供应链金融以其创新的融资方式，在解决中小企业融资难的问题上发挥了重要作用，也为银行拓宽信贷市场提供了新的解决方案，受到广泛关注^[1-4]。而随着互联网及信息技术的革新，供应链金融业务开始由线下转移到线上。特别是由于电子商务的迅猛发展，电商企业的融资需求迅速增加，使得银行开始寻求与电商平台合作，共同为电商融资企业提供供应链金融业务。这成为新的关注点。然而，在银行与电商平台的合作过程中，由于电商平台掌握更多的融资企业交易信息及供应链信息，这些都是授信的重要信息，使得电商平台拥有更多的话语权，进而可获得更高的收益分享水平^[5]。相应地，银行就陷入被动局面，因而只能获得较低的收益分配水平。这种不公平现象的存在，导致一些银行选择自建电商平台，如在2012年1月，交通银行构建“交博汇”线上供应链金融平台^[6]；2012年7月，建设银行构建“善融商务”平台等^[7]，力求摆脱对电商平台的依赖，但“善融商务”等银行自营平台发展相对缓慢。现阶段，银行快速发展与创新供应链金融业务的主要渠道与方式仍然是寻求与电商平台的合作。因此，如何促进银行与电商平台的健康、稳定合作，发挥各自的优势，实现供应链金融业务的快速发展是目前银行面临的主要议题。

目前，关于供应链金融参与主体间的合作机制方面，许多学者已进行了深入研究。Chen等^[8]分析了供应链金融系统中，制造商承诺回购的前提下银行、零售商及制造商的最优均衡策略。Jin和Luo^[9]在一个由银行、供应商和零售商组成的供应链金融系统中，探究了银行具有风险规避特征时零售商的最优库存及保险策略。Yan等^[10-12]利用博弈论的方法系统研究了制造商存在信用担保、零售商存在破产风险、有限融资等不同情形下供应链金融系统的最优融资策略。Yang等^[13]比较分析了零售商提前支付与延迟支付条件下银行、零售商及供应商的最优融资决策。于辉和马云麟^[14]通过构建单周期报童模型探讨了订单转保理融资模式下实现多方合作共赢时的最优订货策略。王宗润等^[15]在考虑隐性股权的前提下，提出了一个由制造商、银行、供应商组成的供应链金融系统，探究了使三方收益最大化的最优决策。以上文献主要研究的是传统供应链金融系统的合作机制，并未考虑电子商务的背景。随着电子商务的快速发展，供应链金融服务逐步从线下向线上转变，合作主体增加了电商角色^[16]。在这一背景下，一些学者进行了相关的研究。Chen和Wang^[17]提了一种将电子商务、现代物流及供应链金融融合在一起的新型企业服务模式。Zhao等^[18]利用演化博弈思想讨论了银行与电子商务平台之间的竞争合作策略。于辉等^[19]基于博弈理论，构建了银行借贷和电商借贷2种模式下的融资博弈批发价契约模型，对比分析了这2种借贷模式对融资企业及供应链绩效的影响，以确定最优的融资合作策略。徐鲲等^[20]在电子商务背景下，利用演化博弈理论分析了银行与供应链联盟的合作机制及溢出价值的分配策略。史金召等^[5]基于委托代理理论，探讨了银行与B2B平台合作过程中的最优激励机制。汪克峰和石岿然^[21]利用演化博弈理论，以委托授信为例，探究了银行与B2B平台的合作策略选择问题。基于鲁宾斯的讨价还价博弈思想，陈金龙和占永志^[22]通过构建供应链金融服务商与银行、融资企业之间讨价还价博弈模型，探究了服务商、银行与融资企业合作过程中的利率定价问题。总体而言，目前关于供应链金融合作机制的研究，主要利用静态博弈论、动态演化博弈论等方法，在不同的条件下探析了参与主体间的最优合作策略，并取得了重要的研究成果，但较少有文献考虑网络效应对合作主体策略选择的影响。事实上，在电子商务环境下，电商平台的加入，为供应链金融参与主体间的合作过程带来了新特点。如电商平台的主要特征之一是具有某种类型的网络外部性，即可以利用双边关系实现无限增值可能性的网络效应，平台的参与主体越多，越能提升平台用户的效用以及平台自身的利润和竞争优势^[23-26]。因此，在考虑网络效应的情形下，分析银行与电商平台的合作策略选择问题，以寻求该情形下的最优合作机制是本文重点关注的问题。

在银行与电商平台的供应链金融业务合作过程中，双方可以根据对方的行为不断学习和调整自己的策略，他们之间所形成的是一种动态演化的博弈关系。但是，以往的文献主要从静态的视角对双方的行为进行刻画，对双方互动演化行为的研究较少；并且，较少关注网络效应对供应链金融业务合作过程的影响。因此，本文在众多研究的基础上，将电商平台的网络效应引入供应链金融业务合作过程，构建演化博弈模型，研究网络效应对银行与电商平台供应链金融业务合作过程的影响，以探析考虑网络效应情形下双方的最优合作策略。

1 未考虑网络效应的演化博弈模型构建及演化策略稳定性分析 1.1 未考虑网络效应的演化博弈模型构建

在实践中，电商平台通常会详实地记录其会员企业在平台上的所有交易，包括网上交易活跃度、交易年限及交易对手评价等信息，形成一个详尽的数据库。而这些数据是电商平台的私有信息。要获得这些信息，银行需与电商平台合作。在供应链金融业务的运作过程中，银行与电商平台的合作主要集中在授信审核及授信后对贷款企业行为的监控。以委托授信为例，银行委托电商平台对融资企业的物流信息、信用信息、交易信息等进行全面审核与监控，以为银行是否决定贷款及后续行为提供依据^[5]。然而，由于信息的不对称、环境的动态变化以及人的思维的局限性，电商平台及银行都是具有有限理性的个体，他们之间的博弈是一个不断学习、动态演化的过程。

因此，假设电商平台有2种策略选择，以概率 $x$ 选择合作策略(即提供真实的融资企业信息给银行)或以概率 $1 - x$ 选择背叛策略(即提供虚假的融资企业信息给银行)。当选择合作策略时，可以获得双方合作授信所带来的收益 $\alpha R$ ，其中，R为双方合作可实现的共同收益(如利息收入)； $\alpha $ 为电商平台的收益分享比例，此时选择合作策略应付出的成本为 ${C_1}$ ；当选择背叛策略时，可以获得融资企业给予的额外回扣 ${R_{\rm B}}$ ，此时应付出的成本为 ${C_3}$ ( ${C_3} < {C_1}$ )。

银行则以概率 $y$ 选择对电商平台进行监督或以概率 $1 - y$ 选择不监督。其中，选择监督策略应付出的成本为 ${C_2}$ ，选择不监督策略则成本为0。且当电商平台选择合作策略时，银行可获得双方合作授信所带来的收益为 $(1 - \alpha )R$ ，其中 $1 - \alpha $ 为银行的收益分享比例。同时，若银行选择监督策略时发现电商平台的背叛行为，会对其进行相应的惩罚 $F$ ，而由于电商平台的背叛行为给银行带来的损失为 $S$ 。

根据上述假设，当电商平台选择合作、银行选择监督策略时，电商平台的收益为 $\alpha R - {C_1}$ ，银行的收益为 $(1 - \alpha )R - {C_2}$ ；当电商平台选择合作、银行选择不监督策略时，电商平台的收益为 $\alpha R - {C_1}$ ，银行的收益为 $(1 - \alpha )R$ ；当电商平台选择背叛、银行选择监督策略时，电商平台的收益为 ${R_{\rm B}} - {C_3} - F$ ，银行的收益为 $ - {C_2} - S + F$ ；当电商平台选择背叛、银行选择不监督策略时，电商平台的收益为 ${R_{\rm B}} - {C_3}$ ，银行的收益为 $ - S$ 。由此可得电商平台与银行的博弈支付矩阵如表1所示。

基于上述博弈矩阵可以得到，电商平台选择合作策略的期望收益为

$\quad\quad{E_x} = y(\alpha R - {C_1}) + (1 - y)(\alpha R - {C_1}),$

(1)

选择背叛策略的期望收益为

$\quad\quad{E_{1 - x}} = y({R_{\rm B}} - {C_3} - F) + (1 - y)({R_{\rm B}} - {C_3}),$

(2)

则电商平台的平均期望收益为

$\quad\quad{\overline E} = x{E_x} + (1 - x){E_{1 - x}}\text{。}$

(3)

由此可得，电商平台的复制者动态方程为

$\quad\quad\frac{{{\rm d}x}}{{{\rm d}t}} = x(1 - x)(\alpha R - {C_1} - {R_{\rm B}} + {C_3} + yF)\text{。}$

(4)

同理可得，银行的复制者动态方程为

$\quad\quad\frac{{{\rm d}y}}{{{\rm d}t}} = y(1 - y)(F - {C_2} - xF)\text{。}$

(5)

因此，银行与电商平台的策略演化可由式(4)、式(5)组成的微分方程系统来描述。对系统的稳定点进行分析，得到5个平衡点 ${F_1}(0,0)$ , ${F_2}(0,1)$ , ${F_3}(1,0)$ , ${F_4}(1,1)$ ， $K$ ( ${x^ * }$ , ${y^ * }$ )。其中，

$ \quad\quad{{x}^{*}}=\frac{F-{{C}_{2}}}{F},\ \ \ {{y}^{*}}=\frac{{{C}_{1}}+{{R}_{\rm B}}-\alpha R-{{C}_{3}}}{F}{\text{。}} $

根据文献[27]，由方程(4)、(5)组成的微分方程系统的雅可比矩阵为

$\quad\;\;\;\; { J} = \left[ {\begin{array}{*{20}{l}} {(1 - 2x)(\alpha R - {C_1} - {R_{\rm B}} + {C_3} + yF)}\quad{x(1 - x)F} \\ { - y(1 - y)F}\quad\quad\quad\quad\quad{(1 - 2y)(F - {C_2} - xF)} \end{array}} \right],$

则该雅可比矩阵的行列式 $\det { J}$ 为

$\begin{split}&\quad\quad\det { J} = (1 - 2x)(\alpha R - {C_1} - {R_{\rm B}} + {C_3} + yF)\times\\ &(1 - 2y)(F - {C_2} - xF) + x(1 - x)y(1 - y){F^2},\end{split}$

(6)

该雅可比矩阵的迹 ${\rm tr}{ J}$ 为

$\begin{split}&\quad\quad{\rm tr}{ J} = (1 - 2x)(\alpha R - {C_1} - {R_{\rm B}} + {C_3} + yF) +\\ &(1 - 2y)(F - {C_2} - xF) + x(1 - x)y(1 - y){F^2}{\text{。}}\end{split}$

(7)

1.2 演化策略稳定性分析

情形1 　当 $\alpha {\text{＜}} \dfrac{{{R_{\rm B}} - {C_3} + {C_1}}}{R}$ 且 $F {\text{＜}} {C_2}$ 时，系统的稳定性分析如表2所示。

系统只有一个稳定点 ${F_1}(0,0)$ ，即当电商平台的收益分享水平较低，且对其背叛行为的惩罚力度较小且不足以弥补银行的监督成本时，系统最终会演化为电商平台选择背叛、银行选择不监督策略。

情形2 　当 $\alpha {\text{＜}} \dfrac{{{R_{\rm B}} - {C_3} + {C_1}\! - \!F}}{R}$ ， $F {\text{＞}} {C_2}$ 时，系统的稳定性分析如表3所示。

系统只有一个稳定点 ${F_2}(0,1)$ ，即当电商平台的收益分享水平较低(对应于银行的收益分享水平较高)，且对电商平台的背叛行为的惩罚达到一定水平时，系统最终会演化为电商平台选择背叛策略，而银行选择监督策略的稳定状态。

情形3 　当 $\alpha {\text{＞}} \dfrac{{{R_{\rm B}} - {C_3} + {C_1}}}{R}$ 时，系统的稳定性分析如表4所示。

系统只有一个稳定点 ${F_3}(1,0)$ ，即当电商平台的收益分享水平较大(对应于银行的收益分享水平较小)，系统最终会演化为电商平台选择合作策略，而银行选择不监督的稳定状态。在这一情形下，虽然电商平台会自觉地提供真实的融资企业信息，银行无需进行监督，但银行必须让利给电商平台，即给予电商平台较高的收益分享水平。

2 考虑网络效应的演化博弈模型构建及演化策略稳定性分析 2.1 考虑网络效应的演化博弈模型构建

随着信息技术与互联网的快速发展，在网络外部性这一理论的基础之上，双边市场理论受到普遍关注。即当某一现实或虚拟组织具有某种类型的网络外部性特征时，就可以通过双边关系来建立和产生无限增值可能性的网络效应^[28-29]。平台作为典型的双边市场，其网络效应是指，随着平台的参与主体越多，不仅能提高平台用户的效用，还可以提升平台的利润和竞争优势^[24,30]。对于电商平台而言，由于平台参与主体的不断增加而产生的网络效应是显而易见的(如参与主体达到一定数量时可以产生广告收入等)。因此，假设电商平台与银行通力合作进行供应链金融服务时，信贷能力大幅提升，可以大大增强平台的吸引力，进而吸引大量企业的加入，产生的网络效应为 ${R_1} = \lambda m(x)$ (其中， $m(x)$ 为企业数量，也即平台规模， $\lambda $ 表示平台规模能转化为具体收益的水平，也即平台的网络效应转化水平)。同时，假设企业的数量 $m(x) = xM$ ( $M$ 为电商平台积极与银行合作时可以吸引的最大企业数量)，表示电商平台合作意愿 $x$ 越高，会促进与银行的长期稳定合作关系，平台的贷款能力和便利性增强，进而吸引更多的企业加入平台^[20]。由此可得，考虑网络效应时，电商平台与银行的博弈支付矩阵如表5所示。

由此可得，电商平台的复制者动态方程为

$\quad\quad\frac{{{\rm d}x}}{{{\rm d}t}} = x(1 - x)(\alpha R - {C_1} - {R_{\rm B}} + \lambda xM + {C_3} + yF)\text{。}$

(8)

此时，银行的复制者动态方程未发生变化，同式(5)。

因此，银行与电商平台的策略演化可由式(5)、式(8)组成的微分方程系统来描述。对系统的稳定点进行分析，得到5个平衡点 ${F_1}(0,0)$ , ${F_2}(0,1)$ , ${F_3}(1,0)$ , ${F_4}(1,1)$ , $K$ ( ${x^ * }$ , ${y^ * }$ )。其中，

$ \quad\quad {x^ * } = \frac{{F - {C_2}}}{F},\ \ {y^ * } = \frac{{{C_1} + {R_{\rm B}} - \alpha R - \lambda xM - {C_3}}}{F}{\text{。}} $

由方程(5)、(8)组成的微分方程系统的雅可比矩阵为

${ J} = \left[ {\begin{array}{*{20}{l}} {(1 - 2x)(\alpha R \!-\! {C_1} \!-\! {R_{\rm B}} \!+\! {C_3} \!+\! \lambda xM \!+\! yF)}\quad{x(1 \!-\! x)F} \\ { - y(1 - y)F}\quad\quad\quad\quad\quad\quad\;\;\;{(1 - 2y)(F - {C_2} - xF)} \end{array}} \right],$

则该雅可比矩阵的行列式 $\det { J}$ 为

$\begin{split}&\quad\quad\det { J} = (1 - 2x)(\alpha R - {C_1} - {R_{\rm B}} + \lambda xM + {C_3} + yF)\times\\ &(1 - 2y)(F - {C_2} - xF) + x(1 - x)y(1 - y){F^2}{\text{。}}\end{split}$

(9)

该雅可比矩阵的迹 ${\rm tr}{ J}$ 为

$\begin{split}&\quad\quad{\rm tr}{ J} = (1 - 2x)(\alpha R - {C_1} - {R_{\rm B}} + \lambda xM + {C_3} + yF) + \\ &(1 - 2y)(F - {C_2} - xF) + x(1 - x)y(1 - y){F^2}{\text{。}}\end{split}$

(10)

2.2 演化策略稳定性分析

情形4 　当 $\alpha {\text{＜}} \min \left( {\dfrac{{{R_{\rm B}}\! -\! {C_3} \!+\! {C_1}}}{R},\dfrac{{{R_{\rm B}} \!-\! {C_3} \!+ \!{C_1}\! - \!F}}{R}} \right)$ ， $F {\text{＜}} {C_2}$ ，且 $\lambda {\text{＜}} \dfrac{{{R_{\rm B}} - {C_3} - \alpha R + {C_1}}}{M}$ 时，系统的稳定性分析如表6所示。

系统只有一个稳定点 ${F_1}(0,0)$ ，即当电商平台的收益分享水平较低，且对其背叛行为的惩罚力度较小且不足以弥补银行的监督成本。同时，双方合作所带来的网络效应转化水平较低时，系统最终仍然会演化为电商平台选择背叛、银行选择不监督策略。

情形5 　当 $\dfrac{{{R_{\rm B}} - {C_3} + {C_1} - F}}{R} {\text{＜}} \alpha {\text{＜}} \dfrac{{{R_{\rm B}} - {C_3} + {C_1}}}{R}$ ， $F {\text{＞}} {C_2}$ ，且 $\lambda {\text{＞}} \dfrac{{{R_{\rm B}} - {C_3} - \alpha R + {C_1}}}{M}$ 时，系统的稳定性分析如表7所示。

系统只有一个稳定点 ${F_3}(1,0)$ ，即当电商平台的收益分享水平在一定范围，且对电商平台的背叛行为的惩罚达到一定水平，同时双方合作所带来的网络效应转化水平较高时，系统最终会演化为电商平台选择合作策略，而银行选择不监督策略的稳定状态。

此时，双方合作时给电商平台带来的网络效应转化水平较高，从而产生一定的额外收益，会对电商平台的策略选择行为产生一定的影响，使其在不要求较高收益分享水平的情况下就能选择合作策略，对收益分享水平具有一定的替代作用。从而在一定程度上缓解了电商平台利用其信息优势要求银行给予较高的收益分享水平才能顺利合作的尴尬局面，银行也无需花费较高的成本对其进行监督，进而促进双方长期稳定合作，充分发挥电商平台和银行各自的优势，促进资源的有效配置。

3 数值分析

本小节将通过数值对比分析进一步探析网络效应对电商平台和银行合作过程的影响。根据第2部分的理论推导所得的各种情形应满足的前提条件，参数选择如下： ${C_1} = 6$ ， ${C_2} = 10$ , $M = 38$ , $R = 40$ , ${R_{\rm B}} = 20$ , ${C_3} = 2$ , $F = 12$ , $\lambda = 0.4$ 。

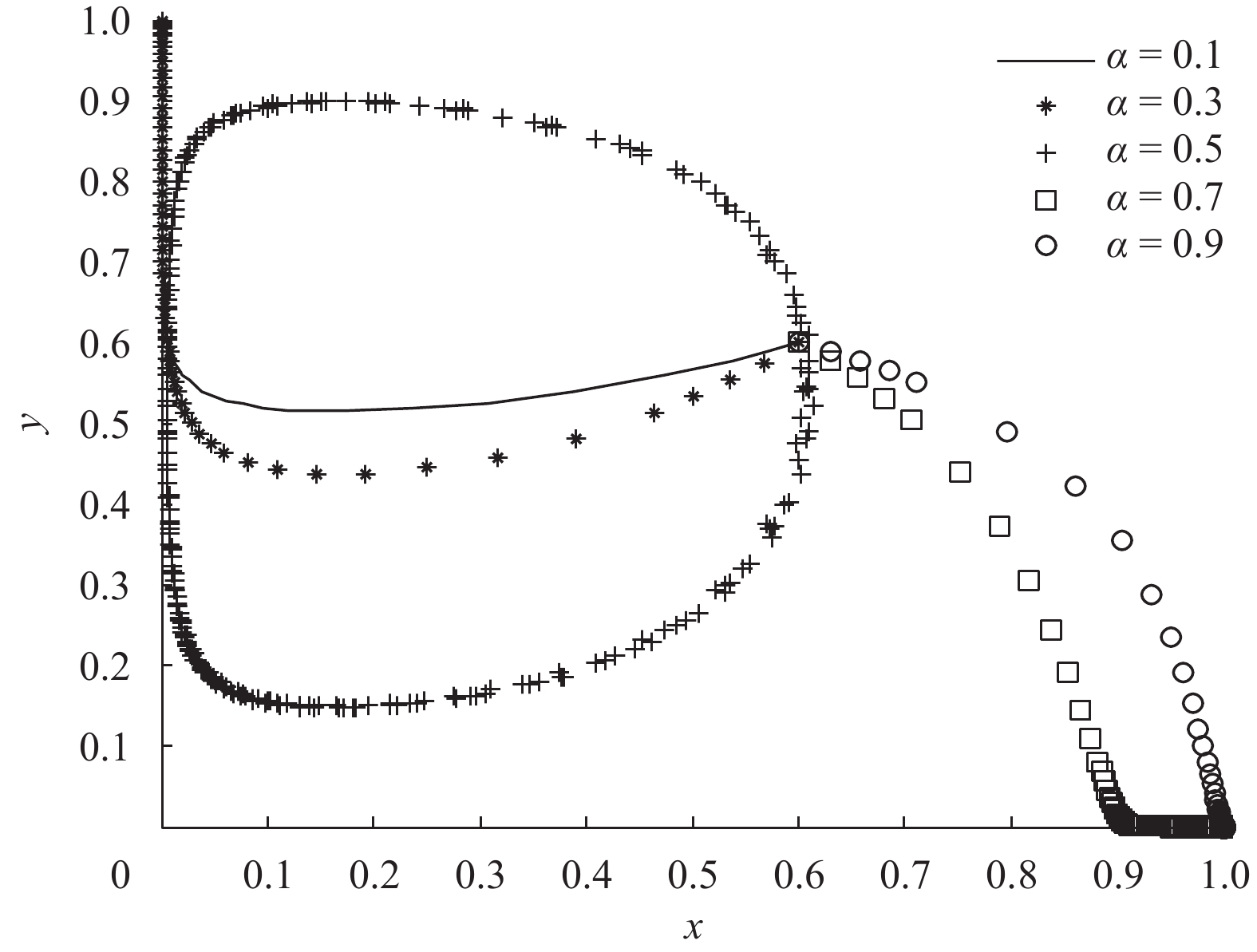
1) 从图1可以看出，在未考虑网络效应的情况下，随着电商平台的收益分享水平 $\alpha $ 的不断增加，系统状态逐步从 ${F_2}(0,1)$ 点趋于 ${F_3}(1,0)$ ，即电商平台只有在享有较高的收益分享水平( $\alpha {\text{≥}} 0.7$ )的情况下，才会选择合作策略，从而造成双方的收益分享不公，阻碍双方的长期稳定合作。

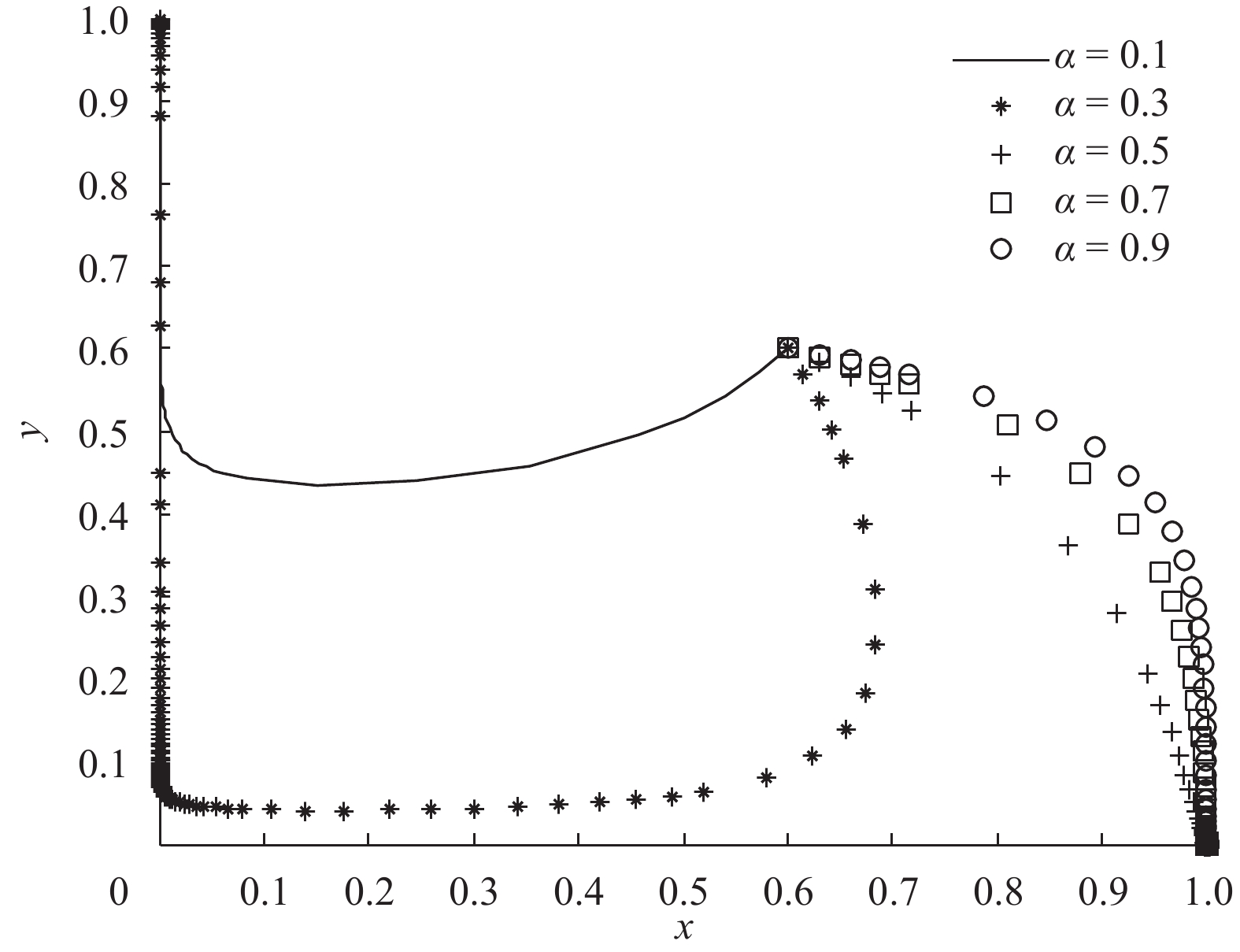
2) 由图2可以看出，在考虑网络效应的情况下，当网络效应转化水平达到一定程度(取 $\lambda = 0.4$ ，此时有 $\lambda {\text{＞}} \dfrac{{{R_{\rm B}} - {C_3} - \alpha R + {C_1}}}{M}$ ， $\lambda $ 在满足这一条件的其他取值也是类似的情况)，可以对电商平台的收益分享水平具有一定的替代作用(此时只要满足 $\alpha {\text{≥}} 0.5$ )，即电商平台要求的收益分享水平较不考虑网络效应时低，就可以促使电商平台选择合作策略，银行也无需进行监督，系统最终演化为 ${F_3}(1,0)$ 的稳定状态，进而可以促进双方的长期稳定合作，发挥各自的优势，实现资源的有效配置。

4 结论与启示 4.1 结论

本文利用演化博弈理论，分别构建不考虑网络效应与考虑网络效应情形下银行与电商平台的演化博弈模型，对比分析了2种情形下银行与电商平台的策略选择，探究了网络效应对双方在供应链金融业务合作过程中的策略选择的影响。

研究表明，在未考虑网络效应的情形下，只有在享有较高的收益分享水平时，电商平台才会选择合作策略，自觉提供真实的融资企业信息，银行无需进行监督；但这意味着银行只能获得较低的收益分享水平，存在不公平的现象，不利于双方的长期合作。在考虑网络效应的情形下，当网络效应转化水平达到一定程度时，对电商平台的收益分享水平具有一定的替代作用；即较未考虑网络效应的情形下，电商平台在更低的收益分享水平下就会选择合作策略，银行也无需进行监督，进而可以促进双方的公平、长期合作，实现优势互补和资源的合理配置。

4.2 管理启示

在互联网背景下，随着电子商务的快速发展，银行要进一步创新与发展供应链金融业务，主要方向还是要加强与电商平台的长期稳定合作，实现优势互补及资源的合理配置。基于本文的研究，要促使银行与电商平台的长期合作，就应有效发挥电商平台的网络效应，使其不只关注与银行合作时所带来的利息收入而要求较高的收益分享水平、造成不公平的合作或在合作过程中存在不道德的行为。因此，在电商平台的成长初期，平台规模较小，此时银行可以通过优惠的贷款利率及较高的服务质量，帮助电商平台提升影响力，进行品牌建设，吸引更多企业的加入，进而通过品牌建设带动网络效应。之后，在平台形成一定规模的条件下，电商平台则可以最大程度地合理利用其网络效应，提高网络效应的转化水平，将网络效应转化为实际的收益，如利用平台的影响力扩大平台的广告收入等，拓宽平台的创收视角，而非只关注与银行合作所带来的利息分配，促进双方的公平、长期合作，进而形成更大的网络效应以获得更多的额外收入，形成良性循环。