2. 经济管理学院/管理科学与工程博士后流动站,四川 成都 610031;
3. 四川省烟草公司成都市公司,四川 成都 610072
2. School of Economics & Management/Post Doctoral Mobile Station in Management Science and Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. Sichuan Provincial Tobacco Companies Chengdu Company, Chengdu 610072, China
自动化立体仓库是一个综合的自动化系统,堆垛机存取系统是其重要的部分。多任务拣选操作控制策略影响仓库的运作效率以及存取系统的性能[1-2]。因此对自动化立体仓库进行堆垛机拣选路径进行优化,可以更加有效地管理自动化立体仓库,提高整体作业效率,从而减少货品搬运量和存储时间,增加企业效益。
关于堆垛机拣选路径优化问题的研究,国内研究方向主要分为堆垛机拣选路径研究和考虑堆垛机拣选作业过程中的约束条件的模型研究。国内外学者大都将堆垛机拣选作业抽象为TSP(travelling salesman problem)问题求解[3-4]。实际自动化立体仓库的堆垛机运行过程中,堆垛机有相应的条件限制,因此将堆垛机拣选作业抽象为TSP问题求解不符合实际情况。针对堆垛机拣选作业,有些学者考虑立体仓库实际约束条件,建立多约束数学模型解决该问题[5-7]。如常发亮等[5]分析自动化立体仓库拣选作业的特点,考虑周转箱的容量限制,建立一种含装箱约束条件的多目标优化数学模型,采用遗传算法求解,结果表明该数学模型有很好的优化效果。蔡安江等[6]分析堆垛机在不同任务下的作业模式,并建立一种基于混合命令序列的堆垛机调度模型,实验验证该模型更具有适用性。方彦军等[7]研究多RGV(rail guided vehicle)和多升降机的自动存取系统,建立相应数学模型,运用智能算法求出系统最优的调度策略。
目前求解堆垛机拣选路径优化问题的方法主要采用智能优化算法求解。智能算法具有求解速度快,处理大规模问题的优点,被广泛用于求解堆垛机拣选路径优化问题。如杨玮[8]提出一种基于模拟退火的混合粒子群算法,与粒子群算法进行比较,虽然该算法得到了有效的应用,但求解精度不高。庞龙等[9]提出了基于蚁群遗传算法,对自动化立体仓库拣选路径进行优化,结果表明该方法可以有效提高仓库拣选作业的效率,但其求解速度慢。周耿烈等[10]提出改进自适应遗传算法,通过对遗传算法进行自适应改进,克服了传统遗传算法的早熟收敛问题。
在模型建立方面,参考已有文献,尚未发现有关考虑半托盘出库的堆垛机复合作业路径拣选问题的研究。已有文献所建立的堆垛机拣选作业优化问题均未考虑半托盘出库的因素,实际上对于烟草物流企业,该因素是不可忽视的。本文结合某烟草物流公司的自动化立体仓库的出入库实际情况,堆垛机存取系统采用整托盘出/入库或者半托盘出/入库,因此不需要考虑堆垛机作业的容量限制,且每个巷道仅有一台堆垛机运行。在求解方法角度,为解决半托盘出库的堆垛机复合作业路径拣选问题,本文采用改进的离散烟花算法(discrete fireworks algorithm, DFWA)求解该问题,得到系统的最优作业拣选时间。
烟花算法是由谭营等[11]于2010年根据对烟花爆炸产生火花这一自然现象的观察提出的一种新型智能优化算法。烟花通过对烟花个体的爆炸操作,产生火花;通过变异操作,产生变异火花并应用映射规则保证变异后的火花仍处于可行域内,最后采用精英策略和类似轮盘赌策略保留最优个体。通过迭代实现对烟花和火花个体的优化,进而获得问题的最优解。
烟花算法发展迅速并在并行计算烟花算法[12]、多目标烟花算法[13]、混合烟花算法[14]等方面设计出衍生算法。这些算法广泛应用于网络构建[15]、滤波器设计[16]等领域。
本文首先以烟草物流公司的堆垛机拣选作业为实例,建立考虑半托盘出库的堆垛机拣选作业模型,然后提出一种离散烟花算法进行求解。将离散烟花算法与粒子群算法(particle swarm optimization, PSO)和蚁群算法(ant colony optimization, ACO)运算结果的比较,验证本文所提算法的有效性。
1 考虑半托盘出库的堆垛机复合作业模型 1.1 堆垛机作业方式堆垛机是自动存取系统中的核心设备,其工作效率决定着物品出入库的效率,堆垛机的调度是影响自动化立体仓库工作效率的重要因素。一般堆垛机作业有单一命令(single command cycle, SC)作业方式和复合命令(dual command cycle, DC)两种作业方式。
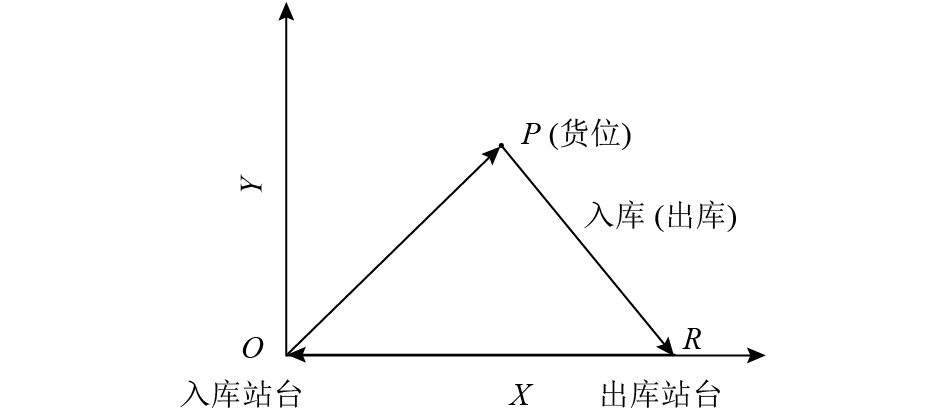
单一命令作业方式指堆垛机完成一次货物的入库作业或者出库作业,如图1所示,O点为入库站台,P为货位点,R为出库站台。假设堆垛机只允许从出库站台出库和入库站台入库,当在P处存货或者取货时,堆垛机的路线为OP→PR→RO。由图可知,堆垛机执行单一作业命令的拣选路线为一个封闭的三角形。所以,堆垛机在执行单一命令时拣选路径与任务的顺序无关。
|
图 1 单一命令作业方式 Fig. 1 Single command cycle |
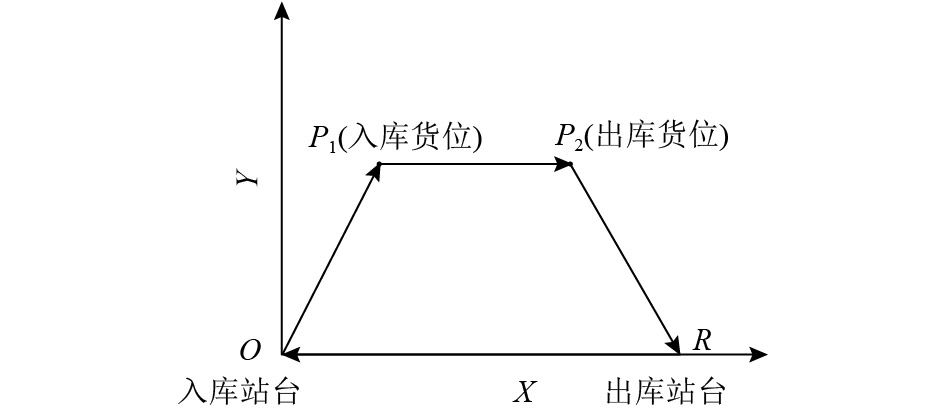
复合命令作业方式是指堆垛机完成一次入库作业和一次出库作业,复合命令作业方式下堆垛机接到一批出/入库作业指令,首先从原点出发执行入库作业命令到达货位P1,执行完入库作业后接着执行出库作业命令到货位P2,取出货物后再运行到巷道口出库站台,最后从出库站台回到入库站台,如图2所示。复合作业方式的效率高,因此在自动化立体仓库中堆垛机一般以复合作业方式存取物品。
|
图 2 复合命令作业方式 Fig. 2 Dual command cycle |
本文提及的半托盘出库作业,即堆垛机接到作业指令,首先从原点出发到出库站台,到达指定货位执行出库作业,执行出库作业后执行入库作业,将拆剁的散盘运行到原来的货位,然后返回巷道口的入库站台,即对一个货位点先执行出库命令,再执行入库命令。
1.2 问题描述堆垛机路径拣选优化问题是指堆垛机接受作业命令,合理地安排路径顺序,完成给定作业任务,实现作业时间最小化。烟草公司出入库采用整托盘出入库方式和半托盘出入库方式,对于卷烟分拣量大的品牌,采用整托盘出库方式,对于卷烟分拣量不大的品牌采用半托盘出库模式,即拆垛后剩余的散盘返库存放供下次使用。本文结合某烟草公司自动化立体仓库的卷烟托盘出入库实际情况,研究考虑半托盘出库情况下的堆垛机复合作业路径优化问题。
1.3 基本假设条件为简化问题作如下假设。
1) 堆垛机运行过程中在水平方向和垂直方向同时匀速运行,水平方向的速度为Vx,垂直方向的速度为Vy,堆垛机的起止过程不作考虑。
2) 堆垛机存货和取货时间忽略不计。
3) 坐标(x, y)表示货位点,(0, 0)表示出/入库台,货格的高度为h1,宽度为h2,h1、h2各为1。
1.4 数学模型本文针对烟草公司堆垛机拣选作业的实际情况,堆垛机复合作业路径优化问题的目标为:保持入库序列P不变,根据条件,出库序列Q和半托盘出库序列W与入库序列组合,使拣选时间T最小,给出如下的数学模型。
设
堆垛机从某一位置P1(
| $\quad\quad T_{{P_1}{P_2}} = \max\; (|x_{1} - x_{2}|/V_{\rm x},|y_{1} - y_{2}|/V_{\rm y});$ | (1) |
| $\quad\quad\left\{ \begin{array}{l} {M} = \max\; (m,n){\text{,}}\\ {N} = \min\; (m,n){\text{。}} \end{array} \right.$ | (2) |
1) 当入库命令数小于出库命令数
| $\quad\quad{T_{\rm L}} = \sum\limits_{i = 1}^{{M} - {N}} {({T_{{O}{{L}_i}}} + } {T_{{{L}_i}{R}}}) + \left( {M - N} \right){T_{OR}}{\text{。}}$ | (3) |
复合作业命令有N个,有N条入库任务和N条出库任务,假设复合作业命令序列为D,堆垛机运行时间为
| $\quad\quad{T_{\rm D}} = \sum\limits_{i = 1}^{N} {({T_{{{D}_{2i - 1}}{O}}}} + {T_{{{D}_{2i}}{O}}}) + \sum\limits_{i = 1}^{N} {{T_{{{D}_{2i - 1}}{{D}_{2i}}}}} + {N}{T_{OR}}{\text{。}}$ | (4) |
w个半托盘出库作业命令的堆垛机运行时间为
| $\quad\quad{T_{\rm W}} = \sum\limits_{i = 1}^w {(2{T_{{{OW}_i}}}} + 2{T_{{{W}_i}{R}}}) + 2w {T_{OR}}{\text{。}}$ | (5) |
总时间为
| $\begin{array}{l} \quad\quad T \!=\! {T_{\rm L}}\! +\! {T_{\rm D}} \!+\! {T_{\rm W}} \!=\! \displaystyle\sum\limits_{i \!= 1}^{M\! - \!{N}} {({T_{{O}{{L}_i}}} \!+\! } {T_{{{L}_i}{R}}})\! +\! \displaystyle\sum\limits_{i \!=\! 1}^{{N}} {({T_{{{D}_{2i - 1}}{O}}}}+\\ {T_{{{D}_{2i}}{O}}}) \!+\!\displaystyle\sum\limits_{i = 1}^{{N}} {{T_{{{D}_{2i - 1}}{{D}_{2i}}}}} \!+\! \displaystyle\sum\limits_{i = 1}^w {(2{T_{{O}{{W}_i}}}} \!+\! 2{T_{{{W}_i}{R}}}) \!+\! ({M} + 2w){T_{OR}}{\text{。}} \end{array}$ | (6) |
2) 当入库命令数大于出库命令数(m>n)时,剩下的入库命令与半托盘出库命令组合,形成复合作业序列。则堆垛机执行复合作业的路径为
| $\quad\quad\left\{ \begin{array}{l} {l_1} = \max\; (M - N,w){\text{,}}\\ {l_2} = \min\; (M - N,w){\text{。}} \end{array} \right.$ | (7) |
单一作业命令有
| $\quad\quad T_{\rm L} = \sum\limits_{i = 1}^{{M} - {N} - {l_2}} {({T_{{O}{{L}_i}}} + } {T_{{{L}_i}{R}}}) + \left( {M-N - l_1} \right){T_{OR}}{\text{。}}$ | (8) |
复合作业命令有
| $\begin{split}&\quad\quad{T_{\rm D}} = \sum\limits_{i = 1}^{N + {l_2}} {({T_{{{D}_{2i - 1}}{O}}}} + {T_{{{D}_{2i}}{O}}}) + \sum\limits_{i = 1}^{N + {l_2}} {{T_{{D_{2i - 1}}{D_{2i}}}}} + \\ &(N + {l_2}){T_{OR}}{\text{。}}\end{split}$ | (9) |
半托盘出库作业命令有
| $\quad\quad{T_{\rm W}} = \sum\limits_{i = 1}^{w - {l_2}} {(2{T_{{O}{{W}_i}}}} + 2{T_{{{W}_i}{R}}}) + (2w - {l_2}){T_{OR}}{\text{。}}$ | (10) |
总时间为
| $\begin{split} &\quad\quad T = {T_{\rm S}} + {T_{\rm D}} + {T_{\rm W}} = \displaystyle\sum\limits_{i = 1}^{{M} - {N} - {l_2}} {({T_{{O}{{L}_i}}} + } {T_{{{ L}_i}{R}}}) +\\ &\displaystyle\sum\limits_{i = 1}^{{N} + {l_2}} {({T_{{{D}_{2i - 1}}{O}}}} + {T_{{{D}_{2i}}{O}}})+ \displaystyle\sum\limits_{i = 1}^{{N} + {l_2}} {{T_{{{D}_{2i - 1}}{{D}_{2i}}}}} +\\ & \displaystyle\sum\limits_{i = 1}^{w - {l_2}} {(2{T_{{O}{{W}_i}}}} + 2{T_{{{W}_i}{R}}}) +({M} + 2w - {l_1}){T_{OR}}{\text{。}} \end{split}$ | (11) |
烟花算法是一种受到烟花爆炸过程的启发而提出的智能优化算法。传统烟花算法主要包括爆炸算子、变异算子、映射规则和选择策略4个部分。烟花算法与一般群体智能优化算法类似,首先随机选择产生N个烟花,每一个烟花代表解空间的一个解。对生成的N个烟花应用爆炸算子和变异算子,产生新的火花,并应用映射规则保证变异后的火花仍处于可行域内,最后采用精英策略保留最优个体,利用选择策略选择出N−1个个体,共同组成新一代的群体。这样逐一迭代,直到满足算法要求。标准的烟花算法流程如下。
Step 1 在一定的解空间内随机产生烟花,每一个烟花代表一个解。
Step 2 计算每一个烟花的适应度值,根据适应度值产生火花,适应度值越好的烟花产生的火花数目越多。
Step 3 烟花的辐射范围内产生火花,计算火花适应度值,烟花进行变异,保证种群多样性。
Step 4 判断是否满足终止,若满足则停止搜索,否则转Step 2。
自动化立体仓库堆垛机拣选路径问题属于离散优化问题,为了使烟花算法适用于求解堆垛机拣选路径问题,需要对烟花算法进行相应改进,使其适用于求解堆垛机拣选路径问题。本文的离散烟花算法主要由爆炸算子、变异算子、选择策略3部分组成。求解堆垛机拣选路径优化问题的离散烟花算法的主要思想如下。1) 采用基于序列组合的实数编码表示烟花个体,每一个个体表示一个可行序列,利用随机化方法初始化种群;2) 利用爆炸算子进行局部搜索和全局搜索,爆炸算子是烟花算法的核心,设计了爆炸操作I和爆炸操作II,产生新的火花以保持种群多样性;3) 为了增强局部搜索能力,使用变异算子提高局部搜索能力,对所有的烟花进行变异操作产生一定数量的火花,只保留结果更优的个体;4) 选择策略应用精英选择策略保留最小适应度值的个体,余下的个体采用类似轮盘赌策略的方式。
2.1 编码由于堆垛机拣选路径问题属于离散优化问题,需要确定出入库组合的拣选序列。因此,采用基于序列组合的实数编码,从左到右的序列编号就是出库序列。以复合作业数目n=5为例,一个可行解s=[1 5 4 3 2],表示出库序列的顺序为1-5-4-3-2。复合作业的序列为{(1, 1) (2, 5) (3, 4) (4, 3) (5, 2)},如图3所示。

|
图 3 编码组合 Fig. 3 Coding combination |
爆炸算子是离散烟花算法的一个重要部分,具有局部搜索和全局搜索作用。在烟花算法中,第
| $\quad\quad{S_i} = m \cdot \dfrac{{1/{{({T_{\max }} - T(i) + \varepsilon )}^2}}}{{\displaystyle\sum\limits_{i = 1}^n {1/{{({T_{\max }} - T(i) + \varepsilon )}^2}} }}{\rm{ }}{\text{。}}$ | (12) |
式(12)中,Si为第i个烟花产生的火花数,m是最大火花数量,Tmax=max{T(i)},ε为一个极小的常数,避免分母为零。同时,为了限制火花数量过多或过少,设定如下的产生火花数量的限制公式:
| $\quad\quad\begin{split}&{S_i} = \left\{ {\begin{array}{*{20}{l}} {{\rm round}(am),S {\text{<}} am},\\ {{\rm round}(bm),S {\text{>}} bm},\\ {{\rm round}({S_i}),{\text{其他}}}, \end{array}} \right.\\ & a {\text{<}} b {\text{<}} 1{\text{。}}\end{split}$ | (13) |
式(13)中,round()为取整函数;a和b为给定的常数。
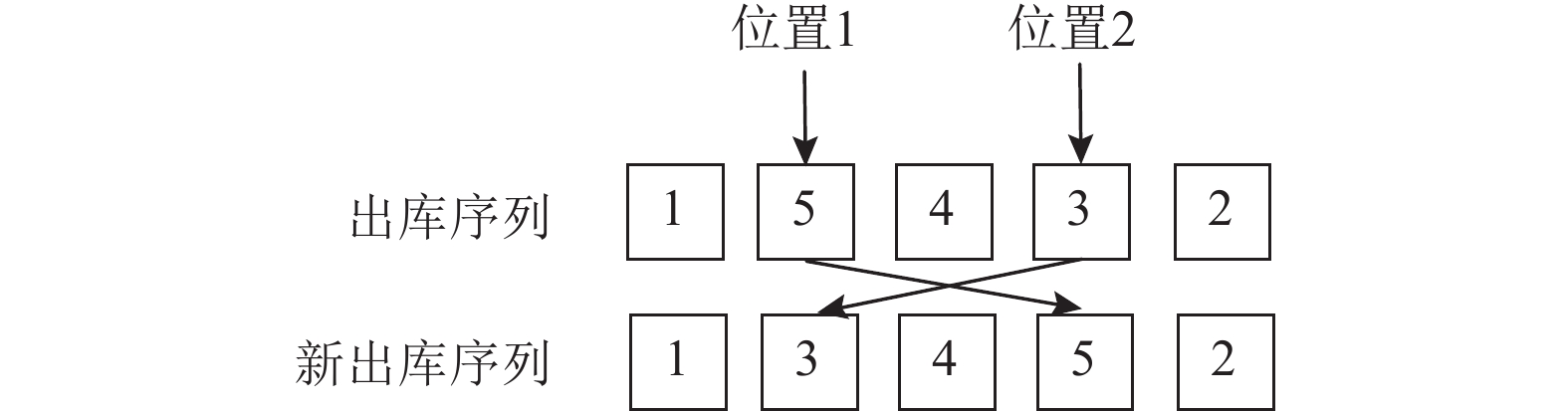
该算法包括了爆炸操作I和爆炸操作II两种爆炸操作。爆炸操作I基本操作为改变两个出库货位的位置。如图4所示,出库序列5和3处产生两个交叉位置,出库序列由原来1-5-4-3-2变成1-3-4-5-2。
|
图 4 爆炸操作I Fig. 4 Explosion operation I |
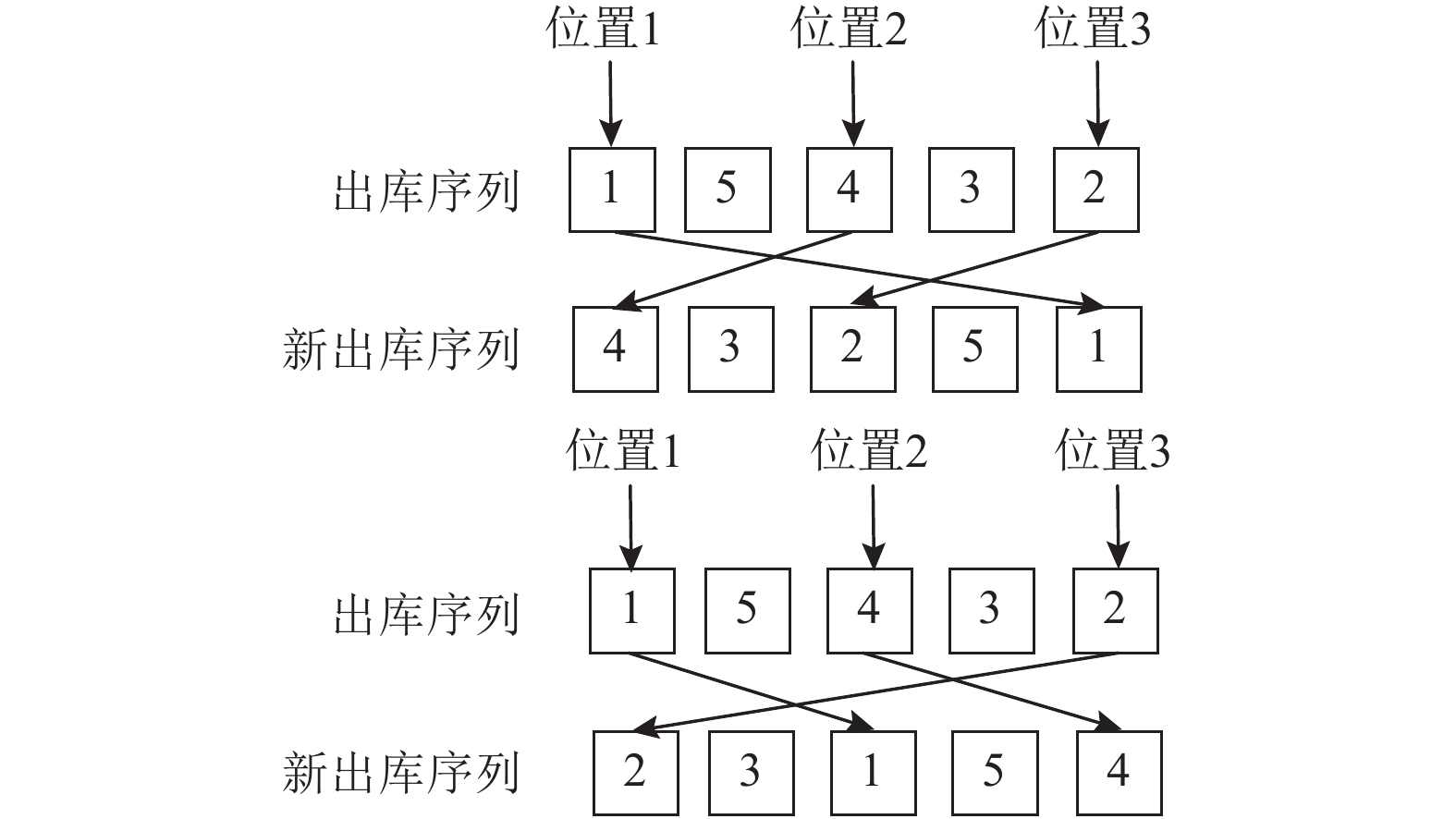
爆炸操作II与爆炸操作I相似,不同的是操作II同时修改3个出库货位的位置。出库序列在1,4,2处产生3个交叉位置,操作II可以生成两种新解。序列1-5-4-3-2变换成4-3-2-5-1或者2-3-1-5-4。爆炸操作II的具体操作如图5所示。
|
图 5 爆炸操作П Fig. 5 Explosion operation П |
爆炸操作I和爆炸操作II并非贪婪选择,计算新的出入库组合的适应度值,产生的新解中,以概率pa接受新的差解。
1) 以概率pa接受新解。
| $\quad\quad p_{\rm a} = \exp ( - \theta T_{\rm m}/T_0 ){\text{。}}$ | (14) |
式(14)中,Tm表示改变后的拣选路径时间,T0表示初始拣选路径时间,θ为控制参数。
2) 若接受差解,将进行一次爆炸操作II进行局部优化,这样的操作为算法跳出局部最优解状态提供可能,并降低跳出局部解被舍弃的概率。
2.3 变异算子变异算子的作用在于局部搜索,为了加强局部搜索进行变异操作。选择全部的烟花个体,对每个烟花进行2-opt操作,随机产生新的火花,计算火花的适应度值,保留适应度值更优的个体,增加种群多样性。产生火花的步骤如下。
Step 1 从烟花个体中随机选择一个烟花作为操作对象。
Step 2 对烟花进行爆炸2-opt操作,产生变异火花,计算火花适应度值,保留适应度值更好的个体。
Step 3 判断是否满足终止,若满足则停止搜索,否则转Step 1。
2.4 烟花个体更新算法的选择策略是为了选择出下一代烟花个体。运用爆炸算子和变异算子产生火花之后,需要从产生的火花中选择部分个体作为下一代烟花。烟花和火花都纳入选择范围,使用精英选择策略,保留最优解的个体,余下的个体采用类似轮盘赌策略的方法。为了保证适应度值小的个体有更大的可能被选择为下一代烟花个体,同时不排除所有的差解,本文设定烟花xi被选择的概率为
| $\quad\quad p({x_i}) = \frac{{1/{{(T(i) - {T_{\min }} + \varepsilon )}^2}}}{{\displaystyle\sum\limits_{i = 1}^n {1/{{(T(i) - {T_{\min }} + \varepsilon )}^2}} }}{\text{。}}$ | (15) |
式(15)中,Tmin=min {T(i)}是最小适应值,ε是平滑参数,防止分母为零。
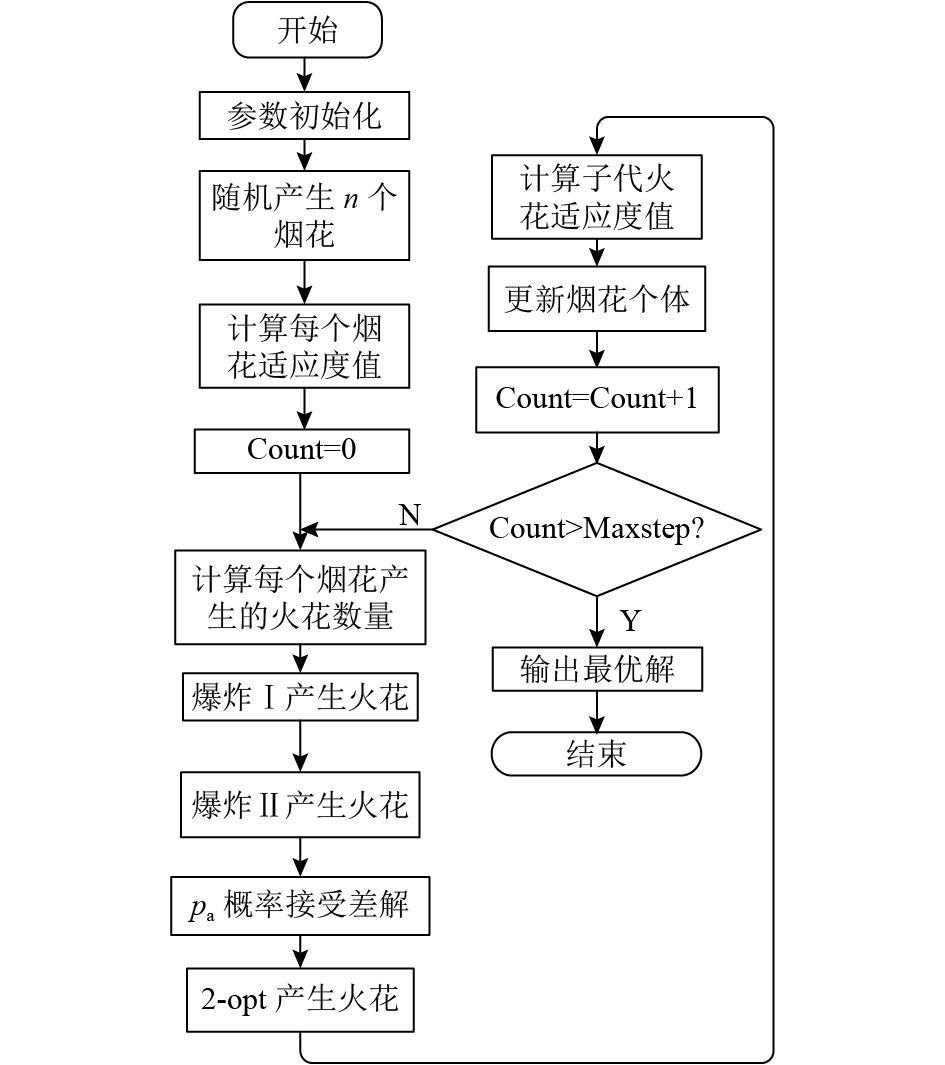
2.5 算法流程在已分析的基础上,离散烟花算法求解堆垛机复合作业拣选路径问题的流程如图6所示。
|
图 6 算法流程图 Fig. 6 Algorithm flowchart |
离散烟花算法具体步骤如下。
Step 1 输入待求解问题的参数:货位坐标、堆垛机速度、入库台坐标、出库台坐标。
Step 2 算法参数初始化:烟花数目n、最小火花数q,最大火花数m、高斯火花数目k、最大迭代次数Maxstep等。
Step 3 确定复合作业的出入库货位。
Step 4 随机产生烟花种群,并计算目标函数的适应度值。
Step 5 开始循环迭代,令count=0。
Step 6 计算每个烟花产生的火花数量。
Step 7 对烟花个体进行爆炸操作I和爆炸操作II,产生火花,计算适应度值,保留更优解的个体,并以概率pa接受差解。
Step 8 对每个烟花个体进行变异操作产生变异火花k个,计算适应度值,仅能接受更优解保存到火花群体中。
Step 9 选择下一代烟花群体n个,从烟花个体和火花个体中保留最优解个体Tmin,计算剩余的个体被选择的概率p,采用轮盘赌策略选择余下的n-1个个体。
Step 10 count=count+1,判断是否达到最大的迭代次数Maxstep,若是,则转到Step 11,否则,转Step 6。
Step 11 输出最优解时间Tmin和出库序列。
3 实验结果分析某物流公司的自动化立体仓库高架库区有14排固定货架,每排货架由32列9层共288个货位组成。货架分布在6个巷道,其中第1~5巷道左右两侧各有1组单深货位,第6巷道两侧各有1组双深货位。本文以单深巷道的固定货架为研究对象,即巷道两旁各有一排货架,如图7所示。

|
图 7 单深巷道 Fig. 7 Single deep roadway |
为了验证离散烟花算法的有效性,随机产生80个货位点的位置坐标对自动化立体仓库堆垛机拣选路径问题进行仿真实验,并与粒子群算法、蚁群算法的结果比较。算法实验所采用的计算机硬件配置为Intel Core i3 -6100,3.7 GHz,4 GB内存,在Windows 7操作系统下使用Matlab 2010 b软件开发了离散烟花算法的实验程序。
设定货架及堆垛机参数:h1=1 m,h2=1 m,水平运行速度vx=3 m/s,垂直运行速度vy=1 m/s。货位点坐标如表1所示,货位属性值:0为出库作业命令,1为入库作业命令,2为半托盘出库命令。离散烟花算法、粒子群算法和蚁群算法的非通用参数设置如表2。
| 表 1 货位坐标 Tab. 1 Cargo position coordinates |
| 表 2 智能优化算法非通用参数设置表 Tab. 2 Intelligent optimization algorithm non-common parameter setting table |
为了准确地说明离散烟花算法的求解性能,分别对拣选货位数为10,50,80的拣选作业进行试验,平均运行30次,共计270个结果。为了更加直观地展现3种算法的计算结果,得到实验结果如表3所示,包含了每种算法在不同拣选货位时的平均拣选时间和最优拣选时间,比较各算法的求解性能。
| 表 3 拣选作业效率对比表 Tab. 3 Comparison of job efficiency |
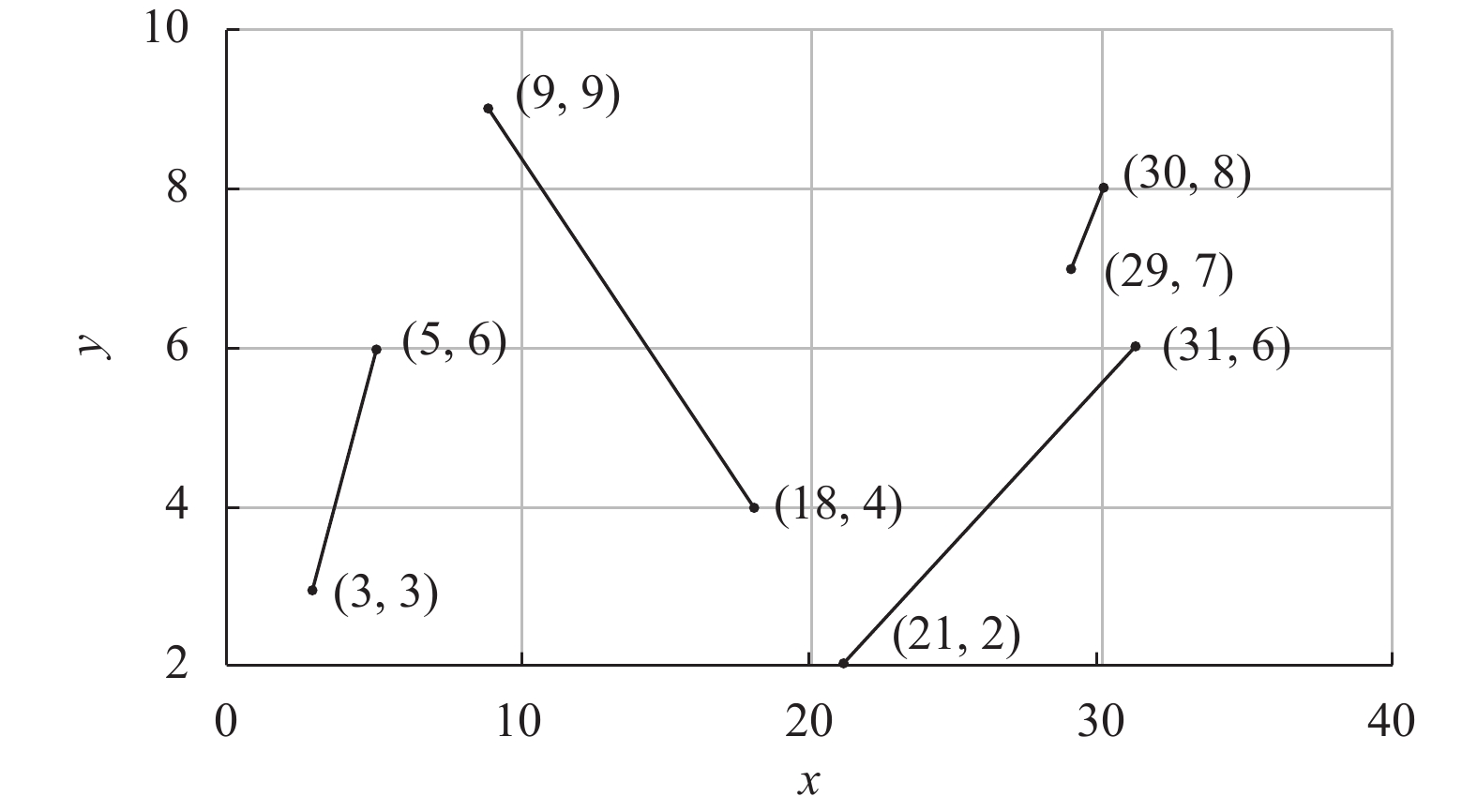
由表1可以看出,当拣选货位数目为10时,有4条入库作业命令,入库作业货位坐标:{(5, 6) (30, 8) (9, 9) (31, 6)};5条出库作业命令,出库作业货位坐标:{(3, 3) (29, 7) (21, 2) (18, 4) (31, 2)}。1条半托盘出库作业命令,货位坐标:{(4, 5)}。入库作业命令小于出库作业命令,因此半托盘出库作业不加入复合作业进行路径优化。3种算法的平均拣选时间与最优拣选时间均为193 s。出入库作业命令最佳组合为{(1, 1) (2, 2,) (3, 4) (4, 3)},复合作业中堆垛机从入库货位到出库货位的路径如图8所示。
|
图 8 堆垛机复合作业路径 Fig. 8 Stacking machine compound operating path |
当拣选货位数为50,分别有20条出库作业命令,21条入库作业命令,9条半托盘出库作业命令。入库作业命令数目大于出库作业命令数,1条半托盘出库命令加入复合作业优化过程,共有21条复合作业命令。
当拣选货位数为80,有28条出库作业命令,36条入库作业命令和16条半托盘出库作业命令。有8条半托盘出库作业命令参与复合作业拣选路径优化过程,共有36条复合作业命令。
将DFWA与ACO、PSO的求解结果进行比较,从表3数据可以看出,在求解质量方面,当复合作业数只有4个的时候,3种算法的求解结果相同。当复合作业数为21时,DFWA的平均拣选时间比PSO的少9.28 s,比ACO的少7.47 s.。当复合作业数为28时,DFWA的平均拣选时间比PSO减少24.54 s,比ACO的求解时间减少38.98 s。由此可以得出,随着测试数据的变大,对于每个规模的复合作业,DFWA的求解时间均小于ACO和PSO,且随着问题规模的增大,ACO与PSO的求解结果与DFWA的求解结果的差距大幅度增加。由此可以表明DFWA较ACO和PSO具有求解优势。
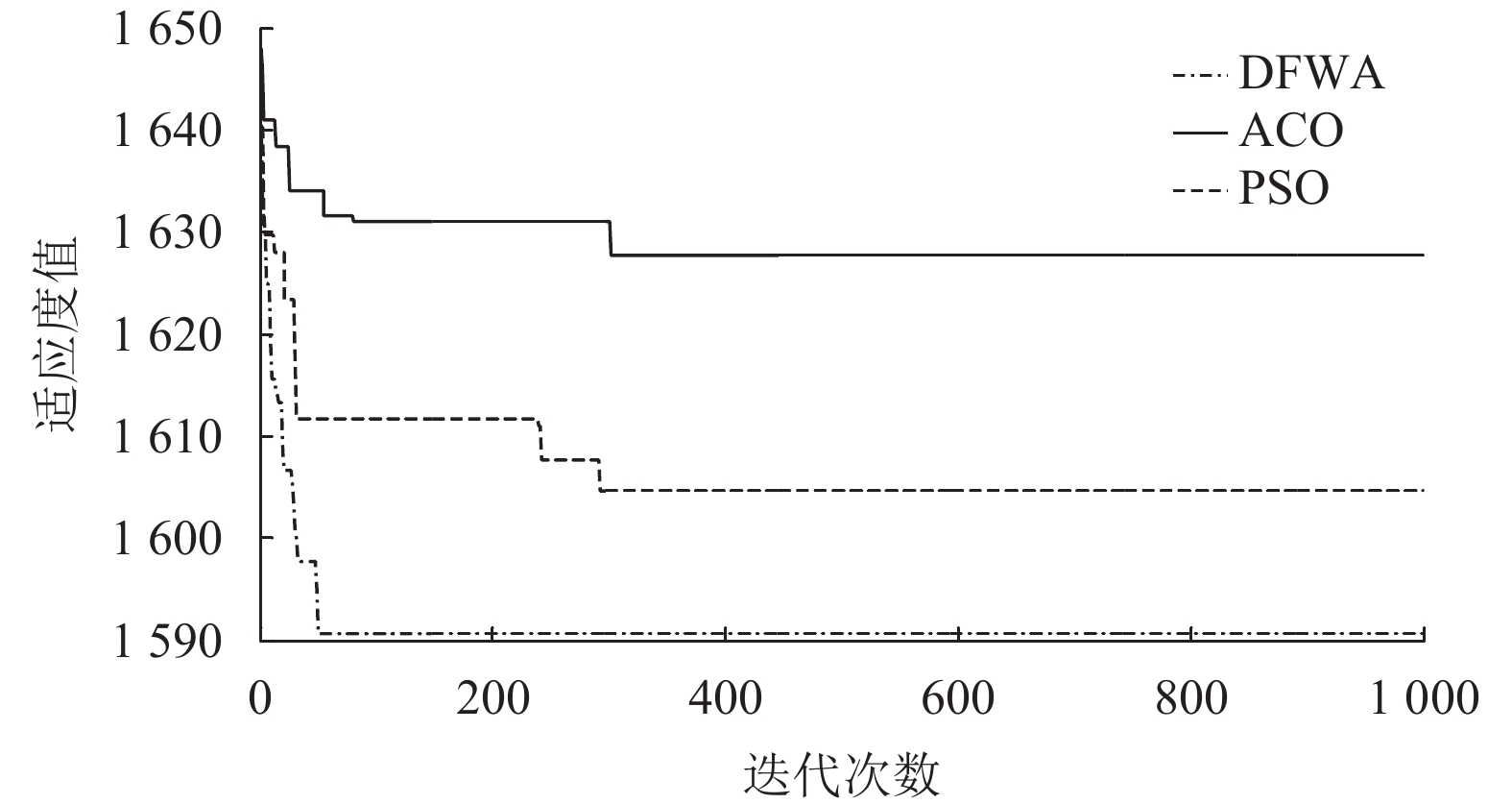
3.2 收敛性验证为更加详细说明DFWA算法的求解特点,选取货位数为80的拣选路径优化问题,迭代次数为1 000,对比ACO算法和PSO算法求解的运算过程,并绘制了相应的算法收敛图。如图9所示。
|
图 9 3种算法迭代曲线 Fig. 9 Three algorithm iterative curves |
从图9中可以看出,与PSO算法和ACO算法相比,DFWA算法具有更快的收敛速度和更高的收敛精度。ACO算法在迭代到301次之后得到最优解,此时最优解为1 627.67 s。PSO算法在执行278次后得到最优解1 606.33 s。DFWA算法执行35次后得到最优解1 592.67 s,适应度值不再降低。由此可知,DFWA算法较其他两种算法,其收敛速度更快,收敛的精度更高,取得更高质量的解。
3.3 运行时间分析货位数与算法运行时间的关系,将3种算法的程序运行时间进行对比。实验参数如表2所示,实验结果如表4所示。
| 表 4 程序运行时间对比表 Tab. 4 Program run time comparison table |
从表4可以看出,随着货位数的增加,3种算法的运行时间也在增加,且ACO算法与PSO算法的运行时间与货位数呈线性关系,DFWA算法运行时间与货位数并没有线性关系。3种算法运行时间相比较,PSO算法的运行时间最长,由于其搜索过程容易陷入局部最优,因此其运行时间较长。DFWA算法的全局搜索和局部搜索能力强,其运行时间最少。结合DFWA的寻优能力、收敛性来看,DFWA在不同任务数下均具有优良的高速收敛性能和优良的寻优性能。
4 结论1) 首次提出考虑半托盘出库作业情况下的堆垛机复合作业路径拣选优化问题,并综合考虑出入库顺序和出入库货位的关系,建立相应的数学模型。采用离散烟花算法,利用爆炸算子进行全局搜索和局部搜索,使用变异算子增强局部搜索能力,并设计择优策略保留选择子代,加快收敛速度,减少求解时间。
2) 基于货位数10、50、80三组数据测试,以DFWA算法所求的结果与ACO算法和PSO算法进行对比,实验证明,DFWA算法对于求解自动化立体仓库堆垛机拣选作业问题更具有有效性和解的优越性。
3) 在未来的研究中,将对目标函数考虑多个目标的优化,进一步完善堆垛机拣选路径问题。在求解方法方面,寻求更加有效的算法从而进一步提高解的质量与求解效率。
| [1] |
VAN DEN Berg J P. Analytic expressions for the optimal dwell point in an automated storage/retrieval system[J].
International Journal of Production Economics, 2002, 76(1): 13-25.
DOI: 10.1016/S0925-5273(01)00149-9. |
| [2] |
Hu Y H, Huang S Y, Chen C, et al. Travel time analysis of a new automated storage and retrieval system[J].
Computers & Operations Research, 2005, 32(6): 1515-1544.
|
| [3] |
Rana K. Order picking in narrow-aisle warehouses[J].
International Journal of Physical Distribution & Logistics Management, 1990, 20(2): 9-15.
|
| [4] |
田国会, 张攀, 尹建芹, 等. 基于混合遗传算法的固定货架拣选优化问题研究[J].
机械工程学报, 2004, 40(2): 141-144.
TIAN Guohui, ZHANG Pan, YIN Jianqin, et al. Research on optimization of fixed shelf selection based on hybrid genetic algorithm[J]. Journal of Mechanical Engineering, 2004, 40(2): 141-144. DOI: 10.3321/j.issn:0577-6686.2004.02.030. |
| [5] |
常发亮, 刘增晓, 辛征, 等. 自动化立体仓库拣选作业路径优化问题研究[J].
系统工程理论与实践, 2007, 27(2): 139-143.
CHANG Faliang, LIU Zengxiao, XIN Zheng, et al. Research on the order picking optimization problem of the automated warehouse[J]. System Engineering Theory and Practice, 2007, 27(2): 139-143. DOI: 10.3321/j.issn:1000-6788.2007.02.019. |
| [6] |
蔡安江, 应嘉奇, 王坚, 等. 分散式立体仓库堆垛机调度模型[J].
计算机集成制造系统, 2016, 22(3): 793-799.
CAI Anjiang, YING Jiaqi, WANG Jian, et al. Scheduling model of crane in distributed automated warehouse[J]. Computer Integrated Manufacturing Systems, 2016, 22(3): 793-799. |
| [7] |
方彦军, 唐猛. 自动小车存取系统复合作业三维空间路径优化[J].
计算机集成制造系统, 2015, 21(3): 702-708.
FANG Yanjun, TANG Meng. Three-dimensional routing optimization for AVS/RS’s composite operation[J]. Computer Integrated Manufacturing Systems, 2015, 21(3): 702-708. |
| [8] |
杨玮, 李程, 傅卫平, 等. 自动化立体仓库固定货架拣选路径问题研究[J].
上海理工大学学报, 2015, 37(1): 84-88.
YANG Wei, LI Cheng, FU Weiping, et al. Chosen path optimization for fixed shelves in AS/RS[J]. Journal of University of Shanghai for Science and Technology, 2015, 37(1): 84-88. |
| [9] |
庞龙, 陆金桂. 基于蚁群遗传算法的自动化立体仓库拣选路径优化[J].
计算机工程与科学, 2012, 34(3): 148-151.
PANG Long, LU Jingui. Order picking optimization of automated warehouses based on the ant colony genetic algorithm[J]. Computer Engineering and Science, 2012, 34(3): 148-151. DOI: 10.3969/j.issn.1007-130X.2012.03.028. |
| [10] |
周耿烈, 冯无恙, 胡赤兵. 基于改进自适应遗传算法求解机床制造企业立体仓库堆垛机路径优化问题[J].
制造技术与机床, 2012(4): 66-70.
ZHOU Genglie, FENG Wuyang, HU Chibing. Solving the warehouse stacker routing problem of machine tool manufacturers based on adaptive genetic algorithm[J]. Manufacturing Technology and Machine Tool, 2012(4): 66-70. DOI: 10.3969/j.issn.1005-2402.2012.04.021. |
| [11] |
谭营, 郑少秋. 烟花算法研究进展[J].
智能系统学报, 2014, 9(5): 515-528.
TAN Ying, ZHENG Shaoqiu. Recent advances in fireworks algorithm[J]. CAAI Transactions on Intelligent Systems, 2014, 9(5): 515-528. |
| [12] |
DING K, ZHENG S, TAN Y. A GPU-based parallel fireworks algorithm for optimization[C/OL]. (2013-06-10). http://www.cil.pkv.edu.cn/publications/papers/2013/DingZhengTanGECCO2013.pdf.
|
| [13] |
ZHENG Y J, SONG Q, CHEN S Y. Multiobjective fireworks optimization for variable-rate fertilization in oil crop production[J].
Applied Soft Computing, 2013, 13(11): 4253-4263.
DOI: 10.1016/j.asoc.2013.07.004. |
| [14] |
ZHENG Y J, XU X L, LING H F, et al. A hybrid fireworks optimization method with differential evolution operators[J].
Neurocomputing, 2015, 148: 75-82.
DOI: 10.1016/j.neucom.2012.08.075. |
| [15] |
MORAMED Imran A, KOWSALYA M, KOTHARI D P. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks[J].
International Journal of Electrical Power & Energy Systems, 2014, 63: 461-472.
|
| [16] |
GAO H, DIAO M. Cultural Firework algorithm and its application for digital filters design[J].
International Journal of Modelling Identification & Control, 2011, 14(4): 324-331.
|
 2019, Vol. 22
2019, Vol. 22