2. 财经学院,江苏 镇江 212013
2. Faculty of Finance and Economics, Jiangsu University, Zhenjiang 212013, China
供应商与承包商组成的二级供应链中,供应商处于供应链源头,对下游承包商的发展起决定性作用。因承包商订货批量不达标,或自身供给能力出现问题等原因导致的供应商退出的现象时有发生。由于供应链构建初期存在不稳定性以及材料产量不确定性,且供应商—承包商之间并未形成长期稳定的合作伙伴关系,导致供应链上游供应商退出风险大大增加,给承包商造成巨大损失[1-4]。新加坡国内建筑材料生产力不足,常年需要从其他国家进口,2001年,印尼和马来西亚同时限制了对新加坡石料与沙的出口,导致新加坡国内石料与沙供不应求,价格飞涨,有些甚至断货致使许多工地停工待料,给承包商带来巨大损失。由此看来供应中断问题在全球越演越烈。
对于供应中断,很多学者对此进行了研究。Yu等[5]分别研究了在单一和双重采购方法下,供应链中断对零售商的影响,结果表明单货源的零售商更容易受到供应中断的影响,但是忽略了中断风险程度对决策的影响。Inderfurth等[6]研究发现在双货源情形下最优订购策略和供应中断风险管理主要受供应商的生产能力及提前期情况影响。造成供应链中断的因素有:需求与供应不确定、提前期不确定、汇率变动和生产能力不确定[7-9]等方面。Gupta等[10]研究了供应中断对零售商利润的影响,并且得到了降低供应风险的策略。邱若臻等[11]在此基础上提出了随机需求下考虑不确定中断概率的鲁棒供应链网络设计模型,结果表明基于线性规划和拉格朗日对偶理论设计的供应链网络能够有效抑制不确定性因素的扰动,具有良好的鲁棒性,但文中仅仅从零售商不确定性进行分析,并没有考虑供应商生产力对供应中断的影响。Kole[12]研究了不同信息水平下合约的有效性以及供应中断情况。把信息水平分为3种情况:完整信息(供应和需求信息),部分信息(仅供应信息),以及无任何信息。结果表明虽然获得完整信息会付出高昂的费用,但可以有效规避供应中断风险。
近年来,建筑材料市场供应商受政策、生产能力、天灾等影响较大,建材的产量很难掌握,部分信息的研究开始受到重视。1957年,Scarf[13]在仅知部分信息情况下研究零售商订货问题,假设只能提前预估需求分布的均值和方差,运用“极大极小利润”方法并求得最差分布下最优决策的存在。但当时Scarf的研究并没有得到重视,直到1993年Gallego等[14]通过对参数进行不同设置,证明了Scarf的研究结果,并使其运用到二次订货、多产品订货等广泛领域。2006年Yue等[15]首次提出了后悔值的概念,并认为是对Scarf研究的再发展。运用“极小极大后悔值”的方法,得到基于后悔情况下的最优订货批量。Muduli[16]认为可以精确估计供需双方不确定信息的上下界,并认为其可以作为最优决策的依据。2014年,孙彩虹[17-20]发现了部分信息下进行鲁棒联合定价与订货决策的价值,并在此基础上于2017年提出运用“极大极小利润”法来测定零售商退出风险对整个供应链的影响,但忽略了供应端不确定性对成本的影响。自此对部分信息下供应链成员退出风险的研究拉开序幕。
本文在以上研究基础上,借鉴Scarf提出的“极大极小值”鲁棒决策方法,分析二级供应链成员间博弈过程,并通过数值仿真清晰刻画了退出标准与最优决策以及承包商成本之间的关系,在一定程度上弥补了部分信息下供应中断研究领域的不足。
1 问题描述假设二级供应链由一个供应商与一个承包商组成,承包商为核心企业,向供应商订购建筑材料,且只能订购一次,没有第二次补货机会。建筑材料供应商对材料生产力不确定,波动较大,产量信息只能通过调查获知均值与方差。双方签订达成协议,约定供应商中途退出的前提。供应商与承包商之间信息对称,供应商能提前预测承包商的决策,以此来制定自身的决策。各个变量及参数具体含义如下。
α为供应商设定的退出标准;
决策顺序如下:供应商确定批发价格以及退出标准,承包商在确定自身需求量情况下向供应商订货。当承包商需求量或者供应商自身生产能力低于一定值时,供应中断。供应链系统如图1所示。

|
图 1 供应链系统图 Fig. 1 Supply chain system diagram |
供应商追求自身鲁棒最优化下期望利益最大化。在仅能获得产量部分信息情况下利用“极大极小值”方法进行博弈分析,供应商的利润函数和期望利润为
| ${\pi _{\rm{S}}} = \left\{ \begin{array}{l} P\min\; \left( {q,D} \right) - {B_{\rm{V}}}D - {h_{\rm{S}}}\left[ {D - \min\; \left( {q,D} \right)} \right],\\ \min\; \left( {q,D} \right) {\text{≥}} \alpha ;\\ P\min\; \left( {q,D} \right) - {B_{\rm{V}}}D - {h_{\rm{S}}}\left[ {D - \min\; \left( {q,D} \right)} \right] - {L_{\rm{S}}},\\ \min\; \left( {q,D} \right){\text{<}} \alpha {\text{。}} \end{array} \right.$ | (1) |
| $\begin{split}& E\left( {{\pi _{\rm{S}}}} \right) = \int_0^{ + \infty } {\left[ {\left( {P + {h_{\rm{S}}}} \right)\min\; \left( {q,x} \right) - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right)x} \right]f\left( x \right){\rm{d}}x -}\!\!\!\!\!\!\!\!\!\!\\ & \int_0^\alpha {{L_{\rm{S}}}f\left( x \right){\rm{d}}x} {\text{。}}\end{split}$ | (2) |
其中,
鲁棒决策最优化,即在最差情况下期望利益最大化:
| $\quad\quad\max\; \min\; E\left( {{\pi _{\rm{S}}}} \right){\text{。}}$ | (3) |
首先分析内部极小化问题
| $\quad\quad\begin{array}{l} \max \;\left[ {{y_1} + \mu {y_2} + \left( {{\mu ^2} + {\sigma ^2}} \right){y_3}} \right]{\text{。}}\\ {y_1} + x{y_2} + {x^2}{y_3} {\text{≤}} \left\{ \begin{array}{l} \left( {P - {B_{\rm{V}}}} \right)x - {L_{\rm{S}}},\\ 0 {\text{≤}} x {\text{≤}} \alpha ;\\ \left( {P - {B_{\rm{V}}}} \right)x,\\ \alpha {\text{<}} x {\text{<}} q;\\ \left( {P + {h_{\rm{S}}}} \right)q - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right)x,\\ x {\text{≥}} q{\text{。}} \end{array} \right. \end{array}$ | (4) |
根据互补松弛条件,最优解应在抛物线
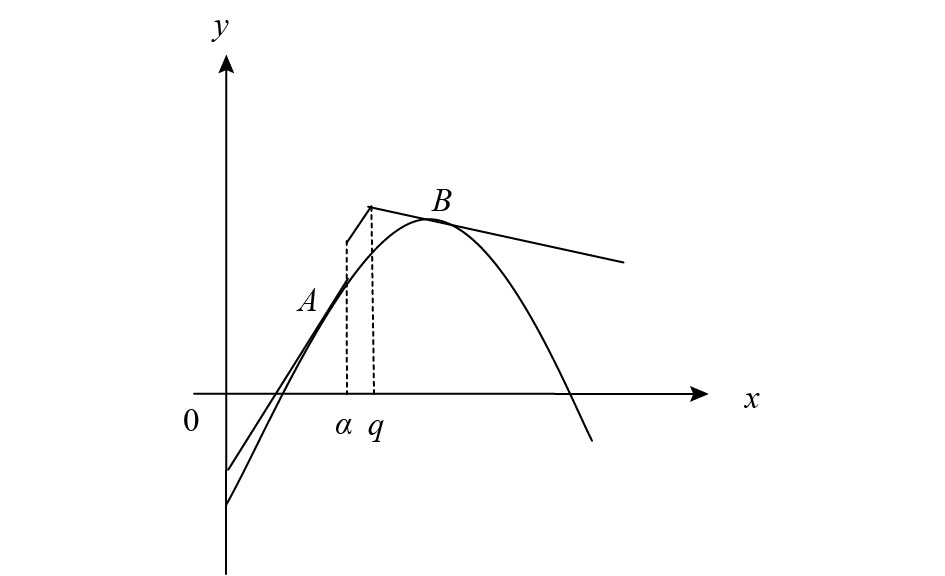
|
图 2 情况1:切于A、B两点 Fig. 2 Case 1: tangent at points A and B |
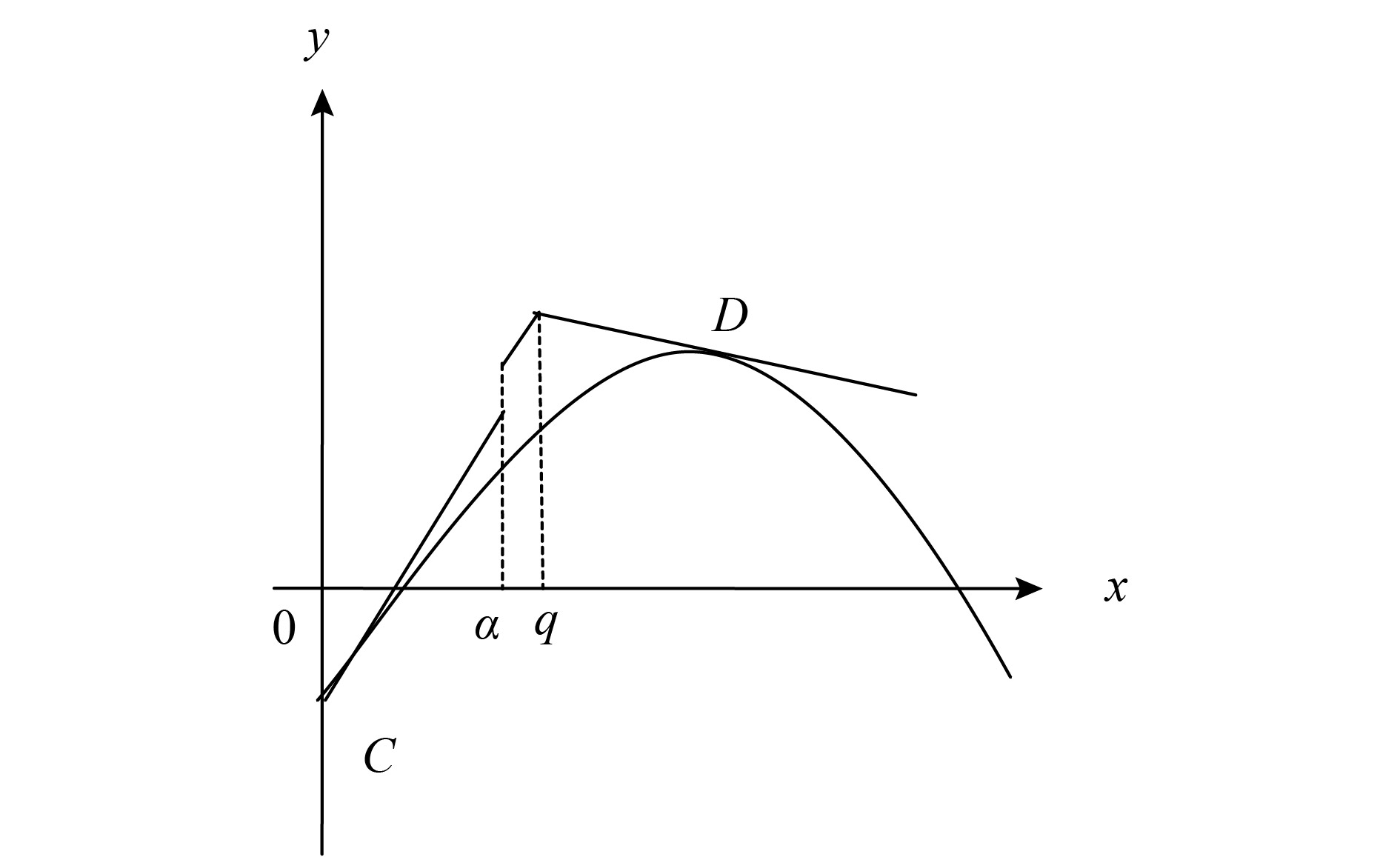
|
图 3 情况2:交于C点,切于D点 Fig. 3 Case 2: intersect at point C, tangent at point D |
1) 情况1:切于A、B两点
(1) 假设两切点的横坐标分别为
| $\quad\quad\left\{\!\!\begin{array}{l} {P_1} = 1 - {P_2},\\ {x_1}{P_1} + {x_2}{P_2} = \mu ,\\ x_1^2{P_1} + x_2^2{P_2} = {\sigma ^2} + {\mu ^2},\\ 0 {\text{<}} {x_1} {\text{≤}} \alpha ,{x_2} {\text{≥}} q{\text{。}} \end{array}\right.$ | (5) |
根据式(5),解得:
| $\quad\quad\left\{\begin{array}{l} {x_1} = \mu - \sigma \sqrt {\dfrac{{1 - {P_1}}}{{{P_1}}}} ,\\ {x_2} = \mu + \sigma \sqrt {\dfrac{{{P_1}}}{{1 - {P_1}}}}{\text{。}} \end{array}\right.$ | (6) |
原问题转化为
| $\begin{split} &\quad\quad\mathop {\min \;}\limits_{{P_1}} \left\{ {\left[ {\left( {P + {h_{\rm{S}}}} \right){x_1} - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right){x_1} - {L_{\rm{S}}}} \right]{P_1} + } \right.\\ &\left. {\left[ {q\left( {P + {h_{\rm{S}}}} \right) - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right){x_2}} \right]\left( {1 - {P_1}} \right)} \right\}{\text{。}} \end{split}$ | (7) |
令式(7)为O,则
| $\quad\quad\begin{split} &\dfrac{{\partial O}}{{\partial {P_1}}} = \left( {P + {h_{\rm{S}}}} \right)\left( {\mu - q} \right) - \dfrac{{\sigma \left( {P + {h_{\rm{S}}}} \right)\left( {1 - 2{P_1}} \right)}}{{2\sqrt {\left( {1 - {P_1}} \right){P_1}} }} - {L_{\rm{S}}},\!\!\!\!\!\!\!\!\!\!\\ &\dfrac{{{\partial ^2}O}}{{\partial {P_1}^2}} = \dfrac{{\sigma \left( {P + {h_{\rm{S}}}} \right)}}{{2{P_1}\left( {1 - {P_1}} \right)\sqrt {\left( {1 - {P_1}} \right){P_1}} }} {\text{>}} 0{\text{。}} \end{split}$ | (8) |
在
| $\quad\quad\left\{\begin{array}{l} {P_1} = \dfrac{1}{2}\left( {1 - \dfrac{A}{{\sqrt {{A^2} + {B^2}} }}} \right),\\ {x_1} = \mu - \dfrac{{\sigma B}}{{\sqrt {{A^2} + {B^2}} - A}},\\ {P_2} = \dfrac{1}{2}\left( {1 + \dfrac{A}{{\sqrt {{A^2} + {B^2}} }}} \right),\\ {x_2} = \mu + \dfrac{{\sigma B}}{{\sqrt {{A^2} + {B^2}} + A}}{\text{。}} \end{array}\right.$ | (9) |
(2) 求解对偶问题:
| $\quad\quad\left\{\begin{array}{l} {y_1} + {x_1}{y_2} + x_1^2{y_3} = \left( {P - {B_{\rm{V}}}} \right){x_1} - {L_{\rm{S}}},\\ {y_1} + {x_2}{y_2} + x_2^2{y_3} = \left( {P + {h_{\rm{S}}}} \right)q - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right){x_2},\\ {y_2} + 2{y_3}{x_1} = P - {B_{\rm{V}}},\\ {y_2} + 2{y_3}{x_2} = - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right) {\text{。}} \end{array}\right.$ | (10) |
通过上式可解得y1、y2、y3,则得对偶问题的最大值为
| $\begin{split} &\quad\quad{y_1} + \mu {y_2} + \left( {{\mu ^2} + {\sigma ^2}} \right){y_3}{\rm{ = }} \mu \left( {P - {B_{\rm{V}}}} \right) -\\ &{L_{\rm{S}}} - \dfrac{{\sqrt {{A^2} + {B^2}} + A}}{2}{\text{。}} \end{split}$ | (11) |
(3) 最差分布下供应商期望利润最大值为
| $\quad\quad E{\left( {{\pi _{\rm{S}}}} \right)_1} = \mu \left( {P - {B_{\rm{V}}}} \right) - {L_{\rm{S}}} - \frac{{\sqrt {{A^2} + {B^2}} + A}}{2}{\text{。}}$ | (12) |
由最优条件得最差分布下供应商最优批发价格为
| $ \begin{split} &\quad\quad{P^ * } = - {h_{\rm{S}}}{\rm{ + }}\\ &\dfrac{{\left( {\mu - q} \right){L_{\rm{S}}} + \sqrt {{{\left( {\mu - q} \right)}^2}L_{\rm{S}}^2 + \dfrac{{4\mu q{L_{\rm{S}}}\left[ {{{\left( {\mu - q} \right)}^2} + {\sigma ^2}} \right]}}{{4\mu q - {\sigma ^2}}}} }}{{{{\left( {\mu - q} \right)}^2} + {\sigma ^2}}} {\text{。}}\!\!\!\!\! \end{split} $ | (13) |
供货商最优批发价与承包商订货量有关,根据式(5)与式(9)订货量满足以下不等式:
| $\begin{split} &\quad\quad\dfrac{{{\mu ^2} + {\sigma ^2}}}{{2\mu }} {\text{<}} q + \\ &\dfrac{{{{\left( {\mu - q} \right)}^2} + {\sigma ^2}}}{{\mu - q + \sqrt {{{\left( {\mu - q} \right)}^2} + \dfrac{{4\mu q{L_{\rm{S}}}\left[ {{{\left( {\mu - q} \right)}^2} + {\sigma ^2}} \right]}}{{4\mu q - {\sigma ^2}}}} }} {\text{<}}\dfrac{{{\mu ^2} + {\sigma ^2} - {\alpha ^2}}}{{2\left( {\mu - \alpha } \right)}} {\text{。}} \end{split}$ | (14) |
2) 情况2:交于C点,切于D点。
(1) C、D两点的横坐标分别为
| $\quad\quad\left\{\!\!\begin{array}{l} {{\hat P}_1} = 1 - {{\hat P}_2},\\ {{\hat x}_2}{{\hat P}_2} = \mu ,\\ x_2^2{{\hat P}_2} = {\sigma ^2} + {\mu ^2}{\text{。}} \end{array}\right.$ | (15) |
解得:
| $\quad\quad\left\{\begin{array}{l} {{\hat P}_1} = \dfrac{{{\sigma ^2}}}{{{\mu ^2} + {\sigma ^2}}},{{\hat x}_1} = 0;\\ {{\hat P}_2} = \dfrac{{{\mu ^2}}}{{{\mu ^2} + {\sigma ^2}}},{{\hat x}_2} = \mu + \dfrac{{{\sigma ^2}}}{\mu }{\text{。}} \end{array}\right.$ | (16) |
(2) 求解对偶问题:
| $\quad\quad\left\{\begin{array}{l} {{\hat y}_1} + {{\hat x}_1}{{\hat y}_2} + \hat x_1^2{{\hat y}_3} = \left( {P - {B_{\rm{V}}}} \right){{\hat x}_1} - {L_{\rm{S}}},\\ {{\hat y}_1} + {{\hat x}_2}{{\hat y}_2} + \hat x_2^2{{\hat y}_3} = \left( {P + {h_{\rm{S}}}} \right)q - \left( {P - {B_{\rm{V}}}} \right){{\hat x}_2},\\ {{\hat y}_2} + 2{{\hat y}_3}{{\hat x}_2} = - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right){\text{。}} \end{array}\right.$ | (17) |
通过式(17)可解得
| $\begin{split} &\quad\quad{{\hat y}_1} + \mu {{\hat y}_2} + \left( {{\mu ^2} + {\sigma ^2}} \right){{\hat y}_3} = - {L_{\rm{S}}} - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right)\mu {\rm{ + }}\\ &\dfrac{{\left[ {{L_{\rm{S}}} + \left( {P + {h_{\rm{S}}}} \right)q} \right]{\mu ^2}}}{{{\mu ^2} + {\sigma ^2}}}{\text{。}} \end{split}$ | (18) |
(3) 最差分布下供应商期望利润为
| $\quad\quad E{\left( {{\pi _{\rm{S}}}} \right)_2} = \frac{{\left[ {{L_{\rm{S}}} + \left( {P + {h_{\rm{S}}}} \right)q} \right]{\mu ^2}}}{{{\mu ^2} + {\sigma ^2}}} - {L_{\rm{S}}} - \left( {{B_{\rm{V}}} + {h_{\rm{S}}}} \right)\mu {\text{。}}\!\!\!\!\!\!\!\!\!\!\!$ | (19) |
对上述
| $\quad\quad\dfrac{{{\mu ^2}q}}{{{\mu ^2} + {\sigma ^2}}} {\text{>}} 0{\text{。}}$ |
此时,在最差情况下,供应商批发价无最优解。
综上所述,供应商在一定范围内可以制定最优决策价格,即
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad{P^ * } = \left\{ \begin{array}{l} \dfrac{{\left( {\mu - q} \right){L_{\rm{S}}} + \sqrt {{{\left( {\mu - q} \right)}^2}L_{\rm{S}}^2 + {{4\mu q{L_{\rm{S}}}\left[ {{{\left( {\mu - q} \right)}^2} + {\sigma ^2}} \right]} / {\left( {4\mu q - {\sigma ^2}} \right)}}} }}{{{{\left( {\mu - q} \right)}^2} + {\sigma ^2}}} - {h_{\rm{S}}},\\ {\text{当}}\dfrac{{{\mu ^2} + {\sigma ^2}}}{{2\mu }} {\text{<}} q + \dfrac{{{{\left( {\mu - q} \right)}^2} + {\sigma ^2}}}{{\mu - q + \sqrt {{{\left( {\mu - q} \right)}^2} + \dfrac{{4\mu q\left[ {{{\left( {\mu - q} \right)}^2} + {\sigma ^2}} \right]}}{{\left( {4\mu q - {\sigma ^2}} \right){L_{\rm{S}}}}}} }} {\text{≤}} \dfrac{{{\mu ^2} + {\sigma ^2} - {\alpha ^2}}}{{2\left( {\mu - \alpha } \right)}};\\ +\infty ,\\ {\text{当}}q + \dfrac{{{{\left( {\mu - q} \right)}^2} + {\sigma ^2}}}{{\mu - q + \sqrt {{{\left( {\mu - q} \right)}^2} + \dfrac{{4\mu q\left[ {{{\left( {\mu - q} \right)}^2} + {\sigma ^2}} \right]}}{{\left( {4\mu q - {\sigma ^2}} \right){L_{\rm{S}}}}}} }} {\text{>}} \dfrac{{{\mu ^2} + {\sigma ^2} - {\alpha ^2}}}{{2\left( {\mu - \alpha } \right)}} {\text{。}} \end{array} \right.$ | (20) |
由式(20)可知,在一定范围内,供应商存在最优批发价格,下面重点分析在此范围内承包商的决策。承包商成本函数为
| $\quad\quad{C_{\rm{R}}} = \left\{ \begin{array}{l} P\min\; \left( {q,D} \right) + \upsilon \left[ {q - \min\; \left( {q,D} \right)} \right],\\ \min\; \left( {q,D} \right) {\text{≥}} \alpha ;\\ P\min\; \left( {q,D} \right) + \upsilon \left[ {q - \min\; \left( {q,D} \right)} \right] - {L_{\rm{R}}},\\ \min\; \left( {q,D} \right) {\text{<}} \alpha {\text{。}} \end{array} \right.$ | (21) |
其中,
| $\begin{split}& \quad\quad E\left[ {{C_{\rm{R}}}} \right] = \int_0^{ + \infty } {\left( {P - \upsilon } \right)} \min\; \left( {q,x} \right)f\left( x \right){\rm{d}}x - \\ &\int_0^\alpha {{L_{\rm{R}}}f\left( x \right){\rm{d}}x} + \upsilon q{\text{。}} \end{split}$ | (22) |
承包商对需求持保守态度,认为预期成本最大化:
| $\quad\quad\max\; \min\; E\left( {{C_{\rm{R}}}} \right){\text{。}}$ | (23) |
根据强对偶性,内部积分问题等价于下述对偶问题:
| $\quad\quad\begin{split} \max \;\left[ {{y_4} + \mu {y_5} + \left( {{\mu ^2} + {\sigma ^2}} \right){y_6}} \right] {\text{。}}\\ {y_4} + x{y_5} + {x^2}{y_6} {\text{≤}} \left\{ \begin{array}{l} \left( {P - \upsilon } \right)\min \;\left( {q,x} \right) - {L_{\rm{R}}},\\ 0 {\text{≤}} x {\text{≤}} \alpha ;\\ \left( {P - \upsilon } \right)\min \;\left( {q,x} \right),\\ x {\text{>}} \alpha {\text{。}} \end{array} \right. \end{split}$ | (24) |
对偶示意图见图4。
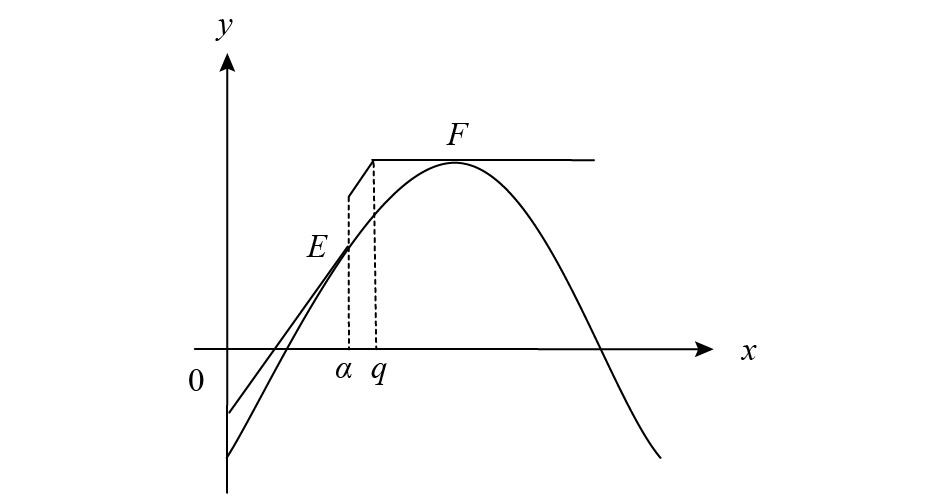
|
图 4 对偶示意图 Fig. 4 Schematic diagram of dual |
根据互补松弛条件,最优解应在抛物线
1) 假设两交点的横坐标分别为
| $\quad\quad\left\{ \begin{array}{l} {P_3} = 1 - {P_4},\\ \alpha {P_3} + {x_4}{P_4} = \mu ,\\ {\alpha ^2}{P_3} + x_4^2{P_4} = {\sigma ^2} + {\mu ^2}{\text{。}} \end{array} \right.$ | (25) |
根据式(25),解得
| $\quad\quad\left\{\begin{array}{l} {P_3} = \dfrac{{{\sigma ^2}}}{{{{\left( {\mu - \alpha } \right)}^2} + {\sigma ^2}}},\;\;{x_3} = \alpha ;\\ {P_4} = \dfrac{{{{\left( {\mu - \alpha } \right)}^2}}}{{{{\left( {\mu - \alpha } \right)}^2} + {\sigma ^2}}},\;\;{x_4} = \dfrac{{\mu \left( {\mu - \alpha } \right) + {\sigma ^2}}}{{\mu - \alpha }}{\text{。}} \end{array}\right.$ | (26) |
2) 对偶问题为
| $\quad\quad\left\{\begin{array}{l} \max \;{y_4} + \mu {y_5} + \left( {{\mu ^2} + {\sigma ^2}} \right){y_6},\\ {y_4} + \alpha {y_5} + {\alpha ^2}{y_6} = \left( {P - \upsilon } \right)\alpha - {L_{\rm{R}}},\\ {y_4} + {x_4}{y_5} + x_4^2{y_6} = \left( {P - \upsilon } \right)q,\\ {y_5} + 2{y_6}{x_4} = 0{\text{。}} \end{array}\right.$ | (27) |
通过式(27)可解得y4、y5、y6,对偶问题的最大值为
| $ \begin{split} &\quad\quad{y_4} + \mu {y_5} + \left( {{\mu ^2} + {\sigma ^2}} \right){y_6}{\rm{ = }}\left( {P - \upsilon } \right)\alpha - {L_{\rm{R}}}{\rm{ + }}\\ &\dfrac{{\left[ {\left( {P - \upsilon } \right)\left( {q - \alpha } \right) + {L_{\rm{R}}}} \right]{{\left( {\mu - \alpha } \right)}^2}}}{{{{\left( {\mu - \alpha } \right)}^2} + {\sigma ^2}}}{\text{。}} \end{split} $ | (28) |
3) 最差分布下承包商成本为
| $ \begin{split} \quad\quad E\left[ {{C_{\rm{R}}}\left( q \right)} \right] = \left( {P - \upsilon } \right)\alpha - {L_{\rm{R}}} + \upsilon q{\rm{ + }}\\ \dfrac{{\left[ {\left( {P - \upsilon } \right)\left( {q - \alpha } \right) + {L_{\rm{R}}}} \right]{{\left( {\mu - \alpha } \right)}^2}}}{{{{\left( {\mu - \alpha } \right)}^2} + {\sigma ^2}}}{\text{。}} \end{split} $ | (29) |
由于供货商最优批发价与承包商最优订货量有关,此时承包商最差情况下最优订货量为
| $\quad\quad{q^ * } = \alpha - \frac{{\left( {{P^{ * '}}\alpha + \upsilon } \right)\left[ {{{\left( {\mu - \alpha } \right)}^2} + {\sigma ^2}} \right]}}{{{{\left( {\mu - \alpha } \right)}^2}{P^{ * '}}}} - \frac{{\left( {{P^ * } - \upsilon } \right)}}{{{P^{ * '}}}}{\text{。}}$ | (30) |
从式(30)可以看出在最差情况下最优订货量
结论1:由式(20)与(30)可知,存在退出风险时,供应商在一定范围内可以作出最优决策,而承包商处于被动局面无法确定其最优决策。且随着承包商订货量的增加,供应商批发价格呈线性增加。双方都选择对自身有利的抉择,而不为对方考虑,导致承包商总体成本上升,建议供需双方之间建立互信合作关系,达到“互利共赢”的目的。
4 数值仿真为更好地刻画供应中断对承包商带来的影响,下面将利用数值仿真来对比分析有无供应中断风险情况下供应商最优批发价格与承包商成本。
某建筑企业有一工程项目,材料采购各项数据如下。以下数据通过正式数据简化而来,具有一定的实际意义:
1) 供应商退出标准对最优决策的影响。
由式(20)可知,供应商的最优批发价格的设定受承包商订货量影响,而承包商不存在最优订货量。图5刻画承包商订货批量对供应商最优决策的影响,并与无退出风险的最优决策进行对比。
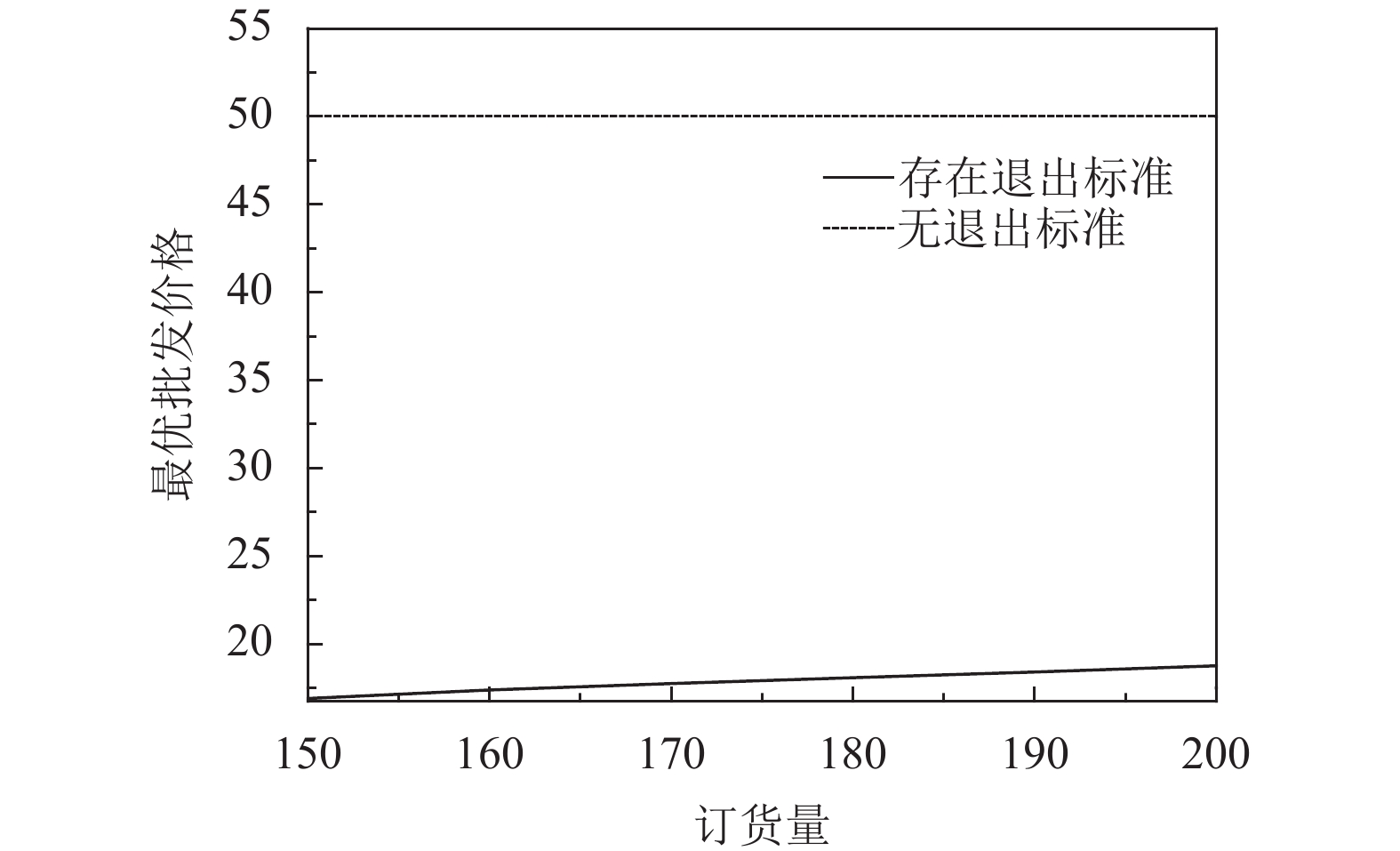
|
图 5 订货量与最优批发价格的关系 Fig. 5 Relationship between wholesale and optimal order |
一方面图5反映出供应商最优批发价受订货量的影响且呈正相关关系,即随着承包商订货量上升供应商的批发价格明显增加;另一方面当存在退出标准时,供应商的最优批发价明显低于无退出风险的情况,说明存在供应中断情况对供应商的最优批发价造成不利影响。
结论2:通过分析有无退出风险情况下供应商最优批发价格与承包商成本可知,存在退出风险情况下的供应商最优决策与承包商成本都远小于无退出风险的情况,说明供应商存在退出风险时对承包商成本产生冲击,建议加强合约制度管理,适当增加违约惩罚费用。
2) 供应商退出标准对承包方成本的影响。
由式(28)可知,承包商成本受供应商最优批发价格、承包商的订货量与退出标准影响,而供应商最优批发价格受承包商的订货量影响。因此只需要刻画在不同退出标准条件下承包商的订货量对承包商成本的影响,并与不存在退出风险的承包商成本进行对比,如图6~图9所示。
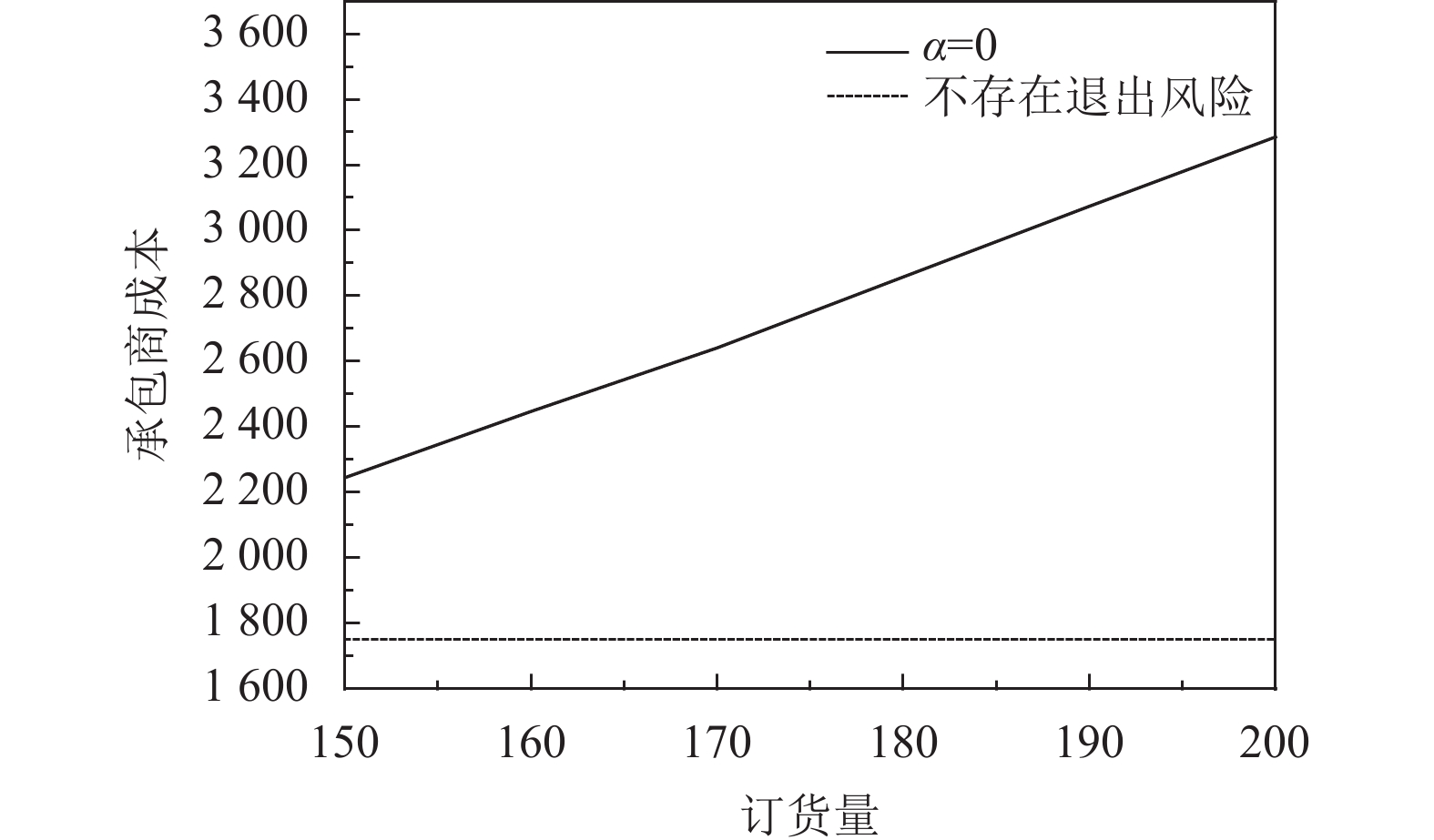
|
图 6 α = 0时订货量与承包商成本的关系 Fig. 6 Relationship between wholesale and Contractor cost, α = 0 |
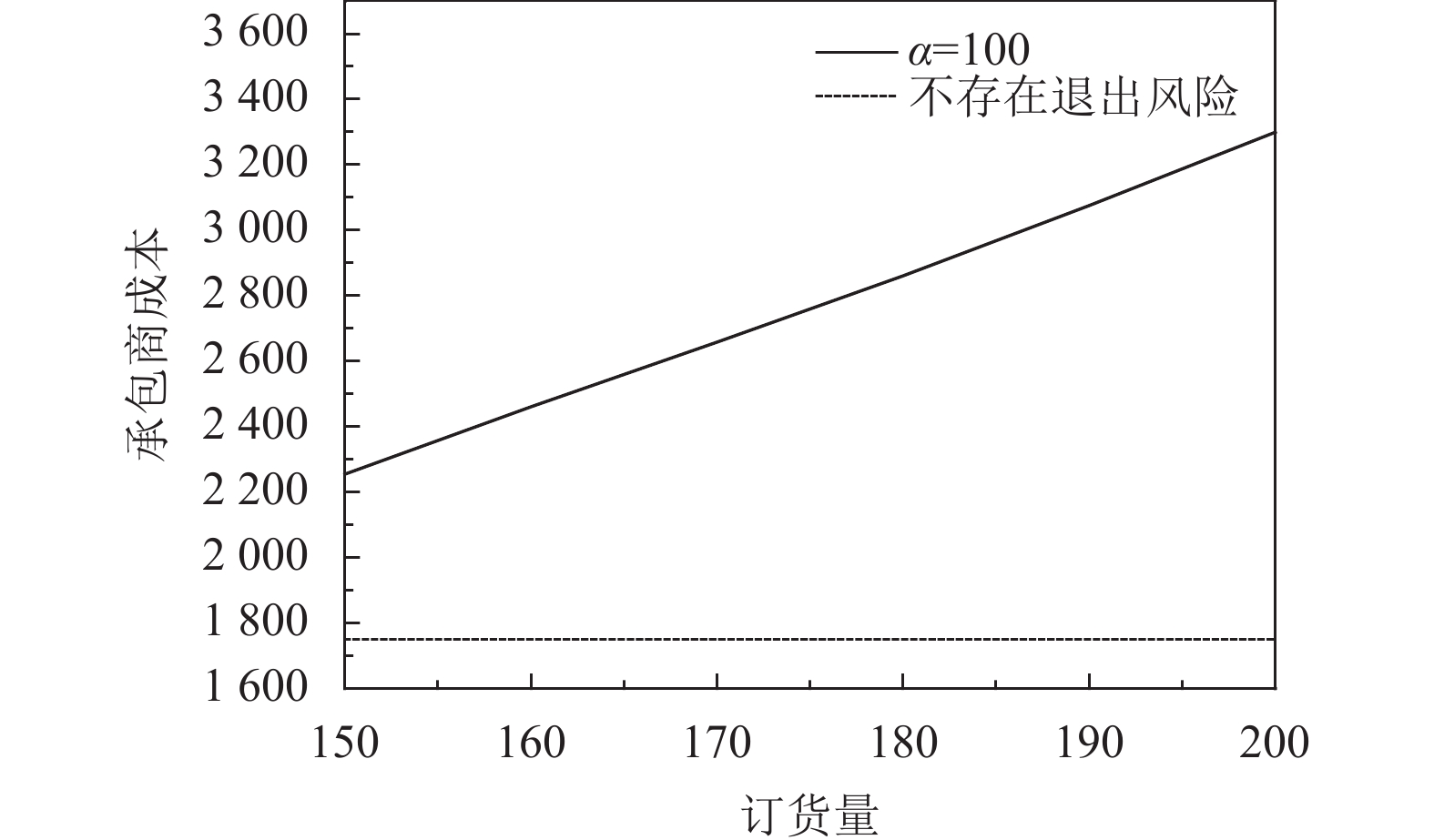
|
图 7 α = 100时订货量与承包商成本的关系 Fig. 7 Relationship between wholesale and Contractor cost, α = 100 |
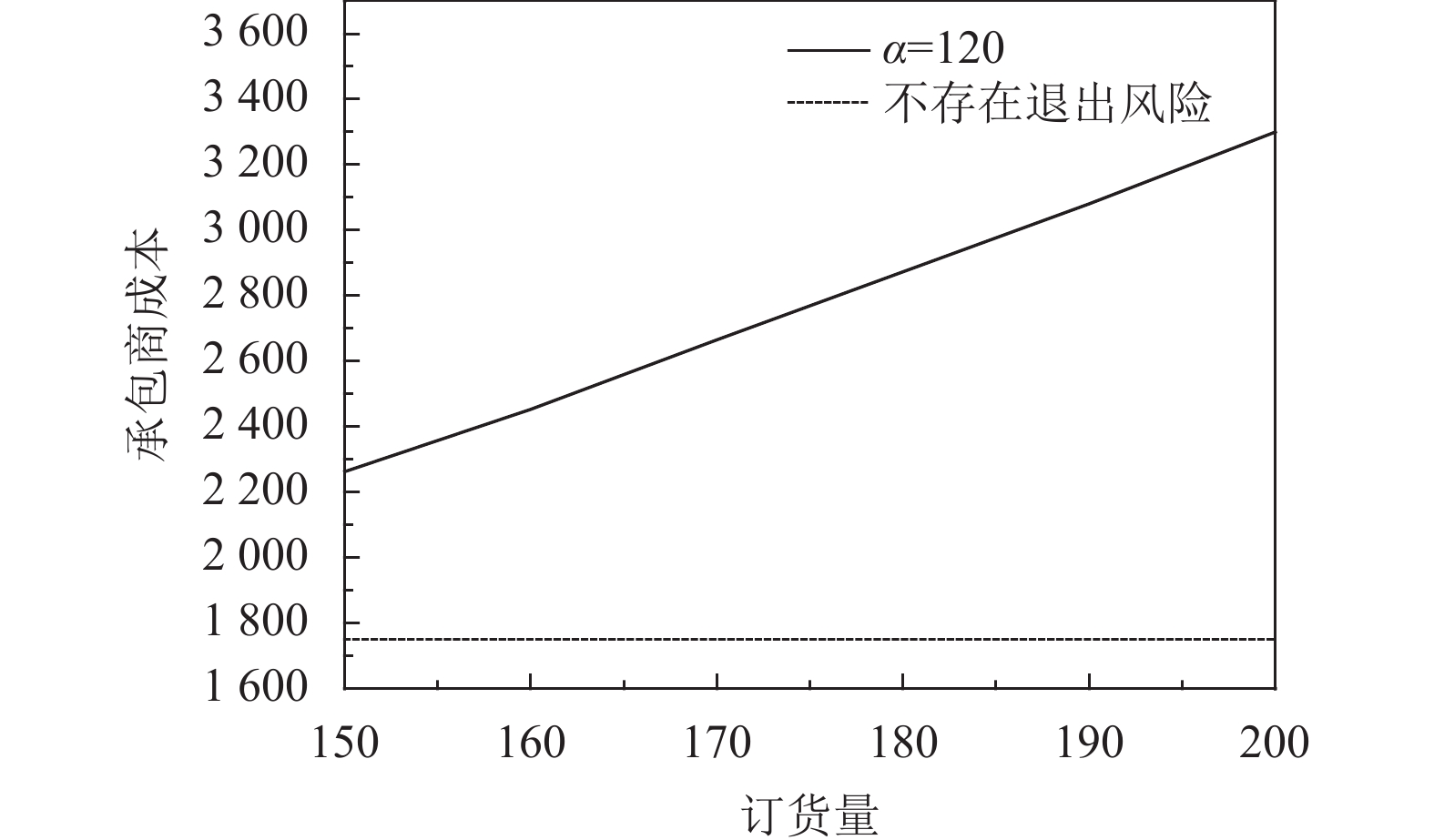
|
图 8 α = 120时订货量与承包商成本的关系 Fig. 8 Relationship between wholesale and Contractor cost, α = 120 |
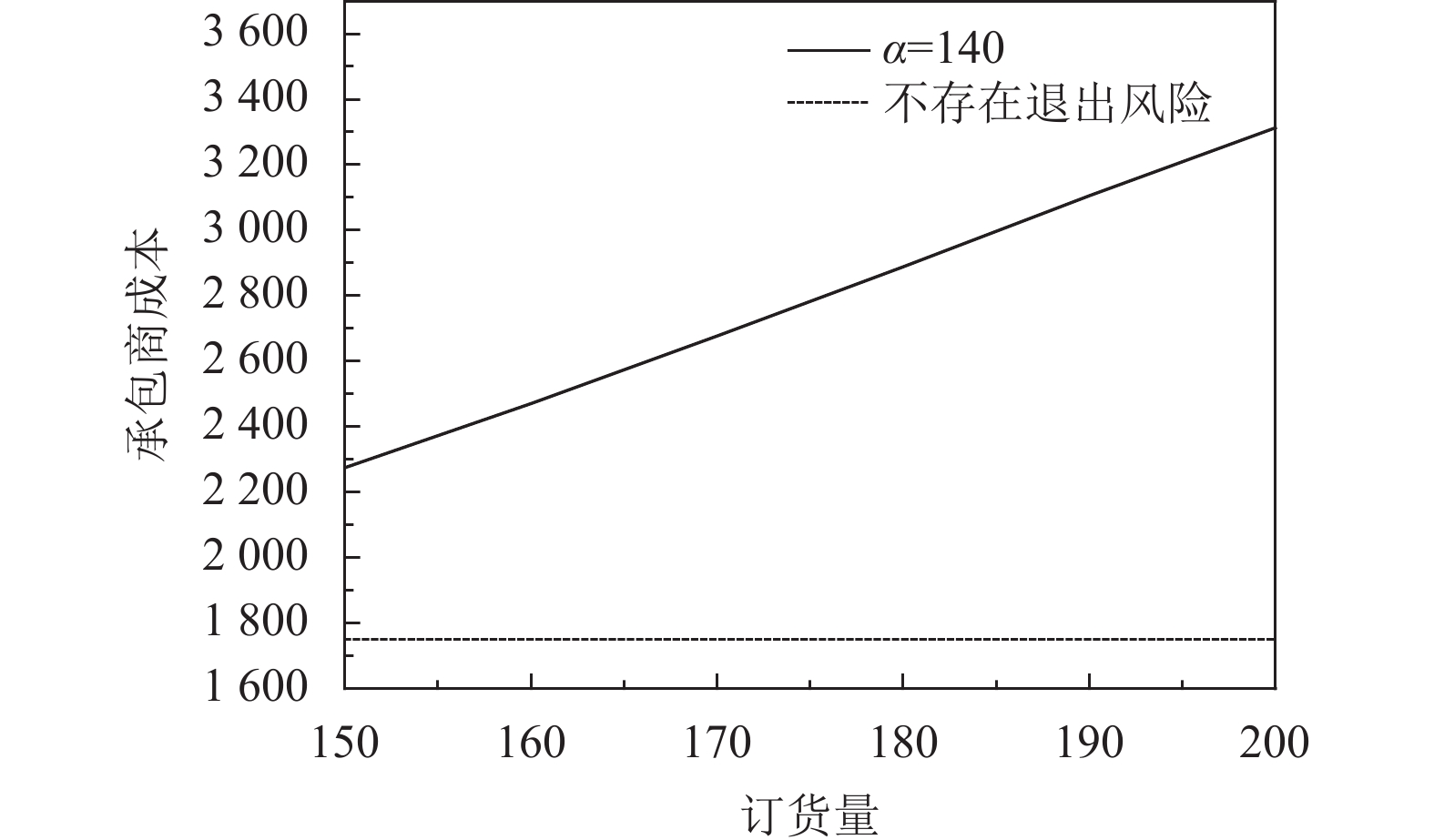
|
图 9 α = 140时订货量与承包商成本的关系 Fig. 9 Relationship between wholesale and Contractor cost, α = 140 |
从图6中可以看出:随着订货量的升高,承包商成本明显增高;随着退出标准的提高,对承包商成本造成冲击,且产量分布未知对承包商成本冲击较大。同时发现当存在退出标准时,承包商成本明显高于无退出风险的情况。
结论3:退出标准给承包商成本造成冲击,同时发现承包商成本增加程度与退出标准大小与订货批量密切相关,建议承包商在可承受范围内,适当减少订货批量、降低退出标准。
5 小结供应链初期不稳定以及生产能力不确定导致了供应链上游供应商存在高退出风险,供应中断对承包商造成巨大损失,冲击了供应链运作基础。本文将Scarf“极小极大值”理论方法运用到供应中断的鲁棒性研究中,刻画了存在退出标准对供应商最优批发价格与承包商成本的影响。近年来众多学者投身于供应链鲁棒性研究中,并取得丰厚成果,但是在部分信息下对供应中断的研究才刚刚起步,需要更多学者投身其中。
| [1] |
PAL B, SANA S S, CHAUDHURI K. A multi-echelon production–inventory system with supply disruption[J].
Journal of Manufacturing Systems, 2014, 33(2): 262-276.
DOI: 10.1016/j.jmsy.2013.12.010. |
| [2] |
HE B, HUANG H, YUAN K. The comparison of two procurement strategies in the presence of supply disruption[M]. UK: Pergamon Press, Inc. 2015.
|
| [3] |
PAUL S K, SARKER R, ESSAM D. A quantitative model for disruption mitigation in a supply chain[J].
European Journal of Operational Research, 2017, 257(3): 881-895.
DOI: 10.1016/j.ejor.2016.08.035. |
| [4] |
ZHANG Juliang, CHEN Jian. Externality of contracts on supply chains with two suppliers and a common retailer[J].
Journal of Industrial & Management Optimization, 2017, 6(4): 795-810.
|
| [5] |
YU H, ZENG A Z, ZHAO L. Single or dual sourcing: decision-making in the presence of supply chain disruption risks[J].
Omega, 2009, 37(4): 788-800.
DOI: 10.1016/j.omega.2008.05.006. |
| [6] |
INDERFURTH Karl, KELLE Peter, KLEBER Rainer. Dual sourcing using capacity reservation and spot market: optimal procurement policy and heuristic parameter determination[J].
European Journal of Operational Research, 2013, 225(2): 298-309.
DOI: 10.1016/j.ejor.2012.08.025. |
| [7] |
ESMAEILIKIE M, FAHIMNIA B, SARKIS J, et al. Tactical supply chain planning models with inherent flexibility: definition and review[J].
Annals of Operations Research, 2016, 244(2): 407-427.
DOI: 10.1007/s10479-014-1544-3. |
| [8] |
IVANOV D, DOLGUII A, SOKOLOV B, et al. Literature review on disruption recovery in the supply chain[J].
International Journal of Production Research, 2017, 55(20): 6158-6174.
DOI: 10.1080/00207543.2017.1330572. |
| [9] |
SAWIK T. A portfolio approach to supply chain disruption management[J].
International Journal of Production Research, 2017, 55(7): 1970-1991.
DOI: 10.1080/00207543.2016.1249432. |
| [10] |
GUPTA V, HE B, SETHI S P. Contingent sourcing under supply disruption and competition[J].
Ssrn Electronic Journal, 2015, 53(10): 3006-3027.
|
| [11] |
邱若臻, 王奕智, 黄小原. 基于不确定中断概率的鲁棒供应链网络设计[J].
计算机集成制造系统, 2016, 22(10): 2458-2468.
QIU Ruozhen, WANG Yizhi, HUANG Xiaoyuan. Robust supply chain network design based on uncertain disruption probability[J]. Computer Integrated Manufacturing Systems, 2016, 22(10): 2458-2468. |
| [12] |
KOLE H, BAKAL I S. Value of information through options contract under disruption risk[J].
Computers & Industrial Engineering, 2017, 103: 85-97.
|
| [13] |
SCARF H E. A min-max solution of an inventory problem[DB/OL]. (1957-06-24). https://www.rand.org/content/dam/rand/pubs/papers/2008/P910.pdf.
|
| [14] |
GALLEGO G, MOON I. The distribution free newsboy problem: review and extensions[J].
Journal of the Operational Research Society, 1993, 44(8): 825-834.
DOI: 10.1057/jors.1993.141. |
| [15] |
YUE J, CHEN B, WANG M C. Expected value of distribution information for the newsvendor problem[J].
Operations Research, 2006, 54(6): 1128-1136.
DOI: 10.1287/opre.1060.0318. |
| [16] |
SHEN L, MUDULI K, BARVE A. Developing a sustainable development framework in the context of mining industries: AHP approach[J].
Resources Policy, 2015, 46: 15-26.
DOI: 10.1016/j.resourpol.2013.10.006. |
| [17] |
孙彩虹. 部分信息下联合鲁棒定价、订货决策的报童模型[J].
系统工程理论与实践, 2014, 34(5): 1122-1130.
SUN Caihong. Jointly robust pricing and order decision newsvendor model under the limited information[J]. System Engineering—Theory & Practice, 2014, 34(5): 1122-1130. |
| [18] |
孙彩虹, 田真真, 于辉. 价格需求函数的供应链合作动力对比分析[J].
工业工程, 2015, 18(4): 58-65.
SUN Caihong, TIAN Zhenzhen, YU Hui. A comparative analysis of supply chain’s collaborative motivation under different price-dependent demand functions[J]. Industrial Engineering Journal, 2015, 18(4): 58-65. DOI: 10.3969/j.issn.1007-7375.2015.04.009. |
| [19] |
孙彩虹, 田真真, 于辉. 零售商退出风险的供应链冲击与协调契约分析[J].
中国管理科学, 2016, 24(6): 38-45.
SUN Caihong, TIAN Zhenzhen, YU Hui. Analysis of supply chain shock and coordinating contract with retailer’s exiting risk[J]. Chinese Journal of Management Science, 2016, 24(6): 38-45. |
| [20] |
孙彩虹, 田真真. 考虑零售商退出风险的供应链鲁棒模型分析[J].
系统科学与数学, 2017, 37(5): 1244-1258.
SUN Caihong, TIAN Zhenzhen. The analysis of robust model of new product supply chain with retailer’s exiting risk[J]. J. Sys. Sci. & Math. Scis, 2017, 37(5): 1244-1258. |
 2019, Vol. 22
2019, Vol. 22