随着互联网的迅速发展,越来越多的制造商通过双渠道销售产品,即传统的零售渠道和在线直销渠道相结合。根据《纽约时报》的调查,在IBM、HP、Nike、Pioneer Electronics、Mattel、Estee Lauder、Compaq、Dell、和Cisco System等多种行业的顶级供应商中,约有42%的供应商通过直销渠道向消费者销售产品。由于各分销渠道的当事人可能具有不同的利益,分销渠道往往不能完全协调。在分销渠道中,上、下游企业依次决策产品价格来实现自身利润最大化,供应链中不同阶段成员的目标发生冲突进而导致每一方获利减少,也就是通常所说的“双重边际效应”现象,这种自利的定价行为导致在独立决策过程中的产品销售价格高于集中决策时的价格。
除价格决策外,产品质量决策也可能受到分销渠道结构的影响。由于准确的产品特性和价格取决于当地市场情况和分销系统,同时提高质量成为企业立足于市场的必要条件,因此许多国际公司基于不同国家的同一产品平台销售不同质量的产品。如何在网络竞争渠道的环境下,制定合理有效的供应链质量决策,提高产品质量,实现不同渠道利益的均衡和渠道整体效益的最大化,成为许多企业亟待解决的问题。
在此背景下,本文研究双渠道供应链中价格和质量决策的问题。虽然制造商努力提高产品质量可以增加产品的吸引力和价值,但是生产高质量的产品需要熟练的劳动力和昂贵原材料,这往往导致高昂的产品质量成本。因此在供应链管理中,产品价格和产品质量水平的决策对企业管理有着重要的战略意义。
1 文献综述已有的关于双渠道运营管理的研究主要集中在定价或质量决策方面,揭示在线直销渠道的作用。虽然直销渠道的开通不能带来直接的利润,但是可给现有的零售商施加潜在竞争压力,增加制造商的谈判能力,同时减少“双重边际效应”。Balasubramanian[1]从战略视角给出双渠道竞争的模型。研究表明,市场覆盖水平可以作为一种机制来控制竞争。Mathieu等[2]研究了零售商店、网上商店和混合销售的利润。他们认为,混合销售将有最大的最优利润。Hua等[3]研究发现当实体书批发价和读者对电子书接受程度均处于较低水平时,出版商应该只销售实体书;否则即使读者对电子书接受程度比较低,出版商也应该销售电子书。也就是说,大多数情况下,出版商应该销售电子书。Chun等[4]分析了传统零售商渠道和直销渠道价格差异的原因。Cattani等[5]证明制造商可以使用定价策略作为增加利润和减少竞争的手段,特别是在直销渠道成本昂贵的情况下。Liu等[6]研究了现有的零售商如何有效抑制电子零售商进入的问题。Cai等[7]讨论了在两个渠道成本结构不同情况下制造商的分销策略,结果表明制造商应在网络渠道成本不高时开通双渠道。Khouja等[8]研究了零售商通过网络和传统渠道销售产品的最优定价策略。Chiang等[9]研究了在考虑顾客对直销渠道接受程度的情形下,制造商和零售商的定价策略。然而,上述文献只关注定价因素,并没有考虑产品质量在直销与零售竞争市场中的战略重要性。
供应链质量管理实践与成员的战略有显著的相关性,同时成员的策略对业务成果和顾客满意度有重要的影响。如Walmart供应链管理者检查制造商提供的产品样本,如果产品可以接受,考虑到市场需求,管理者会根据质量和产品价格进行订货。虽然高质量产品可高价格销售,但是它也导致更高的成本,同时价格和质量影响需求及利润。因此,价格和质量决策对供应链管理实践与成员的战略至关重要。
在已有的双渠道文献中,关于质量改进的研究较少。Chambers等[10]考虑了生产成本变动情况下,制造商在价格和质量的决策对双寡头竞争行为的影响。Xu[11]研究了分销渠道的联合定价与产品质量决策问题。Chao等[12]讨论了制造商和供应商如何制定产品召回成本共享契约,提高产品质量。Hsieh等[13]提出生产过程中的质量改进措施,降低次品率。考虑了两个制造商共享一个特定市场份额下,关于质量改进的供应链。李永飞等[14]研究质量改进对协调销售渠道、价格、销售量及系统总利润等的影响。以上研究集中在制造商和零售商的质量协调问题。
渠道分销对产品质量影响也有一些研究。Jeuland等[15]研究了分销渠道中的质量是否应该更低或相同,Economides[16]拓展了这一结果,并证明了质量有可能取决于边际收益函数的问题。Tsay等[17]的研究表明在直销渠道通过销售努力刺激需求并不是太低效的情况下,直销渠道的引入使得零售商和制造商都获利。Tyagi[18]的研究表明,入侵促使制造商降低批发价格,刺激零售商渠道的需求。Cai[19]研究表明当零售商在基本需求或运营成本方面有足够的成本优势时,可达到双赢的结果。刘咏梅等[20]研究了制造商仅在传统渠道或采用混合渠道进行新产品推广时的产品质量决策问题。Ha等[21]对两个渠道同时存在的情况进行调查,结果表明,根据直销渠道销售成本入侵产品的质量可能较高或较低。Chen等[22]研究了双渠道供应链中制造商零售商定价、利润及产品质量的差异与决策。但是他们没有考虑消费者对渠道的接受程度。与这些文献不同的是,本文在供应链设计中将消费者对直销渠道接受程度与产品质量相结合。以下问题尚无文献进行研究。
1) 在渠道设计中考虑消费者对渠道接受程度不同情形下,引入产品质量后,制造商入侵如何影响产品质量,产品价格以及企业利润?
2) 在渠道设计中考虑消费者对渠道接受程度不同情形下,引入产品质量后,制造商在什么情况下开通双渠道?
下面分别对传统零售渠道模型、分散决策模型和集中决策模型进行研究。希望所得到的结论能为制造商开通双渠道提供一定的理论参考和借鉴。
2 传统零售渠道模型本节介绍了消费者选择的基本模型以及当产品只在传统实体零售商店销售时的渠道定价决策。参考Moorthy等[23]相关文献,假设制造商的单位产品质量成本
零售商以价格
假设由一个垄断型制造商提供的批发价格为
| $\quad\quad{\pi _{\rm r}} = ({p_{\rm r}} - w){Q_{\rm r}} = ({p_{\rm r}} - w)\left(1 - \frac{{{p_{\rm r}}}}{u}\right){\text{。}}$ | (1) |
制造商的利润为
| $\quad\quad{\pi _{\rm m}} = (w - {u^2} - {c_{\rm r}}){Q_{\rm r}} = (w - {u^2} - {c_{\rm r}})\left(1 - \frac{{{p_{\rm r}}}}{u}\right){\text{。}}$ | (2) |
如果制造商和零售商看作一个整体,整体利润为
| $\quad\quad{\pi _{\rm vi}} = ({p_{\rm r}} - {u^2} - {c_{\rm r}})\left(1 - \frac{{{p_{\rm r}}}}{u}\right){\text{。}}$ | (3) |
作为Stackelberg领导者,制造商在零售商决策零售价格
| $\quad\quad w = \frac{{{u^2}{\rm{ + }}u{\rm{ + }}{c_{\rm r}}}}{2}{\text{。}}$ | (4) |
因此,
| $\quad\quad {\pi _{\rm r}}(u) = \frac{{{{({u^2} - u + {c_{\rm r}})}^2}}}{{16u}}\;,{\pi _{\rm m}}(u) = \frac{{{{({u^2} - u + {c_{\rm r}})}^2}}}{{8u}}{\text{。}}$ | (5) |
最后,制造商通过最大化自己的利润
根据式(5)可知,质量
如果质量
现在假设制造商正在考虑向市场开通直销渠道。制造商在零售渠道和直销渠道的边际成本分别为
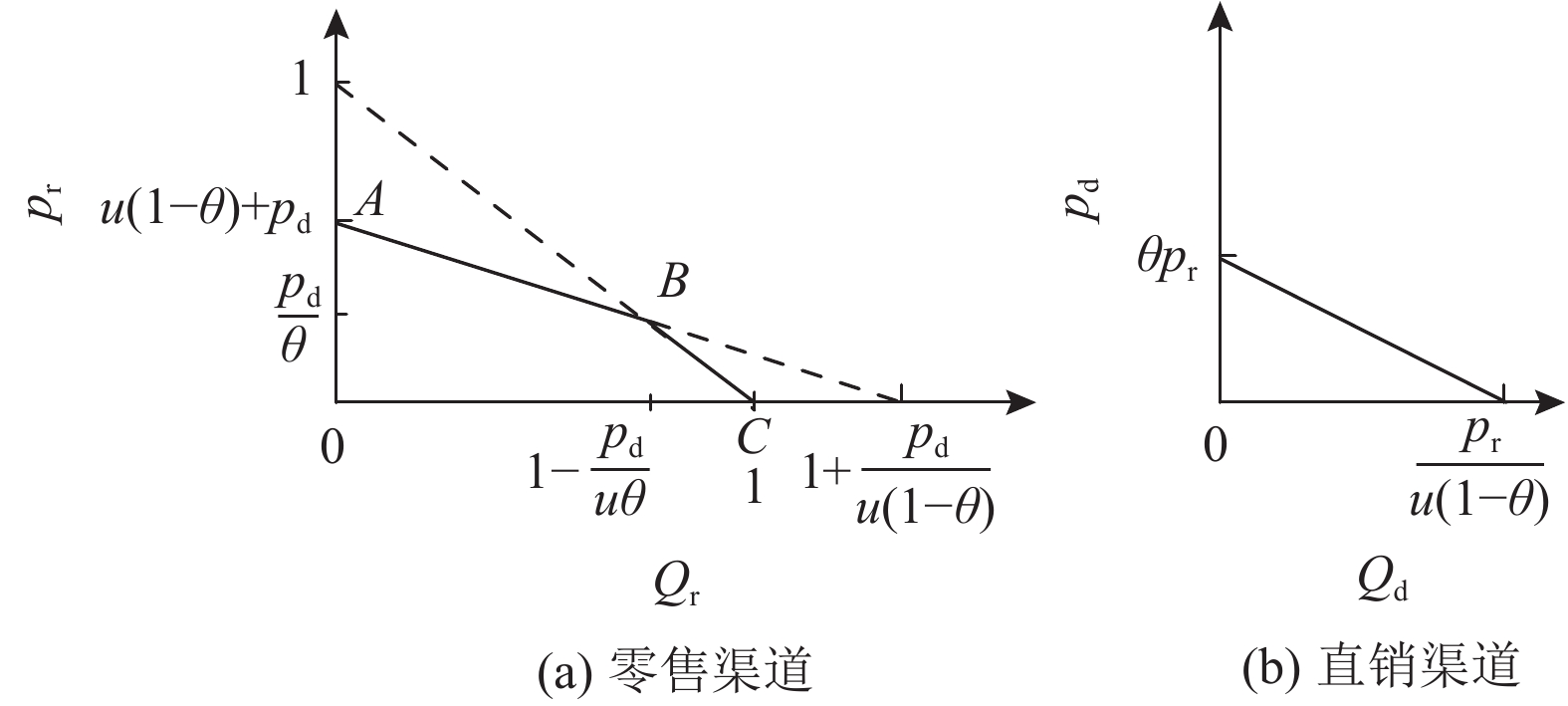
| $\quad\quad{Q_{\rm r}} = \left\{ {\begin{array}{*{20}{l}} {1 - \dfrac{{{p_{\rm r}} - {p_{\rm d}}}}{{u(1 - \theta )}}},&{\text{如果}\dfrac{{{p_{\rm d}}}}{\theta } {\text{≤}} {p_{\rm r}}}{\text{;}}\\ {1 - {p_{\rm r}}/u},&\text{其他} {\text{。}}\end{array}} \right.$ | (6) |
| $\quad\quad{Q_{\rm d}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\theta {p_{\rm r}} - {p_{\rm d}}}}{{u\theta (1 - \theta )}}},&{\text{如果}\dfrac{{{p_{\rm d}}}}{\theta } {\text{≤}} {p_{\rm r}}}{\text{;}}\\ 0,&\text{其他}{\text{。}} \end{array}} \right.$ | (7) |
图1为直销渠道和零售渠道的需求示意图。
|
图 1 零售渠道与直销渠道的需求 Fig. 1 Demand functions of retail store and direct channel |
本节将直销渠道的作用与Stackelberg博弈模型相结合,检验制造商和零售商之间的相互作用。在第1阶段,制造商作为Stackelberg领导者,决定是否开通直销渠道,决策批发价格
| $\quad\quad\max \pi _{\rm m}^{\rm d} = \max \left\{ {({w^{\rm d}} - {u^2} - c_{\rm r}^{\rm d})Q_{\rm r}^{\rm d} + (p_{\rm d}^{\rm d} - {u^2})Q_{\rm d}^{\rm d}} \right\}{\text{,}}$ |
其中零售渠道的需求
零售商决策零售价
|
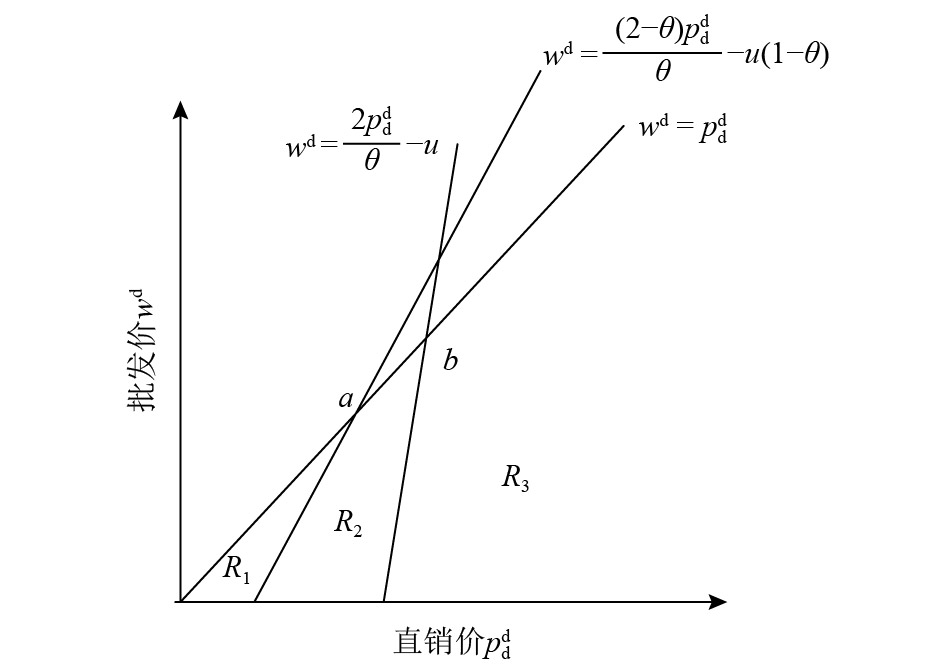
图 2 直销市场和批发价格的可行区域 Fig. 2 Feasible regions for direct market and wholesale price |
| $\quad\quad{R_1} = \left\{ {(p_{\rm d}^{\rm d},w)\left| {\dfrac{{p_{\rm d}^{\rm d} + {w^{\rm d}} + u(1 - \theta )}}{2} {\text{≥}} \dfrac{{p_{\rm d}^{\rm d}}}{\theta },{w^{\rm d}} {\text{≤}} p_{\rm d}^{\rm d}} \right.} \right\}{\text{。}}$ |
接下来,考虑沿
| $\quad\quad{R_3} = \left\{ {(p_{\rm d}^{\rm d},{{ w}^{\rm d}})\left| {\frac{{u + {w^{\rm d}}}}{2} {\text{≤}} \frac{{p_{\rm d}^{\rm d}}}{\theta }{\text{,}}{w^{\rm d}} {\text{≤}} p_{\rm d}^{\rm d}} \right.} \right\}{\text{。}}$ |
最后,如果制造商设置
| $\begin{split} &\quad\quad{R_2} = \left\{ {(p_{\rm d}^{\rm d},{{w}^{\rm d}})\left| {\frac{{p_{\rm d}^{\rm d} + {{w}^{\rm d}} + u(1 - \theta )}}{2} {\text{≤}} \frac{{p_{\rm d}^{\rm d}}}{\theta },} \right.} \right. \\ &\left. { \frac{{u + {{w}^{\rm d}}}}{2} {\text{≥}} \frac{{p_{\rm d}^{\rm d}}}{\theta },{{w}^{\rm d}} {\text{≤}} p_{\rm d}^{\rm d}} \right\} {\text{。}} \end{split} $ |
区域
定理 1 给定制造商产品质量u,批发价wd,直销价
| $p_{\rm r}^{{\rm d}*}({u^{\rm d}},\theta ) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{p_{\rm d}^{\rm d} + {{w}^{\rm d}} + {u^{\rm d}}(1 - \theta )}}{2}}{\text{,}}&{\text{如果}(p_{\rm d}^{\rm d},{{w}^{\rm d}}) \in {R_1}}{\text{;}}\\ {\dfrac{{p_{\rm d}^{\rm d}}}{\theta }}{\text{,}}&{\text{如果}(p_{\rm d}^{\rm d},{{w}^{\rm d}}) \in {R_2}}{\text{;}}\\ {\dfrac{{{u^{\rm d}} + {{w}^{\rm d}}}}{2}}{\text{,}}&{\text{如果}(p_{\rm d}^{\rm d},{{w}^{\rm d}}) \in {R_3}}{\text{。}} \end{array}} \right.$ | (8) |
其中
制造商面临的问题是通过对零售商定价的预测,决策产品质量
首先考虑区域
引理 1 区域
证明 与文献[9]附录1的证明类似,不再赘述。
定理 2 如果产品质量水平为
| $\begin{split} &\quad\quad \hat \theta = \frac{1}{{4{u^2}}}\left.{\Bigg{[}} {{{\left( {{c_{\rm r}} + u} \right)}^2} + 2{c_{\rm r}}{u^2} + 2{u^3} + {u^4}} \right. -\\ & \left. { \left( {{c_{\rm r}} - u\left( {1 - u} \right)} \right)\sqrt {{c_{\rm r}}^2 + 2{c_{\rm r}}u\left( {3 + u} \right) + {u^2}\left( {1 + u\left( {6 + u} \right)} \right)} } \right.{\Bigg{]}}, \!\!\!\!\!\! \end{split} $ | (9) |
使得当
制造商的最优定价为
对应的零售价为
证明 Stackelberg博弈最大化问题的子博弈完美均衡解。
| $\begin{gathered} \;\mathop {{\rm{max}}}\limits_{[(p_{\rm d}^{\rm d},{{w}^{\rm d}}),p_{\rm r}^{{\rm d}*}] \in \varPhi \times {\Re ^ + }} \pi _{\rm m}^{\rm d}(p_{\rm d}^{\rm d},{w^{\rm d}},p_{\rm r}^{{\rm d}*}) {\text{。}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;p_{\rm r}^{{\rm d}*} \in \arg \max \;\pi _{\rm r}^{\rm d}(p_{\rm d}^{\rm d},{w^{\rm d}},p_{\rm r}^{\rm d}){\text{。}} \\ \end{gathered} $ |
其中
在
| $\quad\quad(p_{\rm d}^{\rm d},{{w}^{\rm d}}) = \left(\frac{{u\theta }}{{2 - \theta }},\frac{{u\theta }}{{2 - \theta }}\right){\text{;}}$ | (10) |
在
| $\quad\quad(p_{\rm d}^{\rm d},{{w}^{\rm d}}) = \left(\frac{{u(u + \theta ) + {c_{\rm r}}}}{2},\frac{{u(u + \theta ) + {c_{\rm r}}}}{2}\right){\text{;}}$ | (11) |
在
| $\quad\quad(p_{\rm d}^{\rm d},{{ w}^{\rm d}}) = \left(\frac{{{u^2} + u + {c_{\rm r}}}}{2},\frac{{{u^2} + u + {c_{\rm r}}}}{2}\right){\text{。}}$ | (12) |
显然,如果
| $\quad\quad\!\!\!\begin{array}{l} \max\; {\pi _2}\left(\dfrac{{u(u + \theta ) + {c_{\rm r}}}}{2},\dfrac{{u(u + \theta ) + {c_{\rm r}}}}{2}\right){\text{≥}} \\ \max\; {\pi _3}\left(\dfrac{{{u^2} + u + {c_{\rm r}}}}{2},\dfrac{{{u^2} + u + {c_{\rm r}}}}{2}\right) ,\;{\pi _{\rm r}} {\text{≥}} 0; \end{array} $ |
或等价于
或者,如果
| $\begin{split} &\quad\quad \hat \theta = \frac{1}{{4{u^2}}}\left. \Bigg[ {{{\left( {{c_{\rm r}} + u} \right)}^2} + 2{c_{\rm r}}{u^2} + 2{u^3} + {u^4}} \right. - \\ & \left. {\left( {{c_{\rm r}} - u\left( {1 - u} \right)} \right)\sqrt {{c_{\rm r}}^2 + 2{c_{\rm r}}u\left( {3 + u} \right) + {u^2}\left( {1 + u\left( {6 + u} \right)} \right)} } \right.\Bigg], \end{split} $ |
方程(11)的价格为均衡价格,否则均衡价格为式(12)中的价格。
3.3 渠道均衡解及管理启示本节通过制造商渠道控制问题的完美均衡博弈来描述Stackelberg定价问题。相关结果如表1所示。其中
| 表 1 分散决策模型中,制造商与零售商的均衡结果 Tab. 1 The equilibrium results of manufacturer and retailer in decentralized decision model |
直销渠道的战略性运用是鼓励独立零售商降低零售价,增加销量。这一战略的有效性取决于独立制造商威胁零售渠道直接向消费者销售产品的可行性。
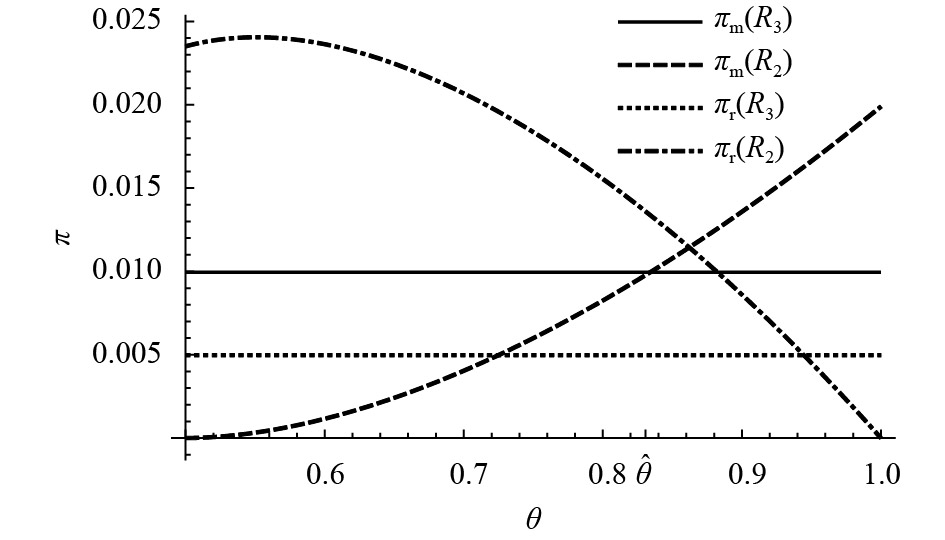
从制造商的角度来看,当
当
|
图 3 企业利润和
|
定理 3 当制造商开通双渠道时,产品质量水平
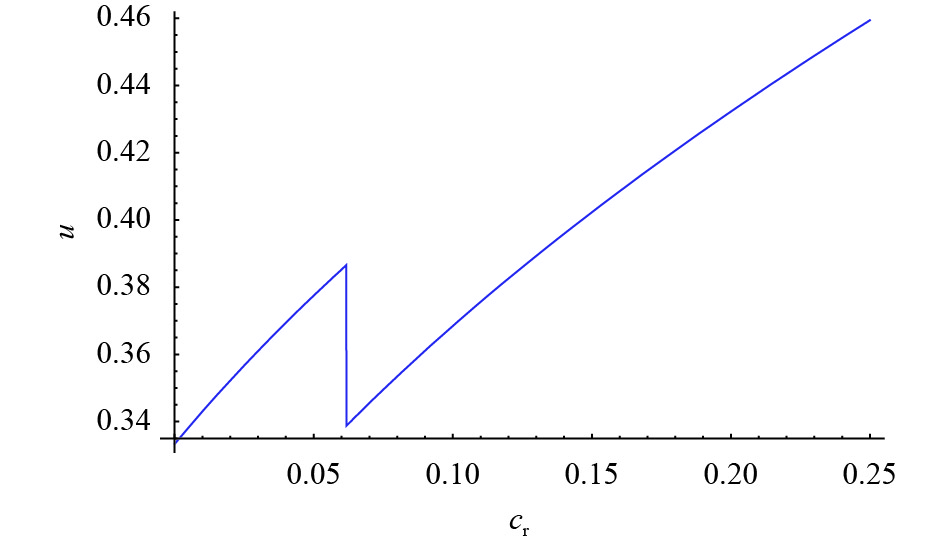
根据表1的结果,对于给定的质量
|
图 4 产品质量与
|
|
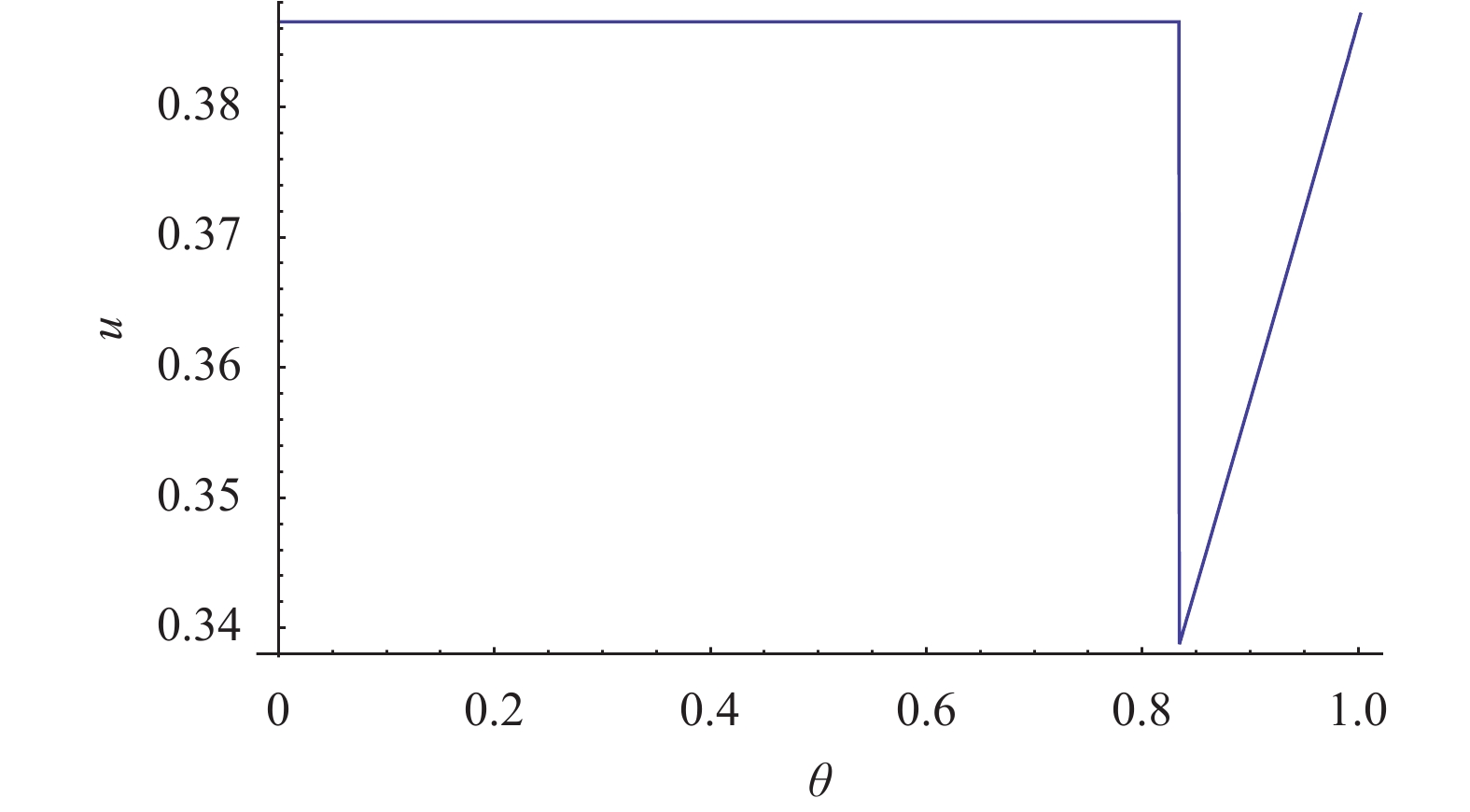
图 5 产品质量与
|
定理 4 存在一个阈值
1) 当制造商入侵时,产品质量
2) 当制造商入侵时,制造商总是提供较低质量的产品,
3) 入侵阈值
如果直销渠道是一个弱的威胁(
随着零售渠道销量和零售利润率的提高,如果
|
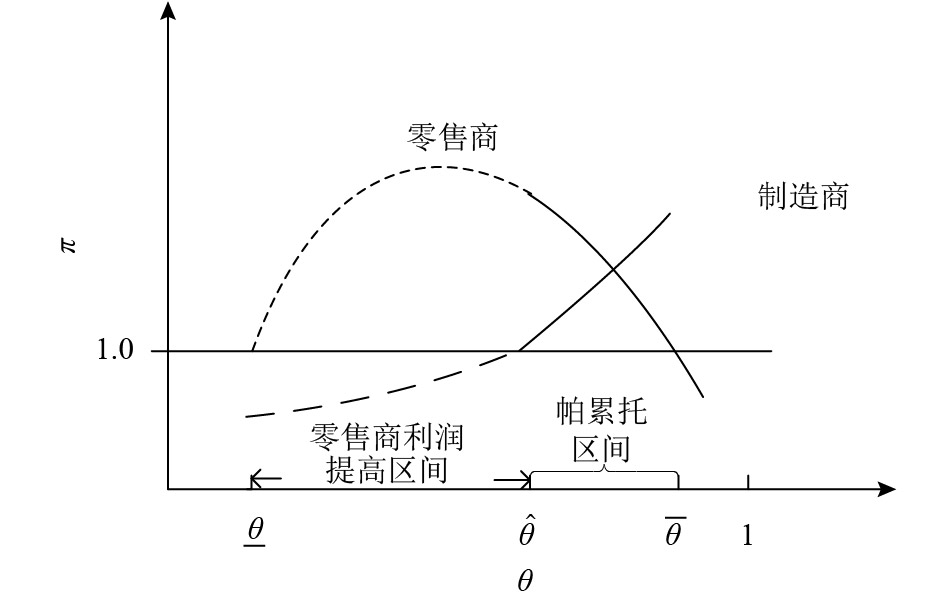
图 6 帕累托区间 Fig. 6 Pareto zone |
当消费者对直销渠道的接受程度在区间
定理 5 存在一个非空区间
证明:由表1可知:
| $\quad\quad{\pi _{\rm r}^{\rm d}}(\theta ) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{({u^2} - u + {c_{\rm r}})}^2}}}{{16u}}}{\text{,}}&{\text{如果}\theta {\text{<}} \hat \theta }{\text{;}}\\ {\dfrac{{(1 - \theta )[{{(u\theta )}^2} - {{({u^2}{\rm{ + }}{c_{\rm r}})}^2}]}}{{4u{\theta ^2}}}}&{\text{,}}\text{其他} {\text{。}}\end{array}} \right.$ |
现在要证明,对
| $\begin{split} &\quad\quad \hat \theta = \dfrac{1}{{4{u^2}}}\left.\Bigg[ {{{\left( {{c_{\rm r}} + u} \right)}^2} + 2{c_{\rm r}}{u^2} + 2{u^3} + {u^4}} \right. - \\ &\left. { \!\left( {{c_{\rm r}}\! - u\left( {1 -\! u} \right)} \right)\sqrt {{c_{\rm r}}^2 +\! 2{c_{\rm r}}u\left( {3 +\! u} \right) +\! {u^2}\left( {1 +\! u\left( {6 + \!u} \right)} \right)} } \right. \Bigg] \text{ 。}\\ \end{split} $ |
证明:因为
| $\quad\quad\begin{gathered} \dfrac{{{\partial ^2}\dfrac{{(1 - \theta )[{{(u\theta )}^2} - {{({u^2}{\rm{ + }}{c_{\rm r}})}^2}]}}{{4u{\theta ^2}}}\;\;\;\;\;}}{{\partial {\theta ^2}}} = \dfrac{{{{({u^2}{\rm{ + }}{c_{\rm r}})}^2}(\theta - {\rm{3}})}}{{2u{\theta ^4}}} {\text{<}} 0, \end{gathered}$ |
所以
又因为
| $\begin{split} &\quad\quad \dfrac{{(1 - \overline \theta )[{{(u\overline \theta )}^2} - {{({u^2}{\rm{ + }}{c_{\rm r}})}^2}]}}{{4u{{\overline \theta }^2}}}\; =\\ & \dfrac{{(1 - \underline \theta )[{{(u\underline \theta )}^2} - {{({u^2}{\rm{ + }}{c_{\rm r}})}^2}]}}{{4u{{\underline \theta }^2}}}= \dfrac{{{{({u^2} - u + {c_{\rm r}})}^2}}}{{16u}}, \end{split} $ |
以及
| $\quad\quad{\pi _{\rm r}}(\hat \theta - \varepsilon ) = \dfrac{{{{({u^2} - u + {c_{\rm r}})}^2}}}{{16u}},\;\;\;\hat \theta \in (\overline \theta ,\;\underline \theta ),$ |
因此对
由图3和图6可知,当
现在假设制造商已经向市场开通直销渠道。与分散决策模型不同的是,企业在考虑实现供应链的整体利润最大化的基础上进行对产品价格和产品质量水平进行决策。方程(6)和(7)中给出了需求函数,如果垂直一体化企业(集中决策模型)以零售价格
| $\quad\quad\pi _{\rm vi}^{\rm c} = (p_{\rm r}^{\rm c} - {u^2} - {c_{\rm r}})Q_{\rm r}^{\rm c} + (p_{\rm d}^{\rm c} - {u^2})Q_{\rm d}^{\rm c}{\text{。}}$ | (13) |
首先假设
| $\begin{split} &\quad\quad \pi _{\rm vi}^{\rm c} = (p_{\rm r}^{\rm c} - {u^2} - {c_{\rm r}})Q_{\rm r}^{\rm c} + (p_{\rm d}^{\rm c} - {u^2})Q_{\rm d}^{\rm c} =\\ &(p_{\rm r}^{\rm c} - {u^2} - {c_{\rm r}})\left(1 - \frac{{p_{\rm r}^{\rm c} - p_{\rm d}^{\rm c}}}{{u(1 - \theta )}}\right) + (p_{\rm d}^{\rm c} - {u^2})\frac{{\theta p_{\rm r}^{\rm c} - p_{\rm d}^{\rm c}}}{{u\theta (1 - \theta )}}{\text{。}} \end{split} $ | (14) |
式(14)中,根据
由表2可知,在集中决策模型中,企业是否开通直销渠道,对零售价没有影响。显然,如果价格相同,那么更高的质量水平的产品总是给同一分割市场带来更多的消费者。一般来说,在一个特定的产品市场,产品以“高质量、高价格”提供给高端客户,构成价格最不敏感的分割市场。在集中决策模型中,企业开通直销渠道后,零售商的利润更大。因此,零售渠道的销售量更高。显而易见的是,在集中决策模型中,企业开通直销渠道后,制造商可以提供更高质量的产品。本文得到如下推论。
| 表 2 集中决策模型中,仅零售渠道或双渠道开通的情况1) Tab. 2 Centralized decision model with only traditional retail channels or dual channels |
推论1 在集中决策模型中,直销渠道的开通,有利于制造商提供更高质量的产品。
5 结论在消费者对直销渠道和零售渠道接受程度有差异的情形下,研究了产品质量为内生的双渠道供应链中价格和质量联合决策问题,得到以下结论。
1) 在集中决策模型中,制造商和零售商视为一个整体。此时制造商开通直销渠道虽然对零售价没有影响,但是能够提高产品质量和供应链整体利润。当接受程度
2) 因为顾客对直销渠道接受程度的价值和批发价效应主导零售商的竞争效应,本文将顾客对直销渠道的接受程度
(1) 当
(2) 当
(3) 当
(4) 当
(5) 当
3) 在分散决策模型中,制造商开通直销渠道降低了产品批发价、直销价、零售价和产品质量水平,刺激需求,所以并不是总对零售商不利。
本文研究存在一些不足之处,仅假设零售渠道和直销渠道的产品是无差异的,没有考虑制造商退货、退款保障以及价格折扣等,这可以作为未来进一步研究。
| [1] |
BALASUBRAMANIAN S. Mail versus mall: a strategic analysis of competition between direct marketers and conventional retailers[J].
Marketing Science, 1998, 17(3): 181-195.
DOI: 10.1287/mksc.17.3.181. |
| [2] |
MATHIEU R G, LEVARY R. Hybrid retail: integrating e-commerce and physical stores[J].
Industrial Management, 2000, 42(5): 6-13.
|
| [3] |
HUA G, WANG S, CHENG T C E. Price and lead time decisions in dual-channel supply chains[J].
European Journal of Operational Research, 2010, 205(1): 113-126.
DOI: 10.1016/j.ejor.2009.12.012. |
| [4] |
CHUN S H, KIM J C. Pricing strategies in B2C electronic commerce: analytical and empirical approaches[J].
Decision Support Systems, 2005, 40(2): 375-388.
DOI: 10.1016/j.dss.2004.04.012. |
| [5] |
CATTANI K, GILLAND W, HEESE H S, et al. Abstract boiling grogs: pricing strategies for a manufacturer adding a direct channel that competes with the traditional channel[J].
Production & Operations Management, 2007, 15(1): 40-56.
|
| [6] |
LIU Y, GUPTA S, ZHANG Z J. Note on self-restraint as an online entry-deterrence strategy[J].
Management Science, 2006, 52(11): 1799-1809.
DOI: 10.1287/mnsc.1050.0566. |
| [7] |
CAI G, ZHANG Z G, ZHANG M. Game theoretical perspectives on dual-channel supply chain competition with price discounts and pricing schemes[J].
International Journal of Production Economics, 2009, 117(1): 80-96.
DOI: 10.1016/j.ijpe.2008.08.053. |
| [8] |
KHOUJA M, PARK S, CAI G. Channel selection and pricing in the presence of retail-captive consumers[J].
International Journal of Production Economics, 2010, 125(1): 84-95.
DOI: 10.1016/j.ijpe.2010.01.005. |
| [9] |
CHIANG W K, CHHAJED D, HESS J D. Direct marketing, indirect profits: a strategic analysis of dual-channel supply-chain design[J].
Marketing Science, 2003, 49(1): 1-20.
|
| [10] |
CHAMBERS C, KOUVELIS P, SEMPLE J. Quality-based competition, profitability, and variable costs[J].
Management Science, 2006, 52(12): 1884-1895.
DOI: 10.1287/mnsc.1060.0581. |
| [11] |
XU X. Optimal price and product quality decisions in a distribution channel[J].
Management Science, 2009, 55(8): 1347-1352.
DOI: 10.1287/mnsc.1090.1023. |
| [12] |
CHAO G H, IRAVANI S M R, SAVASKAN R C. Quality improvement incentives and product recall cost sharing contracts[J].
Management Science, 2009, 55(7): 1122-1138.
DOI: 10.1287/mnsc.1090.1008. |
| [13] |
HSIEH C C, LIU Y T. Quality investment and inspection policy in a supplier–manufacturer supply chain[J].
European Journal of Operational Research, 2010, 202(3): 717-729.
DOI: 10.1016/j.ejor.2009.06.013. |
| [14] |
李永飞, 苏秦, 郑婧. 考虑质量改进的双渠道供应链协调研究[J].
软科学, 2015(7): 35-39.
LI Yongfei, SU Qin, ZHENG Jing. Rearch on dual-channel supply chain coordination with considering quality improvement[J]. Journal of Soft Science, 2015(7): 35-39. |
| [15] |
JEULAND A P, SHUGAN S M. Managing channel profits[J].
Marketing Science, 2008, 27(1): 52-69.
DOI: 10.1287/mksc.1070.0332. |
| [16] |
ECONOMIDES N. Quality choice and vertical integration[J].
International Journal of Industrial Organization, 1999, 17(6): 903-914.
DOI: 10.1016/S0167-7187(97)00063-5. |
| [17] |
TSAY A A, AGRAWAL N. Channel conflict and coordination in the e‐commerce age[J].
Production & Operations Management, 2010, 13(1): 93-110.
|
| [18] |
TYAGI R K. Technological advances, transaction costs, and consumer welfare[J].
Marketing Science, 2004, 23(3): 335-344.
DOI: 10.1287/mksc.1030.0038. |
| [19] |
CAI G. Selection and coordination in dual-channel supply chains[J].
Journal of Retailing, 2010, 86(1): 22-36.
DOI: 10.1016/j.jretai.2009.11.002. |
| [20] |
刘咏梅, 廖攀, 胡军华. 电子商务环境下考虑竞争的新产品开发和定价策略研究[J].
管理工程学报, 2016, 30(2): 210-215.
LIU Yongmei, LIAO Pan, HU Junhua. New product development and pricing strategies in e-commerce environment considering competition[J]. Journal of Industrial Engineering & Engineering Management, 2016, 30(2): 210-215. |
| [21] |
HA A, LONG X, NASIRY J. Quality in supply chain encroachment[J].
Advances in Engineering Software, 2016, 100(2): 215-230.
|
| [22] |
CHEN J, LIANG L, YAO D Q, et al. Price and quality decisions in dual-channel supply chains[J].
European Journal of Operational Research, 2016, 259(3): 935-948.
|
| [23] |
MOORTHY K S, PNG I P L. Market segmentation, cannibalization, and the timing of product introductions[J].
Management Science, 1992, 38(3): 345-359.
DOI: 10.1287/mnsc.38.3.345. |
 2019, Vol. 22
2019, Vol. 22

