近年来,随着社会经济的发展,环境污染和资源短缺等问题日益突出,废旧品回收再利用受到了社会各界的密切关注。再制造是以产品全寿命周期理论为指导,优质、高效、节能、节材、环保为准则,先进技术和产业化生产为手段,进行修复、改造废旧设备产品的一系列技术措施或工程活动。实践证明,再制造在节约资源、降低环境污染和增加社会及企业效益等方面发挥着重要作用,是废旧物品回收再利用的有效方式之一。我国于2011年1月1日起施行《废旧电器电子产品回收处理管理条例》(简称条例),条例规定多渠道回收废旧产品。在实践中,由于OEM不具有再制造相关技术和设备,因而往往只生产销售新产品,第三方再制造商生产销售再制造品。然而,很多产品的再制造过程本身并不破坏废旧品的物理形态,仅对产品进行修复、替代或修理损坏的部件,使得再制造品保持了原产品的外观和内部结构,在再制造品销售中甚至要保留原产品的商标标识。第三方的再制造涉及了OEM的产品声誉、技术专利、消费市场抢占等问题,第三方经OEM授权后才能进行废旧品的回收再制造[1]。例如,苹果公司在2015年授权富士康公司回收再制造废旧手机,并销售再制造品[2]。因此,在授权模式下,研究第三方和OEM在正向供应链销售市场和逆向供应链回收市场的竞争有重要的现实意义。
目前,已有大量的文献研究了再制造的正向供应链销售市场和逆向供应链回收市场的竞争。在正向供应链销售市场竞争方面,伍颖等[3]研究了新产品、制造商和再制造商各自生产的再制造品三者互相竞争的情况下,制造商和再制造商根据再制造节约成本确定新产品和再制造品的生产数量,并进行垄断和竞争两种条件下制造商利润的比较。Mitra[4]假设双寡头在新产品市场进行价格竞争,其中一个制造商引入再制造,研究结果表明制造商引入再制造总比没有再制造更有利可图,而另一竞争者的影响结果是好坏参半。Zou等[2]假设OEM通过授权或外包允许第三方进行再制造,OEM和第三方在生产量和销售价格上进行竞争,研究结果表明当消费者对再制造品的估值较高时,第三方偏好外包模式,否则偏好授权模式,而在这两种情况下OEM通过外包比授权获得更高的利润。Zhang等[5]研究了OEM授权第三方再制造模式下,当新产品和再制造品存在价格竞争时,OEM和第三方的定价策略和协调策略。Yi等[6]假设在正向渠道制造商生产新产品,零售商按契约销售新产品并生产和销售再制造品,在逆向渠道双方同时回收废旧品,研究结果表明制造商在双渠道回收情况下能获利更多。Jena等[7]考虑了在产品需求不确定和废旧品质量不确定情况下,两再制造商通过共同的零售商销售他们的替代产品,在价格和服务两方面存在竞争,研究结果表明当需求波动变大时,直销渠道相比其他渠道模式能提供更好的结果。
在逆向供应链回收市场竞争方面,Liu等[8]研究了OEM和第三方、OEM和零售商、零售商和第三方3种双渠道回收竞争模式,研究结果表明无论竞争强度是多少,对于OEM来说OEM和零售商双渠道回收竞争模式是最好的选择。李凌雁等[9]在制造商授权回收商回收再制造的情形下,建立了包含能进行回收的制造商和具有再制造能力的回收商的闭环供应链模型,结果表明在再制造品短缺的市场中,当回收商再制造成本低于制造商时,制造商才会授权其再制造。闻卉等[10]在专利保护环境下研究了两个再制造商在逆向回收市场进行回收竞争的闭环供应链定价决策问题,在集中决策和分散决策两种情形下探讨了原制造商、两个再制造商和零售商的定价决策。
有些文献同时研究了正向供应链销售市场和逆向供应链回收市场的竞争。Bulmus等[11]建立了OEM和第三方在销售市场和回收市场均存在竞争的两阶段模型,研究结果表明OEM的废旧品采购价格只依赖于自己的成本结构,与第三方的废旧品采购价格无关。Wu[12]建立了当OEM与第三方在回收市场中存在距离竞争以及新产品与再制造品存在价格竞争的两阶段模型,研究结果表明销售市场竞争越激烈,越能促进第三方在回收市场更加努力,这些对于OEM来说都是有利的。Wu等在文献[12]的基础上,进一步假设OEM和第三方在销售市场和回收市场均存在距离竞争时,OEM和第三方的定价和回收策略[13]。田晖等[14]基于新产品与再制造产品存在价格竞争以及制造商和再制造商存在回收竞争,研究固定费用和单位授权费两种不同专利许可策略下供应链成员决策。
本文在已有文献研究的基础上,假设第三方需向OEM缴纳授权费才能回收再制造;在正向供应链销售市场,消费者对新产品更为信赖,双方通过新产品和再制造品的零售价格进行竞争来抢占消费者市场;在逆向供应链回收市场,消费者愿意将废旧品卖给回收价格更高的企业,OEM和第三方通过废旧品回收价格来激励消费者回收进行竞争。本文建立了以双方闭环供应链利润最大化为目标的古诺博弈模型,并求出两企业最优的新产品和再制造品生产量、零售价格以及废旧品回收价格。通过解析方法分析了环保主义者主动无偿返还废旧品数量、废旧品残值对废旧品最优回收价格的影响,单位授权费、第三方从OEM那里购买废旧品的单位价格对新产品和再制造品最优生产量的影响,以及新产品和再制造品的单位生产成本对新产品和再制造品最优生产量、最优零售价格的影响,最后用数值算例方法分析了上述参数对最优利润的影响。
1 符号说明及假设 1.1 符号说明本文用到的参数及决策变量如下:pn/pr表示新产品/再制造品的单位零售价格(决策变量);dn/dr表示新产品/再制造品的生产量(决策变量);ai表示i企业从消费者那里回收废旧品的单位回收价格(决策变量);qi表示i企业从消费者那里回收废旧品的数量;cn/cr表示新产品/再制造品的单位生产成本;s表示第三方回收废旧品的单位残值收入;b表示第三方从OEM那里购买废旧品的单位价格;f表示OEM授权第三方进行回收再制造的单位授权费;α表示环保主义者主动无偿返还废旧品的数量;β表示消费者对废旧品回收的价格敏感系数;θ表示消费者对废旧品回收的交叉价格敏感系数,θ<β;δ表示消费者对OEM生产的新产品的支付意愿,服从[0,1]上的均匀分布;ρ表示消费者对再制造品和对新产品支付意愿的比值,ρ∈(0,1)。其中,i∈{m,t},m和t分别表示OEM和第三方。
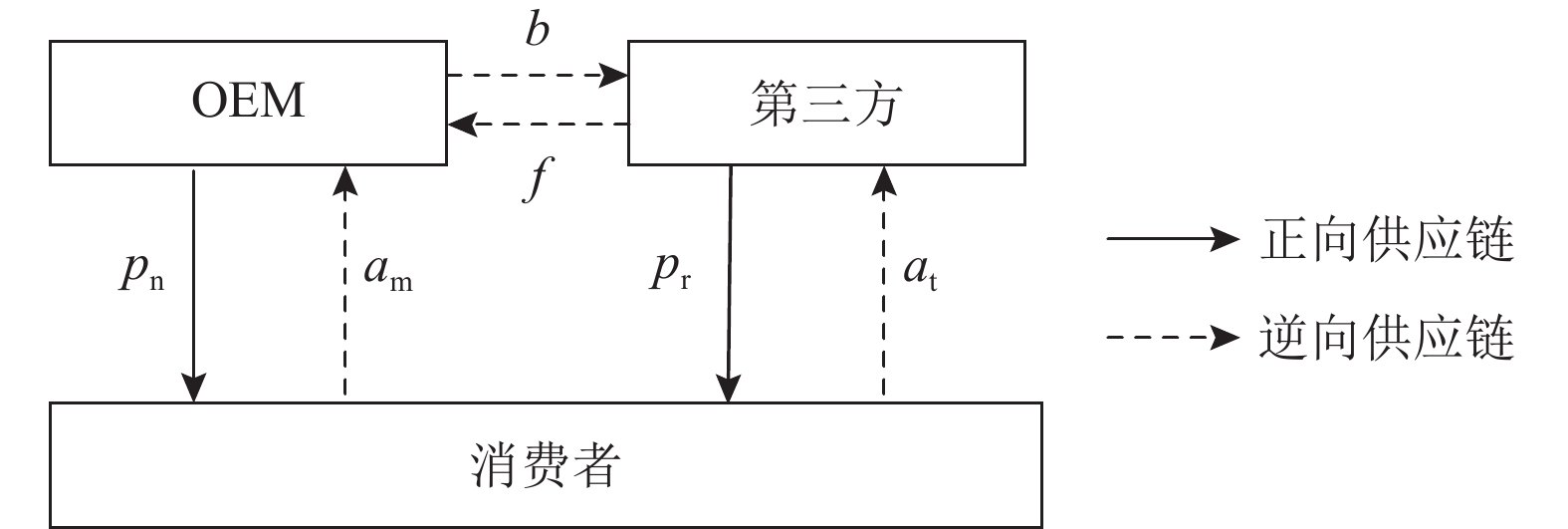
1.2 假设假设1 第三方需向OEM缴纳授权费才能进行回收再制造,OEM和第三方在正向供应销售市场通过新产品和再制造品零售价格竞争,在逆向供应链回收市场通过废旧品回收价格竞争。OEM生产新产品,并将回收的废旧品卖给第三方,第三方生产再制造品,见图1。
|
图 1 模型结构 Fig. 1 Model structure |
假设2 当消费者对新产品支付意愿为δ,对再制造品的支付意愿仅为ρδ,即消费者对新产品更信赖。消费者购买新产品和再制造品的效用分别为Un=δ–pn,Ur=ρδ–pr。当Un>0且Un>Ur时,消费者购买OEM生产的新产品;当Ur>0且Ur>Un时,消费者购买第三方生产的再制造品。通过简单积分求得新产品和再制造产品的需求函数分别为
假设3 在逆向供应链回收市场,废旧品回收数量同时受自身回收价格和竞争企业回收价格的影响,但竞争企业回收价格对该企业回收数量的影响要小于自身回收价格的影响。因此假设OEM和第三方的废旧品回收数量分别为qm=α+βam–θat,qt=α+βat–θam,为计算方便,不失一般性假设β=1,即qm=α+am–θat,qt=α+at–θam,θ<1[15]。
假设4 回收市场的废旧品数量充足,第三方再制造需要的废旧品不仅来源于从消费者那里回收的废旧品,还来源于从OEM那里购买的废旧品。第三方再制造必须满足消费者的再制造品需求,即废旧品的回收量应不少于再制造品的生产量,dr≤qt+qm。
2 模型构建与求解在本模型中,OEM生产和销售新产品,并从消费者那里回收废旧品,然后将废旧品卖给第三方。第三方同时从消费者和OEM那里回收废旧品,进行再制造品的生产销售。OEM和第三方通过回收价格和生产量分别在逆向供应链回收市场和正向供应链销售市场进行竞争,两企业是古诺博弈关系。OEM和第三方同时决策各自废旧品的回收价格am/at和新产品/再制造品的生产数量dn/dr。OEM和第三方的规划模型分别为:
| $\quad\quad\underset{{{d}_{\rm n}},{{ a}_{\rm m}}}{\mathop{\text{max}}\;}{\varPi _{\rm m}} = {p_{\rm n}}{d_{\rm n}} - {c_{\rm n}}{d_{\rm n}} - {a_{\rm m}}{q_{\rm m}} + b{q_{\rm m}} + f{d_{\rm r}},$ | (1) |
| $\begin{split} &\underset{{{d}_{{\rm r}}},{{a}_{{\rm t}}}}{\mathop{\text{max}}\;}{\varPi _{\rm t}} = {p_{\rm r}}{d_{\rm r}} - {c_{\rm r}}{d_{\rm r}} - {a_{\rm t}}{q_{\rm t}} - b{q_{\rm m}} - f{d_{\rm r}} + s({q_{\rm m}} + {q_{\rm t}} - {d_{\rm r}}{{)}}{\text{。}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\ & {\rm{s}}{\rm{.t}}. \quad {d_{\rm r}} {\text{≤}} {q_{\rm m}} + {q_{\rm t}} {\text{。}} \end{split}$ | (2) |
其中,式(1)和式(2)目标函数的第1项和第2项分别表示两企业新产品或再制造品的销售收入和生产成本;第3项分别表示两企业废旧品的回收成本;第4项分别表示OEM废旧品的销售收入和第三方购买OEM废旧品的费用支出;第5项分别表示OEM的授权费收入和第三方的授权费支出;式(2)第6项表示第三方未用于再制造的废旧品的残值收入;式(2)约束条件表示第三方回收的废旧品总量不能低于再制造品的生产量。
命题1 当
| $s {\text{≥}} \dfrac{{(2 - \theta )(\rho (1 + {c_{\rm n}}) - 2(f + {c_{\rm r}})) - \rho (4 - \rho )(2\alpha + b - {\theta ^2}b)}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}}$ |
时,最优解是:
| $\quad\quad a_{\rm m}^{1*} = \frac{{2(b - \alpha ) + \theta (s - \alpha ) + {\theta ^2}(b - s)}}{{4 - {\theta ^2}}},$ |
| $\quad\quad a_{\rm t}^{1*} = \frac{{2(s - \alpha ) + \theta (3b - 2s - \alpha )}}{{4 - {\theta ^2}}},$ |
| $\quad\quad d_{\rm n}^{1*} = \frac{{{c_{\rm r}} - 2{c_{\rm n}} + f - \rho + s + 2}}{{4 - \rho }},$ |
| $\quad\quad d_{\rm r}^{1*} = \frac{{\rho (1 + {c_{\rm n}}) - 2({c_{\rm r}} + f + s)}}{{\rho (4 - \rho )}};$ |
否则,最优解是:
| $ \quad\quad\quad \quad a_{\rm m}^{2*} = \frac{{(4 + 4\rho - {\rho ^2})(b - \alpha ) + \theta (1 - \theta )(\rho (1 + {c_{\rm n}}) - 2({c_{\rm r}} + f)) - 2\theta (\alpha - \theta b) - 2b\rho \theta (4 - \rho ) + \rho {\theta ^2}(\alpha + b)(4 - \rho )}}{{\rho (4 - \rho )(2 - \theta (3 - {\theta ^2})) + 2(4 - {\theta ^2})}}, $ |
| $ a_{\rm t}^{2*} = \frac{{2\rho (1 - \theta )({c_{\rm n}} + 1) + {\rho ^2}(3\alpha + b) + 2\rho \theta (\alpha + b)(4 - \rho ) - 4(\alpha + {c_{\rm r}} + f) - 4\rho (3\alpha + b) - 2\theta (\alpha - 3b - 2{c_{\rm r}} - 2f) + \rho {\theta ^2}(b - \alpha )(4 - \rho )}}{{\rho (4 - \rho )(2 - \theta (3 - {\theta ^2})) + 2(4 - {\theta ^2})}}, $ |
| $\quad\quad\quad\quad\quad\quad\quad d_{\rm n}^{2*} = \frac{{(2 - \theta )(1 - {c_{\rm n}}) - \rho (2{c_{\rm n}} - {c_{\rm r}} - f - 2){{(1 - \theta )}^2} - \rho (2\alpha + b) - \rho {\theta ^2}(\rho - b) - {p^2}(1 - 2\theta )}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}},$ |
| $\quad\quad d_{\rm r}^{2*} = \dfrac{{{{(1 - \theta )}^2}(\rho (1 + {c_{\rm n}}) - 2({c_{\rm r}} + f)) + 2(2\alpha + b - b{\theta ^2})}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}}{\text{。}}$ |
证明 根据OEM与第三方是古诺博弈关系,同时求解am、dn、at、dr。首先对式(1)目标函数
| $\quad\quad{{ H}_1} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\partial ^2}{\varPi _{\rm m}}}}{{\partial a_{\rm m}^2}}}&{\dfrac{{{\partial ^2}{\varPi _{\rm m}}}}{{\partial {a_{\rm m}}\partial {d_{\rm n}}}}} \\ {\dfrac{{{\partial ^2}{\varPi _{\rm m}}}}{{\partial {d_{\rm n}}\partial {a_{\rm m}}}}}&{\dfrac{{{\partial ^2}{\varPi _{\rm m}}}}{{\partial d_{\rm n}^2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 2}&0 \\ 0&{ - 2} \end{array}} \right]{\text{。}}$ |
显然
| $\quad\quad b - \alpha - 2{a_{\rm m}} + \theta {a_{\rm t}} = 0,$ | (3) |
| $\quad\quad 1 - 2{d_{\rm n}} - \rho {d_{\rm r}} - {c_{\rm r}} = 0{\text{。}}$ | (4) |
同时对式(2)目标函数
| $\quad\quad\begin{split} &\dfrac{{\partial {\varPi _{\rm t}}}}{{\partial {a_{\rm t}}}} = - \alpha - 2{a_{\rm t}} + \theta {a_{\rm m}} + b\theta + (1 - \theta )s,\\ &\dfrac{{\partial {\varPi _{\rm t}}}}{{\partial {d_{\rm r}}}} = \rho - 2\rho {d_{\rm r}} - \rho {d_{\rm n}} - {c_{\rm r}} - s - f{\text{。}} \end{split}$ |
进一步求得其Hessian矩阵为
| $\quad\quad{H_2} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\partial ^2}{\varPi _{\rm t}}}}{{\partial a_{\rm t}^2}}}&{\dfrac{{{\partial ^2}{\varPi _{\rm t}}}}{{\partial {a_{\rm t}}\partial {d_{\rm r}}}}} \\ {\dfrac{{{\partial ^2}{\varPi _{\rm t}}}}{{\partial {d_{\rm r}}\partial {a_{\rm t}}}}}&{\dfrac{{{\partial ^2}{\varPi _{\rm t}}}}{{\partial d_{\rm r}^2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 2}&0 \\ 0&{ - 2\rho } \end{array}} \right]{\text{。}}$ |
显然
相应地,规划模型(2)的Lagrange函数为
| $\begin{split} &\quad\quad L{{(}}{a_{\rm t}},{d_{\rm r}},\lambda {{)}} = {p_{\rm r}}{d_{\rm r}} - {c_{\rm r}}{d_{\rm r}} - {a_{\rm t}}{q_{\rm t}} - b{q_{\rm m}} - f{d_{\rm r}} +\\ &s({q_{\rm m}} + {q_{\rm t}} - {d_{\rm r}}{{)}} + \lambda ({q_{\rm m}} + {q_{\rm t}} - {d_{\rm r}}){\text{。}}\end{split}$ |
进而得到式(2)的K-T条件为
| $\quad\quad \left\{\!\!\!\!\begin{array}{l} \dfrac{\partial L({{a}_{\text{t}}},{{d}_{\text{r}}},\lambda )}{\partial {{a}_{\text{t}}}}=-\alpha -2{{a}_{\text{t}}}+\theta {{a}_{\text{m}}}+b\theta +\\ s(1-\theta )+\lambda (1-\theta )=0, \\ \dfrac{\partial L({{a}_{\text{t}}},{{d}_{\text{r}}},\lambda )}{\partial {{d}_{\text{r}}}}=\rho -2\rho {{d}_{\text{r}}}-\rho {{d}_{\text{n}}}-{{c}_{\text{r}}}-s-f-\lambda =0,\!\!\!\!\!\!\!\!\!\\ \lambda (2\alpha +{{a}_{\text{t}}}-\theta {{a}_{\text{m}}}+{{a}_{\text{m}}}-\theta {{a}_{\text{t}}}-{{d}_{\text{r}}})=0{\text{。}} \end{array}\right. $ | (5) |
情形1 当
情形2 当
| $\quad\quad\quad\quad \lambda = \dfrac{{\rho (1 + {c_{\rm n}})(2 - \theta ) - 2(f + {c_{\rm r}} + s)(2 - \theta ) - \rho (2\alpha + b)(4 - \rho ) + \rho {\theta ^2}(b - s)(4 - \rho ) + ps(8\theta - 4 + \rho (1 - 2\theta ))}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{。}} $ |
令
根据命题1的证明过程易知:当
推论1 当
| $ s {\text{≥}} \dfrac{{(2 - \theta )(\rho (1 + {c_{\rm n}}) - 2(f + {c_{\rm r}})) - \rho (4 - \rho )(2\alpha + b - {\theta ^2}b)}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} $ |
时,最优解是:
| $\quad\quad p_{\rm n}^{1*} = \frac{{{c_{\rm r}} + (2 - \rho ){c_{\rm n}} + f + s - 2}}{{4 - \rho }} + 1,$ |
| $\quad\quad p_{\rm r}^{1*} = \frac{{(2 - \rho )({c_{\rm r}} + f + s) + \rho ({c_{\rm n}} + 1)}}{{4 - \rho }};$ |
否则,最优解是:
| $\quad\quad\quad\quad p_{\rm n}^{2*} = 1 - \dfrac{{(2 - \theta + 2\rho {{(1 - \theta )}^2})(1 - {c_{\rm n}}) - \rho ({c_{\rm r}} + f){{(1 - \theta )}^2} + \rho (2\alpha + b) - {\rho ^2}{{(1 - \theta )}^2} - \rho {\theta ^2}b + {{(1 - \theta )}^2}{\rho ^2}(1 + {c_{\rm n}})}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}},$ |
| $p_{\rm r}^{2*} = \rho \left(1 \!-\! \frac{{(2 \!-\! \theta \!+\! 2\rho {{(1 \!-\! \theta )}^2})(1 - {c_{\rm n}}) - (2 - \rho )({c_{\rm r}} + f){{(1 - \theta )}^2} + (2 - \rho )(2\alpha + b) - {\rho ^2}{{(1 - \theta )}^2} + (1 - 2\rho ){\theta ^2}b + {{(1 - \theta )}^2}{\rho ^2}(1 + {c_{\rm n}})}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}}\right){\text{。}}$ |
推论2 在TP和TF两种情形下,新产品的生产量dn都随着单位授权费f的增加而增加,再制造品的生产量dr都随着单位授权费f的增加而减少。
证明
| $\quad\quad \begin{split}& \dfrac{{\partial d_{\rm n}^{1*}}}{{\partial f}} = \dfrac{1}{{4 - \rho }} {\text{>}} 0,\\ &\dfrac{{\partial d_{\rm r}^{1*}}}{{\partial f}} = - \dfrac{2}{{\rho (4 - \rho )}} {\text{<}} 0,\\ &\dfrac{{\partial d_{\rm n}^{2*}}}{{\partial f}} = \dfrac{{\rho {{(1 - \theta )}^2}}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{>}} 0,\\ &\dfrac{{\partial d_{\rm r}^{2*}}}{{\partial f}} = - \dfrac{{2{{(1 - \theta )}^2}}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{<}} 0{\text{。}} \end{split} $ |
推论2得证。
推论2表明,随着单位授权费的增加,对于第三方,再制造显得越来越无利可图。当单位授权费高到一定程度,第三方将会解除与OEM的授权契约关系并退出回收再制造市场。因此,第三方将随着单位授权费的增加而减少再制造品的生产量。对于OEM,当第三方的再制造品的生产量减少时,顾客便会去购买新产品,因此,OEM生产的新产品数量将增加。
推论3 在TP情形下,新产品的生产量dn和再制造品的生产量dr都与第三方从OEM那里购买废旧品的价格b无关;在TF情形下,dn随着b的增加而减少,dr随着b的增加而增加。
证明
| $\begin{split}\quad\quad &\dfrac{{\partial d_{\rm n}^{2*}}}{{\partial b}} = - \dfrac{{\rho (1 - {\theta ^2})}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{<}} 0,\\ &\dfrac{{\partial d_{\rm r}^{2*}}}{{\partial b}} = \dfrac{{2(1 - {\theta ^2})}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{>}} 0{\text{。}} \end{split}$ |
推论3得证。
推论3表明,随着第三方从OEM那里购买废旧品价格的增加,在TP情形下,第三方是部分再制造,第三方只能将多余的废旧品按残值处理,不影响第三方的再制造品生产,从而也不影响OEM的新产品生产。在TF情形下,随着第三方从OEM那里购买废旧品的价格的增加,OEM将废旧品销售给第三方变得越来越有利可图,会回收更多的废旧产品销售给第三方,此时第三方是完全再制造,再制造品生产数量将不断增加。再制造品需求增加侵占了新产品需求,新产品生产数量将不断减少。
推论4 在TP和TF两种情形下,OEM和第三方从消费者那里回收废旧品的单位价格ai(i为t和m)都随着消费者中环保主义者主动无偿返还废旧品数量α的增加而减少。
证明
| $ \begin{split}\quad\quad &\dfrac{{\partial a_{\rm m}^{1*}}}{{\partial \alpha }} = - \dfrac{1}{{2 - \theta }} {\text{<}} 0, \dfrac{{\partial a_{\rm t}^{1*}}}{{\partial \alpha }} = - \dfrac{1}{{2 - \theta }} {\text{<}} 0,\\ &\frac{{\partial a_{\rm m}^{2*}}}{{\partial \alpha }} = - \frac{{\rho (4 - \rho )(1 - {\theta ^2}) + 2(2 + \theta )}}{{\rho (4 - \rho )(2 - \theta (3 - {\theta ^2})) + 2(4 - {\theta ^2})}} {\text{<}} 0,\\ & \dfrac{{\partial a_{\rm t}^{2*}}}{{\partial \alpha }} = \dfrac{{\rho (4 - \rho )(\theta (2 + \theta ) - 3) - 2(2 + \theta )}}{{\rho (4 - \rho )(2 - \theta (3 - {\theta ^2})) + 2(4 - {\theta ^2})}} {\text{<}} 0{\text{。}} \end{split}$ |
推论4得证。
推论4表明,随着消费者中环保主义者主动无偿返还废旧品数量的增加,OEM和第三方都没有必要通过提高废旧品回收价格来获取更多的废旧品。因此,当消费者中环保主义者主动无偿返还废旧品的数量增加时,OEM和第三方都会降低废旧品回收价格。
推论5 在TP情形下,OEM和第三方从消费者那里回收废旧品的单位价格ai都随着废旧品残值s的增加而增加;在TF情形下,ai都与s的变化无关。
证明
推论5表明,在TP情形下,第三方是部分再制造,随着废旧品残值的增加,第三方可以通过增加回收价格以获得更多的废旧品,在满足再制造品需求之后可获得更多的残值收益。由于OEM与第三方在逆向供应链的回收市场是竞争关系,当第三方废旧品回收价格增加时,OEM也会增加废旧品回收价格。在TF情形下,第三方将回收的废旧品完全再制造,无法通过废旧品残值获得收益,因此第三方废旧品回收价格不受废旧品残值的影响,对于和第三方回收竞争的OEM来说,其废旧品回收价格也不受废旧品残值的影响。
推论6 在TP和TF两种情形下,OEM新产品的价格pn都随着新产品的单位生产成本cn的增加而增加,生产量dn都随着cn的增加而减少;第三方再制造品的生产量dr都随着cn的增加而增加。
证明
| $ \begin{split}\quad\quad &\dfrac{{\partial d_{\rm n}^{1*}}}{{\partial {c_{\rm n}}}} = - \dfrac{2}{{4 - \rho }} {\text{<}} 0, \;\dfrac{{\partial d_{\rm r}^{1*}}}{{\partial {c_{\rm n}}}} = \dfrac{\rho }{{\rho (4 - \rho )}} {\text{>}} 0,\\ &\dfrac{{\partial d_{\rm n}^{2*}}}{{\partial {c_{\rm n}}}} = - \dfrac{{2\rho {{(1 - \theta )}^2} + 2 - \theta }}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{<}} 0, \\ &\dfrac{{\partial d_{\rm r}^{2*}}}{{\partial {c_{\rm n}}}} = \dfrac{{\rho {{(1 - \theta )}^2}}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{>}} 0,\\ &\dfrac{{\partial p_{\rm n}^{1*}}}{{\partial {c_{\rm n}}}} = \dfrac{{2 - \rho }}{{4 - \rho }} {\text{>}} 0,\\ &\dfrac{{\partial p_{\rm n}^{2*}}}{{\partial {c_{\rm n}}}} = \dfrac{{\rho (2 - \rho ){{(1 - \theta )}^2} + 2 - \theta }}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{>}} 0{\text{。}} \end{split}$ |
推论6得证。
推论6表明,随着新产品单位生产成本的增加,OEM将通过提高新产品单位价格进行获利,此时顾客会降低对新产品的需求,因此OEM将会减少新产品的生产量。而第三方与OEM在正向供应链的销售市场中是竞争关系,消费者会转向购买第三方的再制造品,从而会导致消费者对第三方再制造品需求量增加,因此第三方将增加再制造品的生产量。
推论7 在TP和TF两种情形下,第三方再制造品的单位价格pr都随着再制造品的单位生产成本cr的增加而增加,生产量dr都随着cr的增加而减少;OEM新产品的生产量dn都随着cr的增加而增加。
证明
| $ \begin{split}\quad\quad &\dfrac{{\partial d_{\rm n}^{1*}}}{{\partial {c_{\rm r}}}} = \dfrac{1}{{4 - \rho }} {\text{>}} 0, \dfrac{{\partial d_{\rm r}^{1*}}}{{\partial {c_{\rm r}}}} = - \dfrac{2}{{\rho (4 - \rho )}} {\text{<}} 0,\\ &\dfrac{{\partial d_{\rm n}^{2*}}}{{\partial {c_{\rm r}}}} = \dfrac{{\rho {{(1 - \theta )}^2}}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{>}} 0,\\ &\dfrac{{\partial d_{\rm r}^{2*}}}{{\partial {c_{\rm r}}}} = - \dfrac{{2{{(1 - \theta )}^2}}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{<}} 0,\\ &\dfrac{{\partial p_{\rm r}^{1*}}}{{\partial {c_{\rm r}}}} = \dfrac{{2 - \rho }}{{4 - \rho }} {\text{>}} 0,\\ &\dfrac{{\partial p_{\rm r}^{2*}}}{{\partial {c_{\rm r}}}} = \dfrac{{\rho (2 - \rho ){{(1 - \theta )}^2}}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}} {\text{>}} 0{\text{。}} \end{split}$ |
推论7得证。
推论7的结果与推论6类似,此处不再赘述。
4 数值算例本节将通过算例分析研究单位授权费f、第三方从OEM那里购买废旧品的单位价格b、环保主义者主动无偿返还废旧品的数量α、废旧品残值s、新产品的单位生产成本cn以及第三方再制造品的单位生产成本cr对OEM和第三方最优利润的影响。在本节中,由命题1,令
| $ \quad\quad\quad\quad\quad\quad\quad\quad\quad{s^ \wedge} = \dfrac{{\rho (1 + {c_{\rm n}})(2 - \theta ) - 2(f + {c_{\rm r}})(2 - \theta ) - \rho (2\alpha + b)(4 - \rho ) + \rho {\theta ^2}b(4 - \rho )}}{{\rho (4 - \rho ){{(1 - \theta )}^2} + 2(2 - \theta )}}{\text{。}} $ |
1) 单位授权费f对OEM和第三方最优利润的影响。
部分参数设置如下:ρ=0.9,θ=0.1,b=0.1,α=0.1,s=0.05,cn=0.4,cr=0.2。将参数代入
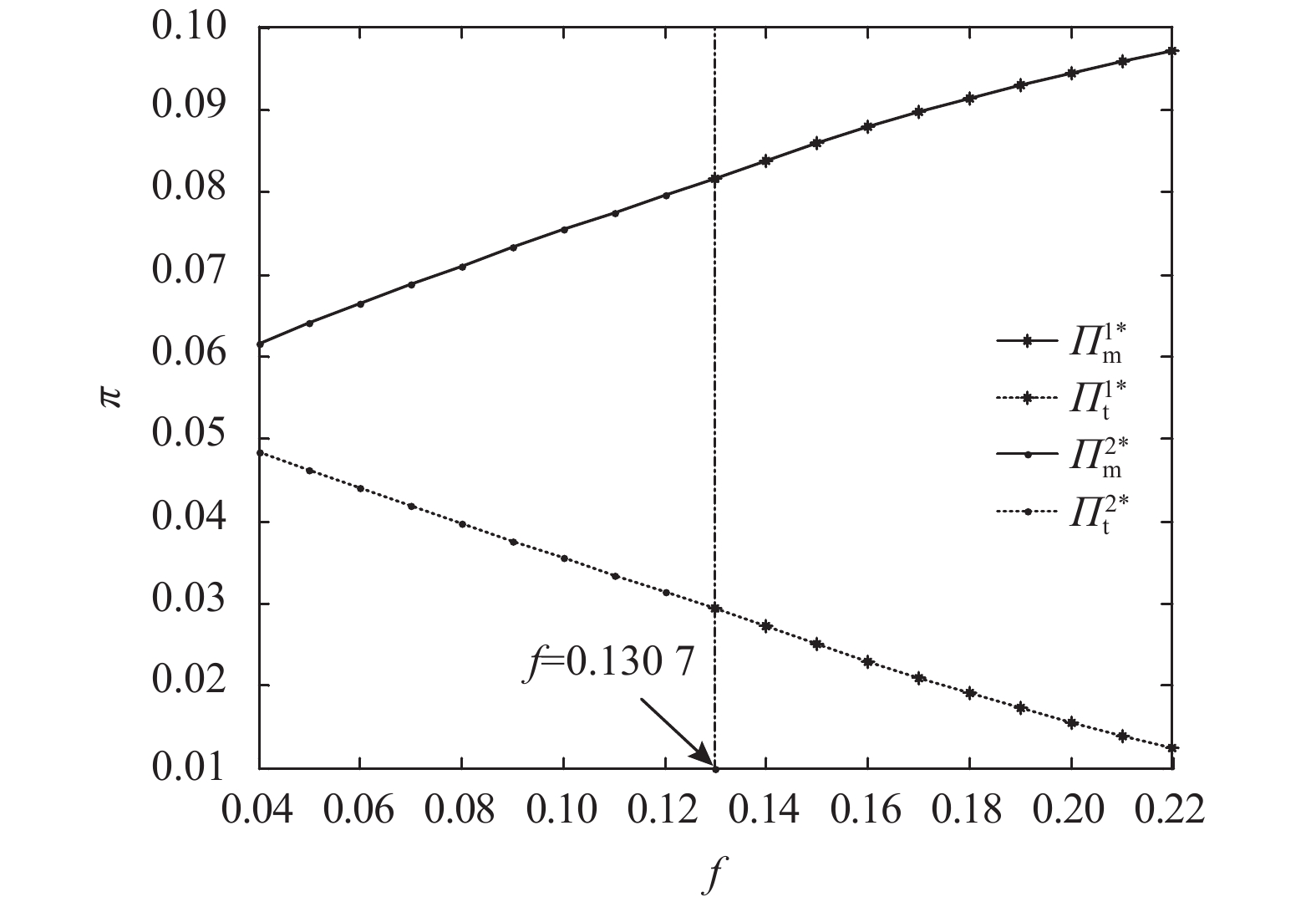
由图2知,在TP、TF两种情形下,OEM最优利润都随着单位授权费的增加而增加;第三方最优利润则随着单位授权费的增加而减少。这是因为随着单位授权费的增加,根据推论2,第三方进行再制造变得越来越无利可图,逐渐减少再制造品生产量,其利润越来越少;而OEM显然能够通过单位授权费增加获得更多的利润。
|
图 2 单位授权费对OEM和第三方最优利润的影响 Fig. 2 The impact of unit licensing fee on the optimal profit of OEMs and third parties |
2) 第三方从OEM那里购买废旧品的单位价格b对OEM和第三方最优利润的影响。
部分参数设置如下:ρ=0.9,θ=0.1,f=0.05,α=0.1,s=0.05,cn=0.4,cr=0.2。将参数代入
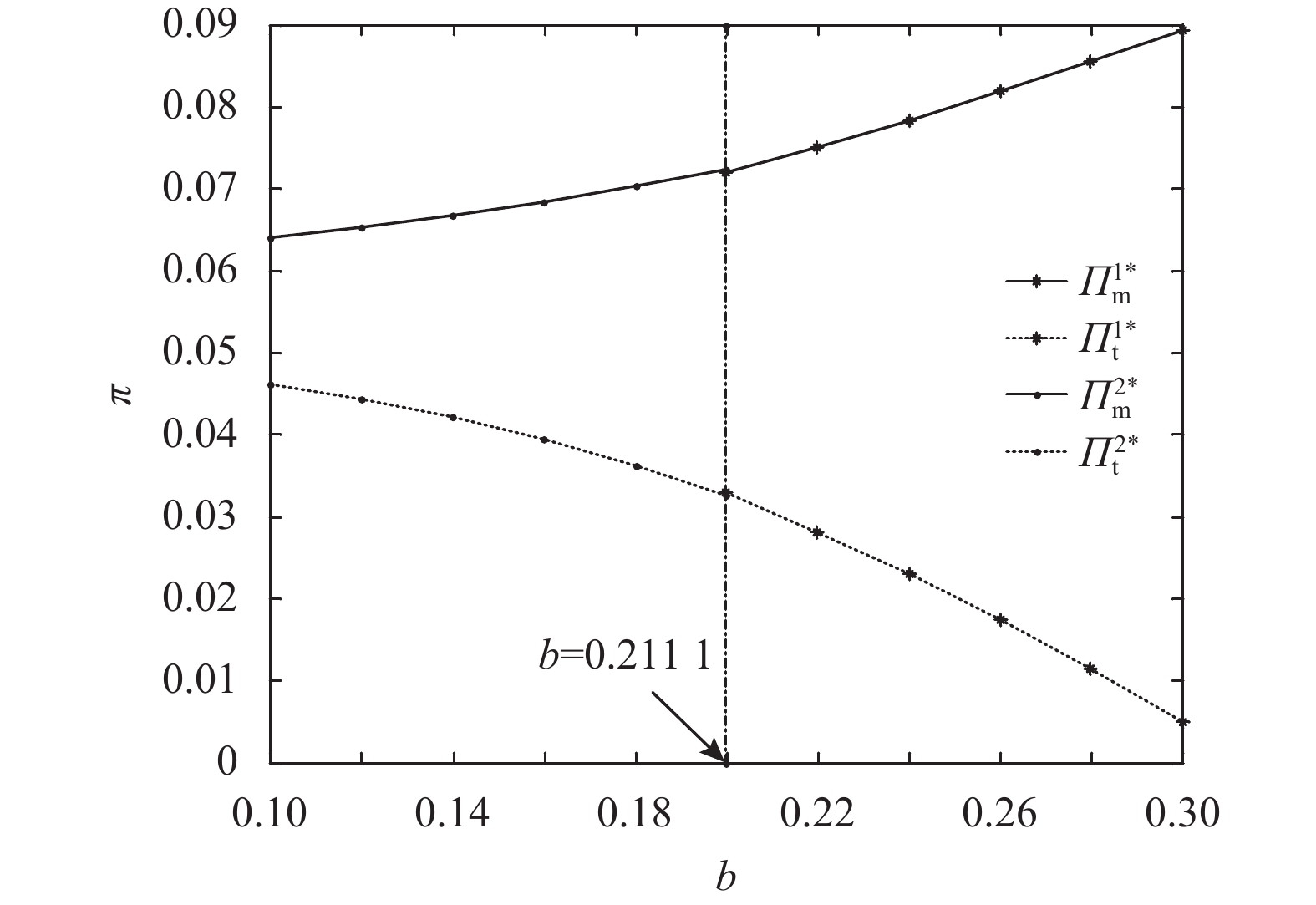
由图3知,在TP、TF两种情形下,OEM最优利润随着第三方从OEM那里购买废旧品的单位价格的增加而增加,而第三方最优利润随着第三方从OEM那里购买废旧品的单位价格的增加而减少。这是因为随着第三方从OEM那里购买废旧品的单位价格的上升,根据推论3,OEM可以通过将废旧品卖给第三方获利,从而最优利润上升。对于第三方,从OEM那里购买废旧品的单位价格的增加会增加再制造成本,最优利润显然会减少。
|
图 3 第三方从OEM那里购买废旧品的单位价格对OEM和第三方最优利润的影响 Fig. 3 The effect of the unit price of third-party purchases of used products from OEMs on the optimal profitability of OEMs and third parties |
3) 环保主义者主动无偿返还废旧品的数量α对OEM和第三方最优利润的影响。
部分参数设置如下:ρ=0.9,θ=0.1,f=0.05,b=0.1,s=0.05,cn=0.4,cr=0.2。将参数代入
由图4知,在TP、TF两种情形下,OEM和第三方最优利润均随着消费者中环保主义者主动无偿返还废旧品数量的增加而增加。这是因为随着消费者中环保主义者主动无偿返还废旧品数量的增加,根据推论4,OEM和第三方废旧品回收价格均会降低,在逆向供应链的回收市场节约了回收成本,从而双方的最优利润均会增加。

|
图 4 环保主义者主动无偿返还废旧品的数量对OEM和第三方最优利润的影响 Fig. 4 The effect of the amount of waste products returned by environmentalists on their initiative to return to the best profits of OEMs and third parties |
4) 废旧品残值s对OEM和第三方最优利润的影响。
部分参数设置如下:ρ=0.9,θ=0.1,f=0.05,b=0.1,α=0.1,cn=0.4,cr=0.2。将参数代入
由图5知,在TP情形下,OEM最优利润均随着废旧品残值的增加而增加,第三方最优利润随残值的增加而减少;在TF情形下,OEM和第三方最优利润都不受废旧品残值影响。这是因为随着废旧品残值的增加,根据推论5,双方均会通过增加回收价格从回收市场那里获得更多的废旧品。对于OEM,尽管提高废旧品回收价格会提高回收成本,但是销售回收的废旧品带来的收益增加会抵消回收成本的增加,从而最优利润上升。对于第三方,废旧品回收价格的增加会增加回收成本,OEM废旧品回收价格的增加也会增加第三方回购废旧品成本。尽管废旧品残值增加可以使第三方在满足正向供应链的再制造品需求后获得更多的残值收益,但残值收益的增加无法抵消回收成本的增加,从而减少最优利润;在TF情形下,第三方是完全再制造,无法通过废旧品残值获得收益,双方的逆向供应链废旧品回收市场的回收价格和正向供应链新产品、再制造品销售市场的零售价格都与废旧品残值无关,因此双方最优利润不受废旧品残值影响。

|
图 5 废旧品残值对OEM和第三方最优利润的影响 Fig. 5 Effect of residual value of waste products on the optimal profits of OEMs and third parties |
5) 新产品单位生产成本cn对OEM和第三方最优利润的影响。
部分参数设置如下:ρ=0.9,θ=0.1,f=0.05,b=0.1,α=0.1,s=0.05,cr=0.2。将参数代入
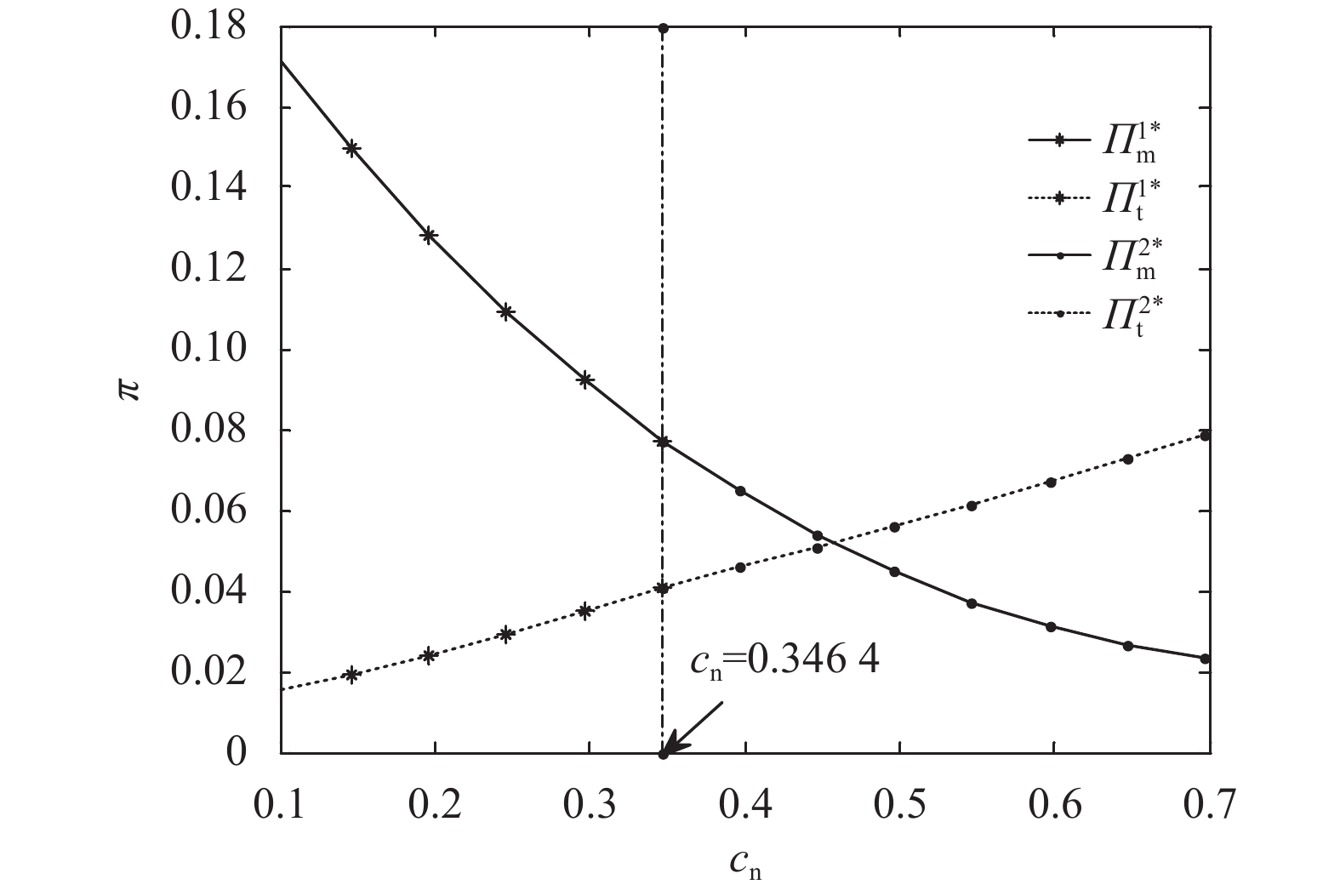
由图6知,在TP、TF两种情形下,OEM最优利润随着新产品单位生产成本的增加而减少,而第三方最优利润都随着新产品单位生产成本的增加而增加。这是因为随着新产品单位生产成本的增加,根据推论6,OEM将减少新产品的生产量,其生产成本增加和产量下降导致自身利润下降是显然的;而对于第三方,会增加再制造品的生产量,从而使最优利润增加。
|
图 6 新产品单位生产成本对OEM和第三方最优利润的影响 Fig. 6 Effect of new product unit production cost on optimal profits of OEMs and third parties |
6) 第三方再制造品单位生产成本cr对OEM和第三方最优利润的影响。
部分参数设置如下:ρ=0.9,θ=0.1,f=0.05,b=0.1,α=0.1,s=0.05,cn=0.4。将参数代入
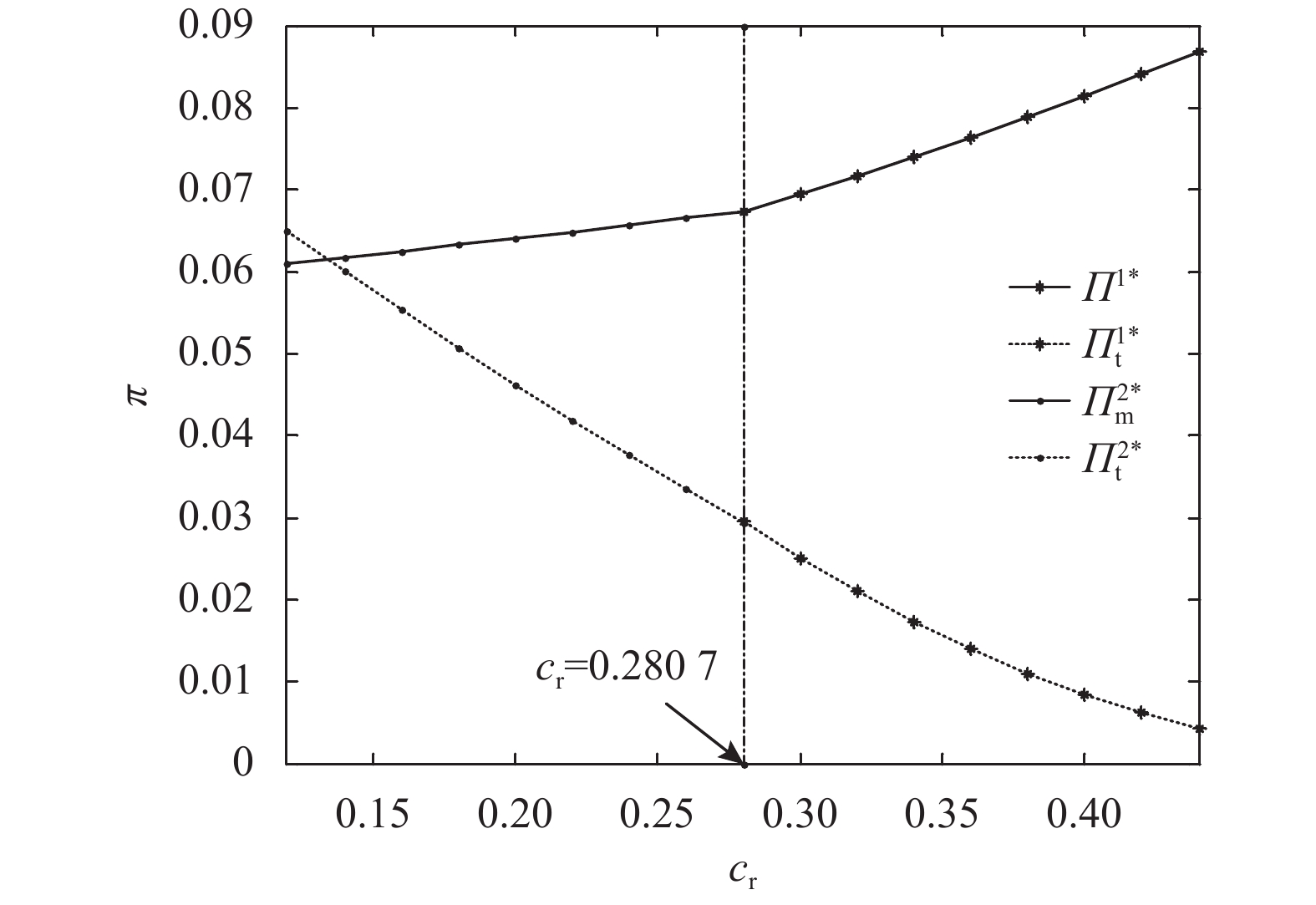
由图7知,在TP、TF两种情形下,第三方最优利润随着第三方再制造品单位生产成本的增加而减少,而OEM最优利润随着第三方再制造品单位生产成本的增加而增加,此结果与图6类似,结果原因此处不再赘述。
|
图 7 第三方再制造品单位生产成本对OEM和第三方最优利润的影响 Fig. 7 Effect of production costs of third party remanufactured units on optimal profits of OEMs and third parties |
本文在OEM授权第三方再制造的背景下,考虑顾客对新产品和再制造产品存在异质需求,OEM和第三方在逆向供应链的回收市场均存在竞争,建立了以双方利润最大化为目标带约束条件的古诺博弈模型,得到两组最优解。结合灵敏度分析和算例分析,本文的研究结果如下。1) 按照废旧品残值所在的区间,得出第三方部分再制造(TP)和第三方完全再制造(TF)两种情形下的新产品与再制造品的生产量、单位零售价格以及OEM和第三方的废旧品回收价格。2) 随着单位授权费的增加,新产品的生产数量不断增加,OEM的最优利润不断增加,再制造品的生产数量不断减少,第三方的最优利润不断减少。3) 随着第三方从OEM那里购买废旧品的单位价格的增加,TP情形下,新产品和再制造品的生产量都不发生变化,TF情形下,新产品的生产量不断增加,再制造品的生产量不断减少,两种情形下,OEM最优利润都不断增加,第三方最优利润都不断减少。4) 随着环保主义者主动无偿返还废旧品数量的增加,OEM和第三方的废旧品回收价格都不断减少,最优利润都不断增加。5) 随着废旧品残值的增加,TP情形下,OEM和第三方废旧品回收价格都不断增加,OEM的最优利润不断增加,第三方的最优利润不断减少;TF情形下,OEM和第三方废旧品回收价格以及双方的最优利润都不发生变化。6) 随着新产品单位生产成本的增加,新产品的单位零售价格不断增加,生产数量不断减少,OEM最优利润不断减少,再制造品的生产数量不断增加,第三方最优利润不断减少。7) 随着再制造品单位生产成本的增加,新产品的生产数量不断增加,OEM最优利润不断增加,再制造品的单位零售价格不断增加,生产数量不断减少,第三方最优利润不断减少。本文的研究结果为授权模式下OEM和第三方产品生产和回收定价决策提供了科学依据。
本文构建的模型是基于一定的假设条件,有一定的局限性。还可以从以下几个方面进行扩展:1) 在逆向供应链回收市场,考虑OEM和第三方两企业以旧换新等其他竞争手段激励消费者回收。2) 在正向供应链回收市场,考虑OEM和第三方两企业服务质量等其他竞争手段吸引消费者购买。3) 考虑其他供应链结构,比如引入零售商等。
| [1] |
PENG W J, SU D Z. Development of an online system for recycling consumer electronic products using the internet, NFC and RFID technologies[J].
Key Engineering Materials, 2014, 572(1): 90-99.
|
| [2] |
ZOU Z B, WANG J J, DENG G S, et al. Third-party remanufacturing mode selection: outsourcing or authorization?[J].
Transportation Research Part E Logistics & Transportation Review, 2016, 87: 1-19.
|
| [3] |
伍颖, 熊中楷. 竞争条件下制造商和再制造商的生产决策[J].
系统工程理论与实践, 2014, 34(2): 291-303.
WU Ying, XIONG Zhongkai. Production strategies of the original equipment manufacturer and independent operator under the condition of competition[J]. Systems Engineering-Theory & Practice, 2014, 34(2): 291-303. |
| [4] |
MITRA S. Models to explore remanufacturing as a competitive strategy under duopoly[J].
Omega, 2016, 59: 215-227.
DOI: 10.1016/j.omega.2015.06.009. |
| [5] |
ZHANG C T, REN M L. Closed-loop supply chain coordination strategy for the remanufacture of patented products under competitive demand[J].
Applied Mathematical Modelling, 2016, 40(13-14): 6243-6255.
DOI: 10.1016/j.apm.2016.02.006. |
| [6] |
YI P, HUANG M, GUO L, et al. Dual recycling channel decision in retailer oriented closed-loop supply chain for construction machinery remanufacturing[J].
Journal of Cleaner Production, 2016, 137(20): 1393-1405.
|
| [7] |
JENA S K, SARMAH S P. Price and service co-opetiton under uncertain demand and condition of used items in a remanufacturing system[J].
International Journal of Production Economics, 2016, 173: 1-21.
DOI: 10.1016/j.ijpe.2015.11.019. |
| [8] |
LIU L, WANG Z, HONG X, et al. Collection effort and reverse channel choices in a closed-loop supply chain[J].
Journal of Cleaner Production, 2017, 144(15): 492-500.
|
| [9] |
李凌雁, 高阳. 基于回收竞争的闭环供应链再制造授权策略研究[J].
科技管理研究, 2017, 37(8): 223-229.
LI Lingyan, GAO Yang. Study on strategy of re-manufacturing authorization for closed-loop supply chain based on recycling competition[J]. Science and Technology Management Research, 2017, 37(8): 223-229. DOI: 10.3969/j.issn.1000-7695.2017.08.032. |
| [10] |
闻卉, 曹晓刚, 黎继子, 等. 专利保护下考虑再制造竞争的闭环供应链定价决策[J].
数学的实践与认识, 2016, 46(21): 64-71.
WEN Hui, CAO Xiaogang, LI Jizi, et al. Pricing decision of the closed-loop supply chain with remanufacturing competition under patent protection[J]. Mathematics in Practice and Theory, 2016, 46(21): 64-71. |
| [11] |
BULMUS S C, ZHU S X, TEUNTRER R. Competition for cores in remanufacturing[J].
European Journal of Operational Research, 2014, 233(1): 105-113.
DOI: 10.1016/j.ejor.2013.08.025. |
| [12] |
WU C H. Strategic and operational decisions under sales competition and collection competition for end-of-use products in remanufacturing[J].
International Journal of Production Economics, 2015, 169(1): 11-20.
|
| [13] |
WU C H, WU H H. Competitive remanufacturing strategy and take-back decision with OEM remanufacturing[J].
Computers & Industrial Engineering, 2016, 98: 149-163.
|
| [14] |
田晖, 孟立军. 基于差异化定价和回收竞争的再制造专利许可决策研究[J].
工业技术经济, 2017, 36(10): 70-78.
TIAN Hui, MENG Lijun. Remanufacturing licensing decision research based on differential pricing strategies and recycling competition[J]. Journal of Industrial Technological Economics, 2017, 36(10): 70-78. DOI: 10.3969/j.issn.1004-910X.2017.10.009. |
| [15] |
MITAR S, WEBSTER S. Competition in remanufaeturing and the effects of government subsidies[J].
International Journal of Production Economies, 2008, 111(2): 287-298.
DOI: 10.1016/j.ijpe.2007.02.042. |
 2019, Vol. 22
2019, Vol. 22