近年来我国电子商务的快速发展极大地促进了物流业的发展，车辆路径的选择作为物流配送服务中的关键环节，对于降低物流企业运作成本，提高配送效率和服务水平有很大影响，因此越来越成为企业关注的重点。在当前激烈的市场竞争中，物流企业对于客户满意度日趋重视，客户关系的维护和新客户的开拓都依赖于客户满意度的提升。在物流企业硬件设施逐步完善的情况下，客户满意度主要受配送服务水平的影响，因此有必要在车辆路径问题(vehicle routing problem，VRP)的研究中考虑客户满意度。

目前，车辆路径问题已得到了国内外学者的广泛关注并取得了丰富的成果。在构建数学模型方面，Sariklis等^[1]对只有车辆装载能力限制的开放式车辆路径问题进行了研究；Calvete等^[2]基于软时间窗建立了多目标车辆路径优化模型；Ubeda等^[3]建立了以燃料和距离为基础的车辆路径模型，并以减少CO₂为评价标准；Kovacs等^[4]研究了考虑车辆容量限制的多目标车辆路径优化问题；李淑琴等^[5]以减少环境污染优化配送路径为目标，考虑时间窗约束，建立多目标环保多车型模型；符卓等^[6]针对带软时间窗的需求依订单拆分车辆路径问题建立相应的数学模型；倪霖等^[7]建立了考虑同时取送货的城市共同配送路径优化模型。在设计求解算法方面，Bianchessi等^[8]分别采用局域搜索算法、构造算法和禁忌搜索算法求解同时取送货车辆路径问题并给出相应算例；Repoussis等^[9]提出了一种多种群的混合进化策略来求解开放式车辆路径问题；Subramania等^[10]研究了元启发式算法求解集送一体化的车辆路径模型；De Oliveira等^[11]采用模拟退火算法和爬山算法来求解带时间窗车辆路径问题；邓爱民等^[12]采用改进的模拟退火算法求解集配货一体化车辆路径问题；王征等^[13]提出改进的变邻域搜索方法求解多车场带时间窗的车辆路径问题；葛显龙等^[14]设计基于自然数序列的改进遗传算法求解带软时间窗约束的车辆路径模型。在现代信息技术应用方面，谷炜等^[15]基于GIS研究末端物流的路径优化。

综合以上分析，已有研究文献主要集中在以降低运输成本为主要目标的基本模型的优化求解上，而针对客户满意度的研究不多。随着客户对配送要求的逐步提高，客户满意度日益成为企业提高核心竞争力的一个重要目标，因此研究考虑客户满意度的车辆路径优化问题是十分必要的。本文从配送准时性、货物完好性两方面衡量客户满意度并建立客户满意度函数，在此基础上建立客户满意度最大和运输成本最小的多目标优化模型，通过算例验证模型的适用性和有效性。

1 客户满意度函数 1.1 问题描述

本文研究的考虑客户满意度的VRP可以描述为：配送中心拥有 $ K $ 辆货车，对 $ N $ 个客户点进行货物配送，货车从配送中心出发，到各客户点去送货，客户点 $ i $ 的位置和配送量 ${D_i}\left( {i = 1, \cdots ,N} \right)$ 确定，每辆货车可服务多个客户，但每个客户最多只能被服务1次，货车配送完毕后返回配送中心，寻找合理的车辆调度方案使目标函数最优。

1.2 时间满意度函数

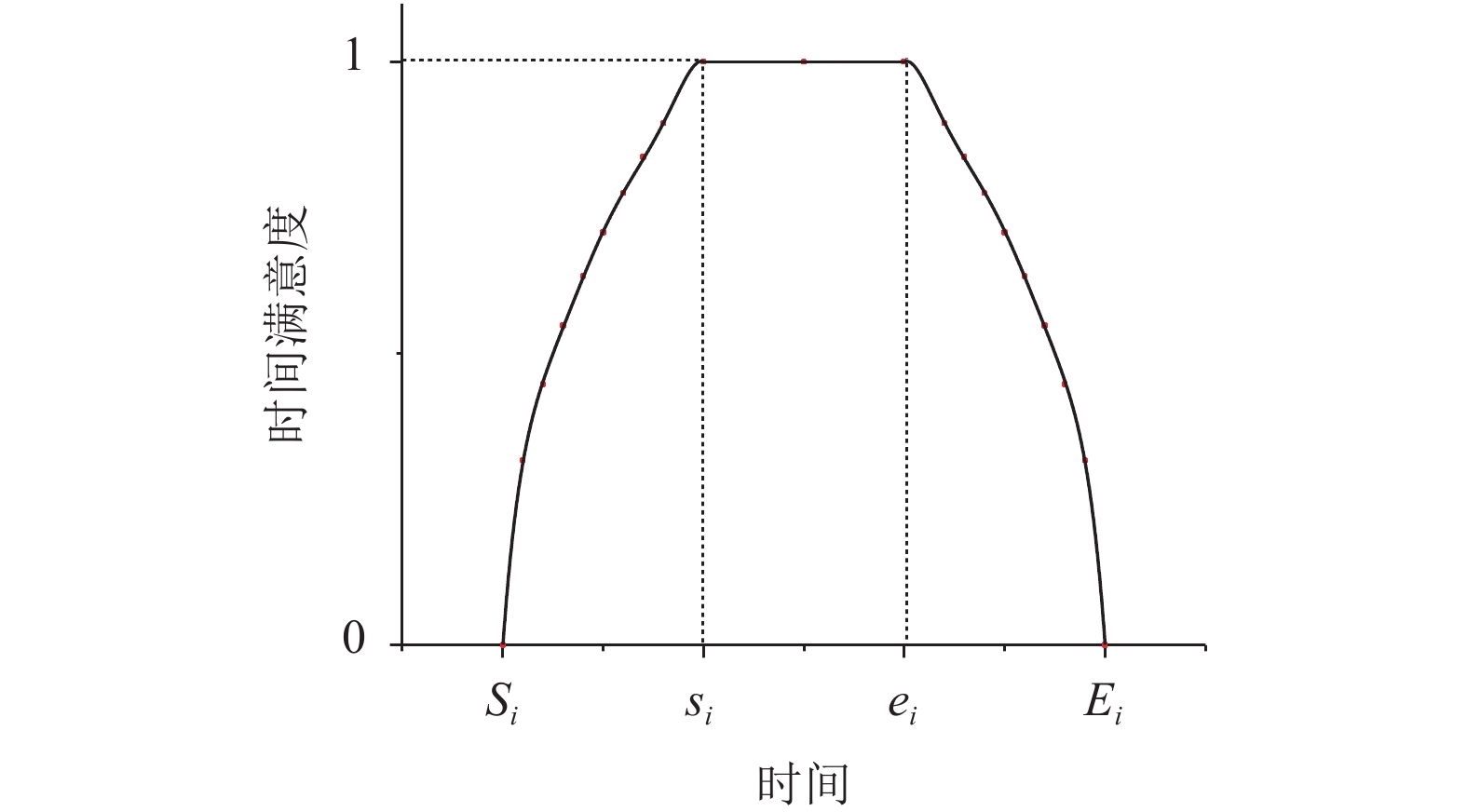
传统的车辆调度问题中的硬时间窗和软时间窗均无法准确反映客户满意度随时间的变化情况，客户可能偏好于在时间窗内的某个特定时间段得到服务，早于或晚于该时间段都会造成客户满意度下降。因此本文对时间窗进行模糊化处理，假设模糊时间窗由一个模糊数表征，用模糊数的隶属度函数表示客户满意度。模糊时间窗包括客户期望得到服务的时间范围和可容忍的服务时间范围。以 $\left[ {{s_i},{e_i}} \right]$ 表示客户 $ i $ 期望得到服务的时间范围，在这个范围内得到服务，客户满意度为100%；以 $\left[ {{S_i},{E_i}} \right]$ 表示客户可容忍的服务时间范围 $\left( {{S_i} < {s_i} {\text{＜}} {e_i} {\text{＜}} {E_i}} \right)$ ，在 $\left[ {{S_i},{s_i}} \right]$ 或 $\left[ {{e_i},{E_i}} \right]$ 内得到服务，客户仍可接受服务，但满意度随服务时间与期望时间的差距增大而降低。在可容忍时间 $\left[ {{S_i},{E_i}} \right]$ 之外，客户不接受服务，客户满意度为0。时间满意度函数如图1所示。

时间满意度函数表示如下：

$\quad\quad{f_i}\left( {{t_i}} \right) = \left\{ \begin{array}{l} {\left[ {\dfrac{{{t_i} - {S_i}}}{{{s_i} - {S_i}}}} \right]^\alpha },{S_i} {\text{＜}} {t_i} {\text{＜}} {s_i};\\ \;\;\;\;\;\;1,\;\;\;\;\;\;\;\;{s_i} {\text{≤}} {t_i} {\text{≤}} {e_i};\\ {\left[ {\dfrac{{{E_i} - {t_i}}}{{{E_i} - {e_i}}}} \right]^\beta },{e_i} {\text{＜}} {t_i} {\text{＜}} {E_i};\\ \;\;\;\;\;\;0,\;\;\;\;\;\;\;\;{\text{其他}}{\text{。}} \end{array} \right.$

(1)

其中 ${t_i}$ 为车辆为客户点 $ i $ 开始服务的时间， $\alpha $ 、 $\beta $ 为客户对时间的敏感系数。

1.3 货物完好满意度函数

配送过程中的货物损坏主要来自两方面，一是装卸搬运不当导致货物挤压、刺穿；二是运输过程中由于颠簸、撞击等造成损坏。货损率与客户满意度呈负相关，货损率越高，客户满意度越低。因此，本文用货损率衡量客户对货物完好性的满意度，假定配送中心运输的货物性质相同或相近，只考虑运输过程中随运输时间累积造成的货损，货损率可用下式计算：

$\quad\quad{y_i} = q\left( {{t_i} - {t_0}} \right){\text{。}}$

(2)

其中， ${y_i}$ 为客户 $ i $ 的货损率， ${t_0}$ 为车辆从配送中心出发的时间， $ q $ 为货物单位时间货损系数。

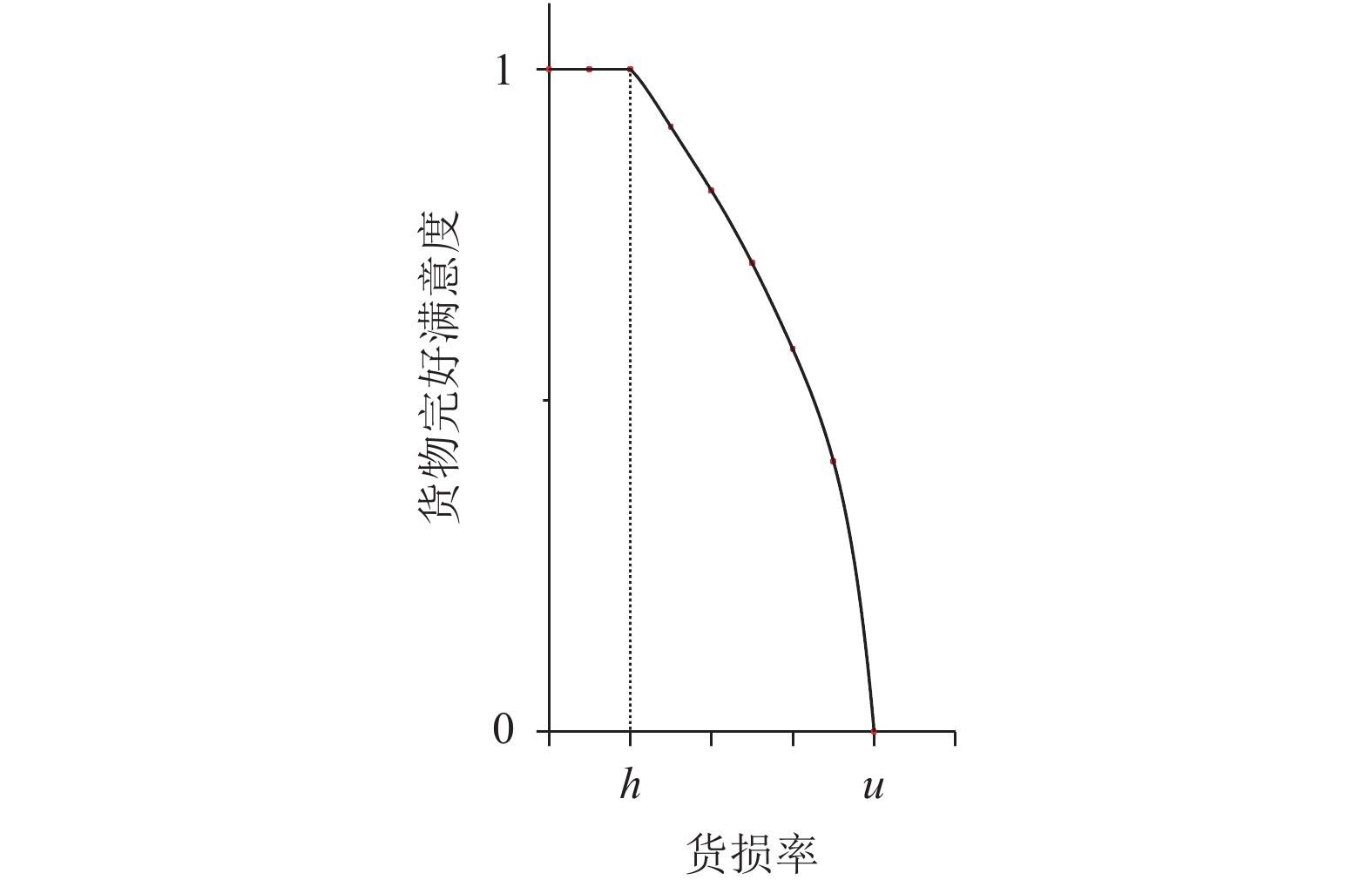
假设客户可接受的货损率范围为 $\left[ {0,h} \right]$ ，在此范围内，客户满意度为100%，客户可容忍的货损率范围为 $\left[ {h,u} \right]$ ，在此范围内，客户满意度随货损率的增加而下降。货物完好满意度函数如图2所示。

货物完好满意度函数表示如下：

$\quad\quad{\mu _i}\left( {{y_i}} \right) = \left\{ \begin{array}{l} \;\;\;\;\;0,\;\;\;\;\;\;{y_i} {\text{＞}} u;\\ {\left[ {\dfrac{{u - {y_i}}}{{u - h}}} \right]^\gamma },h {\text{≤}} {y_i} {\text{≤}} u;\\ \;\;\;\;\;1,\;\;\;\;\;\;0 {\text{≤}} {y_i} {\text{＜}} h{\text{。}} \end{array} \right.$

(3)

其中 $\gamma $ 为客户对货损的敏感系数。

2 数学模型建立 2.1 基本假设与符号说明

在建立模型之前作出如下基本假设：

1) 配送车辆为单一车型，载重量一定；

2) 每一条线路上客户的送货量之和不超过配送车辆的额定载重量；

3) 各个客户的货物可以混装，货物性质相同或相近；

4) 配送中心和各个客户点的位置及其距离、客户的送货量、服务时间要求是已知的；

5) 运输过程中不考虑车辆事故、道路拥堵、天气状况等因素。

由于模型涉及的符号较多，对符号及变量说明如下。

${V}$ 为全部节点集合，即配送中心和客户点的集合， ${V} = \left\{ {0,1,2, \cdots ,N} \right\}$ ，其中0表示配送中心， $\left\{ {1,2, \cdots ,N} \right\}$ 表示客户点集合。

${R}$ 为配送车辆集合， ${R} = \left\{ {1,2, \cdots ,K} \right\}$ 。

${D_i}$ 为客户的送货量。

$ Q $ 为车辆的额定载重量。

$ C $ 为单位车辆固定成本。

$ a $ 为单位距离运输成本。

${d_{ij}}$ 为节点 $ i $ 到节点 $ j $ 的距离。

${l_i}$ 为车辆在客户点 $ i $ 的服务时间。

${t_{ij}}$ 为车辆从客户点 $ i $ 到 $ j $ 的行驶时间。

$\left[ {{s_i},{e_i}} \right]$ 为客户 $ i $ 期望被服务的时间范围， ${s_i}$ 表示下界， ${e_i}$ 表示上界。

$\left[ {{S_i},{E_i}} \right]$ 为客户 $ i $ 可容忍的服务时间范围， ${S_i}$ 表示下界， ${E_i}$ 表示上界。

${f_i}\left( {{t_i}} \right)$ 为时间满意度函数。

$\theta $ 为客户对时间的最低满意度。

$\left[ {0,h} \right]$ 为客户可接受的货损率范围。

$\left[ {h,u} \right]$ 为客户可容忍的货损率范围。

${\mu _i}\left( {{y_i}} \right)$ 为货物完好满意度函数。

$\eta $ 为客户对货物完好性的最低满意度。

$\quad\quad{x_{ijk}} = \left\{ \begin{array}{l} 1,\;\;\;\;{\text{车辆}}k{\text{从节点}}i{\text{行驶到}}j;\\ 0,\;\;\;\;{\text{否则。}} \end{array} \right.$

${\omega _1}$ 、 ${\omega _2}$ 为权重。

2.2 模型建立

基于以上所述，相应的数学模型如下。

$\quad\quad\min\; {Z_1} = C\sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {{x_{0jk}}} } + \sum\limits_{i = 0}^N {\sum\limits_{j = 0\atop i \ne j}^N {\sum\limits_{k = 1}^K {a{d_{ij}}} } } {x_{ijk}};$

(4)

$\min\; {Z_2} = {\omega _1}\left( {1 - \frac{1}{N}\sum\limits_{i = 1}^N {{f_i}\left( {{t_i}} \right)} } \right) + {\omega _2}\left( {1 - \frac{1}{N}\sum\limits_{i = 1}^N {{\mu _i}\left( {{y_i}} \right)} } \right){\text{。}}\!\!\!\!\!\!\!\!\!$

(5)

s.t.

$\quad\quad\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{D_i}} {x_{ijk}}} {\text{≤}} Q,\;\;\;i \ne j,\;\;\;k \in \left\{ {1,2, \cdots K} \right\};$

(6)

$\quad\quad\sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {{x_{0jk}}} } {\text{≤}} K;$

(7)

$\quad\quad\sum\limits_{k = 1}^K {\sum\limits_{i = 0\atop i \ne j}^N {{x_{ijk}}} } = 1,\;\;\;j \in \left\{ {1,2, \cdots N} \right\};$

(8)

$\quad\quad\sum\limits_{k = 1}^K {\sum\limits_{j = 0\atop i \ne j}^N {{x_{ijk}}} } = 1,\;\;\;i \in \left\{ {1,2, \ldots N} \right\};$

(9)

$\sum\limits_{i = 0\atop i \ne p}^N {{x_{ipk}}} = \sum\limits_{j = 0\atop j \ne p}^N {{x_{pjk}}} ,\;\;\;k \in \left\{ {1,2, \cdots K} \right\},\;\;\;p \in \left\{ {1,2, \cdots N} \right\};$

(10)

$\quad\quad\sum\limits_{j = 1}^N {{x_{j0k}}} = \sum\limits_{j = 1}^N {{x_{0jk}}} {\text{≤}} 1,\;\;\;k \in \left\{ {1,2,\cdots,K} \right\};$

(11)

$\quad\quad{f_i}\left( {{t_i}} \right) {\text{≥}} \theta ,\;\;\;\forall i \in \left\{ {1,2, \cdots ,N} \right\};$

(12)

$\begin{split}&\quad\quad{t_j} = \max \;\left\{ {{S_j},\sum\limits_{k = 1}^K {\sum\limits_{i = 0\atop i \ne j}^N {{x_{ijk}}} } \left( {{t_i} + {l_i} + {t_{ij}}} \right)} \right\},{t_j} {\text{≤}} {E_j},\\ &\forall j \in \left\{ {1,2, \cdots ,N} \right\};\end{split}$

(13)

$\begin{split}&\quad\quad{t_i} + {l_i} + {t_{ij}} - H\left( {1 - {x_{ijk}}} \right) {\text{≤}} {t_j},\;\;i,j \in \left\{ {1,2, \cdots N} \right\}{\text{且}}\\ &i \ne j,\;\;k \in \left\{ {1,2, \cdots K} \right\};\end{split}$

(14)

$\quad\quad{\mu _i}\left( {{y_i}} \right) {\text{≥}} \eta ,\;\;\;\forall i \in \left\{ {1,2, \cdots ,N} \right\};$

(15)

$\quad\quad 0 {\text{≤}} {y_i} {\text{≤}} u , \;\;\; \forall i \in \left\{ {1,2, \cdots ,N} \right\};$

(16)

$\quad\quad\begin{array}{l} {x_{ijk}} = 0{\text{或}}1,\;\;\;i \ne j;\\ \forall i \in \left\{ {0,1, \cdots ,N} \right\},\;\;\;\forall j \in \left\{ {0,1, \cdots ,N} \right\},\\ \forall k \in \left\{ {1,2, \cdots ,K} \right\}{\text{。}} \end{array}$

(17)

其中式(4)、(5)为目标函数，式(4)表示最小化运输成本，式(5)表示最小化平均客户不满意度。式(6)~式(17)为约束条件。其中式(6)为车辆装载能力约束；式(7)表示配送车辆数不超过 $ K $ ；式(8)和式(9)表示每个客户有且仅能由一辆车服务；式(10)表示车辆在到达客户点后必须离开客户点；式(11)表示每条线路只有一辆车从配送中心出发且最终返回配送中心；式(12)表示每个客户的时间满意度不低于 $\theta $ ；式(13)表示客户在时间窗内被服务；式(14)表示车辆到达下一客户点的时间晚于到达当前客户点的时间，其中 $ H $ 是一个很大的正数；式(15)表示每个客户的货物完好满意度不低于 $\eta $ ；式(16)表示每个客户货物的货损率在可容忍范围内；式(17)表示决策变量为0-1变量。

2.3 目标函数和约束条件的处理

由于本文建立的模型为多目标优化问题，为了便于求解，通过为两个目标函数分配权重将其转化为单目标优化问题，同时为了使两目标函数量纲统一，对目标函数作如下处理：

$\begin{array}{l} \quad\quad\min\; Z = {\omega _1}\left( {1 - \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{f_i}\left( {{t_i}} \right)} } \right) + {\omega _2}\left( {1 - \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{\mu _i}\left( {{y_i}} \right)} } \right)+\\ {\omega _3}\left( {\dfrac{{C\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{k = 1}^K {{x_{0jk}}} } }}{{{\rm{CN}}}} + \dfrac{{\displaystyle\sum\limits_{i = 0}^N {\displaystyle\sum\limits_{j = 0\atop i \ne j}^N {\displaystyle\sum\limits_{k = 1}^N {a{d_{ij}}{x_{ijk}}} } } }}{{2\displaystyle\sum\limits_{j = 1}^N {a{d_{0j}}} }}} \right){\text{。}} \end{array}$

(18)

其中，CN表示车辆使用数量最大时的固定成本，理论上来说，当每辆车只服务一个客户点时，车辆使用数量最大。本文假设配送中心可用车辆数量不少于客户点数量 $ N $ ，因此车辆使用数量最大为 $ N $ ； $2\displaystyle\sum\limits_{j = 1}^N {a{d_{0j}}} $ 表示运输距离最大时的可变运输成本，最大运输距离为每辆车只服务一个客户点时所有车辆的运输距离之和。

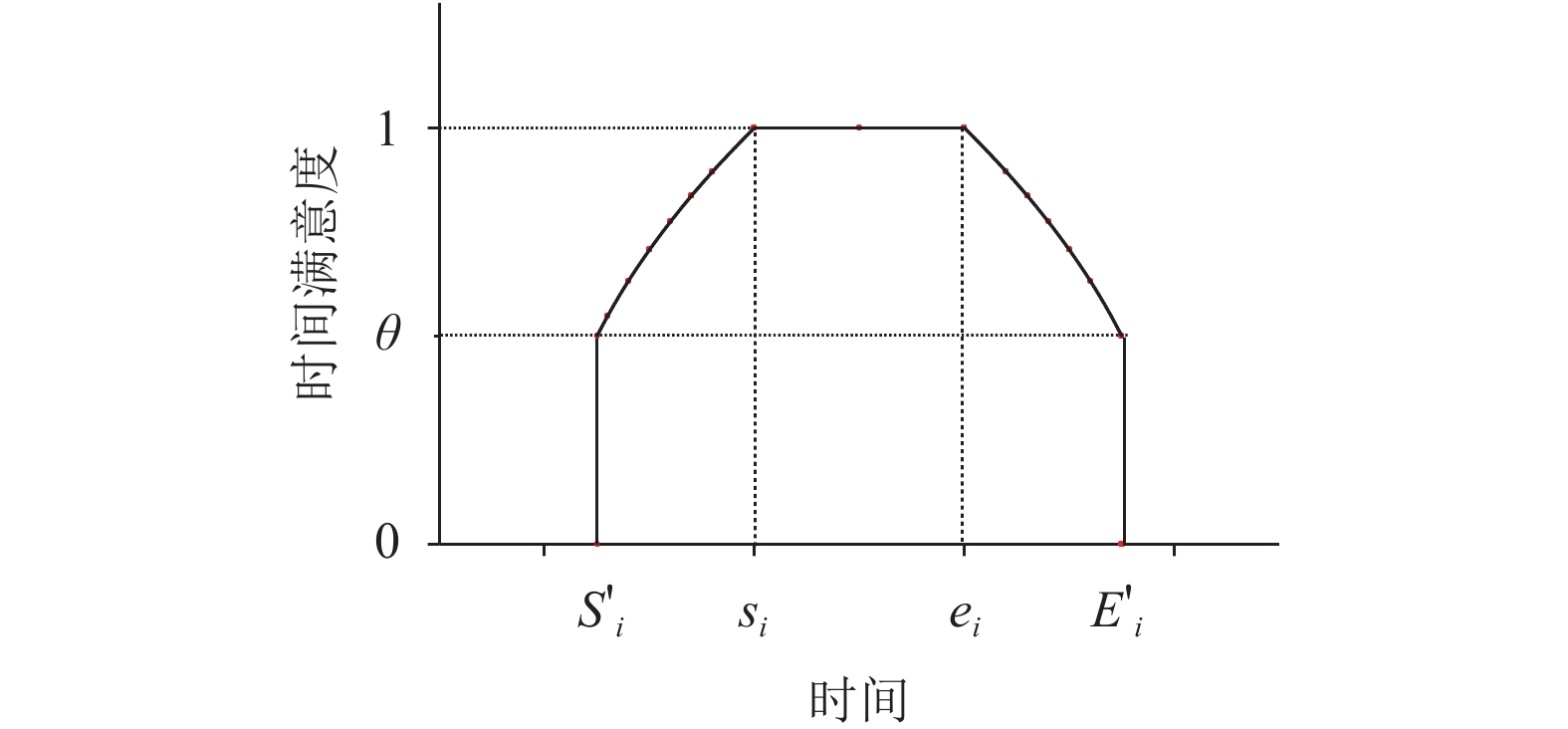
为满足约束条件(9)，即保证任一客户的时间满意度都不低于 $\theta $ ，设可容忍时间范围为 $\left[ {S_i',E_i'} \right]$ ，令 $S_i' = \left\{ {{t_i}\left| {{f_i}\left( {{t_i}} \right) = \theta ,{t_i} {\text{＜}} {s_i}} \right.} \right\}$ ， $E_i' = \left\{ {{t_i}\left| {{f_i}\left( {{t_i}} \right) = \theta ,{t_i} {\text{＞}} {e_i}} \right.} \right\}$ ，则 $S_i' = {\theta ^{1/\alpha }}\left( {{s_i} - {S_i}} \right) + {S_i}$ ， $E_i' = {E_i} - {\theta ^{1/\beta }}\left( {{E_i} - {e_i}} \right)$ ，即截去原可容忍时间范围内客户满意度小于 $\theta $ 的时间段。则改进的时间满意度函数如图3所示。

改进的时间满意度函数表示如下：

$\quad\quad{f_i}\left( {{t_i}} \right) = \left\{ \begin{array}{l} {\left[ {\dfrac{{{t_i} - {S_i}}}{{{s_i} - {S_i}}}} \right]^\alpha },S_i' {\text{＜}} {t_i} {\text{＜}} {s_i};\\ \;\;\;\;\;\;1,\;\;\;\;\;\;\;\;{s_i} {\text{≤}} {t_i} {\text{≤}} {e_i};\\ {\left[ {\dfrac{{{E_i} - {t_i}}}{{{E_i} - {e_i}}}} \right]^\beta },{e_i} {\text{＜}} {t_i} {\text{＜}} E_i';\\ \;\;\;\;\;\;0,\;\;\;\;\;\;\;{\text{其他}}{\text{。}} \end{array} \right.$

(19)

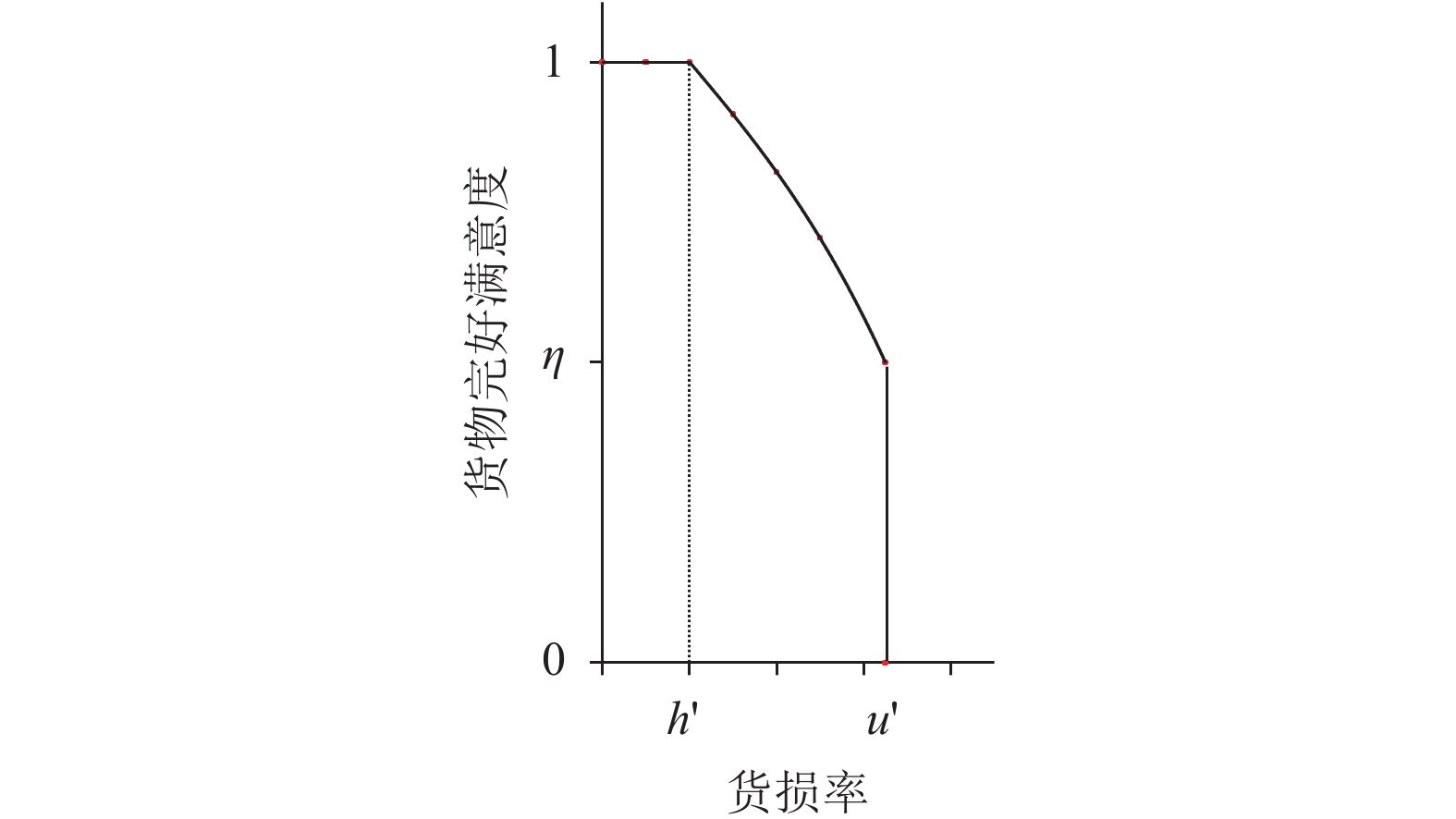
同时为满足约束条件(12)，即保证每个客户的货物完好满意度都不低于 $\eta $ ，设可容忍货损率范围为 $\left[ {{h'},{u'}} \right]$ ，令 ${u'} = \left\{ {{y_i}\left| {{\mu _i}({y_i}) = \eta } \right.} \right\}$ ，则 ${h'} = h$ ， ${u'} = u - $ $ {\eta ^{1/\gamma }}\left( {u - h} \right)$ ，即截去原可容忍货损率范围内客户满意度小于 $\eta $ 的部分。则改进的货物完好满意度函数如图4所示。

改进的货物完好满意度函数表示如下：

$\quad\quad{\mu _i}\left( {{y_i}} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;{y_i} {\text{＞}} {u'},\\ {\left( {\dfrac{{u - {y_i}}}{{u - h}}} \right)^\gamma },{h'} {\text{≤}} {y_i} {\text{≤}} {u'};\\ 1,\;\;\;\;\;\;\;0 {\text{≤}} {y_i} {\text{＜}} {h'}{\text{。}} \end{array} \right.$

(20)

2.4 模型求解

本文所建模型为混合整数非线性规划模型(MINLP)，其中变量类型包含0-1变量与连续变量，约束条件包括线性规划(LP)与非线性规划(NLP)。对于小规模的VRP问题，若采用启发式算法进行求解，求解结果易陷入局部最优解，且求解精度无法保障。而采用精确算法，能够很好地平衡求解精度与时间复杂度之间的关系，从而在可接受的时间范围内，得到质量极高的全局最优解。因此本文采用精确算法，借助Lingo 17.0软件来求解非线性规划模型。Lingo内置的全局求解程序可将非凸的非线性问题转换为多个凸约束和线性子问题，再使用分支定界法来搜索全局最优解。因此根据本文建立的模型特点，调用Lingo 17.0的全局求解程序对模型进行精确求解。同时，本文将Lingo 17.0求得的配送路径优化方案与扫描法进行对比，扫描法具有简单易行且注重节约运输距离的特点，是目前许多中小物流企业进行配送路径规划时采用的方法。通过两种方案在客户满意度和运输成本上的对比，来验证本文构建的优化模型在求解考虑客户满意度的车辆路径问题时的有效性。

3 算例 3.1 算例描述

假设有1个配送中心，可使用的配送车辆为7辆，向7个客户点配送货物。配送中心、送货量及期望服务时间窗等信息参考文献[16]，配送中心坐标为(0, 0)，车辆额定载重量 $ Q $ =3 t，客户可容忍的时间范围上界 ${S_i} = {s_i} - 1$ ，下界 ${E_i} = {e_i} + 1$ 。车辆行驶速度 $ v $ =35 km/h，客户对时间的最低满意度 $\theta = 0.5$ ，时间敏感系数 $\alpha = 0.5$ ， $\beta = 0.8$ ，客户对货物完好性的最低满意度 $\eta = 0.5$ ，货物完好敏感系数 $\gamma = 0.5$ ，客户可接受的货损率范围为[0, 0.2%]，客户可容忍的货损率范围为[0.2%, 1%]，经约束条件(9)转换后，客户可容忍的货损率范围为[0.2%, 0.8%]，单位距离运输成本a=3 元，单位车辆固定成本C=150 元，货物单位时间货损系数q=0.1%，车辆从配送中心出发的时间 ${t_0} = 8$ ， ${\omega _1} = 0.5$ ， ${\omega _2} = 0.3$ ， ${\omega _3} = 0.2$ ，各节点间运输距离见表1，各节点特征数据见表2。

3.2 Lingo优化方案

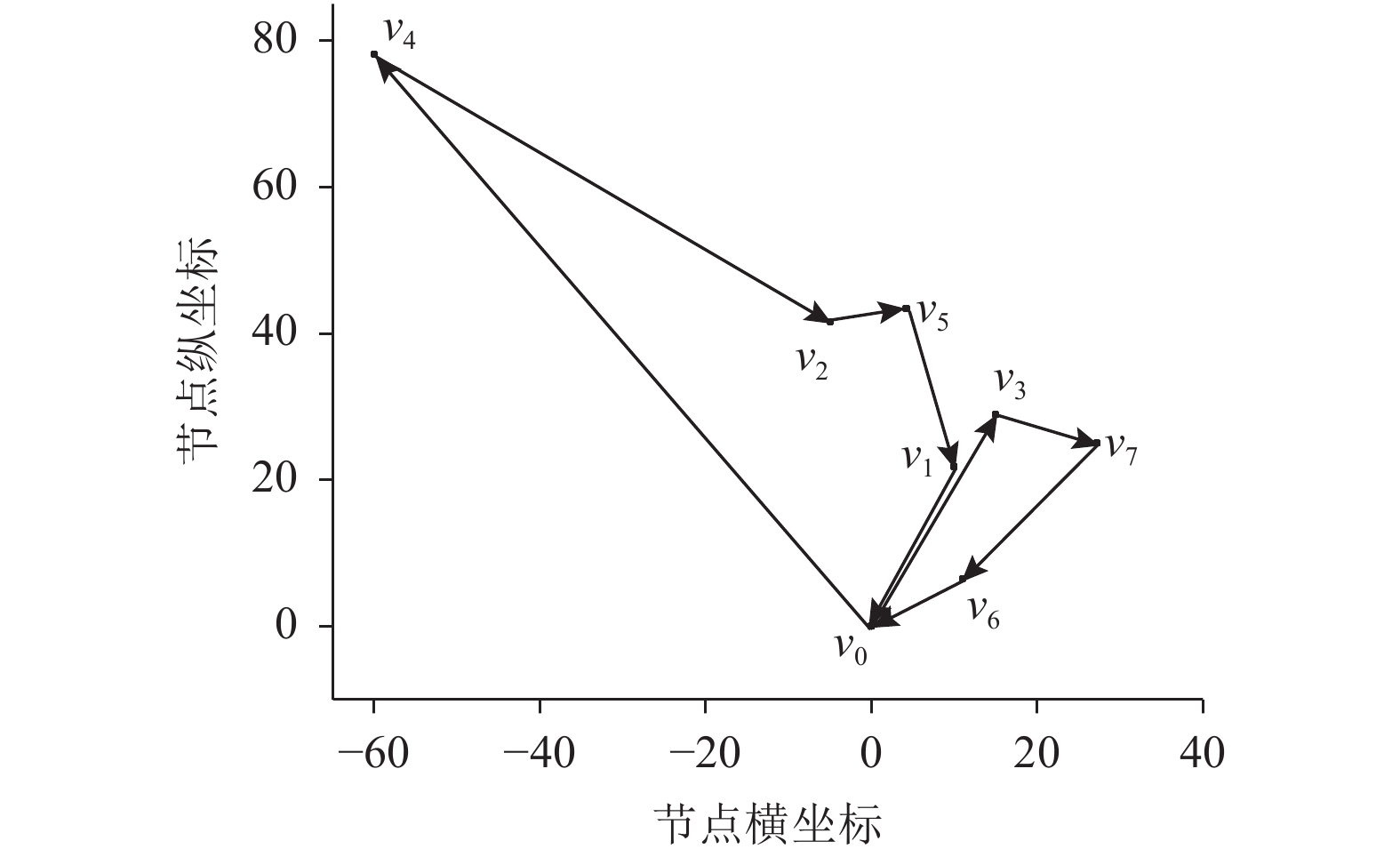
根据前文构建模型，利用Lingo 17.0编程，求解出最优配送路径有2条，分别为：配送中心—客户点1—客户点3—客户点5—配送中心，配送中心—客户点2—客户点4—客户点6—客户点7—配送中心，配送路径如图5所示，平均客户满意度为91.09%，运输总成本为1 276.5元，如表3所示。

3.3 扫描法方案

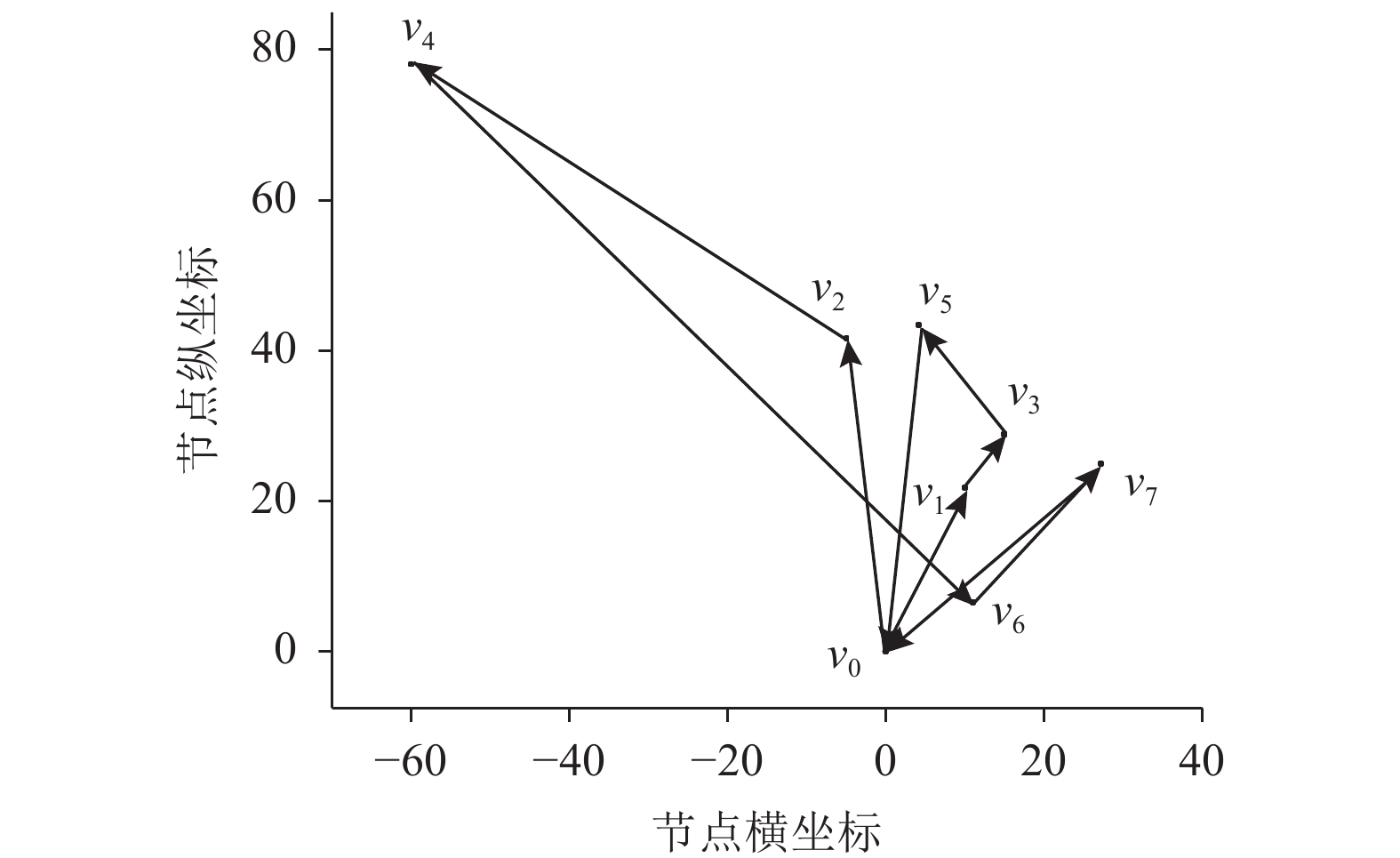
扫描法基本思路为：从配送中心沿任意方向作一条直线，将直线进行顺时针或逆时针旋转，将扫到的客户点依次加入路径中，直到加入某客户点时货物量超出车辆载重量，则剔除此客户点确定一条配送路径，然后从不包含在上条路线中的客户点开始继续旋转构造新的路径，直到所有客户点都被加入到路线中。利用扫描法求解出的配送路径有2条，分别为：配送中心—客户点4—客户点2—客户点5—客户点1—配送中心，配送中心—客户点3—客户点7—客户点6—配送中心，配送路径如图6所示，平均客户满意度为54.79% ，运输总成本为816.3元，如表4所示。

3.4 方案对比

将扫描法与Lingo17.0求解的结果进行对比，可知虽然扫描法求得的方案运输成本较低，但对于客户的送货时间和货物完好性要求并未加以考虑，各客户点的时间满意度不均衡，且在7个客户点中有5个时间满意度为0，两条配送路径的平均时间满意度均偏低。在两种方案运输总成本相差较小的情况下，利用Lingo17.0求得的平均客户满意度比扫描法高出36.3%。同时本文将利用Lingo17.0求解的考虑客户满意度的多目标优化模型与仅考虑运输成本最小的单目标优化模型结果进行对比，可看出，考虑客户满意度的多目标优化模型在运输成本与客户满意度之间达到平衡，而仅考虑运输成本最小的单目标优化模型虽然使运输成本减少了387.6 元，但导致客户满意度降低了19.36%，客户满意度的大幅降低对物流企业的长远发展不利，因此仅考虑运输成本，而忽略提升客户满意度对物流企业来说得不偿失，优化结果对比如表5所示。

4 结论

本文针对车辆路径问题，综合考虑客户满意度和运输成本建立多目标优化模型，并利用LINGO17.0对算例求解，给出2条最优配送路径，通过对比扫描法验证了模型在考虑客户满意度情况下的适用性和有效性，可为物流企业配送路径优化提供理论依据。本文在定义客户满意度函数时，只考虑了时间和货损率两个因素，在实际情况中，收发货的便捷性、配送人员服务态度、配送信息实时性等因素都会对客户满意度产生影响，可考虑作为下一步的研究方向。