云制造是利用物联网技术解决生产企业资源失衡问题的应用实践。李伯虎等^[1]在国内率先提出了“云制造”这一概念，并将其定义为“面向服务的网络化制造”，给出了云制造平台的体系架构。近年来，云制造模式的实践应用得到了快速发展，国内外已相继出现了一些初具雏形的云制造服务平台。比如：国外最大的制造能力服务平台MFG，早在2012年就有50个国家的近20万制造商在平台上提供服务；而国内则有天智网、航天云网等云平台，分别提供区域内和产业内的制造资源交易服务。云制造资源服务组合是云制造模式下完成复杂制造任务的主要方式，涉及合理的多服务组合结构、最优的选择模型和求解方法，对云制造任务的顺利完成和服务质量产生直接影响。基于上述现状，云制造资源分配方法的研究对今后云制造的发展起到十分重要作用。

21世纪，云制造的发展促使制造行业更加重视企业的资源优化配置，故而引起学者们对云制造在制造资源分配方面的关注。制造资源的选择和求解方法的好坏将直接关系资源的分配效率。为此，人工智能算法已广泛应用于制造资源的调度中，主要应用的方法有先进先出调度算法、遗传算法、神经网络算法、蚁群算法、Pareto最优等。

在国内，刘卫宁等^[2]以单一生产任务下服务组合方法为基础，研究了在有多制造任务情况下，以服务质量作为目标函数的多任务服务组合模型，应用改进的遗传算法求解；尹超等^[3]分析了制造资源分配过程的主要特点，以开发新产品为导向，提出八大目标函数资源组合优选模型，模型求解采用灰色关联度的方法；马雪芬等^[4]以成本、时间和质量为目标函数，资源分配模型求解采用改进的遗传算法；周珂等^[5]基于生产任务特点，提出生产任务模型和制造单元资源多目标优化模型，应用自适应精调遗传算法求解；余剑锋等^[6]以时间、成本和质量为目标函数的资源分配模型，用自适应蚁群算法求解；王时龙等^[7]根据物料流以及信息流，设置了影响成本和时间的系数，并通过最大继承法求解云制造资源配置模型；赵道致等^[8]引入前景理论，通过多属性评价，确定匹配主体偏好序，在考虑匹配数量的前提条件下，设计了“多对多”的匹配算法；赵道致等^[9]引入权关系，利用Pontryagin极大值原理求解模型，得出云平台上各企业资源分配的Pareto最优战略。在国外，Dorsch等^[10]分析了不稳定需求下提供供应链服务方案能力规划问题，在完整的排队论系统中建立了同时考虑3种不同能力供应的优化模型；Lee等^[11]研究了制造领域中资源分配模块的智能数据管理的应用，以实现高效运营；Ding等^[12]研究了制造设施中动态授权群体，其修理工作外包的分配模型及启发式方法；Lartigau等^[13]利用改进的仿蜂群算法，基于地理运输可视化的服务质量，分析了云制造服务构成；Liu等^[14]提出了创新的多粒度资源虚拟化和共享战略，匹配了复杂的制造任务与潜在资源；Laili等^[15]基于改进免疫算法的新型云制造服务模式，进一步优化了云制造资源配置。

在已有文献中，虽然有部分学者研究了云制造模式的特征、运营模式、资源分配过程以及不同服务组合结构的特点等，但在资源分配过程中只考虑了制造任务分解的串行结构及需求方的服务质量指标要求，而没有考虑“云”制造环境下面向复杂制造任务以及过程中所存在的大量不确定性，降低了制造服务的应变能力。

基于已有文献存在的上述问题，本文从平台运营方角度出发，研究了复杂制造任务分解涉及的多服务组合结构以及云制造服务的综合评价指标，构建了资源分配双层规划模型(bi-level programming problem，BLPP)，采用改进的快速非支配的遗传算法对模型进行求解^[16]。

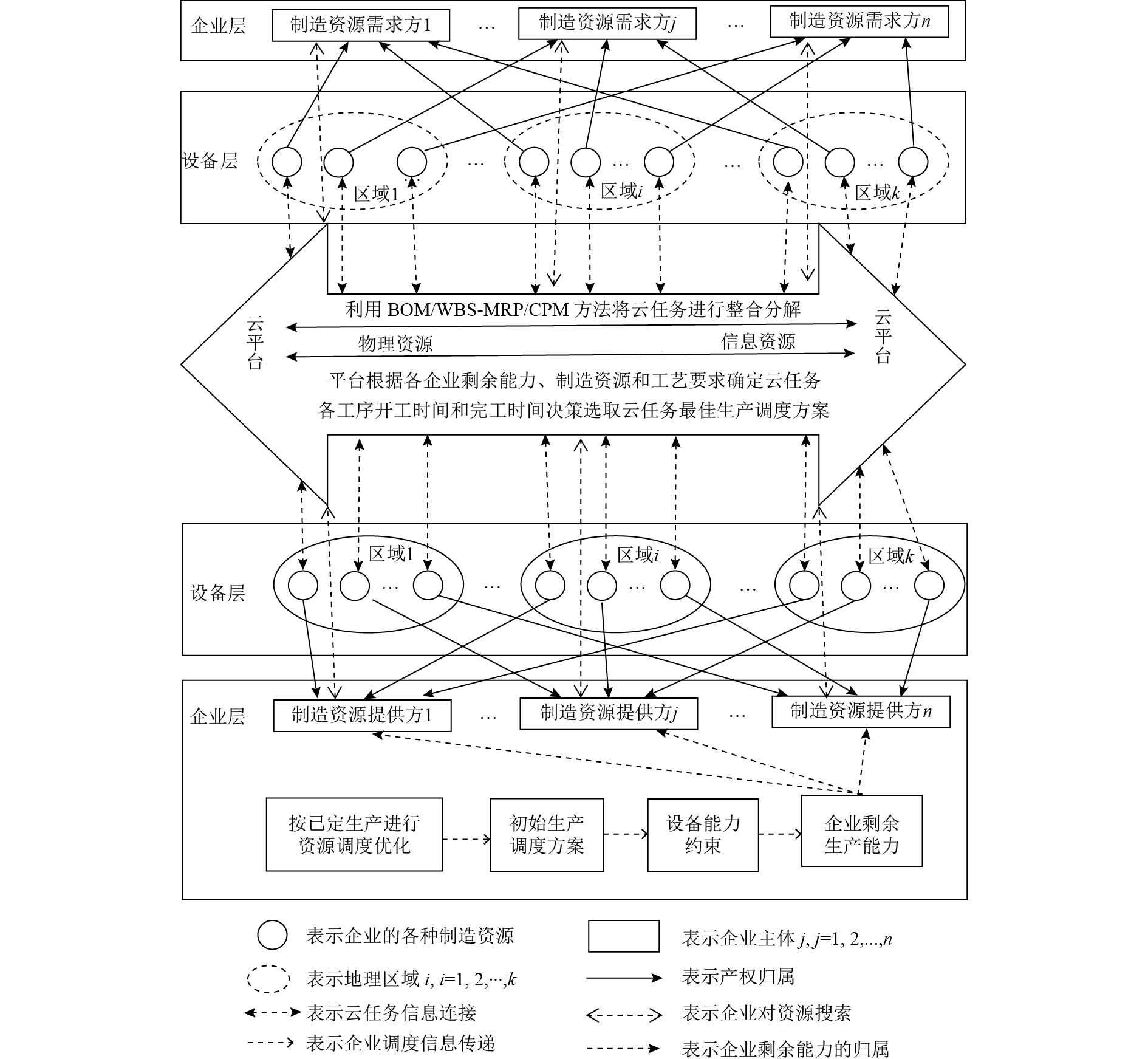
1 云制造资源分配的问题描述

有别于传统的网络化制造，云制造由需求者、资源提供者和云平台运营者组成，如图1所示。云制造资源分配是指需求偏好方将各自的制造任务上传云平台，云平台根据制造任务特点进行合理的解析并将其分解成多个子任务，同时平台上集成了各种企业的剩余能力，形成了云制造服务资源(cloud manufacturing service resource，CMSR)。各项制造子任务驱动云制造平台上各种碎片化资源的共享和集成，突破地理位置的限制并协作完成云需求任务。

云平台基于机器学习得到的知识将订单解析为物料清单(bill of materials，BOM)或工作分解结构(work breakdown structure，WBS)，并按订单的制造与服务的工艺，云资源可用能力和地点将制造任务(manufacturing task，MT)分解为时间序列的加工子任务(manufacturing sub task，MST)。在云需求方和运营方的多目标和多约束条件下，根据物料需求计划(material requirement planning，MRP)或关键路线法(critical path method，CPM)，为不同制造子任务合理分配制造资源服务(manufacturing resource service，MRS)或者服务组合，以满足用户的制造需求。

本文研究云制造资源分配问题，着重考虑需求任务完成分解后，云平台在保证云资源可用能力(云资源具有的能力减现有负荷与已分配负荷)约束前提下，根据制造任务的多服务组合结构和评价指标体系分配云资源，确定可执行的制造服务路径，以完成分解后子任务订单的加工。

2 多服务组合结构与评价指标体系 2.1 云制造资源服务组合的基本结构

在云制造模式下，每一个子任务的完成需要不同的服务组合结构，其复杂程度取决于制造任务的技术含量及生产制造流程的复杂度。这对制造资源服务组合之间的结构有了进一步的丰富和要求。根据云制造模式的过程，将制造服务组合结构分为4种：串联、循环、选择和并行，如图2所示^[17]。

2.2 云制造资源服务组合的评价指标体系

现在的制造资源服务组合以资源计算和Web服务为起点进行研究，但基于云制造模式的特点，利用现有的方法不能解决云制造资源服务组合问题。离线的硬件资源在这一问题中尤为明显，在服务过程中若面对各种任务或资源变化和各种不确定性，要求制造任务具有较高的容错性，会导致既定的组合方案无法高效高质量地完成制造任务。在整个云制造资源分配的过程中，需求方从自身的利益出发，更加关注任务的完成情况，因此以制造资源服务组合的QoS指标作为目标函数。传统的优化模型仅从需求方角度出发，追求需求方利益最大化，忽视了分享经济下平台对柔性指标的要求。柔性指标代表制造服务提供方的服务能力，优质的服务必然会带来一定成本，但劣质的服务对云平台运营方带来了风险，增加重新分配带来的运营成本。制造资源服务组合评价指标是选取和组合制造资源服务的重要依据。因此，在云制造模式下进行资源分配时，需要对需求方的QoS指标和云平台运营方所要求的柔性指标进行优化选择。

2.3 云制造资源服务组合的QoS指标

制造服务的需求方将制造任务上传云平台，在云平台对制造资源的分配过程中，需考虑需求方对于时间、成本和质量等的要求，即上述的制造资源服务组合的QoS指标。云平台为满足客户需求，选择制造资源服务组合时会受QoS指标的影响，进一步选择最优的分配方案。

1) 时间指标T：由每个制造服务资源所需的加工执行时间T_fu、相邻制造服务资源之间资源运输的物流时间T_tr以及任务堆积产生的等待时间T_wa3部分构成。其中， ${T_ {\rm{wa}}} = \displaystyle\sum\limits_{i = 0}^{n - 1} {{T_ {\rm{fu}}}(i)} $ ，n表示任务下达时等待第i个制造服务资源的任务数量。

2) 成本指标C：由每个制造服务资源所需的成本C_fu、相邻服务之间物料资源运输的物流成本C_tr2部分构成。

3) 质量指标Q：云制造模式下制造资源服务完成每个任务都有相应的服务质量(即质量合格率)用Q_se表示。

2.4 云制造资源服务组合的柔性指标

在云制造环境下，制造资源随时需要动态调整。对于云平台来说，面对复杂多变的制造任务，如果制造任务或制造资源发生变化会影响制造任务的完成，则云平台运营方在进行制造资源服务组合的时候就要考虑每一个制造资源的柔性因素。因此云制造资源服务的柔性指标也是资源分配问题中的重点考虑因素。

柔性指标主要由以下3方面构成。

1) 应对制造任务变化的能力F_T：当制造任务发生变化时，制造资源提供方仍能顺利地完成制造任务的能力。主要包括：各个制造资源的服务功能多样性F_fu、资源提供方具有资源的种类F_ty和合作企业的数量F_w。

2) 应对制造资源变化的能力F_R：当制造资源发生变化时，制造资源提供方仍能顺利地完成制造任务的能力。主要包括各个制造资源的服务的可靠性指标F_re、资源提供方提供相同功能资源的数量F_sa和合作企业的数量F_w。

3) 服务评价F_E：建立在历史服务评价的基础上，由制造服务需求方给予0~1之间的满意度来综合评价该项制造服务的历史服务态度、服务能力、服务水平以及服务完成情况。F_E越大则表明制造资源服务的评价越高，应对变化的能力越强。

3 云制造资源分配模型的构建

云制造模式以面向服务的方式将生产过程中的各种资源提供给客户，实时应答动态变化的客户需求，提高云制造环境下的资源利用率，达到减少运营成本、为云平台的用户创造更多经济利益的目的。云制造资源分配问题的实质是根据不同需求方的制造任务，将制造资源进行合理的优化组合，用最经济、最快的速度完成制造任务。云制造生产模式是云平台将复杂的生产任务经过分解后，在上述的评价指标体系的约束下，通过制造资源多服务组合结构的形式完成云制造环境下复杂制造任务。在不同指标评价体系下对云制造的资源进行合理的分配过程属于传统的多目标优化问题(multi-objective optimization problems，MOP)。

基于云平台的运营模式，云平台在不同服务组合下进行制造任务分配时首先满足制造服务需求方的需求，其次还需要考虑云平台运营方因不确定性而带来的运营风险。根据双层规划模型的特点，这可以有效解决本文的资源分配问题，由此构建云制造模式下多服务组合结构的资源分配模型。

3.1 基本假设和符号约定 3.1.1 基本假设

在实际生产运营过程中，云制造模式面对不同的客户需求，分散式的资源，用统一的数学模型很难加以描述。因此，以云制造目标要求和跨区域制造资源分配的本质为出发点，作如下假设：

1) 只考虑跨地域资源分配，不考虑内部资源分配；

2) 考虑实际过程中物流对时间成本的影响；

3) 云平台按照生产工艺标准，将复杂的任务拆分成多个串行的子任务，各子任务的完成依赖于与之对应的多服务组合结构。

3.1.2 符号约定

$\alpha$ 为串联结构中制造服务资源的集合；

$\beta$ 为并行结构中制造服务资源的集合；

$\chi$ 为循环结构中制造服务资源的集合；

$\delta$ 为选择结构中制造服务资源的集合；

N为资源的总数 $\left\{ {\alpha \cup \beta \cup \chi \cup \delta = N} \right\}$ ；

i为制造服务资源的序， ${\rm{MRS}}_{i}=\{{\rm{MRS}}_{i,1}, {\rm{MRS}}_{i,2},$ $ {\rm{MRS}}_{i,3}, \cdots,{\rm{MRS}}_{i,n}\}$ ，n为第i个制造服务资源的个数；

P_i为选择结构中资源 ${\rm MRS}_i $ 被选中的概率， $i \in \delta $ ；

K为循环结构中循环的次数；

T_to为总服务时间；

T_fu(i)为第i个制造服务资源所需的制造加工时间， $i=1,2,\cdots,N $ ；

T_tr(i, i+1)为第i个制造资源与下一制造资源之间的物流时间， $i=1,2,\cdots,N $ ；

T_wa(i)为第i个制造资源任务等待时间， $i=1, $ $2,\cdots,N $ ；

C_to为总服务成本；

C_fu(i)为第i个制造服务资源所需服务成本， $i=1,2,\cdots,N $ ；

C_tr(i,i+1)为第i个制造资源与下一制造资源之间的物流成本 $i=1,2,\cdots,N $ ；

Q_se(i)为第i个制造资源的质量合格率， $i=1,2, $ $ \cdots,N$ ；

F_fu(i)为第i个制造服务资源提供的功能数量， $i=1,2,\cdots,N $ ；

F_ty(i)为第i个制造资源的种类数， $ i=1,2,\cdots,N$ ；

F_w(i)为第i个制造资源的合作企业数量， $i=1, $ $ 2,\cdots ,N$ ；

F_re(i)为第i个制造资源的服务可靠性， $i=1,2,\cdots $ $ N$ ；

F_sa(i)为第i个制造资源提供相同服务的数量， $i=1,2,\cdots,N $ ；

F_E(i)为第i个制造资源的服务评价，取(0~1) $i=1,2,\cdots,N $ ；

ω_T为有需求偏好制造服务需求方的时间权重；

ω_c为有需求偏好制造服务需求方的成本权重；

ω_Q为有需求偏好制造服务需求方的质量权重；

ω_fu为制造资源服务功能多样性的权重系数；

ω_ty为制造资源种类的权重系数；

ω_Tc为任务变化的能力目标下，制造资源提供方合作企业数量的权重系数；

ω_re为制造资源的可靠性的权重系数；

ω_sa为制造资源服务提供相同服务数量的权重系数；

ω_Rc为面对制造资源变化目标下，服务提供方合作企业数量的权重系数；

T_max为需求方要求的最长交货时间；

C_max为需求方要求的最高成本；

Q_min为需求方要求的最低服务质量；

F_{fu min}为云平台运营方要求的最小制造服务功能多样性；

F_{ty min}为云平台运营方要求的最少制造服务资源种类；

F_{re min}为云平台运营方要求的最低可靠性；

F_{sa min}为云平台运营方要求的最少制造资源服务提供相同服务数量；

F_{w min}为云平台运营方要求的最少合作企业数量；

F_{E min}为云平台运营方要求的最低服务评价。

3.2 制造服务需求方的目标函数

制造服务需求方作为双层规划的上层决策主体，从自身的利益出发利用QoS指标作为衡量制造任务完成情况的标准，因此构建模型如式(1)~(3)所示。

$\begin{split} &\quad\quad\min\; T = \min \;{T_ {\rm{to}}} = \min\; ({T_ {\rm{fu}} } + {T_ {\rm{tr}}} + {T_ {\rm{wa}}})= \\ &\min \;\left[{\Big{(}}\sum\limits_{i \in \alpha } {{T_ {\rm{fu}}}(i) + \sum\limits_{i \in \alpha } {{T_ {\rm{tr}}}(i, i + 1) + \sum\limits_{i \in \alpha } {{T_ {\rm{wa}}}(i)} } }+ \right.\\ & \mathop {\max \;}\limits_{i \in \beta } ({T_ {\rm{fu}}}(i) + {T_ {\rm{tr}}}(i, i + 1) + {T_ {\rm{wa}}}(i){\Big{)}}+ \\ &{{K}} \times {{\Big{(}}}\sum\limits_{{{i}} \in {{\chi }}} {{{{T}}_{{\rm{fu}}}}{{(i)}} + \sum\limits_{{{i}} \in {{\chi }}} {{{{T}}_{{\rm{tr}}}}{{(i, i}} + {{1)}} + \sum\limits_{{{i}} \in {{\chi }}} {{{{T}}_{{\rm{wa}}}}{{(i)\Big{)}}}} } }+\\ &\left.\sum\limits_{{{i}} \in {{\delta }}} {{{{T}}_{{\rm{fu}}}}{{(i)}} {{{P}}_{{i}}} + \sum\limits_{{{i}} \in {{\delta }}} {{{{T}}_{{\rm{tr}}}}{{(i, i}} + {{1)}} {{{P}}_{{i}}} + \sum\limits_{{{i}} \in {{\delta }}} {{{{T}}_{{\rm{wa}}}}{{(i)}} {{{P}}_{{i}}}{{)}}} } } \right] ; \end{split} $

(1)

$\begin{split} &\quad\quad \min\; C = \min\; {C_ {\rm{to}}} = \min\; ({C_ {\rm{fu}}} + {C_ {\rm{tr}}}) =\\ & \min\; \left[{\Big(}\sum\limits_{i \in \alpha \cup \beta } {{C_ {\rm{fu}}}(i) + \sum\limits_{i \in \alpha \cup \beta } {{C_ {\rm{tr}}}(i, i + 1)} } +K \times {\Big(}\sum\limits_{i \in \chi } {{C_ {\rm{fu}}}(i) + }\right.\\ & {\sum\limits_{i \in \chi } {{C_ {\rm{tr}}}(i, i + 1){\Big{)}}} }+ \left. \sum\limits_{i \in \delta } {{C_ {\rm{fu}}}(i) {P_i} + \sum\limits_{i \in \delta } {{C_ {\rm{tr}}}(i, i + 1) {P_i}{\Big)}} } \right] ; \end{split} $

(2)

$\begin{split}&\quad\quad \min\; Q = \min\; (1 - {Q_ {\rm{se}}}) =\\ &\min\; \left[1 - {\Big(}\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{Q_ {\rm{se}}}(i) + \sum\limits_{i \in \delta } {{Q_ {\rm{se}}}(i) {P_i}{\Big)}} /N}\right] {\text{。}} \end{split} $

(3)

在云制造模式下，根据不同服务需求方对制造任务要求的时间、成本和质量等指标不尽相同，对于有这种需求偏好的需求方，利用传统的线性加权的方法赋予各个目标不同的权重，将多目标问题转化为单目标问题，并通过与最大指标的值相除达到归一化处理，比较不同需求偏好对于服务组合的影响。

因此，多服务组合结构资源分配问题中需求方的函数可以简化为：

$\min \;{u_1}\left( {T, C, Q} \right) \!=\! {\omega _{{\rm{T}}}}\left( {\frac{T} {{T_{\max }}}} \right)\! +\! {\omega _{\rm{c}}}\left( {{\frac{C} {{{C_{\max }}}}}} \right) \!+\! {\omega _{\rm{Q}}}\left( {{\frac{Q} {Q_{\max }}}} \right){\text{。}}\!\!\!\!$

(4)

$\quad\quad{\rm{s.t}}.\left\{ \begin{array}{l} {T_ {\rm{to}}} {\text{≤}} {T_{\max }};\\ {C_ {\rm{to}}} {\text{≤}} {C_{\max }};\\ {Q_ {\rm{se}}}(i) {\text{≥}}{Q_{\min }}, i = 1, 2, \cdots , N{\text{。}} \end{array} \right.$

(5)

其中， ${\omega _{\rm{T}}} + {\omega _{\rm{C}}} + {\omega _{\rm{Q}}} = 1$ 。

3.3 云平台运营方的目标函数

云平台运营方作为双层规划的下层决策主体，从平台利益出发利用制造资源服务的柔性指标作为制造资源服务组合的可靠性和成功率的标准，因此构建模型如式(6)~(8)所示。

$ \begin{split} &\quad\quad\max\; {F_ {\rm{T}}} = \max\; ( {{\omega _ {\rm{fu}}}{F_ {\rm{fu}}} + {\omega _ {\rm{ty}}}{F_ {\rm{ty}}} + {\omega _ {\rm{Tc}}}{F_ {\rm{w}}}} )= \\ & \max\; \left[{\omega _ {\rm{fu}}}\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{fu}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{fu}}}(i) {P_i}\Big)} /N}+ \right.\\ & {\omega _ {\rm{ty}}}\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{ty}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{ty}}}(i) {P_i}\Big)} /N} +\\ & \left.{\omega _ {\rm{Tc}}}\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{w}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{w}}}(i) {P_i}\Big)} /N} \right] ; \end{split} $

(6)

$ \begin{split} &\quad\quad \max\; {F_ {\rm{R}}} = \max\; \left( {{\omega _ {\rm{re}}}{F_ {\rm{re}}} + {\omega _ {\rm{sa}}}{F_ {\rm{sa}}} + {\omega _ {\rm{Rc}}}{F_ {\rm{w}}}} \right)= \\ & \max\; \left[{\omega _ {\rm{re}}}\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{re}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{re}}}(i) {P_i}\Big)} /N} \right.+\\ & {\omega _ {\rm{sa}}}\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{sa}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{sa}}}(i) {P_i}\Big)} /N}+ \\ &\left. {\omega _ {\rm{Rc}}}\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{w}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{}}}(i) {P_i}\Big)} /N}\right]; \end{split} $

(7)

$ \quad\quad\max\; {F_ {\rm{E}}} = \max\;\left[\Big(\sum\limits_{i \in \alpha \cup \beta \cup \chi } {{F_ {\rm{E}}}(i) + \sum\limits_{i \in \delta } {{F_ {\rm{E}}}(i) {P_i}\Big)} /N}\right] {\text{。}}\!\!\! $

(8)

其中， ${\omega _ {\rm{fu}}} + {\omega _ {\rm{ty}}} + {\omega _ {\rm{Tc}}} = 1$ ， ${\omega _ {\rm{re}}} + {\omega _ {\rm{sa}}} + {\omega _ {\rm{Rc}}} = 1$ 。

因此，多服务组合结构资源分配问题中云平台运营方的函数可以简化为：

$\quad\quad\max\; {u_2}({F_ {\rm{T}}}, {F_ {\rm{R}}}, {F_ {\rm{E}}}){\text{。}}$

(9)

$\quad\quad{\rm{s.t}}.\left\{ \begin{array}{l} {F_ {\rm{fu}}}(i) {\text{≥}} {F_{{\rm{fu}}\min }}, i = 1, 2, \cdots , N;\\ {F_ {\rm{ty}}}(i) {\text{≥}} {F_{{\rm{ty}}\min }}, i = 1, 2, \cdots , N;\\ {F_ {\rm{re}}}(i) {\text{≥}} {F_{{\rm{re}}\min }}, i = 1, 2, \cdots , N;\\ {F_ {\rm{sa}}}(i) {\text{≥}} {F_{{\rm{sa}}\min }}, i = 1, 2, \cdots , N;\\ {F_ {\rm{w}}}(i) {\text{≥}} {F_{{\rm{w}}\min }}, i = 1, 2, \cdots , N;\\ {F_ {\rm{E}}}(i) {\text{≥}} {F_{{\rm{E}}\min }}, i = 1, 2, \cdots , N{\text{。}} \end{array} \right.$

(10)

4 模型的求解 4.1 快速非支配遗传算法

目前，解决MOP的主流算法是进化多目标优化算法，而其中的NSGA-Ⅱ是Deb等于2002年在NSGA(non-dominated sorting genetic algorithm)的基础上提出的改进算法。NSGA-Ⅱ用将种群分层的快速非支配排序方法来简化算法，并提出拥挤度的指标，进一步赋予排序后同级个体中每一个个体适应度值，使得帕累托前沿面内的个体尽可能地均匀分布，并扩展到整个帕累托前沿面。同时NSGA-Ⅱ始终保留精英个体，用选择后的个体所产生的后代与父代个体生成新种群，保留了优势个体，使进化水平得到提升，是目前为止最优秀的进化多目标优化算法之一。

4.2 算法设计

对于MOP优化问题的评价采用非支配排序和拥挤度，即：

$\quad\quad\left\{\begin{array}{l} \mathop {\rm{Rank}}\limits_u\left( {{S\!}_i} \right) {\text{＜}} \mathop {\rm{Rank}}\limits_u\left( {{S\!}_j} \right) ;\\ \mathop {\rm{Distance}}\limits_u\left( {{S\!}_i} \right) {\text{＞}}\mathop {\rm{Distance}}\limits_u\left( {{S\!}_j} \right) , \\ \mathop {\rm{Rank}}\limits_u\left( {{S\!}_i} \right) = \mathop {\rm{Rank}}\limits_u\left( {{S\!}_j} \right){\text{。}} \end{array}\right.$

(11)

式中： $\mathop {\rm{Rank}}\limits_u\left( {{S\!}_i} \right)$ 和 $\mathop {\rm{Rank}}\limits_u\left( {{S\!}_j} \right)$ 分别表示在适应度函数u下 ${{S\!}_i}$ 和 ${{S\!}_j}$ 的非支配等级序列值； $\mathop {\rm{Distance}}\limits_u\left( {{S\!}_i} \right)$ 和 $\mathop {\rm{Distance}}\limits_u\left( {{S\!}_j} \right)$ 分别表示在适应度函数u下个体 ${S\!}_i$ 和 ${S\!}_j$ 的拥挤距离。在NSGA-Ⅱ算法求解MOP优化问题中，若个体 ${S\!}_i$ 和 ${S\!}_j$ 满足式(11)，则说明 ${S\!}_i \succ {S\!}_j$ ，即 ${S\!}_i$ 优于 ${S\!}_j$ 。

对于求解本文研究问题多目标优化问题不能直接应用上述方法，结合式(11)可以得到本文模型中制造资源服务组合方案优劣评价标准：

$\quad\quad\begin{array}{l} {\rm{Rank}}\left( {{S\!}_i} \right) {\text{＜}} {\rm{Rank}}\left( {{S\!}_j} \right) ;\\ {\rm{Distan ce}}\left( {{S\!}_i} \right) {\text{＞}} {\rm{Distan ce}}\left( {{S\!}_j} \right) , \\ {\rm{Rank}}\left( {{S\!}_i} \right) = {\rm{Rank}}\left( {{S\!}_j} \right){\text{。}} \end{array}$

式中：

$\quad\quad \left\{ \begin{array}{l} {\rm{Rank}}({S\!}_i) = \mathop {\rm{Rank}}\limits_{F_ {\rm{T}}}({S\!}_i) + \mathop {\rm{Rank}}\limits_{F _ {\rm{R}}}({S\!}_i) + \mathop {\rm{Rank}}\limits_{F_ {\rm{E}}}({S\!}_i) ,\!\!\!\!\!\!\!\!\!\!\!\! \\ {\rm{Rank}}({S\!}_j) = \mathop {\rm{Rank}}\limits_{F_ {\rm{T}}}({S\!}_j) + \mathop {\rm{Rank}}\limits_{F _ {\rm{R}}}({S\!}_j) + \mathop {\rm{Rank}}\limits_{F_ {\rm{E}}}({S\!}_j) ,\!\!\!\!\!\!\!\!\!\!\!\!\\ {\rm{Distance}}({{S\!}_{i}})=\underset{{{F}_{\rm{T}}}}{\mathop{{\rm Distance}}}\,({{S\!}_{i}})+\\ \quad\underset{{{F}_{\rm{R}}}}{\mathop{\rm{Distance}}}\,({{S\!}_{i}})+\underset{{{F}_{\rm{E}}}}{\mathop{{\rm Distance}}}\,({{S\!}_{i}}), \\ {\rm Distance}({{S\!}_{j}})=\underset{{{F}_{\rm{T}}}}{\mathop{{\rm Distance}}}\,({{S\!}_{j}})+\\ \quad\underset{{{F}_{\rm{R}}}}{\mathop{\rm{Distance}}}\,({{S\!}_{j}})+\underset{{{F}_{\rm{E}}}}{\mathop{{\rm Distance}}}\,({{S\!}_{j}}) {\text{。}} \end{array} \right. $

(12)

基于上式可知： ${\rm{Rank}}({S\!}_i)$ 和 ${\rm{Rank}}({S\!}_j)$ 分别表示方案 ${S\!}_i$ 和 ${S\!}_j$ 在不同目标函数下的非支配等级序列值的和； ${\rm{Distan ce}}\left( {{S\!}_i} \right)$ 和 ${\rm{Distan ce}}\left( {{S\!}_j} \right)$ 分别表示方案 ${S\!}_i$ 和 ${S\!}_j$ 在不同目标函数下拥挤距离的和。当方案 ${S\!}_i$ 和 ${S\!}_j$ 满足式(12)，则说明 ${S\!}_i \succ {S\!}_j$ ；当算法收敛时，若 ${S\!}_i$ 满足 $\mathop {\rm{Rank}}\limits_u\left( {{S\!}_i} \right)$ 和 $\mathop {\rm{Rank}}\limits_u\left( {{S\!}_j} \right)$ 均为3，则得到本模型的下层主体的Pareto解集；将此作为下层主体决策目标的可行解集，代入上层目标函数中计算函数值；然后按照算法对函数值进行分层排序，得到 ${\rm{Rank}}\left( {{S^{_*}}} \right) = {{1}}$ 的解，即为本模型的最优解。

4.3 算法流程

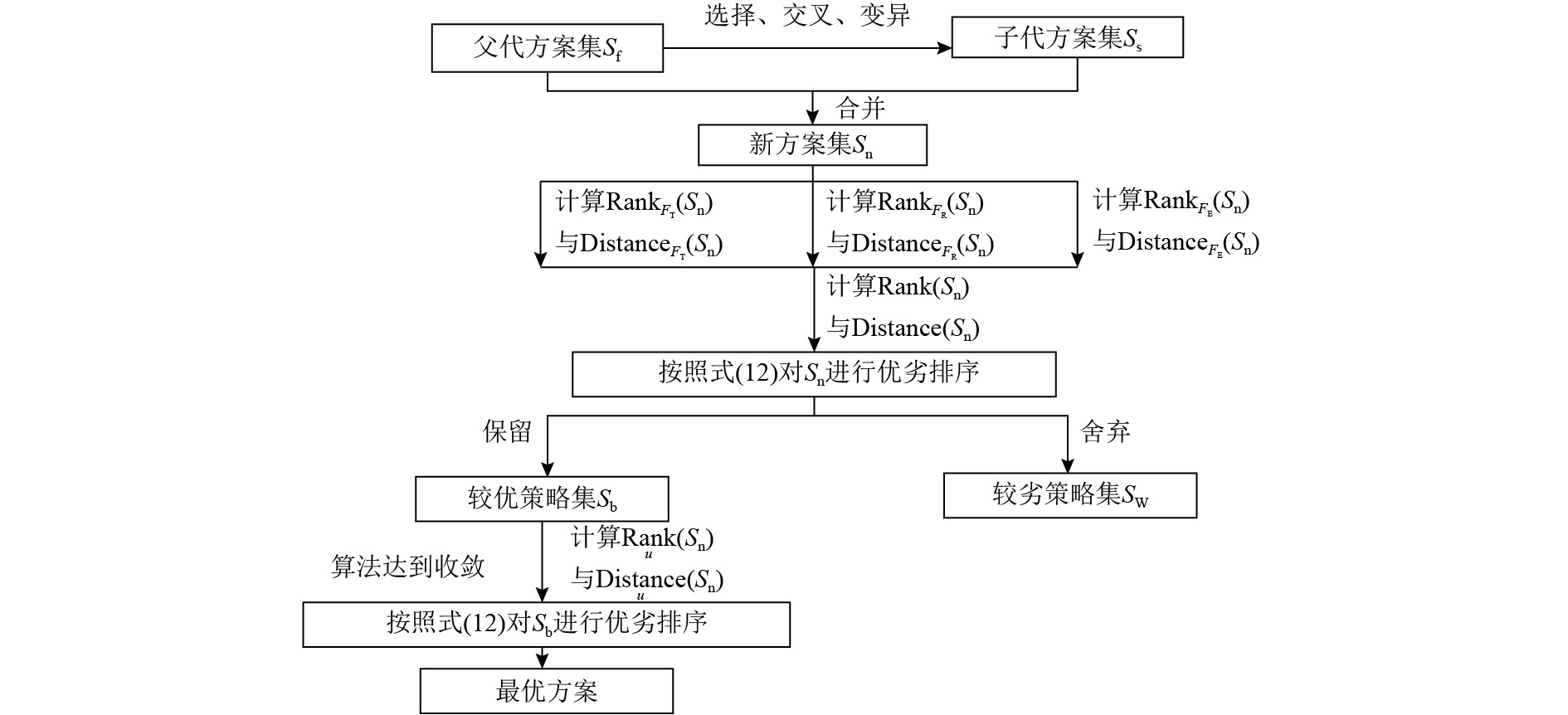
本文提出的云制造资源分配双层规划结构模型包括需求方和云平台运营方，属于双层MOP的求解。而BLPP本身属于NP-Hard问题，因此求解此模型的最优解十分复杂。采用NSGA-Ⅱ算法求解本文模型的一般过程如图3所示。

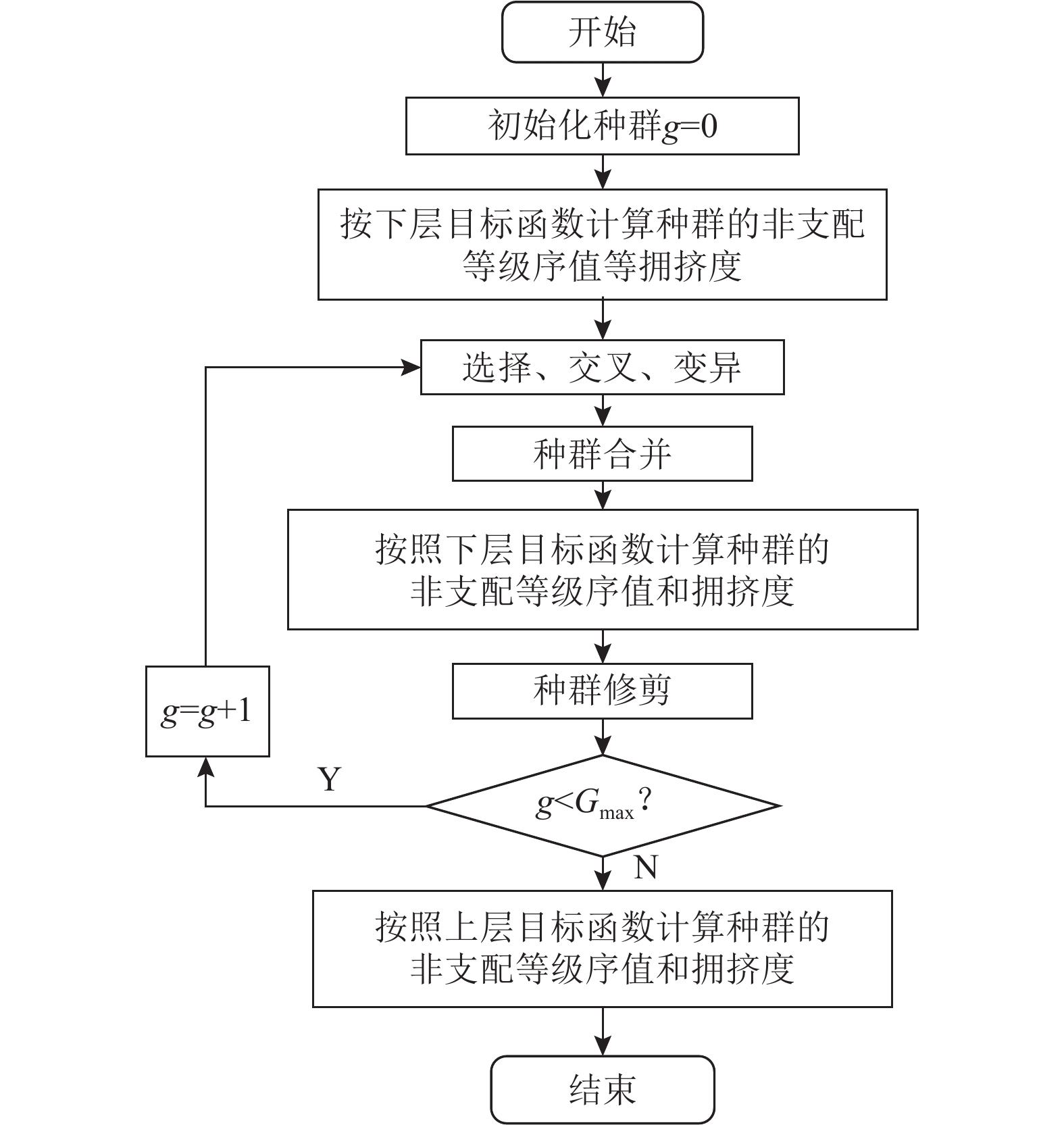
基于上述，结合式(12)和图3对NSGA-Ⅱ算法进行改进。算法中的每一个种群对应多目标优化问题的一个方案，父代方案集S_f通过遗传产生子代方案集S_s并与之合并，构成新的方案集S_n。以式(9)作为适应函数，计算下层主体在方案集S_n下的效用，以式(12)作为判别优劣准则，完成种群的修剪过程，保留优势方案集S_b，进行下一步进化过程。求解本双层规划模型的算法流程如图4所示。

5 算例分析 5.1 模型算例

基于需求方、资源提供方和云平台构成的云制造模式，需求方有一个复杂的生产任务，需要通过云平台完成生产。因此不同的需求方将各自的生产任务和所要求的服务质量指标上传云平台。针对不同的制造任务，云平台可以根据任务的难易程度拆分成子任务MST_k，将其归类并与相应的制造资源服务进行匹配，依赖于不同的服务组合结构来完成。MST_k与MRS_i( $ i=1,2,\cdots,10$ )的组合结构一一对应，如图5所示，其中包括串联、并行、选择和循环4种制造资源服务组合结构。每个制造资源服务对应候选制造资源服务MRS_i，j，如表1所示。

模型参数依据云制造服务需求方的需求偏好设计，可以根据不同需求进行调整。本算例中模型参数设置为：P₅=0.8，P₆=0.2； ${\omega _{\rm{T}}}$ =0.4， ${\omega _{\rm{c}}}$ =0.3， ${\omega _{\rm{Q}}}$ =0.3； ${\omega _ {\rm{fu}}}$ =0.5， ${\omega _ {\rm{ty}}}$ =0.4， ${\omega _{\rm Tc}}$ =0.1， ${\omega _{{\rm{re}}}}$ =0.9， ${\omega _{{\rm{sa}}}}$ =0.08， ${\omega _{{\rm{Rc}}}}$ =0.02；T_max=320 h，C_max=2 000，Q_min=0.90，F_{fu min}=1，F_{ty min}=2，F_{re min}=0.85，F_{sa min}=1，F_{w min}=1，F_{E min}=0.85。

制造资源分配模型算例。

$\quad\quad\min {u_1}\left( {T, C, Q} \right) = 0{\rm{.4}}\left( {{\frac{T} {320}}} \right) + 0{\rm{.3}}\left( {{\frac{C} {{2\;000}}}} \right) + 0{\rm{.3}}\left( {{\frac{Q} {{0 .1}}}} \right){\text{。}}$

$ \quad\quad{\rm{s.t}}.\left\{ \begin{array}{l} {T_ {\rm{to}}} - { {320}} {\text{≤}} 0;\\ {C_ {\rm{to}}} - { {2\;000}} {\text{≤}} 0;\\ 0{\rm{.90 - }}{Q_ {\rm{se}}}(i) {\text{≤}} 0, i = 1, 2, \cdots , {\rm{10}}{\text{。}} \end{array} \right. $

$ \quad\quad\max {u_2}({F_ {\rm{T}}}, {F_ {\rm{R}}}, {F_ {\rm{E}}}){\text{。}} $

$ \quad\quad{\rm{s.t}}\left\{ \begin{array}{l} {\rm{1}} - {F_{{\rm{fu}}\min }} {\text{≥}} 0, i = 1, 2, \cdots , N;\\ {\rm{2}} - {F_{{\rm{ty}}\min }} {\text{≥}} 0, i = 1, 2, \cdots , N;\\ 0{\rm{.85}} - {F_{{\rm{re}}\min }} {\text{≥}} 0, i = 1, 2, \cdots , N;\\ {\rm{1}} - {F_{{\rm{sa}}\min }} {\text{≥}} 0, i = 1, 2, \cdots , N;\\ {\rm{1}} - {F_{{\rm{w}}\min }} {\text{≥}} 0, i = 1, 2, \cdots , N;\\ 0{\rm{.85}} - {F_{{\rm{E}}\min }} {\text{≥}} 0, i = 1, 2, \cdots , N{\text{。}} \end{array} \right. $

5.2 算例求解

本文采用改进的NSGA-Ⅱ算法来求解双层规划模型，利用Matlab编程，计算程序在P4 CPU，内存为2 G，主频为2.81 GHZ的环境下运行，用式(11)和式(12)作为适应度函数。

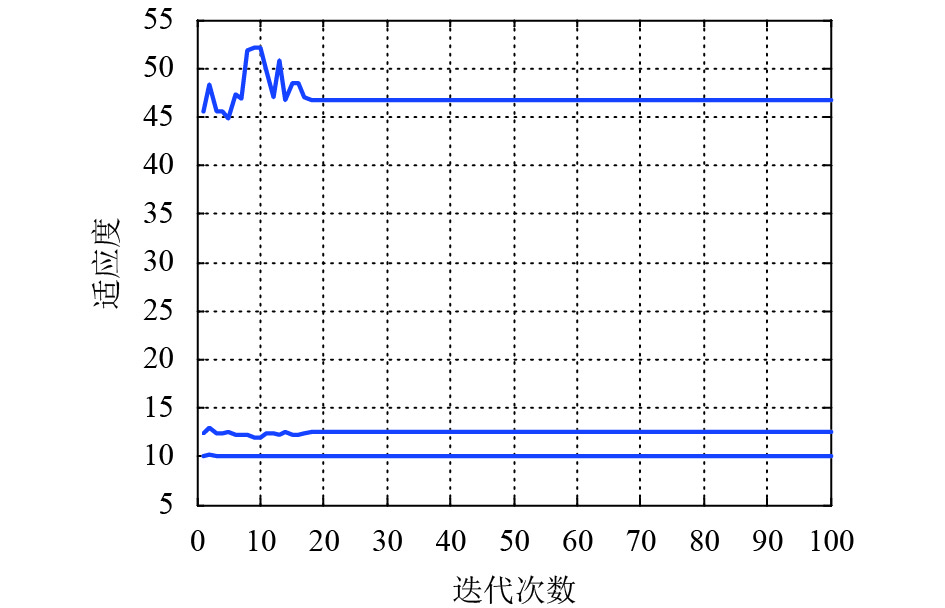
算例中算法参数具体设置为：初始种群100，交叉概率0.8，变异概率0.01，最大遗传代数100，得到种群在每个适应度函数下的平均适应度如图6所示。

从图6中可以看出，在100代的进化过程中，20代后趋于稳定，使算法达到收敛，得到评价指标下的Pareto最优解。根据式(12)的评价标准来判断每个个体是否为上层主体的最优方案，在算法达到收敛时， ${\rm{Rank}}\left( {{S^{*}}} \right)$ =3的个体则为此问题模型下层决策主体目标函数的Pareto解集。云平台将下层主体目标函数的Pareto解集按优劣顺序反馈给云制造服务需求方，作为需求方目标函数的可行解集，分别计算上层目标函数值，根据式(11)进行非支配排序，将 ${\rm{Rank}}\left( {{S^{*}}} \right)$ =1的个体作为模型的最优解。按照优劣顺序对其排序并取前5组解列出，如表2所示。

考虑云制造服务需求方的不同要求，可以选择不同的服务组合方案，例如可以选上层目标函数序列值为1的制造资源服务组合方案 $S_i^*\{\rm MRS_{1,3}, MRS_{2,1},$ $ \rm MRS_{3,2}, MRS_{4,3},\!MRS_{5,3},\!MRS_{7,1},\!MRS_{8,2},\!MRS_{9,2}$ , $ \rm MRS_{10,3}\}$ 为最优方案。

5.3 结果分析

本文采用的双层规划充分考虑了云服务需求方和云平台对于制造资源多服务组合的要求，弥补了传统资源分配对平台利益的忽视。

为验证本文算法的有效性，对本模型的组合方案进行枚举，计算每组服务组合方案的非支配等级序列值，列出柔性指标等级序列值为3的组合方案，如表3所示。表3所示的最优组合方案在表2中都可以找到，且方案1和2的QoS指标和柔性指标的最优非支配等级序列值相同，均为1和3，说明各自目标函数下的等级序列值是完全非支配解，验证了模型算例的求解结果分别满足制造资源服务需求方和云平台运营方的利益最大化，实现了云制造供应链的Pareto最优。

6 结束语

本文针对云制造模式下制造资源的优化分配问题，分析了云制造模式下面对复杂制造任务的资源分配的过程，研究了云制造资源多服务组合结构和评价指标体系，建立了资源分配的双层结构优化决策模型。利用改进的NSGA-Ⅱ评价标准来进行求解，不断地调整方案，使非支配等级序列值向Pareto改进方向进化，解决了云制造模式下资源分配过程中云平台和需求方的利益冲突问题，达到云制造供应链Pareto最优，为平台型企业提高分配资源效率提供了决策方法，并通过算例验证了模型和算法的有效性。

本文主要考虑了制造子任务串行的多服务组合结构情况下的资源分配问题，在下一步工作中，对于实际生产制造过程中任务分解的并行和混合制造子任务的制造资源分配问题将展开深入研究。