2. 综合交通大数据应用技术国家工程实验室,四川 成都 610031
2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Southwest Jiaotong University, Chengdu 610031, China
农业合作社(简称合作社)是农户本着弱者互助的原则自发结成的经济合作组织,是帮助农户增加收入、抵御风险的理想载体,具有天然的“益贫性”[1-2]。国内外众多学者对合作社的作用和运作机理给予了极大的研究兴趣。An等[3]认为农户加入合作社能够获得成本降低、产出提高、环节缩减、品牌效应提升、不确定性降低等益处,因此农户可从中获益并改善自身境况。浦徐进等[4]认为由于农户合作经济组织能够更好地抵御不可抗力原因造成的风险, 降低不守信的龙头企业再次寻找到合作方的概率, 因此能够使参加农户合作经济组织的农户获得更多的利润分成[4]。还有一些学者认为相比于投资人拥有企业,合作社是由农户组成并由农户作为拥有者、控制者的共同体,它的建立使“小农户生产与大市场”实现了有效对接。能帮助小农户应对投资人拥有的寡头企业的强势挤压,应对市场价格不稳定的风险 [5-7]。这些研究都指出合作社在帮助农户增收和抵御风险方面发挥着巨大作用,这也为合作社的发展和兴起提供了理论基础。
近年来,以合作社的迅速崛起为代表,中国的农业产业化、组织化、规模化进程在政府与社会资本的推动下获得了很快的发展。截止到2012年,中国成立了将近60万个农业合作社,吸纳了4600万农户参与合作社[1],到2017年4月底已增至188.8万家。然而在这逐年上升的增量中,小、散、弱型合作社居多。农户盲目加入、地方政府政绩导向、社会资本投机逐利等多种因素交织使许多合作社成立之初严重忽视对农户容量和质量的把控,导致众多合作社出现对接市场能力弱、吸引资金难、品牌培育差、分散恶性竞争等问题,直接影响了产业福利水平和农产品供应链各成员的绩效。
例如,具有典型例证意义的地理标志农产品,因其独特的地理属性和集体知识产权属性使其具有一定的品牌价值,这种品牌价值对于地理范围内的生产者具有共享性,对于非地理范围内的生产者则具有排他性。因此地区内的生产者往往可以通过自组织的方式结成产销合作体,以获得“集体垄断”的竞争优势[8],对应于现实,就是成立农业合作社组织。然而,在实际情况中却出现了一些不和谐的现象,如江西的柑橘类地理标志农产品生产就出现了农户扎堆、合作社林立分散、地理标志保护意识薄弱、产品质量参差不齐等问题[9]。这些现象的出现是因为地理标志农产品具有一定的品牌效应和排他性,会诱使地区范围内的生产者盲目跟风,草率成立或加入一些规模小而分散的农业合作社。这种非理性行为不仅不能够有效提升合作社的竞争力,达到小农户互助脱贫的目的,反而加剧了同行间的竞争损耗,严重破坏了地区内的产销秩序,结果造成合作社对外竞争力和品牌形象的损失,出现经济学中所谓的“公地悲剧”。因此,地区内农户成立合作社以提高其市场竞争力和渠道竞争力的初衷无可厚非,但是需要以理性的态度和方法才能达成这一初衷。
针对农业发展面临的诸多问题,2017年中央一号文件提出深入推进中国农业供给侧改革的要求。其中,就明确指出要积极发展适度规模经营并加强农业合作社的规范建设,保证农户实现有效增收。这一指导方针明确了现存大多数中小型合作社的改进方向。但是,怎样的规模是适度的呢?又需以怎样的标准尺度去界定呢?这成为本文将要着重探讨的问题之一。另外,2017年10月,中国国务院办公厅下发了《国务院办公厅关于积极推进供应链创新与应用的指导意见》,其中,明确指出要创新农业产业组织体系,鼓励农民合作社与农业龙头企业等组织合作建立集农产品生产、加工、流通和服务等于一体的农业供应链体系。这实际上暗示:要解决合作社现有的问题,并不能仅局限于合作社这一主体视角,应该从农产品供应链整体绩效的视角寻找解决问题的思路。
从农产品供应链的视角对该问题进行研究,需要考虑农产品供应链的2个重要特点。1) 农产品供应链参与成员之间存在广泛的博弈与竞争,其中包括同级成员之间的水平竞争和不同层级成员之间的垂直竞争。如售卖生鲜农产品的沃尔玛、家乐福和永辉超市等企业之间的竞争,众多生产和销售具有替代性农产品的农户和合作社之间的激烈竞争。供应链竞争的研究比较成熟,Corbett等[10]、Adida等[11-12]、杨天剑等[13]许多学者从Cournot数量竞争和Bertrand价格竞争两个方面对同级成员的水平竞争进行了深入细致的探讨。而考虑到现实中大多数农产品供应链成员之间存在同质化竞争的现状,本文将以Cournot数量竞争体现同级成员间的水平竞争。2) 农业生产受自然条件影响,具有很强的产出随机性[14]。近年来,许多学者对随机产出下的农产品供应链进行了研究, 大多数研究关注产出随机情况下的农产品供应链协调问题和农户生产决策问题。如He等[15]、凌六一等[16]探讨了产出随机下风险分担合同如何协调供应链;林强等[17]探讨了产出随机下基于协商的收益共享合同如何协调供应链;Huh等[18]和叶飞等[19]分别讨论了产出随机下的农户违约决策和最优生产决策问题。然而,以上研究都还未将随机产出和供应链竞争相结合,也未具体到有合作社参与的农产品供应链中,因此本文在上述研究的基础上做了一定的扩展性研究。
在实际的农产品流通中,合作社多数以“农户+合作社+企业”的结构形式参与到农产品供应链中,而下游企业如沃尔玛等大型企业由于拥有对接市场,实现需求的能力,在农产品供应链中具有较强的渠道权力。因此,基于以上研究和问题,本文考虑随机产出下以由企业为主导,生产农产品的农户与合作社参与的“农户+合作社+企业”三级农产品供应链为载体,在求解供应链成员存在水平Cournot数量竞争和纵向Stackelberg博弈均衡解的基础上,主要探讨两方面问题:1) 如何选择农户,多少容量才有利于供应链整体效益?2) 当上游选择的农户容量已定时,下游成员数量如何影响成员参与博弈的竞争空间,是否存在均衡的供应链结构,此时供应链容纳能力如何?
1 模型描述与假设供应链第一级包含S(
本文假设条件如下。
1) 由于农业生产受季节和天气等自然条件的影响很大,农户的实际产出量通常是随机变量,借鉴文献[16-17, 19]的思想,有
2) S个农户生产的农产品具有同质性。并且,由于农产品生产具有规模不经济的特性,因此假设所有农户的生产成本是关于农资投入的函数
3) 农产品供应链中各级成员之间只通过收购价格契约进行交易,不采用其他形式的供应链契约进行交易。同时假设供应链上的产销总量是对等的。
4) 许多国家已立法规定小农户可从合作社获取一部分返还利润。如《中华人民共和国农民专业合作社法》第五章第三十七条规定:在弥补亏损、提取公积金后的当年盈余,为农民专业合作社的可分配盈余,按成员与本社的交易量(额)比例返还,返还总额不得低于可分配盈余的百分之六十,利润返还政策为农户增收提供了另一个可能性。因此,假设合作社给予农户的利润返还比例的范围为
| 表 1 模型参数说明 Tab. 1 Description of various parameters in the model |
在现实情况中,农户可以同时参与多个合作社,将农产品卖给多个合作社。比如,在美国平均每个农户会参加2.6个专业合作社;荷兰、法国有90%的农民属于某个或几个农民专业合作社成员;几乎所有丹麦农民都参加专业合作社,平均每个农户参加3.6个合作社[18]。同时,合作社也可以与多个下游企业合作,将收购的农产品卖给企业。下面探讨由S个农户、I个合作社、R个企业共同构成三级农产品供应链,此时各级成员间均存在水平Cournot数量竞争,进行横向纳什博弈,不同层级成员间存在主从关系,进行Stackelberg博弈。
给定合作社的收购价格
| $\begin{split}&\quad\quad E\left[ {{\pi _{{\rm{s}},i}}} \right] = E\Bigg[ {{p_{\rm{c}}}{q_{{\rm{s}},i}}-\left({{s_1}\overline {{q_{{\rm{s}},i}}} + \frac{{{s_2}}}{2}{{\left({\overline {{q_{{\rm{s}},i}}} } \right)}^2}} \right) + {b_{\rm{c}}}{\pi _{\rm{c}}}\frac{{{q_{{\rm{s}},i}}}}{{\displaystyle\sum\limits_{i = 1}^S {{q_{{\rm{s}},i}}} }}} \Bigg] = \\&\left({(1-{b_{\rm{c}}}){p_{\rm{c}}}-{s_1} + {b_{\rm{c}}}{p_{\rm{s}}}} \right)\overline {{q_{{\rm{s}},i}}} \cdot \mu -\frac{{{s_2}}}{2}\left({\overline {{q_{{\rm{s}},i}}} } \right){^2}{\text{。}}\quad\quad\;\;\quad\quad\quad(1)\end{split}$ |
此时,第l个合作社将根据农户对其提供的收购价格
| $\begin{split}\quad\quad&E\left[ {{\pi _{{\rm{c}},l}}} \right] = E\left[ {(1-{b_{\rm{c}}})({p_{\rm{s}}}-{p_{\rm{c}}}){q_{{\rm{c}},l}}} \right]{\text{。}}\\&{\rm{s}}{\rm{.t}}{\rm{.}}\;\;{q_{{\rm{c}},l}} + {Q_{{\rm{c}},-l}} = {Q_{\rm{s}}}({p_{\rm{c}}})\;\;{\text{。}}\end{split}$ | (2) |
式(2)中
同理,第k个企业将根据合作社对其提供的收购价格
| $\begin{split}\quad\quad &E\left[ {{\pi _{{\rm{r}},k}}} \right] = E\left[ {\left({(a-bQ)-{p_{\rm{s}}}} \right){q_{{\rm{r}},k}}} \right]{\text{。}}\\&{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{q_{{\rm{r}},k}} + {Q_{{\rm{r}},-k}} = {Q_{\rm{c}}}({p_s}){\text{。}}\end{split}$ | (3) |
式(3)中
对于由企业主导的序贯博弈,采用逆向求解法可得到以下结果。
命题1当供应链各级成员进行横向纳什博弈和纵向Stackelberg博弈时,产出数量、各级价格和各成员的总利润均存在唯一纳什均衡解,如下所示。
产量:
| ${Q^{\rm{d}}} = R{q_{{\rm{r}},k}} = I{q_{{\rm{c}},l}} = S{q_{{\rm{s}},i}} = \frac{{\mu (a-{s_1})RSI}}{{(R + 1)\left[ {b\mu SI + {s_2}(I + 1) \cdot E\left({\displaystyle\frac{1}{\theta }} \right)} \right]}};$ |
价格:
| $\begin{split}\quad\quad &p = a-b{Q^{\rm{d}}},{p_{\rm{s}}} = {s_1} + \frac{{{s_2}(I + 1)}}{{\mu SI}}E\left({\frac{1}{\theta }} \right){Q^{\rm{d}}},\\&{p_{\rm{c}}} = {s_1} + \frac{{{s_2}\left({1-{b_{\rm{c}}}(1 + 1/1In-I)} \right)}}{{\mu (1-{b_{\rm{c}}})S}}E\left({\frac{1}{\theta }} \right){Q^{\rm{d}}}{\text{。}}\end{split}$ |
总利润:
| $\begin{split}\quad\quad &{\pi _{\rm{r}}} = \frac{{a-{s_1}}}{{R + 1}}{Q^{\rm{d}}},{\pi _{\rm{c}}} = \frac{{{s_2}}}{{\mu SI}}E\left({\frac{1}{\theta }} \right){\left({{Q^{\rm{d}}}} \right)^2},\\&\displaystyle\sum\limits_{i = 1}^{\rm{S}} {{\pi _{{\rm{s}},i}}} = {\pi _{\rm{s}}} = \frac{{{s_2}}}{{2S}}{\left[ {E\left({\frac{1}{\theta }} \right)} \right]^2}{\left({{Q^{\rm{d}}}} \right)^2}{\text{。}}\end{split}$ |
其中,
合作社在选择农户加入时,可以以自身利润最优为参考标准,本文将其定义为合作社利润最优策略。由此,可以得到命题2。
命题2 农户之间、合作社之间和企业之间同时存在水平竞争时,能够使合作社总利润最大化的农户容量为
结合命题1和2可知:1)
|
图 1 农户和合作社总利润关于I和R的变化 Fig. 1 The total profit of farmers and cooperatives about I and R(θ~U[0.1, 0.9]) |
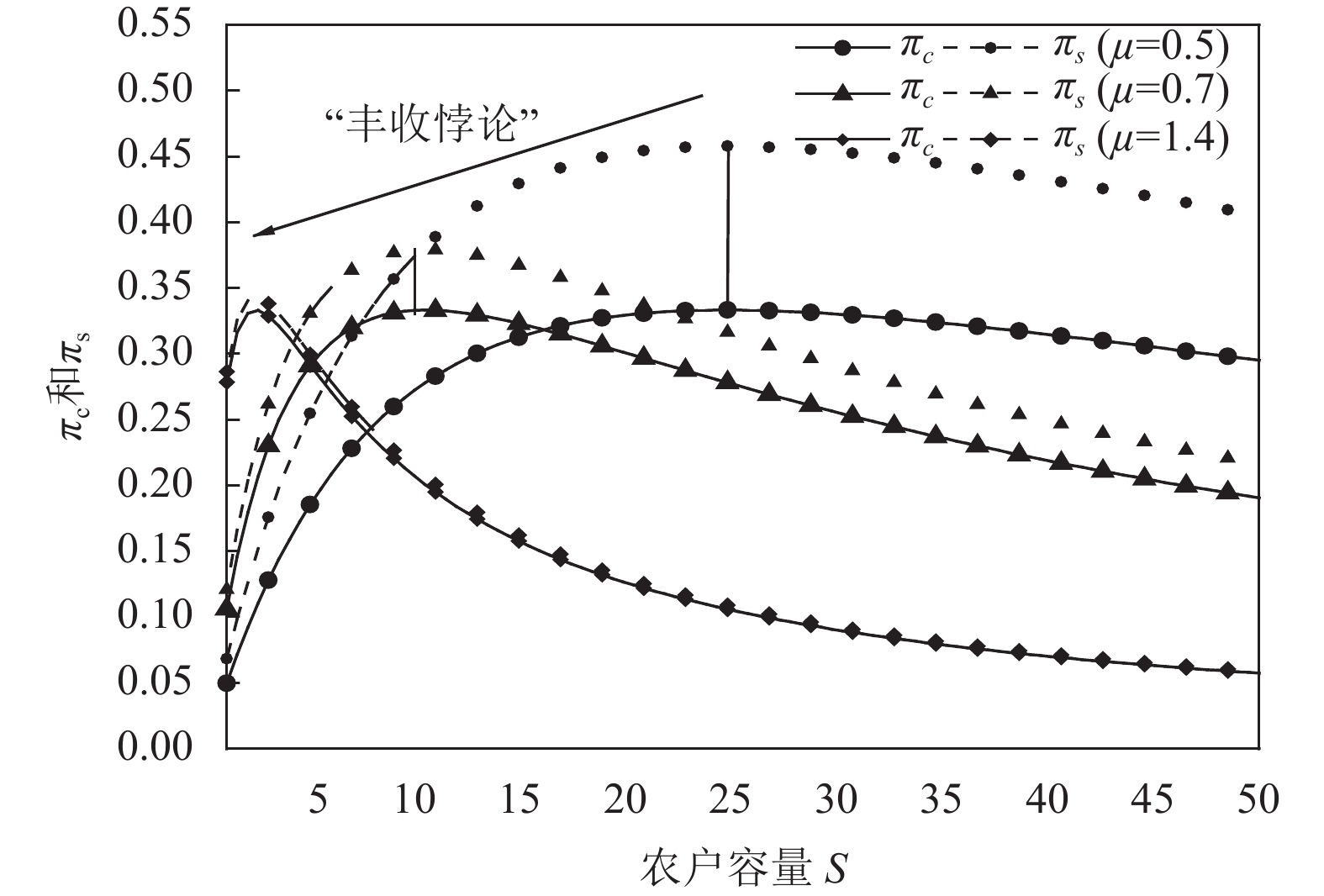
|
图 2 农户和合作社总利润关于均值μ的变化 Fig. 2 The total profit of farmers and cooperatives about μ(R=I=2) |
在均衡条件下,此时的分权农产品供应链的总利润为
命题3 各成员之间同时存在水平竞争时,能够使分权农产品供应链总利润最优的农户容量为
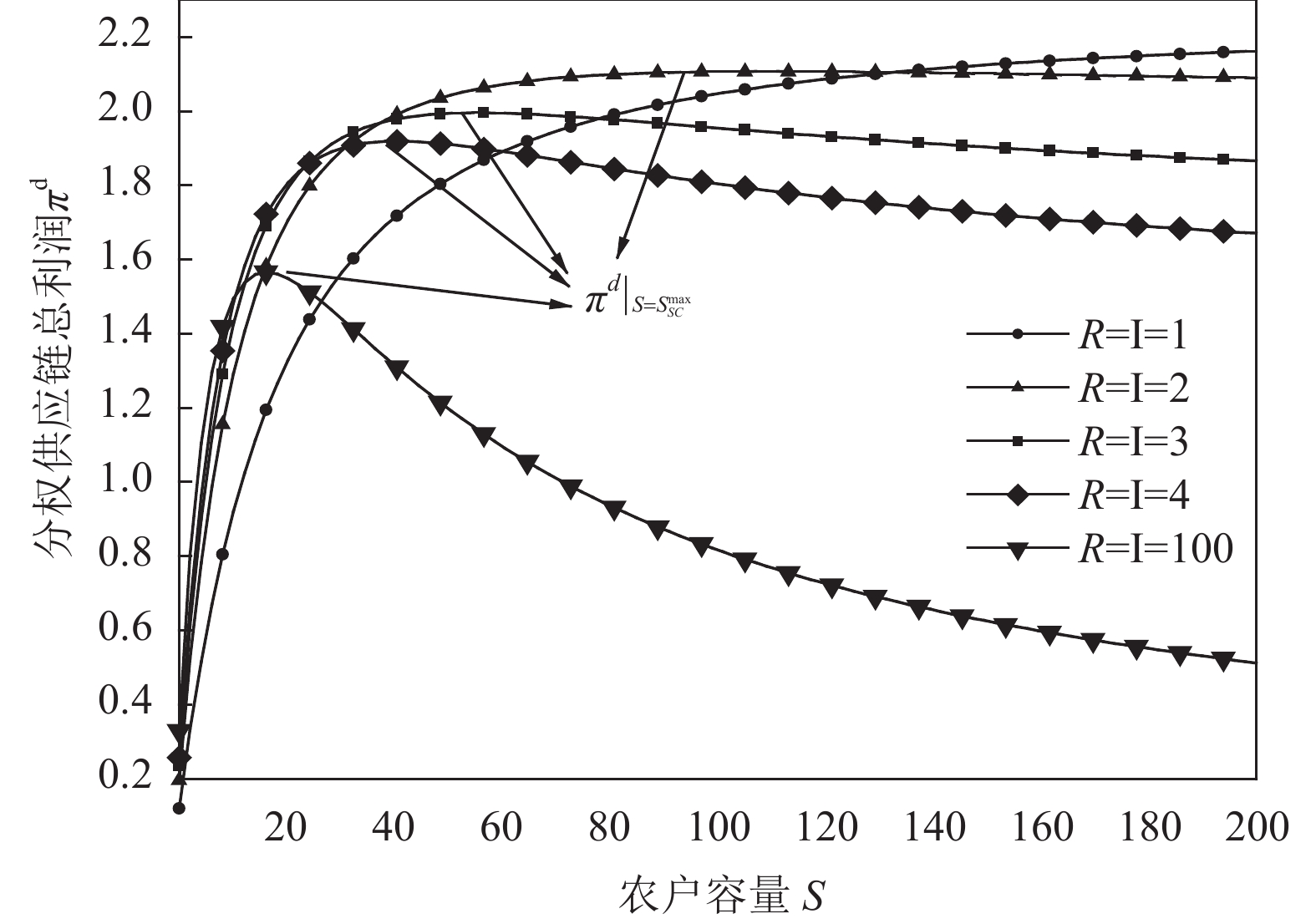
|
图 3 分权供应链总利润关于I和R的变化 Fig. 3 The total profit of decentralized supply chain about I and R(θ~U[0.1, 0.9]) |
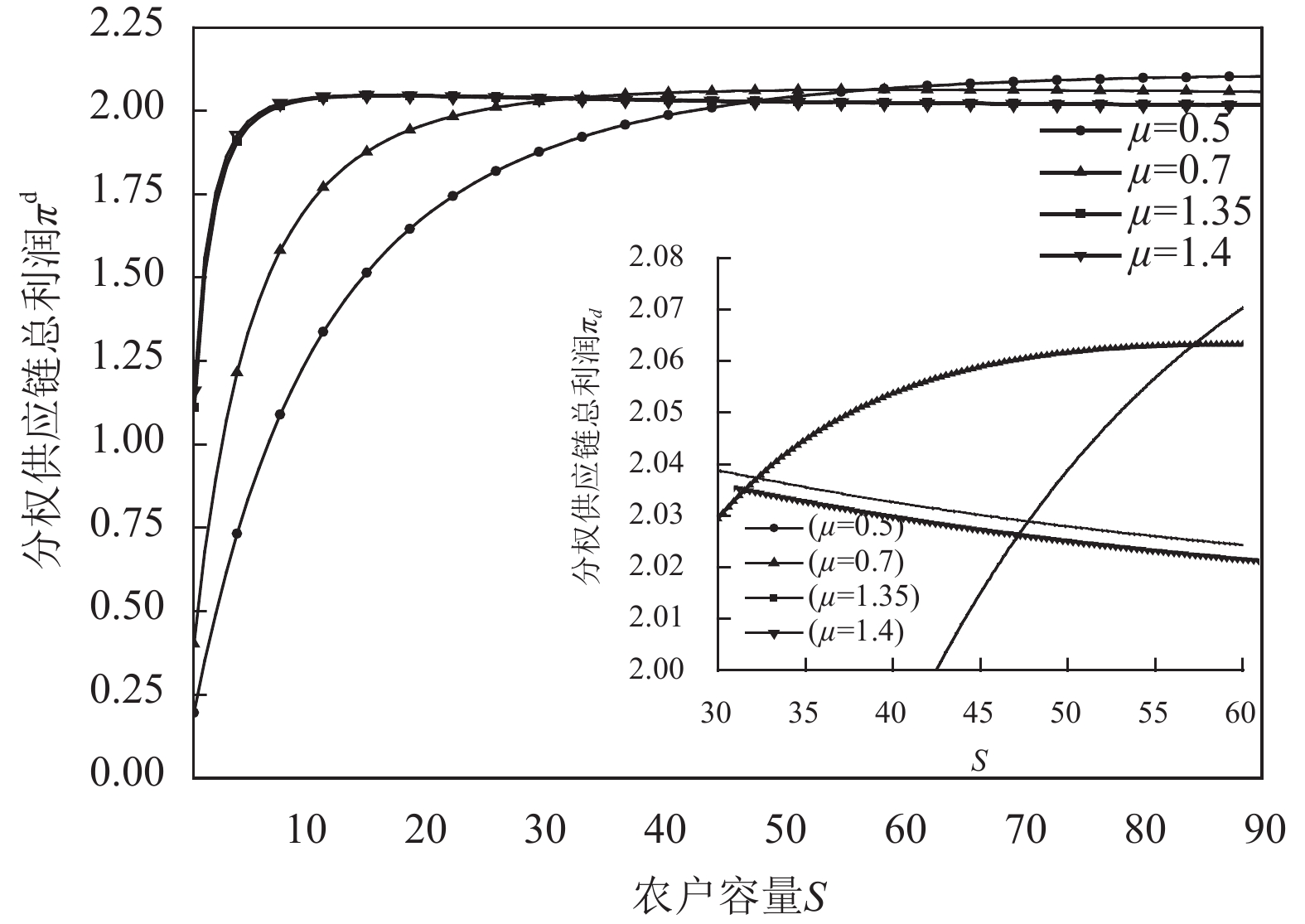
|
图 4 分权供应链总利润关于均值μ的变化 Fig. 4 The total profit of decentralized supply chain about μ(R=I=2) |
在经济学中社会福利也可称为社会总剩余,其构成是消费者剩余和生产者剩余的综合,是衡量经济运行过程中市场主体总获得的有效指标。因此,在本文中社会福利的构成可转化为以下等式:
社会福利=消费者剩余+生产者剩余=(消费者最高支付意愿−消费者实际支付价格)+(企业总收入−企业总支付成本)+(合作社总收入−合作社总支付成本)+(农户总收入−农户总生产成本)=消费者最高支付意愿−农户总生产成本。
同时,借鉴刘天亮等[23]、黄建辉等[24]对社会福利的刻画方式,此时的社会福利可以表示为
| $\begin{split} &\quad\quadW\left({{Q^{\rm{d}}}} \right) = \int\limits_0^{{Q^{\rm{d}}}} {\left({a-bQ} \right)dQ} -\left[ {{s_1}{Q^{\rm{d}}} + \frac{{{s_2}}}{2}{{\left({{Q^{\rm{d}}}} \right)}^2}} \right] = \\&(a-{s_1}){Q^{\rm{d}}}-\frac{{b + {s_2}}}{2}{\left({{Q^{\rm{d}}}} \right)^2}{\text{。}}\end{split}$ |
此时,同命题2和3,可以得到命题4。
命题4 农户之间、合作社之间和企业之间同时存在水平竞争时,能够使社会福利最大化的农户容量为
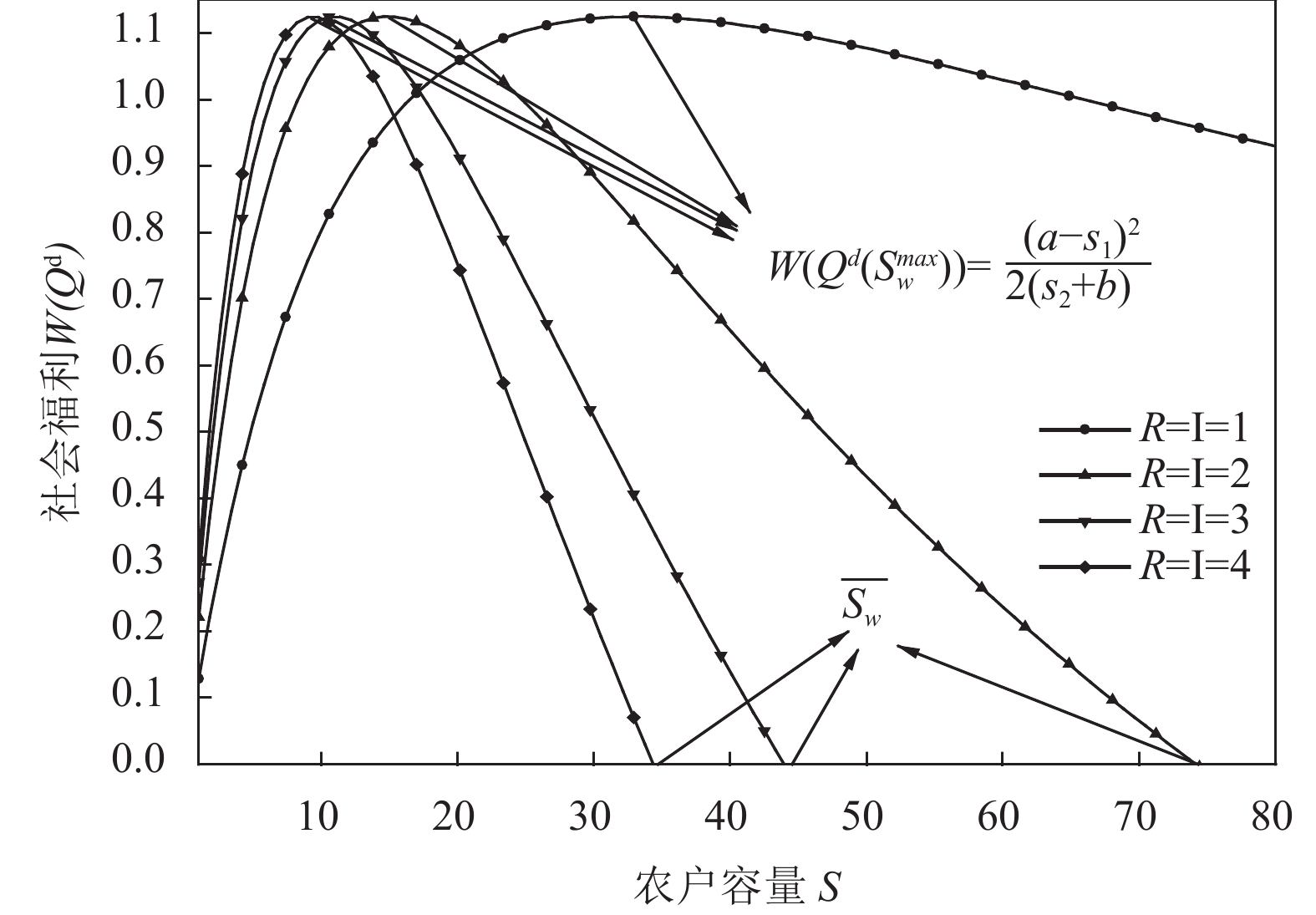
|
图 5 社会福利关于I和R的变化 Fig. 5 The social welfare about I and R(θ~U[0.1, 0.9]) |
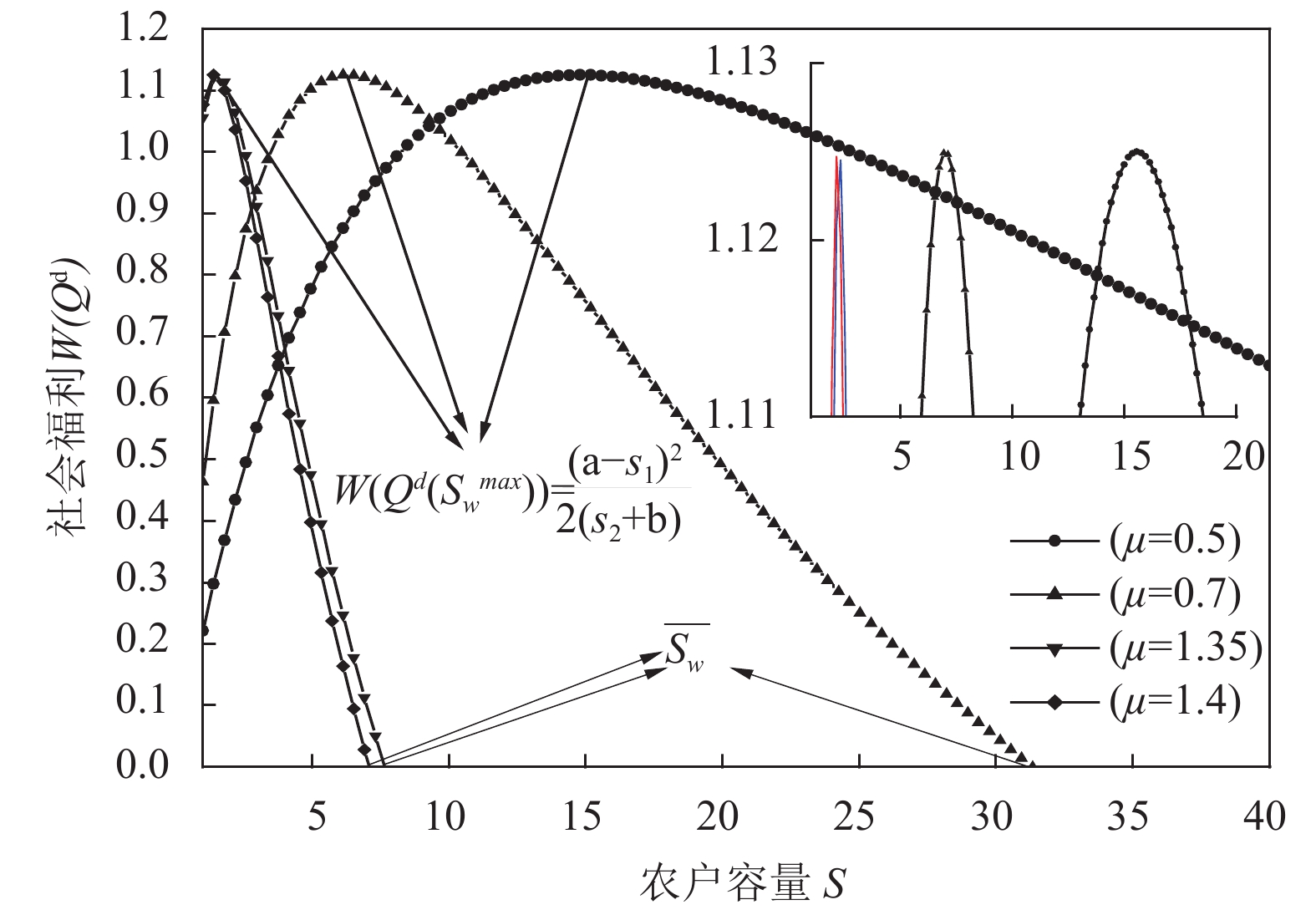
|
图 6 社会福利关于均值μ的变化 Fig. 6 The social welfare about μ(R=I=2) |
在此,本文将
命题5
| $\begin{split}&\quad\quad {\pi ^{{\rm{d1*}}}} = \frac{{R{{(a-{s_1})}^2}}}{{2b{{(R + 1)}^2}}}\left[ {1 + \frac{R}{{2(I + 1)}} + \frac{{\mu RI \cdot E\left({1/\theta } \right)}}{{4(I + 1)}}} \right],\\&\quad\quad{\pi ^{{\rm{d3}}*}} = \frac{{{{(a-{s_1})}^2}}}{{(R + 1)({s_2} + b)}}\left[ {1 + \frac{{{s_2}R-b}}{{({s_2} + b)(I + 1)}} +}\right.\\&\left.{\frac{{\mu I\left({{s_2}R-b} \right) \cdot E\left({1/\theta } \right)}}{{2({s_2} + b)(I + 1)}}} \right]{\text{。}}\end{split}$ |
命题6 存在关于合作社数量I和企业数量R的农户容量区间
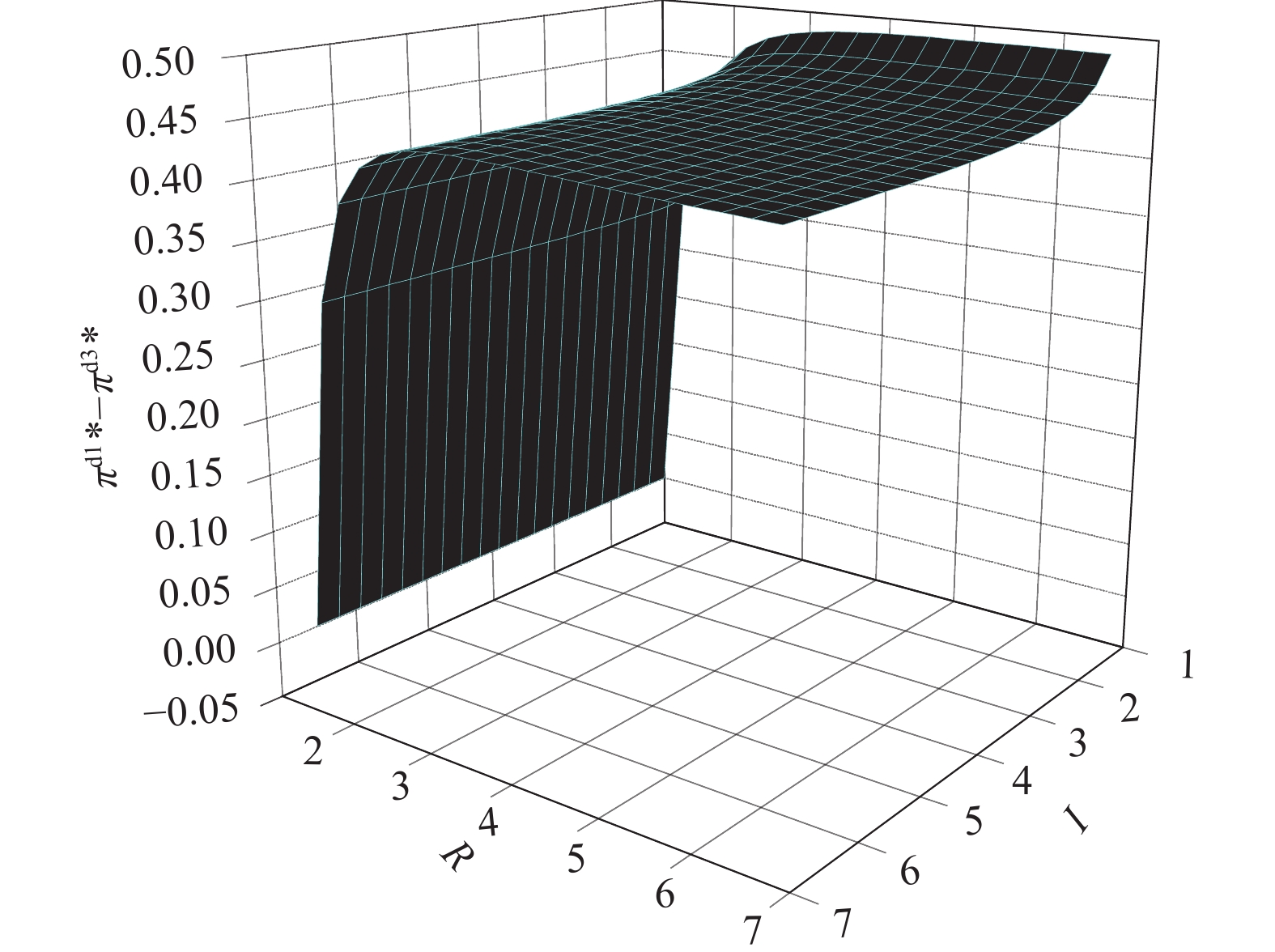
|
图 7 |
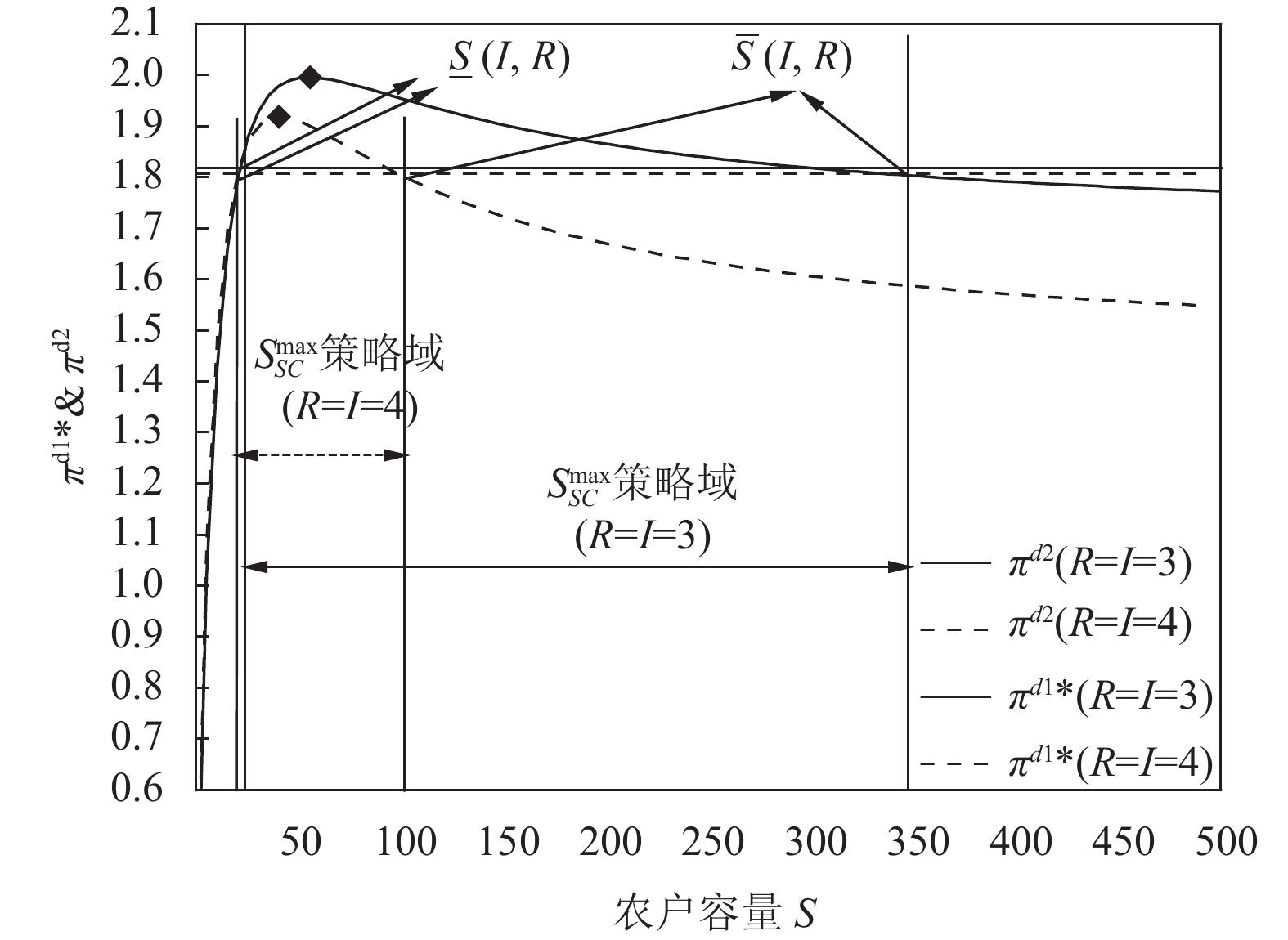
|
图 8 |
命题6表明当
在
| $\quad\quad\begin{array}{l}{\rm{VS}} = \left\{ {\left({I,R} \right):{\pi _{\rm{j}}}\left({{S^{\max }},I,R} \right) {\text{≥}} {F_{\rm{j}}}{\kern 1pt} {\kern 1pt},{\kern 1pt} {\kern 1pt} j = s,c,r} \right\},\\{\rm{VE}} = \left\{ \begin{array}{l}\left({I,R} \right) \in {\rm{VS}}:{\pi _{\rm{s}}}\left({{S^{\max }},I + 1,R} \right) {\text{≤}} {F_{\rm{s}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{或}}\\\quad{\kern 1pt} {\kern 1pt} {\kern 1pt} {\pi _{\rm{s}}}\left({{S^{\max }},I,R + 1} \right) {\text{≤}} {F_{\rm{s}}}\\\left({I,R} \right) \in {\rm{VS}}:{\pi _{\rm{c}}}\left({{S^{\max }},I + 1,R} \right) {\text{≤}} {F_{\rm{c}}}\\\left({I,R} \right) \in {\rm{VS}}:{\pi _{\rm{r}}}\left({{S^{\max }},I,R + 1} \right) {\text{≤}} {F_{\rm{r}}}\end{array} \right\}{\text{。}}\end{array}$ |
则农产品供应链各级成员加入供应链参与博弈和竞争的均衡条件可分别表示为
| $\quad\quad {\pi _{\rm{s}}}\left({{S^{\max }},I + 1,R + 1} \right) {\text{≤}} {F_{\rm{s}}} {\text{≤}} {\pi _{\rm{s}}}\left({{S^{\max }},I,R} \right),$ | (4) |
| $\quad\quad {\pi _{\rm{c}}}\left({{S^{\max }},I + 1,R} \right) {\text{≤}} {F_{\rm{c}}} {\text{≤}} {\pi _{\rm{c}}}\left({{S^{\max }},I,R} \right),$ | (5) |
| $\quad\quad{\pi _{\rm{r}}}\left({{S^{\max }},I,R + 1} \right) {\text{≤}} {F_{\rm{r}}} {\text{≤}} {\pi _{\rm{r}}}\left({{S^{\max }},I,R} \right){\text{。}}$ | (6) |
其中,
结合式(4)~(9),可以将
| $\begin{split}\quad\quad {\pi _{\rm{s}}}\left({S_{\rm{c}}^{\max },I,R} \right) ={\frac{\mu E(1/\theta)(a-s_1)^2}{8b}}\frac{{I{R^2}}}{{(I + 1){{(R + 1)}^2}}},\end{split}$ | (7) |
| $\quad\quad{\pi _{\rm{c}}}\left({S_{\rm{c}}^{\max },I,R} \right) = \frac{{{{\left({a-{s_1}} \right)}^2}}}{{4b}}\frac{{{R^2}}}{{(I + 1){{(R + 1)}^2}}},$ | (8) |
| $\quad\quad {\pi _{\rm{r}}}\left({S_{\rm{c}}^{\max },I,R} \right) = \frac{{{{\left({a-{s_1}} \right)}^2}}}{{2b}}\frac{{{R^2}}}{{{{(R + 1)}^2}}}{\text{。}}$ | (9) |
| $\begin{split}&\quad\quad{\rm{V}}{{\rm{S}}_1} = \left\{ {I {\text{≥}} \frac{{{k_{\rm{s}}}{{(R + 1)}^2}}}{{{R^2}-{k_{\rm{s}}}{{(R + 1)}^2}}}} \right\},{k_{\rm{s}}} =\left({\frac{8bF_s}{{{ \mu E(1/\theta)(a-s_1)^2}}}}\right),\end{split}$ | (10) |
| $\quad\quad{\rm{V}}{{\rm{S}}_2} = \left\{ {I {\text{≤}} \frac{1}{{{k_{\rm{c}}}}}\frac{{{R^2}}}{{{{(R + 1)}^2}}}} \right\},\rm\left({{k_c} = \frac{{4b \cdot {F_{\rm{c}}}}}{{{{\left({a-{s_1}} \right)}^2}}}}\right) ,$ | (11) |
| $\begin{split}&\quad\quad{\rm{V}}{{\rm{S}}_3} = \left\{ {\frac{{-2{k_{\rm{r}}} + 1-\sqrt {1-4{k_{\rm{r}}}} }}{{2{k_{\rm{r}}}}} {\text{≤}} R {\text{≤}}}\right.\\&\left.{ \frac{{-2{k_{\rm{r}}} + 1 + \sqrt {1-4{k_{\rm{r}}}} }}{{2{k_{\rm{r}}}}}} \right\},\left({{k_{\rm{r}}} = \frac{{2b \cdot {F_{\rm{r}}}}}{{{{\left({a-{s_1}} \right)}^2}}} {\text{≤}} \frac{1}{4}} \right),\end{split}$ | (12) |
| $\quad\quad{\kern 1pt} {\rm{V}}{{\rm{S}}_4} = {\kern 1pt} \left\{ {I {\text{<}} \frac{1}{{{k_{\rm{c}}}}}} \right\} {\text{。}}$ | (13) |
| ${\pi _{\rm{s}}}\left({S_{\rm{w}}^{\max },I,R} \right) = \frac{\mu \cdot Eleft(1/heta{\rm{ }} \cdot {\left({a-{s_1}} \right)^2}2}{{({s_2} + b)^2}}\frac{{I({s_2}R-b)}}{{(I + 1)(R + 1)}},$ | (14) |
| ${\pi _{\rm{c}}}\left({S_{\rm{w}}^{\max },I,R} \right) = \frac{{{{\left({a-{s_1}} \right)}^2}}}{{{{({s_2} + b)}^2}}}\frac{{({s_2}R-b)}}{{(I + 1)(R + 1)}} , $ | (15) |
| ${\pi _{\rm{r}}}\left({S_{\rm{c}}^{\max },I,R} \right) = \frac{{{{\left({a-{s_1}} \right)}^2}}}{{{{({s_2} + b)}^2}}}\frac{1}{{(R + 1)}} {\text{。}}$ | (16) |
| $\begin{split}{\rm{V}}{{\rm{S}}_1} \!=\! \left\{ {I {\text{≥}} \frac{{2{k_{\rm{s}}}(R + 1)}}{{\left({{s_2}R\!-\!b} \right)\!-\!2{k_{\rm{s}}}(R \!+\! 1)}}} \right\},\left({k_{\rm{s}}} = {\frac{(s_2+b)^2F_s}{\mu E(1/\theta)(a\!-\!s_1)^2}},\right)\end{split}$ | (17) |
| ${{\rm VS}_2} = \left\{ {I {\text{≤}} \frac{1}{{{k_{\rm{c}}}}}\frac{{\left({{s_2}R-b} \right)}}{{(R + 1)}}-1} \right\},\left({{k_{\rm{c}}} = \frac{{{{({s_2} + b)}^2} \cdot {F_{\rm{c}}}}}{{{{\left({a-{s_1}} \right)}^2}}}} \right),$ | (18) |
| ${{\rm VS}_3} = \left\{ {R {\text{≤}} \frac{{({s_2} + b)}}{{{k_{\rm{r}}}}}-1} \right\},\left({{k_{\rm{r}}} = \frac{{{{({s_2} + b)}^2} \cdot {F_{\rm{r}}}}}{{{{\left({a-{s_1}} \right)}^2}}}} \right){\text{。}}$ | (19) |
由以上公式,可以得到以下命题。
命题7 1) 不等式(10)~(13)和(17)~(19)分别保证了
根据式(4)~(6),可知在集合VS中,上界最大值
| $\begin{split}&\quad\quad{\pi _{\rm{s}}}\left({{S^{\max }},\overline I + 1,R} \right) {\text{<}} {F_{\rm{s}}} {\text{或}} {\pi _{\rm{s}}}\left({{S^{\max }},I,\overline R + 1} \right) {\text{<}} {F_{\rm{s}}}\;\;,\\&{\pi _{\rm{c}}}\left({{S^{\max }},\overline I + 1,R} \right) {\text{<}} {F_{\rm{c}}} , {\pi _{\rm{r}}}\left({{S^{\max }},I,\overline R + 1} \right) < {F_{\rm{r}}}{\text{。}}\end{split}$ |
这意味着供应链中多增加一个成员会使各级成员的利润都低于最低非负均衡利润,出现亏损状况。因此,为避免成员利润亏损,现有成员将会选择阻止其他成员进入供应链参与竞争和博弈,上界最大值
2) 下界组合
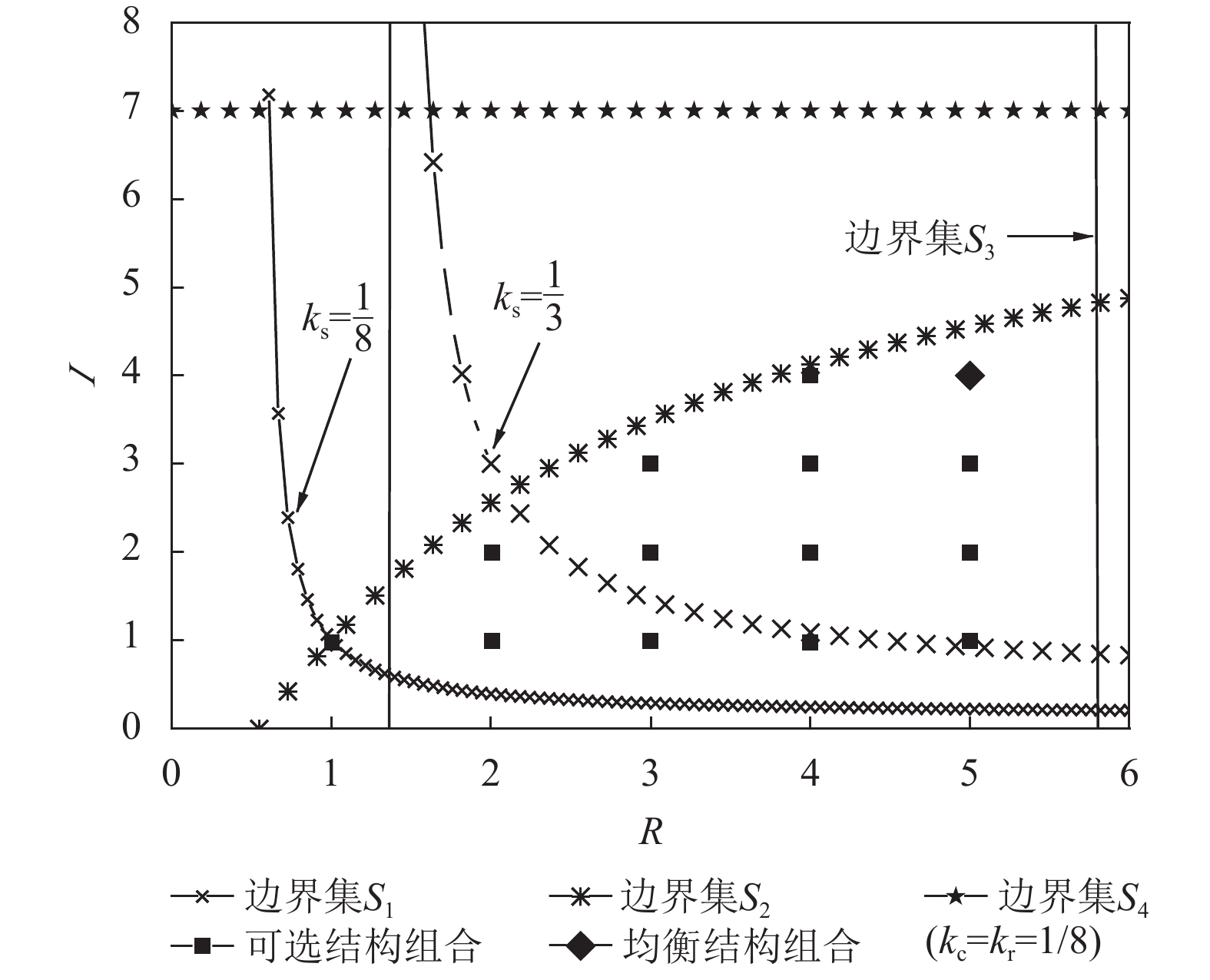
|
图 9 |
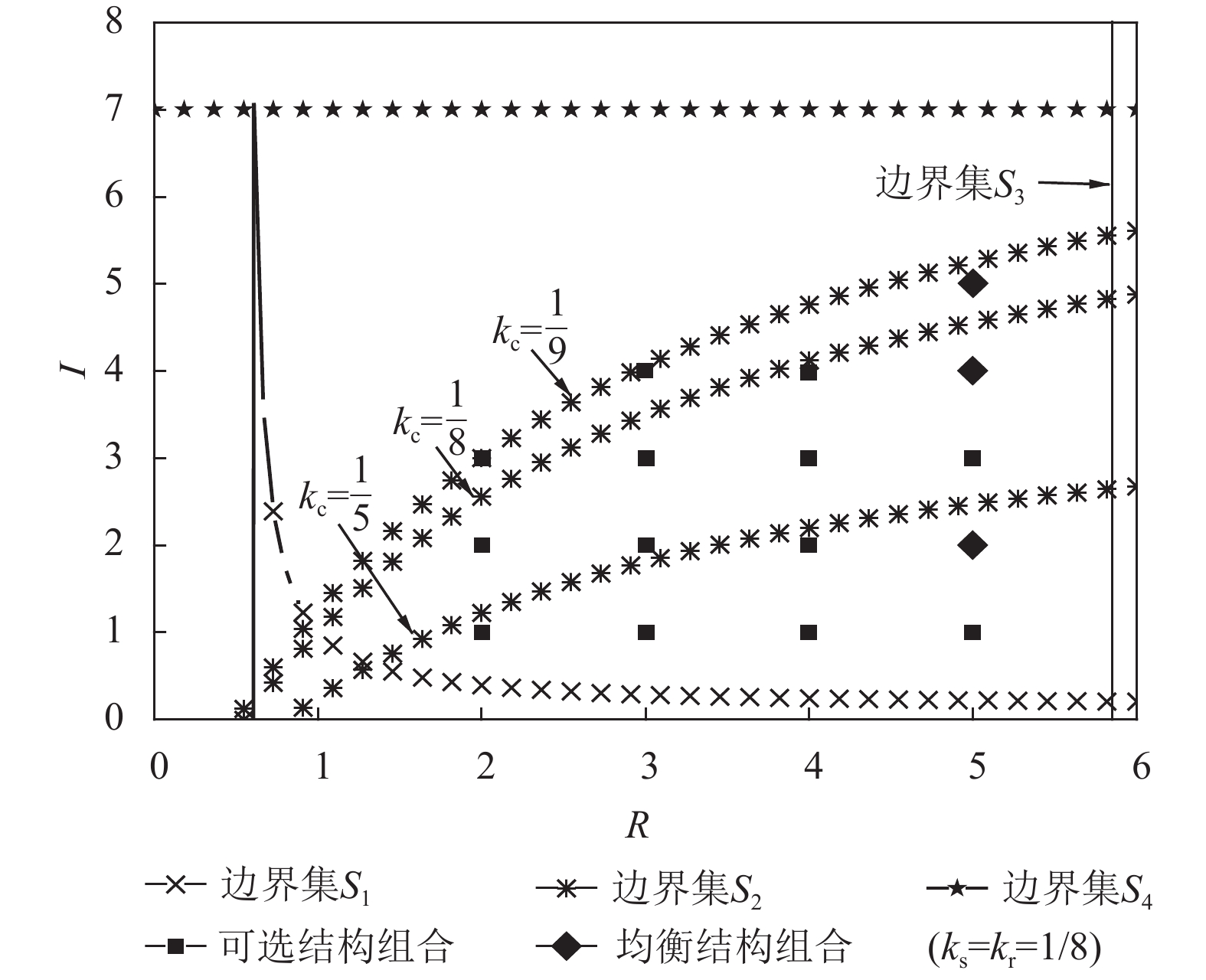
|
图 10 |
3)
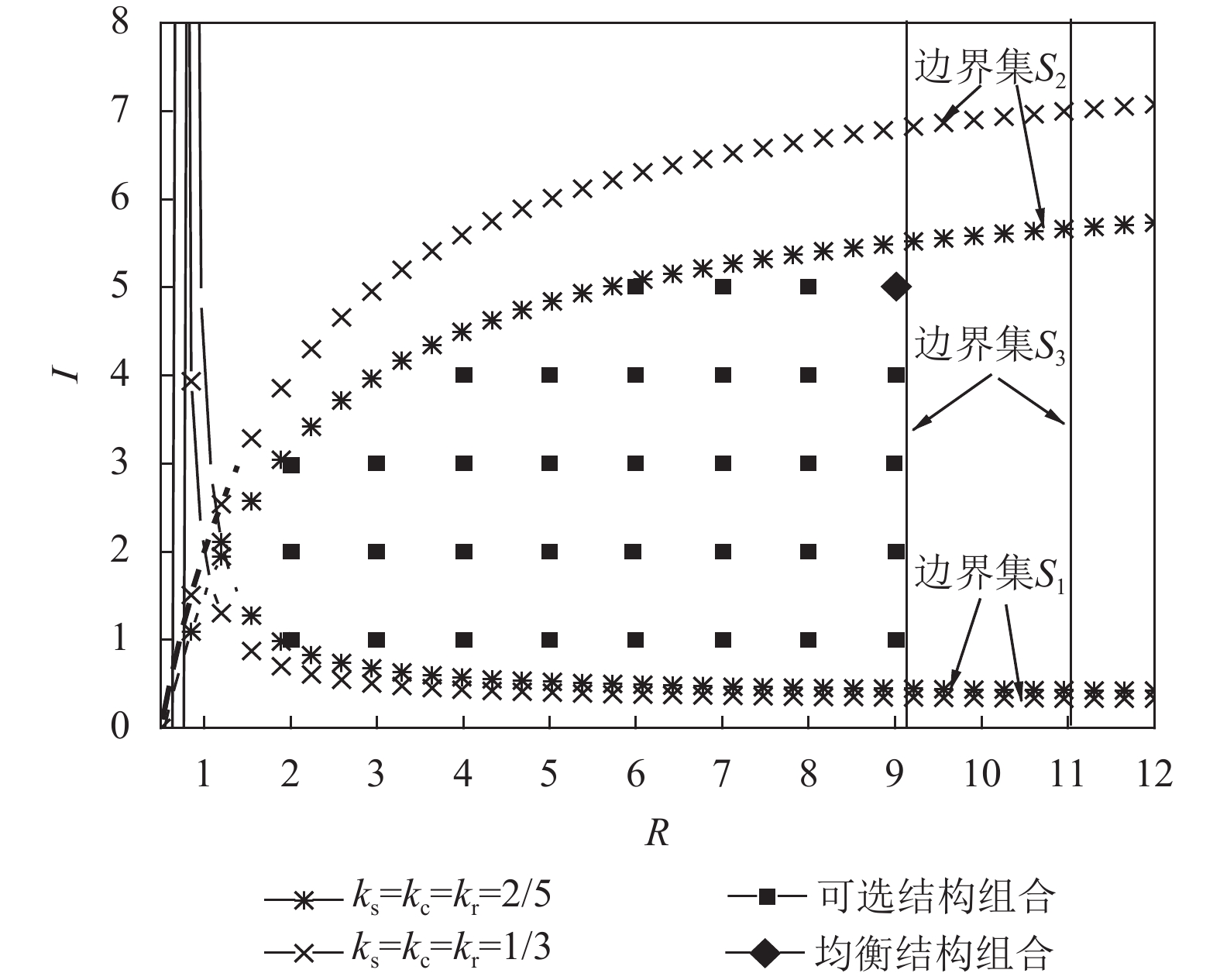
|
图 11 |
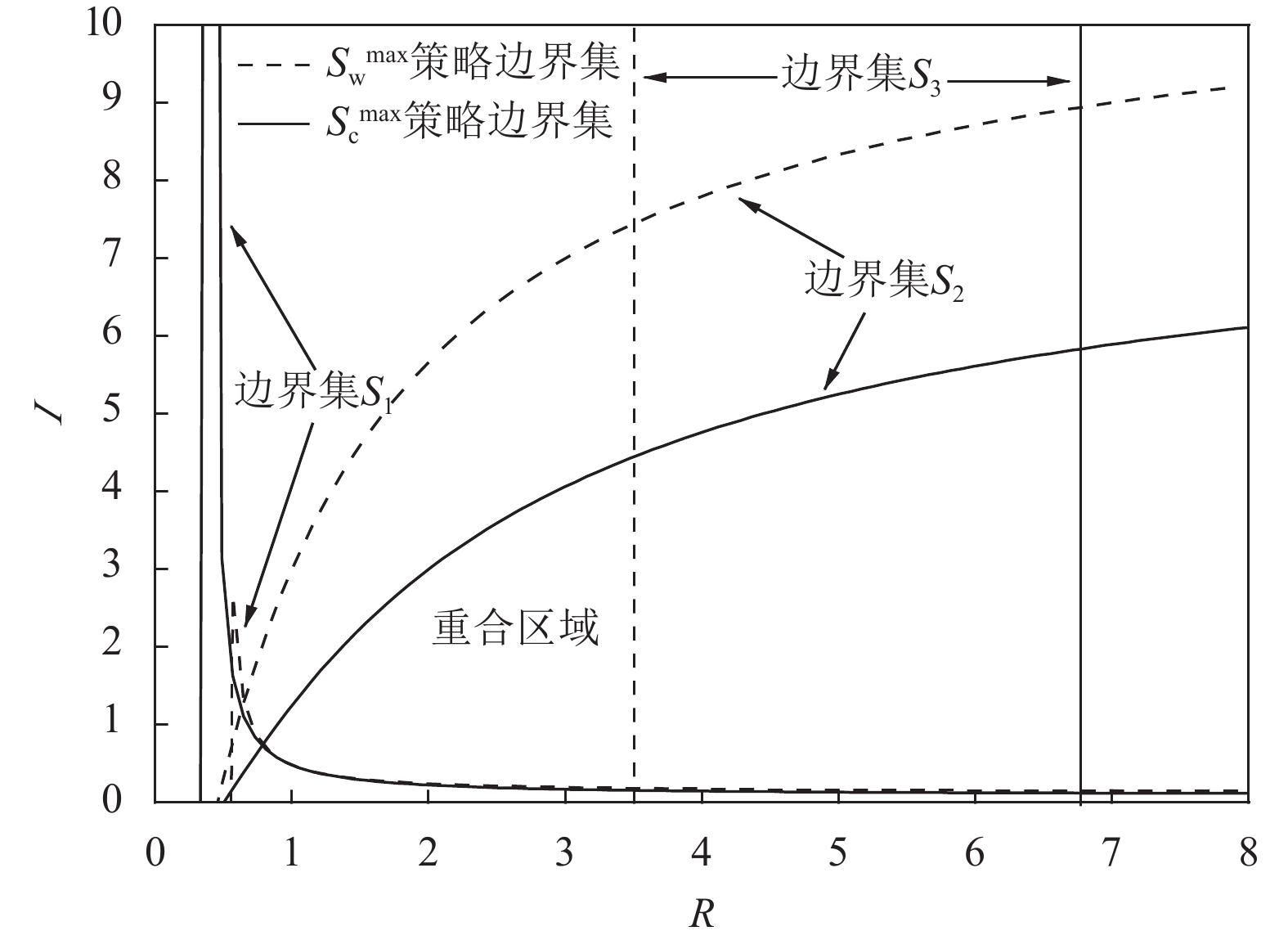
|
图 12 |
本文考虑随机产出下,以由公司为主导,生产农产品的农户与合作社参与的“农户+合作社+公司”三级农产品供应链为载体,在求解供应链成员存在水平竞争和垂直竞争均衡解的基础上,主要探讨了如何确定农户容量、下游成员数量如何影响其参与博弈的竞争空间、供应链的均衡结构和容纳能力等问题。提出合作社利润最优(
1)
2) 在
3) 下游成员数量取上界组合时的农产品供应链结构达到均衡状态,供应链的容纳能力也达到最大值,现有成员将阻止其他主体进入供应链参与博弈与竞争,供应链无法再吸纳其他成员。
4)
本文在得到上述结论和启示的同时,研究内容尚存在一定的不足与展望之处。一,由于
| [1] |
吴彬, 徐旭初. 农民专业合作社的益贫性及其机制[J].
农村经济, 2009, 27(3): 115-117.
WU Bin, XU Xuchu. The benefit poverty and mechanism of farmers' specialized cooperatives[J]. Rural Economy, 2009, 27(3): 115-117. |
| [2] |
孔祥智. 合作社的益贫性[J].
中国农民合作社, 2016, 8(7): 38-38.
KONG Xiangzhi. The benefit poverty of cooperatives[J]. CHINA FARMERS’COOPERATIVES, 2016, 8(7): 38-38. DOI: 10.3969/j.issn.1674-5914.2016.07.019. |
| [3] |
AN J, CHO S, TANG CS. Aggregating smallholder farmers in emerging economies[J].
Production & Operations Management, 2015, 24(9): 1414-1429.
|
| [4] |
浦徐进, 吴林海. 农户合作经济组织的增收效应分析:一个新的委托-代理视角[J].
软科学, 2010, 24(12): 93-96.
PU Xujin, WU Linhai. Analysis of the increased revenues’effect of farmers’cooperative economic organizations-A new principal-agent model[J]. Soft Science, 2010, 24(12): 93-96. DOI: 10.3969/j.issn.1001-8409.2010.12.021. |
| [5] |
SEXTON R J. Imperfect competition in agricultural markets and the role of cooperatives: a spatial analysis[J].
American Journal of Agricultural Economics, 1990, 72(3): 709-720.
DOI: 10.2307/1243041. |
| [6] |
BONTEMS P, FULTON M. Organizational structure, redistribution and the endogeneity of cost: cooperatives, investor-owned firms and the cost of procurement[J].
Journal of Economic Behavior & Organization, 2005, 72(1): 322-343.
|
| [7] |
JANG W, KLEIN C M. Supply chain models for small agricultural enterprises[J].
Annals of Operations Research, 2011, 190(1): 359-374.
DOI: 10.1007/s10479-009-0521-8. |
| [8] |
THIEDIG F, SYLVANDER B S. Welcome to the club? An economical approach to geographical indications in the european union[J].
Agrarwirtschaft, 2000, 49(12): 428-437.
|
| [9] |
许晶晶, 周军, 管珊红. 江西省橘类地理标志农产品发展现状与对策[J].
南方农业学报, 2014, 45(8): 1514-1518.
XU Jingjing, ZHOU Jun, GUAN Shanhong. Developmental status and countermeasures of citrus agricultural products with geographical indication in Jiangxi Province[J]. Journal of Southern Agriculture, 2014, 45(8): 1514-1518. DOI: 10.3969/j:issn.2095-1191.2014.8.1514. |
| [10] |
CORBETT C J, KARMARKAR U S. Competition and Structure in Serial Supply Chains with Deterministic Demand[J].
Management Science, 2001, 47(7): 966-978.
DOI: 10.1287/mnsc.47.7.966.9799. |
| [11] |
ADIDA E, DE MIGUEL V. Supply chain competition with multiple manufacturers and retailers[J].
Operations Research, 2011, 59(59): 156-172.
|
| [12] |
ADIDA E, BAKSHI N, DE MIGUEL V.. Supplier capacity and intermediary profits: can less be more[J].
Production & Operations Management, 2015, 25(4): 630-646.
|
| [13] |
杨天剑, 武兵, 李主贺. 三种由企业主导的双渠道供应链结构在生产成本扰动下的鲁棒性比较[J].
计算机集成制造系统, 2016, 22(3): 846-858.
YANG Tianjian, WU Bing, LI Zhuhe. Robustness comparison of three dual-channel supply chain structure under production cost disruption[J]. Computer Integrated Manufacturing Systems, 2016, 22(3): 846-858. |
| [14] |
LI W, LI W, LI Z. Irrigation and fertilizer effects on water use and yield of spring wheat in semi-arid regions[J].
Agricultural Water Management, 2004, 67(1): 35-46.
DOI: 10.1016/j.agwat.2003.12.002. |
| [15] |
HE Y, ZHANG J. Random yield risk sharing in a two-level supply chain[J].
International Journal of Production Economics, 2008, 112(2): 769-781.
DOI: 10.1016/j.ijpe.2007.06.003. |
| [16] |
凌六一, 郭晓龙, 胡中菊, 等. 基于随机产出与随机需求的农产品供应链风险共担合同[J].
中国管理科学, 2013, 21(2): 50-57.
LING Liuyi, GUO Xiaolong, HU Zhongju, etc. The risk-sharing contracts under random yield and stochastic demand in agricultural supply chain[J]. Chinese Journal of Management Science, 2013, 21(2): 50-57. |
| [17] |
林强, 叶飞. " 公司+农户”型订单农业供应链的Nash协商模型[J].
系统工程理论与实践, 2014, 34(7): 1769-1778.
LIN Qiang, YE Fei. Coordination for" Company+Farmer” contract-farming supply chain under nash negotiation model[J]. Systems Engineering-Theory and Practice, 2014, 34(7): 1769-1778. |
| [18] |
HUH W T, ATHANASSOGLOU S, LALL U. Contract farming with possible reneging in a developing country: Can it work[J].
IIMB Management Review, 2012, 24(4): 187-202.
DOI: 10.1016/j.iimb.2012.06.003. |
| [19] |
叶飞, 黄建辉, 林强. 资金约束下订单农业供应链中的农户最优决策[J].
系统工程理论与实践, 2017, 37(6): 1467-1478.
YE Fei, HUANG Jianhui, LIN Qaing. The optimal production strategies of the farmer in contract-farming supply chain under capital constraint[J]. Systems Engineering-Theory & Practice, 2017, 37(6): 1467-1478. |
| [20] |
徐旭初.中国农民专业合作经济组织的制度分析[M]. 北京: 经济科学出版社, 2005.
|
| [21] |
ALBAKE S, SCHULTZ C.. One cow, one vote[J].
Scand. J. Econ, 1997, 99(4): 597-615.
DOI: 10.1111/sjoe.1997.99.issue-4. |
| [22] |
AGBO M, ROUSSELIÈRE D, SALANIÉ J.. Agricultural marketing cooperatives with direct selling: A cooperative-non-cooperation game[J].
Journal of Economic Behavior & Organization, 2015, 109(1): 56-71.
|
| [23] |
刘天亮, 陈剑, 辛春林. 凸需求情形下分权供应链运作效率及福利分析[J].
管理科学学报, 2011, 14(1): 61-68.
LIU Tianliang, CHEN Jian, XIN Chunlin. Analysis on social welfare and operational efficiency in decentralized supply chains with convex demand[J]. Journal of Management Sciences in China, 2011, 14(1): 61-68. |
| [24] |
黄建辉, 叶飞, 林强. 随机产出下考虑资金约束的农产品供应链补贴机制研究[J].
管理学报, 2017, 14(2): 277-285.
HUANG Jianhui, YE Fei, LIN Qaing. Government subsidy mechanism in agricultural supply chain considering capital constrain under random yield[J]. Chinese Journal of Management, 2017, 14(2): 277-285. DOI: 10.3969/j.issn.1672-884x.2017.02.015. |
 2018, Vol. 21
2018, Vol. 21

