2. 江南大学 商学院,江苏 无锡 200237
2. School of Business, Jiangnan University, Wuxi 200237, China
我国经济建设和工业化进程取得了举世瞩目的成就,但也带来了资源短缺和环境污染等严重问题。再制造是以废旧机电产品为毛坯,运用高新再制造技术对其加工,使再制造产品性能恢复甚至超过新品的过程。它具有节约资源、降低能耗、减少污染物排放的显著功效(可节能60%、节材料70%、减少污染物排放80%以上)[1-2]。因此,它已被各国政府列为节能环保类战略新兴产业,并成为发展循环经济和实现可持续发展的重要战略手段之一[3-4]。
再制造闭环供应链定价问题是目前研究的热点[5]。王玉燕等[6]和Maiti 等[7]采用Stackelberg博弈和Nash均衡探讨了包含制造商、零售商与第三方回收商的闭环供应链定价策略;王文宾等[8]和Gao等[9]采用Stackelberg博弈和Nash均衡探讨集中式和分散式决策情形的二级闭环供应链定价问题,并运用二部定价契约分析制造商主导、零售商主导和垂直Nash均衡等不同渠道权力结构下各主体利益协调问题;郭亚军等[10]、葛静燕等[11]分别研究了第三方回收和零售商回收情况下的二级闭环供应链定价策略;孙浩等[12]、郭军华等[13]和刘家国等[14]则分别单独考虑新产品与再制造品价格差异或质量差异,探讨了制造商与零售商的二级再制造闭环供应链最优差别定价问题。此外,洪宪培等[15] 研究了闭环供应链定价与回收渠道选择问题。国内外学者在再制造闭环供应链定价研究方面取得了丰富成果,然而现有研究仍未成熟,尚未探讨不同渠道权力结构下考虑回收产品质量差异和新产品与再制造品价格差异这一复杂情境的最优定价问题。而该问题是目前各成员企业最为关注的难点。
针对上述情况,本研究拟构建综合考虑不同渠道权力结构和产品双重差异(回收产品拆解质量差异和新产品、再制造产品价格差异)的三级再制造闭环供应链最优定价决策模型,综合运用Stackelberg主从博弈与微分极值法进行模型求解,从而获得各成员企业的单位新产品、再制造品的最优批发价与零售价、单位废旧产品最优回收价及其相关利润。在此基础上,着重分析废旧产品回收率和产品替代系数等关键参数对各成员企业的最优定价及其利润的影响,从而为再制造闭环供应链各成员企业的科学决策提供参考。
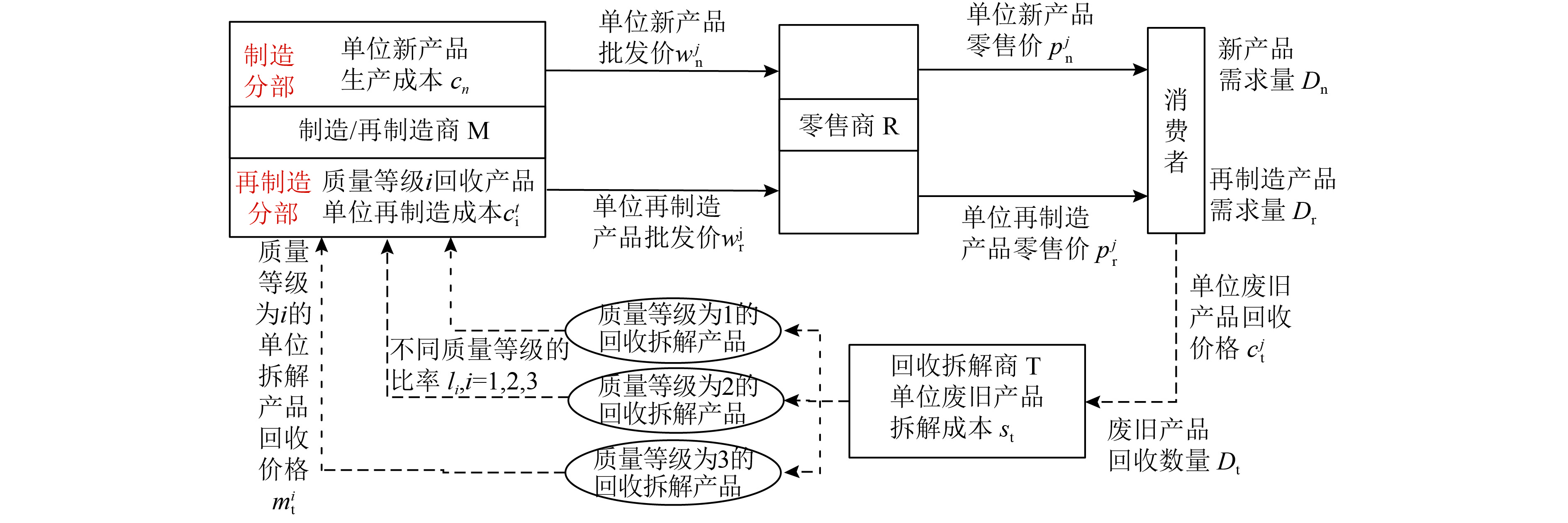
1 问题描述及模型基本假设 1.1 问题描述本文所研究的三级再制造闭环供应链RCLSC(remanufacturing closed-loop supply chain)的结构及其运作流程如图1所示。该闭环供应链具有不同的渠道权力结构j(
|
图 1 三级再制造闭环供应链系统结构及其运作流程图 Fig. 1 Structure and operation flow chart of three-stage remanufacturing closed-loop supply chain system |
研究所涉及的符号及其具体含义如表1所示。
| 表 1 模型的符号定义 Tab. 1 Symbolic definition of the model |
在表1中,单位新产品与再制造产品的批发价
为了确保研究的科学性和针对性,本文结合现实情况提出如下基本假设。
1) 新产品与再制造产品的需求量函数
2) 废旧产品回收量函数
3) 单位废旧产品拆解后分为3个质量等级(采用
4) 为了确保制造与再制造生产能够获得利润,单位产品的批发价、零售价以及生产、再制造成本存在如下关系:
5) RCLSC各成员企业均按照自身利益最大化原则开展决策,且成员企业之间信息透明
2 不同渠道权力结构下RCLSC最优定价策略 2.1 制造/再制造商M为渠道权力主导的RCLSC最优定价策略在以制造/再制造商M为主导的再制造闭环供应链中,制造/再制造商M是Stackelberg博弈的领导者,而零售商R和回收拆解商T为跟随者。前者首先决定单位新产品与再制造产品的批发价
1) 制造/再制造商M的利润
| $\begin{split} &\quad\quad {\text{π}} _{\rm{M}}^{\rm{M}} = {D_{\rm{n}}}(w_{\rm{n}}^{\rm{M}} - {c_{\rm{n}}}) + {D_{\rm{r}}}(w_{\rm{r}}^{\rm{M}} - {c_{\rm{r}}}) - {D_{\rm{t}}}{m_{\rm{t}}} =\\ &({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{M}} + \delta p_{\rm{r}}^{\rm{M}})(w_{\rm{n}}^{\rm{M}} - {c_{\rm{n}}}) + ({d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{M}} + \delta p_{\rm{n}}^{\rm{M}})(w_{\rm{r}}^{\rm{M}} - {c_{\rm{r}}}) -\\ &[\tau ({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{M}} + \delta p_{\rm{r}}^{\rm{M}} + {d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{M}} + \delta p_{\rm{n}}^{\rm{M}}){\rm{ + }}\alpha c_{\rm{t}}^{\rm{M}}]{m_{\rm{t}}}{\text{。}}\end{split}$ |
2) 零售商R的利润
| $\begin{split} &\quad\quad{\text{π}} _{\rm{R}}^{\rm{M}} = {D_{\rm{n}}}(p_{\rm{n}}^{\rm{M}} - w_{\rm{n}}^{\rm{M}}) + {D_{\rm{r}}}(p_{\rm{r}}^{\rm{M}} - w_{\rm{r}}^{\rm{M}}){\rm{ = }}\\&({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{M}} + \delta p_{\rm{r}}^{\rm{M}})(p_{\rm{n}}^{\rm{M}} - w_{\rm{n}}^{\rm{M}}) + ({d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{M}} + \delta p_{\rm{n}}^{\rm{M}})(p_{\rm{r}}^{\rm{M}} - w_{\rm{r}}^{\rm{M}}){\text{。}}\end{split}$ |
3) 回收拆解商T的利润
| $\begin{split}&\quad\quad{\text{π}} _{\rm{T}}^{\rm{M}} = {D_{\rm{t}}}({m_{\rm{t}}} - c_{\rm{t}}^{\rm{M}} - {s_{\rm{t}}}){\rm{ = }}\\&[\tau ({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{M}} + \delta p_{\rm{r}}^{\rm{M}} + {d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{M}} + \delta p_{\rm{n}}^{\rm{M}}){\rm{ + }}\alpha c_{\rm{t}}^{\rm{M}}]({m_{\rm{t}}} - c_{\rm{t}}^{\rm{M}} - {s_{\rm{t}}}){\text{。}}\end{split}$ |
在上述利润函数中,
| $\quad\quad\mathop {\max }\limits_{w_{\rm{n}}^{\rm{M}},w_{\rm{r}}^{\rm{M}}} ({\text{π}}_{\rm{M}}^{\rm{M}}),\;\;\;{\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l}\mathop {\max }\limits_{p_{\rm{n}}^{\rm{M}},p_{\rm{r}}^{\rm{M}}} ({\text{π}} _{\rm{R}}^{\rm{M}}),\\\mathop {\max }\limits_{c_{\rm{t}}^{\rm{M}}} ({\text{π}} _{\rm{T}}^{\rm{M}}){\text{。}}\end{array} \right.$ |
在以零售商R为主导的再制造闭环供应链中,零售商R作为Stackelberg博弈的领导者,此时回收拆解商T和制造/再制造商M为跟随者。零售商R首先根据回收拆解商T和制造/再制造商M的反应函数决定单位新产品与再制造品的零售价
1) 零售商R的利润
| $\begin{split}&\quad\quad{\text{π}} _{\rm{R}}^{\rm{R}} = {D_{\rm{n}}}(p_{\rm{n}}^{\rm{R}} - w_{\rm{n}}^{\rm{R}}) + {D_{\rm{r}}}(p_{\rm{r}}^{\rm{R}} - w_{\rm{r}}^{\rm{R}}) =\\&\left( {{d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{R}} + \delta p_{\rm{r}}^{\rm{R}}} \right)(p_{\rm{n}}^{\rm{R}} - w_{\rm{n}}^{\rm{R}}) + \left( {{d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{R}} + \delta p_{\rm{n}}^{\rm{R}}} \right)(p_{\rm{r}}^{\rm{R}} - w_{\rm{r}}^{\rm{R}}){\text{。}}\end{split}$ |
2) 回收拆解商T的利润
| $\begin{split}&\quad\quad{\text{π}} _{\rm{T}}^{\rm{R}} = {D_{\rm{t}}}({m_{\rm{t}}} - c_{\rm{t}}^{\rm{R}} - {s_{\rm{t}}}) =\\& [\tau ({d_{\rm{n}}} -\varphi p_{\rm{n}}^{\rm{R}} + \delta p_{\rm{r}}^{\rm{R}} + {d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{R}} + \delta p_{\rm{n}}^{\rm{R}}){\rm{ + }}\alpha c_{\rm{t}}^{\rm{R}}]({m_{\rm{t}}} - c_{\rm{t}}^{\rm{R}} - {s_{\rm{t}}}){\text{。}}\end{split}$ |
3) 制造/再制造商M的利润
| $\begin{split}& \quad\quad {\text{π}} _{\rm{M}}^{\rm{R}} = {D_{\rm{n}}}(w_{\rm{n}}^{\rm{R}} - {c_{\rm{n}}}) + {D_{\rm{r}}}(w_{\rm{r}}^{\rm{R}} - {c_{\rm{r}}}) - {D_{\rm{t}}}{m_{\rm{t}}} = \\&({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{R}} + \delta p_{\rm{r}}^{\rm{R}})(w_{\rm{n}}^{\rm{R}} - {c_{\rm{n}}}) + ({d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{R}} + \delta p_{\rm{n}}^{\rm{R}})(w_{\rm{r}}^{\rm{R}} - {c_{\rm{r}}})-\\&[\tau ({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{R}} + \delta p_{\rm{r}}^{\rm{R}} + {d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{R}} + \delta p_{\rm{n}}^{\rm{R}}){\rm{ + }}\alpha c_{\rm{t}}^{\rm{R}}]{m_{\rm{t}}}{\text{。}} \end{split}$ |
在上述利润函数中,由于
| $\quad\quad\mathop {\max }\limits_{p_{\rm{n}}^{\rm{R}},p_{\rm{r}}^{\rm{R}}} ({\text{π}} _{\rm{R}}^{\rm{R}}),\;\;\;{\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l}\mathop {\max }\limits_{w_{\rm{n}}^{\rm{R}},w_{\rm{r}}^{\rm{R}}} ({\text{π}} _{\rm{M}}^{\rm{R}}),\\\mathop {\max }\limits_{c_{\rm{t}}^{\rm{R}}} ({\text{π}} _{\rm{T}}^{\rm{R}}){\text{。}}\end{array} \right.$ |
在以回收拆解商T为主导的RCLSC中,作为Stackelberg博弈领导者,回收拆解商T首先根据制造/再制造商M和零售商R的反应函数决定单位废旧产品的回收价格
1) 回收拆解商T的利润
| $\begin{split}&\quad\quad{\text{π}} _{\rm{T}}^{\rm{T}} = {D_{\rm{t}}}({m_{\rm{t}}} - c_{\rm{t}}^{\rm{T}} - {s_{\rm{t}}}) = \\&[\tau ({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{T}} + \delta p_{\rm{r}}^{\rm{T}} + {d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{T}} + \delta p_{\rm{n}}^{\rm{T}}){\rm{ + }}\alpha c_{\rm{t}}^{\rm{T}}]({m_{\rm{t}}} - c_{\rm{t}}^{\rm{T}} - {s_{\rm{t}}}){\text{。}}\end{split}$ |
2) 制造/再制造商M的利润
| $\begin{split}&\quad\quad {\text{π}} _{\rm{M}}^{\rm{T}} = {D_{\rm{n}}}(w_{\rm{n}}^{\rm{T}} - {c_{\rm{n}}}) + {D_{\rm{r}}}(w_{\rm{r}}^{\rm{T}} - {c_{\rm{r}}}) - {D_{\rm{t}}}{m_{\rm{t}}} = \\ &({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{T}} + \delta p_{\rm{r}}^{\rm{T}})(w_{\rm{n}}^{\rm{T}} - {c_{\rm{n}}}) + ({d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{T}} + \delta p_{\rm{n}}^{\rm{T}})(w_{\rm{r}}^{\rm{T}} - {c_{\rm{r}}}) -\\ & [\tau ({d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{T}} + \delta p_{\rm{r}}^{\rm{T}} + {d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{T}} + \delta p_{\rm{n}}^{\rm{T}}){\rm{ + }}\alpha c_{\rm{t}}^{\rm{T}}]{m_{\rm{t}}}{\text{。}}\end{split}$ |
3) 零售商R的利润
| ${\text{π}}_{\rm{R}}^{\rm{T}} = ( {{d_{\rm{n}}} - \varphi p_{\rm{n}}^{\rm{T}} + \delta p_{\rm{r}}^{\rm{T}}} )(p_{\rm{n}}^{\rm{T}} - w_{\rm{n}}^{\rm{T}}) + ( {{d_{\rm{r}}} - \varphi p_{\rm{r}}^{\rm{T}} + \delta p_{\rm{n}}^{\rm{T}}} )(p_{\rm{r}}^{\rm{T}} - w_{\rm{r}}^{\rm{T}})$ |
在上述利润函数中,由于
| $\quad\quad\mathop {\max }\limits_{c_{\rm{t}}^{\rm{T}}} (\pi _{\rm{T}}^{\rm{T}}){\text{。}}\;\;\;\;\;{\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l}\mathop {\max }\limits_{w_{\rm{n}}^{\rm{T}},w_{\rm{r}}^{\rm{T}}} (\pi _{\rm{M}}^{\rm{T}}),\\\mathop {\max }\limits_{p_{\rm{n}}^{\rm{T}},p_{\rm{r}}^{\rm{T}}} (\pi _{\rm{R}}^{\rm{T}}){\text{。}}\end{array} \right.$ |
不同渠道权力结构下的制造/再制造商M、零售商R和回收拆解商T的最优定价及其利润的均衡解如表2所示。
| 表 2 3种渠道权力结构下的均衡解1) Tab. 2 Equilibrium solution under three channel power structures |
命题1 1) 当制造/再制造商M和零售商R为渠道权力主导时,其对应的成员企业利润
证明 1)由表2可知,
| $\begin{split}&\quad\quad{\text{π}} _{\rm{M}}^{\rm{M}}{\rm{ - }}{\text{π}} _{\rm{M}}^{\rm{R}} = A\displaystyle\frac{{\varphi [{d_{\rm{n}}}{\rm{ - }}\varphi ({c_{\rm{n}}} + \displaystyle\frac{{\tau {m_{\rm{t}}}}}{2})] + \delta [{d_{\rm{r}}} + \delta ({c_{\rm{n}}} + \displaystyle\frac{{\tau {m_{\rm{t}}}}}{2})]}}{{4({\varphi ^2} - {\delta ^2})}} +\\&B\displaystyle\frac{{\varphi [{d_{\rm{r}}}{\rm{ - }}\varphi ({c_{\rm{r}}} + \displaystyle\frac{{\tau {m_{\rm{t}}}}}{2})] + \delta [{d_{\rm{n}}} + \delta ({c_{\rm{r}}} + \displaystyle\frac{{\tau {m_{\rm{t}}}}}{2})]}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\text{。}}\end{split}$ |
结合假设1)中的
| $\begin{split}&\quad\quad{\text{π}} _{\rm{M}}^{\rm{M}}{\rm{ - }}{\text{π}} _{\rm{M}}^{\rm{R}} {\text{>}} A\displaystyle\frac{{\varphi [{d_{\rm{n}}}{\rm{ - }}\varphi p_{\rm{n}}^j] + \delta [{d_{\rm{r}}} + \delta ({c_{\rm{n}}} + \displaystyle\frac{{\tau {m_{\rm{t}}}}}{2})]}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}} +\\&B\displaystyle\frac{{\varphi ({d_{\rm{r}}}{\rm{ - }}\varphi p_{\rm{r}}^j) + \delta [{d_{\rm{n}}} + \delta ({c_{\rm{r}}} + \displaystyle\frac{{\tau {m_{\rm{t}}}}}{2})]}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}} {\text{>}} 0{\text{。}}\end{split}$ |
由此可得
2) 根据表2容易获知
| $\begin{split}& {\text{π}} _{\rm{R}}^{\rm{M}}{\rm{ - }}{\text{π}} _{\rm{R}}^{\rm{T}} \!=\! \left[\frac{{\varphi {d_{\rm{n}}} \!+\! \delta {d_{\rm{r}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{n}}} \!+\! \tau {m_{\rm{t}}}}}{8}\right]A+\left[\frac{{\varphi {d_{\rm{r}}} \!+\! \delta {d_{\rm{n}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{r}}} \!+\! \tau {m_{\rm{t}}}}}{8}\right]B{\rm{ - }}\left[\frac{{\varphi {d_{\rm{n}}} \!+\! \delta {d_{\rm{r}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{n}}} \!+\! \tau {m_{\rm{t}}}}}{8}{\rm{ - }}\frac{{\tau {m_{\rm{t}}}}}{8}\right]C\!{\rm{ - }}\left[\frac{{\varphi {d_{\rm{r}}} + \delta {d_{\rm{n}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{r}}} \!+\! \tau {m_{\rm{t}}}}}{8}{\rm{ - }}\frac{{\tau {m_{\rm{t}}}}}{8}\right]D{\text{。}}\end{split}$ |
由于
| $\quad\quad\left\{ \begin{gathered} \frac{{\varphi {d_{\rm{n}}} + \delta {d_{\rm{r}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{n}}} \!+\! \tau {m_{\rm{t}}}}}{8} \!{\text{>}}\! \frac{{\varphi {d_{\rm{n}}} + \delta {d_{\rm{r}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{n}}} + \tau {m_{\rm{t}}}}}{8}{\rm{ - }}\frac{{\tau {m_{\rm{t}}}}}{8}, \\ \frac{{\varphi {d_{\rm{r}}} + \delta {d_{\rm{n}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{r}}}\! +\! \tau {m_{\rm{t}}}}}{8}\!{\text{>}} \!\frac{{\varphi {d_{\rm{r}}} + \delta {d_{\rm{n}}}}}{{4({\varphi ^2}{\rm{ - }}{\delta ^2})}}{\rm{ - }}\frac{{2{c_{\rm{r}}} + \tau {m_{\rm{t}}}}}{8}{\rm{ - }}\frac{{\tau {m_{\rm{t}}}}}{8}{\text{。}} \\ \end{gathered} \right.$ |
同时
依据上述等式可以获得如下不等式
3) 根据表2可知,
| $\begin{split}&\quad\quad{\text{π}} _{\rm{T}}^{\rm{M}}{\rm{ - }}{\text{π}} _{\rm{T}}^{\rm{T}}{\rm{ = }}(\displaystyle\frac{G}{8} + \tau A + \tau B)({m_{\rm{t}}} - {s_{\rm{t}}} - \displaystyle\frac{G}{{8\alpha }}) - \\&[(\displaystyle\frac{G}{8} + \tau A + \tau B - \displaystyle\frac{{(\varphi - \delta ){\tau ^2}{m_{\rm{t}}}}}{8})({m_{\rm{t}}} - {s_{\rm{t}}} - \displaystyle\frac{G}{{8\alpha }} - \displaystyle\frac{{(\varphi - \delta ){\tau ^2}{m_{\rm{t}}}}}{8})]{\text{。}}\end{split}$ |
由于
4) 依据表2可知,以制造/再制造商M和零售商R为渠道权力主导的RCLSC总利润
综合上述分析结果,可知1)
命题1说明,在RCLSC运行过程中,制造/再制造商M和零售商R为了获得更多利润,必须力争成为再制造闭环供应链的渠道权力主导,此时能够同时实现RCLSC总利润的最大化。而回收拆解商T成为渠道权力主导,则会最小化其自身利润以及RCLSC总利润。
命题2 对于制造/再制造商M和零售商R为渠道权力主导的两种情形,其单位新产品最优零售价
证明 由表2可知如下关系式:
| $\quad\quad\left\{ \begin{array}{l}p_{\rm{n}}^{\rm{M}} = p_{\rm{n}}^{\rm{R}},p_{\rm{n}}^{\rm{T}}{\rm{ - }}p_{\rm{n}}^{\rm{M}} = \displaystyle\frac{{{m_{\rm{t}}}\tau }}{8},\\p_{\rm{r}}^{\rm{M}} = p_{\rm{r}}^{\rm{R}},p_{\rm{r}}^{\rm{T}}{\rm{ - }}p_{\rm{r}}^{\rm{M}} = \displaystyle\frac{{{m_{\rm{t}}}\tau }}{8},\\c_{\rm{t}}^{\rm{M}} = c_{\rm{t}}^{\rm{R}},c_{\rm{t}}^{\rm{T}}{\rm{ - }}c_{\rm{t}}^{\rm{M}} = \displaystyle\frac{{(\varphi - \delta ){m_{\rm{t}}}{\tau ^2}}}{{8\alpha }}{\text{。}}\end{array} \right.$ |
根据假设1)中的
命题2说明:当回收拆解商T为渠道权力主导时,单位新产品与再制造产品的最优批发价
命题3 在3种渠道权力结构情形下,单位新产品与再制造产品的最优批发价
证明 研究以制造/再制造商M为渠道权力主导的情形加以证明,其他情况证明类似。依据表2中的最优定价,并结合假设1)中的
| $\begin{split}\quad\quad&\left\{ \begin{array}{l} \displaystyle\frac{{\text{∂} w_{\rm{n}}^{\rm{M}}}}{{\text{∂} \tau }} = \displaystyle\frac{{\text{∂} w_{\rm{r}}^{\rm{M}}}}{{\text{∂} \tau }} = \displaystyle\frac{{{m_{\rm{t}}}}}{4} {\text{>}} 0, \\ \displaystyle\frac{{\text{∂} w_{\rm{n}}^{\rm{M}}}}{{\text{∂} \delta }} = \displaystyle\frac{{3({\phi ^2} + {\delta ^2}){d_{\rm{r}}} + 2\phi \delta {d_{\rm{r}}}}}{{2{{({\phi ^2} - {\delta ^2})}^2}}} {\text{>}} 0, \\ \displaystyle\frac{{\text{∂} w_{\rm{r}}^{\rm{M}}}}{{\text{∂} \delta }} = \displaystyle\frac{{({\phi ^2} + {\delta ^2}){d_{\rm{n}}} + 2\phi \delta {d_{\rm{r}}}}}{{2{{({\phi ^2} - {\delta ^2})}^2}}} {\text{>}} 0{\text{。}}\end{array} \right.\\&\left\{ \begin{array}{l} \displaystyle\frac{{\text{∂} p_{\rm{n}}^{\rm{M}}}}{{\text{∂} \tau }} = \displaystyle\frac{{\text{∂} p_{\rm{r}}^{\rm{M}}}}{{\text{∂} \tau }} = \displaystyle\frac{{{m_{\rm{t}}}}}{8} {\text{>}} 0, \\ \displaystyle\frac{{\text{∂} p_{\rm{n}}^{\rm{M}}}}{{\text{∂} \delta }} = \displaystyle\frac{{3({\phi ^2} + {\delta ^2}){d_{\rm{r}}} + 6\phi \delta {d_{\rm{n}}}}}{{4{{({\phi ^2} - {\delta ^2})}^2}}} {\text{>}} 0, \\ \displaystyle\frac{{\text{∂} p_{\rm{r}}^{\rm{M}}}}{{\text{∂} \delta }} = \displaystyle\frac{{3({\phi ^2} + {\delta ^2}){d_{\rm{n}}} + 6\phi \delta {d_{\rm{r}}}}}{{4{{({\phi ^2} - {\delta ^2})}^2}}} {\text{>}} 0{\text{。}}\end{array} \right.\end{split}$ |
| $\quad\quad\left\{ \begin{array}{l}\displaystyle\frac{{\text{∂} c_{\rm{t}}^{\rm{M}}}}{{\text{∂} \tau }} = {\rm{ - }}\displaystyle\frac{{[({d_{\rm{n}}} + {d_{\rm{r}}}){\rm{ - }}(\varphi {\rm{ - }}\delta )({c_{\rm{n}}} + {c_{\rm{r}}} + 2{m_{\rm{t}}}\tau )]}}{{8\alpha }} {\text{<}} \\ {\rm{ - }}\displaystyle\frac{{[({d_{\rm{n}}} + {d_{\rm{r}}}){\rm{ - }}(\varphi {\rm{ - }}\delta )(p_{\rm{n}}^{\rm{M}} + p_{\rm{r}}^{\rm{M}})]}}{{8\alpha }}{\rm{ = - }}\displaystyle\frac{{{D_{\rm{n}}} + {D_{\rm{r}}}}}{{8\alpha }} {\text{<}} 0, \\\displaystyle\frac{{\text{∂} c_{\rm{t}}^{\rm{M}}}}{{\text{∂} \delta }} = {\rm{ - }}\displaystyle\frac{{\tau ({c_{\rm{n}}} + {c_{\rm{r}}} + {m_{\rm{t}}}\tau )}}{{8\alpha }} {\text{<}} 0{\text{。}}\end{array} \right.$ |
因此,单位产品与再制造产品的最优批发价
其他渠道权力结构下的证明与之类似,故略。命题3证毕。
4 案例分析:以汽车发电机再制造闭环供应链为例为了验证上述模型的科学性与有效性,本文以我国汽车发电机再制造闭环供应链为案例加以研究。通过深入调研国内最大的两家汽车发电机再制造企业和访谈再制造领域专家学者,获得了如表3所示的汽车发电机再制造闭环供应链模型各项参数数值。
根据表3的模型参数数值,计算获得其他的相关模型参数:
1) 新产品需求量
2) 再制造产品需求量
3)废旧产品回收量
4) 单位拆解产品综合回购价格
5) 单位再制造产品综合生产成本
| 表 3 汽车发动机再制造闭环供应链模型参数数值 Tab. 3 Parameter value of a remanufacturing closed-loop supply chain model for automotive engine |
利用获得的上述模型参数,本文将寻求3种渠道权力结构下RCLSC的最优定价及其成员企业的利润。在此基础上,研究将通过仿真分析重点讨论废旧产品回收率
根据第2节的RCLSC最优定价策略分析,计算并获得3种渠道权力结构下的各成员企业最佳定价及其利润的均衡解,如表4所示。
| 表 4 不同渠道权力结构下RCLSP最优定价及各成员企业利润的均衡解 Tab. 4 Optimal pricing and member’s profit of RCLSP under different channel power structures |
依据表4所示最优定价及成员企业利润均衡解,可以验证本文第3节命题的正确性。
4.2 关键参数对RCLSC最优定价及其利润的影响考虑到目前汽车发电机再制造闭环供应链以制造/再制造商M为渠道权力主导的情形最为常见,因此本文主要依托该渠道权力结构,进一步讨论废旧产品回收率
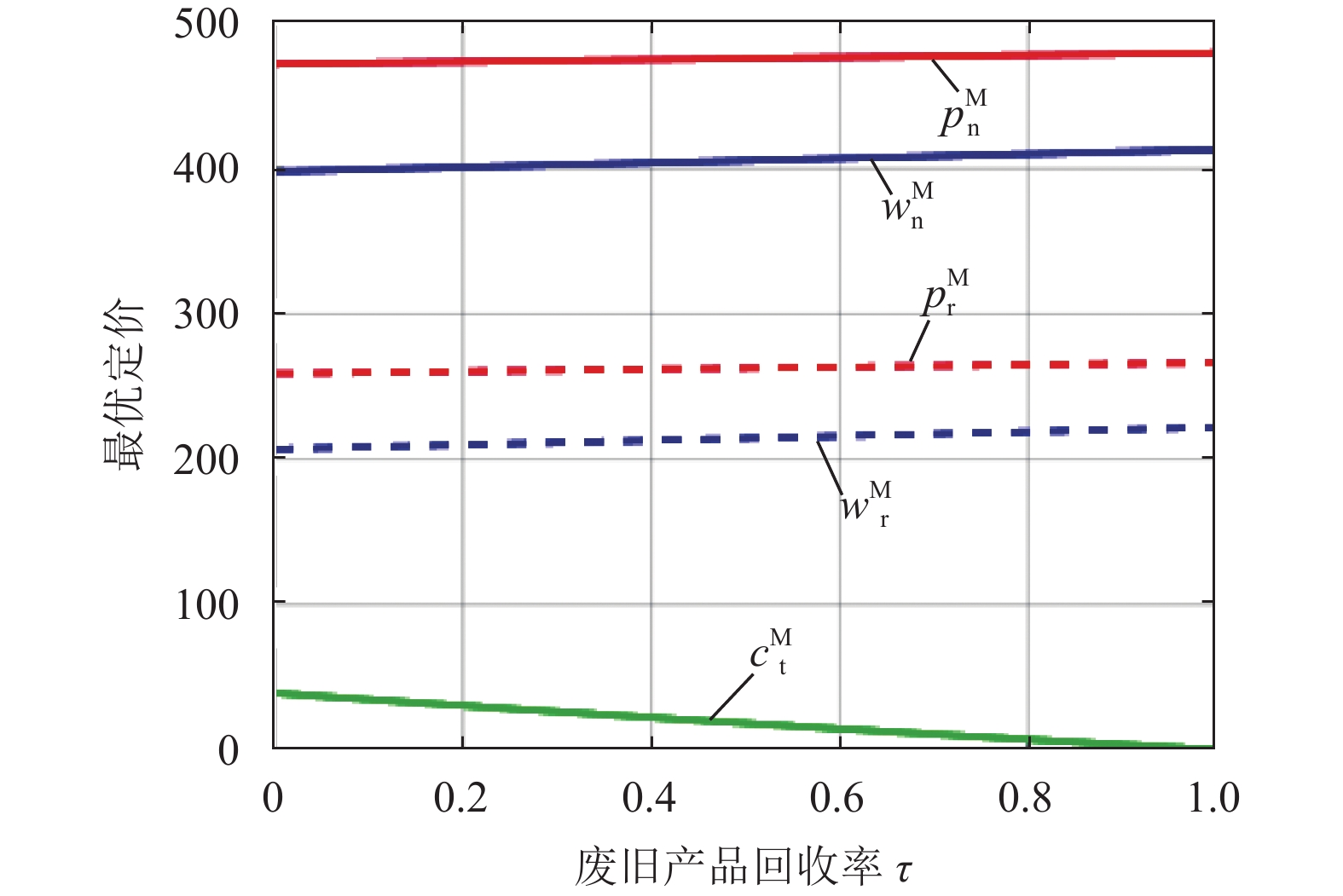
1) 废旧产品回收率
废旧产品回收率
|
图 2 废旧产品回收率
|
① 单位新产品与再制造产品的最优批发价
② 单位废旧产品的最优回收价
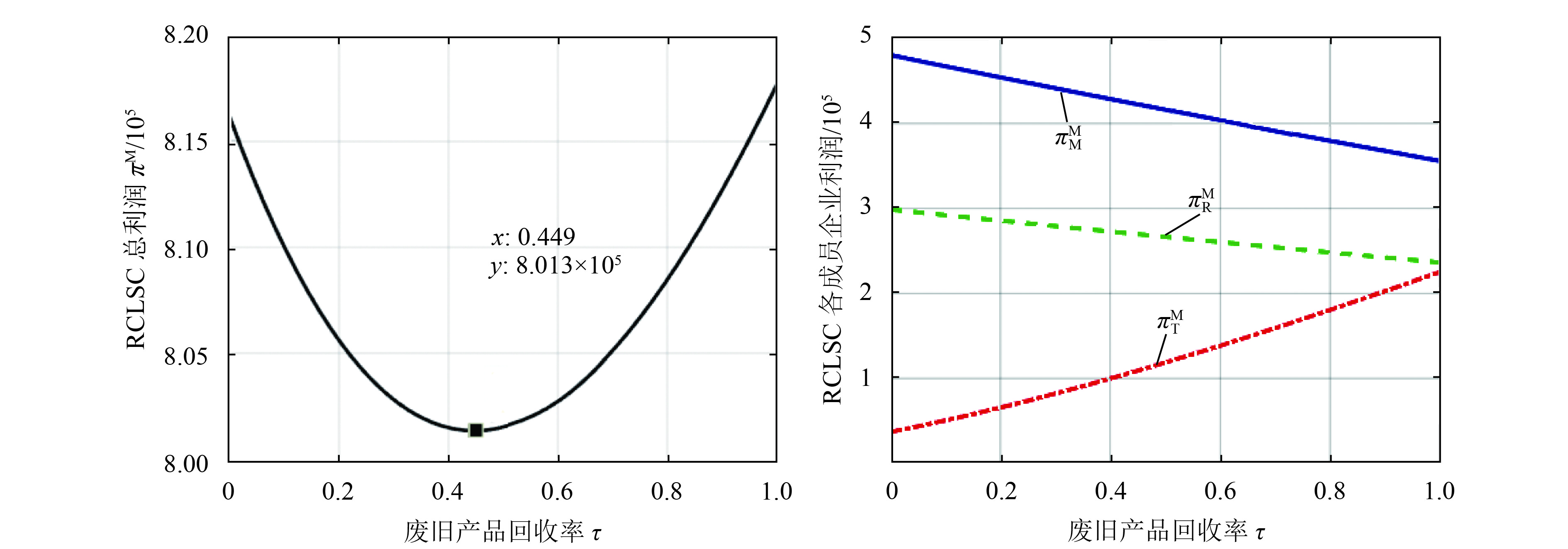
2) 废旧产品回收率
废旧产品回收率
|
图 3 废旧产品回收率
|
① RCLSC总利润
② 制造/再制造商M和零售商R的利润
③ 现行再制造产业政策设定的废旧产品回收利用率目标对于汽车发电机再制造不尽合理。2016年12月我国国务院办公厅印发了《生产者责任延伸制度推行方案》,其主要工作目标是将电器电子产品、汽车等重点推行产品的回收利用率提升到40%~50%。而从本文研究可知,当废旧产品回收率
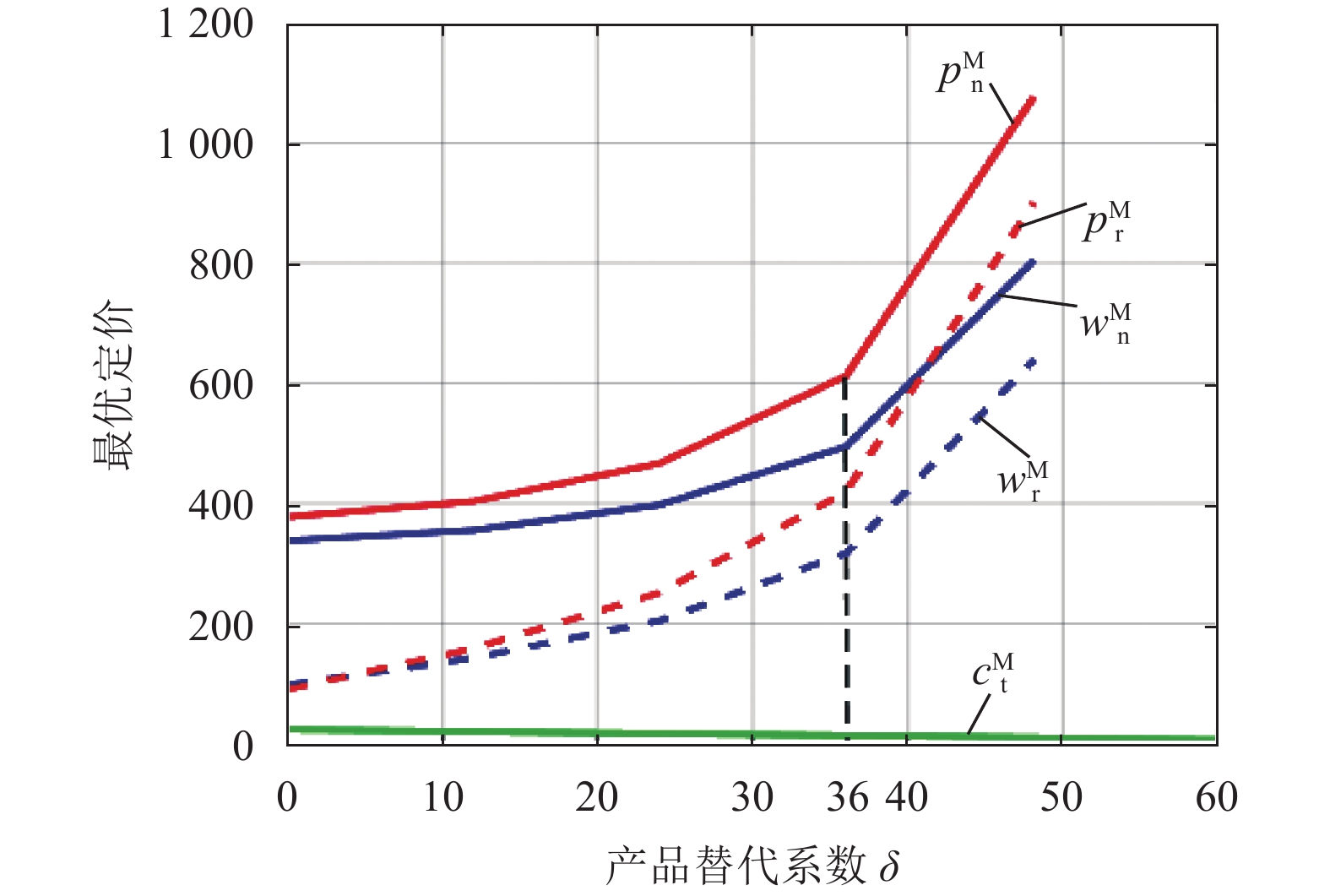
产品替代系数
1) 单位新产品与再制造产品的最优批发价
2) 单位废旧产品最优回收价
|
图 4 产品替代系数
|
本文在考虑不同渠道权力结构和产品双重差异的情形下,研究了以制造/再制造商M、零售商R和回收拆解商T为渠道权力主导的RCLSP最优定价策略问题,获得了单位新产品与再制造品的最优批发价、最优零售价以及单位废旧产品的最优回收价,以及RCLSP总利润和各成员企业的利润。在此基础上,进一步分析了废旧产品回收率
1) 在3种渠道权力结构情形下,当制造/再制造商M和零售商R为主导时,其对应的成员企业利润
2) 以制造/再制造商M和零售商R为渠道权力主导的RCLSC总利润
3) 伴随废旧产品回收率
研究尚存在需要进一步完善之处,譬如研究认为成员企业之间决策信息完全透明,尚未考虑信息不完全透明的情况;研究只考虑单周期RCLSC的最优定价问题,尚未探讨多周期RCLSC的最优定价问题。上述问题有待未来开展研究。
| [1] |
GOVINDAN K, SHANKAR K M, KANNAN D. Application of fuzzy analytic network process for barrier evaluation in automotive parts remanufacturing towards cleaner production e a study in an Indian scenario[J].
Journal of Cleaner Production, 2016, 114: 199-213.
DOI: 10.1016/j.jclepro.2015.06.092. |
| [2] |
RATHORE P, KOTA S, CHAKRABARTI A. Sustainability through remanufacturing in India: a case study on mobile handsets[J].
Journal of Cleaner Production, 2011, 19(15): 1709-1722.
DOI: 10.1016/j.jclepro.2011.06.016. |
| [3] |
GUIDE J, GUIDE V D R, GILVAN C, et al. Time value of commercial product returns[J].
Management Science, 2006, 52(8): 1200-1214.
DOI: 10.1287/mnsc.1060.0522. |
| [4] |
ATASU A, GUIDE V D R, WASSENHOVE L N. Product reuse economics in closed-loop supply chain research[J].
Production & Operations Management, 2010, 17(5): 483-496.
|
| [5] |
SAVASKAN R C, BHATTACHARYA S, WASSENHOVE L N V. Closed-loop supply chain models with product remanufacturing[J].
Management Science, 2004, 50(2): 239-252.
DOI: 10.1287/mnsc.1030.0186. |
| [6] |
王玉燕, 李帮义, 申亮. 供应链、逆向供应链系统的定价策略模型[J].
中国管理科学, 2006, 14(4): 40-45.
WANG Yuyan, LI Bangyi, SHEN Liang. The price decision model for the system of supply chain and reverse Supply chain[J]. Chinese Journal of Management Science, 2006, 14(4): 40-45. DOI: 10.3321/j.issn:1003-207X.2006.04.008. |
| [7] |
MAITI T, GIRI B C. A closed loop supply chain under retail price and product quality dependent demand[J].
Journal of Manufacturing Systems, 2015, 37(3): 624-637.
|
| [8] |
王文宾, 达庆利, 聂锐. 考虑渠道权力结构的闭环供应链定价与协调[J].
中国管理科学, 2011, 19(5): 29-36.
WANG Wenbin, DA Qingli, NIE Rui. The study on pricing and coordination of closed-loop supply chain considering channel power structure[J]. Chinese Journal of Management Science, 2011, 19(5): 29-36. |
| [9] |
GAO Juhong, HAN Hongshuai, HOU Liting, et al. Pricing and effort decisions in a closed-loop supply chain under different channel power structures[J].
Journal of Cleaner Production, 2016, 112(3): 2043-2057.
|
| [10] |
郭亚军, 赵礼强, 李绍江. 随机需求下闭环供应链协调的收入费用共享契约研究[J].
运筹与管理, 2007, 16(6): 15-20.
GUO Yajun, ZHAO Liqiang, LI Shaojiang. Revenue-and-expense sharing contract on the coordination of closed-loop supply chain under stochastic demand[J]. Operations Research & Management Science, 2007, 16(6): 15-20. DOI: 10.3969/j.issn.1007-3221.2007.06.004. |
| [11] |
葛静燕, 黄培清. 价格相依的闭环供应链渠道选择和协调策略[J].
工业工程与管理, 2007, 12(1): 29-34.
GE Jingyan, HUANG Peiqing. The research of closed-loop supply chain coordination[J]. Industrial Engineering & Management, 2007, 12(1): 29-34. DOI: 10.3969/j.issn.1007-5429.2007.01.007. |
| [12] |
孙浩, 达庆利. 基于产品差异的再制造闭环供应链定价与协调研究[J].
管理学报, 2010, 7(5): 733-738.
SUN Hao, DA Qingli. Pricing and coordination of remanufacturing closed-loop supply chain based on product differentiation[J]. Chinese Journal of Management, 2010, 7(5): 733-738. DOI: 10.3969/j.issn.1672-884X.2010.05.017. |
| [13] |
郭军华, 李帮义, 倪明. WTP差异下再制造闭环供应链的定价策略与协调机制[J].
系统管理学报, 2012, 21(5): 617-624.
GUO Junhua, LI Bangyi, NI Ming. Pricing strategies and coordination mechanism of closed-loop remanufacturing supply chain with WTP differentiation[J]. Journal of Systems & Management, 2012, 21(5): 617-624. DOI: 10.3969/j.issn.1005-2542.2012.05.006. |
| [14] |
刘家国, 周学龙, 赵金楼. 基于产品质量差异的闭环供应链定价策略与协调研究[J].
中国管理科学, 2013(s2): 426-431.
LIU Jiaguo, ZHOU Xuelong, ZHAO Jinlou. Study on price decision and coordination of closed-loop supply chain based on quality difference of product[J]. Chinese Journal of Management Science, 2013(s2): 426-431. |
| [15] |
洪宪培, 王宗军, 赵丹. 闭环供应链定价模型与回收渠道选择决策[J].
管理学报, 2012, 9(12): 1848-1855.
HONG Xianpei, WANG Zongjun, ZHAO Dan. Pricing models of closed-loop supply chain and decisions on collecting channel selection[J]. Chinese Journal of Management, 2012, 9(12): 1848-1855. |
 2018, Vol. 21
2018, Vol. 21