在设备批量生产的过程中,一方面为了应对上游可修复设备发生故障导致的停机,另一方面,为了给上游可修复设备提供定期检查的时间,往往在上游设备与下游设备之间设置缓冲区[1]。缓冲区库存最早由Wijngaard[2]提出。Wijngaard考虑了在满足更新系统中的可修复设备的可靠性,运用更新理论与随机模型[3]评估了缓冲区在生产系统中的作用。之后,Karamatsoukis和Kyriakidis[4]在此基础上,考虑了在满足更新系统中的可修复设备的预防维修周期的控制点,即达到预防性维护的阈值,运用马尔可夫决策理论和动态规划[5]来求解。随着生产管理技术和计算机技术的提高,对于缓冲区生产系统下的目标函数模型的建立有了更多的思路和新颖的求解方法。例如,Chelbi和Ait-Kadi[6]考虑了单个运行周期中可能发生的多次故障,建立了期望随机函数;Okasha和Frangopol[7]提出了用遗传算法[7-8]来求解复杂的多目标函数模型。
随着制造业的发展,MRO(maintenance, repair and operation)过程对于企业的成本控制越来越重要,所以,MRO过程的优化成为关键,集中体现在如何优化定期检查周期,如何控制库存的阈值,如何确定故障发生的分布[9]。特别是Christer[10]提出的时间延迟模型克服了许多维修模型存在的因假定条件与实际条件不符而无法应用的问题。之后,Wenbin Wang[11]考虑了实践中设备因缺陷而延迟形成故障,会导致产品质量的劣化过程,而提出对设备的定期重大检查策略,目的是优化检查的检查间隔。
在Chelbi和Ait-Kadi模型的基础上,本文运用了Christer和Wenbin Wang提出的时间延迟模型来确定故障次数。这样将使整个模型的建立更为复杂,但是,却大大提高了模型建立的准确性,即提高了2个决策变量(检查周期和额定库存)的精度。在模型建立后,通过离散迭代算法[12-13]求解,并进行案例分析论证,特别是敏感性分析。将目标函数F1分解成5部分,通过二维图、三维图详细描述了各类费用随联合变量(T,K)的变化情况,得到总费用的主要影响部分,从而作出最优二维联合策略。
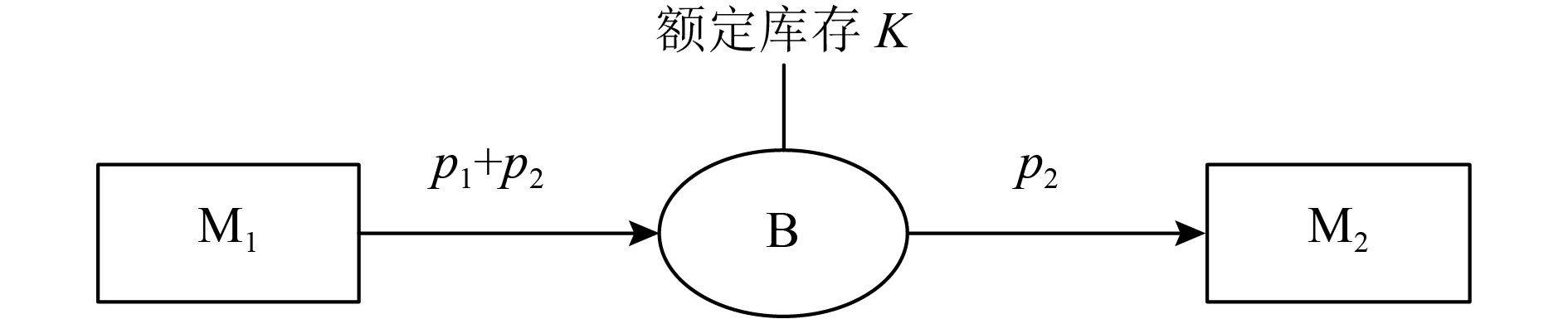
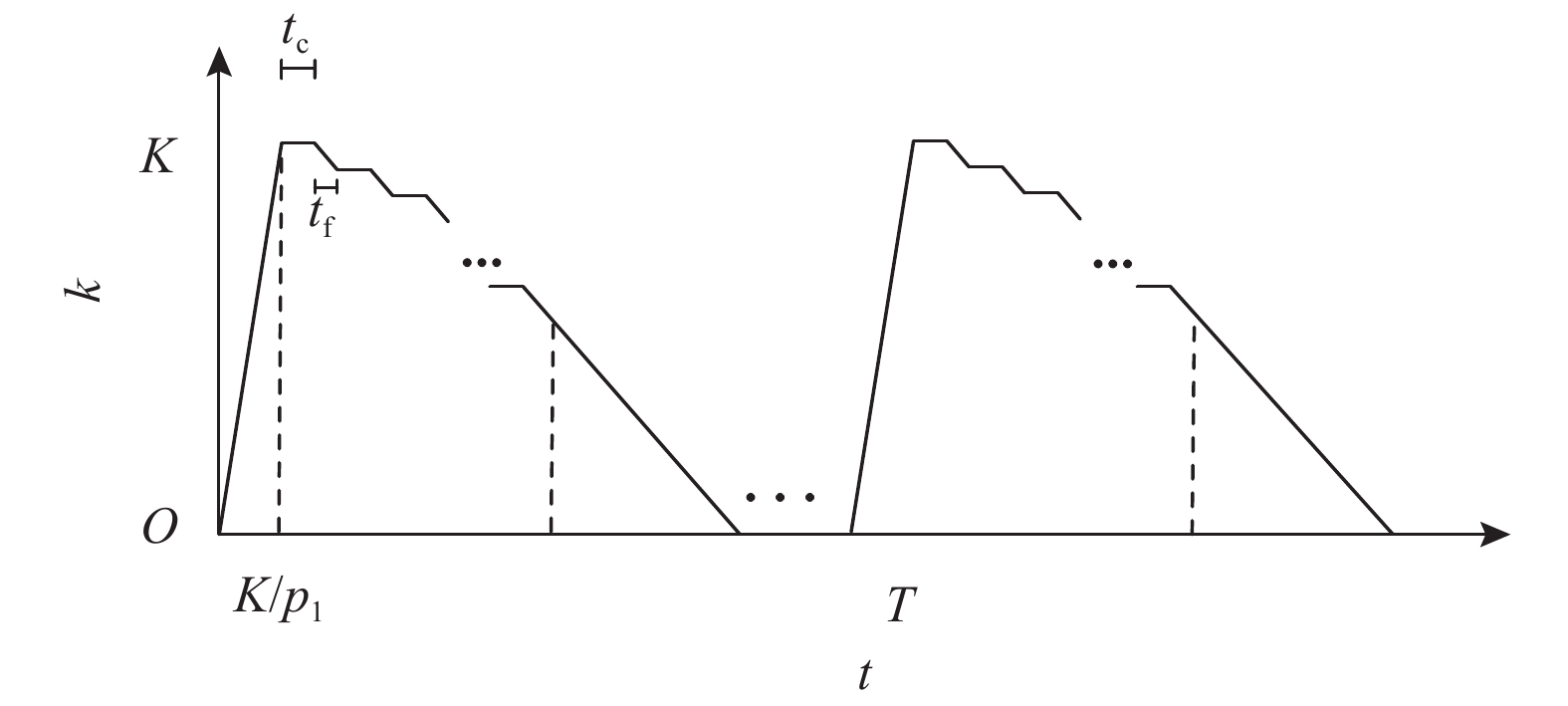
1 问题描述 1.1 带缓冲区的生产系统带缓冲区的设备生产的基本单元如图1所示,该生产系统下,缓冲区的库存变化如图2所示。
|
图 1 带缓冲区的设备生产的基本单元图 Fig. 1 Basic unit diagram of device production with buffer |
设备M1为上游设备,以生产速率p1+p2生产半成品或零件,供应到缓冲区B;M2为下游设备,以p2的需求率从B中获取。因此,B先以p1积累库存,当库存数量达到K时,上游设备开始以速率p2进行生产,以维持库存的平衡。
|
图 2 缓冲区库存k随时间t的变化图 Fig. 2 Buffer inventory k changes with time t |
从B的库存量达到K起,上游设备运行一段时间tc后会发生故障;此时,M1面临维修,同时M2开始消耗B中库存;经历一段时间后,M1修好,又恢复库存的平衡,但是B的库存量减小;接着,M1又会发生故障和面临维修,同时M2消耗B中库存,等待M1修好,与其共同维护缓冲区库存的平衡。如此反复,直至定期检查时刻,M1停止工作,只由M2完全消耗B中剩余库存。
每当B中库存降为零时,M1立即工作,再以生产速率p1+p2进行下一个运行周期的投产。
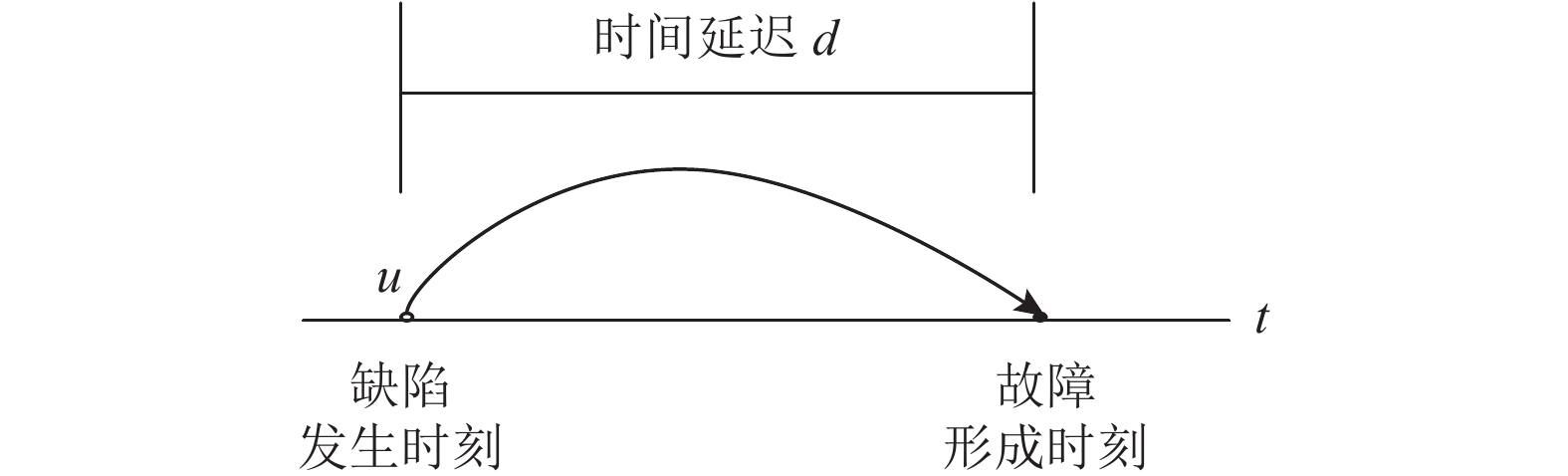
1.2 时间延迟概念时间延迟[10, 14]是指从缺陷发生到进一步恶化成为故障所经历的的时间。在时间延迟理论下,故障的形成如图3所示。
|
图 3 缺陷延迟形成故障图 Fig. 3 Defect delay forming fault diagram |
缺陷在u时刻发生,经过一段时间d后才形成故障。在每个运行周期内从上游设备开始运行到定期检查期间,会有故障导致的停机。该停机时间段不可能再有缺陷发生。因此,当应用时间延迟理论求解每个运行周期的平均故障次数时,u的取值范围必然在上游设备运行的任意时刻。
2 模型建立 2.1 假设和符号假设1 上游设备经每次定期检查维护后能修复如新,不考虑下游设备的故障带来的影响,即下游设备在定期检查之前一直正常运行。一旦到了定期检查时刻,设备都停止运行,直到检查完毕且库存降为零,再进行下一个运行周期。
假设2 定期检查发现的缺陷能立即并完全排除。检查的时间和排除缺陷的时间相对整个运行周期较小,所以忽略不计,而且排除缺陷不会引发任何故障。
假设3 额定库存量K是有界的,一方面,
假设4 缺陷有多个,每个缺陷独立同分布,而且缺陷发生率服从齐次泊松分布,缺陷发生率记作λ,缺陷的发生与缺陷进一步劣化成为故障是相互独立的事件。
假设5 从缺陷发生到故障形成这一时间间隔称为时间延迟,记为d,d是一随机变量,其概率密度函数和分布函数分别记为f(d)和F(d),而且F(d)服从负指数分布。
基本符号描述如表1所示。
| 表 1 符号描述 Tab. 1 Symbol description |
设A1为第一次库存降为零的时刻,An(n≥2)为第n次库存降为零的时刻,由于每次库存降为零后,系统又立即重新进入下一个运行周期,所以,{An, n=1,2,3…}构成一个更新过程[15]。
由于函数的决策变量是T和K,系统单位时间的总费用记为F1(T,K),由更新酬劳定理,即
| $\quad\quad{F_1}\left( {T,K} \right)=\mathop { \lim }\limits_{t \to \infty } \frac{{\left[ {0,t} \right]{\text{内的总费用}}}}{t} = \frac{{{\rm EC}\left( T \right)}}{{E\left( T \right)}}{\text{。}}$ | (1) |
同样地,由基本更新定理,得到上游设备单位时间的平均停机时间,该函数记为F2(T,K),即
| $\quad\quad{F_2}\left( {T,K} \right) \!=\!\mathop { \lim }\limits_{t \to \infty } \frac{{\left[ {0,t} \right]{\text{内的总停机时间}}}}{t} \!=\! \frac{{{\rm ET}\left( T \right)}}{{E\left( T \right)}}{\text{。}}$ | (2) |
先来表达一个运行周期的总费用期望值EC(T)
| $\quad\quad{\rm{EC}}\left( T \right) ={\rm E}{{\rm C}_{\rm{p}}} + {\rm E}{{\rm C}_{\rm{f}}} + {\rm EC}{_{\rm{r}}} + {\rm EC}{_{\rm{h}}} + {\rm EC}{_{\rm{w}}}{\text{。}}$ | (3) |
其中,ECp已知,只需要表达出ECf、ECr、ECh、ECw关于T和K的函数。
| $\begin{split}&\quad\quad {{\rm EC}_{\rm h}} = {C_{{\rm h}}}\left[ {\frac{{{K^2}}}{{2{p_1}}} + \frac{{{{( {K - {P_2}{t_f}{E_{\rm Nf}}} )}^2}}}{{2{p_2}}} +}\right.\\&\left.{\left( {T - \frac{K}{{{p_1}}}} \right)\left( {K - {p_2}{t_{\rm f}}{E_{\rm Nf}}} \right) + \frac{1}{2}\left( {T - \frac{K}{{{p_1}}}} \right){p_2}{t_{\rm f}}{E_{\rm Nf}} +}\right.\\&\left.{\frac{1}{2}{t_{\rm c}}{p_2}{t_{\rm f}}{E_{\rm Nf}}} \right]{\text{。}}\end{split}$ | (4) |
由图2可知,tc与T、K满足
| $\quad\quad\left( {{t_{\rm c}} + {t_{\rm f}}} \right){E_{\rm Nf}} = T - \frac{K}{{{p_1}}} \Rightarrow {t_{\rm c}} = \frac{{{p_1}T - {p_1}{t_{\rm f}}{E_{\rm Nf}} - K}}{{{E_{\rm Nf}}}}{\text{。}}$ | (5) |
将式(5)代入式(4)中,并整理,得到
| $\begin{split}&\quad\quad{{\rm EC_h}} = {C_{{\rm h}{\rm{}}}}\left[ {TK - \frac{{{K^2}}}{{2{p_1}}} + \frac{{{{\left( {K - {p_2}{t_{\rm f}}{E_{\rm Nf}}} \right)}^2}}}{{2{p_2}}} +}\right.\\&\left.{{p_2}{t_{\rm f}}{E_{\rm Nf}}\left( {\frac{K}{{2{p_1}}} - \frac{T}{2} + \frac{{{p_1}T - {p_1}{t_{\rm f}}{E_{\rm Nf}} - K}}{{2{E_{\rm Nf}}}}} \right)} \right],\end{split}$ | (6) |
| $\quad\quad {{\rm EC}_{\rm w}} = {c_1}\frac{K}{{{p_1}}} + {c_2}\left( {T - \frac{K}{{{p_1}}} - {t_{\rm f}}{E_{{\rm Nf}}}} \right),$ | (7) |
| $\quad\quad {\rm EC_f} = {c_{\rm f}}{E_{\rm Nf}},$ | (8) |
| $\quad\quad{\rm EC_r} = {c_{\rm r}}{E_{\rm Nr}}{\text{。}}$ | (9) |
现在具体来看ENf、ENr的表达,从而表达出ECf和ECr,在一个运行周期内,由时间延迟理论,通过积分变换,有
| $\quad\quad{E_{\rm Nf}} = \mathop \int \limits_0^{\tau {\rm{}}} \lambda F\left( {\tau - u} \right){\rm d u} = \mathop \int \limits_0^{\tau {\rm{}}} \lambda F\left( u \right){\rm d u}{\text{,}}$ | (10) |
| $\quad\quad F\left( u \right) = 1 - {{\rm e}^{ - \alpha u}},\;u {\text{>}} 0{\text{。}}$ | (11) |
因为在一个运行周期内,上游设备实际运行的时间
| $\quad\quad \tau = T - {t_{\rm f}}{E_{\rm Nf}}{\text{。}}$ | (12) |
将式(11)、(12)代入式(10)中,得到ENf和T的关系式如下
| $\lambda {t_{\rm f}}{{\rm e}^{ - \alpha \left( {T - {t_{\rm f}}{E_{\rm Nf}}} \right)}} + \alpha \left( {1 + \lambda {t_{\rm f}}} \right)\left( {T - {t_{\rm f}}{E_{\rm Nf}}} \right) - \lambda {t_{\rm f}} - \alpha T = 0{\text{。}}$ | (13) |
可看出ENf和T具有一一映射关系,但是,ENf难以直接用T表示出来,因此,再将式(12)代入式(13)中,分别得到T和ENf关于τ的表达式。
| $\quad\quad T = \frac{{\lambda {t_{\rm f}}}}{\alpha }\left( {{{\rm e}^{ - \alpha \tau }} - 1} \right) + \left( {1 + \lambda {t_{\rm f}}} \right)\tau, \;\;{\text{记为}}\;\;T = g\left( \tau \right);$ | (14) |
| $\quad\quad {E_{\rm Nf}} = \frac{\lambda }{\alpha }\left( {{{\rm e}^{ - \alpha \tau }} - 1} \right) + \lambda \tau, \;\;{\text{记为}}\;\;{E_{\rm Nf}} = h\left( \tau \right);$ | (15) |
| $\quad\quad {E_{\rm Nr}} = \mathop \int \limits_0^{\tau {\rm{}}} \lambda \left[ {1 - F\left( {\tau - u} \right)} \right]{{\rm d u}} = {\rm{}}\frac{\lambda }{\alpha }\left( {1 - {{\rm e}^{ - \alpha \tau }}} \right){\text{。}}$ | (16) |
接下来,将式(14)中的T和式(15)中的ENf代入式(6)~(8)中,将式(16)中的ENr代入式(9)中,最后代入式(3),得到
| $\begin{split}&\quad\quad{\rm EC}\left( T \right) = {{\rm EC}_p} + {\rm{}}{C_{{\rm h}{\rm{}}}}\left[ {g\left( \tau \right)K - \displaystyle\frac{{{K^2}}}{{2{p_1}}} + \displaystyle\frac{{{{\left( {K - {p_2}{t_{\rm{f}}}h\left( \tau \right)} \right)}^2}}}{{2{p_2}}} + } \right.\\&\displaystyle\left. {{p_2}{t_{\rm{f}}}h\left( \tau \right)\left( {\frac{K}{{2{p_1}}} - \frac{{g\left( \tau \right)}}{2} + \frac{{{p_1}g\left( \tau \right) - {p_1}{t_{\rm{f}}}h\left( \tau \right) - K}}{{2h\left( \tau \right)}}} \right)} \right] + {c_1}\frac{K}{{{p_1}}} + \\&\displaystyle{c_2}\left[ {g\left( \tau \right) - \frac{K}{{{p_1}}} - {t_{\rm{f}}}h\left( \tau \right)} \right] + {\rm{}}{c_{\rm{f}}}h\left( \tau \right) + {c_{\rm{r}}}\frac{\lambda }{\alpha }\left( {1 - {{\rm{e}}^{ - \alpha \tau }}} \right){\text{。}}\end{split}$ | (17) |
再来计算一个运行周期的平均总停机时间ET(T),其中,
| $\quad\quad{t_g} = \frac{{K - {p_2}{t_{\rm{f}}}{E_{\rm Nf}}}}{{{p_2}}} = \frac{{K - {p_2}{t_{\rm{f}}}h\left( \tau \right)}}{{{p_2}}},$ | (18) |
| $\quad\quad {\rm ET}\left( T \right) = {E_{\rm Nf}}{t_{\rm f}} + {t_{\rm g}}{\text{。}}$ | (19) |
将式(15)、(18)代入式(19)中,得到
| $\quad\quad {\rm ET}\left( T \right) = \frac{K}{{{p_2}}}{\text{。}}$ | (20) |
另外,
| $\begin{split}&\quad\quad E\left( T \right) = T + {t_{\rm g}} = T + \frac{{K - {p_2}{t_{\rm f}}{E_{\rm Nf}}}}{{{p_2}}} =\\&g\left( \tau \right) + \frac{{K - {p_2}{t_{\rm f}}h\left( \tau \right)}}{{{p_2}}} = \tau + \frac{K}{{{p_2}}}{\text{。}}\end{split}$ | (21) |
最后将式(17)、(21)代入式(1)就可以得到第1个目标函数的最后结果,将式(20)、(21)代入式(2)可以得到第2个目标函数的最后结果。
2.3 约束条件 2.3.1 非线性不等式约束为了和假设4保持一致,一方面为了保证p1足够大,即达到K的过程时间非常短,即认为不会发生故障,同时为了简化积分运算,从而对服从时间延迟分布的故障次数的计算的积分下限可处理成0。另一方面,额定库存量K不能太小,即不小于一个运行周期内故障维修时缓冲区库存的期望消耗量,保证不会产生缺货。即
| $\quad\quad{p_2}{t_{\rm f}}{E_{\rm Nf}} {\text{≤}} K \ll {p_1}T \Leftrightarrow {p_2}{t_{\rm f}}h\left( \tau \right) {\text{≤}} K \ll {p_1}g\left( \tau \right){\text{。}}$ |
决策变量和大于一个周期的故障次数ENf、ENr非负,即
| $\quad\quad K {\text{>}} 0,T {\text{>}} 0,{E_{\rm Nf}} {\text{>}} 0,\;{E_{\rm Nr}} {\text{>}} 0 \Leftrightarrow K {\text{>}} 0,\tau {\text{>}} 0{\text{。}}$ |
在这里,证明一下第2个约束条件的等价转换为什么成立。证明如下。
式(14)、式(15)和式(16)分别对τ求导得到
| $\begin{split}\quad\quad &\displaystyle\frac{{{\rm d} T }}{{{\rm d} \tau }} = g'\left( \tau \right) = \lambda {t_{\rm f}}\left( {1 - {{\rm e}^{ - \alpha \tau }}} \right);\\&\displaystyle\frac{{{\rm d} {{E_{{\rm Nf}}}} }}{{{\rm d} \tau }} = h'\left( \tau \right) = \lambda \left( {1 - {{\rm e}^{ - \alpha \tau }}} \right);\\&\displaystyle\frac{{{\rm d} {{E_{{\rm Nr}}}}} }{{{\rm d} \tau }} = {E_{{\rm Nr}}}{\rm{'}}\left( \tau \right) = \lambda {{\rm e}^{ - \alpha \tau }}{\text{。}}\end{split}$ |
当τ>0时,由于λ、tf和α均为正参数,
该模型为2个目标函数的联合优化问题,属于非线性规划。另外,模型存在2个决策变量T和K,(将T转换为τ处理)同时在满足两个约束条件的情况下,要从理论上得到最优解的表达式相当困难,所以本文将借助离散迭代算法的思想,该算法的核心是降维,具体如下。
先赋予其中一自变量的初始值,转换为因变量与另一自变量的函数关系,确定当函数值最优时另一变量的值;然后,以定步长连续迭代其初始值,每迭代一次,确定另一自变量最优解,直至在可行域全部迭代完毕,将所有组最优联合二元变量再次代入目标函数,进行比较,找到最终的最优解。
求解前,根据实际情况和经验确定缓冲区额定库存K和检测周期T的范围,以及确定生产过程中总停机时间的上限,即最大平均时间的累计停机时间MADT,步长ΔK和ΔT也根据实际情况确定。
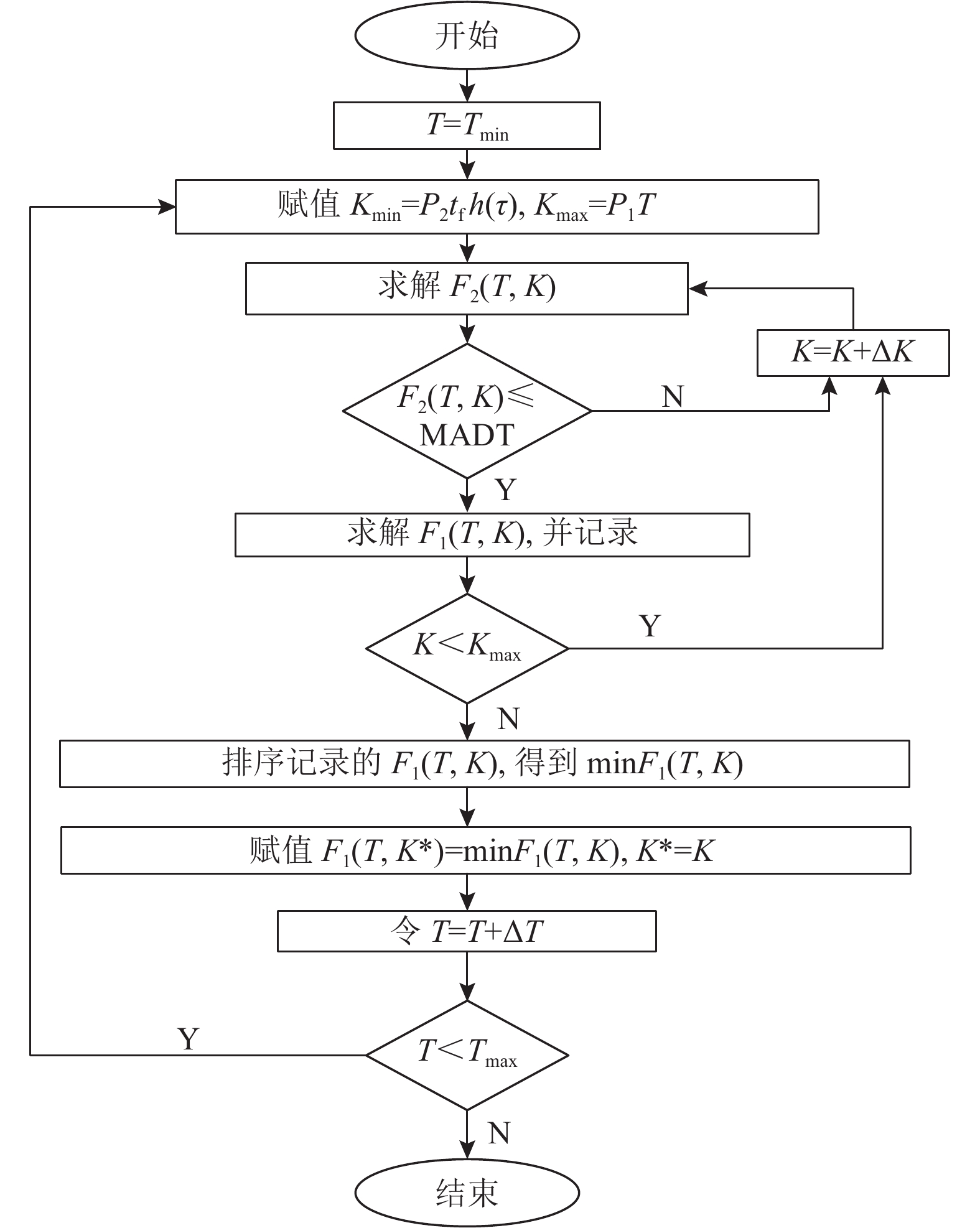
在算法的基础上,最后通过Matlab编程,求出当不超过MADT时,最小费用对应的T和K。程序框图如图4所示。具体算法步骤如下。
步骤1 赋值T=Tmin,τ=g−1(Tmin)
1) Kmin=p2tfh(τ),Kmax=p1T,令K=Kmin。
2) 求解F2(T,K)。
3) 判断F2(T,K)>MADT如果成立,则赋值K=K+ΔK,并转2),否则转4)。
4) 求解F1(T,K),并记录F1(T,K),F2(T,K),T,K。
5) 判断K<Kmax,如果成立,赋值K=K+ΔK,否则转6)。
6) 将所有记录的F1(T,K)进行排序,取最小值。
7) 赋值F1(T,K*)=minF1(T,K),K*=K。
8) 令T=T+ΔT。
9) 判断T≤Tmax,如果成立,转1),否则,程序结束。
步骤2 通过步骤1能够排序得到在满足F2(T,K)≤MADT的情况下,不同检查周期下的最佳额定库存K*和对应的单位时间的最低总费用值F1(T,K*)。最后再经过排序就能得到所有检查周期下的最低总费用值和对应的最优联合策略(T,K)。
|
图 4 算法流程 Fig. 4 Algorithm flow chart |
有一带缓冲区的生产系统,上游设备的缺陷发生服从齐次泊松分布,参数
| 表 2 参数设置 Tab. 2 Parameter setting table |
| 表 3 各变量的取值范围及迭代步长 Tab. 3 Value range and iteration step size of each variable |
将表2数据代入最后的优化模型
| $\quad\quad\left\{ \begin{array}{l}{F_1}\left( {T,K} \right) = \displaystyle\frac{{{\rm EC}\left( T \right){\rm{}}}}{{E\left( T \right)}},\\{\rm{max}}\;\;{F_2}\left( {T,K} \right) = \displaystyle\frac{{{\rm ET}\left( T \right){\rm{}}}}{{E\left( T \right)}} = {\rm MADT}{\text{。}}\end{array} \right.$ |
再根据算法的步骤1和步骤2,结合表3数据,计算结果如表4所示。T、ENf随τ的变化如图5、图6所示,F1、F2随T和K的变化如图7、图8所示。将单位时间的总费用分解成5部分单位时间的费用,各部分费用随T和K的变化如图9~13所示。
| 表 4 不同检查周期T下的最佳K*、最优F1(T,K*)和对应的F2(T,K*)和ENf、ENr值 Tab. 4 Best K*, the optimal F1(T, K*) and the corresponding F2(T,K*) and ENf、ENr under different inspection periods T |

|
图 5 T随τ的变化 Fig. 5 The variation of T with τ |
1) 敏感性分析。
从图7和图8可看到,当K*值固定,随着T的增大,F1的总体变化趋势是减小,但是F2在不断增加;当T值固定,随着K*的增大,F1在起伏变化,达到多个极小值,而且最小值线对应的K*值在1 200附近,F2也在起伏不定;因此,为了达到F1和F2的平衡,T不能无限增加,而且最优库存K*应该接近1 200。
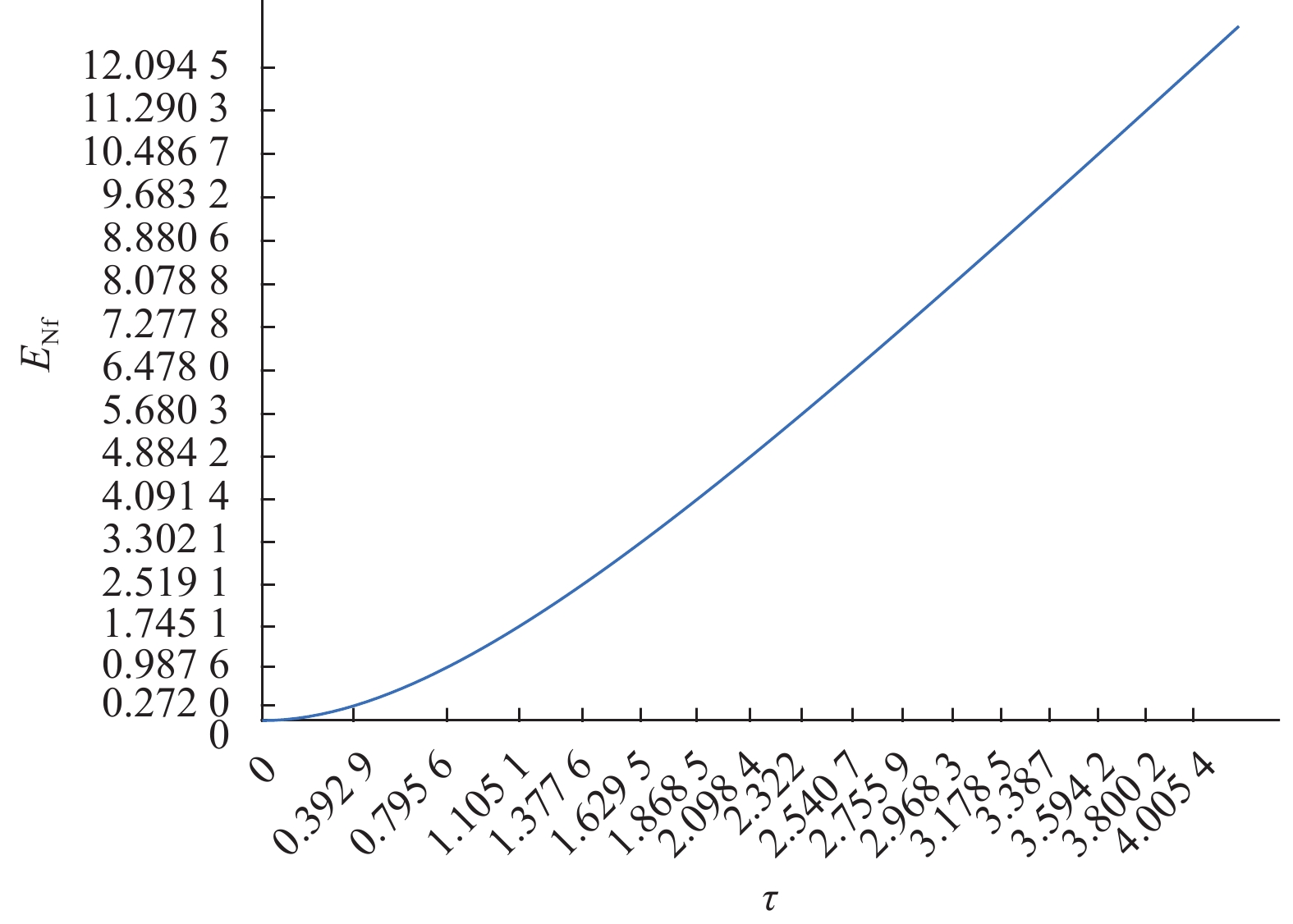
从图5和图6可看出T和ENf都随τ的增大而增大,因此得到T关于ENf也是单调递增函数,当T较小时,ENf也较小,从表4的求解结果看出,当T和K*较小时,F1较大,结合图9~13,看到F1的主要来源是单位时间的定期检查费和库存费。原因是ECP不随T的变化而改变,当T和K*偏小,ECP偏大;ECh/E(T)起初很大,是因为分母
|
图 6 ENf随τ的变化 Fig. 6 The variation of ENf with τ |

|
图 7 F1随T和K的变化 Fig. 7 The variation of F1 with T and K |

|
图 8 F2随T和K的变化 Fig. 8 The variation of F2 with T and K |

|
图 9 单位时间的检查费随T和K的变化 Fig. 9 The inspection cost per unit time varies with T and K |

|
图 13 单位时间的缺陷排除费随T和K的变化 Fig. 13 The defect elimination cost per unit time varies with T and K |
当T增加到25,τ增加到3.387,ENf增加到9.683 2,而且对应的最佳库存K*为1 195.02时,F1取到极小值,即F1(25,1 195.02)=22 739.95,而且,F2(25,1 195.02)=0.199<0.2。这也符合生产系统的停机时间要求。对应地,K/p1=1.49 d,即需要1.49 d达到额定库存量。另外,将T、K*、ENf、p2和tf的值代入式(21)得到运行周期的平均长度E(T)=30.05 d。在整个运行周期中,平均故障次数大约发生10次,故障导致的停机时间为22.32 h,库存降为零需要的停机时间为E(T)–T=5.05 d。
2) 管理意义。
相应的企业可做出如下决策:每月初投产1 195件产品或零件,花费1.5 d时间只启动上游设备。然后,启动下游设备,大约在第25 d末同时关闭上、下游设备并检查和维护,然后一直等到库存降为零,即大约在下月初再进行同一规模、同一方式的投产。

|
图 10 单位时间的库存费随T和K的变化 Fig. 10 The inventory cost per unit time varies with T and K |

|
图 11 单位时间的运行费随T和K的变化 Fig. 11 The operating cost per unit time varies with T and K |

|
图 12 单位时间的故障维修费随T和K的变化 Fig. 12 The maintenance cost per unit time varies with T and K |
3) 创新点和不足。
由于故障次数对于MRO的优化相当关键,而故障次数的确定较理想而可行的方法是借助时间延迟模型,因此将时间延迟理论融入带有缓冲区的可修复设备的生产系统中,建立的多目标优化模型是有效而精确的。而且,通过案例分析,验证了该模型的可行性。
本文的模型适用的其中一个条件是上游设备经每次定期检查维护后能修复如新,而且不考虑下游设备的故障带来的影响,然而,实际生产中,很难保证修复如新。另外,模型忽略了检查和排除缺陷的时间,如果该时间相对于运行周期来说是较长的,甚至在库存降为零之前尚未修好,就会产生缺货现象,需要重新建立模型。这是进一步研究的内容。
总之,本文的研究对某些企业的成本控制、停机时间控制、缓冲区库存控制和检查周期的确定具有一定的指导意义。
| [1] |
PAVITSOS A, KYRIAKIDIS E G. Markov decision models for the optimal maintenance of a production unit with an upstream buffer[J].
Computers & Operations Research, 2009, 36(6): 1993-2006.
|
| [2] |
WIJNGAARD J. The effect of interstage buffer storage on the output of two unreliable production units in series, with different production rates[J].
Iie Transactions, 1977, 11(1): 374-390.
|
| [3] |
SHELDON M Ross. 应用随机过程: 概率模型导论[M]. 龚光鲁(译). 北京: 人民邮电出版社, 2011.
|
| [4] |
KYRIAKIDIS E G, DIMITRAKOS T D. Optimal preventive maintenance of a production system with an intermediate buffer[J].
European Journal of Operational Research, 2006, 168(1): 86-99.
DOI: 10.1016/j.ejor.2004.01.052. |
| [5] |
严正峰, 刘猛. 带有中间缓冲区的生产系统设备维修策略研究[J].
组合机床与自动化加工技术, 2015(9): 81-85.
YAN Zhengfeng, LIU Meng. The study of maintenance policy in a production system with an intermediate buffer[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(9): 81-85. |
| [6] |
CHELBI A, AIT-KADI D. Analysis of a production/inventory system with randomly failing production unit submitted to regular preventive maintenance[J].
European Journal of Operational Research, 2004, 156(3): 712-718.
DOI: 10.1016/S0377-2217(03)00254-6. |
| [7] |
OKASHA N M, FRANGOPOL D M. Lifetime-oriented multi-objective optimization of structural maintenance considering system reliability, redundancy and life-cycle cost using GA[J].
Structural Safety, 2009, 31(6): 460-474.
DOI: 10.1016/j.strusafe.2009.06.005. |
| [8] |
韩帮军, 范秀敏, 马登哲. 用遗传算法优化制造设备的预防性维修周期模型[J].
计算机集成制造系统, 2003, 9(3): 206-209.
HAN Bangjun, FAN Xiumin, Ma Dengzhe. Genetic algorithm is used to optimize the pre-defense of manufacturing equipment[J]. Computer Integrated Manufacturing Systems, 2003, 9(3): 206-209. DOI: 10.3969/j.issn.1006-5911.2003.03.009. |
| [9] |
方淑芬, 吕文元. 设备维修管理智能决策支持系统的研究[J].
系统工程理论与实践, 2001, 21(12): 53-59.
FANG Shufen, LYU Wenyuan. Research on a maintenance intelligent decision support system[J]. System Engineering Theory and Practice, 2001, 21(12): 53-59. DOI: 10.3321/j.issn:1000-6788.2001.12.010. |
| [10] |
CHRISTER A H, WALLER W M. Delay time models of industrial inspection maintenance problems[J].
Journal of the Operational Research Society, 1984, 35(5): 401-406.
DOI: 10.1057/jors.1984.80. |
| [11] |
WANG Wenbin. An inspection model for a process with two types of inspections and repairs[J].
Reliability Engineering & System Safety, 2009, 94(2): 526-533.
|
| [12] |
陆志强, 王佳跃, 周炳海. 带缓冲区的可修复设备多目标预防性维护决策模型[J].
计算机集成制造系统, 2010, 16(10): 2124-2128.
LU Zhiqiang, WANG Jiayue, ZHOU Binghai.. Multi-objective preventive maintenance decision-making model for repairable equipment with buffer[J]. Computer Integrated Manufacturing Systems, 2010, 16(10): 2124-2128. |
| [13] |
成国庆, 周炳海, 李玲. 考虑缓冲区库存的退化系统最优维修更换策略[J].
计算机集成制造系统, 2015, 21(6): 1593-1600.
CHENG Guoqing, ZHOU Binghai, LI Ling.. Optimal maintenance strategy for deteriorating systems with intermediate buffers[J]. Computer Integrated Manufacturing Systems, 2015, 21(6): 1593-1600. |
| [14] |
吕文元, 郑睿, 张乐. 非齐次缺陷发生率情况下时间延迟模型比较研究[J].
计算机集成制造系统, 2008, 14(8): 1529-1532.
LYU Wenyuan, ZHENG Rui, ZHANG Le. Comparative research on delay-time-based models in case of non-homogeneous defect arrival rate[J]. Computer Integrated Manufacturing Systems, 2008, 14(8): 1529-1532. |
| [15] |
Ross S M. Stochastic processes[M]. 2nd ed. New York: John Wiley & Sons, 1996.
|
 2018, Vol. 21
2018, Vol. 21