干道信号协调控制一直是城市交通控制领域研究的热点，对解决城市交通拥堵问题具有重要的意义，而干道交叉口之间的相位差作为干道信号协调控制中的关键参数，对信号协调控制起着至关重要的作用。经过多年的研究，干道相位差优化取得了很多重要的成果。结合法^[1]根据各交叉口连线的相位差与延误时间对应关系，利用串行或并行的思想对交叉口连线进行两两结合，将整个路网压缩简化为一条连线，然后反推确定路网中所有交叉口的最佳相位差取值。广义结合法^[2]运用图论思想，理论上将结合法推广到任意复杂路网的应用。英国的TRANSYT^[3]系统采用“爬山法”进行相位差优化，在实践中取得了较好的效果。美国的TRANSYT-7F8.1^[4]以后的版本采用遗传算法进行相位差优化，以克服传统“爬山法”容易陷入局部最优的不足。除此之外，数解法和图解法^[5]作为两种实用的相位差优化方法，思路简便，效果直观，但由于考虑因素较少，在实践过程中受到限制。近年来国内学者对相位差优化方法进行了相关探索，主要体现在相位差优化模型和算法改进方面。常云涛等^[6]考虑到传统绿波设计方法涉及的因素太少，提出应该考虑相交道路转弯车辆的影响和车辆行驶离散性等因素，并引入遗传算法求解改进后的优化模型。谷远利等^[7]结合中国实际交通流特性，基于Robertson模型分析相邻交叉口的车流运行规律，建立相邻交叉口相位差优化的数学模型，并采用遗传算法求解模型。卢凯等^[8]综合考虑各路段的平均车速、车流的离散性、转向车流以及车辆到达的不均匀性等各种影响因素，以干道总延误与总停车次数为优化目标建立相位差优化模型，利用Matlab编程实现相位差的优化。鄢小文等^[9]利用交通波理论建立了不同周期下相邻交叉口间的延误模型，在此基础上进行相位差优化。文献[6-9]均以相邻交叉口为基础，通过考虑不同的约束条件，建立精确的数学模型研究相位差——延误关系，在此基础上对相位差进行滚动优化，最终获得各条路段的相位差配时参数。

综上可知，传统研究大多以相邻交叉口为基础，忽略了连续交叉口对应的多个相位差之间的内在相关性，它实质基于假设前提：两个交叉口之间，某一行驶方向的车流所受到阻滞延误仅仅取决于这两个交叉口的相位差，与其他相邻的交叉口无关。这种假设没有充分考虑车流运动的基本特点，只适用于高饱和度的交通状况。基于此，本文以连续交叉口的多个相位差为研究对象，引入基于多个相位差相关性分析的干道效用函数，运用神经网络描述多个相位差和干道延误的关系，同时采用遗传算法寻找模型的最优解。因此，本文主要研究仿真优化方法在多个交叉口相位差优化中的应用，暂不考虑转向车辆、路段车速、车辆到达不均匀性等因素对优化效果的影响。

1 问题描述 1.1 干道效用函数

在信号协调控制中，Gartner等^[10]提出干道效用函数(link performance function)的概念并将其应用于混合整数线性规划模型中，该函数的表现形式为相邻交叉口相位差和干道车辆延误的对应关系。干道效用函数是相邻交叉口相关性的集中体现：包括交通流特征(流量、密度、速度、转向交通和车流离散特性等)、道路物理特征(交叉口间距、道路宽度和坡度等)和信号配时参数特征(周期、绿信比和相位差等)。传统相位差优化模型采用简化的干道效用函数进行相位差优化(即认为某路段车辆的延误只取决于该路段交叉口的相位差，而与其他交叉口之间的相位差无关)，难以匹配实际的交通流特性。实践发现，对于一条由多路段、多交叉口构成的城市主干道，受交通流运行状态的影响，连续交叉口间的多个相位差存在一定的内在关联性，表现车辆在干道的延误取决于上游连续交叉口间的多个相位差。针对该问题，近年相关学者进行了研究探讨^[11]。对于不同路段饱和度条件下，相位差与延误的相关性界定，国外研究作了一个大致划分^[12]，如表1所示。

由表1可知，当路段饱和度大于0.9时，路段下游交叉口的延误只与该路段对应的相位差相关；当路段饱和度处于[0.3，0.9]时，路段下游交叉口的延误不仅与该路段本身的相位差有关，还与该路段上游相邻的一条路段的相位差相关；当路段饱和度小于0.3时，路段下游交叉口的延误与上游3条或更多相邻路段的相位差相关。对于多个相位差的相关性，国外研究通常采用傅里叶函数进行数学建模，但需要首先确定干道效用函数的具体形式，且实践证明该干道效用函数仅能近似描述干道车辆延误与交叉口相位差之间的关系。为解决该问题，本文拟采用神经网络来描述干道车辆延误与相位差之间的关系，求解干道协调控制的最优相位差。

2 模型建立 2.1 基于BP神经网络的干道效用函数模型

相关研究表明，多个交叉口之间的相位差存在相互影响，且很难采用精确的数学公式来表达这种非线性关系，而神经网络由于能够拟合任意非线性系统而应用广泛。因此，本文拟采用BP神经网络，利用其强大的非线性逼近能力来拟合干道车辆延误与多个交叉口相位差之间的关系，以达到描述干道效用函数的作用^[13]。

其中，神经网络基本框架如图1所示，主要结构包括输入层、隐含层、输出层和各层之间连接权值。

图1中： ${x_i}$ 表示输入层第 $i$ 个节点的输入值， $i = 1,2, \cdots ,n$ ； ${z_j}$ 表示隐含层第 $j$ 个节点输入值， $j = 1,2, \cdots ,p$ ； ${y_k}$ 表示输出层第 $k$ 个节点的输出值， $k = 1,2, \cdots ,m$ ； ${\theta _j}$ 表示隐含层第 $j$ 个节点的阈值； $\phi \left( x \right)$ 表示隐含层的激励函数； ${b_k}$ 表示输出层第 $k$ 个节点的阈值； $\psi \left( x \right)$ 表示输出层的激励函数； ${w_{ij}}$ 表示输入层第 $i$ 个节点到隐含层第 $j$ 个节点之间的权值； ${v_{jk}}$ 表示隐含层第 $j$ 个节点到输出层第 $k$ 个节点之间的权值。

而由文献[12]可知，神经网络各层之间存在一定关系，且可由式(1)、(2)表达：

$\quad\quad{z_j} = \phi \left( {\sum\limits_{i = 1}^n {{w_{ij}}{x_i} + {\theta _j}} } \right),$

(1)

${y_k} = \psi \left( {\sum\limits_{j = 1}^p {{v_{jk}}{z_j} + {b_k}} } \right) = \psi \left[ {\sum\limits_{j = 1}^p {{v_{jk}} \phi \left( {\sum\limits_{i = 1}^n {{w_{ij}}{x_i} + {\theta _j}} } \right) + {b_k}} } \right]{\text{。}}$

(2)

根据式(2)求得预测值后，可与实际结果进行对比，得出预测误差。即对 $N$ 个训练样本的总误差准则函数为

$\quad\quad E = \frac{1}{2}\sum\limits_{p = 1}^N {\sum\limits_{k = 1}^m {{{\left( {t_k^p - y_k^p} \right)}^2}} } {\text{。}}$

(3)

式中： $E$ 为总误差准则函数， $t_k^p$ 和 $y_k^p$ 分别表示第 $p$ 个训练样本输出层第 $k$ 个节点的真实值和计算值。

然后根据误差梯度下降法依次修正输出层权值的修正量 $\Delta {v_{jk}}$ ，输出层阈值的修正量 $\Delta {b_k}$ ，隐含层权值的修正量 $\Delta {w_{ij}}$ ，隐含层阈值的修正量 $\Delta {\theta _j}$ 。

$\quad\quad\Delta {v_{jk}} = - \eta \frac{{\partial E}}{{\partial {v_{jk}}}} = \eta \sum\limits_{p = 1}^N {\sum\limits_{k = 1}^m {\left( {t_k^p - y_k^p} \right) \cdot } } {\psi '}\left( {{z_k}} \right) \cdot {y_k},$

(4)

$\quad\quad\Delta {b_k} = - \eta \frac{{\partial E}}{{\partial {b_k}}} = \eta \sum\limits_{p = 1}^N {\sum\limits_{k = 1}^m {\left( {t_k^p - y_k^p} \right) \cdot } } {\psi '}\left( {{z_k}} \right),$

(5)

$\begin{split}&\quad\quad\Delta {w_{ij}} = - \eta \frac{{\partial E}}{{\partial {w_{ij}}}} = \eta \sum\limits_{p = 1}^N {\sum\limits_{k = 1}^m {\left( {t_k^p - y_k^p} \right)} } \cdot\\&{\psi '}\left( {{z_k}} \right) \cdot {v_{jk}} \cdot {\phi '}\left( {{z_j}} \right) \cdot {x_i},\end{split}$

(6)

$\quad\quad\Delta {\theta _j} = - \eta \frac{{\partial E}}{{\partial {\theta _j}}} = \eta \sum\limits_{p = 1}^N {\sum\limits_{k = 1}^m {\left( {t_k^p - y_k^p} \right)} } \cdot {\psi '}\left( {{z_k}} \right) \cdot {v_{jk}} \cdot {\phi '}\left( {{z_j}} \right){\text{。}}$

(7)

式中 $\eta $ 为学习率。

综上可知，在设定好BP神经网络的结构后，通过输入和输出样本对网络进行训练，即周而复始地进行信号的正向传播与误差的反向传播两个过程，对网络的权值和阈值不断学习修正，直到网络输出的误差减少到可接受的程度，从而实现给定的输入/输出映射关系。依据构建神经网络的基本思路，本文将一条干道上各交叉口的相位差作为输入变量，以干道车辆延误作为输出变量，设置神经网络的基本结构并给出期望的误差范围，然后依据样本数据对构建好的网络不断学习训练，直到满足误差要求，最后就可以实现对干道效用函数的高效拟合。其中相位差和车辆延误的数据可以通过微观仿真软件产生。因此，其干道效用函数的形式和式(2)一致，但针对不同干道，式(2)中的相关参数的取值不一样。

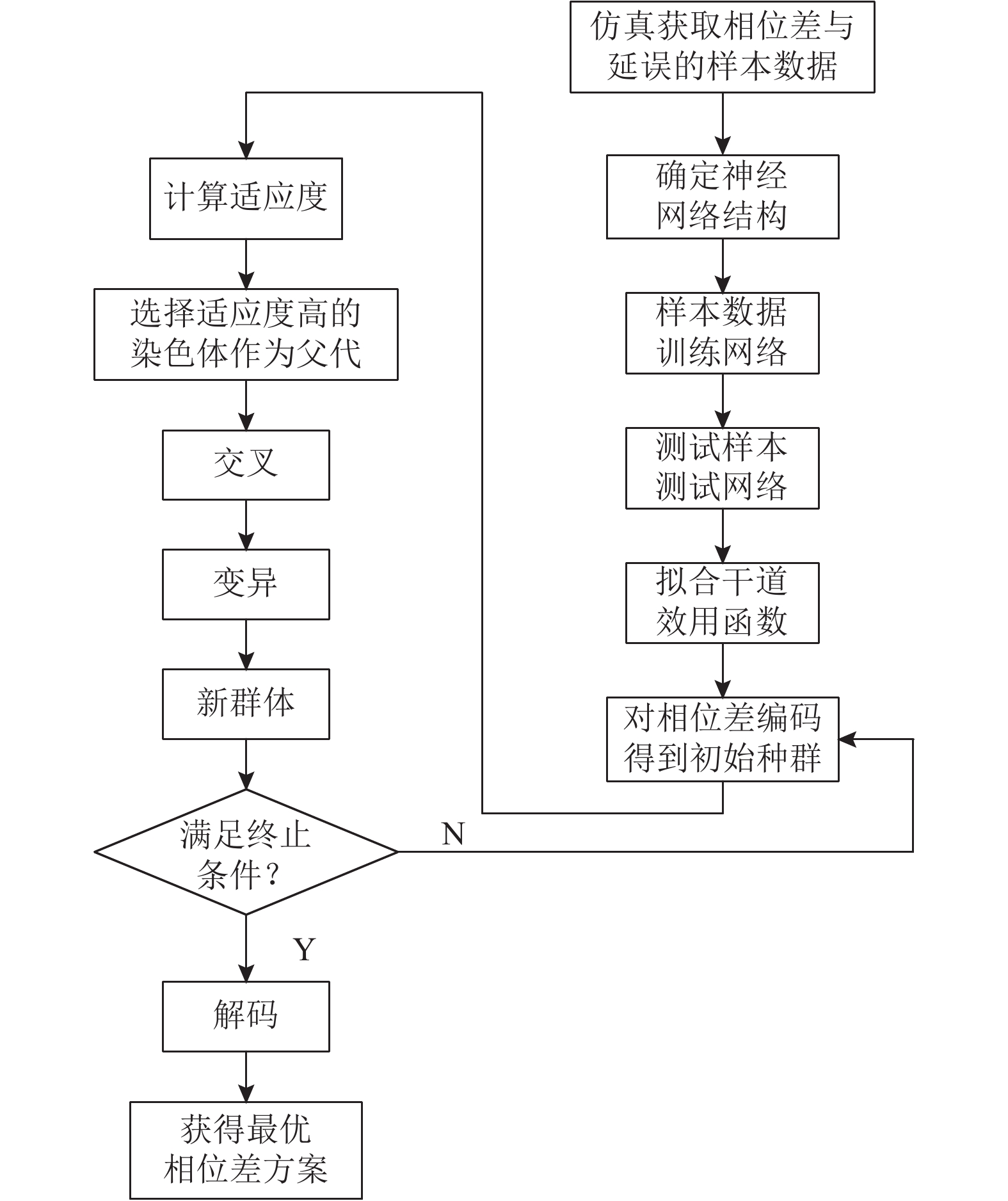
2.2 基于遗传算法的干道仿真优化

在利用神经网络拟合干道车辆延误和相位差的关系后，需要寻找神经网络中干道延误最小时对应的相位差组合，该相位差组合即为干道协调的最佳相位差方案。考虑到一般算法很难找到神经网络输出的最小值，而遗传算法具有良好的全局搜索能力^[14]，可以快速地将解空间中的全体解搜索出，而不会陷入局部最优；并且利用它的内在并行性，可以方便地进行分布式计算，加快求解速度。因此，本文采用遗传算法来寻找神经网络输出的最优值，即干道车辆最小延误值。具体优化流程如图2所示。

具体实施步骤如下。

1) 结合实际数据搭建微观仿真环境，在此环境下通过不断输入不同的相位差方案获取延误数据，即获得相位差——延误数据，以此作为神经网络的数据样本。对于一条包含n个交叉口的主干道，交叉口周期一致为C，以步距为1进行优化，则会产生 Cⁿ个相位差配时方案。为了提高仿真效率，只随机对其中一部分方案进行仿真，然后以此作为神经网络的数据样本。

2) 以干道上各交叉口的相位差 ${\lambda _1},{\lambda _{_2}},\cdots,{\lambda _n}$ 作为输入变量，车辆延误 ${D_1},{D_2},\cdots,{D_n}$ 作为输出变量，一个相位差方案 ${\left\{ {{\lambda _1},{\lambda _{_2}},\cdots,{\lambda _n}} \right\}_i}$ 对应输出一个延误值 ${D_i}$ ，i为相位差方案编号，设置神经网络的基本结构并给出期望的误差范围，然后通过BP神经网络对数据样本不断学习训练，实现干道效用函数的拟合。

3) 采用实数编码对各个相位差 ${\lambda _1},{\lambda _{_2}},\cdots,{\lambda _n}$ 进行编码，以干道车辆延误的倒数作为适应度函数： $f(n) = 1/{D_n}$ ，染色体长度为n–1，设置初始种群规模、最大遗传代数、交叉概率、变异概率等参数，通过选择、交叉、变异不断遗传进化，保留适应度大的个体作为父代，最后获得最优相位差方案。

3 案例分析 3.1 基础数据

以一条主干道上的4个连续交叉口为基础进行仿真实验，并将本文模型的优化结果与Synchro软件的结果进行对比分析。交叉口间距分别为300 m、350 m和400 m，4个连续交叉口的交通流分布如图3所示。对于周期、绿信比等基本信号配时参数，可以依据传统方法结合交通流量数据计算获得，本文只研究相位差优化方法。

3.2 仿真步骤

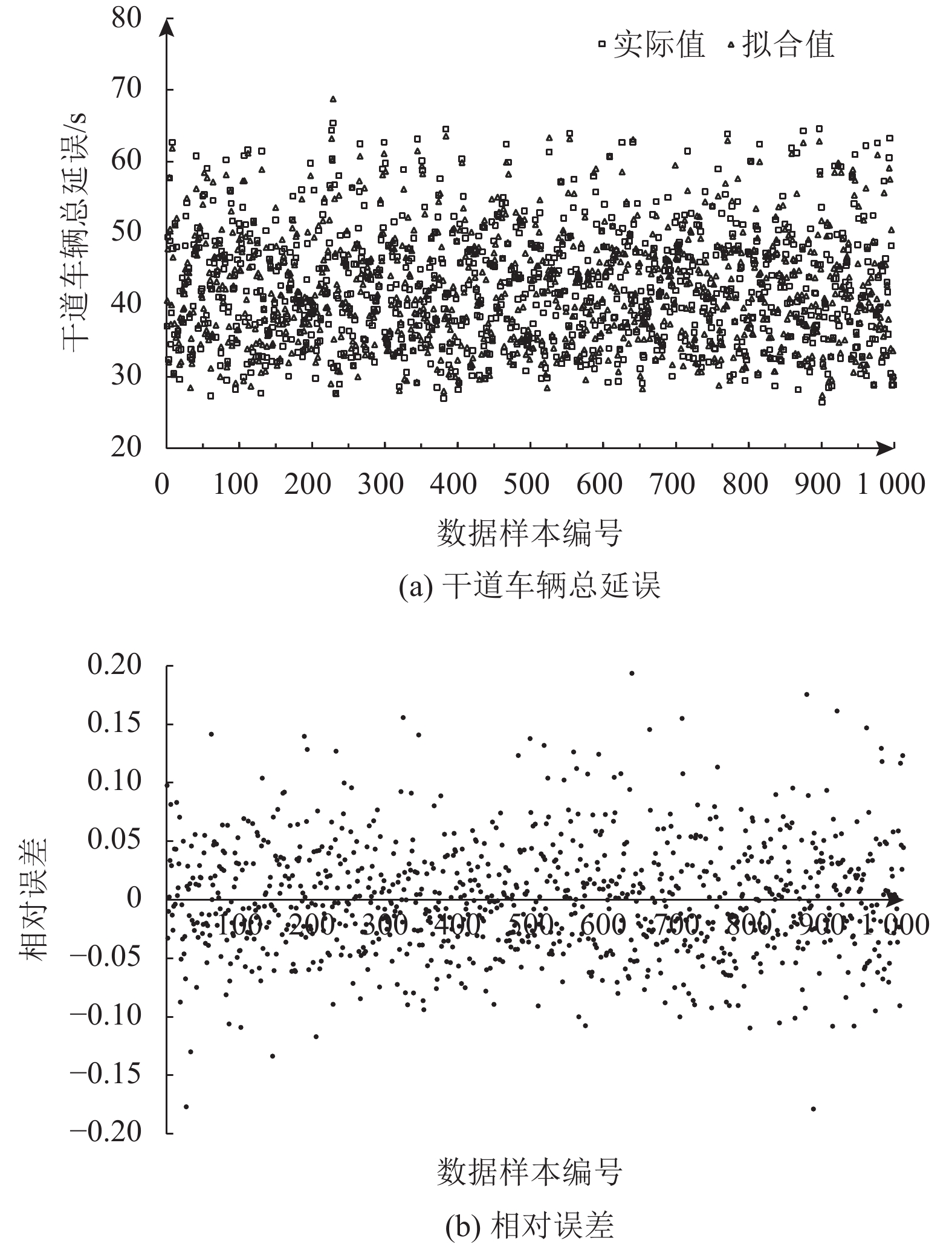
首先，利用Vissim软件搭建微观仿真环境，然后在该仿真环境下，输入交通流量、信号周期和绿信比等基本参数，接着利用Matlab编程对Vissim进行二次开发。这样可以不断改变交叉口之间的相位差，通过对不同相位差方案下的车辆行驶状况进行仿真，可以获得该相位差方案对应的干道车辆延误数据。相邻交叉口之间的相位差取值范围为[0，60)，若步距为1，则理论上可以生成60³个相位差配时方案。为了提高仿真效率，借助编程随机仿真运行其中的1 000个相位差配时方案，即可以获得1 000组数据样本。在此基础上，借助BP神经网络对数据样本不断训练学习，从而实现对干道效用函数的拟合。神经网络拟合误差如图4所示。

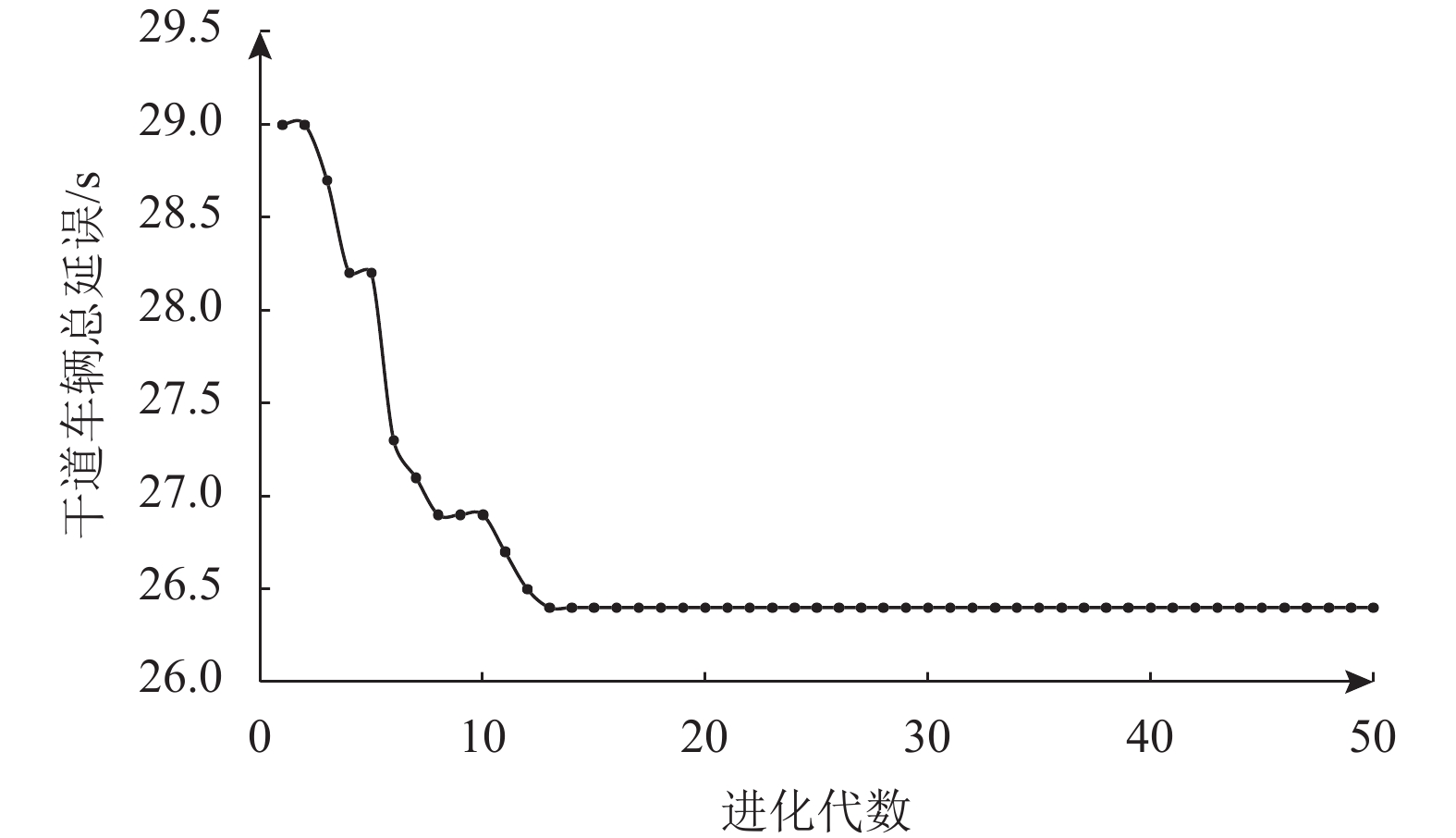
分析图4可知，神经网络对1 000组数据样本学习训练后，干道车辆延误的拟合值与实际值拟合度较高：二者的相对误差分布符合高斯分布，说明拟合效果较为可靠；相对误差范围大多在10%以内，表明拟合效果较好。考虑到一般算法很难找到神经网络输出的最小值，因此采用遗传算法寻找全局最优解。本文对个体采用实数编码的方式，以干道车辆延误的倒数作为适应度函数，初始种群规模为20，最大遗传代数为50次。设置好相关参数后，对个体进行选择，保留适应度大的个体作为父代，通过交叉、变异不断遗传进化。进化过程如图5所示。

分析图5可知，经过15代遗传进化后干道总延误达到最小值并处于稳定状态，此时获得最佳相位差配时方案为(31, 34, 4)，即对应的交叉口AB、BC、CD之间的相位差分别为31 s、34 s、4 s，该方案对应的干道延误值为26.42 s。

3.3 模型比较分析

为了证明本文模型的效果，同时利用Synchro软件仿真获得相位差优化方案。Synchro软件以美国HCM2000中的信号配时理论作为支撑，在延误计算方面，Synchro采用较为复杂的百分比延误计算方法，该计算方法对于近饱和和过饱和这两种情况下的信号配时具有良好的适用性。该方法分为2步进行，第1步是计算百分比车道组流量的情况下的每周期延误和每车延误，第2步是计算百分比车道组调整流量和平均百分比延误。本文先根据现场收集的交叉口几何渠化方案、交通流量、信号控制方案等，在Synchro搭建仿真环境，通过测试后，运行优化，得到优化后信号配时方案下的干道车辆延误值。

以干道车辆平均延误数据作为评价指标，对二者进行比较分析。两种模型的优化结果如表2所示。

由表2可知，与Synchro优化的配时方案相比，本文模型获得的相位差配时方案效果更好，使车辆在干道的平均延误减少7.57 s，控制效果提升22.27%。分析可知其主要原因在于：1) 模型考虑了连续交叉口中的多个相位差与延误的相关性，更符合实际的干道交通流特性；2) 模型的仿真优化基于神经网络和遗传算法，对于相位差的优化不是单个滚动求解，而是直接对整体的相位差组合优化求解，执行效率和优化效果更好。

4 结论

本文针对传统研究的不足，提出基于神经网络和遗传算法的干道相位差优化模型。通过实例分析可得出以下结论。

1) 神经网络能够很好地拟合干道车辆延误和多个交叉口相位差之间的关系，可以用来描述干道效用函数；

2) 遗传算法能够寻找获得神经网络的输出最小值，即最小干道车辆延误所对应的干道相位差方案；

3) 与Synchro信号配时优化软件相比，文中模型干道车辆平均延误减少了22.27%。

未来可采用深度学习等算法来描述干道车辆延误与交叉口相位差之间的关系，从而进一步提升相位差优化效果。对于多个相位差与延误的相关性，目前只有国外对不同饱和度的划分方式，未来可结合国内实际交通特性界定饱和度条件，同时也可以进一步研究受不同交通因素(交叉口转向比、饱和度等)影响的情况下本文模型的适用性。