2. 华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074
2. State Key Lab of Digital Manufacturing Equipment & Technology, Huazhong University of Science and Technology, Wuhan 430074, China
开放车间调度问题(open shop scheduling problem,OSSP)是典型的NP-hard完全问题,对此可以有如下描述:用m种机器加工n个工件,每个工件必须在每台机器上进行加工,即每个工件有m道工序,每个工序的加工时间均是一个定值。机器和工件也有一定的约束:工件没有工序顺序约束,即工件可以按照任意顺序在各台机器上加工;每台机器在任意时刻至多加工一个工件(允许机器空闲);任何时刻工件都不允许在多台机器上加工。零时刻时,所有的工作都是相互独立且可加工的。每个工作可以任意顺序通过机器,即所有的工作都没有预定的加工顺序[1]。由于对工件的加工路径没有任何限制,调度者可以赋予每个工件不同的加工顺序,在满足约束的同时,确定所有加工机器和工件的组合路径,使最大制造期Makespan最小。
相较于作业车间问题(job-shop scheduling problem,JSP)和流水车间问题(flow-shop scheduling problem,FSP)来说,OSSP具有更大的可行解空间,复杂度更高。目前,精确算法和启发式规则都可以用来解决OSSP。Brucker等[2]针对最小化Makespan的多台机器的OSSP,采用基于析取图的分枝定界法,首次求得了Taillard[3]部分算例的最优解,但同时承认在某些情况下,该分枝定界法不如启发式规则有效。Rock等[4]引入基于两个机的情况下,用于求解多项式可行解的机器聚集算法,一些更有前途的方法集中在所谓密集调度(dense schedules)即如果没有设备处于闲置状态,或没有准备在该机器上处理的工序,一个开放的车间调度就被认为是密集的。Ahmadizar等[5]针对OSSP搜索空间大,一般算法搜索效率低下等问题,利用多种启发式规则缩小搜索空间,提高了算法的进化效率。Doulabi等[6]为消除初始解对粒子群优化产生的影响,提出采用多目标模拟退火方法生成初始种群,然后采用蚁群算法求解多目标的OSSP,得到了标准算例的最新下界。Gueret等[7]发布了每个操作具有两个优先项的表调度启发式和具有本地搜索改进程序的匹配启发式算法。王军强等[8]在开放式车间调度问题的优化求解中,提出了一种基于多样性增强的自适应遗传算法,实验结果表明多样性增强算子提高了求解质量,自适应交叉变异算子加快了算法的收敛速度。展勇等[9]针对多并行机可中断开放车间调度问题,提出了基于网络流的调度算法,同时针对OSSP的特点,建立了以制造期最短为目标的整数规划模型,提出了工件有就绪时间约束时制造期下界的计算方法,求得各机器上工件的加工顺序。
本文主要通过对文化基因算法(memetic algorithm, MA)核心思想的研究,用其来求解OSSP,使用Taillard[3]的基准实例来测试算法,为解决柔性检测调度优化问题提供理论和技术支持。
1 问题数学模型开放式车间调度问题可用如下数学模型表示。
目标函数:minCmax,即最小化最大制造期。
约束条件如下。
| $\quad\quad{X_{j, i, k}} = \left\{ {\begin{array}{*{20}{c}}{1, }&{{\text{工序}}{{{O}}_{{{k}}, {{i}}}}{\text{之后马上进行}}{{{O}}_{{{j}}, {{i}}}}{\text{加工}}};\\0,&{\text{其他情况。}}\end{array}} \right.$ | (1) |
| $\quad\quad \sum \limits_{k = 0, k \ne j}^n {X_{j, i, k}} = 1,\quad\quad\forall j, i;$ | (2) |
| $\quad\quad \sum \limits_{{{j}} = 1, {{j}} \ne {{k}}}^{{n}} {{{X}}_{{{j}}, {{i}}, {{k}}}} {\text{≤}} 1,\quad\quad\forall {{i}}, {{k}} {\text{>}} 0;$ | (3) |
| $\quad\quad \sum \limits_{{{j}} = 1}^{{n}} {{{X}}_{{{j}}, {{i}}, 0}} = 1,\quad\quad\forall {{i}};$ | (4) |
| $\quad\quad{X_{j, i, k}} + {X_{k, i, j}} {\text{≤}} 1,\quad\quad\forall i, k {\text{<}} n, k {\text{>}} j;$ | (5) |
| $\quad\quad{C_{j, i}} {\text{≥}} {C_{k, i}} + {P_{j, i}} + {X_{j, i, k}},\quad\quad\forall j, i, k, k \ne j;$ | (6) |
| $\quad\quad{C_{j, i}} {\text{≥}} {C_{j, i}} + {P_{j, i}} + \left( {1 - {X_{j, i, l}}} \right) B,\quad\quad\forall j, i {\text{<}} m, l {\text{>}} i;$ | (7) |
| $\quad\quad {C_{j, i}} {\text{≥}} {C_{j, i}} + {P_{j, i}} + {X_{j, i, l}}B,\quad\quad\forall j, i {\text{<}} m, l {\text{>}} i{\text{。}}$ | (8) |
式中:Oj, i表示工件j在机器i上加工;Pj, i、Cj, i表示Oj, i的加工时间、完工时间;i表示机器序号,j表示工件序号;B是一个足够大的正数;式(1)用于判断工序之间的先后加工关系;式(2)表示每个工序都能在每台机器上加工一次;式(3)表示每台机器加工每道工序后最多只有一个工序;式(4)表示工序0可以成为每台机器上一个工序的前者;式(5)表示保证了一道工序不能同时是另一个工序的前者和后者;式(6)表示使Oj, i不能在Ok, i之前开始加工;式(7)、(8)表示与操作相关的约束。
2 析取图模型析取图模型常用来描述和分析车间调度问题,由一系列节点组成[10]。在析取图模型中,每道工序都对应一个节点。节点编号从1到N,其中N=m×n是工序的总数目。此外,还有两个虚节点,节点0和节点N+1,分别代表一个调度的开始和结束。对于属于同一工序的每对操作{i, j},两个圆弧(i, j)和(j, i)代表相反的加工方向。同样的,对于需要同一个机器加工的每对工序{i, j},两个圆弧(i, j)和(j, i)代表相反的加工方向。两道工序间的反向弧表示一个事实,即每一台机器可以同时处理至多一个工序和各作业至多同时在一个机器上进行处理。圆弧(i, j)对应的工序i时长为di。最后,对于每个节点
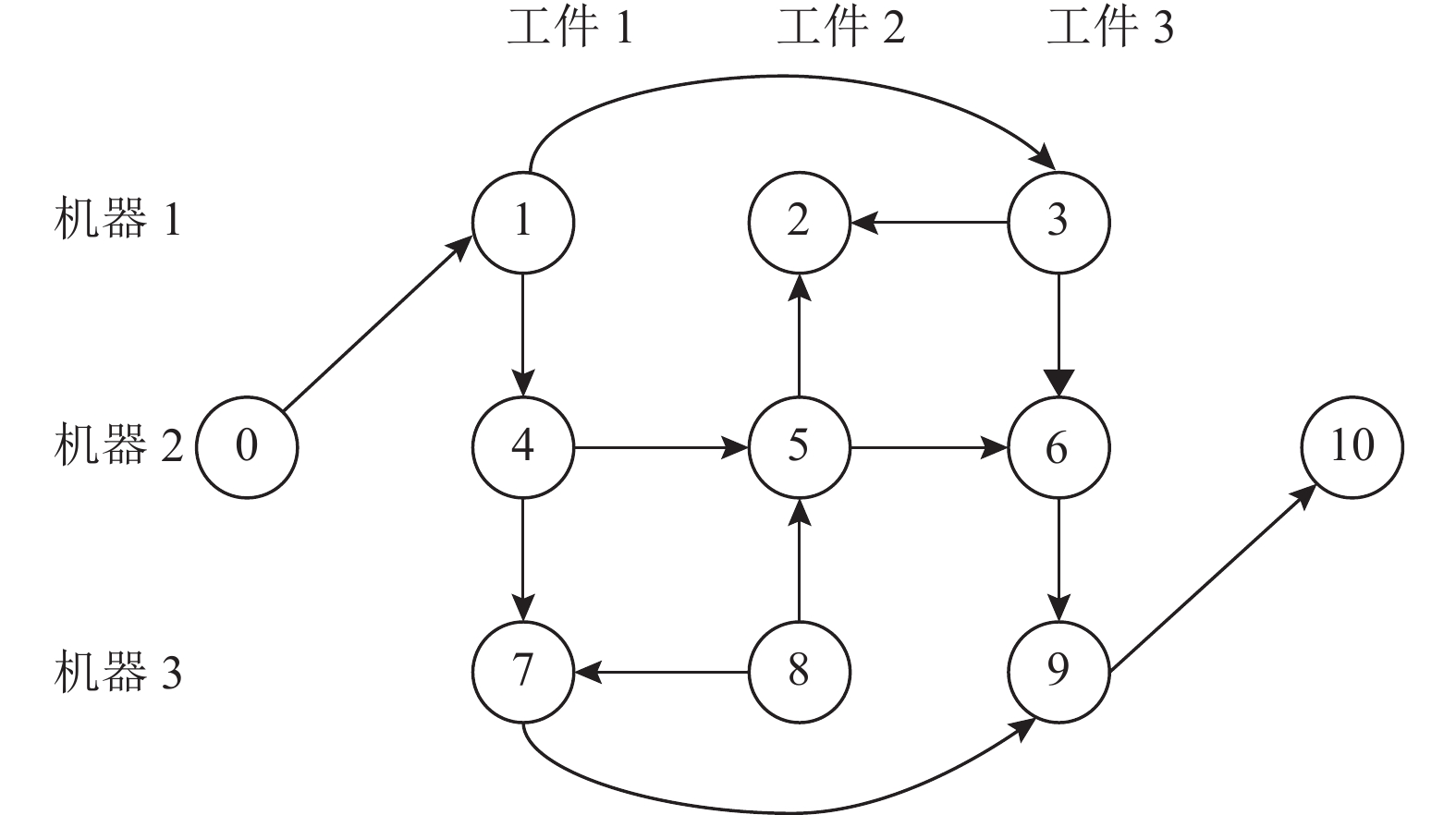
开放车间调度问题可以建立析取图模型进行求解,每一个非连通的析取图都对应调度问题的一个可行解,所有析取图中的从节点0到节点N的最长距离就是所有可行解的最大完工时间,节点0到节点N的最大路径即为关键路径。一般情况下,关键路径有多条,包含了操作的有序序列。这些由关键路径分解而成的工序的序列,称之为关键块,关键块是在同一台机器上加工某一作业的工序的最大序列。一个关键块必须具有至少两个工序,对于任何两个相邻的关键块,其中一个由同一作业的工序组成,另一个由在同一机器上加工的工序组成[11]。
图1给出了在求解一个3台机器和3个工件的开放车间调度问题时的一个可行调度的析取图模型的关键路径(图中实线箭头为关键路径),把本实施案例的关键路径0 −1−4−5−6−9−10分解成3块:1−4、4−5−6和6−9。模块1−4含有作业1的工序;模块4−5−6包括机器2上加工的工序;模块6−9由作业3的工序组成。
|
图 1 3×3问题的一个析取图模型 Fig. 1 A disjunctive graph model for 3×3 problems |
现在对引入的附加符号进行如表1的说明,其中
| 表 1 附加符号说明 Tab. 1 Additional symbol specification |
当且仅当ei+di+li=Cmax时,工序i就被称为关键工序,那么这一条加工路径即为一条关键路径。需要注意的是,对每个工序i以下条件成立:
| $\quad\quad{e_i} = {\rm{max}}\;\left\{ {{e_{{\rm PM}\left( i \right)}} + {d_{{\rm PM}\left( i \right)}}, {e_{{\rm PJ}\left( i \right)}} + {d_{{\rm PJ}\left( i \right)}}} \right\},$ |
| $\quad\quad{l_i} = {\rm{max}}\;\left\{ {{l_{{\rm SM}\left( i \right)}} + {d_{{\rm SM}\left( i \right)}}, {l_{{\rm SJ}\left( i \right)}} + {d_{{\rm SJ}\left( i \right)}}} \right\}{\text{。}}$ |
对于未定义的i,ei,di和li等于0。每个工序i的ei,li的值可以用Bellman[12]算法计算。
3 文化基因算法 3.1 基本原理文化基因算法(MA)的框架在业务流程上与遗传算法基本相同,不同的是文化基因算法还在此基础上加入局部邻域搜索的方法,使每次迭代的全部个体都能够达到局部最优。遗传算法的全局搜索对种群进行全局广度搜索,局部搜索对个体进行局部深度搜索。结合遗传算法和局部搜索算法的优点,文化基因算法的全局搜索能力非常强大,而且在每次交叉和变异操作后均进行局部搜索,然后比较种群的分布情况,及时淘汰适应度较差的个体,从而达到用更少的迭代次数,更快得出算法的最优解的目的。因此,该算法不仅获得的最优解的收敛性能比较高,而且获得最优解的质量也非常的好。在某些问题领域里,与传统的遗传算法相比,文化基因算法的搜索效率能够大幅度提高[13]。
MA的程序结构流程图,如图2所示。

|
图 2 MA程序结构流程图 Fig. 2 The flow chart of procedure of MA |
MA的全局搜索策略可以从遗传算法、模拟退火算法、进化策略等多种现成的进化算法中选择,这些全局搜索的策略都确保父代的特点能够顺利地延续到子代上,同时要最大限度地让子代发生变异。本文采用研究比较普遍的遗传算法(genetic algorithm,GA),作为MA的全局搜索策略。
GA通过模拟生物进化过程中的自然选择和遗传中发生的交叉和变异过程的计算模型来搜索最优解[14]。从一个随机产生的初始种群开始,经过一系列的选择、交叉和变异,得到一群适应度更高的子代,使种群朝着更好的方向进化,随着时间的推移,种群不断进化,最终得到一群适应度最高的个体,也就求得了问题的最优解。一个简单GA的伪代码如图3所示,其中P(t)表示t代种群,初代种群P(0)是随机产生的。

|
图 3 遗传算法伪代码 Fig. 3 The pseudo code of GA |
遗传算法的关键环节如下。
1) 编码方案。遗传算法求解问题的关键不是在问题的解空间上,而是利用解的特定编码表示。选用不同的编码方案,会对算法的性能和效率等产生截然不同的影响。
2) 确定适应度函数。适应度用来度量解的质量高低,适应度的大小一般取决于解的行为与解空间的关系。通常表示为目标函数或用度函数的形式。可行解的适应度是算法在计算时进行选择操作的参考标准。
3) 进化操作。主要是变异、交叉等进行操作,进化操作的合理程度直接影响到进化算法的性能。一般需要根据所选的编码方法和需求解的问题特征来设计进化操作。
4) 选择策略。选择策略体现在2个方面:①进行第3)步之前,选择符合要求的父代个体作为初始种群;②在完成第3)步之后,选择一部分优秀的子代个体保留下来。通常会选择轮盘赌、线性排名选择等选择策略。
5) 控制参数。控制参数主要包括种群的初始规模、算法执行的迭代次数、交叉操作的概率、变异操作的概率等控制参数。
3.3 局部搜索策略开放车间调度问题的邻域结构与作业车间调度问题邻域解的产生类似,由交换关键块上的相邻工序产生,每交换一次称为移动[10]。尽管有相关理论表明,关键块的某些工序交换后得到的解的质量会有所下降,但是N5邻域结构会避免此类情况的发生。
N5领域结构的主要思想如下。
1) 除了第1个和最后1个关键块以外,交换其他所有关键块的首尾工序。
2) 如果关键路径的尾块上的工序数大于2时,则将与块首连着的工序进行交换;如果此情况发生在第1个关键块上,就交换和块尾相连的工序;如果只有2个工序时,只需将这2个工序进行交换。
3) 如果只有1个工序时,不需要进行交换。
与作业车间调度相比,开放车间调度问题中的关键块中的工序是在同一个机器上加工,而不是属于同一个工作。所以在进行交换时,需要分为两种情况,而对于工序(i, j)有4种移动方式。
第1种情况:当工件i,j在一台机器上加工时(此时称为机器类型)。
1) 交换(i, j);
2) 交换(i, j)和(PJ(j), j);
3) 交换(i, j)和(i, SJ(j));
4) 交换(i, j), (PJ(j), j)和(i, SJ(j))。
第2种情况:当工件i, j为同一个工件时(此时称为工件类型)。
1) 交换(i,j);
2) 交换(i, j)和(PM(j), j);
3) 交换(i, j)和(i, SM(i));
4) 交换(i, j), (PM(j), j)和(i, SM(i))。
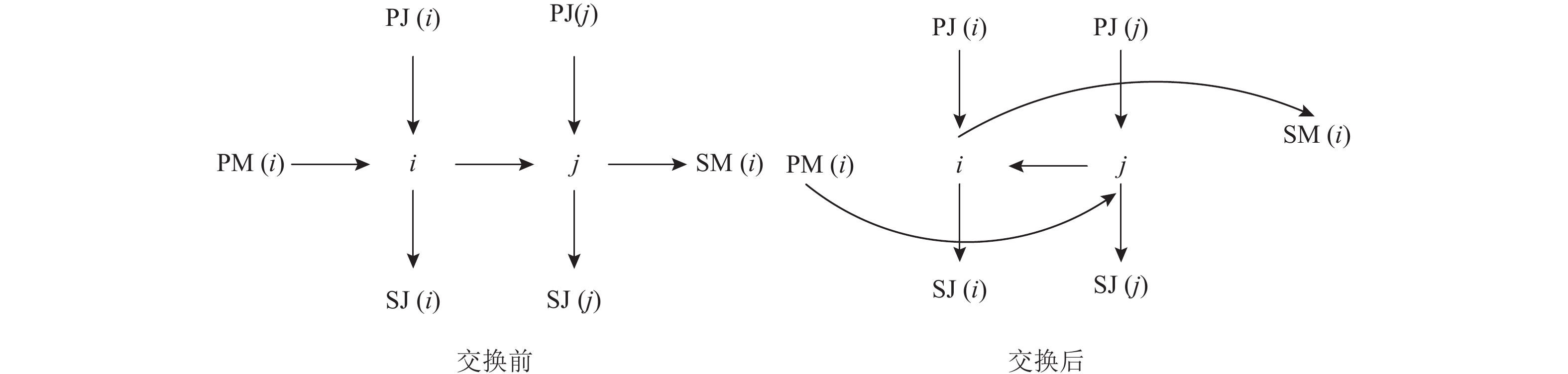
对于第1种情况,交换前后的析取图如图4所示。
|
图 4 交换(i, j)前后的析取图 Fig. 4 Disjunctive graphs of around the exchange (i, j) |
文中采用的爬山法是所有局部搜索策略中最简单、效率最高的,其算法过程描述如下。
1) 选择一个当前解s;
2) 根据邻域结构产生一个领域解集N(s);
3) 剔除解集中质量比s差的解,得到一个新集合N(s)';
4) 计算N(s)'中解的个数num;
5) 如果num不等于0,就从N(s)'中根据一定策略选择一个解换掉s,跳到第2步,否则结束算法。
在计算过程中,如何定义邻域结构和如何选取可行解尤其重要。对于在作业调度问题上的爬山法,Mattfeld[15]给出了3种邻域解的选择策略:随机选取、顺序选取和最优选取。根据爬山法的特性,在求解过程中爬山法会剔除不如当前解法的邻域解,只保留更好的领域解,因而易形成局部最优。当然也有能跳出局部最优的局部搜索算法,比如模拟退火法,变邻域搜索和禁忌搜索等,但是它们的迭代次数较多,花费时间比爬山法多,所以这里采用爬山法进行局部搜索。
4 算法性能分析设定机器数量m有4、5、7、10四种情况,工件加工时间的计算是采用Taillard[3]提供的标准算例,对每台机器进行10组算例试验。将上述文化基因算法在 Visual Studio 6.0 开发环境用 C++语言编程,来求得程序的最优解,并将程序取得的最后结果与每个实例的下限值LB进行比较。
| $\quad\quad{\rm{LB}} = {\rm{max}}\left\{ {\mathop {\max }\nolimits_{{{{M}}_{{i}}} \in {{M}}} \left\{ {\mathop \sum \limits_{{{j}} = 1}^{{n}} {{{p}}_{{{ij}}}}} \right\}, \mathop {\max }\nolimits_{{{{J}}_{{j}}} \in {{J}}} \left\{ {\mathop \sum \limits_{{{i}} = 1}^{{m}} {{{p}}_{{{ij}}}}} \right\}} \right\}{\text{。}}$ |
在算法运行过程中,文化基因算法的相关参数设置如下:种群数量为500,交叉概率为0.35,变异概率为0.05,最大迭代次数为100。
为了分析制造期偏离最优值的偏离程度,定义偏离程度指标Dc的计算公式为:
| $\quad\quad{D_{\rm c}} = \frac{{{C_{\rm d}}}}{{{C_{\rm opt}}}},$ |
其中,Cd是MA的制造时间,Copt是两个对比算法中制造期的较小的值,在文中即是LB的计算值。
下面是MA得出的调度结果与每个问题所给下限值的比较情况,如表2~5所示。
| 表 2 Taillard 4×4问题调度结果 Tab. 2 The problem of scheduling results Taillard 4×4 |
| 表 3 Taillard 5×5问题调度结果 Tab. 3 The problem of scheduling results Taillard 5×5 |
| 表 4 Taillard 7×7问题调度结果 Tab. 4 The problem of scheduling results Taillard 7×7 |
| 表 5 Taillard 10×10问题调度结果 Tab. 5 The problem of scheduling results Taillard 10×10 |
表2~5是两种算法的调度结果,4组算例中的工件数n都等于机器种类数m。MA所得解均与最优解下限值有一定的偏差,偏离程度指标的范围为:1.00<Dc<1.60。这说明当n=m时,本算法的求解质量虽然达不到算例的下限值,但也达到了Dc<2.0的指标,说明本文的MA符合算法求解的有效性。虽然开放车间调度问题在约束上比其他车间调度问题要少得多,但它也因此具有了较为宽广的搜索空间,更体现了局部搜索的重要性。文化基因算法是在全局搜索遗传算法的基础上加入局部搜索,在解决开放车间调度问题上表现出了自己良好的优越性。
5 结束语针对开放车间调度问题,本文提出了文化基因算法的框架与操作流程,该算法不仅沿用了遗传算法的基本操作,并且还在此基础上加入局部搜索策略,使每次迭代的全部个体都可以先得到局部最优解。遗传算法进行种群的全局广度搜索求解,局部搜索策略进行个体的局部深度搜索求解。MA汲取了遗传算法和爬山算法的优点,因此不仅具有很强的全局搜索能力,同时在每次交叉和变异操作后通过爬山算法均进行局部搜索,通过优化种群分布、及时删除不良个体,进而减少迭代次数,加快算法的求解速度,既保证了算法较高的收敛性,又确保能获得高质量的解。基于40个标准算例的测试,通过与下界值LB的比较分析,测试结果表明:1) 利用本文提出的MA基本上可以求解出基准实例的最优解,而且都达到Dc<2.0的指标要求,证明了MA的有效性;2) MA继承了遗传算法的基本操作,具有较强全局搜索能力,能够扩大算法的搜索范围,避免陷入局部最优;3) 在全局搜索策略过程中加入局部搜索策略可以改善种群结构,增强算法的局部寻优能力,进而加快算法的求解速度;4) 随着问题规模的增大,MA在求解开放车间调度时仍然能够得出质量符合要求的解,说明所提算法在解决具有较大规模和较大搜索空间的调度问题时,拥有更有效的算法性能。
| [1] |
LOW C F, YEH Y. Genetic algorithm-based heuristics for an open shop scheduling problem with setup processing and removal times separated[J].
Robotics and Computer-Integrated Manufacturing, 2009, 25(2): 314-322.
DOI: 10.1016/j.rcim.2007.07.017. |
| [2] |
BRUCKER P, HURINK J, JURISCH B, et al. A branch & bound algorithm for the open-shop problem[J].
Discrete Applied Mathematics, 1997, 76(1-3): 43-59.
DOI: 10.1016/S0166-218X(96)00116-3. |
| [3] |
TAILLARD E D. Benchmark for basic scheduling problems[J].
European Journal of Operational Research, 1993, 64(2): 278-285.
DOI: 10.1016/0377-2217(93)90182-M. |
| [4] |
ROCK H, SCHMIDT G. Machine aggregation heuristics in shop-scheduling[J].
Methods of Operations Research, 1983, 45: 303-314.
|
| [5] |
AHMADIZAR F, FARAHANI M H. A novel hybrid genetic algorithm for the open shop scheduling problem[J].
The International Journal of Advanced Manufacturing Technology, 2012, 62(5-8): 775-787.
DOI: 10.1007/s00170-011-3825-1. |
| [6] |
DOULABI S, AVAZBEIUI M, ARAB S, et al. An effective hybrid simulated annealing and two mixed integer linear formulations for just-in-time open shop scheduling problem[J].
The International Journal of Advanced Manufacturing Technology, 2012, 59(9-12): 1143-1155.
DOI: 10.1007/s00170-011-3546-5. |
| [7] |
GUERET C, PRINS C. Classical and new heuristics for the open-shop problem: a computational evaluation[J].
European Journal of Operational Research, 1998, 107(2): 306-314.
DOI: 10.1016/S0377-2217(97)00332-9. |
| [8] |
王军强, 郭银洲, 崔福东, 等. 基于多样性增强的自适应遗传算法的开放式车间调度优化[J].
计算机集成制造系统, 2014, 20(10): 2479-2493.
WANG Junqiang, GUO Yinzhou, CUI Fudong, et al. Diversity enhancement based adaptive genetic algorithm for open-shop scheduling problem[J]. Computer Integrated Manufacturing Systems, 2014, 20(10): 2479-2493. |
| [9] |
展勇, 邱长华, 祝海涛. 基于网络流的多并行机可中断开放车间调度算法[J].
计算机集成制造系统, 2011, 17(5): 990-996.
ZHAN Yong, QIU Changhua, ZHU Haitao. Algorithm of preemptive open-shop scheduling with parallel machines based on network flow[J]. Computer Integrated Manufacturing Systems, 2011, 17(5): 990-996. |
| [10] |
ROY B, SUSSMAN B. Les problèmes d’ordonnancement avec contraintes disjonctives[C/OL].(2017-08-01).http://www. scirp.org/(S(i43dyn45teexjx455qlt3d2q))/reference/ReferencesPapers.aspx?ReferenceID=1201138.
|
| [11] |
PINEDO M. 调度: 原理、算法和系统[M]. 张智海, 译. 北京: 清华大学出版社, 2007.
|
| [12] |
BELLMAN R E. On a routing problem[J].
Quarterly Applied Mathematics, 1958, 16: 87-90.
DOI: 10.1090/qam/1958-16-01. |
| [13] |
刘漫丹. 文化基因算法(Memetic Algorithm)研究进展[J].
自动化技术与应用, 2007, 26(11): 1-4, 18.
LIU Mandan. The development of the memetic algorithm[J]. Techniques of Automation & Application, 2007, 26(11): 1-4, 18. DOI: 10.3969/j.issn.1003-7241.2007.11.001. |
| [14] |
玄光男, 程润伟. 遗传算法与工程优化[M]. 北京: 清华大学出版社, 2004.
|
| [15] |
MATTFELD D C. Evolutionary Search and The Job Shop[M]. Berlin: Springer, 1995.
|
 2018, Vol. 21
2018, Vol. 21

