2. 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China
公交线路调度的重要依据是线路的客流出行需求[1-2],现有的线路调度主要采用单模式调度,对于如何利用现有的数据,通过分析客流出行特征,优化调度模式缺乏相关研究。文献[3-5]研究表明乘客乘坐公交出行具有一定的规律,从非集计分析层面来说,乘客的上下车的站点较为固定,从集计层面来说不同站点的上下车乘客较为固定。文献[6]指出在高峰出行时段部分线路主要客流需求是通勤客流,而采用传统的一条线路一种调度模式会造成乘客出行时间总体过长,公交运行效率不高等问题。据此本文提出,通过公交IC卡的数据分析,得到线路的通勤客流,并据此设计单线路的多模式调度的方式提高公交系统运行效率。
现有的关于线路多模式调度的研究主要集中在大站快车的线路设计及调度。如文献[7-9]考虑线路载客能力,提出了单条线路大站快车设计的模型。文献[10] 基于已经确定的线路集,提出了线网大站快车的线路选择及发车频率设计方法。但这些研究主要集中在已经确定客流需求情况下的大站快车设计研究,对于如何结合公交IC卡,结合数据挖掘技术,缺乏相应的深入探讨。
与现有的大站快车设计不同,本文主要针对早晚高峰出行中,通勤比例较高,出行量急剧增加这一现象,提出基于IC卡识别通勤客流识别技术的公交线路多模式调度。多模式调度仅服务于高峰时段,平峰时段时恢复原有的公交服务。
1 问题及相关概念描述 1.1 公交调度模式及出行时间分析现有的公交调度模式主要是采用单线路的调度模式,也就是公交车在运行过程中沿着既定线路,不论站点上下客多少,每个站点都会停靠。而实际上,公交车在进站之前要进行减速直至停靠至站点,离开站点时要加速至正常运行速度,这一过程中减少了车辆的平均运行速度,增加了线路的运行时间[11],增加部分与停靠站点无上下车关系的乘客的出行时间。而在早晚高峰期,大部分出行需求为通勤出行[6],站点相对固定,针对这一特定的公交出行行为,本文提出单线多调模式,以此减少整体乘客出行时间。
1.2 线路客流特征描述文献[12]根据公交IC卡数据分析表明,工作日的高峰时段公交出行需求主体主要是通勤客流,通勤乘客是城市公共交通系统服务的主要对象。而通勤客流主要由上下班乘客构成,其出行起始点相对固定且集中,且其出行时间主要集中在早晚高峰时段。
1.3 公交IC卡数据公交IC卡在公交出行中广泛使用,随着计算机技术的发展,学者们对IC提取客流出行特征展开了大量研究。文献[13-14]利用公交IC卡信息,基于公交出行链对乘客提出了乘客下车站点判断模型。文献[15-16]利用IC卡信息,实现了公交OD的推导。与这些研究不同,本文主要是对单条线路的通勤客流进行识别,在此基础上推导通勤客流的主要上下车点。
1.4 单线多调模式思路描述本文所指的单线多调模式,是指在高峰期时段内,通过识别通勤客流基础上确定通勤站点,以节约乘客总体出行时间为目的,将原有单线路模式设计为通勤线路和一般线路的多调度模式。
2 通勤客流识别及线路多调模式模型构建 2.1 通勤客流识别模型2.1.1 模型假设
本研究结合乘客公交出行的实际特征,做出如下模型的条件假设。
1) 公交通勤客流出行构成封闭的出行链,即乘客下车站点为乘客的下次出行的上车站点;
2) 乘客工作日出行次数到达一定频次,且符合通勤出行特征,即认为其为通勤客流;
3) 本文所指的通勤客流时段为出行时间在早高峰和晚高峰时段。
2.1.2 模型构建
通过对以往研究分析,结合文中研究对象是针对的通勤客流,确定了对原始客流数据进行2个方面进行判断,从而筛选出通勤客流。2个方面分别为客流出行时间段是否为通勤客流时间段;周出行次数是否达到一定的比例。定义向量
1) 通勤时段判断模型构建。
通勤时段是指客流出行时间是否满足早晚高峰出行特征,因此在通勤客流识别中含有来去2个指标,分别为去程
① 客流时间段判断模型构建。
| $\quad\quad{t_{ij}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} 1,&{{t_{ij}} \in {t_{\rm{k}}},i,j \in N}; \\ 0,&{{t_{ij}} \notin {t_{\rm{k}}},i,j \in N}{\text{。}} \end{array}} \right.$ | (1) |
其中,i为标号为
② 通过去回程客流判断标示符作乘积运算可以得到客流是否满足通勤时段。
| $\quad\quad {\varepsilon _{ij}} = {t_{ij}} \times {t_{ji}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} 1,&{{t_{ij}} \in {t_{\rm{k}}} \cap {t_{ji}} \in {t_{\rm{k}}},i,j \in N} ;\\ 0,&{{t_{ij}} \notin {t_{\rm{k}}} \cup {t_{ji}} \notin {t_{\rm{k}}},i,j \in N} {\text{。}}\end{array}} \right.$ | (2) |
其中,
2) 出行频次判断模型构建。
出行频次判断方法是指一周内工作日出行频次是否满足通勤客流特征,当满足就取1,否则,取0
| $\quad\quad{\varphi _{ij}} = \left\lceil {({p_{ij}} - c)/c} \right\rceil {\text{。}}$ | (3) |
其中,
3) 通勤客流判断模型构建。
| $\quad\quad{f_{ij}} = {\varepsilon _{ij}} \times {\varphi _{ij}}{\text{。}}$ | (4) |
其中,
模型说明,通勤客流识别模型是从出行时段和出行频次来衡量公交出行是否为通勤客流的,只有当出行在通勤时段且出行频次到达额定次数,才认其为通勤客流。
2.2 线路多调模式模型2.2.1 模型假设
1) 乘客总是可以乘坐第一辆车离开;
2) 假定乘客在站点的随机到达率与车辆离开过程无关,在一定周期内是个常量模型构建;
3) 假定通勤客流优先选择通勤线路出行。
| $\quad\quad \min {T = } {T_{\rm{w}}} + {T_{\rm{t}}}{\text{。}}$ | (5) |
s.t.
| $\quad\quad V_{\rm{t}}^{\rm{n}} + V_{\rm{t}}^{\rm{c}} = V_{\rm{t}};$ | (6) |
| $\quad\quad\sum\limits_{i,j \in N\atop i \ne j} {r_{ij}^{\rm{n}} {\text{≤}} 1}; $ | (7) |
| $\quad\quad\sum\limits_{{i_{\rm{c}}},{j_{\rm{c}}} \in {N_{\rm{c}}}\atop{i_{\rm{c}}} \ne {j_{\rm{c}}}} {r_{{i_{\rm{c}}}{j_{\rm{c}}}}^{\rm{c}} {\text{≤}} 1}; $ | (8) |
| $\quad\quad r_{ii}^{\rm{n}} = 0,i \in N;$ | (9) |
| $\quad\quad r_{_{{i_{\rm{c}}}{i_{\rm{c}}}}}^{\rm{c}} = 0,{i_{\rm{c}}} \in {N_{\rm{c}}}{\text{。}}$ | (10) |
其中,
式(5)为模型的目标函数,即乘客总的出行时间最小;式(6)为约束条件,表示设计通勤线路之后,车队规模与现有的公交线路保持一致;式(7)和式(8)表示在非通勤线路中每个站点在一条线路最多出现一次;式(9)和式(10)表示在通勤线路中每个站点在一条线路也最多出现一次;
乘客总的等待时间与乘客出行量和发车间隔有关,乘客在车旅行时间与乘客出行距离、车速以及停靠站点数量有关。由于多模式调度与单模式调度主要影响是在乘客等待时间以及站点停靠时间,因此上述模型可以重塑如下。
| $ \quad\quad \min {T = } {T_{\rm{w}}} + {T_{\rm{t}}}{\text{。}}$ | (11) |
s.t.
| $\quad\quad{V_{\rm{t}}^{\rm{n}}} + V_{\rm{t}}^{\rm{c}} = {V_{\rm{t}}};$ | (12) |
| $\quad\quad\sum\limits_{i,j \in N\atop i \ne j} {r_{ij}^{\rm{n}}{\text{≤}} 1};$ | (13) |
| $\quad\quad\sum\limits_{{i_{\rm{c}}},{j_{\rm{c}}} \in {N_{\rm{c}}}\atop{i_{\rm{c}}} \ne {j_{\rm{c}}}} {r_{{i_{\rm{c}}}{j_{\rm{c}}}}^{\rm{c}}{\text{≤}} 1};$ | (14) |
| $\quad\quad r_{ii}^{\rm{n}} = 0,i \in N;$ | (15) |
| $\quad\quad r_{{i_{\rm{c}}}{i_{\rm{c}}}}^{\rm{c}} = 0,{i_{\rm{c}}} \in {N_{\rm{c}}};$ | (16) |
| $\begin{split}&\quad\quad {T_{\rm{w}}} = {E_{ij}}({T^{\rm{n}}}) \left(\displaystyle\sum\limits_{{i_{\rm{n}}} \in {N_{\rm{n}}}} {\displaystyle\sum\limits_{{j_{\rm{n}}} \in {N_{\rm{n}}}} {{d_{{i_{\rm{n}}}{j_{\rm{n}}}}}} } + \displaystyle\sum\limits_{{i_{\rm{n}}} \in {N_{\rm{n}}}} {\displaystyle\sum\limits_{{j_{\rm{c}}} \in {N_{\rm{c}}}} {{d_{{i_{\rm{n}}}{j_{\rm{c}}}}}} } + \right. \\&\left.\displaystyle\sum\limits_{{i_{\rm{c}}} \in {N_{\rm{c}}}} {\displaystyle\sum\limits_{{j_{\rm{n}}} \in {N_{\rm{n}}}} {{d_{{i_{\rm{c}}}{j_{\rm{n}}}}}} } \right) + {E_{ij}}({T^{\rm{c}}}) \displaystyle\sum\limits_{{i_{\rm{c}}}} {\displaystyle\sum\limits_{{j_{\rm{c}}}} {{d_{{i_{\rm{c}}}{j_{\rm{c}}}}}}};\end{split} $ | (17) |
| $\begin{split}&\quad\quad{T_{\rm{t}}} = \displaystyle\sum\limits_{{i_{\rm{n}}} \in {N_{\rm{n}}}} {\displaystyle\sum\limits_{{j_{\rm{n}}} \in {N_{\rm{n}}}} {{d_{{i_{\rm{n}}}{j_{\rm{n}}}}}} } [({l_{{i_{\rm{n}}}{j_{\rm{n}}}}}/v) + ({j_{\rm{n}}} - {i_{\rm{n}}} - 1) s]+\\& \displaystyle\sum\limits_{{i_{\rm{n}}} \in {N_{\rm{n}}}} {\displaystyle\sum\limits_{{j_{\rm{c}}} \in {N_{\rm{c}}}} {{d_{{i_{\rm{n}}}{j_{\rm{c}}}}}[({l_{{i_{\rm{n}}}{j_{\rm{c}}}}}/v) + } } ({j_{\rm{c}}} - {j_{\rm{n}}} - 1) s]+ \\& \displaystyle\sum\limits_{{i_c} \in {N_c}} {\displaystyle\sum\limits_{{j_{\rm{n}}} \in {N_{\rm{n}}}} {{d_{{i_{\rm{c}}}{j_{\rm{n}}}}}[} } ({l_{{i_{\rm{c}}}{j_{\rm{n}}}}}/v + ({j_{\rm{n}}} - {i_{\rm{c}}} - 1) s]+\\ & \displaystyle\sum\limits_{{i_{\rm{c}}} \in {N_{\rm{c}}}} {\displaystyle\sum\limits_{{j_{\rm{c}}} \in {N_{\rm{c}}}} {{d_{{i_{\rm{c}}}{j_{\rm{c}}}}}} } [({l_{{i_{\rm{c}}}{j_{\rm{c}}}}}/v) + \left( {{j_{\rm{c}}} - {i_{\rm{c}}} - {\rm{skip}}_{{j_{\rm{c}}}{i_{\rm{c}}}}^{{r_{\rm{c}}}}} \right)]{\text{。}}\end{split}$ | (18) |
其中,
目标函数中乘客出行等待时间主要与发车间隔有关,因此如何构建乘客等待时间与发车间隔的关系是求解目标函数的关键,根据文献[13]的相关分析,乘客等待时间与发车间隔关系推导如下。
设
T =
随机到达乘客的平均等待时间为
| $\begin{split} &\quad\quad E(t) = \left(\int\nolimits_{0}^\infty {0.5h\lambda hf(h){\rm{d}}h} \right)/\left(\int\nolimits_{0}^\infty {\lambda hf(h){\rm{d}}h} \right) = \\ &0.5E({h^2})/ E(h){\text{。}} \end{split} $ | (19) |
通过
| $\quad\quad E(t) = 0.5E(h)[1 + {\rm{Var}}(h)/{E^2}(h)]{\text{。}}$ | (20) |
算法解决的问题,实际上就是在通勤客流识别确定通勤站点的基础上,如何分配通勤客流与非通勤客流的车辆问题,本文提出采用客流比例分配产生初始解,然后用遗传算法求出最佳分配方式。
Step1 产生初始分配方案,即生成初始解。
为了便于算法快速找到最优解,在初始解生成过程中,考虑出行供给与出行需求相互匹配原则,通过通勤客流比例和非通勤客流比例,确定2种调度模式的车辆分配方案区间。
| $\quad\quad V_{{\rm{int}}}^{\rm{c}} = {V_{\rm{t}}} \left[ {\frac{{\displaystyle\sum\limits_{i \in {N_{\rm{c}}},j \in {N_{\rm{c}}}} {{d_{ij}}} }}{{\displaystyle\sum\limits_{i \in N,j \in N} {{d_{ij}}} }}} \right],$ | (21) |
| $\quad\quad V_{{\rm{int}}}^{\rm{n}} = {V_{\rm{t}}} - V_{{\rm{int}}}^{\rm{c}}{\text{。}}$ | (22) |
其中,
Step 2 按照式(11)计算目标函数值;
Step 3 对于种群进行交叉变异处理;
Step 4 将父代与子代混合,挑选出优势个体作为新的种群;
Step 5 按照式(11)计算新种群的目标函数;
Step 6 判断是否到达算法停止条件即是否达到预设代数,如果是,则输出最优解,如果不是,则进入Step3。
其中停止条件为遗传算法设定的最大迭代代数。
算法步骤如图1所示。
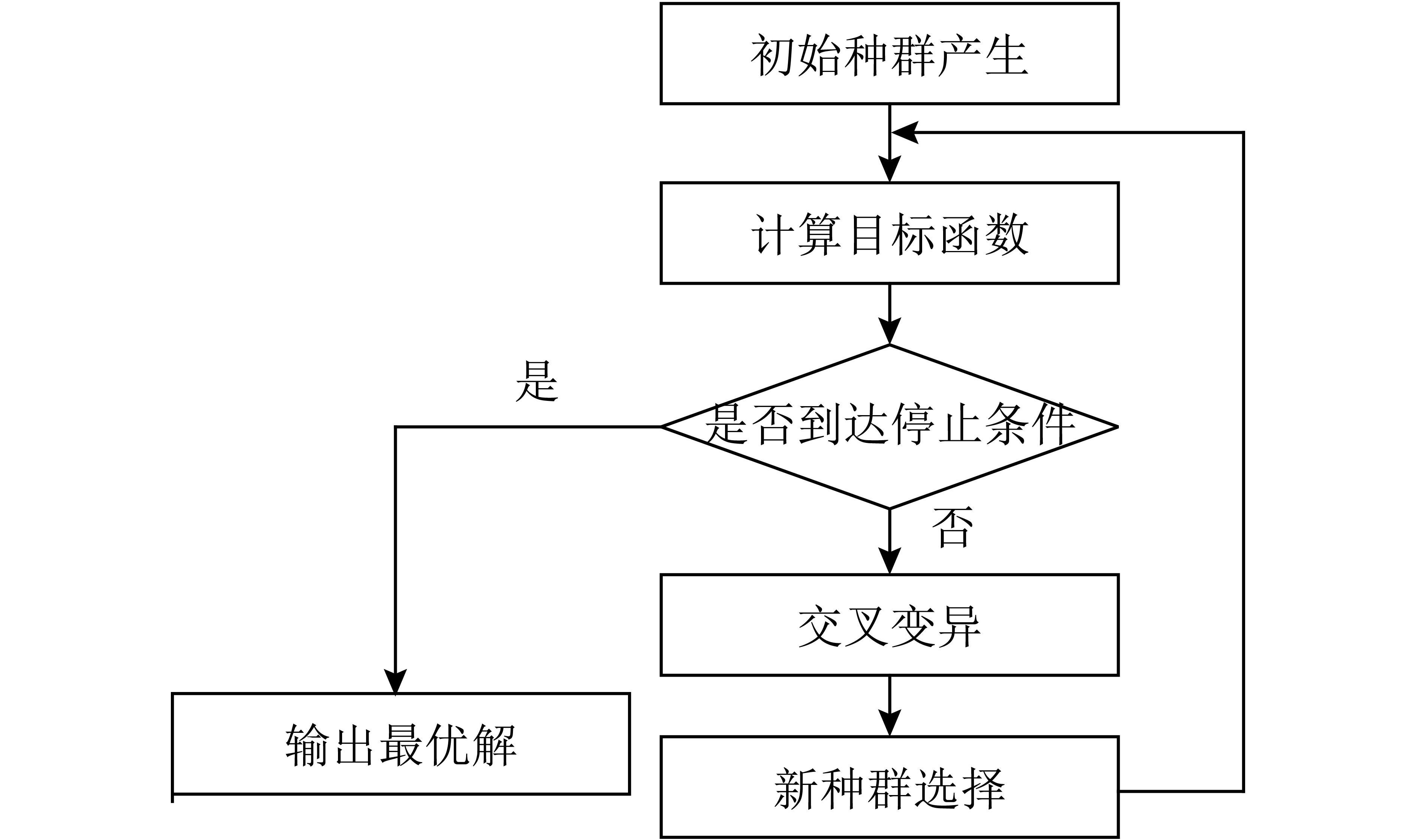
|
图 1 遗传算法流程 Fig. 1 The flow chart of genetic algorithm |
取100路公交线路作案例分析。
由于乘客在乘坐公交车时,只需要在上车时使用公交卡,因此公交卡IC卡数据中缺失下车站点信息,因此本文下车站点信息按照文献[17]的方法进行识别。结合本文构建的模型及相应的算法,占高峰期总出行人次的77.59%,将去程高峰时段设定为7:30到9:00,回程高峰时段设定在4:30到6:00,且周工作日出行频次设定在8次以上认为是通勤客流,识别得到通勤客流为786人,占高峰期总出行人次的77.59%。
4.2 公交线路现有的运行数据该线路在高峰时段出行人次为1 013人,其中通勤客流所占为786人,占高峰期总出行人次的77.59%,线路车队规模为11辆,公交站点平均停靠时间为2 min,乘客平均出行时间为37.5 min。其中线路站点信息如表1。
| 表 1 100路公交线路运行站点和标号 Tab. 1 Route 100 bus running sites and labels |
根据上述数据,运用遗传算法求解,设置算法运行最大代数为200代,求解出最佳多模式调度方案与原方案对比如表2。
根据上述求解结果总出行时间对比可知,原有的乘客出行时间为37 987.5 min,通过多模式调度的方案出行时间为32 696.6,比原有出行时间减少了5 290.9 min,优化效率达到13.93%。但需要说明的是,采用该模式也同时会对非通勤客流的出行时间产生影响。
| 表 2 100路公交线路对比研究 Tab. 2 A comparative study on the route 100 bus line |
本文提出利用在高峰期公交客流出行站点分布不均匀的特性,通过公交IC卡出行数据识别通勤客流的模型,并在此基础上依据高峰期出行特征设计了单线路多调度模式。该模式通过适应高峰期站点客流分配不均匀的特性,提升公交运行效率。最后通过一实际案例数据验证该方法的合理性和有效性。案例结果表明,通过单线多调模式,在公交资源配置不变的情况下,能够显著地减少乘客总体出行时间,减少比例到达13.93%,为客流具有分布不均匀的特征的公交线路提供了一种提高其运营效率的调度模式。本文工作主要是针对单条线路客流出行特征设计公交线路多模式调度,未来可以延伸至网络层面,对公交线网多模式调度展开相关研究。
| [1] |
COLLINS C, HASAN S, UKKUSURI S V. A novel transit rider satisfaction metric: Rider sentiments measured from online social media data[J].
Journal of Public Transportation, 2013, 16(2): 21-45.
DOI: 10.5038/2375-0901. |
| [2] |
LEE Y Y, BALDICK R. A frequency-constrained stochastic economic dispatch model[J].
Power Systems, IEEE Transactions on, 2013, 28(3): 2301-2312.
DOI: 10.1109/TPWRS.2012.2236108. |
| [3] |
胡继华, 邓俊, 黄泽. 结合出行链的公交IC卡乘客下车站点判断概率模型[J].
交通运输系统工程与信息, 2014, 14(2): 62-67.
HU Jihua, DENG Jun, HUANG Ze. Trip-chain based probability model for identifying alighting stations of smart card passengers[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(2): 62-67. DOI: 10.3969/j.issn.1009-6744.2014.02.010. |
| [4] |
芦方强, 陈学武, 胡晓健. 基于公交OD数据的居民公交出行特征研究[J].
交通运输工程与信息学报, 2010, 8(2): 31-36.
LU Fangqiang, CHEN Xuewu, HU Xiaojian. Characteristic research of resident’s bus trip based on bus OD data[J]. Journal of Transportation Engineering and Information, 2010, 8(2): 31-36. DOI: 10.3969/j.issn.1672-4747.2010.02.007. |
| [5] |
赵新. 厦门市快速公交系统出行链特征指标调查研究[J].
城市公共交通, 2012(11): 37-41.
ZHAO Xin. Investigation research on the characteristic index of Xiamen bus rapid transit system passengers travel chain[J]. Urban Public Transport, 2012(11): 37-41. DOI: 10.3969/j.issn.1009-1467.2012.11.011. |
| [6] |
NIJLAND L, DIJST M. Commuting-related fringe benefits in the Netherlands: Interrelationships and company, employee and location characteristics[J].
Transportation Research Part A: Policy and Practice, 2015, 77(1): 358-371.
|
| [7] |
CHEN J, LIU Z, ZHU S, et al. Design of limited-stop bus service with capacity constraint and stochastic travel time[J].
Transportation research part E: logistics and transportation review, 2015, 83: 1-15.
DOI: 10.1016/j.tre.2015.08.007. |
| [8] |
徐大伟, 裴玉龙. 公共交通大站快车调度模型[J].
哈尔滨工业大学学报, 2008, 40(4): 580-584.
XU Dawei, PEI Yulong. Express bus scheduling model and application[J]. Journal of Harbin Institute of Technology, 2008, 40(4): 580-584. DOI: 10.3321/j.issn:0367-6234.2008.04.016. |
| [9] |
魏明, 陈学武, 孙博. 配合大站快车的单线公交组合调度模型[J].
交通运输系统工程与信息, 2015(2): 136-142.
WEI Ming, CHEN Xuewu, SUN Bo. A model and an algorithm of schdule coordination for multi-mode regional bus transit[J]. Journal of Highway and Transportation Research and Development, 2015(2): 136-142. |
| [10] |
LEIVA C, MUÑOZ J C, GIESEN R, et al. Design of limited-stop services for an urban bus corridor with capacity constra- ints[J].
Transportation Research Part B: Methodological, 2010, 44(10): 1186-1201.
DOI: 10.1016/j.trb.2010.01.003. |
| [11] |
孙祥龙, 陆建. 公交站点间行程时间估计[J].
武汉理工大学学报(交通科学与工程版), 2013, 37(1): 67-70.
SUN Xianglong, LU Jian. Travel time estimation between bus stops[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2013, 37(1): 67-70. |
| [12] |
DEVILLAINE F, MUNIZAGA M, TRÉPANIER M. Detection of activities of public transport users by analyzing smart card data[J].
Journal of the Transportation Research Board, 2012(2276): 48-55.
|
| [13] |
DEWULF B, NEUTENS T, VANLOMMEL M, et al. Examining commuting patterns using floating car data and circular statistics: Exploring the use of new methods and visualizations to study travel times[J].
Journal of Transport Geography, 2015, 48(1): 41-51.
|
| [14] |
邓伟伟. 基于IC卡数据的OD矩阵生成技术及其应用研究[D]. 成都: 电子科技大学, 2015.
DENG Weiwei. Research on generation and application of OD matrix based on bus IC card data[D]. Chengdu: University of Electronic Science and Technology of China, 2015. |
| [15] |
HU X H, ZHANG Y. The application of fluid analogy method for estimating transit route ODs using IC card on-off passenger data[J]. Applied Mechanics and Materials, 2014, 694(1): 73-79.
|
| [16] |
CEDER A. Public transit planning and operation[M]. London: Butterworth-Heinemann, 2007.
|
| [17] |
TRÉPANIER M, TRANCHANT N, CHAPLEAU R. Individual trip destination estimation in a transit smart card automated fare collection system[J].
Journal of Intelligent Transportation Systems, 2007, 11(1): 1-14.
DOI: 10.1080/15472450601122256. |
 2018, Vol. 21
2018, Vol. 21