2. 综合大数据应用技术国家工程实验室,四川 成都 610031
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China
随着我国城市规模的迅速扩大和机动化进程的加快,城市交通拥堵问题日益严重,而交叉口作为城市交通网络的重要组成部分,往往是城市拥堵的多发地。提升交叉口的运行效率是缓解城市交通拥堵的重要手段之一。合理的信号配时方案能够使得交通流在交叉口的时间和空间中均衡分布,有效提高交叉口甚至整个路网的运行效率。
国内外学者对交叉口信号配时优化模型进行了大量研究,提出了多种信号配时优化模型。Webster[1]提出TRRL信号配时法。该方法以车辆通过交叉口的总延误时间为唯一衡量指标,对信号配时方案进行优化。Akcelik[2]在TRRL法的基础上提出了ARRB配时法。该方法的衡量指标同时考虑了车辆延误和停车次数,并修正了延误计算公式。Park[3]提出了一种能同时对周期、相位差和绿信比进行优化的定周期随机信号优化模型。Roshandeh等[4]建立了以交叉口机动车延误和行人延误为优化目标的信号配时优化模型。Li等[5]针对过饱和交叉口,提出了一种以平均排队长度最小和通行能力最大为目标的多目标优化模型。高云峰等[6]以非饱和交叉口为研究对象建立了定周期信号控制参数的多目标优化模型,并以非支配排序遗传算法为基础建立了直接求解单个交叉口交通信号多目标控制模型的相容优化方法。颜艳霞等[7]建立了以车辆延误、停车次数和通行能力的多目标信号配时优化模型,并以蚂蚁优化算法进行求解。杨锦东等[8]基于灰色控制理论,提出以延误和排队车辆数最小为目标函数的两目标优化模型。王秋平等[9]在分析了单点交叉口交通流特性的基础上,建立以平均延误和平均停车次数为目标的优化模型,并以遗传算法和遗传退火算法对模型进行求解。张萌萌等[10]提出一种以平均延误时间最短,通行能力最大,以及鲁棒性最好即流量波动时车辆延误标准差最小为目标的多目标优化模型,并以遗传算法求解,该模型能有效减小平均延误,提高信号配时方案的鲁棒性。陈小红等[11]针对交通方式混行的交叉口,提出一种以通行能力最大、车辆停车率及出行者平均延误最小为目标的多目标优化模型。另外,为了迅速获得最优控制方案,许多学者将现代寻优算法应用于配时优化研究中,如遗传算法[12]、人工神经网络[13]、免疫算法[14]、蚁群算法[15]等。
虽然国内外的配时优化模型成果很多,但是现有的配时优化模型大多数都是针对单环结构(非搭接)相位方案进行配时优化,针对双环结构(含搭接)相位方案的配时优化模型较少。由于我国城市交叉口多使用传统单环相位方案,当交叉口车流量不均衡时时,即使对其应用配时优化模型进行优化,也难免会因为同一相位内各流向交通量不均衡而造成交叉口时空资源的浪费。针对这种情况,对交叉口信号配时采用双环相位方案能够有效减少交叉口时空资源的浪费,所以研究建立双环信号配时优化模型对提高交通运行效率,缓解交通拥堵有重要的作用。
因此,本文旨在建立一种双环相位信号配时优化模型,以解决传统信号配时方案同一相位不同流向流量不均衡而导致的交叉口时空资源的浪费。首先,针对双环相位方案,建立以交叉口平均延误最少为目标函数,各相位绿灯时长为优化变量的双环信号配时优化模型;然后,考虑到模型目标函数的复杂性和遗传算法的求解非线性问题的优越性,采用自适应遗传算法对模型进行求解;最后,通过实际调查数据,对比了文中模型和经典的Webster模型,证明了文中模型的有效性和优越性。
1 双环信号配时优化模型 1.1 相位方案选择相位控制方案从结构上可分为单环相位方案和双环相位方案,单环相位方案是指在方案中不包含搭接相位,而双环相位方案则与之相反。单环相位方案和双环相位方案分别如图1a和图1b所示(由于右转不受控制,这里不作考虑)。由图可知,双环相位方案和单环相位方案由8个流向组成;流向1、2、5、6和流向3、4、7、8分别组成2条道路的流向组,且2个组被“分隔线”隔开;流向1、2、3、4和流向5、6、7、8分别组成2个相位环。在同一方向里面,2个环可以独立运行,也就是说任意调整同环同一方向里的相位的顺序和时间都不会与其他相位产生相位冲突。在单环相位方案中,相位环所对应的2个流向必须同时开始和结束,如流向1和流向5必须同时开始和结束;但在双环相位方案中,只有遇到“分隔线”时,分别处于2个环内的2个流向才必须同时开始或结束,只要不遇到“分隔线”,2个环所对应的2个流向便可以不同时开始或结束,如流向1和流向5可以不同时结束。

|
图 1 相位方案 Fig. 1 Phase scheme |
与传统单环相位方案相比,双环相位方案更加灵活,可以根据实际情况随时调整相位时长和相位顺序。为了更有效地利用时空资源,本文选择在交叉口采用双环相位方案的基础上建立配时优化模型。这也是双环信号配时优化模型与Webster法等传统配时优化模型最大不同之处。
1.2 模型建立针对非饱和交叉口,目前研究[12-18]所采用的交叉口交通效益的评价指标通常有交叉口延误、交叉口通行能力、停车次数、排队长度等。需要注意的是对于一个信号控制交叉口,这些指标并不能同时达到最优。例如想要减少停车次数或增加通行能力,就需要加长信号周期,这样又会导致交叉口延误增加。对于非饱和交叉口来说,车辆延误时间是交叉口拥堵程度最直观的体现,因此本文选取交叉口平均延误
| $\quad\quad {d_i} = \sum\limits_j {\frac{{C{{(1 - {{{g_{{\rm{e}}i}}} / C})}^2}}}{{2(1 - ({{{g_{{\rm{e}}i}}} / C}){v_{ij}})}}} {\text{。}}$ | (1) |
式中,
信号周期内各个流向的车辆延误的加权平均值即为交叉口平均车辆延误
| $\quad\quad D = {{\displaystyle\sum\limits_{i = 1}^8 {{d_i}{q_i}} }}{\Big{/}}{{\displaystyle\sum\limits_{i = 1}^8 {{q_i}} }}{\text{。}}$ | (2) |
式中,
将平均延误
| $\quad\quad R = \min \;D{\text{。}}$ | (3) |
由于优化模型是在双环相位方案的基础上建立,所以对于主干路来说,上下2个相位环的时间应当一致。由此可得主干路对应的4个流向的绿灯时间满足以下约束:
| $\quad\quad{g_1} + {g_2} - {g_5} - {g_6} = 0{\text{。}}$ | (4) |
式中,
同理,对于次干路来说,上下2个相位环长度也应当一致,所以次干路所对应的4个流向的绿灯时长应满足以下约束:
| $\quad\quad{g_3} + {g_4} - {g_7} - {g_8} = 0{\text{。}}$ | (5) |
且任意相位环内的各流向绿灯时间之和等于信号周期长度:
| $\quad\quad{g_1} + {g_2} + {g_3} + {g_4} - C = 0{\text{。}}$ | (6) |
同时,由于考虑到行人过街等因素以及在实际应用中各流向绿灯时间必须为正整数,各流向的绿灯时间必须满足以下约束:
| $\quad\quad{g_i}^{\min} {\text{≤}} {g_i} {\text{≤}} {g_i}^{\max},$ | (7) |
| $\quad\quad{g_i} \subseteq {{\rm{N}}^*}{\text{。}}$ | (8) |
式中,
另外,每个流向都由损失时间和有效绿灯时间组成,所以有效绿灯时间和损失时间应满足
| $\quad\quad{g_i} = {g_{{\rm{e}}i}} + {l_i}{\text{。}}$ | (9) |
式中,
模型中信号周期
| $\quad\quad C = \frac{{1.5L + 5}}{{1 - Y}}{\text{。}}$ | (10) |
式中,
综上可知,双环信号配时优化模型为
| $\quad\quad\begin{gathered} R = \min {{\displaystyle\sum\limits_{i = 1}^8 {{d_i}{q_i}} }}{\Big{/}}{{\displaystyle\sum\limits_{i = 1}^8 {{q_i}} }}{\text{。}}\\ {\rm{s.t.}} \left\{ \begin{array}{l} {g_1} + {g_2} - {g_5} - {g_6} = 0 , \\ {g_3} + {g_4} - {g_7} - {g_8} = 0, \\ {g_1} + {g_2} + {g_3} + {g_4} - C = 0 , \\ {g_i}^{\min} {\text{≤}} {g_i} {\text{≤}} {g_i}^{\max}, \\ {g_i} = {g_{{\rm{e}}i}} + {l_i}, \\ {g_i} \subseteq {{\rm{N}}^*}, \\ C = {{(1.5L + 5)} / {(1 - Y)}}, \\ {d_i} = \displaystyle\sum\limits_j {\displaystyle\frac{{C{{(1 - {{{g_{{\rm{e}}i}}} / C})}^2}}}{{2(1 - ({{{g_{{\rm{e}}i}}} / C}){v_{ij}})}}}{\text{。}} \\ \end{array} \right. \\ \end{gathered} $ | (11) |
该模型以交叉口平均延误最小为优化目标,以各流向绿灯时间为优化参数,且各流向绿灯时间均为正整数,是一种非线性整数优化模型。该模型中目标函数较为复杂,优化参数和约束条件较多。对于这类复杂的非线性整数规划模型,传统优化算法很难对其进行求解,但现代寻优算法往往能够求解出较好的局部最优解甚至全局最优解。目前,应用于非线性整数规划模型求解的现代寻优算法主要有:模拟退火算法[19]、遗传算法[20]、蚁群算法[21]、粒子群算法[22]等。其中,遗传算法由于其良好的全局搜索能力和极强的鲁棒性,十分适合求解复杂的非线性优化问题;而由遗传算法改进而来的自适应遗传算法更是克服了遗传算法的早熟、收敛速度过慢等问题。因此,这里考虑采用自适应遗传算法对双环信号配时优化模型进行求解。
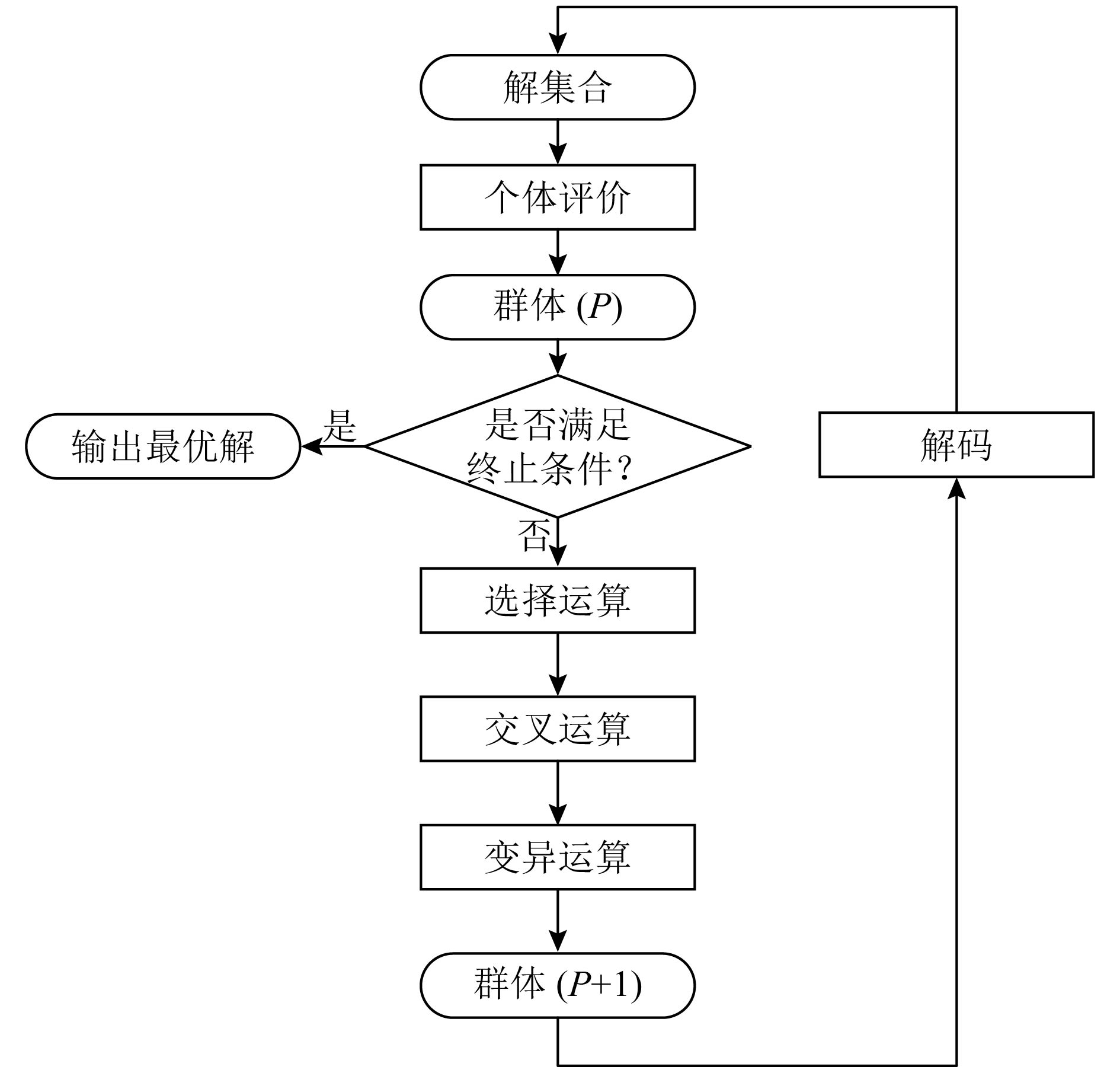
2 自适应遗传算法遗传算法是基于自然原则原理和自然遗传机制的寻优算法,其实质是通过群体搜索技术,根据适者生存的原则逐代进化,最终得到最优解。遗传算法首先需要随机产生初始群体并得到每一个体的适应度,然后对个体的基因进行选择、交叉、变异等操作,得到下一代群体,按此方法使群体逐代进化,直到满足进化终止条件。图2为遗传算法的运算过程示意图。
|
图 2 遗传算法运算过程示意图 Fig. 2 The schematic diagram of the genetic algorithm |
本文采用自适应遗传算法,对双环信号配时模型参数进行优化。在遗传操作中使用改进的选择算子,保证了算法能够收敛于全局最优解;并引入自适应的交叉概率和变异概率。自适应遗传算法具体操作步骤如下。
2.1 编码为了方便处理双环信号配时模型的约束条件和提高算法的运算效率,自适应遗传算法采用真值编码的方式,以信号配时模型相位结构中的绿灯时间
在遗传算法中,以个体适应度值的大小来评定个体的优劣程度。本算法中,以交叉口平均延误函数D为目标函数,适应度函数
| $\quad\quad F = \left\{ \begin{array}{l} \max - D, \max {\text{>}} D ; \\ 0, \quad\quad\;\;\;\max {\text{≤}} D{\text{。}} \\ \end{array} \right.$ | (12) |
式中,
自适应遗传算法的选择算子使用随机联赛选择法和最优保存策略相结合的选择策略,在避免非成熟收敛的同时保证了算法的全局收敛性[23]。随机联赛选择法的基本思想是每次选择几个个体中适应度最高的一个个体到下一代群体中,重复M次即可得到下一代群体的M个个体。而最优保存策略是为了保证适应度最好的个体基因尽可能地遗传到下一代群体中,其具体操作如下。首先找出当代群体中适应度最高的个体和适应度最低的个体;若当前群体中最佳个体的适应度比总的迄今为止的最好个体的适应度还要高,则以当前群体中的最佳个体作为新的迄今为止的最好个体;否则用迄今为止的最好个体替换当前群体中的最差个体。
2.3.2 自适应交叉算子本算法中,交叉算子采用单点交叉,为了保证种群的多样性和算法的全局收敛性,交叉运算采用自适应的交叉概率。交叉概率公式[24-25]为
| $\quad\quad{P_{\rm{c}}} = \left\{ \begin{array}{l} {P_{\rm cmax}},\quad\quad\quad\quad\quad\quad\quad\quad{f'} {\text{<}} {f_{\rm avg}}; \\ {P_{\rm cmin}} + \frac{{{P_{\rm cmax}} - {P_{\rm cmin}}}}{{1 + \exp \left[\displaystyle\frac{{2A({f'} - {f_{\rm avg}})}}{{{f_{\max}}}}\right]}}, {f'} {\text{≥}} {f_{\rm avg}}{\text{。}} \\ \end{array} \right.$ | (13) |
式中,
本算法中,为提高算法的全局收敛性,变异算子采用非均匀变异。染色体基因为
| $\quad\quad{x'}\!= \!\left\{\!\!\! \begin{array}{l} {x_k} + \Delta (t,{g_k}^{\max} - {x_k}), {\rm{if\; random}}(0,1) = 0; \\ {x_k} - \Delta (t,{x_k} - {g_k}^{\min}), {\rm{if\; random}}(0,1) = 1{\text{。}\!\!\!}\!\end{array} \right.$ | (14) |
式中,
| $\quad\quad\Delta (t,y){\rm{ = }}y(1 - {r^{0.5(1 - {t / T})}}){\text{。}}$ | (15) |
式中,r为
为了防止早熟现象的发生,变异算子采用自适应的变异概率。变异概率公式[24-25]为
| $\quad\quad{P_{\rm m}} = \left\{ \begin{array}{l} {P_{\rm mmax}},\quad\quad\quad\quad\quad\quad\quad\quad f {\text{<}} {f_{\rm avg}}; \\ {P_{\rm mmin}} + \frac{{{P_{\rm mmax}} - {P_{\rm mmin}}}}{{1 + \exp \left[\displaystyle\frac{{2A(f - {f_{\rm avg}})}}{{{f_{\max}}}}\right]}}, f {\text{≥}} {f_{\rm avg}}{\text{。}} \\ \end{array} \right.$ | (16) |
式中,
设置最大进化代数
本文自适应遗传算法可分为以下6个步骤。
Step1 随机产生满足模型约束的初始父代群体
Step2 计算个体的适应度,判断是否满足终止条件。若满足终止条件,则输出最优解;否则进行Step 3。
Step3 使用随机联赛选择法对群体
Step4 使用自适应交叉概率对群体
Step5 使用自适应变异概率对群体
Step6 使用最优保存策略对群体
本文以4个交叉口为例,实地调查了4个交叉口晚高峰流量数据,分别使用Webster配时模型和双环信号配时优化模型对4个交叉口进行配时优化。4个交叉口的渠化如图3所示,控制方案如图4所示。晚高峰流量如表1所示。

|
图 3 交叉口渠化图 Fig. 3 The diagram of intersection channelization |

|
图 4 交叉口相位控制方案 Fig. 4 The signal control scheme of intersection |
| 表 1 交叉口流量 Tab. 1 Intersections traffic flow |
首先对4个交叉口使用传统Webster配时优化模型对其进行配时优化,其中每相位信号损失时间为3s。交叉口采用传统四相位控制,相位控制方案如图4所示。计算出各相位有效绿灯时间后,通过Webster延误公式计算交叉口平均延误。4个交叉口的配时优化方案分别如图5~图8所示,优化结果分别如表2~表5所示。然后对4个交叉口使用双环信号配时优化模型对其进行配时优化,并通过Python语言编写自适应遗传算法程序对模型进行求解。程序求解过程如图9所示。各流向最大绿灯时长设为60s,最小绿灯时长设为10s,每相位损失时间为3s。另外自适应遗传算法中一些参数设置为:种群大小设为100,最大进化代数设为200。4个交叉口的配时优化方案分别如图5~图8所示,优化结果分别如表2~表5所示。
|
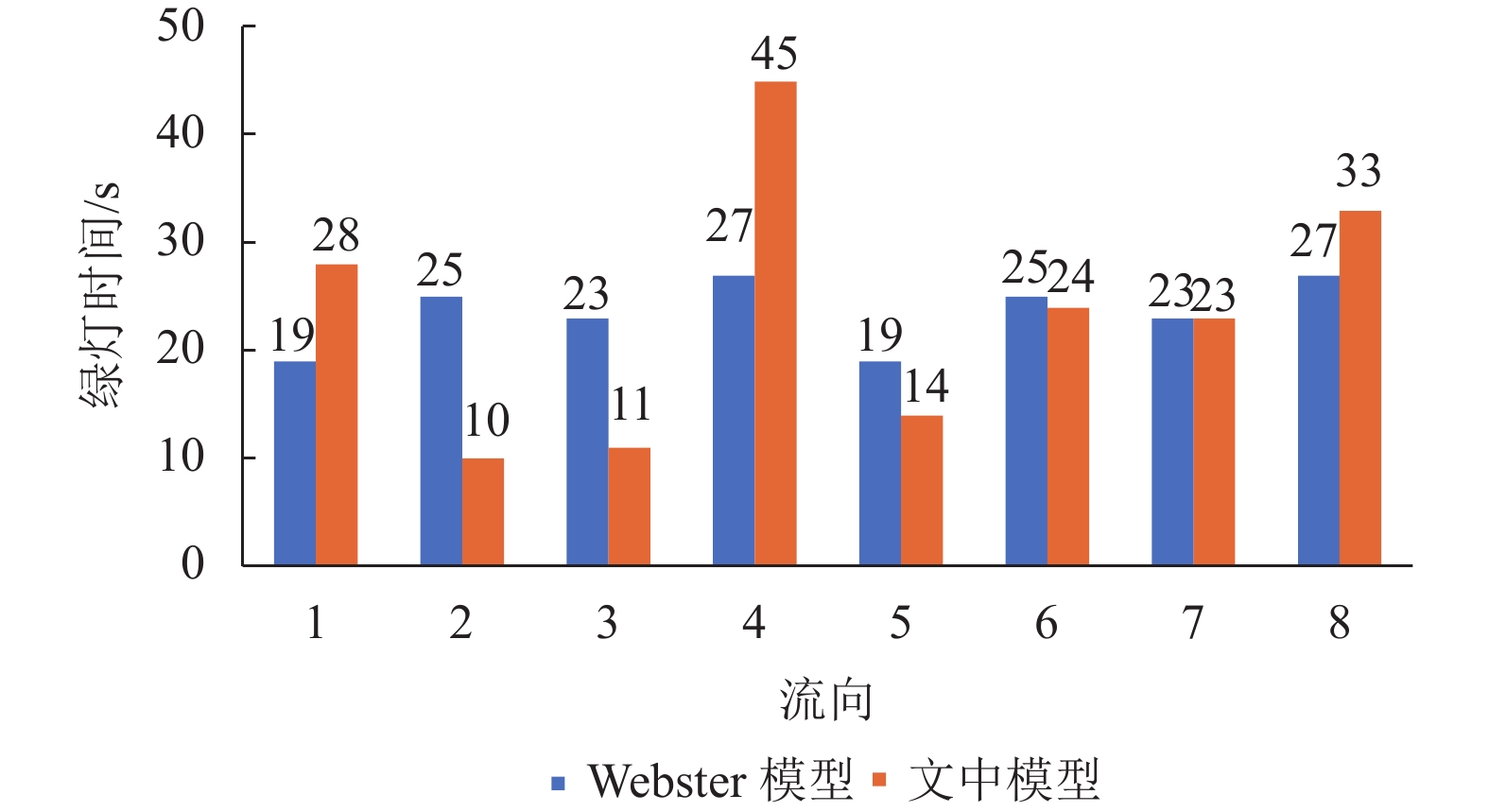
图 6 交叉口2信号配时方案 Fig. 6 The signal timing scheme of intersection 2 |
|
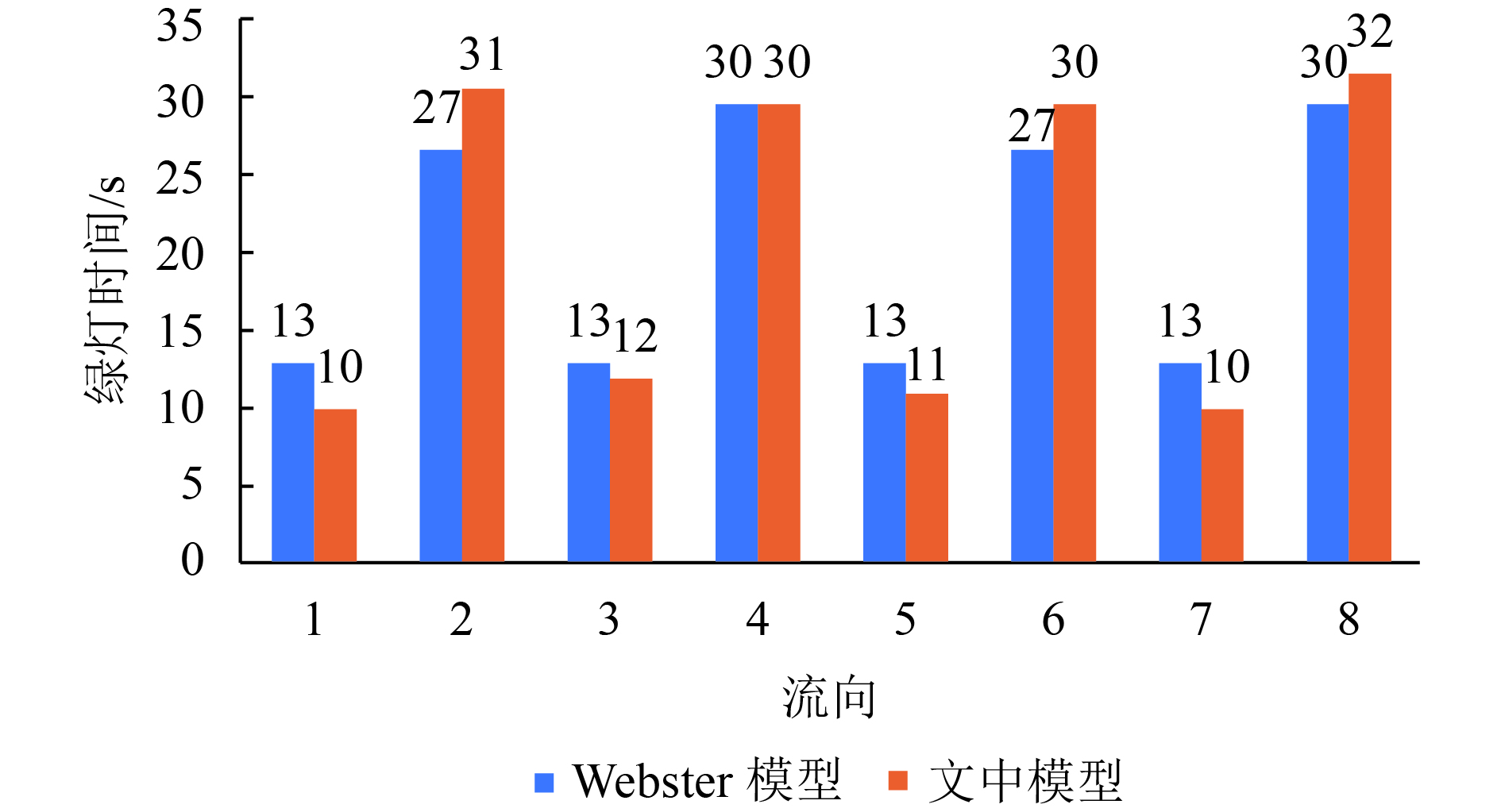
图 7 交叉口3信号配时方案 Fig. 7 The signal timing scheme of intersection 3 |
|
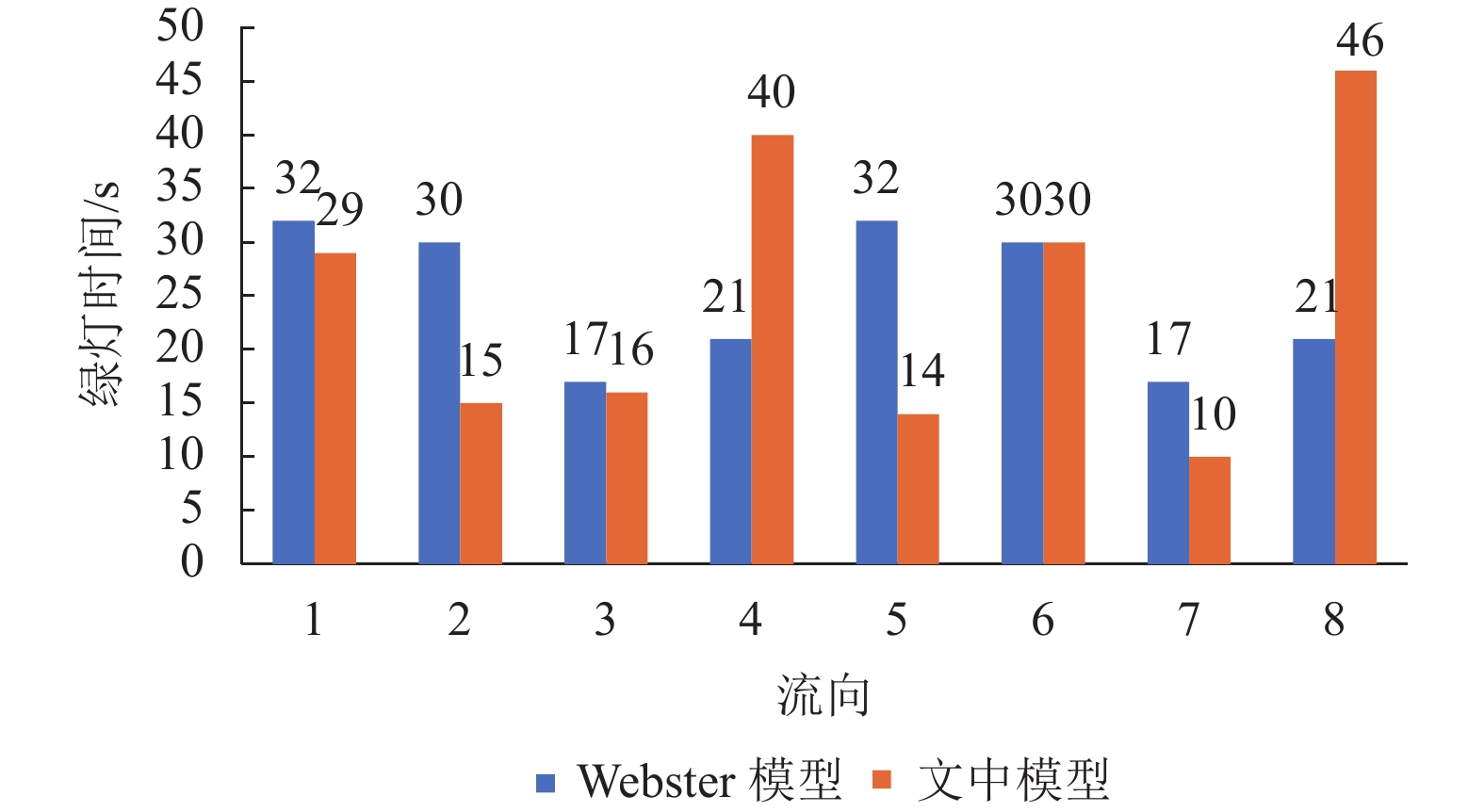
图 8 交叉口4信号配时方案 Fig. 8 The signal timing scheme of intersection 4 |
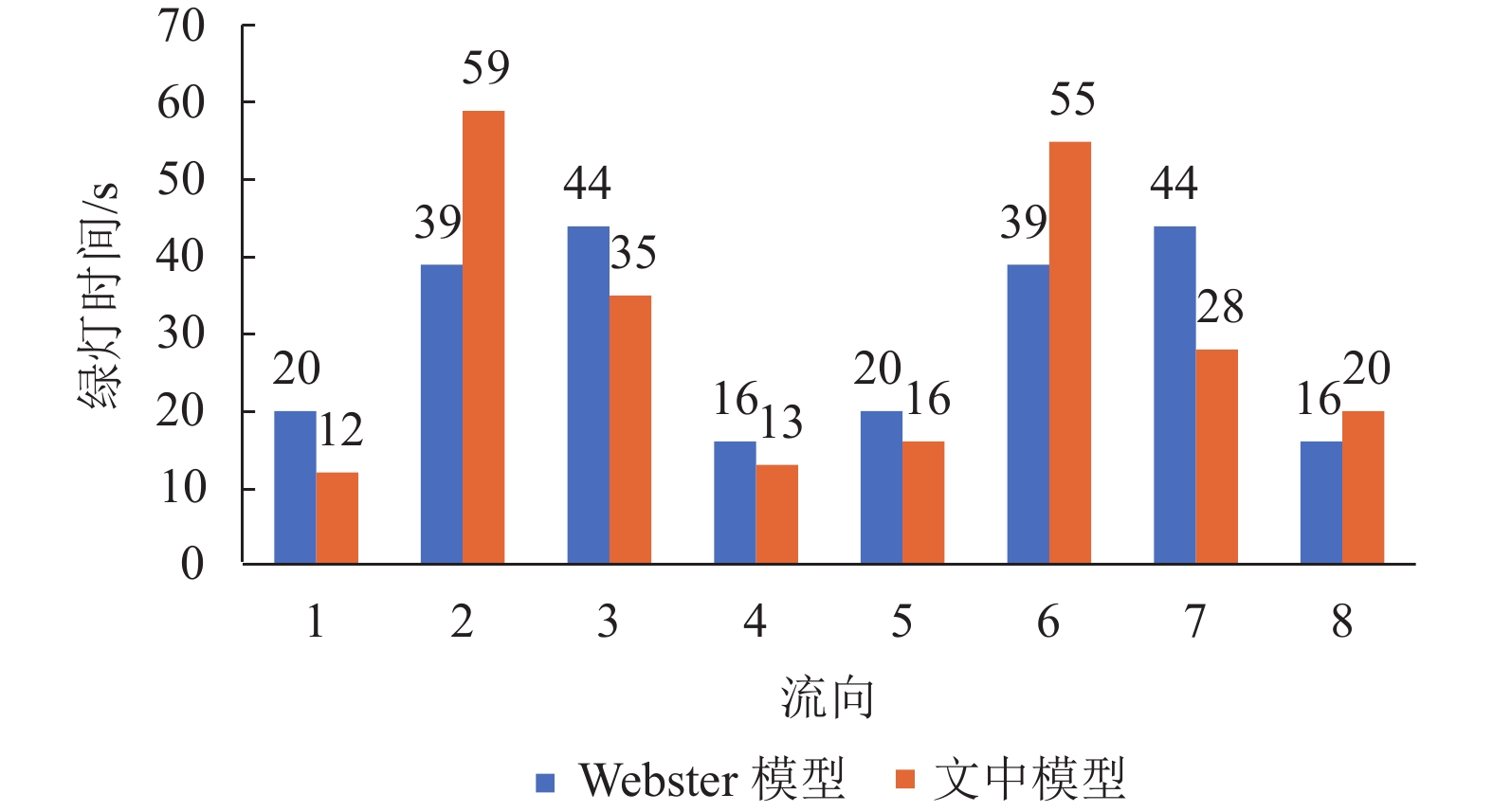
|
图 5 交叉口1信号配时方案 Fig. 5 The signal timing scheme of intersection 1 |
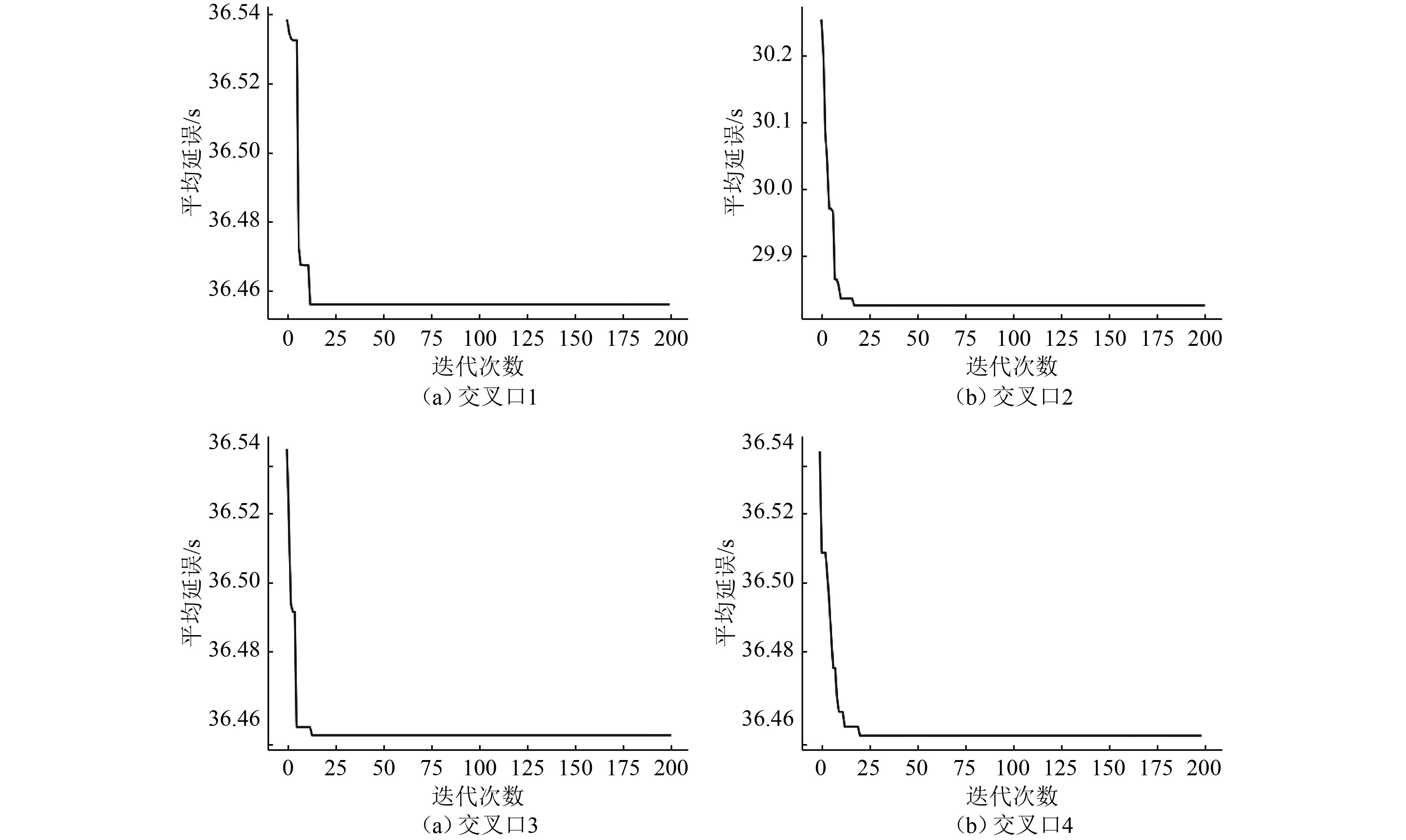
|
图 9 自适应遗传算法进化流程 Fig. 9 The evolution flowchart of adaptive genetic algorithm |
由表2可知,对交叉口1应用Webster模型进行配时优化,交叉口平均延误为41.12s;应用双环信号配时优化模型后,交叉口平均延误变为36.45s;与Webster法优化结果相比,平均延误降低了11.36%。由表3可知:对交叉口2应用Webster模型进行配时优化,交叉口平均延误为34.58s;应用双环信号配时优化模型后,交叉口平均延误变为29.83s;与Webster法优化结果相比,平均延误降低了13.74%。由表4可知,对交叉口3应用Webster模型进行配时优化,交叉口平均延误为28.21s;应用双环信号配时优化模型后,交叉口平均延误变为27.16s;与Webster法优化结果相比,平均延误降低了3.72%。由表5可知,对交叉口4应用Webster模型进行配时优化,交叉口平均延误为37.41s;应用双环信号配时优化模型后,交叉口平均延误变为34.04s;与Webster法优化结果相比,平均延误降低了9.00%。由此可见,双环信号配时优化模型优化结果优于传统Webster模型,可以有效减少交叉口平均延误,一定程度上提高了交叉口服务水平。
| 表 2 交叉口1优化结果 Tab. 2 The optimize results of intersection 1 |
| 表 3 交叉口2优化结果 Tab. 3 The optimize results of intersection 2 |
| 表 4 交叉口3优化结果 Tab. 4 The optimize results of intersection 3 |
另外,由表2~表5可知,4个交叉口同相位各流向流量间的不均衡情况排序依次为交叉口2>交叉口1>交叉口4>交叉口3;而对4个交叉口分别应用双环信号配时优化模型后,交叉口2的平均延误下降了13.74%,交叉口1下降了11.36%,交叉口4下降了9.00%,交叉口3下降了3.72%,平均延误下降幅度排序情况和交叉口同相位各流向流量间的不均衡情况相同。所以,交叉口同相位内的2个流向的流量越不均衡,应用双环信号配时优化模型后的优化结果越好。
| 表 5 交叉口4优化结果 Tab. 5 The optimize results of intersection 4 |
在双环相位方案的基础上建立了以交叉口平均延误为目标函数的双环信号配时优化模型,并采用自适应遗传算法对模型进行求解。以4个交叉口为例,分别使用传统Webster模型和双环信号配时优化模型进行优化,根据交叉口优化结果,得出以下结论。
1) 双环信号配时优化模型的优化效果比传统Webster模型更好,可以有效减少交叉口平均延误。
2) 交叉口同相位不同流向间的流量分布越不均衡,双环信号配时优化模型的优化效果越好。
| [1] |
WEBSTER F V. Traffic signals[J].
Road Research Technical Paper, 1966, 56(4): 206-207.
|
| [2] |
AKCELIK R. Traffic signals: capacity and timing analysis[R]. Melbourne: Australian Road Research Board, 1981.
|
| [3] |
PARK B. Enhanced genetic algorithm for signal-timing optimization of oversaturated intersections[J].
Transportation Research Record, 2000, 1727: 32-41.
DOI: 10.3141/1727-05. |
| [4] |
ROSHANDEH A M, LEVINSON H S, LI Z, et al. New methodology for intersection signal timing optimization to simultaneously minimize vehicle and pedestrian delays[J].
Journal of Transportation Engineering, 2014, 140(5): 1-10.
DOI: 10.1061/(ASCE)TE.1943-5436.0000658. |
| [5] |
LI Yan, YU Lijie, AOSiran T, et al. Multi-objective optimization of traffic signal timing for oversaturated intersection[J].
Mathematical Problems in Engineering, 2003(1683): 1-9.
|
| [6] |
高云峰, 徐立鸿, 胡华, 等. 交叉口定周期信号控制多目标优化方法[J].
中国公路学报, 2011, 24(5): 82-88.
GAO Yunfeng, XU Lihong, HU Hua, et al. Multi-objective optimization method for fixed-time signal control at intersection[J]. China Journal of Highway and Transport, 2011, 24(5): 82-88. |
| [7] |
颜艳霞, 李文权. 单点交叉口信号实时配时模型及蚂蚁算法[J].
公路交通科技, 2006, 23(11): 116-119.
YAN Yanxia, LI Wenquan. Ant colony optimization for signalized intersection[J]. Journal of Highway and Transportation Research and Development, 2006, 23(11): 116-119. DOI: 10.3969/j.issn.1002-0268.2006.11.027. |
| [8] |
杨锦冬, 杨东援. 城市信号控制交叉口信号周期时长优化模型[J].
同济大学学报(自然科学版), 2001, 29(7): 789-794.
YANG Jindong, YANG Dongyuan. Optimized signal time model in signaled intersection[J]. Journal of Tongji University(Natural Science), 2001, 29(7): 789-794. DOI: 10.3321/j.issn:0253-374X.2001.07.007. |
| [9] |
王秋平, 谭学龙, 张生瑞. 城市单点交叉口信号配时优化[J].
交通运输工程学报, 2006, 6(2): 60-64.
WANG Qiuping, TAN Xuelong, ZHANG Shengrui. Signal timing optimization of urban single-point intersections[J]. Journal of Traffic and Transportation Engineering, 2006, 6(2): 60-64. DOI: 10.3321/j.issn:1671-1637.2006.02.014. |
| [10] |
张萌萌, 贾磊, 邹难, 等. 单点交叉口鲁棒优化信号配时研究[J].
公路交通科技, 2011, 28(1): 107-111.
ZHANG Mengmeng, JIA Lei, ZOU Nan, et al. Robust optimal traffic signal timing of urban single-point intersection[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 107-111. DOI: 10.3969/j.issn.1002-0268.2011.01.020. |
| [11] |
陈小红, 钱大琳, 石冬花. 基于慢行交通的交叉口信号配时多目标优化模型[J].
交通运输系统工程与信息, 2011, 11(2): 106-111.
CHEN Xiaohong, QIAN Dalin, SHI Donghua. Multi-objective optimization method of signal timing for the non-motorized transport at intersection[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(2): 106-111. DOI: 10.3969/j.issn.1009-6744.2011.02.016. |
| [12] |
首艳芳, 徐建闽. 信号交叉口多目标动态决策模型及其优化方法[J].
公路交通科技, 2012, 29(11): 92-97.
SHOU Yanfang, XU Jianmin. Multi-objective dynamic decision-making model of signalized intersection and its optimization method[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 92-97. DOI: 10.3969/j.issn.1002-0268.2012.11.017. |
| [13] |
董超俊, 刘智勇. 多层反馈混沌神经网络及其在交叉口优化控制中的应用[J].
公路交通科技, 2006, 23(6): 121-126.
DONG Chaojun, LIU Zhiyong. Multi-layer chaotic neural network with feedback and its application in urban signal intersection optimization control[J]. Journal of Highway and Transportation Research and Development, 2006, 23(6): 121-126. DOI: 10.3969/j.issn.1002-0268.2006.06.030. |
| [14] |
顾榕, 曹立明, 王小平. 免疫遗传算法在交叉口信号配时优化中的应用[J].
同济大学学报(自然科学版), 2007, 35(2): 208-212.
GU Rong, CAO Liming, WANG Xiaoping. Application of lmmunogenetic algorithm optimization in intersection signal timing[J]. Journal of Tongji University(Natural Science), 2007, 35(2): 208-212. DOI: 10.3321/j.issn:0253-374X.2007.02.013. |
| [15] |
肖业伟, 黄辉先, 王宸昊. 基于蚁群算法的交叉路口多相位信号配时优化[J].
计算机工程与应用, 2008, 44(19): 241-244.
XIAO Yewei, HUANG Huixian, WANG Chenhao. Multiphase traffic signal timing optimization of intersection based on ant colony algorithm[J]. Computer Engineering and Applications, 2008, 44(19): 241-244. DOI: 10.3778/j.issn.1002-8331.2008.19.074. |
| [16] |
张鹏, 李文权, 常玉林. 基于Ring-Barrier相位的交叉口车道功能判分与信号配时协同优化模型[J].
东南大学学报(自然科学版), 2013, 43(3): 659-663.
ZHANG Peng, LI Wenquan, CHANG Yulin. Collaborative optimization model of lane markings and signal timings based on Ring-Barrier phase at intersections[J]. Journal of Southeast University(Natural Science Edition), 2013, 43(3): 659-663. |
| [17] |
蒲琪, 谭永朝, 杨超. 交叉口信号配时优化模型研究[J].
上海铁道大学学报, 1999, 20(4): 31-34.
PU Qi, TAN Yongzhao, YANG Chao. Signal-planning optimal model for intersection[J]. Journal of Shanghai Tiedao University, 1999, 20(4): 31-34. DOI: 10.3969/j.issn.1008-0392.1999.04.007. |
| [18] |
刘爽, 岳芳, 郭彦东, 等. 基于模式搜索算法的交叉口信号配时优化研究[J].
交通运输系统工程与信息, 2011, 11(s1): 29-35.
LIU Shuang, YUE Fang, GUO Yandong, et al. Optimization research on signal timing for urban intersections based on pattern search algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(s1): 29-35. |
| [19] |
刘学智, 袁荣湘, 刘涤尘. 模拟退火算法在输电网络扩展规划中的应用[J].
电力系统及其自动化学报, 2010, 22(2): 11-14.
LIU Xuezhi, YUAN Rongxiang, LIU Dichen. Application of simulated annealing algorithm on transmission network expansion planning[J]. Proceedings of the CSU-EPSA, 2010, 22(2): 11-14. DOI: 10.3969/j.issn.1003-8930.2010.02.003. |
| [20] |
张萌萌, 贾磊, 邹难. 单点定时信号配时的多目标优化模型[J].
计算机工程, 2011, 37(6): 27-29.
ZHANG Mengmeng, JIA Lei, ZOU Nan. Multi-objective optimization model for signal timing of signalized intersection[J]. Computer Engineering, 2011, 37(6): 27-29. DOI: 10.3969/j.issn.1000-3428.2011.06.010. |
| [21] |
郭茜, 聂润兔, 王超. 蚁群算法在解决空中交通飞行冲突中的应用[J].
交通运输工程与信息学报, 2009, 7(2): 116-119.
GUO Qian, NIE Runtu, WANG Chao. Aplication of ant colony algorithm to aircraft conflict resolution[J]. Journal of Transportation Engineering and Information, 2009, 7(2): 116-119. DOI: 10.3969/j.issn.1672-4747.2009.02.021. |
| [22] |
张兰, 雷秀娟, 马千知. 基于粒子群优化算法的多交叉口信号配时[J].
计算机应用研究, 2010, 27(4): 1252-1254.
ZHANG Lan, LEI Xiujuan, MA Qianzhi. Multi-cross signal timing based on particle swarm optimization algorithm[J]. Application Research of Computers, 2010, 27(4): 1252-1254. |
| [23] |
田丰, 边婷婷. 基于自适应遗传算法的交通信号配时优化[J].
计算机仿真, 2010, 27(6): 305-308.
TIAN Feng, BIAN Tingting. Traffic signal timing optimization based on adaptive genetic algorithm[J]. Computer Simulation, 2010, 27(6): 305-308. DOI: 10.3969/j.issn.1006-9348.2010.06.073. |
| [24] |
邝航宇, 金晶, 苏勇. 自适应遗传算法交叉变异算子的改进[J].
计算机工程与应用, 2006, 42(12): 93-96.
KUANG Hangyu, JIN Jing, SU Yong. Improving crossover and mutation for adaptive genetic algorithm[J]. Computer Engineering and Applications, 2006, 42(12): 93-96. DOI: 10.3321/j.issn:1002-8331.2006.12.028. |
| [25] |
王蕾, 沈庭芝, 招扬. 一种改进的自适应遗传算法[J].
系统工程与电子技术, 2002, 24(5): 75-78.
WANG Lei, SHEN Tingzhi, ZHAO Yang. An improved adaptive genetic algorithm[J]. System Engineering and Electronics, 2002, 24(5): 75-78. DOI: 10.3321/j.issn:1001-506X.2002.05.023. |
| [26] |
卢长娜, 王如云, 陈耀登. 自适应遗传算法[J].
计算机仿真, 2006, 23(1): 172-175.
LU Changna, WANG Ruyun, CHEN Yaodeng. An adaptive genetic algorithm[J]. Computer Simulation, 2006, 23(1): 172-175. DOI: 10.3969/j.issn.1006-9348.2006.01.048. |
 2018, Vol. 21
2018, Vol. 21