绿色供应链以供应链技术和绿色制造理论为基础,在理论和实践上涉及到绿色供应链的管理、供应商选择、绩效评价、政企博弈、定价、风险管理和收益分配等诸多方面。相对于传统的供应链,绿色供应链不仅节能环保,而且运作效率更高。因为一个完整的供应链涉及到供应商、制造商、零售商和消费者等诸多经济行为主体,同时从产品的原材料采购、生产加工、储存运输到消费回收的各个环节,都存在着巨大的节能减排和资源能源效率提升的潜力。正因为如此,近些年来绿色供应链的构建、推广和管理日益受到重视。
自绿色供应链概念被提出以来[1],国内外关于绿色供应链的研究文献逐渐增多。目前国外的文献大多集中于运用博弈论的方法进行分析。Sheu和Chen[2]运用三阶段的博弈模型分析了政府财政干预对绿色供应链的影响。Barari等[3]提出了一个包括生产绿色产品的制造商和零售商的演化博弈模型。Ghosh和Shah[4]运用博弈论研究了渠道结构对绿色产品的价格和利润的影响、绿化成本和消费者的环境意识对绿色产品生产的影响。Basiri和Heydari[5]采用博弈论的方法研究了一条包括制造商和零售商的二级供应链同时生产和销售绿色和非绿色产品。
也有国外学者构建其他数理模型进行研究。Madani和Rasti-Barzoki[6]建立了一个政府为领导者,两条竞争的非绿色、绿色供应链为追随者的数学模型,发现政府补贴比政府税收的作用更大而且显著提高了政府和供应链的利润和绿色产品的持续性,集中决策能为他们带来更多的利润和绿色产品。Jamali和Rasti-Barzoki[7]构建了2个制造商、2个零售商和2种产品(它们各自分别与绿色产品和非绿色产品对应)模型,发现集中决策实现的产品绿色度更高。
国内有关绿色供应链的研究起步较晚,但是研究的文献不断增多。首先是关于政府参与背景下绿色供应链中不同关系人博弈问题的研究。徐伟和郑燕飞[8]在研究绿色供应链政企博弈关系时考虑了消费者的举报行为,分别得出了纳什均衡解和混合策略均衡解。申亮[9]运用演化博弈论针对政府激励机制对制造商生产策略演化行为的积极作用进行了深入研究。朱庆华和窦一杰[10]综合考虑政府补贴、产品绿色度水平、消费者效用建立了一个政府与采取不同战略制造商的三阶段博弈模型。陈志松[11]运用契约理论和纳什谈判理论分析了政府激励政策下人造板绿色供应链的集中优化决策、分散均衡决策和谈判协调决策模型下相应的收益分享—成本分担契约谈判协调机制。张艳丽等[12]基于消费者策略行为建立了无政府补贴、政府对绿色产品制造商进行补贴和绿色消费者3种情况的绿色供应链决策模型,发现政府的补贴有利于绿色产品制造商的发展。田一辉和朱庆华[13]通过建立三阶段演化博弈模型研究了在政府价格补贴下竞争企业间绿色供应链管理的扩散过程,认为政府的价格补贴可以促进绿色产品的销量和价格上升。
有些文献侧重于绿色供应链定价策略及其影响问题的研究。例如,江世英和李随成[14]以包括一个制造商和一个零售商的二级供应链为背景,对以制造商为主导的Stackelberg博弈模型、以零售商为主导的Stackelberg博弈模型、纳什均衡模型和合作博弈模型在产品绿色度、产品价格以及批发价格等方面进行了比较分析。梁喜和马春梅[15]分析了不同市场结构下绿色闭环供应链的成员的决策和绩效,认为无领导的垂直纳什结构最理想,但考虑实际情况零售商控制市场较好。邱国斌[16]基于博弈论研究了制造商的最优定价策略和零售商的最优订货策略,发现订货量和批发价格随着损失厌恶增加而减少,环保意识能够促使制造商降低批发价格。
也有一些文献从偏好和风险规避的角度探讨了绿色供应链的相关问题。刘会燕和戢守峰[17]考虑消费者偏好,针对由制造商和排他性零售商组成的两条竞争供应链,构建了3种链—链之间竞争结构模型,分析各情况下最优价格和绿色度的决策以及消费者偏好和供应链之间竞争对产品选择和绩效的影响。江世英等[18]在风险规避型的制造商、零售商的前提下建立了集中决策博弈模型和制造商领导Stackelberg博弈模型,比较了2种博弈模型中产品绿色度、批发价格、产品价格与风险规避度的相互影响,以及风险规避度对制造商、零售商效用的影响。
此外,还有一些文献从信息角度探讨了绿色供应链的决策问题。曹裕和刘子豪[19]在信息不对称下建立了三级供应链的非合作博弈模型和引入收益共享合约的合作决策模型,证明了信息不对称下合作决策的优越性。陈杰等[20]分析了供应商和制造商在不完全信息条件下,双方在不同的市场环境下的判断和采取的策略。曹柬等[21]针对供应链采购环节中原材料绿色度隐匿的逆向选择问题,研究了不对称信息下制造商的激励契约的设计过程。徐莉等[22]分析了信任对绿色供应链知识共享的调节作用。
通过对国内外文献的梳理可以发现,已有的文献大都着重于政府的财政干预与绿色供应链的博弈关系、不同市场结构下绿色供应链的决策与绩效等。但是,关于绿色供应链的成员的风险态度类型,几乎所有的研究都假设制造商和零售商是风险中性的。只有江世英等的研究[18]假设了制造商与零售商是风险规避型企业,但也仅研究了集中决策模型和制造商领导的Stackelberg博弈模型,没有继续研究其他市场结构下的情况。由于信息不对称和有限理性,所以研究风险规避型企业对绿色供应链的影响具有重要的理论和现实意义。本文在考虑制造商、零售商风险规避的基础上,建立集中决策与分散决策模型,深入分析绿色供应链的定价问题。
1 基础模型和研究假设为了简化研究问题,本文考虑由一个制造商、一个零售商和消费者组成的二级绿色供应链。首先是消费者根据自己的偏好选择绿色产品,形成市场需求函数。然后,绿色产品制造商根据市场需求生产绿色产品,并且以批发价格卖给零售商。最后,零售商以市场价格把绿色产品卖给消费者,这样就形成了一条绿色供应链。
为了建立数学模型,本文做出如下假设。
1) 消费者普遍偏好绿色度高、价格便宜的产品。也就是说,市场需求与绿色产品的价格和绿色度相关。产品价格越高,市场需求越小;产品绿色度越高,产品越环保,市场需求越大,且市场需求具有不确定性。即市场需求函数可以表示为
| $\quad\quad D = \alpha - \beta p + \tau \theta + \varepsilon{\text{。}} $ | (1) |
这里,α代表绿色产品的市场容量;β代表产品的需求价格弹性,α、β均大于0;p代表绿色产品价格;τ是需求的绿色度敏感性系数;θ代表产品绿色度;ε代表需求的不确定性,它是均值为0,方差为σ2的随机变量,服从正态分布。
2) 制造商生产单位绿色产品的成本为c1。为了提高产品绿色度而产生的研发成本是研究成果的二次函数
| $\quad\quad {\pi _1} = \left( {\omega - {c_1}} \right)D - \frac{1}{2}\eta {\theta ^2}{\text{。}}$ | (2) |
再假设制造商为风险规避者,风险规避度为λ1>0。那么,效用函数可以表示为
| $\begin{split}&\quad\quad{U_1} = E\left( {{\pi _1}} \right) - {\lambda _1}{\rm{var}}\left( {{\pi _1}} \right) = \left( {\omega - {c_1}} \right)\left( {\alpha - \beta p + \tau \theta } \right) -\\ &\displaystyle\frac{1}{2}\eta {\theta ^2} - {\lambda _1}{\left( {\omega - {c_1}} \right)^2}{\sigma ^2}{\text{。}}\end{split}$ | (3) |
3) 零售商销售绿色产品的单位成本为c2,那么零售商的利润函数表示为
| $\quad\quad{\pi _2} = \left( {p - \omega - {c_2}} \right)D{\text{。}}$ | (4) |
假设零售商同样为风险规避者,风险规避度为λ2 >0,则零售商和供应链的效用函数可以分别表示为
| $\begin{split}&\quad\quad{U_2} = E\left( {{\pi _2}} \right) - {\lambda _2}{\rm{var}}\left( {{\pi _2}} \right) =\\ &\left( {p - \omega - {c_2}} \right)\left( {\alpha - \beta p + \tau \theta } \right) -{\lambda _2}{\left( {p - \omega - {c_2}} \right)^2}{\sigma ^2}{\text{。}}\end{split}$ | (5) |
| $\begin{split}&\quad\quad{U_{{\rm{SC}}}} = {U_1} + {U_2}= \left( {p - {c_1} - {c_2}} \right)\left( {\alpha - \beta p + \tau \theta } \right) - \\ &\displaystyle\frac{1}{2}\eta {\theta ^2} - \left[ {{\lambda _1}{{\left( {\omega - {c_1}} \right)}^2} + {\lambda _2}{{\left( {p - \omega - {c_2}} \right)}^2}} \right]{\sigma ^2}{\text{。}}\end{split}$ | (6) |
集中决策模型就是制造商和零售商相互串通成为一个系统,系统确定最优的产品价格、批发价格和绿色度使得供应链整体的效用最大化,该模型用数学表达为
| $\quad\quad\left\{ {\begin{array}{*{20}{l}}{\mathop {\max }\limits_{p,\omega ,\theta } {U_{{\rm{SC}}}} = {U_1} + {U_2},}\\{{\rm{s}}.{\rm{t}}.p {\text{≥}} \omega + {c_2},\omega {\text{≥}} {c_1},\theta {\text{≥}} 0,{U_1} {\text{>}} 0,{U_2} {\text{>}} 0}{\text{。}}\end{array}} \right.$ | (7) |
引理1 集中决策模型下的均衡产品价格、批发价格和绿色度,可以通过对式(6)分别求关于p、ω、θ的偏导数,并令偏导数等于零求解得出
| ${p^{*}} = \frac{{\left[ {\alpha \eta + \left( {\beta \eta - {\tau ^2}} \right)\left( {{c_1} + {c_2}} \right)} \right]\left( {{\lambda _1} + {\lambda _2}} \right) \!+\! 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}\left( {{c_1} \!+\! {c_2}} \right)}}{{\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}}},$ | (8) |
| $\quad\quad{\omega ^{*}} = \frac{{{\lambda _1}{c_1} + {\lambda _2}\left( {{p^{*}} - {c_2}} \right)}}{{\left( {{\lambda _1} + {\lambda _2}} \right)}},$ | (9) |
| $\quad\quad{\theta ^{*}} = \frac{{\tau \left( {{p^{*}} - {c_1} - {c_2}} \right)}}{\eta }{\text{。}}$ | (10) |
证明 该绿色供应链效用函数的Hessian矩阵为
| $\begin{split}&\quad\quad{{H}}\left( {U_{{\rm{SC}}}} \right)= \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} {p^2}}}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} p\text{∂} \omega }}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} p\text{∂} \theta }}}\\{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} \omega \text{∂} p}}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} {\omega ^2}}}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} \omega \text{∂} \theta }}}\\{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} \theta \text{∂} p}}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} \theta \text{∂} \omega }}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} {\theta ^2}}}}\end{array}} \right] =\\&\left[ {\begin{array}{*{20}{c}}{ - 2\left( {\beta + {\lambda _2}{\sigma ^2}} \right)}&{2{\lambda _2}{\sigma ^2}}&\tau \\{2{\lambda _2}{\sigma ^2}}&{ - 2{\sigma ^2}\left( {{\lambda _1} + {\lambda _2}} \right)}&0\\\tau &0&{ - \eta }\end{array}} \right]{\text{。}}\end{split}$ | (11) |
由式(11)可知,该Hessian矩阵的一阶顺序主子式M1=–2(β+λ2σ2)<0,二阶顺序主子式
命题1 集中决策模型下,产品的批发价格随着产品的绿色度增加而增加,产品价格随着绿色度的增加而增加,产品价格随着批发价格的增加而增加。
证明 联立式(9)和(10),可以得出
命题2 当α>β(c1+c2)时,制造商的风险规避度越大,产品的价格越低,产品绿色度越低,零售商的风险规避度越大,产品的价格越低,产品绿色度越低;当α<β(c1+c2)时,制造商风险规避度越大,产品价格越高,产品绿色度越高,零售商风险规避度越大,产品价格越高,产品绿色度越高。
证明 根据式(8),可得
| $\begin{array}{l}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\displaystyle\frac{{\text{∂} {p^{*}}}}{{\text{∂} {\lambda _1}}} = \displaystyle\frac{{\left\{ {\left[ {\alpha \eta + \left( {\beta \eta - {\tau ^2}} \right)\left( {{c_1} + {c_2}} \right)} \right] + 2\eta {\lambda _2}{\sigma ^2}} \right\}\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right] }}{{{{\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right]}^2}}}-\\\quad\quad\quad\quad\quad\quad\quad\quad{\displaystyle\frac{\left( {2\beta \eta - {\tau ^2} + 2\eta {\lambda _2}{\sigma ^2}} \right)\left\{ {\left[ {\alpha \eta + \left( {\beta \eta - {\tau ^2}} \right)\left( {{c_1} + {c_2}} \right)} \right]\left( {{\lambda _1} + {\lambda _2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}\left( {{c_1} + {c_2}} \right)} \right\}}{{\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right]}^2}} =\\ \quad\quad\quad\quad\quad\quad\quad\quad\displaystyle\frac{{ - 2{\eta ^2}{\lambda _2}^2{\sigma ^2}\left[ {\alpha - \beta \left( {c + {c_2}} \right)} \right]}}{{{{\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right]}^2}}},\end{array}$ |
| $\begin{array}{l}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\displaystyle\frac{{\text{∂} {p^{*}}}}{{\text{∂} {\lambda _2}}} = \displaystyle\frac{{\left\{ {\left[ {\alpha \eta + \left( {\beta \eta - {\tau ^2}} \right)\left( {{c_1} + {c_2}} \right)} \right] + 2\eta {\lambda _1}{\sigma ^2}} \right\}\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right] }}{{{{\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right]}^2}}}-\\\quad\quad\quad\quad\quad\quad\quad\quad{\displaystyle\frac{ \left( {2\beta \eta - {\tau ^2} + 2\eta {\lambda _1}{\sigma ^2}} \right)\left\{ {\left[ {\alpha \eta + \left( {\beta \eta - {\tau ^2}} \right)\left( {{c_1} + {c_2}} \right)} \right]\left( {{\lambda _1} + {\lambda _2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}\left( {{c_1} + {c_2}} \right)} \right\}}{{\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right]}^2}}=\\\quad\quad\quad\quad\quad\quad\quad\quad \displaystyle\frac{{ - 2{\eta ^2}{\lambda _1}^2{\sigma ^2}\left[ {\alpha - \beta \left( {c + {c_2}} \right)} \right]}}{{{{\left[ {\left( {{\lambda _1} + {\lambda _2}} \right)\left( {2\beta \eta - {\tau ^2}} \right) + 2\eta {\lambda _1}{\lambda _2}{\sigma ^2}} \right]}^2}}}{\text{。}}\end{array}$ |
当α>β(c1+c2)时,
命题2的经济意义在于:当市场的容量越大,需求价格弹性越小时,消费者对价格越不敏感,价格上升会使得供应链系统的利润增加,但是如果供应链系统是风险规避者,则风险规避度越大,产品价格上升反而降低了供应链整体的效用;当市场容量越小,需求价格弹性越大,消费者对价格越敏感,风险规避的供应链系统为了增加系统的效用,则会制定较高的产品价格。
2.2 分散决策模型分散决策模型的特点是参与博弈的各方分散决策、相互竞争,只考虑自己的利益最大化。实际上,分散决策模型在现实社会中更为常见。比较常见的有一方领导,一方追随的Stackelberg模型和各方同时进行决策的纳什均衡模型。因此,本文将进一步研究分散决策模型下的绿色供应链的定价问题。在这之前,有必要证明引理2。
引理2 当2ηλ1σ2–τ2>0时,制造商的效用函数是关于批发价格ω、绿色度θ的联合凹函数,有极大值;零售商的效用函数是关于产品价格p的凹函数,有极大值。
证明 制造商效用函数的Hessian矩阵如式(12)所示。
| $\quad\quad{{H}}\left({U_1}\right) = \left[\!\! {\begin{array}{*{20}{c}}{\displaystyle\frac{{{\text{∂} ^2}{U_1}}}{{\text{∂} {\omega ^2}}}}&{\displaystyle\frac{{{\text{∂} ^2}{U_1}}}{{\text{∂} \omega \text{∂} \theta }}}\\{\displaystyle\frac{{{\text{∂} ^2}{U_1}}}{{\text{∂} \theta \text{∂} \omega }}}&{\displaystyle\frac{{{\text{∂} ^2}{U_{{\rm{SC}}}}}}{{\text{∂} {\theta ^2}}}}\end{array}} \!\!\right] = \left[\!\! {\begin{array}{*{20}{c}}{ - 2{\lambda _1}{\sigma ^2}}&\tau \\\tau &{ - \eta }\end{array}} \!\!\right]{\text{。}}$ | (12) |
其一阶顺序主子式M1=–2λ1σ2<0,二阶顺序主子式M2=2ηλ1σ2–τ2>0。根据定义,该Hessian矩阵是负定矩阵。因此,制造商效用函数是关于批发价格ω、绿色度θ的联合凹函数,有极大值。
对零售商效用函数求关于产品价格p的二阶偏导数,有
在制造商领导的Stackelberg模型中,制造商作为领导者,零售商作为跟随者,该供应链的决策顺序为:首先是制造商根据其效用最大化原则确定其最优批发价格和产品的绿色度;然后零售商在最优批发价格和产品绿色度的基础上根据它的效用最大化原则决定产品的价格。其数学模型可以表示为
| $\left\{ \!\!\!{\begin{array}{*{20}{l}}{\mathop {\max }\limits_{\omega ,\theta } {U_1}},\\{{\rm{s}}.{\rm{t}}.p = {\rm{argmax}}{U_2},p {\text{≥}} \omega + {c_2},\omega {\text{≥}} {c_1},\theta {\text{≥}} 0,{U_1} {\text{>}} 0,{U_2} {\text{>}} 0{\text{。}}}\end{array}} \right.$ | (13) |
该模型可用逆向归纳法求解:第1步,首先对式(5)求关于p的一阶偏导数,并令导数等于零,可以得出
| $\quad\quad p = \frac{{\alpha + \tau \theta + \left( {\beta + 2{\lambda _2}{\sigma ^2}} \right)\left( {\omega + {c_2}} \right)}}{{2\left( {\beta + {\lambda _2}{\sigma ^2}} \right)}}{\text{。}}$ | (14) |
第2步,把式(14)代入式(3),并对其分别求关于ω、θ的一阶偏导数,可以求出均衡时的批发价格、绿色度为
| $\begin{split}\quad\quad\quad\quad\quad\quad&\quad\quad{\omega ^{{**}}} = \displaystyle\frac{{2\eta {\beta ^3}\left( {{c_1} + {c_2}} \right) + 2\eta {\beta ^2}{\sigma ^2}\left( {2{c_1}{\lambda _1} + 3{c_1}{\lambda _2} - {c_2}{\lambda _2}} \right) + 4\eta \beta {c_1}{\lambda _2}{\sigma ^4}\left( {{\lambda _2} + {\lambda _1}} \right) }}{{4\eta {\beta ^3} + 4\eta {\beta ^2}{\sigma ^2}\left( {3{\lambda _2} + 2{\lambda _1}} \right) + 8\eta \beta {\lambda _2}{\sigma ^4}\left( {2\beta {\lambda _1} + {\lambda _2} + {\lambda _1}{\lambda _2}{\sigma ^2}} \right) - {\tau ^2}{{\left( {\beta + 2{\lambda _2}{\sigma ^2}} \right)}^2}}}+\\&{\displaystyle\frac{2\alpha \eta {\beta ^2} + 6\alpha \eta \beta {\lambda _2}{\sigma ^2} + 4\eta {\lambda _2}^2{\sigma ^4}\left( {\alpha - \beta {c_2}} \right) + 8\eta {\lambda _1}{\lambda _2}{\sigma ^4}\left( {{\lambda _2}{\sigma ^2} + \beta } \right) - {\tau ^2}{{\left( {\beta + 2{\lambda _2}{\sigma ^2}} \right)}^2}}{4\eta {\beta ^3} + 4\eta {\beta ^2}{\sigma ^2}\left( {3{\lambda _2} + 2{\lambda _1}} \right) + 8\eta \beta {\lambda _2}{\sigma ^4}\left( {2\beta {\lambda _1} + {\lambda _2} + {\lambda _1}{\lambda _2}{\sigma ^2}} \right) - {\tau ^2}{{\left( {\beta + 2{\lambda _2}{\sigma ^2}} \right)}^2}}}{\text{,}}\end{split}$ | (15) |
| $\quad\quad{\theta ^{{**}}} = \frac{{\tau \left( {2{\lambda _2}{\sigma ^2} + \beta } \right)\left( {{\omega ^{{**}}} - {c_1}} \right)}}{{2\eta \left( {{\lambda _2}{\sigma ^2} + \beta } \right)}}{\text{。}}$ | (16) |
第3步,把式(15)、(16)代入式(14),则均衡的产品价格为
| $\quad\quad{p^{{**}}} = \frac{{\alpha + \tau {\theta ^{{**}}} + \left( {\beta + 2{\lambda _2}{\sigma ^2}} \right)\left( {{\omega ^{{**}}} + {c_2}} \right)}}{{2\left( {\beta + {\lambda _2}{\sigma ^2}} \right)}}{\text{。}}$ | (17) |
在零售商领导的Stackelberg模型中,零售商作为领导者,制造商作为跟随者,零售商首先决定产品的价格,制造商在其基础上决定批发价格、产品绿色度,其数学模型表示为
| $\quad\quad\!\!\left\{\!\!{\begin{array}{*{20}{l}}{\mathop {\max }\limits_p {U_2}}{\text{,}} \\{{\rm{s}}.{\rm{t}}.\; \omega = {\rm{argmax}}{U_1},\;\theta = {\rm{argmax}}{U_1},}\;{p {\text{≥}} \omega + {c_2},\;}\\\quad\quad{\omega {\text{≥}} {c_1},\;\theta {\text{≥}} 0,\;{U_1} {\text{>}} 0,\;{U_2} {\text{>}} 0}{\text{。} }\end{array}} \right.$ | (18) |
同样地,用逆向归纳法求解该模型。第1步,对式(3)分别求关于ω、θ的一阶偏导数,并令导数等于零,求解得到
| $\quad\quad\omega = {c_1} + \frac{{\eta \left( {\alpha - \beta p} \right)}}{{2\eta {\lambda _1}{\sigma ^2} - {\tau ^2}}}{\text{。}}$ | (19) |
| $\quad\quad\theta = \frac{{\tau \left( {\alpha - \beta p} \right)}}{{2\eta {\lambda _1}{\sigma ^2} - {\tau ^2}}}{\text{。}}$ | (20) |
第2步,把式(19)、(20)代入式(5),并对其求关于p的一阶偏导数,令导数等于零,可以求出均衡时的产品价格,结果得到
| $\quad\quad\quad\quad{\bar p} = \frac{{A\left\{ {A\left[ {\alpha + B\left( {\beta + 2E} \right)} \right] + \left[ {2\alpha \beta \eta + {\tau ^2}\left( {\alpha - \beta } \right) + \beta {\tau ^2}B + 2\eta E\left( {\alpha + \beta {c_1}} \right)} \right]} \right\} + \beta \eta \left[ {{\tau ^2}\left( {2\alpha - \beta ) + 2\alpha \eta E} \right)} \right]}}{{\eta {\beta ^2}\left( {{\tau ^2} + 2E} \right) + \beta A\left[ {2\eta \beta + {\tau ^2}\left( {1 + \eta \beta } \right) + 2E\left( {1 + \eta } \right)} \right] + 2{A^2}\left( {\beta + E} \right)}}{\text{。}}$ | (21) |
其中,A=2ηλ1σ2–τ2,B=c1+c2,E=λ2σ2。
第3步,把式(21)分别代入式(19)、(20),则可导出均衡时的批发价格、产品绿色度为
| $\quad\quad\bar \omega = {c_1} + \frac{{\eta \left( {\alpha - \beta {{\bar p}}} \right)}}{{2\eta {\lambda _1}{\sigma ^2} - {\tau ^2}}}{\text{。}}$ | (22) |
| $\quad\quad\bar \theta = \frac{{\tau \left( {\alpha - \beta {{\bar p}}} \right)}}{{2\eta {\lambda _1}{\sigma ^2} - {\tau ^2}}}{\text{。}}$ | (23) |
在纳什均衡模型中,制造商和零售商的决策没有先后顺序,他们同时进行决策,制造商确定批发价格和产品绿色度,零售商确定产品价格,其数学模型表示为
| $\left\{ {\begin{align} \; & {\mathop {\max }\limits_{\omega ,\theta } {U_1}}{\text{,}} \\\; & {\mathop {\max }\limits_p {U_2}}{\text{,}}\\\; & {\rm{s}}.{\rm{t}}.p {\text{≥}} \omega + {c_2},\omega {\text{≥}} {c_1},\theta {\text{≥}} 0,{U_1} {\text{>}} 0,{U_2} {\text{>}} 0{\text{。}}\end{align}} \right.$ | (24) |
其均衡时的批发价格、产品绿色度和产品价格,可以通过令其效用函数的一阶偏导数等于零,得出
| $\quad\quad \bar {\bar \omega} = {c_1} + \frac{{\eta \left( {\alpha - \beta \bar{\bar p}} \right)}}{{2\eta {\lambda _1}{\sigma ^2} - {\tau ^2}}} {\text{,}}$ | (25) |
| $\quad\quad\bar {\bar\theta} = \frac{{\tau \left( {\alpha - \beta \bar{\bar p}} \right)}}{{2\eta {\lambda _1}{\sigma ^2} - {\tau ^2}}}{\text{,}}$ | (26) |
| $\quad\quad\bar{\bar p} = \frac{{\alpha \left( {2{\lambda _1}{\sigma ^2} + \beta \eta + 2\eta E} \right) + {\rm{AB}}\left( {\beta + 2E} \right)}}{{2A\left( {\beta + E} \right) + \beta \left( {{\tau ^2} + \beta \eta + 2\eta E} \right)}}{\text{。}}$ | (27) |
其中,A=2ηλ1σ2–τ2,B=c1+c2,E=λ2σ2。
命题3 在3种分散决策模型中,制造商领导的Stackelberg模型里,产品绿色度越高,批发价格越高,并且产品价格与产品绿色度、批发价格之间呈现出正相关关系;在零售商领导的Stackelberg模型和纳什均衡模型中,产品绿色度越高,批发价格越高,而产品价格与产品绿色度、批发价格之间则呈现负相关关系。
证明 对式(16)进行变形处理,可以得到
命题3表明,在制造商具有领导优势时,制造商生产产品的绿色度越高,产品的批发价格和零售价格都将随之涨价,因为产品的绿色度越高,制造商需要付出更多的生产成本,因此抬高了批发价格和零售价格,这与现实情况是符合的;而在制造商没有领导优势时,对于零售商给定的零售价格,由于制造商是风险规避的,制造商倾向于降低产品的绿色度来降低生产成本以提高效用。命题3的现实意义是,对于消费者和整个社会而言,相比于零售商主导市场,制造商主导市场能带来绿色度更高的产品,给社会带来更少的污染。
3 结果与讨论 3.1 制造商与零售商风险态度不同时的均衡本文的第3部分分析了制造商和零售商都是风险规避者时各模型的均衡结果,而这部分主要分为以下3种情况讨论风险态度对各模型均衡时的批发价格、产品绿色度和产品价格的影响:1) 制造商与零售商都是风险中性的厂商;2) 制造商是风险中性型,零售商是风险规避型厂商;3) 制造商是风险规避型,零售商是风险中性型厂商。其结果如表1~表4所示。
| 表 1 集中决策模型均衡解 Tab. 1 Solution of centralized decision model |
| 表 2 制造商领导的Stackelberg模型均衡解 Tab. 2 Solution of Stackelberg model with manufacturer as leader |
| 表 3 零售商领导的Stackelberg模型均衡解 Tab. 3 Solution of Stackelberg model with retailer as leader |
| 表 4 纳什均衡模型均衡解 Tab. 4 Solution of Nash equilibrium model |
从表1可以看出,对于集中决策模型而言,在制造商与零售商中至少有一个是风险中性时,厂商的风险态度不影响绿色产品的价格与产品绿色度,但是对产品的批发价有影响。值得注意的是,当制造商风险规避,零售商风险中性时,此时的最优批发价格ω=c1,这样制造商将无利可图;当制造商风险中性,零售商风险规避时,此时的最优批发价格ω=p–c2,零售商将无利可图,也就是说,这样的情况在现实生活中不存在。
命题4 在集中决策模型中,制造商风险规避、零售商风险中性时的最优批发价格ω2*,制造商与零售商均为风险规避时最优批发价格ω*,制造商风险中性、零售商风险规避时的最优批发价格ω1*,他们之间的大小关系是ω2*<ω*<ω1*。
从表4可以看出,对于分散决策模型中的纳什均衡模型而言,制造商风险中性,零售商风险规避与制造商和零售商均为风险中性时的最优批发价格、最优绿色度和最优产品价格没有差别,只与α、β、τ、η、c1、c2有关,与零售商的风险规避度无关。
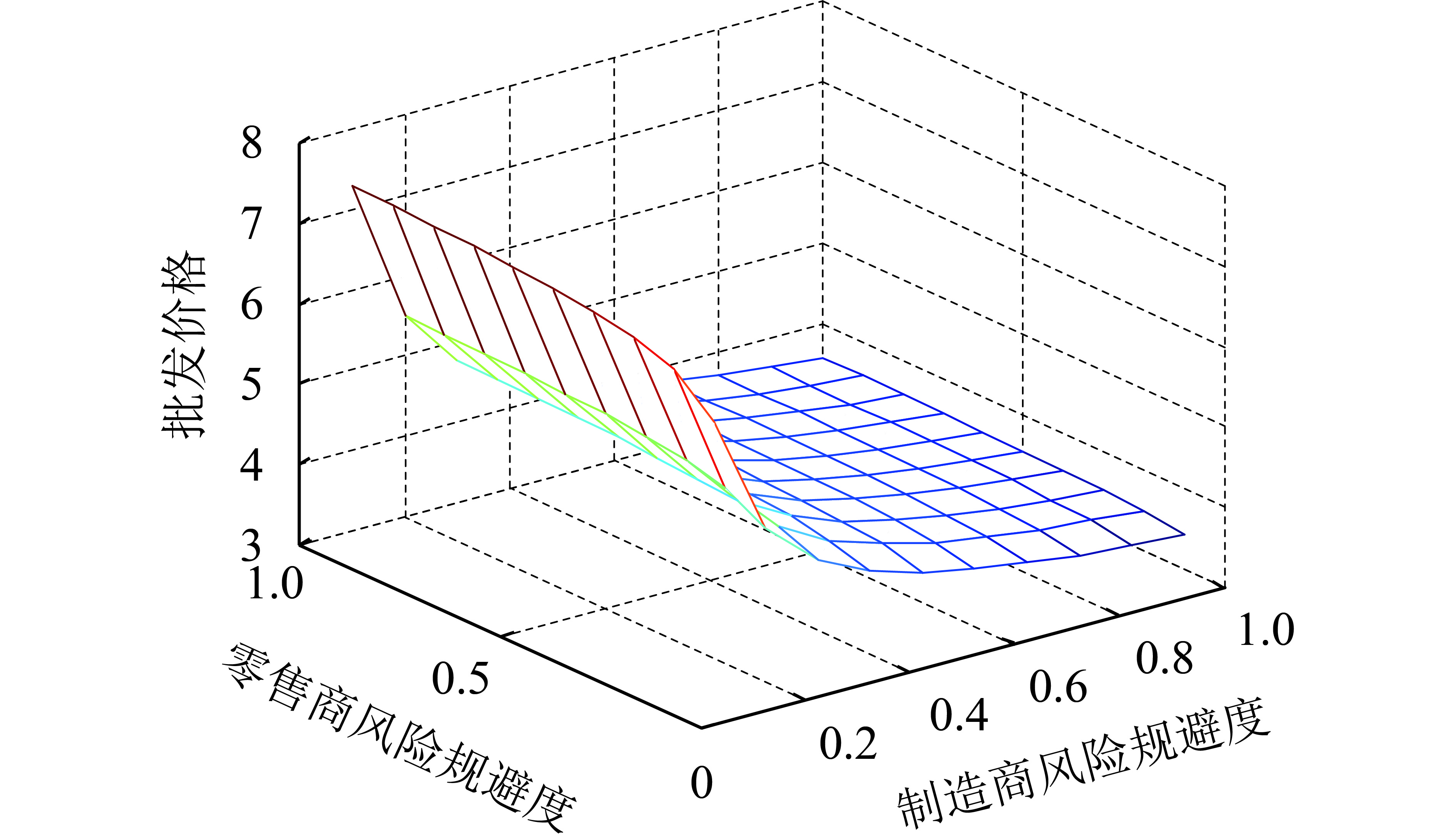
3.2 数值仿真由于模型参数较多,表达式比较复杂,为了更好地研究风险规避度对绿色供应链的影响,接下来的部分将用Matlab软件对模型进行检验,以便得到更加准确的结论,为供应链厂商的决策提供参考依据。由于篇幅限制,这里仅对集中决策模型进行数值分析。依据引理1对模型的参数进行赋值:α=10,β=1,η=0.6,τ=1,σ=2,c1=3,c2=2,λ1、λ2在[0.1,1)的范围内变动,步长为0.1。利用Matlab软件绘制的(λ1,λ2,ω)、(λ1,λ2,θ)、(λ1,λ2,p)和(λ1,λ2,USC)的三维立体图分别如图1~图4所示。图5是在取λ1=λ2=0.5时,产品绿色度与供应链效用之间的关系图。
|
图 1 风险规避对批发价格的影响 Fig. 1 Impact of risk aversion on wholesale prices |
|
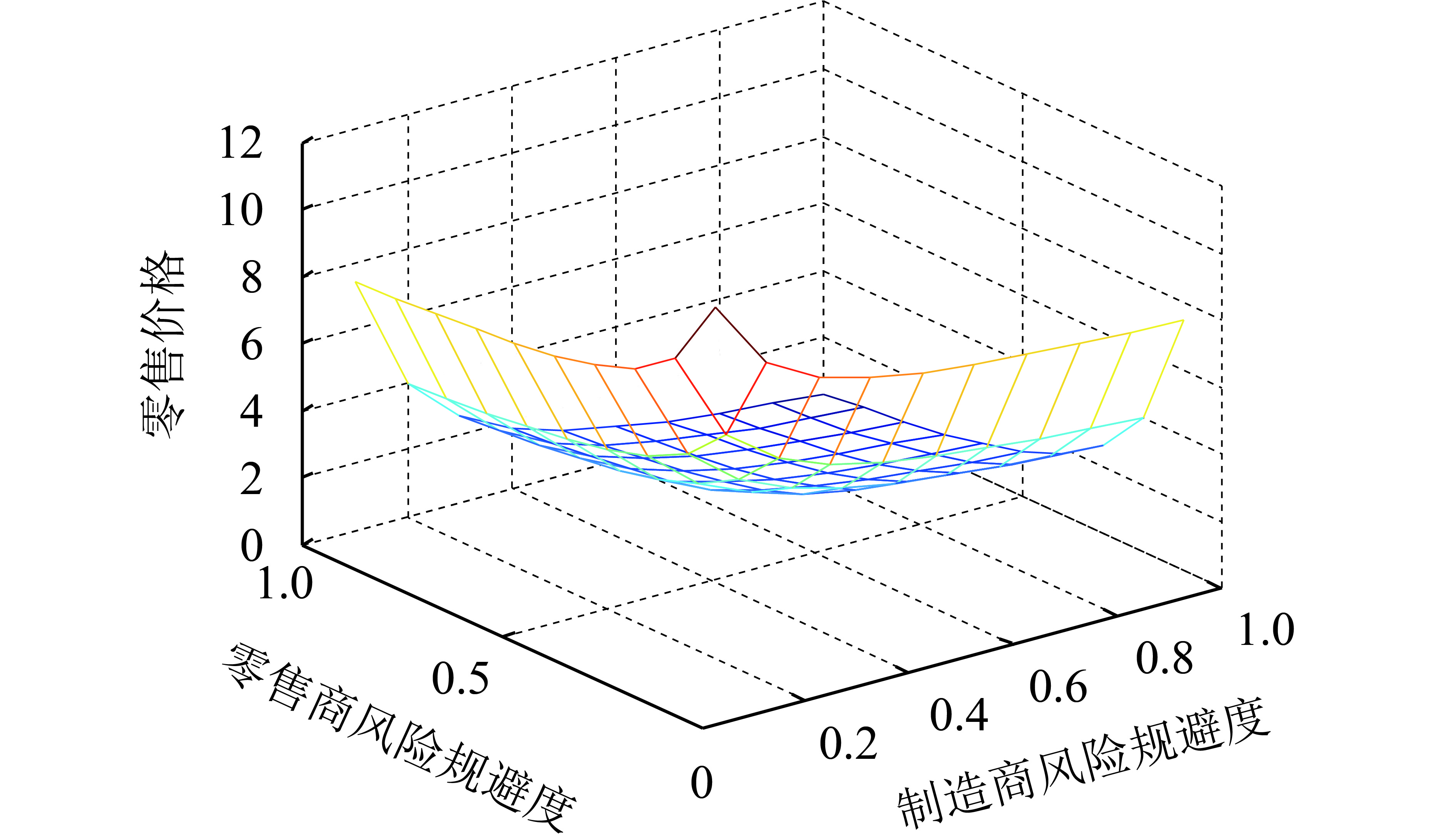
图 3 风险规避对零售价格的影响 Fig. 3 Impact of risk aversion on retail prices |
一是风险规避对供应链的影响。在α>β(c1+c2)的条件下,从图1可以看到,当零售商风险规避度不变时,随着制造商风险规避度的增加,产品的批发价格一直下降,λ1在0至0.2区间时,批发价格下降最快。λ1在0.2至0.4区间时,批发价格下降速度变缓。λ1在0.6至1区间时,批发价格趋于平缓。当制造商风险规避度不变时,随着零售商风险规避的度的增加,批发价格呈现出缓慢上升的趋势,但是上升程度不大。综合来看,制造商风险规避对批发价格的影响程度要大于零售商。
仔细观察图2~图4不难发现,这3个图形非常相似且对称,表明λ1和λ2对它们的影响程度是相同的,当制造商、零售商的风险规避度增加时,产品绿色度、零售价格和供应链的期望效用都在下降。不同的是,这三者的下降速度不一样,厂商风险规避度对零售价格影响程度最大,其次是产品绿色度,最后是供应链系统的效用。
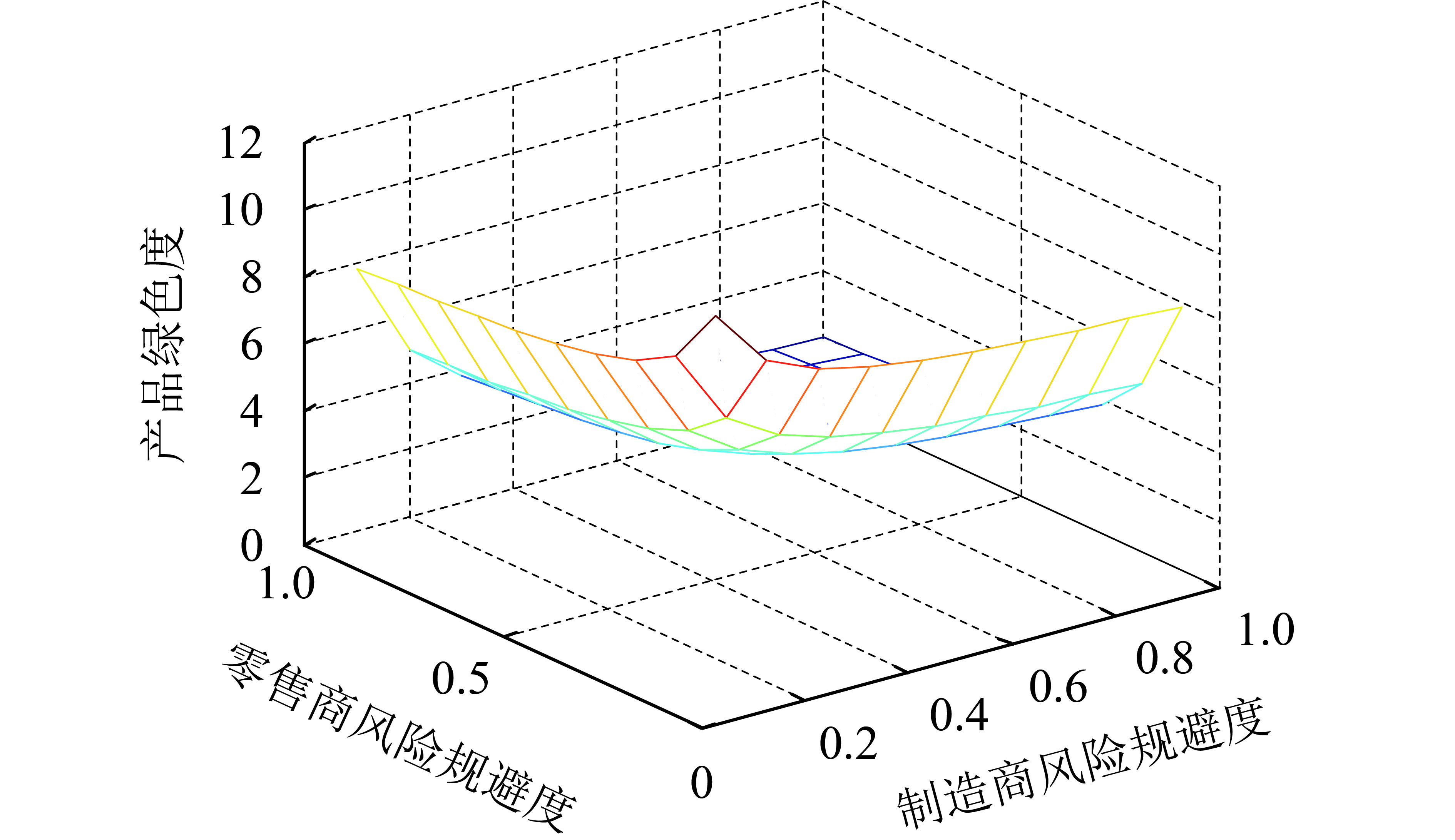
|
图 2 风险规避对绿色度的影响 Fig. 2 Effect of risk aversion on greenness |

|
图 4 风险规避对供应链效用的影响 Fig. 4 Impact of risk aversion on supply chain utility |
二是产品绿色度对供应链期望效用的影响。从图5可以看出,在给定的条件下,存在一个最优的产品绿色度使得期望供应链的效用最大,在3.3至3.4之间。在这个最优绿色度之下,随着绿色度的增加,供应链的期望效用也增加。在最优绿色度之上,随着绿色度的增加,供应链的期望效用降低,直到供应链期望效用等于零时,有一个最大的产品绿色度,大约是7.8。此后,制造商将不会提高产品绿色度。

|
图 5 产品绿色度对供应链效用的影响 Fig. 5 Effect of product greenness on supply chain utility |
本文以由风险规避型的制造商、零售商组成的二级绿色供应链为背景,考虑了产品绿色度,利用博弈论的方法建立了集中决策模型与分散决策模型,分散决策模型包括制造商领导的Stackelberg模型、零售商领导的Stackelberg模型和纳什均衡模型,分别得出了各个模型下的均衡批发价格、产品绿色度和产品价格,并进行了对比分析。在此基础上,进一步分析了制造商与零售商风险态度不同时的各模型的均衡结果。
研究结果表明,在集中决策模型中,产品绿色度、批发价格和零售价格这三者之间存在正相关关系,而制造商与零售商的风险规避度对供应链的影响与市场容量、需求价格弹性、厂商的成本等因素有关。而对于分散决策模型而言,在制造商领导的Stackelberg模型中,产品绿色度越高,制造商的批发价格和零售商的零售价格均提高;在零售商领导的Stackelberg模型和纳什均衡模型中,零售价格越高,制造商选择的产品绿色度越低,批发价格越低。
由于篇幅限制,文章没有分析市场容量、需求价格弹性系数、绿色度敏感系数、成本等对绿色供应链的影响,文章的下一步可以采用数学软件对此进行数值仿真。同时,为了更切合实际,不对称信息和非线性需求函数则是以后的研究方向。
| [1] |
HANDFIELD R B, WALTON S V, GOIZUETA R C, etal. Green supply chain: Best practice from the furniture industry. Proceedings of Annual Meeting of Decision Science Institute[C]. Orlando, FL, USA: Decision Science Institute, 1996: 1295-1297.
|
| [2] |
SHEU J B, CHEN Y J. Impact of government financial intervention on competition among green supply chains[J].
International Journal of Production Economics, 2012, 138(1): 201-213.
DOI: 10.1016/j.ijpe.2012.03.024. |
| [3] |
BARARI S, AGARWAL G, ZHANG W J, etal. A decision framework for the analysis of green supply chain contracts: An evolutionary game approach[J].
Expert Systems with Applications, 2012, 39(3): 2965-2976.
DOI: 10.1016/j.eswa.2011.08.158. |
| [4] |
GHOSH D, SHAH J. A comparative analysis of greening policies across supply chain structures[J].
International Journal of Production Economics, 2012, 135(2): 568-583.
DOI: 10.1016/j.ijpe.2011.05.027. |
| [5] |
BASIRI Z, HEYDARI J. A mathematical model for green supply chain coordination with substitutable products[J].
Journal of Cleaner Production, 2017, 145(1): 232-249.
|
| [6] |
MADANI S R, RASTI-BARZOKI M. Sustainable supply chain management with pricing, greening and governmental tariffs determining strategies: A game-theoretic approach[J].
Computers & Industrial Engineering, 2017, 105(3): 287-298.
|
| [7] |
JAMALI M B, RASTI-BARZOKI M. A game theoretic approach for green and non-green product pricing in chain-to-chain competitive sustainable and regular dual-channel supply chains[J].
Journal of Cleaner Production, 2018, 170(1): 1029-1043.
|
| [8] |
徐伟, 郑燕飞. 绿色供应链管理中有举报行为的政企博弈分析[J].
中国管理科学, 2008, 16(S1): 450-454.
XU Wei, ZHENG Yanfei. Analysis of government-enterprise game with reporting behavior in green supply chain management[J]. Chinese Journal of Management Science, 2008, 16(S1): 450-454. |
| [9] |
申亮. 绿色供应链演化博弈的政府激励机制研究[J].
技术经济, 2008, 27(3): 110-113.
SHEN Liang. Research on government incentive mechanism of evolutionary game in green supply chain[J]. Technology Economics, 2008, 27(3): 110-113. DOI: 10.3969/j.issn.1002-980X.2008.03.022. |
| [10] |
朱庆华, 窦一杰. 基于政府补贴分析的绿色供应链管理博弈模型[J].
管理科学学报, 2011, 14(6): 86-95.
ZHU Qinghua, DOU Yijie. Green supply chain management game model based on government subsidy analysis[J]. Journal of Management Sciences in China, 2011, 14(6): 86-95. |
| [11] |
陈志松. 政府激励政策下人造板绿色供应链谈判-协调机制研究[J].
中国管理科学, 2016, 24(2): 115-124.
CHEN Zhisong. Research on the negotiation of green supply chain based on government incentive policies - coordination mechanism[J]. Chinese Journal of Management Science, 2016, 24(2): 115-124. |
| [12] |
张艳丽, 胡小建, 杨海洪, 等. 政府补贴下考虑消费者策略行为的绿色供应链决策模型[J].
预测, 2017, 36(2): 57-63.
ZHANG Yanli, HU Xiaojian, YANG Haihong, et al. Green supply chain decision model considering consumers' strategic behavior under government subsidy[J]. Forecasting, 2017, 36(2): 57-63. |
| [13] |
田一辉, 朱庆华. 政府价格补贴下绿色供应链管理扩散博弈模型[J].
系统工程学报, 2016, 31(4): 526-535.
TIAN Yihui, ZHU Qinghua. Diffusion game model of green supply chain management under government price subsidy[J]. Journal of Systems Engineering, 2016, 31(4): 526-535. |
| [14] |
江世英, 李随成. 考虑产品绿色度的绿色供应链博弈模型及收益共享契约[J].
中国管理科学, 2015, 23(6): 169-176.
JIANG Shiying, LI Suicheng. Green supply chain game model considering product green degree and revenue sharing contr- act[J]. Chinese Journal of Management Science, 2015, 23(6): 169-176. |
| [15] |
梁喜, 马春梅. 不同市场结构下绿色闭环供应链决策分析[J].
工业工程, 2016, 19(1): 135-141.
LIANG Xi, MA Chunmei. Analysis of green closed-loop supply chain decision under different market Structure[J]. Industrial Engineering Journal, 2016, 19(1): 135-141. DOI: 10.3969/j.issn.1007-7375.2016.01.021. |
| [16] |
邱国斌. 基于损失厌恶的绿色供应链博弈研究[J].
当代经济管理, 2013, 35(12): 18-23.
QIU Guobin. Research on green supply chain game based on loss aversion[J]. Contemporary Economy & Management, 2013, 35(12): 18-23. |
| [17] |
刘会燕, 戢守峰. 考虑消费者绿色偏好的竞争性供应链的产品选择与定价策略[J].
管理学报, 2017, 14(3): 451-458.
LIU Huiyan, JI Shoufeng. Product Selection and pricing strategy of competitive supply chain considering consumers' green preferences[J]. Chinese Journal of Management, 2017, 14(3): 451-458. DOI: 10.3969/j.issn.1672-884x.2017.03.014. |
| [18] |
江世英, 李随成, 王欢. 考虑风险规避的绿色供应链定价决策[J].
系统工程, 2016, 34(3): 94-100.
JIANG Shiying, LI Suicheng, WANG Huan. Green supply chain pricing decision considering risk aversion[J]. Systems Engineering, 2016, 34(3): 94-100. DOI: 10.3969/j.issn.1001-2362.2016.03.064. |
| [19] |
曹裕, 刘子豪. 无政府激励的绿色供应链管理的可行性分析[J].
管理工程学报, 2017, 31(2): 119-127.
CAO Yu, LIU Zihao. Feasibility analysis of green supply chain management without government incentive[J]. Journal of Industrial Engineering and Engineering Management, 2017, 31(2): 119-127. |
| [20] |
陈杰, 屠梅曾, 孙大宁. 生态供应链下绿色采购的信号博弈[J].
系统工程学报, 2004, 19(2): 202-206.
CHEN Jie, TU Meizeng, SUN Daning. Signaling game of green purchasing under ecological supply chain[J]. Journal of Systems Engineering, 2004, 19(2): 202-206. DOI: 10.3969/j.issn.1000-5781.2004.02.017. |
| [21] |
曹柬, 吴晓波, 周根贵. 不对称信息下绿色采购激励机制设计[J].
系统工程理论与实践, 2013, 33(1): 106-116.
CAO Jian, WU Xiaobo, ZHOU Gengui. Green procurement incentive mechanism design under asymmetric information[J]. System Engineering Theory and Practice, 2013, 33(1): 106-116. DOI: 10.3969/j.issn.1000-6788.2013.01.012. |
| [22] |
徐莉, 库陶菲, 朱同斌. 基于信任调节机制的绿色供应链知识共享研究[J].
技术经济, 2009, 28(3): 119-123.
XU Li, KU Taofei, ZHU Tongbin. Study on knowledge sharing of green supply chain based on trust regulatory mechanism[J]. Technology Economics, 2009, 28(3): 119-123. DOI: 10.3969/j.issn.1002-980X.2009.03.023. |
 2018, Vol. 21
2018, Vol. 21