随着自然资源短缺和环境污染问题的日益严重,资源的可持续发展与循环经济逐渐受到了政府和社会各界的强烈关注。我国于2009年正式实施的《循环经济促进法》确立了循环经济减量化、再利用、资源化,减量化优先的原则,并作出了一系列的制度安排。2010年由我国11部委提出的《关于推进再制造产业发展的意见》指出“再制造从源头减少能源资源消耗和废弃物排放,改变‘大量生产大量废弃’的传统增长方式和消费模式,形成‘资源-产品-到寿产品-再制造产品’的循环经济模式,实现产品生命周期效益最大化与拥有成本最小,高效利用资源,受到了国家高度重视,被视为循环经济“再利用”的高级形式”。2013 年国务院印发《循环经济发展战略及近期行动计划》持续推进社会各层面发展循环经济。相关法律法规的出台体现了坚持节约资源和保护环境的基本国策,企业与社会各界也将继续全面贯彻创新、协调、绿色、共享、开放这样一个新的发展理念。而加快发展再制造产业是建设资源节约型、环境友好型社会的客观要求,鉴于此,加强对回收再制造模式的研究具有重要的理论和实践意义。回收与再制造过程往往可以节约更多的能源与原材料消耗,因此相对于使用原材料生产的新产品来说再制造具有更小的环境影响[1]。但是对于制造商而言,回收再制造与原材料生产的成本不同,用不同质量的回收产品进行再制造的成本也会有所差异,不同的产品质量会有不同的市场占有率[2]。对此,在考虑新产品质量的情况下,选择合适的再制造模式,能够为企业带来更大的经济效益与社会效益。
目前,越来越多的学者针对产品的回收再制造展开了研究。Savaskan等[3]针对3种回收模式:制造商回收、零售商回收、第三方回收下闭环供应链最优回收模式的选择进行研究,得出由零售商主导回收的回收模式要优于制造商与第三方主导回收的模式。在以上研究基础上,Savaskan和Wassenhove[4]分析得出当存在2个零售商竞争、1个制造商的回收渠道选择时,零售商之间的竞争在一定程度会影响制造商的回收渠道决策。熊中楷等[5]建立了受专利保护的原制造商授权第三方再制造的闭环供应链模型,并在传统收益分享契约的基础上,将契约形式进行拓展。Ferguson[6]提出在原制造商面对第三方制造商对其具有销售竞争情况时,原制造商会进行再制造或者提前回收废旧产品来维持自身利益。Majumder[7]的研究证明原制造商通过与销售商进行竞争可以降低再制造成本。黄宗盛等[8]研究发现在专利保护的背景下,第三方再制造商的进入可以增加原制造商利润。Mitra等[9]在考虑政府补贴情景下建立了原制造商与再制造商两阶段定价与决策模型。黄祖庆等[10]研究了5种直线型再制造供应链决策结构下的供应链收益,结果表明回收再制品的潜在期望收益是回收再制造的驱动因素。Zou等[11]通过比较原制造商选择外包模式或者授权模式进行再制造的最优价格与利润,发现第三方制造商在消费者对再制品价值预估较低时倾向于授权模式,而原制造商均倾向于外包模式。以上文献主要从产品回收的角度探讨最优回收渠道或闭环供应链模式,而忽略了新产品与再制品之间的差异及消费者的选择过程。
而针对产品质量差异对回收再制造过程的选择,也有一些学者进行了研究。Pokharel和Liang[12]建立考虑再制品质量进行最优收购价格与数量的模型,并通过算例分析再制品质量对其影响。谢家平等[13]从制造商的角度出发,将产品质量水平作为内生变量,考虑其对回收废旧产品降级率的影响,研究结果表明随着降级率的增大,制造商会降低再制造比例。许民利等[14]通过博弈论研究了3种情景下的生产决策并考虑消费者对新产品和再制造产品的不同偏好,分析原制造商授权或自行再制造应满足的条件,得出结论原制造商只有当自身再制造的成本较低且有利润时才愿意生产再制造产品。刘家国等[15]考虑再制品与新产品之间存在质量差异,从而会引发不同的市场需求。由此构建了由一个制造商和一个零售商组成的闭环供应链系统模型,并运用博弈理论分析在集中决策和分散决策情况下的最优产品定价策略与利润。曹俊等[16]通过建立两阶段的动态博弈模型,探讨了新件制造商和再制造商同时进入存在消费转移的市场后,如何进行质量和价格竞争,从而实现各自的利润最大化。
Örsdemir等[17]研究了原制造商在面对独立第三方再制造商时的竞争策略,原制造商处于竞争优势地位时会将产品质量作为一个与独立再制造商竞争的手段,处于劣势时会通过控制产品数量与再制造商进行竞争。熊中楷等[18]采用三阶段的动态博弈模型,研究了单个制造商和单个销售商构成的分散式闭环供应链中旧产品回收质量的控制问题。Galbreth和Blackburn[19]研究当回收产品供给与质量不确定时回收策略的制定,以及如何安排回收产品进行再制造。Ferguson等[20]运用动态规划思想建立了一个多周期回收再制造模型,表明对再制品的质量进行区分可以提高企业的利润。
基于此,考虑到产品质量对于闭环供应链最优回收渠道的影响,本文着重于探讨外包再制造模式与专利保护下授权的供应链再制造模式选择问题。利用博弈理论分别探讨原制造商与第三方再制造两种模式下最优策略,并对2种决策模型结果进行比较分析,期望所得到的结论能为闭环供应链中原制造商的外包及授权策略和再制造模式选择提供一定的理论参考。
1 问题描述和假设考虑受到新产品质量影响的情况下,原材料制造商对废旧产品回收再制造有2个途径并对此建立模型:1)原制造商将再制造工作外包给第三方制造商完成(模型O);2)授权第三方制造商进行再制造(模型R)。在模型O中,原制造商独立生产新产品的同时销售新产品与再制品,通过支付给第三方制造商外包费分离再制造工作。在模型R中,原制造商仅生产及销售新产品。并向第三方制造商收取授权费,回收产品的再制造与销售工作只由第三方制造商进行。原制造商决定新产品零部件质量,较高的新产品质量意味着更高的生产成本与市场需求。
符号与变量说明如下。
本文讨论2个再制造模型——模型O与模型R,
根据以上假设,通过简单的内部计算,可以得到以下的需求函数。
| $\quad\quad\begin{split} &{Q_{\rm n}} = 1 + \displaystyle\frac{{{p_{\rm n}} - {p_{\rm r}}}}{{s(\delta - 1)}},\\&{Q_{\rm r}} = \displaystyle\frac{{\delta {p_{\rm n}} - {p_{\rm r}}}}{{s\delta (1 - \delta )}}{\text{。}}\end{split}$ | (1) |
所有的决策均考虑单阶段决策,根据需求函数,可以推导出逆需求函数为
| $\quad\quad \begin{split}&{p_{\rm n}} = s(1 - {Q_{\rm n}} - \delta {Q_{\rm r}}),\\&{p_{\rm r}} = s\delta (1 - {Q_{\rm n}} - {Q_{\rm r}}){\text{。}}\end{split}$ | (2) |
原制造商(OEM)通过支付外包费用给第三方制造商进行制造工作,原制造商仍然针对新产品及再制品销售工作。原制造商为Stackelberg博弈领导者,第三方制造商为追随者。原制造商与第三方制造商的利润函数为
| $\quad\quad\begin{split}&\mathop {\varPi _O^O}\limits_{{Q_{\rm n}},{p_{\rm o}}} = ({p_{\rm n}} - cs){Q_{\rm n}} + {p_{\rm r}}{Q_{\rm r}} - {p_{\rm o}}{Q_{\rm r}},\\&\mathop {\varPi _R^O}\limits_\lambda = ({p_{\rm o}} - \beta cs){Q_{\rm r}} - 1/2{Q_{\rm r}}^2{\text{。}}\end{split}$ | (3) |
根据博弈顺序,首先原制造商决定新产品质量
| $\begin{split}\quad\quad&{Q_{\rm n}}^{O*} = \displaystyle\frac{{{\delta ^2}s - [1 + (\beta - 1)c]s\delta + c - 1}}{{2{\delta ^2}s - 2\delta s - 2}}\text{,}\\&{Q_{\rm r}}^{O*} =\displaystyle\frac{{cs(\beta - \delta )}}{{2\left( {{\delta ^2}s - \delta s - 1} \right)}}\text{。}\end{split}$ | (4) |
| $\begin{split}&\quad\quad{p_{\rm o}}^{O*} = \displaystyle\frac{{2\left[ {\beta \delta \left( {\delta - 1} \right)s - \frac{1}{2}\left( {\beta + \delta } \right)} \right]cs}}{{\left( {2{\delta ^2} - 2\delta } \right)s - 2}},\\&\quad\quad{\lambda ^{O*}} = \displaystyle\frac{{cs\left( {\beta - \delta } \right)}}{{{\delta ^2}s - \delta s\left[ {1 + \left( {\beta - 1} \right)c} \right] + c - 1}}{\text{。}}\end{split}$ | (5) |
得到原制造商与第三方制造商最优利润为
| $\quad\quad\begin{array}{l} \varPi _O^{O*} \!\!\!=\!\!\! \displaystyle\frac{{\left( \!{\left( {\left(\!\! {2c \!-\! 1} \right)\!{\delta ^2} \!\!+\!\! \left( \!{1 \!+\! \left( {1 \!- \!2\beta } \!\right)\!{c^2} \!\!-\!\! 2c} \right)\delta \!\!+\!\! {c^2}{\beta ^2}} \!\right)\!\!s \!+\! {{\left( \!{c \!-\! \!1} \right)}^2}} \!\right)\!\!s}}{{4\left[\! {1 \!-\! \!\!s\left( \!{{\delta ^2} \!+\! 4}\right)} \!\right]\!}}\!\!,\\\varPi _R^{O*} = \displaystyle\frac{{{c^2}{s^2}{{\left( {\beta - \delta } \right)}^2}}}{{8{{\left[ {\left( {{\delta ^2} - \delta } \right)s - 1} \right]}^2}}}{\text{。}}\end{array}$ | (6) |
新产品与再制品的最优销售价格为
| $\quad\quad\begin{split}& p_{\rm n}^{O*} = \displaystyle\frac{{\left( {c + 1} \right)\left[ {s\left( {{\delta ^2} - \delta } \right) - 1} \right]s}}{{\left( {2{\delta ^2} - 2\delta } \right)s - 2}}, \\&p_{\rm r}^{O*} =\displaystyle\frac{{\left[ {\left( {\delta - 1} \right)\left( {\beta c + \delta } \right)s - c - 1} \right]\delta s}}{{\left( {2{\delta ^2} - 2\delta } \right)s - 2}}{\text{。}}\end{split}$ | (7) |
在授权再制造模型中,原制造商与第三方制造商存在2种关系。一方面,原制造商通过对第三方制造商收取授权费,第三方制造商通过再制造获得收益,二者为合作关系。另一方面,由于原制造商决定了新产品质量也就间接影响了新产品的销售情况,对此二者存在竞争关系。与模型O类似,原制造商为Stackelberg博弈领导者,第三方制造商为追随者。原制造商与第三方制造商的利润函数为
| $\quad\quad\begin{split}&\mathop {\varPi _O^R}\limits_{{Q_{\rm n}},{p_{\rm s}}} = \left( {{p_{\rm n}} - cs} \right){Q_{\rm n}} + {p_{\rm s}}{Q_{\rm r}},\\&\mathop {\varPi _R^R}\limits_\lambda = \left( {{p_{\rm r}} - \beta cs} \right){Q_{\rm r}} - {p_{\rm s}}{Q_{\rm r}} - 1/2{Q_{\rm r}}^2{\text{。}}\end{split}$ | (8) |
原制造商决定新产品质量s、数量
| $\quad\quad\begin{split} &Q_{\rm n}^{R*} =\displaystyle\frac{{{\delta ^2}s - \left[ {2 + \left( {\beta - 2} \right)c} \right]s\delta + c - 1}}{{2\left( {{\delta ^2}s - 2\delta s - 1} \right)}},\\&Q_{\rm{r}}^{R*} = \displaystyle\frac{{cs\left( {\beta - \delta } \right)}}{{2\left( {{\delta ^2}s - 2\delta s - s} \right)}}{\text{。}}\end{split}$ | (9) |
| $\quad\quad\begin{split} &p_{\rm s}^{R*} = 1/2s\left( {\delta - \beta c} \right),\\&{\lambda ^{R*}} = \displaystyle\frac{{cs\left( {\beta - \delta } \right)}}{{{\delta ^2}s - \delta s\left[ {2 + \left( {\beta - 2} \right)c} \right] + c - 1}}{\text{。}}\end{split}$ | (10) |
得到原制造商与第三方制造商的最优利润为
| $\quad\quad\begin{array}{l}\varPi _O^{R*}\!\! \!=\!\!\! \displaystyle\frac{{\left(\! {\left(\! {\left( {2c \!- \!1}\! \right){\delta ^2} \!+ \!\left( \!{1 \!+\! \left(\! {1 \!-\! 2\beta } \!\right)\!{c^2} \!\!-\!\! 2c}\! \right)\!\delta \!+\! {c^2}{\beta ^2}} \!\right)\!s \!\!+\! {{\left(\! {c \!-\! 1} \!\right)}\!^2}} \!\right)\!s}}{{4s\left( {1 - {\delta ^2} + \delta } \right)}}\!\!,\\\varPi _R^{R*} = \displaystyle\frac{{{s^2}{{\left( {\beta - \delta } \right)}^2}{c^2}\left( {2\delta s + 1} \right)}}{{8{{\left[ {\left( {{\delta ^2} - 2\delta } \right)s - 1} \right]}^2}}}{\text{。}}\end{array}$ | (11) |
模型R中新产品与再制品的销售价格为
| $\quad\quad\begin{array}{l} p_{\rm n}^{R*} = \displaystyle\frac{{\left( {c + 1} \right)\left[ {s\left( {{\delta ^2} - 2\delta } \right) - 1} \right]s}}{{2\left( {{\delta ^2} - 2\delta } \right)s - 1}}, \\p_{\rm r}^{R*} =\displaystyle\frac{{\left( {\left( {{\delta ^2} + ((\beta - 1)c - 2)\delta - \beta c} \right)s - c - 1} \right)\delta s}}{{2\left( {{\delta ^2} - 2\delta } \right)s - 2}}\text{。}\end{array}$ | (12) |
本节首先基于命题1与命题2针对2个模型求解的均衡结果与利润函数进行比较,并对2个模型的消费者剩余与社会福利进行比较分析,最后讨论考虑新产品质量情况下的环境影响。
3.1 均衡结果与利润函数比较命题1 模型O与模型R回收率满足当
证明
| $ \begin{array}{l}\quad\quad{\lambda ^{O*}} \!-\! {\lambda ^{R*}} = \\\displaystyle\frac{{c{s^2}\left( {\beta \!-\! \delta } \right)\delta \left( {c \!-\! 1} \right)}}{{\left( {\left( {1 \!+\! \left( {\beta \!-\! 1} \right)c} \right)s\delta \!-\! {\delta ^2}s - c \!+\! 1} \right)\left( {\left({2 \!+\! \left( {\beta \!-\! 2} \right)c} \right)s\delta -{\delta ^2}s \!-\! c \!+\! 1} \right)}}{\text{。}}\end{array}$ | (13) |
通过简单的计算可得,
命题1表明当回收再制品的规模
命题2 考虑新产品质量影响下2个模型的利润函数满足
1) 当
2) 当
证明 首先比较模型O与模型R的原制造商最优利润函数。
| $\quad\quad\varPi _O^{O*} - \varPi _O^{R*} = \displaystyle\frac{{{s^3}{c^2}\delta {{\left( {\beta - \delta } \right)}^2}}}{{4\left( {{\delta ^2}s - \delta s - 1} \right)\left( {{\delta ^2}s - 2\delta s - 1} \right)}} > 0,$ | (14) |
| $\varPi _{\rm{R}}^{O*} - \varPi _{\rm{R}}^{R*}{\rm{ = }}\frac{{{c^2}\left[ {2{\delta ^2}s - {\delta ^3}s - \delta \left( {s - 1} \right) - \displaystyle\frac{1}{2}} \right]{s^4}{{\left( {\beta - \delta } \right)}^2}{\delta ^2}}}{{4{{\left( {{\delta ^2}s - \delta s - 1} \right)}^2}{{\left( {{\delta ^2}s - 2\delta s - 1} \right)}^2}}}\text{。}$ | (15) |
解关于s的方程

|
图 1 |
命题2表明再制品的潜在利润与消费者对于再制品的接受情况有关,即与再制品价值折扣
1) 当
2) 当
命题3 考虑新产品质量影响下,原制造商进行外包再制造情况下的供应链效率要高于授权再制造模式。
证明 原制造商外包再制造模型中供应链总利润为
| $\begin{split}&\quad\quad {\varPi ^{sO}} - {\varPi ^{sR}} = \\&- \displaystyle\frac{{{s^3}{{\left( {\beta - \delta } \right)}^2}\delta {c^2}\left[ {{\delta ^3}{s^2} - 1 + \left( {s - {s^2}} \right){\delta ^2} - \displaystyle\frac{5}{2}\delta s} \right]}}{{4{{\left( {{\delta ^2}s - \delta s - 1} \right)}^2}{{\left( {{\delta ^2}s - 2\delta s - 1} \right)}^2}}}>0{\text{。}}\end{split}$ | (16) |
在这个部分,针对模型O与模型R的消费者剩余(CS)与社会福利(SW)进行比较,消费者剩余函数与社会福利函数为
| $\begin{array}{l}\quad\quad {\rm{CS}} = \displaystyle\int_{1 - {Q_{\rm n}} - {Q_{\rm r}}}^{1 - {Q_{\rm n}}} {\left( {\delta \phi s - {p_{\rm r}}} \right)} {\rm{d}}\phi + \displaystyle\int_{1 - {Q_{\rm n}}}^1 {\left( {\phi s - {p_{\rm n}}} \right)} {\rm{d}}\phi \to\\ CS = 1/2s\left[ {\left( {2{Q_{\rm n}}{Q_{\rm r}} + {Q_{\rm r}}^2} \right)\delta + {Q_{\rm n}}^2} \right],\end{array}$ | (17) |
| $\;\;\quad\quad {\rm{SW}} = {\varPi _O} + {\varPi _R} + {\rm{CS}}{\text{。}}$ | (18) |
由此得到模型O的最优消费者剩余与最优社会福利为
| $\quad\quad\quad\quad\quad\quad{\rm{C}}{{\rm{S}}^{O*}} = \frac{{\left( {\left( {\left( {2c - 1} \right){\delta ^2} + \left( {1 + \left( {1 - 2\beta } \right){c^2} - 2c} \right)\delta + {c^2}{\beta ^2}} \right)\left( {1 - \delta } \right)\delta {s^2} - {{\left( {c - 1} \right)}^2}\left( {2\delta \left( {\delta - 1} \right)s - 1} \right)} \right)s}}{{8{{\left( {s\left( {{\delta ^2} - \delta } \right) - 1} \right)}^2}}},$ | (19) |
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad{\rm{S}}{{\rm{W}}^{O*}} = \frac{{3\left( {\left( {\left( {2c - 1} \right){\delta ^2} + \left( {1 + \left( {1 - 2\beta } \right){c^2} - 2c} \right)\delta + {c^2}{\beta ^2}} \right)s + {{\left( {c - 1} \right)}^2}} \right)}}{{8\left( {1 - {\delta ^2} + \delta } \right)}}{\text{。}}$ | (20) |
模型R的最优消费者剩余与最优社会福利为
| ${\rm{C}}{{\rm{S}}^{R*}} = \frac{{\left( {{{\left( {c - 1} \right)}^2} - \left( {\left( {2c - 1} \right){\delta ^3} + \left( {4 + \left( {3 - 2\beta } \right){c^2} - 8c} \right){\delta ^2} + \left( {\left( {{\beta ^2} + 2\beta - 4} \right){c^2} + 8c - 4} \right)\delta - {c^2}{\beta ^2}} \right)\delta {s^2} - 2\delta {{\left( {c - 1} \right)}^2}\left( {\delta - 2} \right)s} \right)s}}{{8{{\left[ {\left( {{\delta ^2} - 2\delta } \right)s - 1} \right]}^2}}},$ | (21) |
| $ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad{\rm{S}}{{\rm{W}}^{R*}} = - \frac{3}{{8{{\left[ {\left( {{\delta ^2} - 2\delta } \right)s - 1} \right]}^2}}}\left( {{H_1} + {H_2} + {H_3}} \right),$ | (22) |
其中,
| $\quad\quad {\begin{split}&{{H_1} = \delta {s^3}\left( {\left( {2c - 1} \right){\delta ^3} + \left( {4 + \left( {\displaystyle\frac{5}{3} - 2\beta } \right){c^2} - 8c} \right){\delta ^2} + \left( {\left( {{\beta ^2} + \displaystyle\frac{{14}}{3}\beta - 4} \right){c^2} - 4 + 8c} \right)\delta - \displaystyle\frac{7}{3}{c^2}{\beta ^2}} \right)} ,\\& {{H_2} = {s^2}\left( {\left( {{c^2} - 4c + 2} \right){\delta ^2} + \left( {\left( {2\beta - 4} \right){c^2} + 8c - 4} \right)\delta - {c^2}{\beta ^2}} \right)}, \\& {{H_3} = - s{{\left( {c - 1} \right)}^2}} {\text{。}}\end{split}} $ | (23) |
命题4 考虑新产品质量s时,消费者剩余与社会福利在模型O与模型R中满足以下关系:
证明 首先比较模型O与模型R的CS与SW。
| $\begin{split}&\quad\quad{\rm{C}}{{\rm{S}}^{O*}} - {\rm{C}}{{\rm{S}}^{R*}} =\\&\displaystyle\frac{{{{\left( {\beta - \delta } \right)}^2}{c^2}\left( {{\delta ^2}s - \displaystyle\frac{3}{2}s\delta - 1} \right)\left( {\delta - 1} \right){s^4}{\delta ^2}}}{{{{\left( {{\delta ^2}s - \delta s - 1} \right)}^2}{{\left( {{\delta ^2}s - 2\delta s - 1} \right)}^2}}} > 0, \end{split}$ | (24) |
| $\begin{split}&\quad\quad {\rm{S}}{{\rm{W}}^{O*}} - {\rm{S}}{{\rm{W}}^{R*}} = \\&\displaystyle\frac{{\left( {2{\delta ^2}s - 5\delta s - 2} \right){{\left( {\beta - \delta } \right)}^2}{c^2}{s^3}\delta }}{{8\left( {{\delta ^2}s - \delta s - 1} \right){{\left( {{\delta ^2}s - 2\delta s - 1} \right)}^2}}} > 0{\text{。}} \end{split}$ | (25) |
命题4表明随着质量水平s的提高,模型O中的消费者剩余与社会福利均高于模型R。对于政策制定者与企业来说由原制造商采取外包再制造模式进行回收再制造可以为社会带来更多效益。
3.3 环境影响比较根据Raz等[21]的研究,将环境影响分为制造阶段与使用阶段,
命题5 当
证明 根据假设,环境影响函数为
| $\quad\quad E = {Q_{\rm n}}\left( {e_{\rm n}^{\rm m} + e_{\rm n}^{\rm u}} \right) + {Q_{\rm r}}\left( {e_{\rm r}^{\rm m} + e_{\rm r}^{\rm u}} \right){\text{。}}$ | (26) |
将式(4)代入式(26)与将式(9)代入式(26)分别得到模型O与模型R的最优环境影响函数。比较2种模式选择下产生的环境影响为
| $\quad\quad{E^{O*}} - {E^{R*}} = \frac{{\left[ {\delta \left( {e_{\rm n}^{\rm m} + e_{\rm n}^{\rm u}} \right) - e_{\rm r}^{\rm m} - e_{\rm r}^{\rm u}} \right]{s^2}\left( {\beta - \delta } \right)\delta c}}{{2\left( {{\delta ^2}s - \delta s - 1} \right)\left( {{\delta ^2}s - 2\delta s - 1} \right)}}{\text{。}}$ | (27) |
当
命题5表明环境影响不仅与再制品的数量相关,同时与新产品的数量有关。当消费者对于再制品的价值折扣
命题6 1) 随着再制品价值折扣系数
考虑新产品质量水平s时增加一个质量成本,表示为
由图2可以看出,当再制品价值折扣系数

|
图 2 不同再制造模式下的
|

|
图 3 不同再制造模式下的
|
在图3中可以看出,2种模式中的新产品质量s随着规模系数
2) 当考虑新产品质量成本
设参数
可以看出,当考虑新产品质量成本
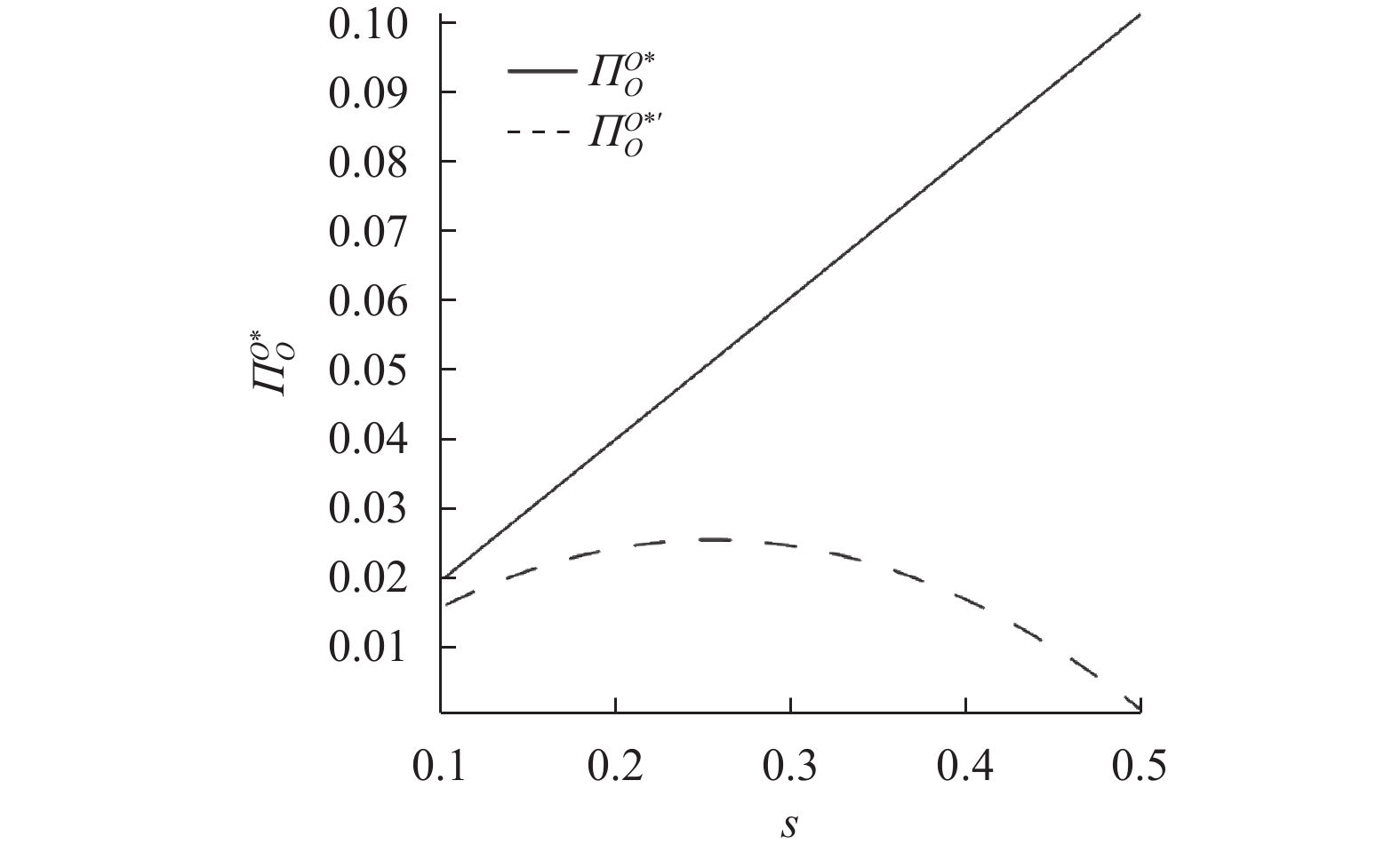
|
图 4 模型O考虑新产品质量成本OEM利润变化 Fig. 4 The change of OEM profits in model O |
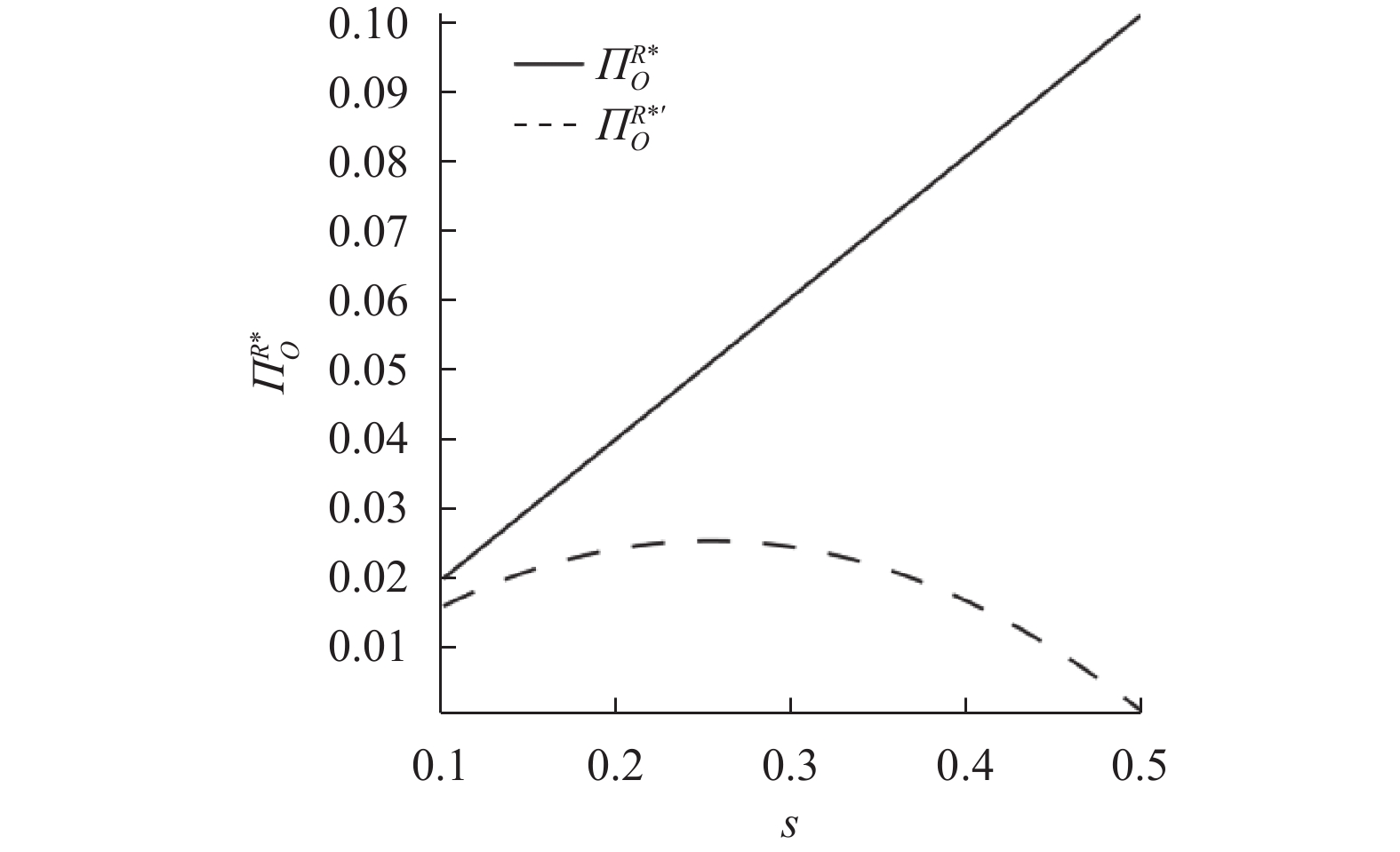
|
图 5 模型R考虑新产品质量成本OEM利润变化 Fig. 5 The change of OEM profits in model R |
下面通过数值算例来验证以上模型的结果。有关参数为
|
表 1 |
|
表 2 |
由表1、表2容易验证命题1~命题4成立。从表1可以看出,在
从表2还可以看到,原制造商的利润在外包再制造模式中总是大于授权再制造模式,而第三方制造商的利润与回收规模与再制品价值折扣有关。外包再制造模式的供应链总利润与消费者剩余、社会福利也总是大于授权再制造的供应链总利润。
图6、图7比较了外包再制造模式与授权再制造模式的环境影响。

|
图 6 |
在图6中,当再制品的制造阶段的环境友好程度比新产品更加友好,同时消费者对于再制品的接受程度较低时,可以看出外包再制造模式(模型O)要比授权再制造模式(模型R)对环境更加友好。但是当再制品的制造阶段不及新产品的环境友好程度时,同时消费者对于再制品的接受程度较高时,选择授权再制造模式(模型R)对环境更加友好。
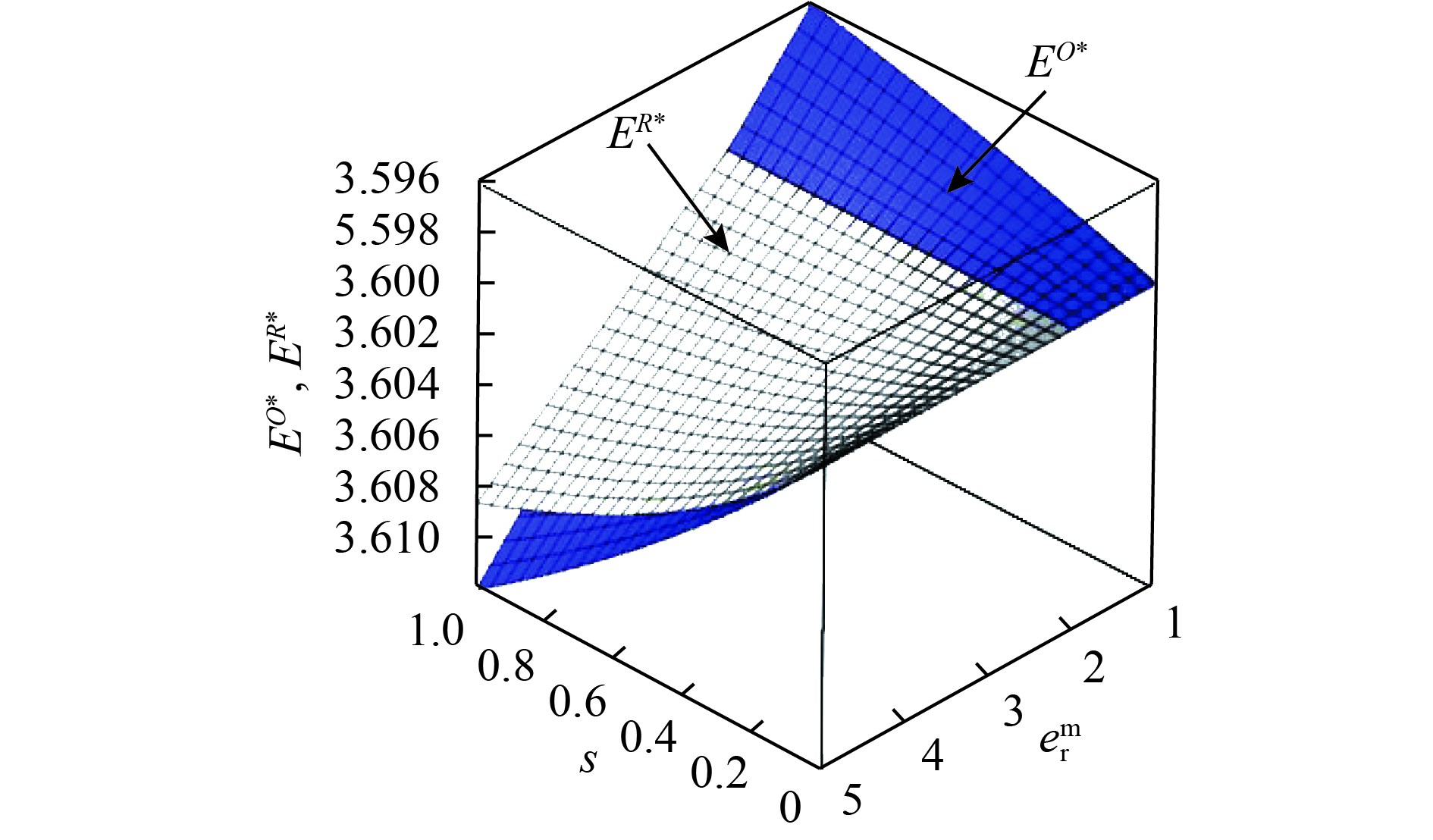
|
图 7 |
图7有关参数为
本文研究了新产品质量对于原制造商再制造模式选择的影响,针对原制造商对于废旧产品回收的2种途径建立了外包再制造模型(模型O)与授权再制造模型(模型R),通过逆推归纳法得出了2种模型中均衡结果。分析了回收再制品规模与再制品价值折扣以及新产品质量对企业再制造模式选择策略的影响。并从消费者剩余、社会福利与环境影响3个方面进行了对比分析。结果表明:1) 当回收再制品的规模大于再制品价值折扣时,采用外包再制造模式的再制品回收率要小于授权再制造模式,反之则结果不同。2) 原制造商选择外包再制造模式的利润大于授权再制造模式,而当再制品价值折扣很低时,第三方制造商从授权再制造模式中会获得比外包再制造模式更大的利润。3) 外包再制造模式下总供应链利润、消费者剩余与社会福利均优于授权再制造模式。4) 在考虑新产品质量成本的条件时,随着再制品价值折扣系数与规模系数的增大,两种模式中的新产品质量水平先降低后增加,而原制造商利润先增加后减小。5) 当再制品价值折扣系数与再制品回收规模满足一定条件,而且新产品质量较高时,原制造商采取外包模式产生的环境影响要小于授权制造模式。最后通过算例分析,验证了相关结论。由本文研究结论可以对制造企业再制造模式选择带来一定的启示,原制造商通过控制新产品质量水平选择外包再制造模式可以获得更高的利润与社会影响,而第三方制造商在消费者对于再制品价值评估较低时,应该选择授权再制造模式提高收益。
本文进一步的研究可以考虑:1)两阶段决策情况下对再制造模式选择策略的影响,即原制造商在第1阶段只进行新产品的制造与销售,在第2阶段,原制造商与第三方制造商生产新产品与再制品。2)进一步讨论由零售商或者第三方同时进行再制造的模式选择策略。
| [1] |
CHEN J M,. The co-operative strategy of a closed-loop supply chain with remanufacturing[J].
Transportation Research Part E, 2012, 48(2): 387-400.
DOI: 10.1016/j.tre.2011.10.001. |
| [2] |
聂佳佳, 邓东方. 再制造产品质量对闭环供应链回收渠道的影响[J].
工业工程与管理, 2014, 19(1): 1-7.
NIE Jiajia, DENG Dongfang. Effect of remanufacturing product quality on recovery channel in closed-l oop supply chain[J]. Industrial Engineering and Management, 2014, 19(1): 1-7. DOI: 10.3969/j.issn.1007-5429.2014.01.001. |
| [3] |
SAVASKAN R C, BHATTACHARYA S, WASSENHOVE L N. Closed-loop supply chain models with product remanufacturing[J].
Management Science, 2004, 50(2): 239-252.
DOI: 10.1287/mnsc.1030.0186. |
| [4] |
SAVASKAN R C, WASSENHOVE L N. Reverse channel desi- gn: the case of competing retailers[J].
Management Science, 2006, 52(1): 1-14.
DOI: 10.1287/mnsc.1050.0454. |
| [5] |
熊中楷, 申成然, 彭志强. 专利保护下再制造闭环供应链协调机制研究[J].
管理科学学报, 2011, 14(6): 76-85.
XIONG Zhongkai, SHEN Chengran, PENG Zhiqiang. Closed loop supply chain coordination research with remanufacturing under patent protection[J]. Journal of Management Sciences in China, 2011, 14(6): 76-85. |
| [6] |
FERRER G, SWAMINATHAN J M. Managing new and remanufactured Products[J].
Management Science, 2006, 52(1): 15-26.
DOI: 10.1287/mnsc.1050.0465. |
| [7] |
MAJUMDER P, GROENEVELT H. Competition in remanufacturing[J].
Production and Operations Management, 2001, 10(2): 125-141.
|
| [8] |
黄宗盛, 聂佳佳, 胡培. 专利保护下的闭环供应链再制造模式选择策略[J].
工业工程与管理, 2012, 17(6): 15-21.
HUANG Zongsheng, NIE Jiajia, HU Pei. Research on the remanufacturing models of closed-loop supply chain under patent licensing[J]. Industrial Engineering and Management, 2012, 17(6): 15-21. DOI: 10.3969/j.issn.1007-5429.2012.06.003. |
| [9] |
MITRA S, WEBSTER S. Competition in remanufacturing and the effects of government subsidies[J].
International Journal of Production Economics, 2008, 111(2): 287-298.
DOI: 10.1016/j.ijpe.2007.02.042. |
| [10] |
黄祖庆, 达庆利. 直线型再制造供应链决策结构的效率分析[J].
管理科学学报, 2006, 9(4): 51-57.
HUANG Zuqing, DA Qingli. Study on efficiency of serial supply chains with remanufacture[J]. Journal of Management Sciences in China, 2006, 9(4): 51-57. DOI: 10.3321/j.issn:1007-9807.2006.04.007. |
| [11] |
ZOU Z B, WANG J J, DENG G S, et al. Third-party remanufacturing mode selection: outsourcing or authorization?[J].
Transportation Research Part E, 2016, 87(3): 1-19.
|
| [12] |
POKHAREL S, LIANG Y J. A model to evaluate acquisition price and quantity of used products for remanufacturing[J].
International Journal of Production Economics, 2012, 138(1): 170-176.
DOI: 10.1016/j.ijpe.2012.03.019. |
| [13] |
谢家平, 迟琳娜, 梁玲. 基于产品质量内生的制造/再制造最优生产决策[J].
管理科学学报, 2012, 15(8): 12-23.
XIE Jiaping, CHI Linna, LIANG Ling. Optimal manufacturing/remanufacturing production decision based on endogenous pro- duct quality[J]. Journal of Management Sciences in China, 2012, 15(8): 12-23. DOI: 10.3969/j.issn.1007-9807.2012.08.002. |
| [14] |
许民利, 张璇, 简惠云. 考虑品牌优势和成本差异的再制造决策[J].
管理学报, 2016, 13(8): 1241-1249.
XU Minli, ZHANG Xuan, JIAN Huiyun. Remanufacturing decision based on brand advantages and cost difference[J]. Chinese Journal of Management, 2016, 13(8): 1241-1249. DOI: 10.3969/j.issn.1672-884x.2016.08.015. |
| [15] |
刘家国, 周学龙, 赵金楼. 基于产品质量差异的闭环供应链定价策略与协调研究[J].
中国管理科学, 2013, 21(S2): 426-431.
LIU Jiaguo, ZHOU Xuelong, ZHAO jinlou. Study on price decision and coordination of closed-loop supply chain based on quality difference of product[J]. Chinese Journal of Management Science, 2013, 21(S2): 426-431. |
| [16] |
曹俊, 熊中楷, 刘莉莎. 闭环供应链中新件制造商和再制造商的价格及质量水平竞争[J].
中国管理科学, 2010, 18(5): 82-90.
CAO jun, XIONG Zhongkai, LIU Lisha. Price and quality competition between the new and remanufactured producer in the closed-loop supply chain[J]. Chinese Journal of Management Science, 2010, 18(5): 82-90. |
| [17] | |
| [18] |
熊中楷, 曹俊, 刘克俊. 基于动态博弈的闭环供应链回收质量控制研究[J].
中国管理科学, 2007, 15(4): 42-50.
XIONG Zhongkai, CAO Jun, LIU Kejun. Study on the quality control policy in the closed loop supply chain based on the dynamic game theory[J]. Chinese Journal of Management Science, 2007, 15(4): 42-50. DOI: 10.3321/j.issn:1003-207x.2007.04.007. |
| [19] |
GALBRETH M R, BLACKBURN J D. Optimal acquisition and sorting policies for remanufacturing[J].
Production and Operation Management, 2006, 15(3): 384-392.
|
| [20] |
FERGUSON M, GUIDE V D, KOCA E, et al. The value of quality grading in remanufacturing[J].
Production and Operation Management, 2009, 18(3): 300-314.
DOI: 10.1111/poms.2009.18.issue-3. |
| [21] |
RAZ G, DRUEHL C T, BLASS V. Design for the environment: life-cycle approach using a newsvendor model[J].
Production & Operations Management, 2013, 22(4): 940-957.
|
 2018, Vol. 21
2018, Vol. 21