2. 交通运输学院,重庆 400074
2. School of Traffic and Transportation, Chongqing Jiaotong University, Chongqing 400074, China
自航空管制放松以来,作为收益管理重要技术的动态定价已广泛应用于航空公司机票销售实践[1]。但是动态定价意味着不同时间机票价格不同,使得乘客在各个时期购买产品的效用有差异,导致策略乘客选择购买时机最大化自身效用成为了可能。特别是在“互联网+”背景下,乘客获得机票价格信息渠道越来越丰富,更增加了其策略行为。近几年的收益管理研究表明,策略乘客选择购买时机的行为减少了航空公司的期望收益。如Ovchinnikov和Milner[2]、Levin和McGil[3]等发现,如果航空公司在决策过程中不考虑乘客的策略行为,会造成20%~35%的收益损失。面对策略乘客行为,航空公司需要合理的定价并提出易于操作的销售机制,才能保障在激烈的市场竞争中立于不败之地。
收益管理中关于消费者策略行为的研究已成为研究热点。本文的内容涉及消费者策略行为下的动态定价及应对机制有效性分析两个方面。第一方面的文献主要以价格为变量,探究在消费者策略行为下零售商定价策略的变化。Anderson和Wilson[4]通过建立航空公司销售期末开放舱位的收益管理模型,分析了等待至最后时刻和购买低价舱位两类乘客对航空公司收益的影响,指出在航空公司管理决策过程中应重点关注这两类购买行为。Levin和McGil[5]用效用折现因子来刻画消费者的策略等待行为,通过建立多周期随机动态规划模型,分析了零售商的动态定价策略。Papanastasiou和Savva[6]在策略消费者等待行为下考虑了需求不确定环境,建立了零售商需求学习下的贝叶斯均衡模型,研究表明虽然需求学习下零售商的定价小于需求确定情况,但能提升收益水平。第二方面的文献主要通过引入新的销售机制,比较该机制与传统销售模式下的收益来验证缓解消费者策略行为的效果。Liu和Zhang[7]建立了具有服务质量差异的两零售商多周期竞争定价模型,并分析价格承诺机制对零售商均衡价格的影响以及对均衡收益的提升作用。Prasad等[8]在航空公司机票销售实践中引入机票绑定和预留机票定价机制来缓解策略行为的影响,研究表明在需求或策略程度较小时,预留机票机制下的收益大于机票绑定。Yan和Ke[9]提出了零售商销售的PM和DPM两种策略,分析了2种策略下零售商在正常销售季和打折销售季的价格,并讨论了基于供应水平和策略程度下两种机制的适用范围。
目前在机票销售实践中出现一种新的销售机制:中介商销售。比如国内外著名网站hotwire.com、onetravel.com、携程、去哪儿网等虽然不是机票的直接提供者,但将机票销售作为其经营业务的一部分。作为季末清仓机制,航空公司通过把部分季末剩余机票交由中介商销售,获得中介商销售的收益分配,而中介商通过销售机票获得额外收益提成。关于中介商销售机制下的定价和收益管理策略,国内外文献主要集中在零售商和中介商的定价与收益分配问题,没有探讨该机制的有效性。杨道箭等[10]在零售商与中介商组成的销售供应链中考虑了顾客策略行为与风险偏好,分析该机制下的最优收益分享契约。官振中和李伟[11]分析了投机商和策略消费者的行为,得出了在两者的共同作用下零售商的定价策略,并分析了策略型消费者所占比例、消费者保留价格变动系数等因素对产品价格和零售商定价和收益产生的影响。有文献讨论了中介商销售机制的有效性。Su[12]在市场上有中介商(投机商)的情况下研究了销售固定数量产品零售商的均衡定价及收益。研究表明,中介商的存在增加了零售商的收益,其实质是用中介销售替代零售商动态定价行为。Jerath等[13]讨论了航空公司机票销售实践中模糊中介商销售机制缓解乘客策略行为的效果,指出当乘客的偏好较低时,模糊销售机制具有有效性,但文章没有考虑乘客等待的效用损失。周杰和李豪[14]从航空公司和模糊销售中介的视角分析了该机制缓解乘客策略行为的效果,得出了当乘客的策略程度位于某一范围时,模糊销售可以缓解乘客的策略行为,具有实施的可行性。但文章假定乘客对机票的估价固定,缺乏一定的实践性。
基于此,本文在上述研究的基础上,通过假定乘客的估价服从均匀分布,建立了两周期定价博弈模型,分析了中介商销售机制下航空公司和中介商的均衡定价策略,从航空公司和中介销售商的角度探讨了该机制的有效性,对航空公司面对策略乘客时实施有效的销售策略、提高收益具有一定的借鉴意义。
1 问题描述及符号假设考虑航空公司和中介商同时存在的机票销售市场。销售分为2周期。在周期1,市场上只有航空公司销售机票;在周期2,航空公司和中介商分别定价、共同存在,形成双渠道机票销售市场。航空公司与中介商通过制定销售价格实现收益最大化。
为了刻画乘客的策略选择行为,假定所有乘客均在销售期初到达市场。乘客购买机票的效用由航空公司机票价格和对机票的估价组成。其中,估价为乘客的私人信息,对航空公司来说,认为估价服从
以上标A表示航空公司,S表示销售中介,以下标
综上所述,航空公司、中介商和乘客的决策过程如图1所示。

|
图 1 航空公司、中介商和乘客的决策 Fig. 1 Decisions for airlines, intermediaries, and passengers |
因为乘客购买机票的效用随估价的增加而增加,因此在任何周期如果估价为
1) 乘客只在中介商购买。
在此情况下,乘客在中介购买的效用大于在航空公司购买的效用,即
| $\quad\quad p_2^ {\rm{A}} {\text{≥}} (1 - \theta ){V_2} + p_2^ {\rm{S}}{\text{。}}$ | (1) |
在
在
| $\quad\quad {V_2}^{\prime \prime } = \frac{{p_2^ {\rm{S}}}}{\theta }{\text{。}}$ | (2) |
因此中介商销售机票获得的总收益为
| $\quad\quad R_2^ {\rm{A}} = \beta p_2^ {\rm{S}}\left({V_2} - \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta }\right),$ |
| $\quad\quad {R^ {\rm{S}}} = (1 - \beta )p_2^ {\rm{S}}\left({V_2} - \frac{{p_2^ {\rm{S}}}}{\theta }\right){\text{。}}$ |
2) 所有乘客均在航空公司购买。
要满足在航空公司购买,需要保证
| $\quad\quad R_2^ {\rm{A}} = p_2^ {\rm{A}}({V_2} - p_2^ {\rm{A}}),$ |
| $\quad\quad {R^ {\rm{S}}} = 0{\text{。}}$ |
3) 乘客在航空公司和中介之间选择购买。
此时在
| $\quad\quad {R^ {\rm{S}}} = (1 - \beta )p_2^ {\rm{S}}\left(\frac{{p_2^ {\rm{A}} - p_2^ {\rm{S}}}}{{1 - \theta }} - \frac{{p_2^ {\rm{S}}}}{\theta }\right),$ |
| $\quad\quad R_2^ {\rm{A}} = \beta {p^ {\rm{S}}}\left(\frac{{p_2^ {\rm{A}} - p_2^ {\rm{S}}}}{{1 - \theta }} - \frac{{p_2^ {\rm{S}}}}{\theta }\right) + p_2^ {\rm{A}}\left({V_2} - \frac{{p_2^ {\rm{A}} - p_2^ {\rm{S}}}}{{1 - \theta }}\right){\text{。}}$ |
综合上述分析可知在周期2,航空公司和中介商的收益如式(3)和式(4)所示。
| $R_2^ {\rm{A}} = \left\{ {\begin{array}{*{20}{l}} \beta \left[p_2^ {\rm{S}}\left({V_2} - \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta }\right)\right],\quad p_2^ {\rm{A}} {\text{≥}} p_2^ {\rm{S}} + (1 - \theta ){V_2}; \\ p_2^ {\rm{A}}\left({V_2} - \displaystyle\frac{{p_2^ {\rm{A}} - p_2^ {\rm{S}}}}{{1 - \theta }}\right) + \beta p_2^ {\rm{S}}\left(\displaystyle\frac{{p_2^ {\rm{A}} - p_2^ {\rm{S}}}}{{1 - \theta }} - \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta }\right),\\\quad\quad \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta } {\text{<}} p_2^ {\rm{A}} {\text{<}} p_2^ {\rm{S}} + (1 - \theta ){V_2} ;\\ p_2^ {\rm{A}}({V_2} - p_2^ {\rm{A}}),\quad p_2^ {\rm{A}} {\text{<}} \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta } {\text{。}}\\ \end{array}} \right.$ | (3) |
| ${R^ {\rm{S}}} = \left\{\!\! {\begin{array}{*{20}{l}} (1 - \beta )p_2^ {\rm{S}}\left({V_2} - \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta }\right),\quad p_2^ {\rm{A}} {\text{≥}} p_2^ {\rm{S}} + (1 - \theta ){V_2}; \\ (1 - \beta )p_2^ {\rm{S}}\left(\displaystyle\frac{{p_2^ {\rm{A}} - p_2^ {\rm{S}}}}{{1 - \theta }} - \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta }\right),\\ \quad\quad\displaystyle\frac{{p_2^ {\rm{S}}}}{\theta } {\text{<}} p_2^ {\rm{A}} {\text{<}} p_2^ {\rm{S}} + (1 - \theta ){V_2} ;\\ 0,\quad p_2^ {\rm{A}} {\text{<}} \displaystyle\frac{{p_2^ {\rm{S}}}}{\theta }{\text{。}} \\ \end{array}} \right.$ | (4) |
由式(3)和式(4)直接可得周期2航空公司和中介商的市场均衡,如定理1所示。
定理1 周期2航空公司和中介商销售的均衡价格为
| $\quad\quad p_2^{{\rm{A}}*} = \frac{{\xi (1 - \theta ) + \lambda }}{{2\xi }}{V_2},\quad p_2^{{\rm{S}}*} = \frac{{\theta (1 - \theta )}}{\xi }{V_2}{\text{。}}$ |
均衡收益为
| $\quad\quad R_2^ {\rm{A}*} = \left[\frac{{\xi (1 - \theta ) + \lambda }}{{2\xi }} \cdot \frac{{2 - \theta \beta }}{\xi } + \frac{{\beta \theta (1 - \theta )}}{{{\xi ^2}}}\right]V_2^2,$ | (5) |
| $\quad\quad R_{}^{{\rm{S}}*} = (1 - \beta )\frac{{\theta (1 - \theta )}}{{{\xi ^2}}}V_2^2{\text{。}}$ | (6) |
其中,
证明 当
当
| $\quad\quad R_2^ {\rm{A}*} = \frac{{\beta \theta }}{4}V_2^2,$ | (7) |
| $\quad\quad R_2^{{\rm{S}}*} = \frac{{(1 - \beta )\theta }}{4}V_2^2{\text{。}}$ | (8) |
当
| $\quad\quad p_2^{{\rm{S}}*} = \frac{{\theta (1 - \theta )}}{\xi }{V_2},$ |
| $\quad\quad p_2^{{\rm{A}}*} = \frac{{\xi (1 - \theta ) + \lambda }}{{2\xi }}{V_2},$ |
| $\quad\quad R_2^ {\rm{A}*} = \left[\frac{{\xi (1 - \theta ) + \lambda }}{{2\xi }} \cdot \frac{{2 - \theta \beta }}{\xi }) + \frac{{\beta \theta (1 - \theta )}}{{{\xi ^2}}}\right]V_2^2,$ |
| $\quad\quad R_2^{{\rm{S}}*} = (1 - \beta )\frac{{\theta (1 - \theta )}}{{{\xi ^2}}}V_2^2{\text{。}}$ |
由式(5)和式(7)可得
| $\begin{array}{l}\quad\quad\left[\displaystyle\frac{{\xi (1 - \theta ) + \lambda }}{{2\xi }} \cdot \displaystyle\frac{{2 - \theta \beta }}{\xi }) + \displaystyle\frac{{\beta \theta (1 - \theta )}}{{{\xi ^2}}} - \displaystyle\frac{{\beta \theta }}{4}\right]V_2^2 = \\\left[\displaystyle\frac{{4(1 - \theta ) \!+\! \theta \beta \cdot (6 - 3\beta - \theta \beta )}}{{4\xi }} \!+\!\! \right. \left. \displaystyle\frac{{\lambda (2 - \theta \beta ) \!+\! 2\theta \beta (1 - \theta )}}{{2{\xi ^2}}}\right]V_2^2\!{\text{≥}}\!0{\text{。}}\end{array}$ |
因此,在
下面证明在
证毕。
定理1表明,在中介商销售机制下周期2的市场均衡为航空公司与中介商共同销售,不存在任何一方独占市场的情况。
2.2 周期1均衡分析基于收益最大化考虑,航空公司在周期1的定价应满足
| $\quad\quad {V_2} = \frac{{p_1^ {\rm{A}} \cdot 2\xi }}{{(1 - \gamma ) \cdot 2\xi + \gamma ((1 - \theta )\xi + \lambda )}}{\text{。}}$ | (9) |
通过销售,在周期1航空公司的收益为
令
化简可得
| $\quad\quad p_1^{{\rm{A}}*} = \frac{{(1 - \gamma ) \cdot 2\xi + \gamma ((1 - \theta )\xi + \lambda )}}{{4\xi }}V{\text{。}}$ | (10) |
将式(10)代入式(9)求得
| $\quad\quad {V_2} = \frac{1}{2}V{\text{。}}$ | (11) |
因此,周期1航空公司的收益为
| $\quad\quad R_1^{{\rm{A}}*} = \frac{{(1 - \gamma ) \cdot 2\xi + \gamma ((1 - \theta )\xi + \lambda )}}{{8\xi }}{V^2}{\text{。}}$ |
综合两周期的收益,并将式(11)代入式(5)和式(6)可得,在整个销售期航空公司和中介商的收益分别为
| $\begin{split}&\quad\quad {R^{{\rm{A}}*}} = R_1^{{\rm{A}}*} + R_2^{{\rm{A}}*} = {V^2} \cdot \left[ {\displaystyle\frac{{\xi (1 - \theta ) + \lambda }}{{8\xi }} \cdot \displaystyle\frac{{2 - \theta \beta }}{\xi } + } \right.\\&\left. {\displaystyle\frac{{\beta \theta (1 - \theta )}}{{4{\xi ^2}}} + \displaystyle\frac{{(1 - \gamma ) \cdot 2\xi + \gamma ((1 - \theta )\xi + \lambda )}}{{8\xi }}} \right],\end{split}$ | (12) |
| $\quad\quad {R^{{\rm{S}}*}} = (1 - \beta )\frac{{\theta (1 - \theta )}}{{4{\xi ^2}}}{V^2}{\text{。}}$ | (13) |
推论1 在中介商销售机制下,乘客策略程度越大,航空公司的收益越低。
证明 由式(12)可知
| $\quad\quad \frac{{\partial {R^{{\rm{A}}*}}}}{{\partial \gamma }} = \left[\frac{{ - 4 - 2\theta (1 - \beta )}}{{8\xi }}\right]{V^2} {\text{<}} 0{\text{。}}$ |
证毕。
推论1表明在中介商销售机制下,乘客的策略等待行为导致航空公司的收益降低,且策略程度越大,航空公司的收益越低。这与Su[17]、Cachon等[18]在无中介商销售下的结论相同。
3 中介商销售机制的有效性分析本节讨论航空公司传统直销模式下的收益,并与中介商销售机制下的收益相比较。重点讨论中介商销售机制的有效性。
3.1 航空公司直销模式下的收益分析定义上标“-”为航空公司直销模式下的决策变量。为了保持策略乘客等待行为的有效性,仍假定销售为两周期。按照前述思路分析,可得在周期2在
周期1在
| $\quad\quad{\bar V_2} = \frac{{2\bar p_1^ {\rm{A}}}}{{2 - \gamma}}{\text{。}}$ |
由上式得周期1航空公司的收益为
| $\quad\;\;\begin{array}{l}\bar R_1^{\rm{A}} = \bar p_1^{\rm{A}}(V - {{\bar V}_2}) = \bar p_1^{\rm{A}}\left( {V - \displaystyle\frac{{2\bar p_1^{\rm{A}}}}{{2 - \gamma }}} \right){\text{。}}\end{array}$ |
令
| $\quad\quad\bar p_1^{{\rm{A}}*} = \frac{{2 - \gamma }}{4}V,$ |
| $\quad\quad\bar R_1^{{\rm{A}}*} = \frac{{2 - \gamma }}{8}{V^2}{\text{。}}$ |
综上可得,在直销模式下航空公司的总收益为
| $\quad\quad {\bar R^{{\rm{A}}*}} = \frac{{2 - \gamma }}{8}{V^2} + \frac{{\bar V_2^2}}{4} = \frac{{5 - 2\gamma }}{{16}}{V^2}{\text{。}}$ | (14) |
推论2
证明 在周期1,
| $\begin{array}{l}\quad\quad p_1^{{\rm{A}}*} - \bar p_1^{{\rm{A}}*} = \displaystyle\frac{{(1 - \gamma ) \cdot 2\xi + \gamma [(1 - \theta)\xi + \lambda ]}}{{4\xi }}V - \displaystyle\frac{{2 - \gamma }}{4}V =\\ \displaystyle\frac{{\theta \gamma (\beta - 3)}}{{4\xi }}V {\text{<}}0{\text{。}}\end{array}$ |
在周期2,
| $\begin{array}{l}\quad\quad p_2^{{\rm{A}}*} - \bar p_2^{{\rm{A}}*} = \left(\displaystyle\frac{{\xi (1 - \theta ) + \lambda }}{{4\xi }} - \displaystyle\frac{1}{4}\right)V = \\\displaystyle\frac{{\theta (\beta - 3)}}{{4\xi }}V {\text{<}}0{\text{。}}\end{array}$ |
证毕。
推论2表明,在中介商销售机制下航空公司的最优定价策略小于传统直销模式。主要原因在于周期1航空公司需要通过较低的价格满足高需求乘客的需求,以获得最大收益;在周期2又面临中介商的竞争(由定理1,过高价格导致航空公司收益损失),因此价格低于传统直销模式。
3.2 两种模式下收益的比较分析本节主要从航空公司和中介商的角度探讨中介商销售机制的有效性,即中介商的存在是否能够缓解乘客的策略行为,是否具有实施的可行性。为了方便讨论,令
定理2
| $\quad\quad\left\{ {\begin{array}{*{20}{l}} \displaystyle\frac{1}{{2\beta }} {\text{<}} \theta {\text{<}} 1,& \displaystyle\frac{1}{2} < \beta {\text{<}} 1 ;\\ \displaystyle\frac{{4 - \gamma }}{{4 - 2\beta \gamma }} {\text{<}} \theta {\text{<}} 1,& 0 {\text{<}} \beta {\text{<}} \displaystyle\frac{1}{2} {\text{。}}\\ \end{array}} \right.$ | (15) |
证明 式(12)减去式(14),化简可得
| $\begin{array}{l}\quad\quad \Delta R = \displaystyle\frac{{{V^2}\theta }}{{16{\xi ^2}}} \cdot \left[ {4({\beta ^2}\gamma - 2\beta \gamma ){\theta ^2} + } \right.\\\left. {4(2\beta \gamma + \beta - {\beta ^2}\gamma )\theta + \beta (\beta - 4)} \right]{\text{。}}\end{array}$ |
可知
| $\quad\quad\left\{ {\begin{array}{*{20}{l}}\displaystyle \frac{1}{{2\beta }} {\text{<}} \theta {\text{<}} 1,& \displaystyle\frac{1}{2} {\text{<}} \beta {\text{<}} 1; \\ \displaystyle\frac{{4 - \gamma }}{{4 - 2\beta \gamma }} {\text{<}} \theta {\text{<}} 1, &0 {\text{<}} \beta {\text{<}} \displaystyle\frac{1}{2}{\text{。}} \\ \end{array}} \right.$ |
证毕。
定理2表明,在
定理3 对任意的
证明: 由式(6)知,
证毕。
定理3表明,中介商进入销售市场后,收益大于不进入市场的情况(为0),从中介商的角度,中介商销售机制具有实施的可行性。
推论3:
证明:
| $\begin{array}{l}\quad\quad \displaystyle\frac{{\partial \Delta R}}{{\partial \gamma }} = \displaystyle\frac{{{V^2}\theta }}{{16{\xi ^2}}} \cdot [4{\beta ^2} - 2\beta {\theta ^2} + 8\beta \theta - 4{\beta ^2}\theta ] = \\\displaystyle\frac{{{V^2}\theta \beta }}{{16{\xi ^2}}} \cdot [4\beta - 2\theta (\theta - 4 + 2\beta )]{\text{≥}}0{\text{。}}\end{array}$ |
证毕。
推论3表明,乘客策略程度
本节通过数值模拟(利用Matlab2014b)验证以上理论分析的结果,重点分析各参数对中介商销售机制有效性的影响。
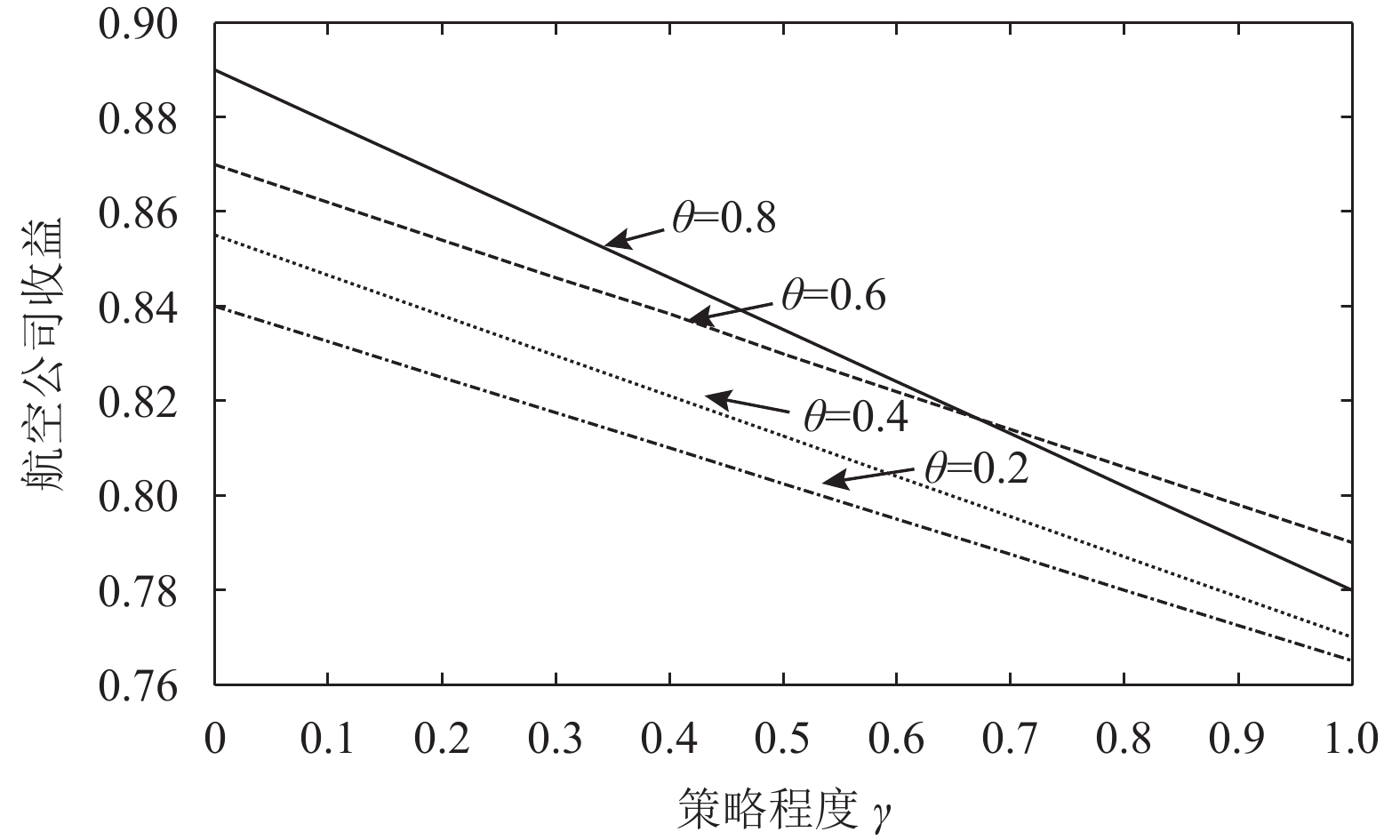
4.1 乘客策略程度对收益的影响首先令
|
图 2 不同
|
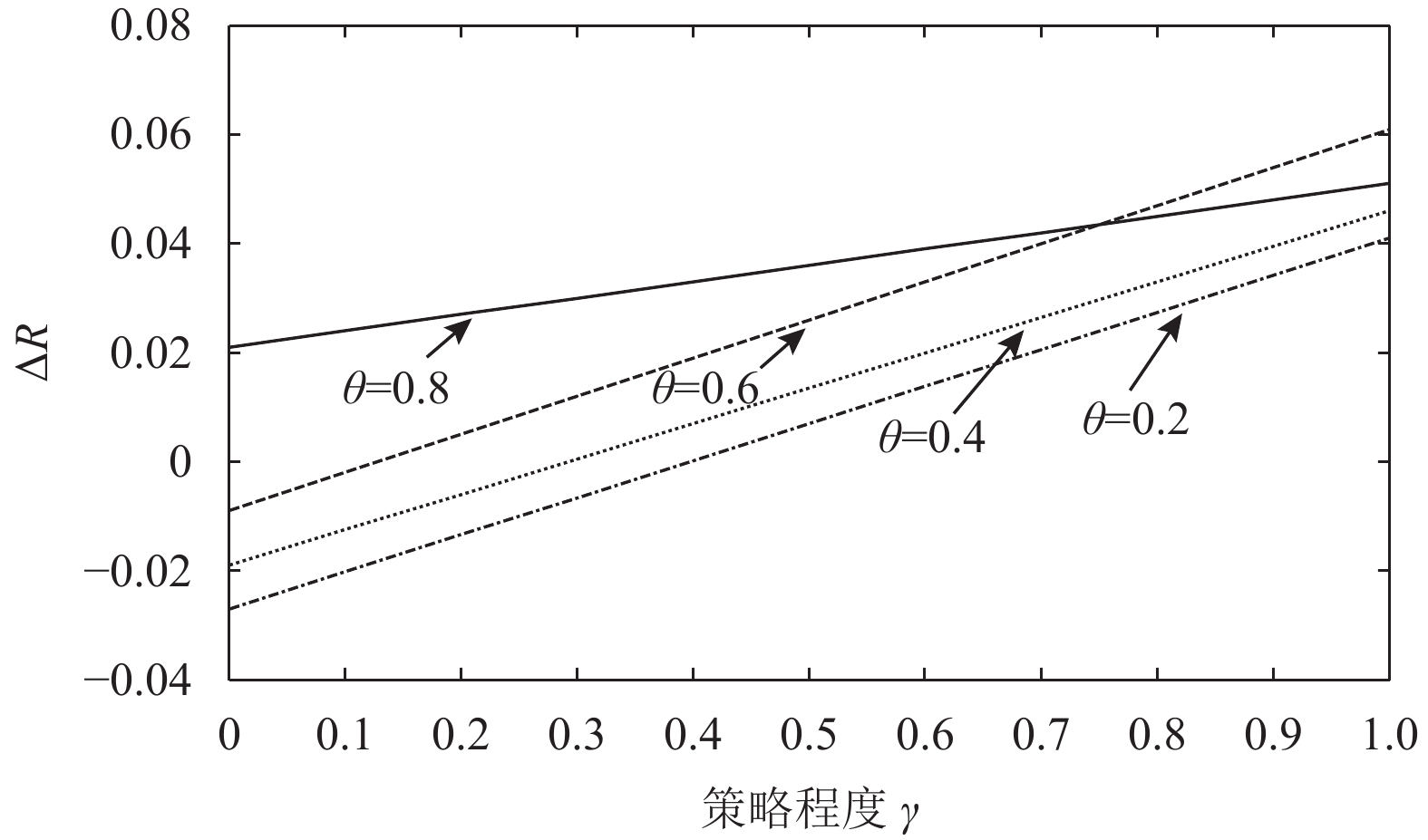
|
图 3 不同
|
可以看到,对所有的
令
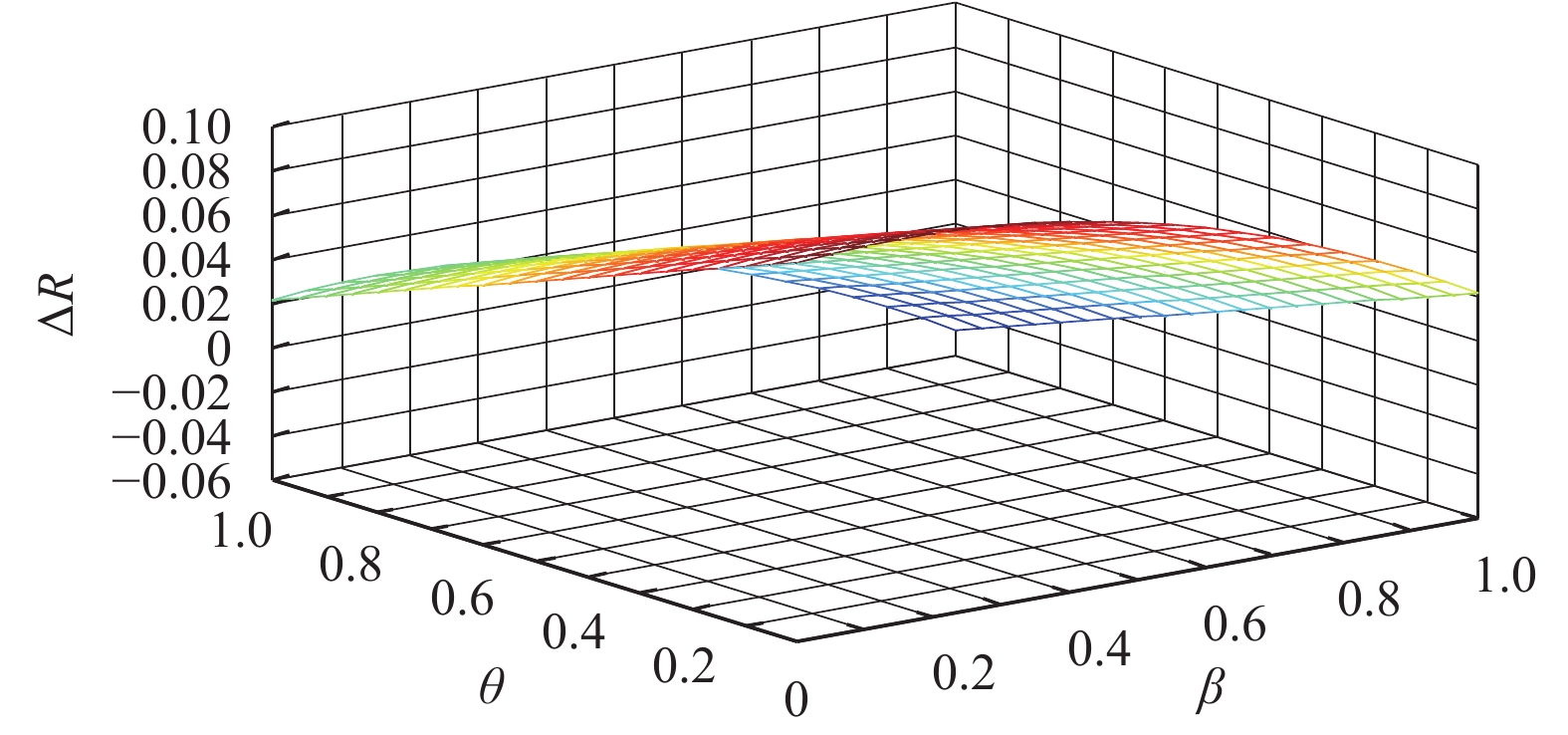
|
图 4 不同
|

|
图 5 不同
|

|
图 6 不同
|
可以看出:
1) 在特定的乘客策略程度下,在式(15)有效性范围内,航空公司在中介商销售机制下的收益大于传统销售,而中介商也获得非负的收益。即中介商销售机制可以增加航空公司和中介商的收益,可以有效地缓解乘客的策略行为对航空公司收益的影响。验证了定理2和定理3。
2) 随着
3) 中介商的收益随着
本文在乘客具有策略行为以及估价不确定的背景下,研究中介商销售机制下航空公司与中介商的定价策略及该机制的有效性。根据问题的特点,假定航空公司在周期1销售机票,并在周期2与中介商共同销售,形成双渠道机票销售供应链,通过逆向求解探讨了航空公司和中介商的均衡定价策略,将均衡收益与传统直销渠道相比较,并通过算例进行验证。研究表明:
1) 在乘客估价不确定下,当乘客对中介商的估价折扣位于某一范围时,中介商销售机制不仅可以缓解乘客的策略行为,也具有实施的可行性。但该机制不能完全消除策略行为对航空公司收益的影响。
2) 航空公司和中介商一定程度的竞争可能带来更高的收益。
3) 乘客策略程度越高,中介销售机制缓解乘客策略行为的效果越明显。
中介商销售机制在国内外航空客运机票销售实践中已被使用,应用前景广泛。本文的研究将进一步扩展需求不确定下该机制的应用,在一定程度上能够辅助航空公司在复杂的市场环境下实施有效的销售策略,实现收益最大化。
后续研究还可以从以下几个方面加以展开:1) 从供应链的角度探讨航空公司与中介商的最优收益分享比例;2) 在竞争环境,即多个航空公司和多个中介商存在时,探讨该机制有效性。
| [1] |
GALLEGO G, RYZIN G V. Optimal dynamic pricing of inventories with stochastic demand over finite horizons[J].
Management Science, 1994, 40(3): 999-1020.
|
| [2] |
OVCHINNIKOV A, MILNER J M. Strategic response to wait-or-buy: revenue management through last minute deals in the presence of customer learning[C]. Toronto: University of Toronto, 2005.
|
| [3] |
LEVIN Y, MCGILL J. Dynamic pricing in the presence of strategic consumers and oligopolistic competition[J].
Management Science, 2009, 55(1): 32-46.
DOI: 10.1287/mnsc.1080.0936. |
| [4] |
ANDERSON C K, WILSON J G. Wait or buy? The strategic consumer: pricing and profit implications[J].
Journal of the Operational Research Society, 2003, 54(3): 299-306.
DOI: 10.1057/palgrave.jors.2601497. |
| [5] |
LEVIN Y, MCGILL J. Optimal dynamic pricing of perishable items by a monopolist facing strategic consumers[J].
Production and Operations Management, 2009, 50(1): 128-143.
|
| [6] |
PAPANASTASIOU Y, SAWA N. Dynamic pricing in the presence of social learning and strategic consumers[J]. Management Science, 2016, 63(4): 919-939.
|
| [7] |
LIU Q, ZHANG D. Dynamic pricing competition with strategic customers under vertical product differentiation[J].
Management Science, 2013, 59(1): 84-101.
DOI: 10.1287/mnsc.1120.1564. |
| [8] |
PRASAD A, VENKATESH R, Mahajan V. Product bundling or reserved product pricing? Price discrimination with myopic and strategic consumers[J].
International Journal of Research in Marketing, 2015, 32(1): 1-8.
DOI: 10.1016/j.ijresmar.2014.06.004. |
| [9] |
YAN B, KE C. Two strategies for dynamic perishable product pricing to consider in strategic consumer behavior[J].
International Journal of Production Research, 2015, 3(12): 1-16.
|
| [10] |
杨道箭, 齐二石, 魏峰. 顾客策略行为与风险偏好下供应链利润分享[J].
管理科学学报, 2011, 14(12): 50-59.
YANG Daojian, QI Ershi, WEI Feng. Supply chain profit sharing under strategic customer behavior and risk preference[J]. Journal of Management Sciences in China, 2011, 14(12): 50-59. |
| [11] |
官振中, 李伟. 存在投机商和策略型消费者的零售商定价研究[J].
系统工程理论与实践, 2015, 35(2): 308-314.
GUAN Zhenzhong, LI Wei. Optimal pricing research with speculators and strategic consumers[J]. Systems Engineering-Theory & Practice, 2015, 35(2): 308-314. |
| [12] |
SU X M. Optimal pricing with speculators and strategic consumers[J].
Management Science, 2010, 56(1): 24-40.
|
| [13] |
JERATH K, NETESSINE S, SENTHIL K. Revenue management with strategic customers: Last-minute selling and opaque selling[J].
Management Science, 2010, 56(3): 430-448.
DOI: 10.1287/mnsc.1090.1125. |
| [14] |
周杰, 李豪. 考虑乘客策略行为的航空客运机票模糊销售机制研究[J].
工业工程与管理, 2016, 21(1): 150-158.
ZHOU Jie, LI Hao. The study of opaque selling mechanism for airline with strategic passengers[J]. Industrial Engineering and Management, 2016, 21(1): 150-158. DOI: 10.3969/j.issn.1007-5429.2016.01.022. |
| [15] |
杨慧, 周晶, 宋华明. 考虑消费者短视和策略行为的动态定价研究[J].
管理工程学报, 2010, 24(4): 133-137.
YANG Hui, ZHOU Jing, SONG Huaming. A dynamic pricing model with strategic and myopic consumers[J]. Journal of Industrial Engineering and Engineering Management, 2010, 24(4): 133-137. DOI: 10.3969/j.issn.1004-6062.2010.04.021. |
| [16] |
JOSEF B, PAAT R. Dynamic pricing under a general parametric choice model[J].
Operations Research, 2012, 60(4): 965-980.
DOI: 10.1287/opre.1120.1057. |
| [17] |
SU X M. Intertemporal pricing with strategic customer behavior[J].
Management Science, 2007, 53(5): 726-741.
DOI: 10.1287/mnsc.1060.0667. |
| [18] |
CACHON G, RARD P, FELDMAN P. Price commitments with strategic consumers: Why it can be optimal to discount more frequently than optimal[J].
Ssrn Electronic Journal, 2015, 17(3): 399-410.
|
 2018, Vol. 21
2018, Vol. 21