应急管理是国内外学术界广泛关注的科学问题，其研究范围涉及到工程技术与社会心理学等多学科领域，对于不同类别和发生机理的突发事件需要开展针对性研究。就重大事故应急管理而言，其主要特征是参与部门多、流程复杂且应急资源存在相互配合关系(即多部门联动)，通常可以描述为由多个关联性任务组成的复杂工作流系统。有关自然灾害、人为事故应急管理过程中的科学决策，通常包括应急资源选址及配置^[1-3]、应急车辆路径规划^[4]、应急流程优化^[5]及其集成问题^[6]等。在现实应急管理实践过程中，需要从整体上把握以上决策内容间的相互关系，以便从全局优化而非局部的角度进行科学决策。因此，如何将车辆路径规划、应急资源配置等决策内容，体现到完整的应急管理流程模型中，以及如何通过流程模型为前两项决策优化提供指导依据(如模型中的约束条件)，就成为将应急管理理论付诸实践的重要步骤。

应急管理是多个相关联应急活动或作业的有机组合，各应急作业间可能存在顺序、并行等关系，应急作业具有时间属性，且取决于作业所需要的资源供应量。因此，应急流程具有显著的时间属性并与可用资源密切相关。流程管理是应急管理过程中赖以决策的重要依据，研究者广泛关注应急流程建模研究,提出了任务网(task network)^[5]、工作流(workflow)^[7]等方法。其中，工作流是信息管理领域广泛应用的流程建模工具。它由荷兰学者van der Aalst提出，并由其研究团队在模型属性、应用领域方面不断加以拓展。用Petri网进行工作流建模形成工作流网，则进一步提高了工作流理论在不同领域的适用性。工作流网的研究主要包括结构特性研究^[7-8]、时间属性拓展研究^[9-11]、资源约束拓展研究^[12]等。需要指出的是，应急管理过程中存在明显的应急活动时间不确定性特征，且受应急资源的影响。这就表明，传统的工作流网模型难以满足应急管理流程建模需要，应急工作流网应同时体现资源约束和不确定性时间属性。对此，Wang等^[13]提出具有活动和资源库所的工作流网，通过活动库所的输入与输出变迁来定义该活动的开始与终止，同时，为活动持续时间给出了最早和最晚完成时间定义。Liu等^[14]研究在资源约束下，考虑不确定应急活动执行时间窗并建立应急响应流程模型。也有研究将库所赋予时间属性，进行应急救援情形下具有资源和时间双重属性的工作流网研究^[15]。以上对于工作流网的拓展工作，对应急流程图形化建模研究具有重要的借鉴意义，但将工作流网理论应用于应急管理还存在差距：1) 应急工作流应与管理决策优化相结合，以实现通过整体流程控制来指导科学决策的目的；2) 实际应急处置过程中的基本特征应在工作流网中得以体现，比如资源运输的行程时间具有不确定性，对于可消耗类资源并不满足资源守恒条件等等。

为此，本文从管理部门需要把握全局流程进行决策的特点出发，以工作流网为分析工具对应急处置作业环节所涉及到的资源需求、时间属性进行描述，以应急管理总流程的全局性经济指标、时间指标为优化目标，进行应急资源调度与路径规划集成问题研究。首先提出一种具有时间和资源属性的应急工作流网模型，以揭示多资源与多活动之间的对应关系；在此基础上，进行应急资源配置与路径规划集成问题描述与建模；针对问题存在不确定约束条件的特点，提出一种混合随机优化求解算法，并设计数值仿真案例对模型与算法进行验证。

1 多部门联合应急工作流网模型

为实现对应急作业流程进行定量描述和分析，本文借助Petri网思想将工作流网扩展为具有资源约束和不确定性时间属性的应急工作流网。

定义1 　Petri网可以定义为一个五元组PN = $ (P,T,F,W,{S_0})$ ，其中，

$P = \{ {p_1},{p_2},\cdots,{p_n}\} $ 为包含n个库所的非空有限集合；

$T = \{ {t_1},{t_2},\cdots,{t_m}\} $ 为包含m个变迁或活动的非空有限集合，且 $P \cap T = \varphi $ ；

$F = \rm{Pre} \cup \rm{Post}$ 为有向弧的非空有限集合， ${\rm{Pre}}:(P \times T) \to N$ 是从库所到变迁的带权重有向弧， ${\rm{Post}}:(T \times P) \to N$ 是从变迁到库所的带权重有向弧， $N = \{ 0,1,2,\cdots\} $ ；

$W:F \to N$ 为一个映射，表达有向弧的权重；

${S_0}:P \to N$ 为每个库所中托肯分布及数目的初始状态。

定义2 　 具有资源约束和不确定性时间属性的应急工作流网，定义为 $ < {\rm{PN}},{I_p} > $ 。

1) ${\rm{PN}} = (P,T,F,W,{S_0})$ ，为有标识的P-time Petri网。P表示库所集合，包括状态库所、动作库所、资源库所三类，其中状态和动作库所具有时间属性；其他如定义1所示。

2) ${I_{\rm{p}}} = [\rm{EF},\rm{LF}]$ ，为动作库所和状态库所对应的时间区间，EF为动作或状态的最早完成时间，LF为相应的最晚完成时间。根据应急处置过程中时间属性的不同，将I_P分为可视时间I_v(已知量，用于应急流程控制)、静态时间I_s(给定量，用于推导可视时间)、可变时间I_d(未知量，与资源供应量相关)。

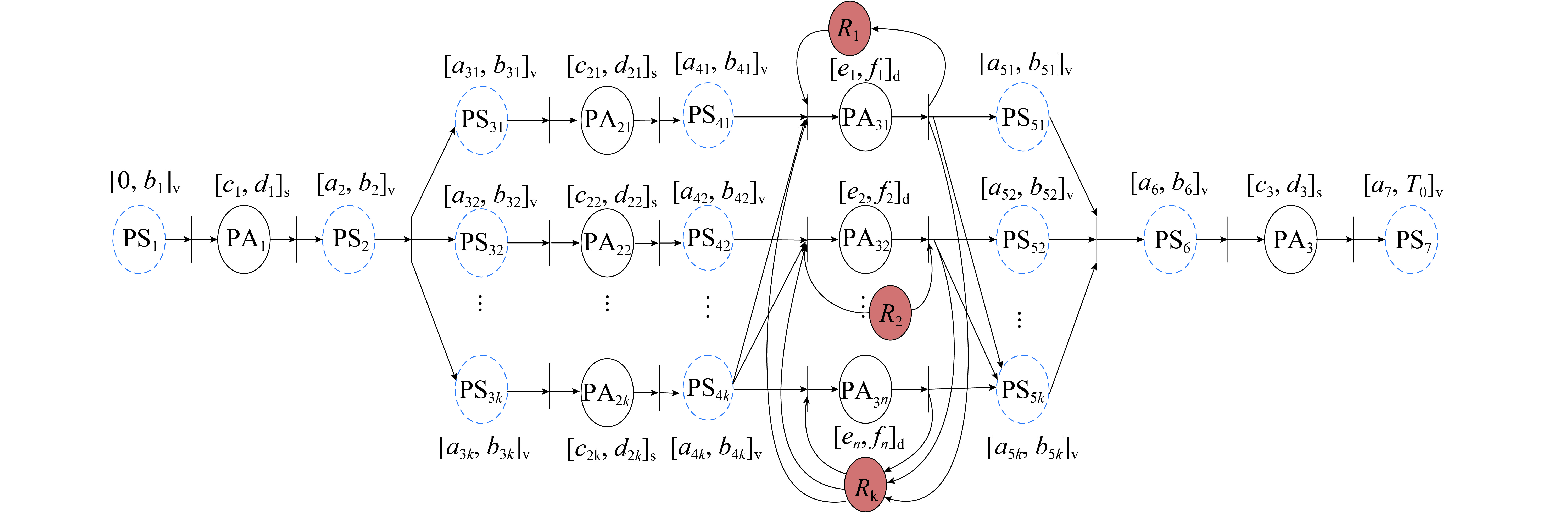
在应急处置的现场作业过程中，广泛存在多资源共享与多活动联动特点。为此，建立具有k种资源以及n个救援活动的联合应急工作流网模型如图1所示。该模型具有3类库所，其中状态库所(4+3k个)与动作库所(2+k+n个)具有时间属性，资源库所(k个)不具备时间属性，相关说明见表1。

在应急管理过程中，静态时间 ${[c,d]_{\rm{s}}}$ 是指根据经验判断或统计出的活动完成区间范围，比如应急响应时间范围、调配车辆到达现场的时间范围，以及现场清理与恢复所需时间范围。在完成静态时间估计的前提条件下，就可以按照工作流网模型的不确定时间计算规则，分别进行状态库所的可视时间参数计算和动作库所的持续时间估计。需要指出的是， ${\rm{P}}{{\rm{A}}_{2k}}$ 对应的应急资源运输时间，作为软约束用于估算可视控制时间；应急资源的实际运输时间取决于优化路径，实际运输时间与已知的运输时间(软约束)间允许存在差异，这种差异将产生相应的惩罚成本。对于实际应急管理的意义在于，静态时间的经验估计一定程度上存在不合理性，若将不合理的静态时间参数作为硬约束，有可能导致无可行解问题。

可视时间 ${[a,b]_{\rm{v}}}$ 用于流程控制，在给定最大允许救援时间 $\rm{TT}$ 的情况下，可以自后向前推导出各阶段可视控制的最晚完成时间： ${b_6} = {\rm{TT}} - {d_3}$ , ${b_{5n}} = {b_6}$ , ${b_{4k}} = {b_{5n}} - {f_n},$ ${b_{3k}} = {b_{4k}} - {d_{2k}}$ ， ${b_2} = \min \{ {b_{3k}}\} $ ， ${b_1} =$ $ {b_2} - {d_1}$ 。其中， $n = 1,2,...,N$ ， $k = 1,2,...,K$ 。同理，已知应急起始时间为0的情况下，自前向后可推导出可视控制的最早完成时间： ${a_2} = 0 + {c_1}$ ， ${a_{3k}} = {a_2}$ ， ${a_{4k}} = {a_{3k}} + {c_{2k}}$ ， ${a_{5k}} = \max \{ {e_l}\} + {a_{4k}}$ ， ${a_6} = \max \{ {a_{5k}}\} $ ， ${a_7} = {a_6} + {c_3}$ 。其中， $l = 1,2,..,L$ 为所有作业中与第 $k$ 类资源相关的活动。

本文假定第 $n$ 类作业与多种资源相关，但其总体执行时间仅取决于第 $k$ 种关键资源，且作业执行时间随资源量增加而递减，并存在极限值 ${z_n}$ (即作业最早完成时间 ${e_n} = {z_n}$ )。这里采用Sigmoid函数近似表达上述非线性关系，则作业最晚完成时间可通过式(1)计算。

$\quad\quad{f_n}({r_k}) = {u_n}\frac{{{{\rm{e}}^{ - {s_n}{r_k}}}}}{{1 + {{\rm{e}}^{ - {s_n}{r_k}}}}} + {z_n}{\text{。}}$

(1)

其中， ${u_n}$ 为时间系数；常数 $\rm{e}$ 为自然对数的底数； ${s_n}$ 为资源消耗速度参数； ${r_k}$ 为影响第n类作业效率的关键资源； ${z_n}$ 为作业完成最短时间。

至此，在已知应急启动时间为0并期望在时间TT内完成的情况下，通过应急工作流网 $ < \rm{PN},{I_p} > $ 的工作原理，就可以根据2+k个静态时间参数，计算得到所有4+3k个状态库所的可视时间参数值(包括最早和最晚完成时间)。同时，也可以根据应急资源供应量，估算出相应作业的最早完成时间(极限值)和最晚完成时间。以上建模及时间属性分析过程，既考虑了资源对应急流程的影响，也考虑了所有作业存在的时间不确定性(即用最早和最晚完成时间来表达时间属性)，因此，符合实际应急管理工作的现实需求。

本文提出的扩展型应急工作流网，具备以下3个特征：1)能直观展现应急过程中资源运输与现场作业之间的紧前紧后时序关系；2)借助最早与最晚完成时间区间，表达应急流程中各环节的时间不确定性；3)能体现资源供应量对现场作业时间效率的相互关系，从而揭示资源对整个应急过程的主导性作用。对于实际应急管理中的资源配置与路径规划等决策问题，若能够从应急过程的整体流程出发，借助应急工作流网推算各作业环节的最早、最晚完成时间，则既可以用于应急预案的推演和评判，也可以为应急资源的配置数量和运输路径决策提供参考依据。

2 应急资源配置与路径规划集成问题建模

在应急管理决策过程中往往涉及多部门协同，因此，指挥中心从全流程控制的角度出发，通过集成决策为各部门提供相应的应急资源配置与路径规划参考方案，有利于大幅度提高多方协同处置效率。集成决策背景下，首先应根据接警信息和处置预案，预判应急处置所需资源种类及数量；其次，参考同类事件最晚完成时间，借助应急工作流网估算现场作业和资源运输的最早和最晚时间参数；再次，以资源运输允许的时间窗作为软约束条件，经优化计算得到相应的行驶路径。总体而言，由于应急资源分配既与现场作业时间效率相关，也影响到资源运输的软时间窗，这就使得两类决策问题存在耦合关系，因此需要研究相应的集成问题。

定义3 　应急资源配置与路径规划集成问题。假定应急处置需要消耗类和工具类应急资源，且资源配送车辆的行程时间随机，需考虑如下问题：如何从 $M$ 个备选应急站点中选取K个站点即 $K$ 种不同应急资源(假定每个点仅提供一种资源)；如何为 $K$ 种资源配送车辆规划行驶路径并对现场 $N$ 个作业活动合理分配资源，从而在满足应急作业总时间限制条件下，尽可能地降低应急处置总成本。

与之相对应的集成决策模型如下。

$\quad\quad\min F = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {[{\rm{C}}{{\rm{C}}_{mn}} + {\rm{C}}{{\rm{U}}_{mn}}]} } + {\rm{CT}} + {\rm{CP}}{\text{。}}$

(2)

$\begin{split}&\quad\quad{\rm{s}}{\rm{.t}}{\rm{.}}\\&\quad\quad{\rm{C}}{{\rm{C}}_{mn}} = (w_{mn}^{{\rm{out}}}{\rm{ - }}w_{mn}^{{\rm{in}}}){x_{mn}} C_{mn}^{\rm{c}}{\text{。}}\end{split}$

(3)

$\quad\quad{\rm{C}}{{\rm{U}}_{mn}} = {f_n}(w_{mn}^{{\rm{in}}} {y_{mn}}) C_{mn}^{\rm{u}}{\text{。}}$

(4)

$\quad\quad{\rm{CT}} = {C^{\rm{t}}}\sum\limits_{i = 1}^U {\sum\limits_{j = 1}^U {\sum\limits_{k = 1}^K {{x_{ijk}}E[{{\tilde t}_{ijk}}]} } } {\text{。}}$

(5)

$\begin{split}&\quad\;\;\;\;{\rm{CP}} = {C^{\rm{l}}} \displaystyle\sum\limits_{k = 1}^K {\max (E[{{\tilde t}_k}] - {b_{4k}},0)} + \\&{C^{\rm{e}}} \displaystyle\sum\limits_{k = 1}^K {\max ({a_{4k}} - E[{{\tilde t}_k}],0)} {\text{。}}\end{split}$

(6)

$\quad\quad{\tilde t_k} = \sum\limits_{i = 1}^U {\sum\limits_{j = 1}^U {{x_{ijk}}{{\tilde t}_{ijk}}} } + t_k^0{\text{。}}$

(7)

$\quad\quad{\rm{Pr}}\left\{ {{a_{4k}} {\text{≤}} {{\tilde t}_k} {\text{≤}} {b_{4k}}} \right\} {\text{≥}} {\beta _k}{\text{。}}$

(8)

$\quad\quad{\rm{w}}{{\rm{s}}_{mn}} {\text{≤}} w_{mn}^{{\rm{out}}} {\text{≤}} {\rm{w}}{{\rm{b}}_{mn}}{\text{。}}$

(9)

$\quad\quad\sum\limits_{n = 1}^N {w_{mn}^{{\rm{out}}}} {\text{≤}} {Q_m}{\text{。}}$

(10)

$\quad\quad\sum\limits_{m = 1}^M {({x_{mn}} + {y_{mn}})} {\text{≤}} K{\text{。}}$

(11)

$\quad\quad\sum\limits_{i = 1}^U {\sum\limits_{k = 1}^K {{x_{ijk}}} {\text{≤}} 1} ,\forall j \in [1,U]{\text{。}}$

(12)

$\quad\quad\sum\limits_{j = 1}^U {\sum\limits_{k = 1}^K {{x_{ijk}}} {\text{≤}} 1} ,\forall i \in [1,U]{\text{。}}$

(13)

$\quad\quad{x_{ijk}} = \left\{ {\begin{array}{*{20}{l}}{1,}&{\text{运输资源}k\text{的车辆经过路段}(i,j);}\\{0,}&{\text{否则。}}\end{array}} \right.$

(14)

$\quad\quad{x_{mn}} = \left\{ {\begin{array}{*{20}{l}}{1,}&{\text{活动}n\text{使用可消耗资源}m;}\\{0,}&{\text{否则。}}\end{array}} \right.$

(15)

$\quad\quad{y_{mn}} = \left\{ {\begin{array}{*{20}{l}}{1,}&{\text{活动}n\text{占用不可消耗资源}m;}\\{0,}&{\text{否则。}}\end{array}} \right.$

(16)

其中， $U$ 为路网节点数； $m \in [1,M]$ 为可供使用的资源标识， $n \in [1,N]$ 为活动标识， $k \in [1,K]$ 为实际使用的资源标识， $M,N,K$ 均为给定值；决策变量 ${x_{ijk}}$ 、 ${x_{mn}}$ 、 ${y_{mn}}$ 均为0-1变量, ${x_{ijk}}$ 为标识第 $k$ 类资源运输路径的变量， ${x_{mn}}$ 与 ${y_{mn}}$ 分别为标识活动 $n$ 占用消耗、工具类资源的变量。

目标函数(2)表示应急处置总成本，包括资源消耗成本、资源占用成本、资源运输成本(与行程时间相关)，以及资源到达时间不符合时间窗产生惩罚成本。式(3)为活动 $n$ 所消耗资源的经济成本， $w_{mn}^{\rm{out}}{\rm{ - }}w_{mn}^{{\rm{in}}}$ 为活动消耗资源量，由资源供给量与返回量的差值决定， $C_{mn}^{\rm{c}}$ 为资源消耗成本系数。式(4)为活动 $n$ 占用工具资源的时间成本， ${f_n}( \cdot )$ 为活动完成时间函数， $C_{mn}^{\rm{u}}$ 为资源占用成本系数。式(5)为资源运输成本， ${C^{\rm{t}}}$ 为单位运输时间成本系数，第 $k$ 类资源在路段 $(i,j)$ 上的行程时间 ${\tilde t_{ijk}}$ 服从正态分布。式(6)为资源提前及延迟到达产生的惩罚成本，第1项为资源到达时间超出 ${b_{4k}}$ 产生的延误成本， ${C^{\rm{l}}}$ 为延误惩罚成本系数；第2项为资源先于 ${a_{4k}}$ 到达产生的等待成本， ${C^{\rm{e}}}$ 为等待惩罚成本系数。需要说明的是，现实中通常不考虑对资源早到产生的等待情况进行惩罚，本文侧重各种资源的相互配合在此给出一种通式，在实际应用中可调整系数 ${C^{\rm{e}}}$ 来适应具体案例需求。式(7)中 ${\tilde t_k}$ 为第 $k$ 类资源实际到达现场的时间，第1项表示资源运输的在途行程时间，第2项 $t_k^0$ 为资源出发起始时间。

约束(8)表明，第 $k$ 类资源在时间窗 $[{a_{4k}},{b_{4k}}]$ 内到达处置现场的概率,应大于置信度 ${\beta _k}$ ,该时间窗即图1中PS_4k库所的时间属性。资源约束(9)表明，活动 $n$ 执行所需资源应高于最低启动量，同时低于资源供应量上限。资源约束(10)表示，应急处置活动对第 $k$ 类资源的需求量，不超过应急站点资源容量 ${Q_k}$ 。约束条件(11)限定任意活动 $n$ 所需的资源种类数不超过 $K$ 。式(12)、(13)限定资源运输路径不能重复访问任意路网节点，即不存在环或者重复路段。

3 粒子群与遗传算法混合优化求解

以上集成决策模型属于随机规划模型^{[4, 16]}，其计算量主要来自2个方面：1)通过随机模拟处理机会约束(8)带来的计算量；2)资源配置与路径规划方案优选过程中，产生的计算量。当备选站点规模及路网规模较大时，以上随机规划问题求解的时间复杂度将随之迅速增加。由于粒子群算法用于路径优化效率较高，而遗传算法广泛应用于大规模复杂问题求解，故本文采用2种算法相结合的混合优化算法^{[6, 17]}对集成问题进行求解。

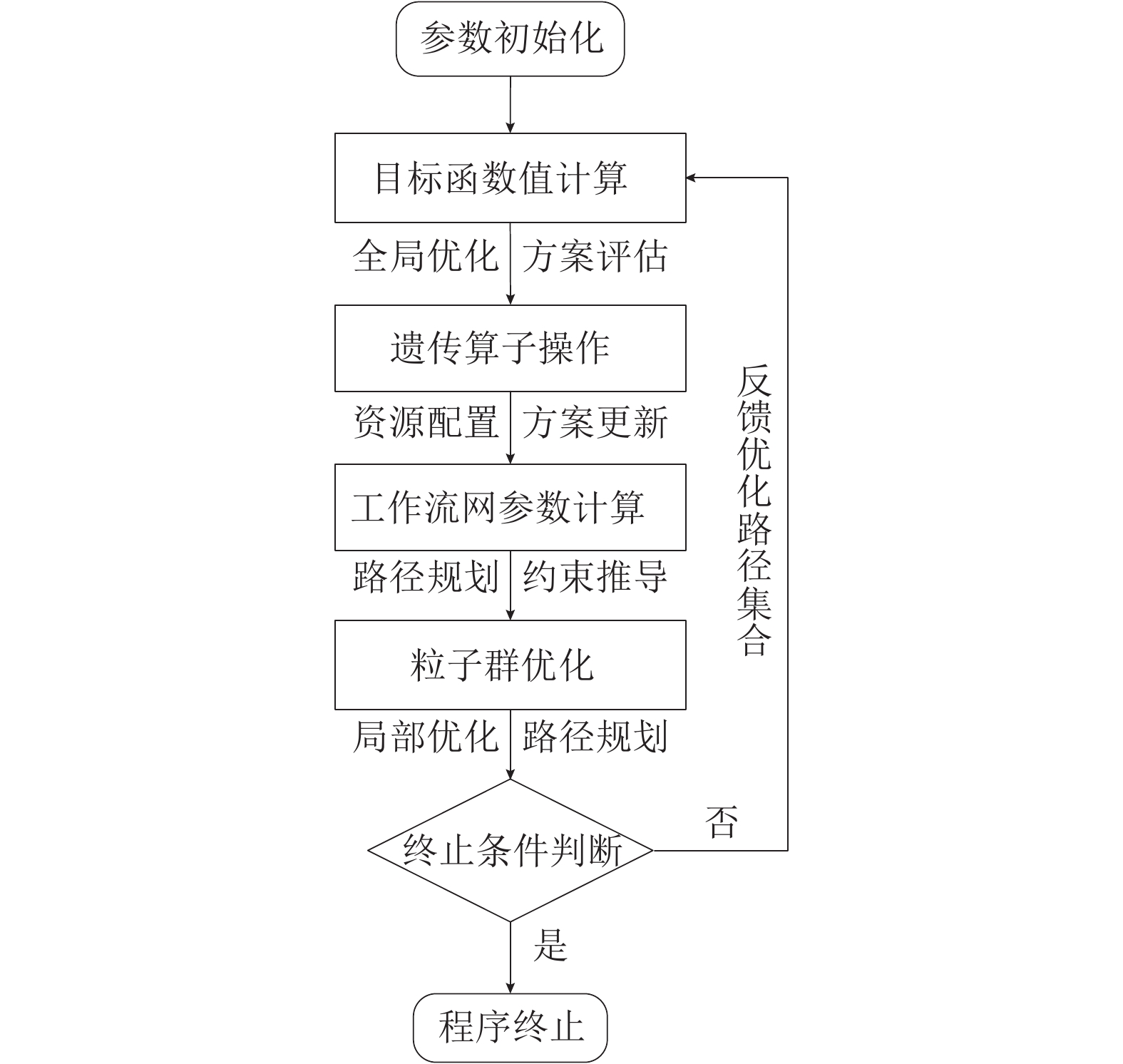
图2所示混合优化算法分为4个层次。1) 资源分配优化层，利用遗传算法进行二进制染色体编码，生成可行的应急站点选取及应急活动资源配置方案并进行进化。2) 工作流网参数计算层，根据资源分配方案与应急工作流网计算得到应急资源允许到达的时间窗约束。3) 运输路径优化层，利用离散粒子群算法，对应急资源运输路径规划问题进行0-1编码和迭代更新。4) 目标函数计算层，则通过计算4类关联成本构成的目标函数值或适应值，评价应急站点选取与资源分配方案、运输路径方案的优劣，以筛选优秀种群参与下一代进化。限于篇幅，这里省略具体编码和相关计算公式，有关理论可参考文献[17-18]。

以上混合优化流程中，遗传算法用于资源配置方案优化，粒子群算法用于资源运输路径优化，两者之间相互协调共同构成集成决策问题的完整解。具体求解流程设计如下。

Step 1 　应急资源初始化。根据现有 $M$ 种备选资源类型、数量及其分布情况，参考同类事件预案库确定本次应急处置所需资源数 $K$ ；按照以往经验规则生成一组资源分配方案，并通过约束条件(9)、(10)进行可行性判断。

Step 2 　工作流网初始化。根据应急作业环节及其与资源间的关系，绘制形如图1的应急工作流网；根据经验预设应急工作完成最晚时间参数 $T$ ，以及事件检测与现场清理等辅助性作业的静态时间区间；根据资源分配方案及其与作业时间之间的函数关系，推导出状态库所的可视控制时间参数，由此构造约束条件(8)。

Step 3 　运输路径初始化。根据上层可行应急资源分配方案集，通过工作流网计算相应的运输车辆到达时间窗，据此产生一系列初始路径集合，用随机模拟方法判断初始路径群体是否满足约束条件(9)~(11)，确保种群达到粒子群算法所需的规模。

Step 4 　遗传算子操作。针对以上初始化方案和参数，进行目标函数值计算即总成本评估，选取应急资源配置方案群体中的精英个体，通过遗传、交叉、变异算子，生成新的应急资源配置方案，并进行可行性校验。

Step 5 　工作流网分析。根据以上资源分配方案，进行 $n$ 个作业活动执行时间及 $k$ 种资源消耗量的计算；根据全局可视控制时间、经验给定的静态时间参数(如据经验估计的应急资源到达时间窗)，得出受资源约束的活动可变时间间隔，并推导出局部可视控制时间参数；根据资源消耗量与占用时间情况，计算资源消耗、资源占用成本。

Step 6 　粒子群算子操作。以运输成本和惩罚成本为目标函数，根据更新后的局部可视控制时间窗(应急资源到达时间窗)，进行种群中各粒子的速度和位置进行迭代更新，得到一组与资源配置方案相对应的最优资源运输路径集。

Step 7 　种群评估与优选。根据Step 4得到的资源消耗与占用成本，以及Step 6得到的运输成本与惩罚成本，计算出总成本用以评估应急资源配置方案种群适应值，优选总成本较小配置方案对应的精英个体，进入下次遗传进化操作。转入Step 4。

Step 8 　算法终止判断。如满足最大迭代次数或目标函数减少幅度趋于收敛的预设条件，则输出应急资源站点的选择方案、针对各应急作业的资源分配方案，以及资源的具体运输路径方案；算法终止。

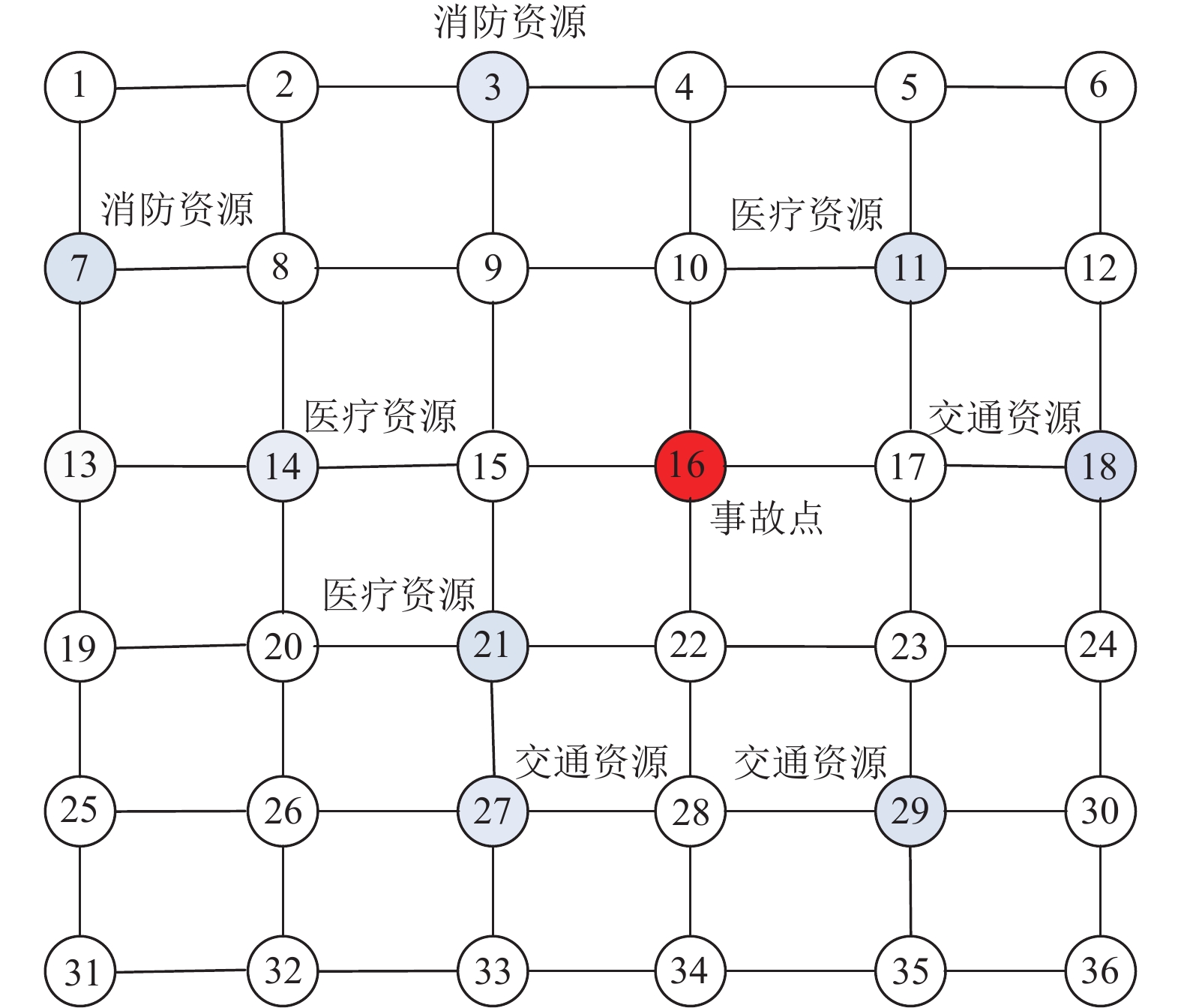
4 集成优化仿真案例分析

仿真案例中，以假定在图3所示的路网中，在第16节点处发生车辆燃烧、人员受伤的重大交通事故。应急指挥中心在接到事故求救电话后，需要根据事故情况和应急资源储备情况，从现有的3类共8个备选应急站点中，选择并配置应急资源赶赴事故现场展开处置作业，要求应急处置总体时间应控制在45 min内完成。

案例中路网节点数 $U = 36$ ，需要从8个备选站点( $M = 8$ )中，选取消防 ${R_1}$ 、医疗 ${R_2}$ 、交通 ${R_3}$ 三类资源即 $K = 3$ ，为现场三类作业提供资源供应即 $N = 3$ 。假定现场消防作业 ${\rm{P}}{{\rm{A}}_{31}}$ 需消防与交通资源，该作业启动的最低资源需求量为 $({\rm{w}}{{\rm{s}}_{11}},{\rm{w}}{{\rm{s}}_{21}},{\rm{w}}{{\rm{s}}_{31}}) = (5,0,2)$ ；人员救治作业 ${\rm{P}}{{\rm{A}}_{32}}$ 需医疗与交通资源，该作业启动的最低资源需求量 $({\rm{w}}{{\rm{s}}_{12}},{\rm{w}}{{\rm{s}}_{22}},{\rm{w}}{{\rm{s}}_{32}}) = (0,6,2)$ ；维持秩序作业仅需交通资源，故其最低资源需求量 $({\rm{w}}{{\rm{s}}_{13}},{\rm{w}}{{\rm{s}}_{23}},{\rm{w}}{{\rm{s}}_{33}}) = (0,0,8)$ 。

静态时间参数根据预案库推测给定，其中事件检测库所 ${\rm{P}}{{\rm{A}}_1}$ 的时间属性 ${[{c_1},{d_1}]_{\rm{s}}} = {[3,4]_{\rm{s}}}$ ，消防、医疗、交通资源抵达库所 ${\rm{P}}{{\rm{A}}_{21}}$ 、 ${\rm{P}}{{\rm{A}}_{22}}$ 、 ${\rm{P}}{{\rm{A}}_{23}}$ 的时间属性分别为 ${[{c_{21}},{d_{21}}]_{\rm{s}}} = {[15,20]_{\rm{s}}}$ 、 ${[{c_{22}},{d_{22}}]_{\rm{s}}} = {[18,21]_{\rm{s}}}$ 、 ${[{c_{23}},{d_{23}}]_{\rm{s}}} = {[10,19]_{\rm{s}}}$ ，现场恢复库所 ${\rm{P}}{{\rm{A}}_3}$ 的时间属性 ${[{c_3},{d_3}]_{\rm{s}}} = {[4,8]_{\rm{s}}}$ ，单位为min。

仿真路网中任意两相邻节点间的行程时间，服从均值为2的不同方差的正态分布；资源消耗时间系数 ${u_n} = 1/3$ ，资源消耗速度控制因子 ${s_n} = 0.2$ ，最少执行时间 ${z_n} = 10$ ；运输成本系数 ${C^{\rm{t}}} = 10$ ，惩罚因子 ${C^{\rm{l}}} = {C^{\rm{e}}} = 10$ 。利用Matlab编程进行仿真，对应急资源配置优化的遗传操作，交叉概率为0.6,变异概率为0.3，种群规模100；对运输路径的粒子群进化，种群规模为100，最大迭代次数为100次。

1) 应急资源配置优化方案。表2第2列为应急处置所需资源总量，其中消防资源量为6，医疗资源量为6，交通资源量为12；第3列表明消防和医疗作业，均需配备2单位的交通资源予以协助；第4列则是根据应急工作流网的时间参数计算规则，得出的消防、医疗、交通资源到达时间窗(实际到达不在时间窗内则产生惩罚成本)。

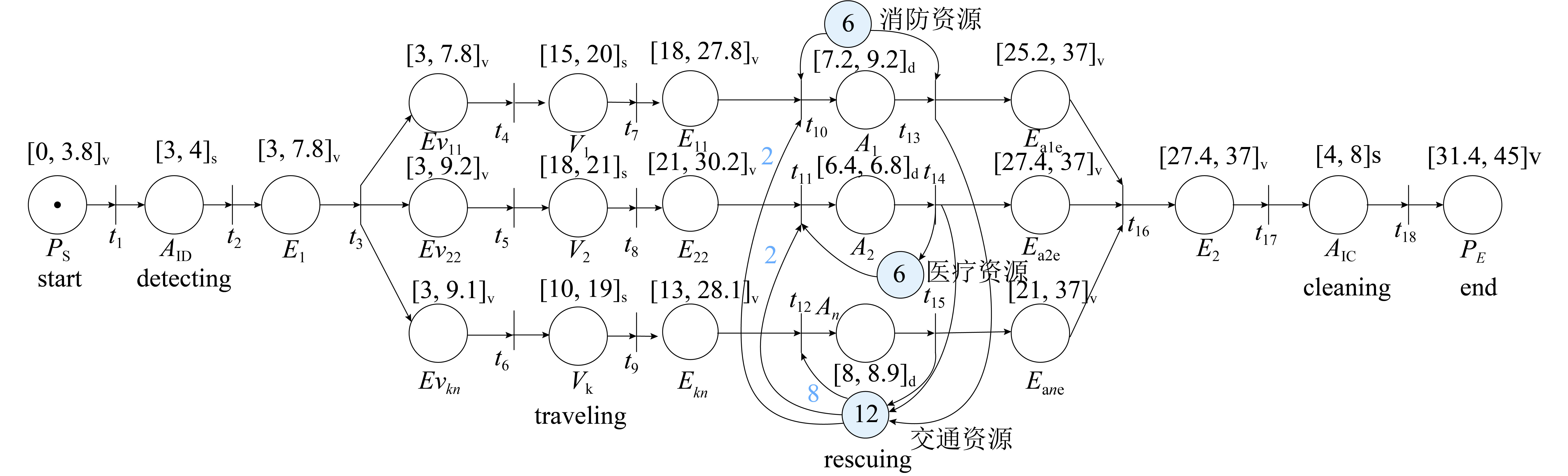
图4为最优资源配置方案对应的应急工作流网模型，其中全局可视控制时间窗表明，在确保45 min完成应急处置并最小化应急管理总成本的情况下，应急处置最早完成时间为31.4 min，最晚为45 min；根据事件检测、运输行程与现场清理等静态时间参数，可得到局部可视控制时间参数，如现场应急作业应在[27.4, 37.0] min范围内完成，以及消防、医疗和交通资源的理论达到时间窗(与表格第4列相同)。

2) 应急资源运输路径优化方案。本文考虑应急站点受容量约束限制，在最优应急资源分配方案基础上，将各类资源总量和应急车辆调度时间窗作为车辆调度依据。通过仿真计算，得到最优资源配置下的车辆路径方案。

表3表明，为了实现应急处置时间限制下的总成本最优，3类资源运输的最佳运输路径分别为7-8-9-15-16、14-20-21-22-16、27-28-22-16，由于图3路网中各路段的行程时间为随机数，对应的行程时间期望值分别为9.47 min、13.38 min、17.14 min。

由于本文优化目标既包含运输成本(对应行程时间)又包含惩罚成本(早到迟到产生的成本)，案例中假定接到处置信息3 min后所有车辆全部出发，因此提前到达车辆也将产生惩罚成本。故在这一假设条件下，由本算法优化得到的资源运输路径并非最短路径，如表3第3列所示。若假设车辆出发时间可以调整，则可以避免早到产生的惩罚成本，表3中第14个站点出发的医疗资源也可避免绕路行为。

假定运输应急资源的车辆出发时间可控，则按照表2第4列的时间窗，给出如表3第4列的推荐出发时间窗。为使惩罚成本最低，将应急站点7的车辆出发时间控制在[8.53, 18.33] min内，即最早在检测确认事件报警之后5.53 min发车；应急站点14的车辆出发时间控制在[7.62, 16.82] min内，即最早在检测确认事件报警之后4.62 min发车；应急站点27的交通资源可以在[0.00, 10.96]内出发。以上参数均为行程时间随机模拟数的均值，存在不满足表2第4列时间窗要求的情况，故产生表3第5列的惩罚成本期望值。

5 结论

针对突发事件应急管理受多种资源影响，决策内容复杂且相互关联的特点，借助应急工作流网模型来揭示应急处置流程中的作业、时间与资源关联关系，从而进行应急资源配置与路径规划集成问题研究。论文首先提出一种具有资源约束和不确定时间属性的应急工作流网模型，模型中包含状态库所、动作库所和资源库所，其中又将资源分为可消耗资源与可占用资源两类；同时，通过可视控制时间、静态时间、可变时间，来分别刻画应急流程过程的总体时间控制、局部时间预判、现场时间变化等复杂情形。

本文研究的集成模型以给定的全局应急处置总时间为前提，以应急处置过程所产生的总成本作为目标函数，其成本包括应急管理所需的资源成本、应急车辆运输过程产生的运输成本和未在预定时间内到达的惩罚成本。通过遗传算法中嵌套粒子群算法对集成模型求解，可得到包括应急储备点选择和资源配置方案、应急车辆发车时间、车辆路网行驶路径方案和现场资源分配方案。因此，本文面向实际应急管理特点所建立的集成模型，可提供相对完整的应急处置决策方案。

未来研究方向包括，应急工作流网的结构合理性与动态性能研究、大规模路网中的实际案例分析、针对不同突发事件应急处置的建模与分析等。