股权战略联盟是企业之间为了实现共同的目标而形成的合作伙伴关系[1],这在供应链管理中是一种非常普遍的现象。上游供应商与下游制造商的单向持股作为其主要表现形式之一,在各行各业均较常见。在汽车行业,如德国发动机供应商戴姆勒公司持有汽车生产商阿斯顿·马丁公司5%的股份[2];在新兴电动汽车领域,作为丰田与特斯拉的电池供应商,日本松下公司同样对丰田公司实施了持股策略;美国漆料供应商杜邦公司持有生产商通用公司25%的股份[3]。长安汽车集团投资5亿元间接持有动力电池供应商宁德时代0.39%的股权[4]。在食品行业,中粮包装公司(加多宝供应商)花费20亿元增资凉茶制造商清远加多宝公司,对其持股近31%[5]。这种优势互补的合作一方面可以巩固供应商在所属行业中的领导地位,也缓解了制造商公司的资金紧张问题,扩大了生产,备受各大企业的青睐。
近些年来,供应链中企业的持股问题受到学者的广泛关注,持股形式主要包括上游供应商与下游制造商的单向持股[6-7]以及企业之间的交叉持股[8-11]两种类型,研究内容集中于持股比例对产品生产成本投资,供应链产量与消费者剩余以及供应链系统利润的影响。在企业单向持股情形下,Morita等[12]认为制造商持股上游企业可以避免供应商定制投资产生的问题。着眼于消费者群体,Greenlee等[6]认为在不对称成本下,同质产品可以增加生产者总剩余,而差异化产品可能会对消费者不利。企业交叉持股背景下,Güth等[10]指出垂直交叉持股可以增加交易的可能性。Flath[11]发现存在多个供应商与多个制造商时,交叉持股使得供应链产品产量得以增长。张汉江等[8]研究了企业交叉持股之后市场行为与绩效的原始创新性,认为交叉持股虽然使得产品市场价格有所降低,但却增加了供应链总收益。Cai等[13]基于一个多市场竞争的分析框架,认为在现有市场的某些条件下,相比于独立进入,企业更喜欢联盟进入市场。此外,还有部分学者致力于研究供应链持股模型的协调问题[2, 14]。在市场需求不确定时,张楠等[2]讨论供应商对制造商单向持股的供应链协调问题,分析认为该持股模型不能消除“双重边际效应”,进而设计出基于回购与补贴策略的契约使得供应链各方收益得到完美协调。在下游制造商持股上游供应商背景下,付红等[14]通过引入回购策略实现了组装供应链协调。
关于产品定价问题的研究也较为丰富,学者考虑了不同因素对产品定价策略的影响。从碳配额交易体系出发,马秋卓等[15]研究了低碳产品定价问题以及企业的最优碳排放策略。在供应链竞争环境下,Zhu等[16]探讨绿色产品设计及最优定价问题。从消费者角度出发,基于消费者低碳偏好,赵道致等[17]分析了企业产品线的定价问题。周木生等[18]与王春萍等[19]分别考虑消费者非线性边际支付意愿与寡头市场结构下信息产品的定价策略。基于产品数字化以及产品盗版问题,Dinah等[20]研究企业的最优定价问题。
可以看出,虽然上述文献部分涉及到单向持股或交叉持股背景下企业产品的定价问题,然而大部分学者却忽视了在垄断供应商与竞争性制造商的供应链组成中,供应商的纵向持股对于市场地位不同的制造商竞争策略以及产品定价的影响。基于此,建立供应商单向持股制造商模型,细化市场结构,研究Nash静态博弈以及Stackelberg动态博弈下竞争性制造商的产品定价与竞争策略,分析供应商持股比例对产品需求量、各博弈方收益以及供应链整体利润的影响。本文所考虑的供应商持股模型与竞争制造商市场地位的差异情形更加符合现实情况,更能反映供应链各方之间的合作与竞争关系,希望所得结论可为相关企业的定价决策提供理论参考。
1 模型描述 1.1 模型假设考虑市场上存在垄断供应商
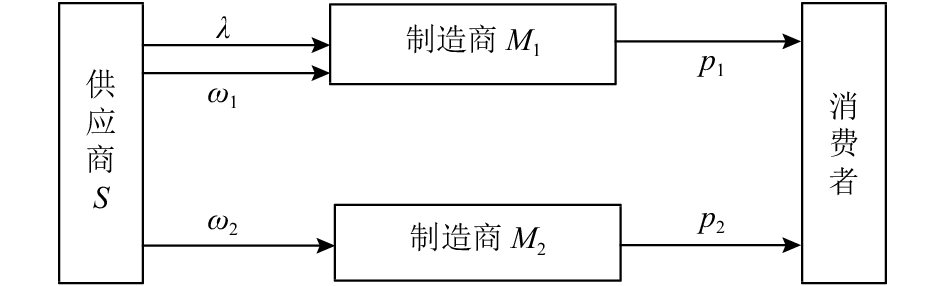
|
图 1 供应商持股模型 Fig. 1 Shareholding model of supplier |
根据Yue等[22]、陈忠等[23]和艾兴政等[24]对竞争渠道产品的研究,制造商
| $\quad\quad\begin{array}{l}{q_1} = ra - b{p_1} + d\left( {{p_2} - {p_1}} \right),\\{q_{\rm{2}}} = \left( {1 - r} \right)a - b{p_2} + d\left( {{p_1} - {p_2}} \right){\text{。}}\end{array}$ | (1) |
其中,
其他假设:1) 供应商和制造商均按照订单生产(make-to-order),各博弈方均没有库存[22, 25];2) 供应商的生产成本
考虑双寡头制造商市场地位相同,在利润最大化的基础上,供应商以
| $\max \mathop {\varPi _1^{\rm{DN}}}\limits_{p_1^{\rm{DN}}} = \left( {1 - \lambda } \right)\left( {p_1^{\rm{DN}} - w_1^{\rm{DN}}} \right)\left( {ra - p_1^{\rm{DN}} + \frac{1}{2}\left( {p_2^{\rm{DN}} - p_1^{\rm{DN}}} \right)} \right),$ | (2) |
| $\max \mathop {\varPi _2^{\rm{DN}}}\limits_{p_2^{\rm{DN}}} = \left( {p_2^{\rm{DN}} - w_2^{\rm{DN}}} \right)\left( {\left( {1 - r} \right)a - p_2^{\rm{DN}} + \frac{1}{2}\left( {p_1^{\rm{DN}} - p_2^{\rm{DN}}} \right)} \right){\text{。}}$ | (3) |
供应商的利润函数为
| $\max \mathop {\varPi _{\rm{S}}^{\rm{DN}}}\limits_{w_1^{\rm{DN}}{\rm{ }}w_2^{\rm{DN}}} = w_1^{\rm{DN}}q_1^{\rm{DN}} + w_2^{\rm{DN}}q_2^{\rm{DN}} + \lambda \left( {p_1^{\rm{DN}} - w_1^{\rm{DN}}} \right)q_1^{\rm{DN}}{\text{。}}$ | (4) |
根据逆向归纳法,首先将式(2)、式(3)分别对
| $\quad\quad p_1^{\rm{DN}} = \frac{{2\left( {5r + 1} \right)a + 3\left( {6w_1^{\rm{DN}} + w_2^{\rm{DN}}} \right)}}{{35}},$ | (5) |
| $\quad\quad p_{\rm{2}}^{\rm{DN}} = \frac{{2\left( { - 5r + 6} \right)a + 3\left( {w_1^{\rm{DN}} + 6w_2^{\rm{DN}}} \right)}}{{35}}{\text{。}}$ | (6) |
将式(5)和式(6)代入式(4),并联立方程组
| $\quad\quad\begin{array}{l}w_1^{{\rm{DN}}*} = \displaystyle\frac{{\left( {74\lambda r + 25\lambda - 70r - 35} \right)a}}{{8\left( {17\lambda - 35} \right)}},\\w_2^{{\rm{DN}}*} = \displaystyle\frac{{\left( {3 - 2r} \right)a}}{8}{\text{。}}\end{array}$ | (7) |
经验证,式(4)的海塞矩阵(Hessian Matrix)负定,可保证供应商利润取得极大值。
将式(7)代入式(5)和式(6),制造商的最优零售价格分别为
| $\quad\quad p_1^{\rm{DN}*} = \frac{{\left( {74\lambda r + 25\lambda - 110r - 43} \right)a}}{{8\left( {17\lambda - 35} \right)}},$ | (8) |
| $\quad\quad p_2^{\rm{DN}*} = \frac{{\left( {50\lambda r - 75\lambda - 110r + 153} \right)a}}{{8\left( {35 - 17\lambda } \right)}}{\text{。}}$ | (9) |
制造商和供应商的最优需求和利润分别为
| $\quad\quad\begin{array}{l}q_1^{{\rm{DN}}*} = \displaystyle\frac{{3\left( {5r + 1} \right)a}}{{70 - 34\lambda }},\\q_2^{{\rm{DN}}*} = \displaystyle\frac{{3\left( {2\lambda r - 3\lambda - 5r + 6} \right)a}}{{70 - 34\lambda }},\end{array}$ | (10) |
| $\quad\quad\varPi _1^{\rm{DN}*} = \frac{{3{{\left( {5r + 1} \right)}^2}\left( {1 - \lambda } \right){a^2}}}{{2{{\left( {17\lambda - 35} \right)}^2}}},$ | (11) |
| $\quad\quad\varPi _2^{\rm{DN}*} = \frac{{3{{\left( {2\lambda r - 3\lambda - 5r + 6} \right)}^2}{a^2}}}{{2{{\left( {17\lambda - 35} \right)}^2}}},$ | (12) |
| $\quad\quad \varPi _{\rm{S}}^{{\rm{DN}}*} = \frac{{3\left[ {4\left( {\lambda \! -\! 5} \right){r^2} + 4\left( {5 \!-\! 3\lambda } \right)r \!+\! 9\lambda \!-\! 19} \right]{a^2}}}{{16\left( {17\lambda - 35} \right)}}{\text{。}}$ | (13) |
在产品市场上,制造商
| $\max \mathop {\varPi _1^{\rm{LN}}}\limits_{p_1^{\rm{LN}}} = \left( {1 - \lambda } \right)\left( {p_1^{\rm{LN}} - w_1^{\rm{LN}}} \right)\left( {ra - p_1^{\rm{LN}} + \frac{1}{2}\left( {p_2^{\rm{LN}} - p_1^{\rm{LN}}} \right)} \right),$ | (14) |
| $\max \mathop {\varPi _2^{\rm{LN}}}\limits_{p_2^{\rm{LN}}} = \left( {p_2^{\rm{LN}} - w_2^{\rm{LN}}} \right)\left( {\left( {1 - r} \right)a - p_2^{\rm{LN}} + \frac{1}{2}\left( {p_1^{\rm{LN}} - p_2^{\rm{LN}}} \right)} \right),$ | (15) |
| $\max \mathop {\varPi _{\rm{S}}^{\rm{LN}}}\limits_{w_1^{\rm{LN}}{\rm{ }}w_2^{\rm{LN}}} = w_1^{\rm{LN}}q_1^{\rm{LN}} + w_2^{\rm{LN}}q_2^{\rm{LN}} + \lambda \left( {p_1^{\rm{LN}} - w_1^{\rm{LN}}} \right)q_1^{\rm{LN}}{\text{。}}$ | (16) |
根据逆向归纳法,首先将式(15)对
| $\quad\quad p_2^{\rm{LN}} = \frac{{p_1^{\rm{LN}} + 3w_2^{\rm{LN}} + 2\left( {1 - r} \right)a}}{6}{\text{。}}$ | (17) |
将式(17)代入式(14),对
| $\quad\quad p_1^{\rm{LN}} = \frac{{17w_1^{\rm{LN}} + 3w_2^{\rm{LN}} + 2\left( {5r + 1} \right)a}}{{34}}{\text{。}}$ | (18) |
把式(17)与式(18)代入式(16),同时对
| $w_1^{\rm{LN}*} = \frac{{\left( {74\lambda r + 25\lambda - 68r - 34} \right)}}{{136\left( {2\lambda - 1} \right)}},\\w_2^{\rm{LN}*} = \frac{{\left( {3 - 2r} \right)a}}{8}{\text{。}}$ | (19) |
把式(19)代入式(17)和(18)可求得两制造商的最优零售价格:
| $\quad\quad p_1^{\rm{LN}{\rm{*}}} = \frac{{\left( {74\lambda r + 25\lambda - 108r - 42} \right)a}}{{136\left( {\lambda - 2} \right)}},$ | (20) |
| $\quad\quad p_2^{\rm{LN}{\rm{*}}} = \frac{{\left( {150\lambda r - 225\lambda - 320r + 446} \right)a}}{{408\left( {2 - \lambda } \right)}}{\text{。}}$ | (21) |
同理,也可求得制造商和供应商的最优需求和利润:
| $q_1^{\rm{LN}*} = \frac{{\left( {5r + 1} \right)a}}{{12\left( {2 - \lambda } \right)}},\\q_2^{\rm{LN}*}\frac{{\left( {12\lambda r - 18\lambda - 29r + 35} \right)a}}{{68\left( {2 - \lambda } \right)}},$ | (22) |
| $\quad\quad\begin{array}{l}\varPi _1^{\rm{LN}*} = \displaystyle\frac{{{{\left( {5r + 1} \right)}^2}\left( {1 - \lambda } \right){a^2}}}{{204{{\left( {\lambda - 2} \right)}^2}}},\\\varPi _2^{{\rm{DN}}*} = \displaystyle\frac{{{{\left( {12\lambda r - 18\lambda - 29r + 35} \right)}^2}{a^2}}}{{6\;936{{\left( {\lambda - 2} \right)}^2}}},\end{array}$ | (23) |
| $\varPi _{\rm{S}}^{{\rm{DN}}*} \!=\! \frac{{\left[ {\left( {36\! -\! 172} \right){r^2} \!+\! \left( {176 \!-\! 108\lambda } \right)r \!+\! 81\lambda \!-\! 166} \right]{a^2}}}{{816\left( {\lambda - 2} \right)}}{\text{。}}$ | (24) |
制造商
| $\max \mathop {\varPi _1^{\rm{ON}}}\limits_{p_1^{\rm{ON}}} = \left( {1 - \lambda } \right)\left( {p_1^{\rm{ON}} - w_1^{\rm{ON}}} \right)\left( {ra - p_1^{\rm{ON}} + \frac{1}{2}\left( {p_2^{\rm{ON}} - p_1^{\rm{ON}}} \right)} \right),$ | (25) |
| $\max \mathop {\varPi _2^{\rm{ON}}}\limits_{p_2^{\rm{ON}}} = \left( {p_2^{\rm{ON}} - w_2^{\rm{ON}}} \right)\left( {\left( {1 - r} \right)a - p_2^{\rm{ON}} + \frac{1}{2}\left( {p_1^{\rm{ON}} - p_2^{\rm{ON}}} \right)} \right),$ | (26) |
| $\max \mathop {\varPi _{\rm{S}}^{\rm{ON}}}\limits_{w_1^{\rm{ON}}{\rm{ }}w_2^{\rm{ON}}} \!=\! w_1^{\rm{ON}}q_1^{\rm{ON}} \!+\! w_2^{\rm{ON}}q_2^{\rm{ON}} \!+\! \lambda \left( {p_1^{\rm{ON}} \!-\! w_1^{\rm{ON}}} \right)q_1^{\rm{ON}}{\text{。}}$ | (27) |
求解过程与3.2节类似,整理
| 表 1 DN、LN与ON模型的均衡解1) Tab. 1 Equilibrium solution of model DN、LN and ON |
本部分通过对比
命题1 供应商持股比例
1)被持股制造商
2) (1) 当
(2) 当
(3) 当
证明 将3种市场结构下的制造商
| $\quad\quad\begin{array}{l}p_1^{\rm{DN}*} - p_1^{\rm{ON}*} = \displaystyle\frac{{\left( {\lambda - 1} \right)\left( {2\lambda r - 3\lambda - 5r + 6} \right)a}}{{1\;683{\lambda ^2} - 6\;933\lambda + 7\;140}} {\text{<}} 0,\\p_1^{\rm{LN}*} - p_1^{\rm{ON}*} = \displaystyle\frac{{\left( {\lambda - 1} \right)\left( {2\lambda r - 3\lambda - 34r} \right)a}}{{1\;683{\lambda ^2} - 6\;834\lambda + 6\;936}} {\text{>}} 0{\text{。}}\end{array}$ |
即
对于制造商2,
| $\quad\quad\begin{array}{l}p_2^{\rm{DN}*} - p_2^{\rm{LN}*} = \displaystyle\frac{{\left( {\lambda - 1} \right)\left( {5r + 1} \right)a}}{{1\;734{\lambda ^2} - 7\;038\lambda + 7\;140}} {\text{<}} 0,\\p_2^{\rm{DN}*} - p_2^{\rm{ON}*} = \displaystyle\frac{{\left( {\lambda - 2} \right)\left( {2\lambda r - 3\lambda - 5r + 6} \right)a}}{{561{\lambda ^2} - 2\;311\lambda + 2\;380}} {\text{<}} 0{\text{。}}\end{array}$ |
下面只需比较
| $\quad\quad p_2^{{\rm{LN}}*} - p_2^{{\rm{ON}}*} = \frac{{{G_1}a}}{{3\;366{\lambda ^2} - 13\;668\lambda + 13\;872}}{\text{。}}$ | (28) |
其中
命题1表明,在供应商对制造商
命题2 不同市场结构对制造商最优产量的影响:
1) 被持股制造商
2) 制造商
证明 传统制造商在3种市场结构下的需求函数满足:
| $\quad\quad\begin{array}{l}q_1^{\rm{DN}*} - q_1^{\rm{LN}*} = \displaystyle\frac{{\left( {1 - \lambda } \right)\left( {5r + 1} \right)a}}{{204{\lambda ^2} - 828\lambda + 840}} {\text{>}} 0,\\q_1^{\rm{DN}*} - q_1^{\rm{ON}*} = - \displaystyle\frac{{\left( {2\lambda r - 3\lambda - 5r + 6} \right)a}}{{1\;122{\lambda ^2} - 4\;622\lambda + 4\;760}} {\text{<}} 0,\end{array}$ |
即
| $\quad\quad\begin{array}{l}q_2^{\rm{DN}*} - q_2^{\rm{LN}*} = \displaystyle\frac{{\left( {\lambda - 1} \right)\left( {5r + 1} \right)a}}{{1\;156{\lambda ^2} - 4\;692\lambda + 4\;760}} {\text{<}} 0,\\q_2^{\rm{DN}*} - q_2^{\rm{ON}*} = - \displaystyle\frac{{\left( {8\lambda - 17} \right)\left( {2\lambda r - 3\lambda - 5r + 6} \right)a}}{{3\;366{\lambda ^2} - 13\;866\lambda + 14\;280}} {\text{>}} 0,\end{array}$ |
即
命题2表明无论是何种市场结构,产品制造商的最优生产量在竞争对手处于强势地位时高于两者处于同等地位时的生产量,在自身处于“领导者”地位时生产量最低,并且不受到两者市场份额占比以及供应商持股比例的影响。出现此现象的原因在于,处于“领导者”地位的制造商决策的价格要高于竞争对手处于“领导者”地位时的价格,而对于同种类型的产品,“价格优势”更能得到消费者的青睐。另外,由命题1可知,处于同等地位的两制造商的零售价格最低,但此时激烈的竞争迫使产品的需求量并不能达到最高。
命题3 供应商持股比例
1)当供应商对制造商
2)当供应商对制造商
证明 制造商
| $\varPi _1^{\rm{DN}*} - \varPi _1^{\rm{LN}*} = \frac{{\left( {1 - \lambda } \right){{\left( {5r + 1} \right)}^2}\left( {17{\lambda ^2} - 34\lambda - 1} \right){a^2}}}{{204{{\left( {17\lambda - 35} \right)}^2}{{\left( {\lambda - 2} \right)}^2}}} {\text{<}} 0,$ | (29) |
| $\!\!\begin{array}{l}\quad\quad\varPi _1^{\rm{DN}*} - \varPi _1^{\rm{ON}*} =\\\!\!\displaystyle\frac{{\left( {1 \!-\! \lambda } \right)\left( {988\lambda r \!+\! 201\lambda \!-\! 2\;035r \!-\! 414} \right)\left( {2\lambda r \!-\! 3\lambda \!-\! 5r \!+\! 6} \right){a^2}}}{{6{{\left( {17\lambda \!-\! 35} \right)}^2}{{\left( {33\lambda - 68} \right)}^2}}} {\text{<}}\!0,\end{array}$ | (30) |
| $\quad\quad\varPi _1^{{\rm{LN}}*} - \varPi _1^{{\rm{ON}}*} = \frac{{\left( {\lambda - 1} \right){G_2}{a^2}}}{{204{{\left( {\lambda - 2} \right)}^2}{{\left( {33\lambda - 68} \right)}^2}}}{\text{。}}$ | (31) |
其中
| ${\lambda _{3,4}} = \displaystyle\frac{{1\;088{r^2} + 1\;224r + 204 \pm \left( {290{r^2} + 118r - 12} \right)\sqrt {34} }}{{1\;369{r^2} + 942r + 135}},$ |
其中
制造商
| $\quad\quad\varPi _2^{{\rm{DN}}*} - \varPi _2^{{\rm{LN}}*} = \frac{{\left( {1 - \lambda } \right)\left( {5r + 1} \right){G_3}{a^2}}}{{6\;936{{\left( {17\lambda - 35} \right)}^2}{{\left( {\lambda - 2} \right)}^2}}}{\text{。}}$ | (32) |
其中
| $\varPi _2^{\rm{DN}*} - \varPi _2^{\rm{ON}*} = - \frac{{\left( {25{\lambda ^2} - 68\lambda + 34} \right){{\left( {2\lambda r - 3\lambda - 5r + 6} \right)}^2}{a^2}}}{{6{{\left( {17\lambda - 35} \right)}^2}{{\left( {33\lambda - 68} \right)}^2}}}{\text{。}}$ | (33) |
当
| $\quad\quad\varPi _2^{\rm{LN}*} - \varPi _2^{\rm{ON}*} = - \frac{{50{a^2}{G_4}}}{{867{{\left( {\lambda - 2} \right)}^2}{{\left( {33\lambda - 68} \right)}^2}}}{\text{。}}$ | (34) |
其中,
命题3指出供应商对制造商
命题4 供应商持股比例
1)当制造商
2)当制造商
证明 将3种市场结构下供应商的最优利润两两作差可得:
| $\quad\quad\varPi _{\rm{S}}^{\rm{DN}*} - \varPi _{\rm{S}}^{\rm{LN}*} = \frac{{\left( {1 - \lambda } \right){{\left( {5r + 1} \right)}^2}{a^2}}}{{204\left( {17\lambda - 35} \right)\left( {\lambda - 2} \right)}} {\text{>}}0,$ | (35) |
| $\quad\quad\varPi _{\rm{S}}^{\rm{DN}*} - \varPi _{\rm{S}}^{\rm{ON}*} = \frac{{{{\left( {2\lambda r - 3\lambda - 5r + 6} \right)}^2}{a^2}}}{{6\left( {17\lambda - 35} \right)\left( {33\lambda - 68} \right)}} > 0,$ | (36) |
| $\begin{split}&\quad\quad\varPi _{\rm{S}}^{\rm{LN}*} - \varPi _{\rm{S}}^{\rm{ON}*} =\\&\displaystyle\frac{{\left[ {2{{\left( {2r - 3} \right)}^2}{\lambda ^2} + 3\left( {3{r^2} + 42r - 23} \right)\lambda - 68\left( {2r - 1} \right)} \right]{a^2}}}{{204\left( {\lambda - 2} \right)\left( {33\lambda - 68} \right)}}{\text{。}}\end{split}$ | (37) |
式(37)的正负由
| ${\lambda _{7,8}} = \displaystyle\frac{{ - 9{r^2} - 126r + 69 \pm \sqrt {\left( {81{r^2} - 22r - 9} \right)\left( {{r^2} + 82r + 15} \right)} }}{{4{{\left( {2r - 3} \right)}^2}}},$ |
命题4表明供应商的利润与制造商市场份额
本节将通过数值算例分析供应商持股比例
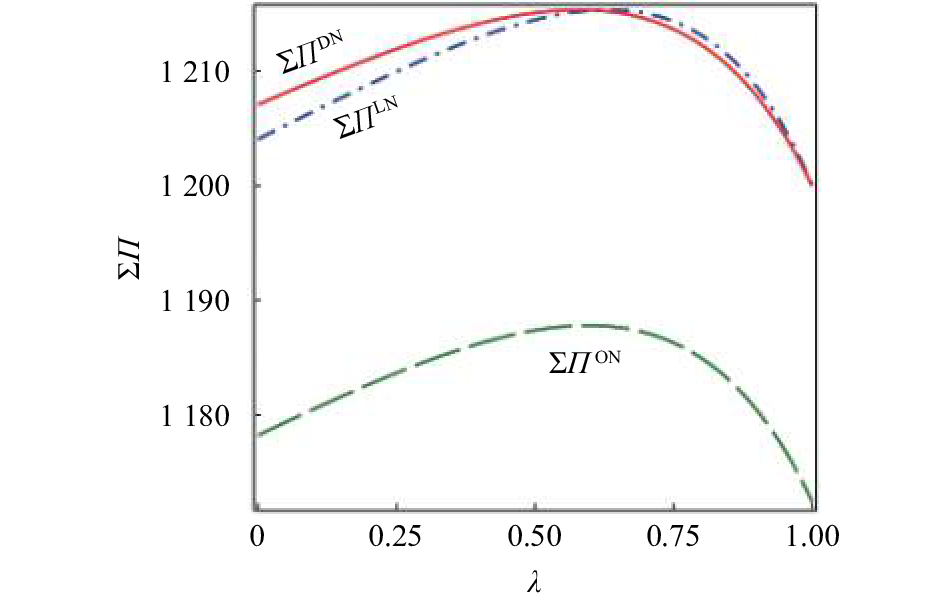
|
图 2 |
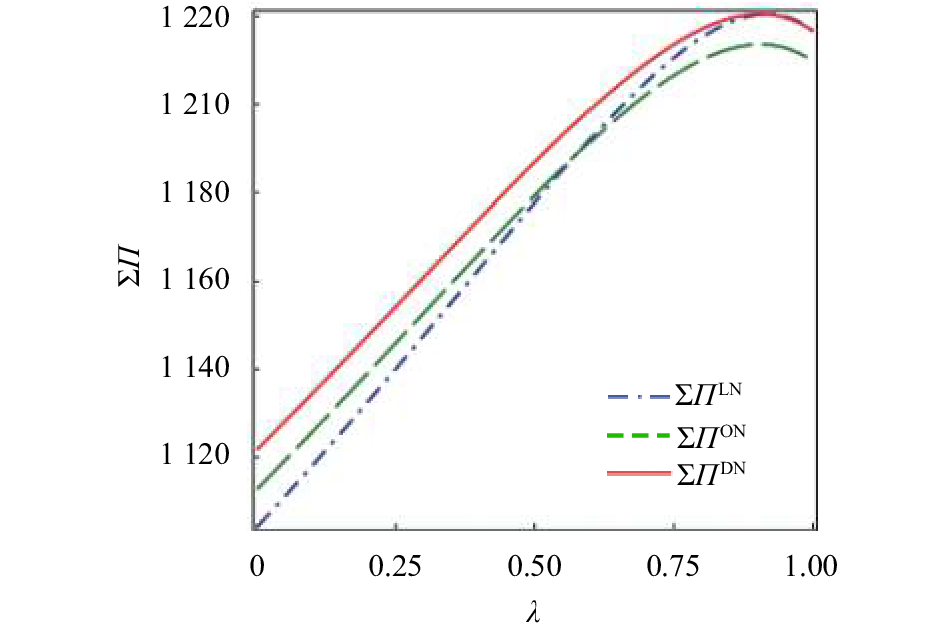
|
图 3 |
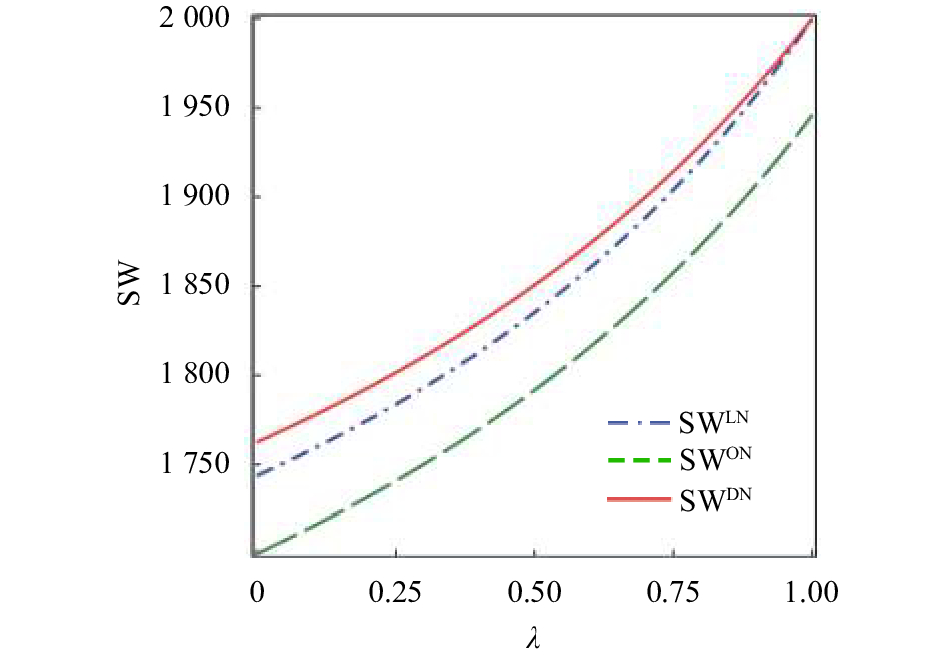
|
图 4 |
|
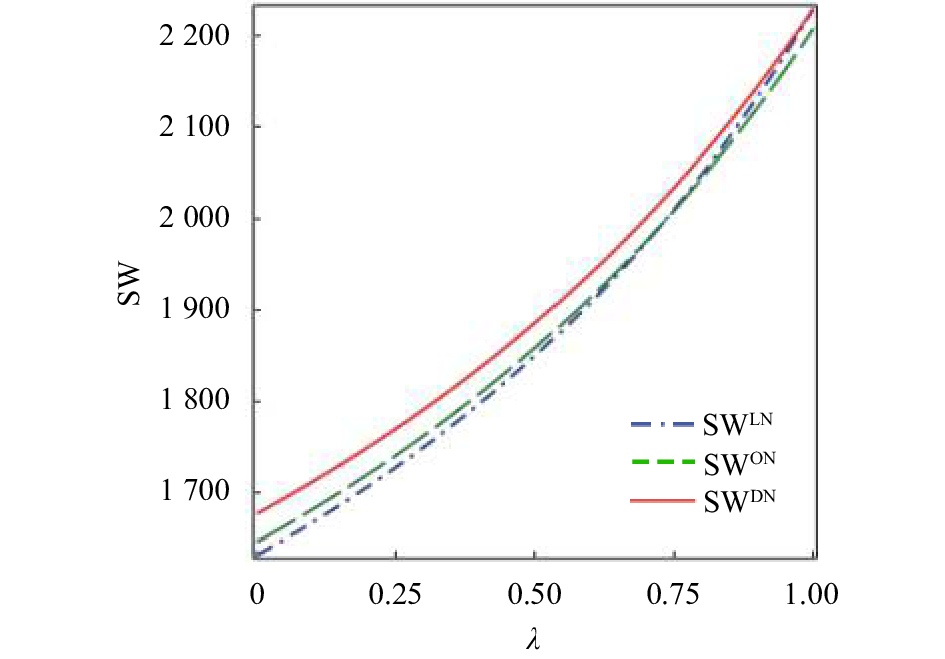
图 5 |
由图4与图5的变化趋势可以看到,3种市场结构下社会福利与供应商持股比例均呈正相关。图4说明制造商
在垄断供应商持股双寡头制造商的背景下,研究供应商持股比例对产品定价、产品需求量以及各方企业利润的影响,根据不同的市场结构,建立双寡头领导者、被持股制造商为领导者与未被持股制造商为领导者3种持股模型,通过对比制造商静态博弈与动态博弈下的均衡结果发现:1) 被持股制造商
可以从以下几个方面进行扩展研究:1) 本文仅考虑了供应商与制造商的单向持股,研究企业之间的交叉持股对产品定价策略的影响;2) 产品需求函数中可以加入某些影响因子,如制造商服务水平等因素。
| [1] |
CHILD J, FAULKNER D. Strategies of cooperation: managing alliances, network, and joint ventures [M]. New York: Oxford University Press, 1998
|
| [2] |
张楠, 周宗放. 供应商持股制造商的供应链协调[J].
系统工程, 2016, 34(4): 89-93.
ZHANG Nan, ZHOU Zongfang. Coordinating a supply chain when supplier holds equity in manufacturer[J]. Systems Engineering, 2016, 34(4): 89-93. DOI: 10.3969/j.issn.1001-2362.2016.04.070. |
| [3] |
BLAIR R D, KASERMAN D L. Law and economics of vertical integration and control [M]. New York: Academic Press, 1983
|
| [4] |
今日头条. 长安汽车投资5.19亿间接持股宁德时代0.3855%股权好戏还在后头[EB/OL].(2017-11-02). https://www. toutiao.com/i6483708365280117262/
|
| [5] |
今日头条. 中粮包装20亿持股加多宝, 可口可乐销售良好, 饮料行业蓄势待发? [EB/OL].(2017-11-01). https://m.toutiao.com/ i6483274056589115917/
|
| [6] |
GREENLEE P, RASKOVICH A. Partial vertical ownership[J].
European Economic Review, 2006, 50(4): 1017-1041.
DOI: 10.1016/j.euroecorev.2005.01.004. |
| [7] |
ELDAIF S M, LEE R, ADAMS K N, et al. Backwards integration and strategic delegation[J].
Social Science Electronic Publishing, 2012, 97(6): 1959-1965.
|
| [8] |
张汉江, 宫旭, 廖家旭. 线性需求供应链中企业交叉持股的定价和绩效变化研究[J].
中国管理科学, 2010, 18(6): 65-70.
ZHANG Hanjiang, GONG Xu, LIAO Jiaxu. Research on pricing and performance of cross-shareholdings in the supply chain of linear demand[J]. Chinese Journal of Management Science, 2010, 18(6): 65-70. |
| [9] |
SHIMOKAWA K. Japan and the global automotive industry [M]. UK: Cambridge University Press, 2010
|
| [10] |
GÜTH W, NIKIFORAKIS N, Normann H T. Vertical cross-shareholding: theory and experimental evidence[J].
International Journal of Industrial Organization, 2007, 25(1): 69-89.
DOI: 10.1016/j.ijindorg.2006.02.001. |
| [11] |
FLATH D. Vertical integration by means of shareholding interlocks[J].
International Journal of Industrial Organization, 1989, 7(3): 369-380.
DOI: 10.1016/0167-7187(89)90004-0. |
| [12] |
MORITA H. Partial ownership induces customised investments under repeated interaction: an explanation of Japanese manufacturer-suppliers relationships[J].
Scottish Journal of Political Economy, 2003, 48(3): 345-359.
|
| [13] |
CAI C J, RAJU J S. Keeping your enemies closer: when market entry as an alliance with your competitor makes sense[J].
Marketing Science, 2016, 35(5): 743-755.
DOI: 10.1287/mksc.2016.0988. |
| [14] |
付红, 马永开, 唐小我. 制造商持股供应商情形下的组装供应链协调[J].
系统工程理论与实践, 2014, 34(9): 2265-2273.
FU Hong, MA Yongkai, TANG Xiaowo. Coordination of assembly supply chain when manufacturer holds equity in suppliers[J]. Systems Engineering-Theory&Practice, 2014, 34(9): 2265-2273. |
| [15] |
马秋卓, 宋海清, 陈功玉. 碳配额交易体系下企业低碳产品定价及最优碳排放策略[J].
管理工程学报, 2014, 28(2): 127-136.
MA Qiuzhuo, SONG Haiqing, CHEN Gongyu. A study on low-carbon product pricing and carbon emission problems under the cap-and-trade system[J]. Journal of Industrial Engineering/Engineering Management, 2014, 28(2): 127-136. DOI: 10.3969/j.issn.1004-6062.2014.02.017. |
| [16] |
ZHU W, HE Y. Green product design in supply chains under competition[J].
European Journal of Operational Research, 2016, 258(1): 165-180.
|
| [17] |
赵道致, 原白云, 徐春秋. 考虑消费者低碳偏好未知的产品线定价策略[J].
系统工程, 2014, 32(1): 77-81.
ZHAO Daozhi, YUAN Baiyun, XU Chunqiu. Product line pricing based on the unknown consumer low-carbon preference[J]. Systems Engineering, 2014, 32(1): 77-81. DOI: 10.3969/j.issn.1005-2542.2014.01.012. |
| [18] |
周木生, 张玉林. 基于非线性边际支付意愿的信息产品定价策略研究[J].
系统工程理论与实践, 2014, 34(3): 710-716.
ZHOU Musheng, ZHANG Yulin. Study of pricing of information goods on the basis of nonlinear marginal willingness to pay[J]. Systems Engineering –Theory &Practice, 2014, 34(3): 710-716. |
| [19] |
王春苹, 南国芳, 李敏强, 等. 寡头市场信息产品与服务的最优定价策略[J].
管理科学学报, 2016, 19(3): 92-106.
WANG Chunping, NAN Guofang, LI Minqiang, et al. Optimal pricing for information goods and complementary services in duopoly markets[J]. Journal of Management Sciences in China, 2016, 19(3): 92-106. DOI: 10.3969/j.issn.1007-9807.2016.03.007. |
| [20] |
VERNIK D A, PUROHIT D, DESAI P S. Music downloads and the flip side of digital rights management[J].
Marketing Science, 2011, 30(6): 1011-1027.
DOI: 10.1287/mksc.1110.0668. |
| [21] |
聂佳佳, 石纯来. 零售商纵向持股对制造商直销渠道选择的影响[J].
软科学, 2016, 30(3): 130-135.
NIE Jiajia, SHI Chunlai. The effect of retailer's vertical sharing on supplier's launching direct channels[J]. Soft Science, 2016, 30(3): 130-135. DOI: 10.3969/j.issn.1002-9753.2016.03.011. |
| [22] |
YUE X, LIU J. Demand forecast sharing in a dual-channel supply chain[J].
European Journal of Operational Research, 2006, 174(1): 646-667.
DOI: 10.1016/j.ejor.2004.12.020. |
| [23] |
陈忠, 艾兴政. 双渠道信息共享与收益分享合同选择[J].
系统工程理论与实践, 2008, 28(12): 42-51.
CHEN Zhong, AI Xingzheng. Choice of forecasting information sharing and revenue sharing contract between dual-channel[J]. Systems Engineering –Theory &Practice, 2008, 28(12): 42-51. DOI: 10.3321/j.issn:1000-6788.2008.12.005. |
| [24] |
艾兴政, 唐小我, 马永开. 传统渠道与电子渠道预测信息分享的绩效研究[J].
管理科学学报, 2008, 11(1): 12-21.
AI Xingzheng, TANG Xiaowo, MA Yongkai. Performance of forecasting information sharing between traditional channel and E-channel[J]. Systems Engineering –Theory &Practice, 2008, 11(1): 12-21. DOI: 10.3321/j.issn:1007-9807.2008.01.002. |
| [25] |
聂佳佳. 预测信息分享对制造商开通直销渠道的影响[J].
管理工程学报, 2012, 26(2): 106-112.
NIE Jiajia. The effect of forecast information sharing on manufacturer's launching direct channels[J]. Journal of Industrial Engineering/Engineering Management, 2012, 26(2): 106-112. DOI: 10.3969/j.issn.1004-6062.2012.02.015. |
 2018, Vol. 21
2018, Vol. 21

