随着城市经济的发展，小汽车数量不断增加，由此带来的交通拥堵造成了巨大的社会经济损失。根据韩国交通运输研究所的交通拥堵成本估算，在2007年由交通拥堵造成的经济损失约为14.4万亿美元^[1]。而信号控制作为缓解城市交通拥堵的有效途径之一，发挥着其重要的作用。

当今的信号控制方法主要分为：定时控制、感应控制和自适应控制。定时控制方法^[2]是基于历史数据，通过对交叉口历史数据的收集，计算获得信号配时方案，其基本假设为交叉口的交通需求保持不变，并没有考虑到需求的波动性。感应控制是通过在交叉口停车线上游设置检测器，通过检测结果判断当前相位绿灯时间是否延长，其一定程度上解决了固定信号配时方法的不足；但其基于简单判断规则，并不能使交叉口的效益最大化。自适应控制则是在预测未来交通需求的基础上优化交叉口信号配时方案，能够很大程度上降低交叉口的车辆延误。现有的自适应控制系统主要有：澳大利亚的SCATS^[3]、英国的SCOOT^[4]、法国的PRODYN^[5]、意大利的UTOPIA^[6]、美国的OPAC^[7]、法国的CRONOS^[8]和美国的RHODES^[9]等。

但现有的自适应控制系统主要依赖于传统的线圈或者视频检测设施，这将带来以下两个缺陷。1)线圈检测器只能检测固定位置的车辆通过信息，并不能直接获取车辆的状态信息(如：位置、速度和加速度等)，视频检测器主要可以收集交通流量、空间占有率和排队长度等宏观信息。2)自适应控制系统对检测器的要求非常高，其检测的可靠性对控制系统有很大的影响，一旦检测器故障或失效将会使控制效果骤降，且检测器具有安装、维护成本高和使用寿命低等缺点^[10]。近年来，在电子信息和无线通信等技术^[11]的推动下，“车路协同”系统以车—车、车—路通信为基础，实现了信息在系统内部的快速、准确和有效的传输。因此，在车路协同环境下，很容易获取车辆的位置和速度等信息^[12]；且由于车路协同车载装置基于车辆个体，个别故障不会对整体产生较大的影响；因此，基于此构建的信号控制系统鲁棒性较好。随后，相关学者^[13-20]研究了如何有效利用车路协同数据优化信号配时方案。Priemer等^[13]首次概念性地提出车路协同技术在信号控制上的应用，其假设交叉口通讯设施与车载装置的无线通讯距离可能达到300 m。通讯的数据包括：车辆牌号、位置、速度、时间戳以及车载装置收集的其他交通信息等。受到通讯距离的限制，其优化步长为5 s，优化时间窗为20 s，采用动态规划和完全枚举算法寻找最优解。张存保等^[14]研究了基于车路协同的单点信号控制优化方法，提出了如何利用车路协同数据计算交叉口延误和停车次数。Lee等^[15-16]基于车速恒定假设，研究了车路协同环境下交叉口动态信号配时方法，该方法优化时间步长为5 s，优化时长为20 s，采用全枚举算法求解模型。同时，车路协同技术在协调控制的研究也相继展开。吴伟等^[17]研究了车路协同环境下基于动态车速的相位差优化方法。Feng等^{[10, 18]}在车联网环境下，以COP算法^[19]为基础，建立了以车辆延误和排队长度为优化目标，相位绿灯时长为约束的双环信号结构优化模型，讨论了车载设施渗透率对模型优化结果的影响；并提出了车联网环境下单交叉口控制优化体系的基本框架^[20]。

综上可知，车路协同设施相对于传统的检测设施和设备，具有较好的鲁棒性，且检测的交通信息更为全面，如：可实时检测车辆的位置、速度、加速度和与之相关的时间戳信息，基于此优化的信号配时方案将更能适应交通需求特征。同时，从现有研究来看，虽然有效地利用了车路协同数据来提高交叉口的信号控制效率，但存在一些缺点，如：优化时间步长过长，优化时间区间较短和大多采用枚举算法，存在求解效率低等问题。

为解决现有的研究缺陷，充分利用车路协同环境提供的交通信息，本文提出了一种车路协同环境下基于遗传算法的交叉口自适应实时控制优化模型。在车路协同环境下，首先，基于车辆的位置和速度等信息采用文献[21]中的车辆到达预测方法预测下游交叉口的到达分布；然后，以预测结果作为输入，交叉口车辆平均延误为优化目标，各相位绿灯时长为决策变量，最小绿灯时长为约束条件，建立信号配时优化模型。该模型不再受优化时长的约束，可以根据实际预测区间和相位绿灯时长，设定优化时长。最后，采用遗传算法求解模型，实现了交叉口实时自适应控制。

1 车路协同环境下的自适应信号配时优化模型 1.1 车辆到达预测

传统的交通流预测模型往往是基于集计思想，如只能知道未来1分钟或者几分钟甚至1小时的交通流量，不能对每辆车的到达时间进行预测，使自适应控制系统达不到理想的控制效果。而在车路协同环境下，很容易获得车辆位置和速度等信息，基于此可对车辆到达交叉口的时间进行预测。所以文中采用文献[21]中的方法对各个方向的车流进行预测。将预测的车辆到达结果作为优化模型的基础数据，根据建立优化模型和算法，实现对交叉口信号配时方案的优化。

1.2 优化模型

对一个典型的四路交叉口来说，可能存在多个转向，在不考虑右转车辆的情况下，通常分为4个方向的左转和直行，共8个转向。为了使文中优化模型具有普遍性，假设交叉口转向集合为 $P = \{ 1,2, \cdots, p\} $ ，即共 $ p $ 个转向，优化时长为 $ T $ 。则可用信号状态矩阵表示各转向各个时刻的信号灯色，其中 ${{M}}$ 表示整个优化时长各转向的信号灯色矩阵。

$\quad\quad{{M}} = \left\{ {{X_1},{X_2}, \cdots ,{X_T}} \right\}{\text{。}}$

(1)

$\quad\quad{{{X}}_t} = \left(\!\! {\begin{array}{*{20}{c}}{{x_{1,t}}}\\{{x_{2,t}}}\\ \vdots \\{{x_{p,t}}}\end{array}}\!\! \right),{x_{p,t}} = \left\{\! {\begin{array}{*{20}{c}}{0,} & {{\text{红灯信号}}}\\{1,} & {{\text{绿灯信号}}}\\{2,} & {{\text{黄灯信号}}}\end{array}} \right.\!\!\!,\;t \in \left[ {1,T} \right]{\text{。}}$

(2)

式中， ${{{X}}_t}$ 表示 $ t $ 时刻各个转向信号灯色状态矩阵， ${x_{p,t}}$ 表示 $ t $ 时刻转向 $ p $ 的信号灯状态值。

随着交叉口信号的变化，各个转向的车辆排队长度随着时间不断变化，表示为

$\quad\quad{{{L}}_t} = \left( {\begin{array}{*{20}{c}} {{l_{1,t}}} \\ {{l_{2,t}}} \\ \vdots \\ {{l_{p,t}}} \end{array}} \right),t \in \left[ {1,T} \right]{\text{。}}$

(3)

式中， ${{{L}}_t}$ 表示 $ t $ 时刻各个转向的排队车辆数矩阵， ${l_{p,t}}$ 表示 $ t $ 时刻转向 $ p $ 的排队车辆数；其中，初始排队矩阵用 ${{{L}}_0}$ 表示，车路协同环境下，可以通过设置车辆速度阈值来判断车辆是否处于停车状态，并结合车辆位置信息直接计算获得各个进口道的排队车辆数。

采用文献[21]中的方法对下游各个时刻(粒度为1 s)的到达车辆数进行预测，其中左转、直行车辆按交叉口历史转向信息分配^[22]，所以各转向的 $ t $ 时刻到达的车辆数矩阵表示为

$\quad\quad{{{A}}_t} = \left( {\begin{array}{*{20}{c}} {{a_{1,t}}} \\ {{a_{2,t}}} \\ \vdots \\ {{a_{p,t}}} \end{array}} \right),t \in \left[ {1,T} \right]{\text{。}}$

(4)

式中， ${a_{p,t}}$ 表示 $ t $ 时刻转向 $ p $ 到达的车辆数。

而各转向 $ t $ 时刻离去的车辆数矩阵表示为

$\quad\quad{{{D}}_t} = \left( {\begin{array}{*{20}{c}} {{d_{1,t}}} \\ {{d_{2,t}}} \\ \vdots \\ {{d_{p,t}}} \end{array}} \right),t \in \left[ {1,T} \right]{\text{。}}$

(5)

式中， ${d_{p,t}}$ 表示 $ t $ 时刻转向 $ p $ 离去的车辆数。

同时，各个转向的饱和流率矩阵表示为

$\quad\quad{{S}} = \left( {\begin{array}{*{20}{c}} {{s_1}} \\ {{s_2}} \\ \vdots \\ {{s_p}} \end{array}} \right){\text{。}}$

(6)

式中， ${s_p}$ 表示转向 $ p $ 的饱和流率，辆/s，可由该转向的车道组的饱和流率直接计算获得。

式(5)中当前时刻该转向离去车辆数与当前时刻的初始排队车辆数、信号灯色和饱和流率有关，以下将具体分析不同情况下离去车辆数量的计算方法，以 $ t $ 时刻转向 $ p $ 为例。可分为以下3种情况进行讨论。

1) 当该转向的信号灯色为红灯时，即 ${x_{p,t}} = 0$ 时，由于该转向不放行，则离去车辆数为0，即 ${d_{p,t}} = 0$ 。

2) 当该转向的信号灯色为绿灯或者黄灯时，即 ${x_{p,t}} = 1$ 或 ${x_{p,t}} = 2$ 时，且当该转向的初始排队车辆数和到达车辆数小于等于最大离去车辆数(与该转向的饱和流率有关)，即 ${a_{p,t}} + {l_{p,t - 1}} {\text{≤}} {s_p}$ ，则此时的离去车辆为该转向的排队车辆数和到达的车辆数之和，即 ${d_{p,t}} = {a_{p,t}} + {l_{p,t - 1}}$ 。

3) 与情况2类似，且当该转向的排队车辆数和到达车辆数大于最大离去车辆数，即 ${a_{p,t}} + {l_{p,t - 1}} {\text{＞}} {s_p}$ ，则此时的离去车辆为最大离去车辆数(饱和流率)，即 ${d_{p,t}} = {s_p}$ 。

综上分析可知，式(5)可表示为

${d_{p,t}} \!= \!\left\{\!\!\! {\begin{array}{*{20}{l}} {0,}&{{x_{p,t}} \!=\! 0}; \\ {{q_{p,t}} + {l_{p,t - 1}},}&{\left( {{x_{p,t}} \!=\! 1 \vee {x_{p,t}} \!=\! 2} \right) \wedge \left( {{a_{p,t}} \!+\! {l_{p,t - 1}} {\text{≤}} {s_p}} \right)}; \\ {{s_p},}&{\left( {{x_{p,t}} \!=\! 1 \vee {x_{p,t}} \!=\! 2} \right) \wedge \left( {{a_{p,t}} \!+\! {l_{p,t - 1}} {\text{＞}} {s_p}} \right)}{\text{。}}\end{array}} \right.$

(7)

式中， $ \vee $ 和 $ \wedge $ 分别表示并集和交集操作符号。

则根据车辆累计算法(IQA算法^[23])， $ t $ 时刻排队车辆数可由 $ t - 1 $ 时刻的排队车辆数、 $ t $ 时刻的到达车辆数和离去车辆数计算得出，计算公式如式(8)所示：

$\quad\quad{{{L}}_t} = {{{L}}_{t - 1}} + {{{A}}_t} - {{{D}}_t},\;\; {t {\text{≥}} 1} {\text{。}}$

(8)

式中，当 $t = 1$ ， ${{{L}}_0}$ 表示各个转向的初始排队车辆数，而在车路协同环境下，各个转向的初始排队车辆很容易获取，而在后文VISSIM^[24]车路协同仿真环境下可用COM^[25]接口提供的排队计数器模拟车路协同环境获取初始排队长度。

采用IQA延误计算模型可通过累计排队车辆数计算交叉口的累计延误。由于文中时间离散步长为1 s，因此，每个时间步长的车辆数等于车辆的总延误值。当优化时间区间为 $ T $ 时，采用IQA延误模型可计算延误为

$\quad\quad{\rm{Delay}} = \sum\limits_{i = 1}^p {\sum\limits_{t = 1}^T {{l_{i,t}}} } {\text{。}}$

(9)

式中 ${\rm{Delay}}$ 为给定信号配时方案下，该方案总的车辆延误值，单位为s。

实际信号配时方案中，各个转向的绿灯时长矩阵可表示为

$\quad\quad{{G}} = \left( {\begin{array}{*{20}{c}} {{g_1}} \\ {{g_2}} \\ \vdots \\ {{g_p}} \end{array}} \right){\text{。}}$

(10)

式中， ${g_p}$ 表示转向 $p$ 的绿灯时长。

可以发现，式(9)中计算延误需要给定式(1)中的各个转向的信号状态矩阵 $ {{M}} $ 。以下将通过一个具体实例来说明信号配时方案 $ {{G}} $ 如何与各个转向的信号状态矩阵 $ {{M}} $ 相互转换。假设一个交叉口为8个转向，4个放行相位，相序为东西左转、东西直行、南北左转和南北直行。若相位清空时间r=0 s，黄灯时间y=3 s，优化时长T=102 s。假设一个信号配时方案为(20 s, 30 s, 30 s, 10 s)，则其中 $ G $ 可表示为(20 s, 30 s, 30 s, 10 s, 20 s, 30 s, 30 s, 10 s)。则

${{M}} = \left\{ {{{{X}}_{\rm{1}}},{{{X}}_{\rm{2}}}, \cdots ,{{{X}}_{{\rm{102}}}}} \right\} = \left(\!\! {\begin{array}{*{20}{c}} {{x_{1,1}}}&{{x_{1,2}}}& \!\!\!\!\cdots\!\!\!\! &{{x_{1,102}}} \\ {{x_{2,1}}}&{{x_{2,2}}}& \!\!\!\!\cdots \!\!\!\!&{{x_{2,102}}} \\ \vdots & \vdots & & \vdots \\ {{x_{8,1}}}&{{x_{8,2}}}& \!\!\!\!\cdots\!\!\!\! &{{x_{8,102}}} \end{array}} \!\!\right){\text{。}}$

(11)

所以， $ {{M}} $ 与 ${{G}}$ 之间存在映射关系，可用函数表示：

$\quad\quad{{M}} = f\left( {{{G}},y,r} \right){\text{。}}$

(12)

式中，f表示某种映射函数关系，y表示黄灯时长，r表示清空全红时长。

考虑到信号配时中需要考虑最小绿灯时长约束，如式(13)所示：

$\quad\quad{{G}} {\text{≥}} {{{G}}_{\min }}{\text{。}}$

(13)

其中，

$\quad\quad{{{G}}_{\min }} = \left( {\begin{array}{*{20}{c}} {{g_{1,\min }}} \\ {{g_{2,\min }}} \\ \vdots \\ {{g_{p,\min }}} \end{array}} \right){\text{。}}$

(14)

同时，必须保证各个相位的绿灯时长、清空时长之和等于优化时长，如式(15)所示：

$\quad\quad\sum\limits_{j = 1}^k {\left( {{g_j} + y + r} \right)} = T{\text{。}}$

(15)

式中，k表示相位数，若2个转向同时放行，如典型的8转向4相位的交叉口中，东西左转一起放行，即为一个相位；所以所有放行相位时长之和为总的优化时长。实际优化时，若优化时长不足4个相位的总时长，可采取3个或2个相位优化一次的滚动优化方法。

综上可知，交叉口信号配时优化模型可表示如下：

$\quad\quad\left\{ \begin{array}{l}\min \; \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^p {\displaystyle\sum\limits_{t = 1}^T {{l_{i,t}}} } }}{{\displaystyle\sum\limits_{i = 1}^p {\displaystyle\sum\limits_{t = 1}^T {{d_{i,t}}} } }}{\text{。}}\\{\rm{s.t.}}\\{\begin{array}{l}{{{M}} = f\left( {G,y,r} \right),}\\{\displaystyle\sum\limits_{i = 1}^k {\left( {{g_i} + y + r} \right)} = T,}\\{{{G}} {\text{≥}} {{{G}}_{\min }}{\text{。}}}\end{array}} \end{array} \right.$

(16)

式中， $t = 1$ 时的初始排队为已知值，在式(8)中已说明。从模型(16)可知，决策变量为交叉口各个相位的绿灯时长；目标函数为交叉口的车均延误最小；约束条件为各相位的最小绿灯时长和优化时长约束。其中目标函数和决策变量为隐性函数关系，即给定决策变量取值，目标函数不能直接通过决策变量计算得出，但可以通过式(1)~(15)计算得到。因此，该模型可以认为是一个非线性优化问题，充分考虑到遗传算法具有一定的全局搜索能力，文中采用遗传算法求解该模型。

遗传算法涉及到解的编码与解码、选择规则、交叉规则、变异规则和参数的选取等问题。以下将讨论这几部分的内容。其中解的编码与解码必须要满足约束条件。以下将对相应的算法操作进行具体说明。

2 遗传算法 2.1 编码与解码

1) 编码。

常用的编码技术有二进制编码和实数编码，其中二进制编码不利于对等式约束的处理，文中模型涉及到等式约束，所以可用实数编码技术。针对k信号相位阶段，采用 $ k $ 个0–1之间的实数 $ {{R}} = $ $\left\{ {{R_1},{R_2}, \cdots ,{R_k}} \right\}$ 作为一个解。

2) 解码。

解码是通过基因来获得实际变量的取值，即通过 ${{R}}$ 来获得各个相位的绿灯时长，由于式(15)等式约束的影响，可采用以下方法解码获取各个相位的绿灯时长。

${g_i} = {g_{i,\min }} + \left\lfloor {\frac{{{R_i}}}{{\sum\limits_{i = 1}^k {{R_i}} }}\left( {T - \sum\limits_{i = 1}^k {\left( {{g_{i,\min }} + y + r} \right)} } \right)} \right\rfloor ,i = 1,2, \cdots ,k - 1;$

(17)

$\quad\quad{g_k} = T - \sum\limits_{i = 1}^{k - 1} {\left( {{g_i} + y + r} \right)} - y - r{\text{。}}$

(18)

从式(17)和(18)很容易知道，解码得到的绿灯时长不仅满足最小绿灯时长的约束，还满足式(15)中的等式约束。同时可根据相位和转向的关系获取各个转向的绿灯时长。

2.2 选择规则

遗传算法常用的选择规则有轮盘赌选择、随机遍历抽样选择和局部选择等方法，考虑轮盘法能够有效地保留较好的解，使算法更早地收敛，所以文中遗传算法采用轮盘赌选择规则。

2.3 交叉规则

常用的交叉规则有单点交叉和多点交叉，考虑到信号配时方案中基因较短，采用多点交叉可能会使解的稳定性降低，所以文中采用单点交叉规则。交叉规则的实现过程为首先随机选择交叉位置，再在交叉位置实现基因之间的交叉。如有两组基因分别(0.1, 0.2, 0.3, 0.4)和(0.4, 0.3, 0.2, 0.1)，若交叉点为第2个位置，则交叉产生的新的基因为：(0.1, 0.2, 0.2, 0.1)和(0.4, 0.3, 0.3, 0.4)。

2.4 变异规则

变异也分为多点变异和单点变异，考虑到可能与交叉出现相同的情况，即避免解的波动性太大，不能收敛，采用单点变异规则。首先确定变异的位置，再在变异位置产生新的随机数替代原来的随机数，形成新的基因。如基因：(0.1, 0.2, 0.3, 0.4)，若变异点为第2个点，则交叉产生的新的个体为：(0.1, 0.5, 0.3, 0.4)。

2.5 参数设置

通过实验测试不同参数模型的优化效果，最终文中遗传算法相关参数设置如表1所示。

3 实例分析

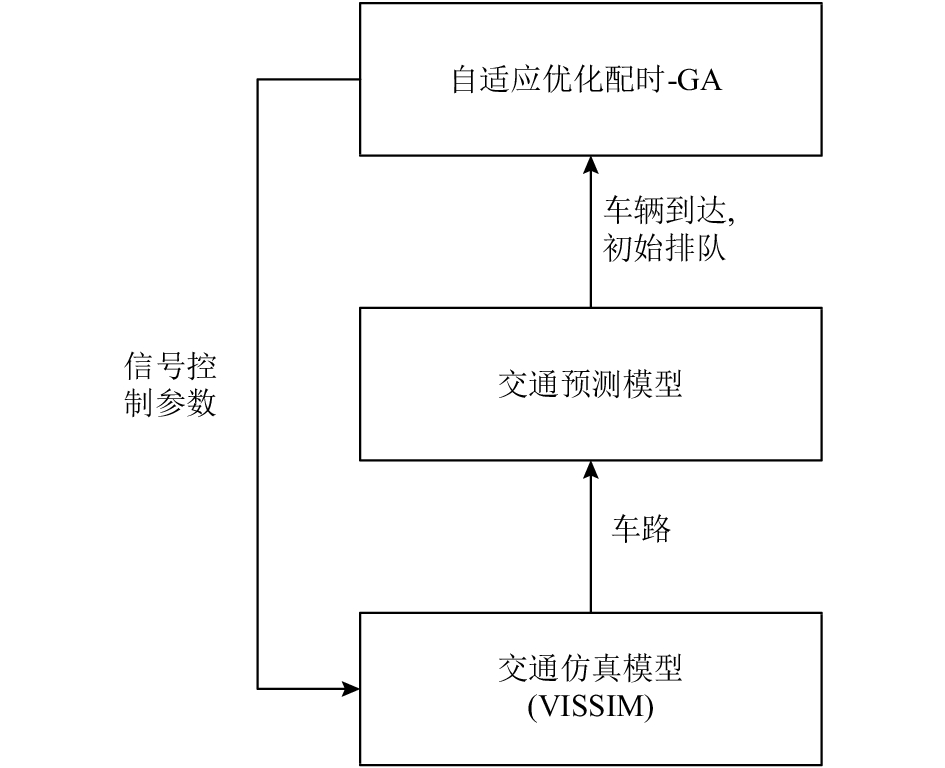
为证明文中模型的有效性，在VISSIM^[24]中构建车路协同环境，通过获取车辆状态信息实现车辆到达预测，从而根据预测数据采用遗传算法对交叉口信号配时方案进行优化，并将优化结果反馈到VISSIM中的信号控制机中，实时调整信号配时方案。同时，在相同交通条件下构建感应控制，以交叉口车均延误为控制目标，测试文中模型和感应控制的效果。文中仿真实验具体框架如图1所示。

首先在成都市选取合适的交叉口，如图2所示。现场调查收集交叉口的几何尺寸、交通流量、转向比和渠化情况等相关信息。通过现场调查可知，该交叉口所处路网为方格型路网，由于左转车流较大，进口道均设有左转专用车道。目前实施的信号配时方案为感应控制，且拥有4个相位，即东西左转、东西直行、南北左转和南北直行相位。通常情况下该交叉口处于非饱和状态，即每个周期积累的排队车辆均可在该周期内消散。

在不考虑右转车流的情况下，仅控制该交叉口8个转向即4个相位的车流，如图2中转向箭头所示。根据调查交叉口几何尺寸和渠化情况在VISSIM中构建仿真路网，并设置流量和转向比等信息。同时，为构建车路协同仿真环境，可通过Matlab访问VISSIM中的COM接口实时获取车辆的位置、速度和加速度等相关信息，用来模拟车路协同环境。且在交叉口各个车道组设置排队计数器和车辆延误检测器，检测车辆的初始排队长度和各个转向的车辆平均延误等信息。

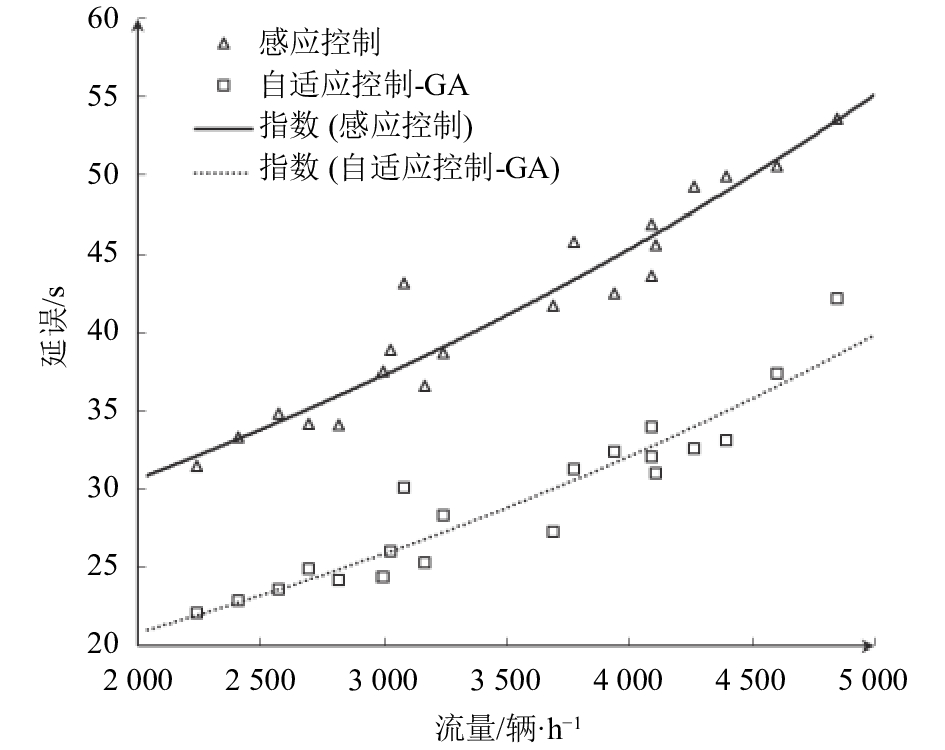
为证明文中模型的控制效果，以车均延误为评价目标，将文中自适应控制和感应控制进行比较分析。通过在仿真环境下改变路网输入流量(2 000~6 000 辆/h)，仿真不同流量状态(即非饱和状态到过饱和状态)下，文中自适应控制和感应控制的控制延误。不同交通流状态下文中模型和感应控制延误效果图如图3所示。

由图3可知，两种算法的车均延误均随车流量呈现指数增长趋势，与实际结果相符。与感应控制相比，文中自适应控制下交叉口的车辆平均延误减少了30%，证明了文中模型能够更好地优化交叉口信号配时方案。同时，在不同交通流状态下(即非饱和状态和过饱和状态)，文中自适应控制效果更优，说明文中自适应控制模型能够适用于各种交通流状态。

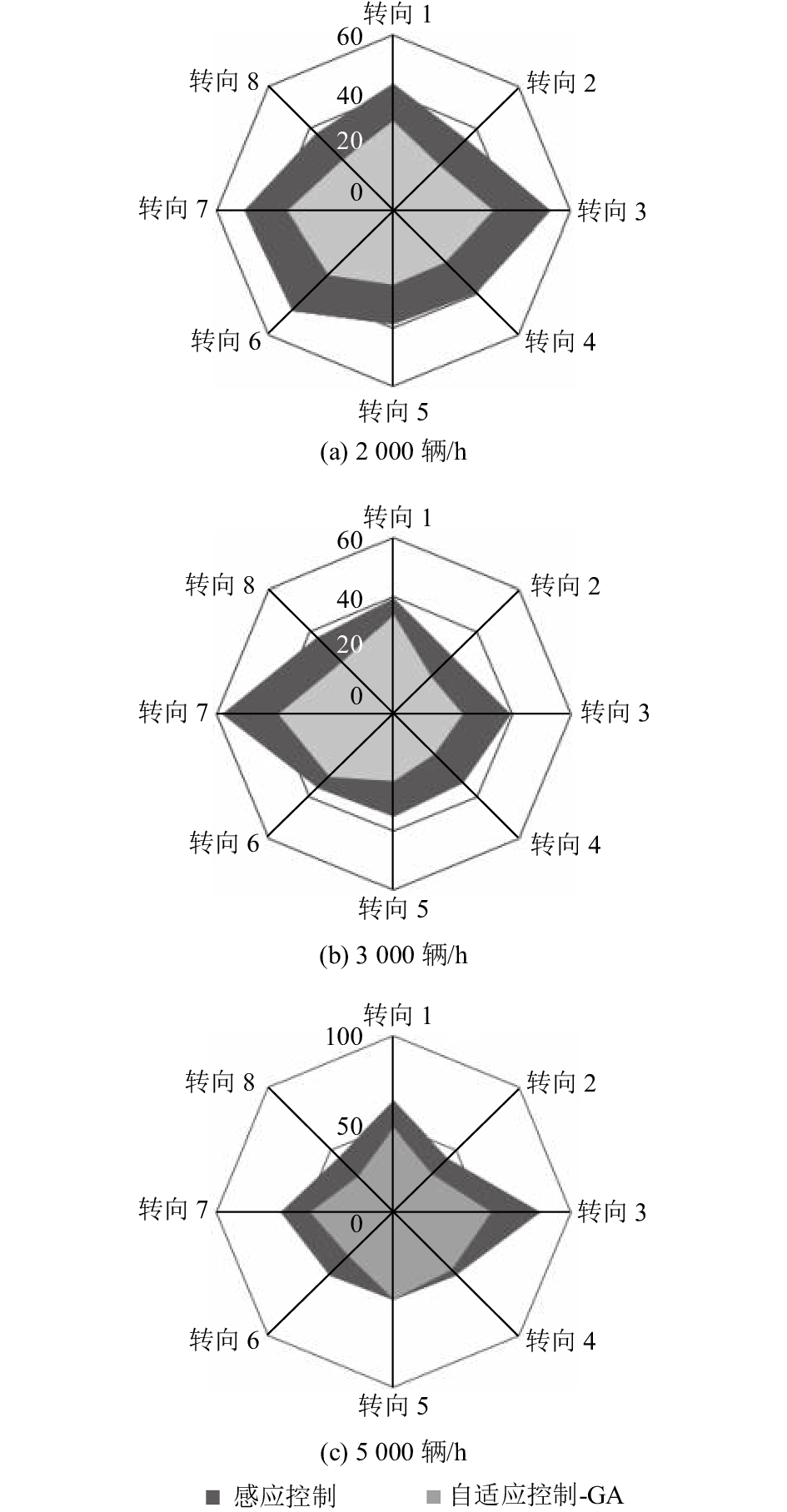
为比较两种控制方法在不同交通流状态下交叉口各个转向的车均延误，分别仿真交叉口流量在2 000、3 000和5 000 辆/h的情况下，文中自适应控制和感应控制两种不同控制方法的控制效果。根据VISSIM中的延误检测模块获取各个转向的车均延误，3种不同交通流条件下文中自适应控制和感应控制各转向车辆延误对比如图4所示，同时为比较各个转向延误均衡性，可计算各个转向的延误标准差值，计算结果如表2所示。

从图4可知，当交叉口流量变化时，文中自适应控制下交叉口各个转向的车均延误均比感应控制要小。同时根据表2可知，与感应控制相比，文中自适应控制下交叉口各个转向的延误标准差值更小，说明文中模型不仅能够优化交叉口的车均延误，还能够保证各个转向的延误均衡，这是因为车路协同环境下能够准确地获取交叉口各个转向的初始排队，使得优化模型能够均衡各个信号转向的排队长度，从而达到均衡转向延误的效果。

4 结论

本文提出了一种车路协同环境下基于遗传算法的交叉口自适应实时控制优化模型。基于实际调查数据在VISSIM构建车路协同微观仿真环境，并通过仿真实验证明了文中自适应控制优化模型的有效性。通过与感应控制相比，可以得出结论：1)文中模型使交叉口的平均延误减少了30%；2)同时能够保证交叉口各个转向的车辆延误均衡。

考虑到文中模型仅适用于单交叉口，未来将考虑在车路协同环境下多交叉口的协同优化算法，实现多交叉口的实时协同优化。同时，由于本文模型优化目标为延误最小，大多适用于非饱和状态交叉口，且文中并未考虑对交叉口相序的优化。因此，未来可针对饱和状态的交叉口或将相序引入优化模型，构建新的优化模型和算法，以达到改善交叉口运行状态的目的。