航空战略联盟(简称航空联盟)是航空公司之间合作的组织结构方式,也是一种国际竞争战略[1]。国内学术界对于航空联盟的定义是,通过一定的方式形成的收益共享、风险共担、资源共享的组织安排或者合作方式[2]。国内外关于航空联盟的成因有很多的研究。Dresner等[3]认为航空战略联盟形成的主要原因,是企业加入战略联盟后产生了正向的效应,产生了更多的收入和更多的利润。Youssef[4]认为是规模经济以及共同市场力这两种因素促进航空公司结成航空联盟。Oum等[5]将航空战略联盟形成的原因归为成本节约、营销优势、合作定价等6个方面。而Gudmundsson等[6]研究发现航空业形成战略联盟的因素可以分为4类。Evans[7]将航空公司加入航空战略联盟的动因分为外因和内因两种。国内学者张怀明[8]认为航空战略联盟的动因主要是各国政府对国际航空市场管制的放松。黎群[9]从航空业网络经济性的角度研究得出,航空战略联盟能够降低生产成本和交易成本。谢泗薪等[10] 的研究与Evans[7]类似,将航空公司加入航空联盟的原因分为内外两种。
有很多文献是研究航空联盟对航空公司绩效的影响。Drenser等[3]认为航空联盟能增加收入和降低成本。而Brueckner[11]通过实证研究验证了2个航空公司在结盟前后价格上升了5%,但并没有显著性。Park等[12]通过实证研究得出参与航空联盟的成员的旅客运输量会上升,运价会下降。Oum等[13]发现航空联盟会使枢纽之间航线增加,业务量会增大。Chua等[14]认为航空联盟对大型航空公司的成本有消极的影响,对小型航空公司有较小的积极影响。Du[15]通过实证分析认为代码共享能够提高航空公司的价格和运输量。Iatrou等[16]认为航空联盟不同合作方式会因为成本、运输量、收益不同而有不同的影响。王新安等[17]认为代码共享能提高航空公司的运营效率,但限制了竞争。
目前收益分配机制的研究已经由单个航空公司扩展到了航空联盟。收益管理通过构建模型来预测未来的需求,确定最优的价格和存量[18]。Wright等[19]以2个航空公司的Markov模型来分析不同成员对收益分配机制的影响。Wynne[20]研究了航线距离的分配机制可能导致联盟收益比单独运营少。Netessine等[21]研究2条航线的航线网络收益分享机制。Vinod[22]提出了基于转移价格的动态收益分配方法,对集中决策下和分散式决策下的收益分配机制进行了对比分析。de Man等[23]从动态的角度分析航空联盟的收益分配机制,认为航空联盟通过平均分配可以使航空联盟更稳定。Graf等[24]将期权的思想运用到收益分配机制中。Talluri等[25]提出了静态和动态的舱位收益控制方法。Goetz等[26]研究航空联盟从合作到竞争的影响因素。Cavalcante [27]研究得出合作关系决定航空联盟之间的定价。
一般而言,收益分配机制可以分为静态和动态。静态的收益分配方法主要包括固定比例分配、固定份额以及航程比例分配等。静态的收益分配方法比动态的收益分配方法简单,动态的收益分配方法主要是Nash谈判模型、收益/风险分配比例、Shapley值收益模型等。因为实际操作问题,动态的收益分配方法运用得比较少。但动态收益分配方法是未来的发展方向。本文要解决的问题是,结合动态的收益分配方法,考虑航班的实际运营成本以及航班的市场特质,对航空联盟内部成员的代码共享合作提出了一个完整的收益分配方案,实现双方利益的最大化。
1 基本决策模型理性决策者从利益最大化出发进行决策,航空公司加入航空联盟的主要目的也是为了获得更高的收益,因此假设航空公司都是理性的决策者,追求自身的收益最大化。本文参考Flores-Fillol[28]的启发式算法的函数构建收益分配模型。
1.1 前提和假设假设考虑一个由2个航空公司(设为航空公司1和2)和3个城市(设为A,H,B)组成的航线网络,其中H是A和B城市的中转枢纽城市。2个航空公司和3个城市的航线网络结构如图1所示。本文在建立模型之前,提出如下假设:1) 航空公司1和2都采用点—点的全对称航线网络结构,因此AH、BH和AB 3条航线都是直飞(对于枢纽的航线网络结构在航线AB上航空公司1和2可以选择直飞,或者经停H城市,此类网络结构另文进行了研究);2) AH、BH、AB这3条航线都没有其他外部选择(如汽车、高铁等),所有的旅客都选择飞机作为出行方式;3) 航线网络AH、BH和AB由航空公司1和航空公司2来承担。随着科学技术的发展,人们可以选择飞机、高铁、动车或自驾等不同交通工具便捷出行,而飞机往往是对于时间敏感的商务人士首选,且远距离出行时(如:广州至新疆、广州至洛杉矶等,若是选乘其他交通,需耗费较长时间或是较难到达)也将优先考虑飞机,因此本文假设研究的航线上没有外部选择。此外,各航空公司相互合作组成航空联盟,该联盟将与其他航空公司、航空联盟或其他出行方式等进行竞争,以期获取更多的“蛋糕”,之后航空联盟中的合作航空公司将基于一定规则分配所获得的“蛋糕”,那么航空联盟如何在竞争市场上获取更大的“蛋糕”,以及如何分配“蛋糕”,都是值得研究的问题。本文主要研究“蛋糕”的分配问题,因此并未涉及其他出行方式的影响,这也与Cavalcante[27]、Wan等[29]、李实萍等[30]研究假设一致。
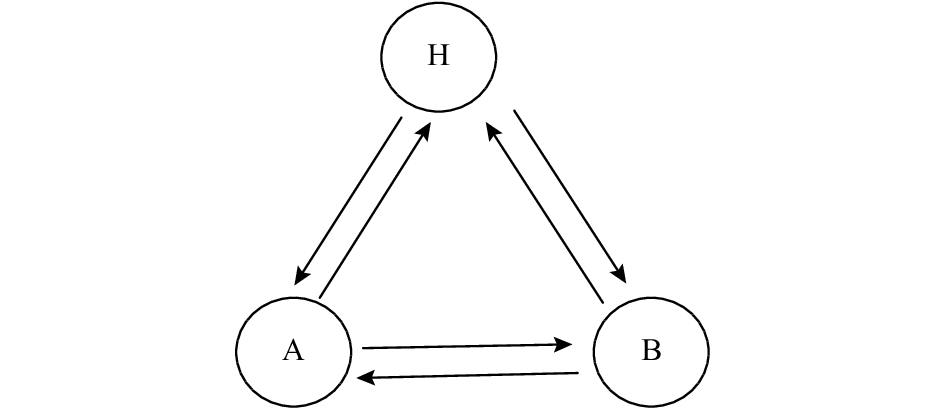
|
图 1 航空战略联盟航线网络结构 Fig. 1 Airline strategic alliance route network structure |
本文所采用的变量如表1所示。
| 表 1 变量定义 Tab. 1 Variable definitions |
1) 效用函数。
本文构建的效用函数由3部分组成,分别是消费支出、服务质量和旅行福利。其中,消费支出
另外,本文考虑顾客的忠诚度对航空公司决策的影响。假设顾客对航空公司
综上所述,航空公司
| $\quad\quad U = y + {f_i} - {p_i} + a{\text{。}}$ | (1) |
其中y=Y+b,且a>0表示顾客偏好于航空公司1。
2) 需求函数。
根据假设可知AH、BH、AB为3条不同的航线,但本文研究的是全航线网络结构,因此AH、HB和AB可视为同类型的航线,因此可以类似讨论。对于J(J=AH,BH,AB) 航线而言,由于顾客没有其他外部选择,则可以认为完全被航空公司承运。如果旅客对航空公司1有偏好,也即是具有忠诚度(即a>0),所以选择航空公司1出行。其条件表达如下:
| $\quad\quad y + {f_{1,J}} - {p_{1,J}} + a {\text{>}} y + {f_{2,J}} - {p_{2,J}}{\text{。}}$ | (2) |
即
区别于Brueckner[11]设定需求函数,本文认为旅客1忠诚于航空公司1,即a>0的情况下,顾客做出决策时也会对另外一家航空公司的服务质量有歧视[11]。除了在总量上两家航空公司的效用相差a之外,本文假设顾客对另外一家航空公司的航班价格和航班频次的认知都有歧视,设这种服务的差异为参数λ(0<λ≤1)。相应地,顾客选择航空公司1的前提条件可改写为
| $\quad\quad a {\text{>}}{p_{1,J}} - \lambda {p_{2,{\rm{J}}}} - {f_{1,J}} + \lambda {f_{2,J}}{\text{。}}$ | (3) |
此外,航空公司1承担J(J=AH,BH,AB)航线运营的需求函数是
| $\begin{split}\quad\quad{q_{1,J}} = \displaystyle\int_{{p_{1,J}} - \lambda {p_{2,J}} - {f_{1,J}} + \lambda {f_{2,J}}}^{\frac{\beta }{2}} {\frac{1}{\beta }{\rm{d}}a =}\\{\displaystyle\frac{1}{2} - \frac{1}{\beta }\left( {{p_{1,J}} - \lambda {p_{2,J}} - {f_{1,J}} + \lambda {f_{2,J}}} \right)} {\text{。}}\end{split}$ | (4) |
同理可得,航空公司2的需求函数是
| $\begin{split}\quad\quad{q_{2,J}} = \displaystyle\int_{ - \frac{\beta }{2}}^{{p_{1,J}} - \lambda {p_{2,J}} - {f_{1,J}} + \lambda {f_{2,J}}} {\frac{1}{\beta }{\rm{d}}a =}\\ {\displaystyle\frac{1}{2} - \frac{1}{\beta }\left( {{p_{2,J}} - \lambda {p_{1,J}} - {f_{2,J}} + \lambda {f_{1,J}}} \right)} {\text{。}}\end{split}$ | (5) |
3) 成本函数。
由于本文研究的是全航线网络结构,假定航空公司在AH、BH和AB航线上的运营成本包括该航线起飞的成本和每一个座位服务的成本,即
综上所述,航空公司i(i=1,2)在航线J(J=AH、BH、AB)上的总运营成本为
| $\quad\quad{C_{1,J}}\left( {{q_{1,J}},{f_{1,J}}} \right) = \theta {f_{1,J}} + \tau {s_{1,J}} = \theta {\left( {{f_{1,J}}} \right)^2} + \tau {q_{1,{\rm{J}}}}{\text{。}}$ | (6) |
假设航空公司1和2没有合作组成航空战略联盟,它们是个体理性的分散决策个体,此时各个航空公司都由自身利益最大化的角度出发来决定各航线上航班的机票价格和航班的频率等。
基于前文假设,航空公司1的收益函数
| $\quad\quad{\pi _1} = \mathop \sum \limits_{J = {\rm{AH}},{\rm{BH}},{\rm{AB}}} \left\{ {{p_{1,J}}{q_{1,J}} - \left[ {\theta {{\left( {{f_{1,J}}} \right)}^2} + \tau {q_{1,J}}} \right]} \right\}{\text{。}}$ | (7) |
在全航线网络结构中,A、B、H是对等的,所以说AB、AH和BH3个市场是完全对等的,则可以得到每个航空公司在3个不同市场的票价和航班频率是一致的,对于航空公司1而言,则有
| ${\pi _1} = 3\left[ {\left( {{p_1} - \tau } \right)\left( {\frac{1}{2} - \frac{1}{\beta }\left( {{p_1} - \lambda {p_2} \!-\! {f_1} \!+\! \lambda {f_2}} \right)} \right) \!- \theta {{\left( {{f_1}} \right)}^2}} \right]{\text{。}}$ | (8) |
根据式(8)易证π1是票价p1和航班频率f1的联合凹函数,通过一阶导数分别对票价和航班频率求导,可以得到票价和航班频率的最优解是关于航空公司2的票价和航班频率的函数。类似地,可以建立航空公司2的收益函数π2,求解后可得其最优票价和航班频率是关于航空公司1的票价和航班频率的函数。因此,联立后可求解得:
| $\quad\quad{p_{i,{\rm{AB}}}}^* = {p_{i,{\rm{AH}}}}^* = {p_{i,{\rm{BH}}}}^* = \frac{{\theta {\beta ^2} + 2\beta \tau \theta - \tau + \lambda \tau }}{{4\theta \beta - 2\beta \lambda \theta - 1 + \lambda }},$ | (9) |
| $\quad\quad{f_{i,{\rm{AB}}}}^* \!=\! {f_{i,{\rm{AH}}}}^* = {f_{i,{\rm{BH}}}}^* \!=\! \frac{{\beta - 2\tau + 2\lambda \tau }}{{2\left( {4\theta \beta \!-\! 2\beta \lambda \theta \!-\! 1 \!+\! \lambda } \right)}}{\text{。}}$ | (10) |
其中,i=1,2。
1.4 集中决策模型当航空公司1和航空公司2进行合作决策时,即合作双方在航空战略联盟中采用集中决策的模式,那么航空公司之间不存在效用的转移。本模型同样考虑全对称的航线网络结构,3个城市A、B、H对市场都是直达的,也就是说,3个城市之间是相互连接,独立运行。整个收益函数如下所示:
| $\quad\quad{{\pi} _{\rm{C}}} \!=\! {\pi _1} \!+\! {\pi _2} \!=\! \mathop \sum \limits_{i = 1}^2 \left\{ {\underbrace {3{p_i}{q_i}}_{{\rm{AH}},{\rm{BH}},{\rm{AB}}} \!- 3\underbrace {\left[ {\theta {{\left( {{f_i}} \right)}^2} + \tau {q_i}} \right]}_{{C_{i,{\rm{AH}}}} = {C_{i,{\rm{BH}}}} = {C_{i,{\rm{AB}}}}}} \right\}{\text{。}}$ | (11) |
其中i=1,2表示航空公司1和2,且3个航线是完全对称的,即AB=AH=BH。
对于航空公司i(i=1,2)而言,由于AH、BH和AB3个航空市场是完全对等的,因此
| ${p_{i,{\rm{AB}}}}^{\rm{C}} = {p_{i,{\rm{AH}}}}^{\rm{C}} = {p_{i,{\rm{BH}}}}^{\rm{C}} = \frac{{\theta {\beta ^2} + 2a\tau \theta \left( {1 - \lambda } \right) - {{\left( {1 - \lambda } \right)}^2}\tau }}{{\left( {1 - \lambda } \right)\left( {4\theta \beta - 1 + \lambda } \right)}},$ | (12) |
| $\quad\quad{f_{i{\rm{AB}}}}^{\rm{C}} = {f_{i,{\rm{AH}}}}^{\rm{C}} = {f_{i,{\rm{BH}}}}^{\rm{C}} = \frac{{\beta - 2\tau \left( {1 - \lambda } \right)}}{{2\left( {4\theta \beta - 1 + \lambda } \right)}}{\text{。}}$ | (13) |
前文的航空联盟收益分配模型得到的是航空公司之间通过合作能获取的最大收益,但是并没有涉及具体的收益分配方案,因此下文将确定航空联盟公平合理的收益分配方案。目前有多种收益分配机制,例如:Shapley值收益分配法、Nash谈判模型的收益分配方法、收益/风险分配方法以及基于核心理论的收益分配方法等。本文选择基于Shapley值来讨论航空战略联盟的收益分配方案。Shapley值模型是由Shapley L.S.提出的用来解决多人合作决策的问题,Shapley值模型是合作博弈中对所有参与者都有公平性的解。
2.1 基于Shapley值的分配模型战略联盟由多个成员组成,战略联盟成立的原因是因为战略联盟产生的收益大于单个成员收益之和。联盟成员之间的合作具有非对抗性,那么加入联盟的成员增加并不会引起总收益的减少,而会带来最大的收益。基于Shapley值的分配模型考虑了各联盟成员对联盟总目标的贡献程度,避免了分配上的平均主义,比单独考虑资源投入价值、资源配置效率及将两者结合的分配方式更为合理、公平,同时也体现联盟中各成员之间的博弈过程。Shapley值模型的参数定义如表2所示。
| 表 2 基于Shapley值分配模型的参数定义 Tab. 2 Parameter definitions based on the Shapley value allocation model |
设有限集合I={1,2,…,n},对于集合I存在任何一个子集合S对应存在一个实值函数ν(s),满足以下条件:
| $\begin{array}{l}\quad\quad\nu \left( \varnothing \right) = 0,\\\nu \left( {{s_1}\mathop \cup \nolimits {s_2}} \right) {\text{≥}} \nu \left( {{s_1}} \right) \!+\! \nu \left( {{s_2}} \right),{s_1}\mathop \cap \nolimits {s_2} \!=\! \varnothing ,{s_1} \!\subseteq\! I,{s_2} \!\subseteq\! I{\text{。}}\end{array}$ | (14) |
这个实值函数ν(s)是多人协作集合I对策的特征函数。
同时,满足联盟的最大效益是大于单个成员效益之和,即
| $\quad\quad\mathop \sum \limits_{i = 1}^n {x_i} = v\left( I \right)\text{且}{x_i} {\text{>}} v\left( i \right),\;\;\;i = 1,2,3, \ldots ,n{\text{。}}$ | (15) |
其中,每个成员可得到的分配量为
| $\quad\quad{\varphi _i}\left( v \right) = \mathop \sum \limits_{s \in {s_i}} \omega \left( {\left| s \right|} \right)\left[ {v\left( s \right) - v\left( {\left( {s/i} \right)} \right)} \right]{\text{。}}$ | (16) |
其中
Shapley值收益分配方法不仅考虑了个体对整体的贡献,还考虑了个体的投资以及风险。Shapley值具有配置集体理性,任何合作博弈都拥有Shapley值,加上这种方法是不会分配利益给对联盟没有贡献的参与人,所以被认为是比较公平的方法,因为将所有人对联盟的贡献都考虑在内,但是Shapley值方法并没有考虑主导企业的作用。
2.2 考虑风险的Shapley值收益分配模型在基本的Shapley值收益分配模型中加入风险因素。其中,风险因素的调整因子(简称风险因子)是
| $\quad\quad 1 + {{\Delta }}{r_i} = 1 + \left( {{r_i} - \frac{1}{n}} \right),\;\;i = 1,2, \ldots ,n{\text{。}}$ | (17) |
风险因子1+Δri表示航空公司根据风险程度所应得到的实际收益。当1+Δri<1,则表明航空公司i相对于联盟中其他航空公司所承担的风险较小,则应该分配的收益要少。反之亦然,当1+Δri>1,表明航空公司i所承担的风险较大,应该得到的收益更多。所以航空战略联盟中航空公司i在考虑风险的情况下,应得收益是
| ${\varphi _i}\left( v \right)' = \left( {1 + {\rm{\Delta }}{r_i}} \right){\varphi _i}\left( v \right) = \left[ {1 + \left( {{r_i} - \frac{1}{n}} \right)} \right]{\varphi _i}\left( v \right),\;\;i = 1,2, \ldots ,n{\text{。}}$ | (18) |
基于Shapley值的利益分配中假设航空战略联盟中各成员风险分担均等,为此加入航空业的风险因素对Shapley值法的利益分配方案进行适当的修正。航空战略联盟合作存在的不确定因素和不可控制的因素较多,导致了航空战略联盟的风险呈现复杂性。按照风险的来源可以将风险分为外部风险和内部风险两种,外部风险包括政治风险、市场风险、经济风险、意外灾害风险等;内部风险包括运营风险、技术风险、合作风险、投资风险等。
确定不同航空公司的风险评价方法有很多,常用的方法有DEA数据包络法、灰色关联分析法、敏感性分析法等。航空公司承受的风险指标很多都不能用量化描述的定量指标,更多是定性指标。本文采用模糊综合评价方法对航空战略联盟风险系数进行测算。模糊综合评价法是以模糊数学理论为基础,应用模糊关系合成原理将一些不易量化的因素进行定量处理,根据不同的因素对对象进行综合评价。模糊综合评价法的优点是简单易掌握,对多因素、多层次的复杂问题评价效果较好。
根据航空战略联盟所面临的风险分析,可以得到航空战略联盟风险的影响因素,如表3所示。据模糊综合评价法,用R表示航空战略联盟中各个航空公司承担的风险,可以得到风险因素集G={政治风险,市场风险,经济风险,意外灾害风险,运营风险,技术风险,合作风险,投资风险}。根据航空战略联盟风险影响程度的不同,针对不同的因素赋予权重
模糊综合评价法中,从风险因素集合U到V的模糊关系矩阵,也即是计算指标权重大小的方法,本文采用德尔菲法,这是一种主观赋权法,通过邀请航空业或者该领域的专家对不同的评判指标进行衡量并赋予相应的权重系数。针对9个风险因素对航空战略联盟中航空公司风险的贡献程度进行评分,为了便于统计,将专家的评价结果转化成[0,1]区间,可以得到不同风险因素的模糊向量。
| 表 3 航空战略联盟风险的影响因素评价表 Tab. 3 Factors affecting the evaluation of airline strategic alliance risk |
完成不同风险因素的评价结果统计后,将评价结果组成一个矩阵,即可以得到从G到V的模糊关系矩阵
| $\quad\quad\begin{array}{l}{R} = {\left( {{X_{\text{政治风险}}},{X_{\text{市场风险}}},{X_{\text{经济风险}}},{X_{\text{意外灾害风险}}},{X_{\text{运营风险}}},{X_{\text{能力风险}}},{X_{\text{合作风险}}},{X_{\text{投资风险}}}} \right)^{\rm{T}}} =\left[ {\begin{array}{*{20}{c}}{{r_{11}}}& \cdots &{{r_{15}}}\\ \vdots &{}& \vdots \\{{r_{91}}}& \cdots &{{r_{95}}}\end{array}} \right]{\text{。}}\end{array}$ | (19) |
通过模糊关系矩阵对评价对象进行模糊综合评判,并通过矩阵运算得到权重值,而如果Z中各分子的分量之和不等于1,则进行归一化处理。
| $\begin{array}{l}{Z} \!=\! {XR} \!=\! \left( {{w_1},{w_2},{w_3},{w_4},{w_5},{w_6},{w_7},{w_8},{w_9}} \right)\left[ \!\!{\begin{array}{*{20}{c}}{{r_{11}}}&\!\!\!\!\!\!\!\! \cdots \!\!\!\!\!\!\!\!&{{r_{15}}}\\ \vdots &\!\!\!\!\!\!\!\!{}\!\!\!\!\!\!\!\!& \vdots \\{{r_{91}}}& \!\!\!\!\!\!\!\!\cdots\!\!\!\!\!\!\!\! &{{r_{95}}}\end{array}} \!\!\right] =\\\left[ {{z_1},{z_2},{z_3},{z_4},{z_5}} \right],\end{array}$ | (20) |
| $\quad\quad{R'} = {Z'}{{V}^{\rm{T}}}。$ | (21) |
传统的Shapley值法是注重公平,无风险偏好的收益分配方法,定义每一个联盟成员所承受的风险是一致的。但是在现实中,不同联盟成员的风险存在差异,不同的航空公司的规模,所处的市场环境,自身的技术能力等方面都存在差异,不同航空公司所承受的风险是不一样的。所以本文通过德尔菲法和模糊综合评价方法对航空公司所承受的风险进行评价,得到风险因子,将风险因子加入收益分配模型中,得到航空公司在考虑风险的情况下应得的收益,如式(17)和式(18)所示。
2.4 考虑航空联盟风险的Shapley值收益分配模型设航空战略联盟的合作对策I=(N,v), N={1,2}(1和2分别代表航空公司1和航空公司2),ν(s)是合作对策I的特征函数。ν({1})和ν({2})分别是航空公司1和航空公司2不结盟时所取得的各自收益。ν({1,2})是两家航空公司构成联盟的总收益。
在基本决策模型中,讨论了集中决策下所得到的收益表示联盟后的收益,以及分散决策下的收益表示不联盟各自运营的收益。结合Shapley值的收益分配模型,可以得到联盟的特征值
| $\left\{ {\begin{array}{*{20}{l}}{\nu \left( {\left\{ \varnothing \right\}} \right) = 0;}\\{\nu \left( {\left\{ 1 \right\}} \right) = 3\left[ {\left( {{p_1} \!-\! \tau } \right)\left( {\displaystyle\frac{1}{2} \!-\! \displaystyle\frac{1}{\beta }\left( {{p_1} \!-\! \lambda {p_2} \!-\! {f_1} \!+\! \lambda {f_2}} \right)} \right) - \theta {{\left( {{f_1}} \right)}^2}} \right];}\\{\nu \left( {\left\{ 2 \right\}} \right) = 3\left[ {\left( {{p_2} \!-\! \tau } \right)\left( {\displaystyle\frac{1}{2} \!-\! \displaystyle\frac{1}{\beta }\left( {{p_2} \!-\! \lambda {p_1} \!-\! {f_2} \!+\! \lambda {f_1}} \right)} \right) \!-\! \theta {{\left( {{f_2}} \right)}^2}} \right];}\\{\nu \left( {\left\{ {1,2} \right\}} \right) = 3\left( {p - \tau } \right) - \displaystyle\frac{6}{\beta }\left( {1 - \lambda } \right)\left( {p - f} \right) - 6\theta {f^2}{\text{。}}}\end{array}} \right.$ | (22) |
其中:
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\left\{ {\begin{array}{*{20}{l}}\displaystyle{p = \frac{{\theta {\beta ^2} + 2 \beta \tau \theta \left( {1 - \lambda } \right) - {{\left( {1 - \lambda } \right)}^2}\tau }}{{\left( {1 - \lambda } \right)\left( {4\theta \beta - 1 + \lambda } \right)}},}\quad {f = \displaystyle\frac{{\beta - 2\tau \left( {1 - \lambda } \right)}}{{2\left( {4\theta \beta - 1 + \lambda } \right)}};}\\\displaystyle{{p_1} = \frac{{\theta {\beta ^2} + 2\beta \tau \theta - \tau + \lambda \tau }}{{4\theta \beta - 2\beta \lambda \theta - 1 + \lambda }},}\quad {{f_1} = \displaystyle\frac{{\beta - 2\tau + 2\lambda \tau }}{{2\left( {4{\rm{\theta }}\beta - 2\beta {\rm{\lambda \theta }} - 1 + {\rm{\lambda }}} \right)}};}\\\displaystyle{{p_2} = \frac{{\theta {\beta ^2} + 2\beta \tau \theta - \tau + \lambda \tau }}{{4\theta \beta - 2\beta \lambda \theta - 1 + \lambda }},}\quad {{f_2} = \displaystyle\frac{{\beta - 2\tau + 2\lambda \tau }}{{2\left( {4\theta \beta - 2\beta \lambda \theta - 1 + \lambda } \right)}}{\text{。}}}\end{array}} \right.$ |
将其代入式(22)可得到特征值的数值。
根据考虑风险的Shapley值模型,ri是通过模糊综合评价方法得到的风险因子,每个成员所分配得到的收益是
| $\quad\quad{\varphi _i}\left( v \right)' = \mathop \sum \limits_{s \in {s_i}} \left( {1 + \left( {{r_i} - \frac{1}{n}} \right)} \right)\omega \left( {\left| s \right|} \right)\left[ {v\left( s \right) - v\left( {\frac{s}{i}} \right)} \right]{\text{。}}$ | (23) |
其中
所以航空公司1和航空公司2分配得到的收益分别为:
| $\begin{split}& {\varphi _1}\left( v \right)' = \left( {1 + \left( {{r_1} - \displaystyle\frac{1}{2}} \right)} \right)\left\{ {\left[ {\nu \left( {\left\{ 1 \right\}} \right) - \nu \left( {\left\{ \varnothing \right\}} \right)} \right]\displaystyle\frac{{\left( {2 - \left| 1 \right|} \right)!\left( {\left| 1 \right| - 1} \right)!}}{{2!}} + \left[ {\nu \left( {\left\{ {1,2} \right\}} \right) - \nu \left( {\left\{ 2 \right\}} \right)} \right]\displaystyle\frac{{\left( {2 - \left| 2 \right|} \right)!\left( {\left| 2 \right| - 1} \right)!}}{{2!}}} \right\}=\\& \displaystyle\frac{{\left( {1 - 2{r_1}} \right)\left( {{\pi _{\text{分散},1}} + {\pi _{\text{集中},1\mathop \cup \nolimits 2}} - {\pi _{\text{分散},2}}} \right)}}{4} = \displaystyle\frac{{\left( {1 - 2{r_1}} \right)\left\{ {2\left( {\lambda - 1} \right){p^2} + \left[ {1 + 2\left( {1 - \lambda } \right)f + 2\left( {1 - \lambda } \right)\tau } \right]p + 2\beta \theta {f^2} + 2\lambda \tau f - \beta \tau } \right\}}}{{4\beta }},\end{split}$ | (24) |
| $\begin{split}& {\varphi _2}\left( v \right)' = \left( {1 + \left( {{r_2} - \displaystyle\frac{1}{2}} \right)} \right)\left\{ {\left[ {\nu \left( {\left\{ 2 \right\}} \right) - \nu \left( {\left\{ \varnothing \right\}} \right)} \right]\displaystyle\frac{{\left( {2 - \left| 1 \right|} \right)!\left( {\left| 1 \right| - 1} \right)!}}{{2!}} + \left[ {\nu \left( {\left\{ {1,2} \right\}} \right) - \nu \left( {\left\{ 1 \right\}} \right)} \right]\displaystyle\frac{{\left( {2 - \left| 2 \right|} \right)!\left( {\left| 2 \right| - 1} \right)!}}{{2!}}} \right\}=\\& \displaystyle\frac{{\left( {1 - 2{r_2}} \right)\left( {{\pi _{\text{分散},2}} + {\pi _{\text{集中},1\mathop \cup \nolimits 2}} - {\pi _{\text{分散},1}}} \right)}}{4} \!=\! \displaystyle\frac{{\left( {1 - 2{r_2}} \right)\left\{ {2\left( {\lambda - 1} \right){p^2} \!+\! \left[ {1 + 2\left( {1 - \lambda } \right)f + 2\left( {1 - \lambda } \right)\tau } \right]p + 2\beta \theta {f^2} + 2\lambda \tau f - \beta \tau } \right\}}}{{4\beta }}{\text{。}}\end{split}$ | (25) |
本文在构建航空战略联盟收益分配方案的基础上,对南航和X航空公司在A-B-H航线网络中的合作收益,考虑风险的Shapley值收益分配模型进行收益分配。本文参数的确定是参考两家航空公司的对外公布的数据和信息进行调整。南航与航空战略联盟中的X航空公司进行合作,选取其中一个航线网络结构A-H-B城市,双方在城市A和城市B,中转城市H这3个航空市场中展开合作。两家航空公司的规模、营业收入等方面接近,所以将南航(N航)和X航的边际航班运营成本和座位的边际成本设为相等,其中旅客对南航的忠诚度较高。相关参数的确定如下,影响旅客对航空公司的忠诚度a的产品差异化程度β=2;每个航班起飞的边际运行成本θ=2.5;每一个座位的边际成本τ=0.02, 消费者心理感知偏差λ=0.3。
两家航空公司在集中决策的收益分配模型下所取得的收益是双方合作能取得的最大收益值,在分散决策情况下的收益分配模型所取得的是双方各自单独运行所取得的收益。根据上面的基本决策模型,计算可得集中和分散决策模式下的最优决策及其收益,具体如表4所示。
| 表 4 集中与分散决策模式下的均衡结果 Tab. 4 Equilibrium results in centralized and decentralized decision models |
两家航空公司合作可以记为I={N,X},两家航空公司独立运营得到的收益为v(N)=0.288, v(X)=0.288,两家航空公司合作的集合收益是v(N∪X)=0.683。
根据Shapley值可以计算得到两家航空公司分配得到的收益,具体如表5和表6所示。
| 表 5 N航空公司的分配收益 Tab. 5 Distribution benefits of N Airlines |
| 表 6 X航空公司的分配收益 Tab. 6 Distribution benefits of X Airlines |
此外,两家航空公司得到的收益比单独运营时得到的收益高。由于两家航空公司的规模不同,所处的市场特性不同,公司的员工素质和技术水平不同,所以两家航空公司所承担的风险也不一样。风险承受得越高,则分配得到的收益则越高。根据上面对航空联盟中不同航空公司的风险因子确定办法,分别对N和X航空公司进行风险因素的确定。假设得到两家公司的风险影响因子是RN=0.9, RX=0.6,进行归一化处理可以得到修正后的风险因子是rN=0.6, rX=0.4,从而对以上的Shapley值进行修正,可以得到:
| $\begin{split}\quad\quad\displaystyle{\varphi _{\rm{N}}}{\left( v \right)'} = {\varphi _{\rm{N}}}\left( v \right)\left[ {1 + \left( {{r_{\rm{N}}} - \frac{1}{n}} \right)} \right] =0.342 \times {\Bigg{[}}1+\\\displaystyle \left. { \left( {0.6 - \frac{1}{2}} \right)} \right] = 0.376, \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\end{split}$ | (26) |
| $\begin{split}\quad\quad\displaystyle{\varphi _{\rm{X}}}{\left( v \right)'} = {\varphi _{\rm{X}}}\left( v \right)\left[ {1 + \left( {{r_{\rm{X}}} - \frac{1}{n}} \right)} \right] =0.342 \times{\Bigg{[}}1 +\\\displaystyle \left. { \left( {0.4 - \frac{1}{2}} \right)} \right] = 0.307{\text{。}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\end{split}$ | (27) |
由于N航空公司在运营A-B-H航线的时候比X航空公司承受更大的风险,所以在经过风险因素的修正之后,N航空公司分配得到更多的收益。不同分配方式的结果如表7所示。
| 表 7 不同分配方式的结果对比 Tab. 7 Comparison of the results of different allocation methods |
平均分配的方法并不能反映双方的投入程度,会对收益偏小的一方产生消极的影响。按照单干比例分配收益,在单干情况收益较大的一方将获得更大份额的收益,但是不能反映双方合作后的增效作用。在Shapley值收益分配模型之下,可以反映贡献较大的一方所应该得到的收益。考虑了风险因素之后,在考虑公平性的前提下考虑各航空公司所承担的风险因素,则更能与自身情况相匹配,从而得到一个较为合理有效的收益分配方法。
4 结论本文考虑航空公司的产品差异性、心理感知偏差、航班起飞和座位的成本,构建航空战略联盟的收益决策模型,并且分别讨论集中决策和分散决策模式下的最优定价和频次。然后,通过考虑风险的Shapley值方法对最大化的收益进行合理的分配,从而为航空公司提供一个收益分配的解决方案。最后将模型的研究结论运用到实际中,研究南航的航空联盟收益分配方案。
当然,本文是在一定基本合理假设基础上展开的研究,因此存在以下几方面继续研究的可能性。1) 本文只考虑了全对称的航线网络结构情况,其他不同航线网络结构的收益分配方案值得进一步研究。2) 本文构建的收益分配模型中,只考虑了两家航空公司3个市场的简单情况,但是实际中航线网络结构更复杂,如:航空公司进行多方面的合作、竞争对手有可能是多个、存在国内外多个竞争市场对航空联盟产生影响等,考虑更为复杂且贴近实际的航空联盟收益分配问题是未来研究方向。3) 本文假设各航线上没有其他外部选择,而现今社会人们可以选择飞机、高铁、动车或自驾等交通工具出行,如何将航线上的其他外部选择纳入决策模型之中,研究航空战略联盟与其他外部选择进行竞争时的收益分配问题。
| [1] |
文军. 航空联盟形成机理及协调管理中若干问题研究[D]. 成都: 西南交通大学, 2008
WEN Jun. Research on some issues of the formation mechanism and coordination management about airline alliance[D]. Chengdu: Southwest Jiaotong University, 2008 |
| [2] |
聂金艳. 航空联盟的经济动因及低成本航空联盟的可行性分析[J].
空运商务, 2011(19): 4-8.
|
| [3] |
DRESNER M E, WINDLE R J. Alliances and code-sharing in the international airline industry[J].
Built Environment, 1996, 22(3): 201-211.
|
| [4] |
YOUSSEF W. Causes and effects of international airline equity alliances[D]. USA: University of California at Berkeley, 1992
|
| [5] |
OUM T H, PARK J, ZHANG A. Globalization and strategic alliances: the case of the airline industry[J].
Transportation Quarterly, 2000, 57(3): 179-180.
|
| [6] |
GUDMUNDSSON S V, RHOADES D L. Airline alliance survival analysis: typology, strategy and duration[J].
Transport Policy, 2001, 8(3): 209-218.
DOI: 10.1016/S0967-070X(01)00016-6. |
| [7] |
EVANS N. Collaborative strategy: an analysis of the changing world of international airline alliances[J].
Tourism Management, 2001, 22(3): 229-243.
DOI: 10.1016/S0261-5177(01)00024-3. |
| [8] |
张怀明. 从" 开放天空协定”看美国的国际航空政策[J].
国际航空, 1998(9): 48-50.
ZHANG Huaiming. View the int'l air transportation policy of US through Open Sky Treaty[J]. International Aviation, 1998(9): 48-50. |
| [9] |
黎群. 航空公司战略联盟的网络经济性分析[J].
北京交通大学学报(社会科学版), 2003, 2(3): 20-24.
LI Qun. Analysing the economies of network about airline alliance[J]. Journal of Beijing Jiaotong University (Social Sciences Edition), 2003, 2(3): 20-24. DOI: 10.3969/j.issn.1672-8106.2003.03.005. |
| [10] |
谢泗薪, 康燕, 周尚志. 航空公司战略联盟新视野[J].
中国民用航空, 2001(3): 40-46.
Xie Sixin, KANG Yan, ZHOU Shangzhi. A new perspective on strategic alliance of airlines[J]. China Civil Aviation, 2001(3): 40-46. |
| [11] |
BRUECKNER J K. The economics of international codesharing: an analysis of airline alliances[J].
International Journal of Industrial Organization, 2004, 19(10): 1475-1498.
|
| [12] |
PARK J H, ZHANG A. Airline alliances and partner firms’ outputs[J].
Transportation Research Part E Logistics & Transportation Review, 1998, 34(4): 245-255.
|
| [13] |
OUM T H, ZHANG A. Key aspects of global strategic alliances and the impacts on the future of Canadian airline industry[J].
Journal of Air Transport Management, 2001, 7(5): 287-301.
DOI: 10.1016/S0969-6997(01)00023-0. |
| [14] |
CHUA C L, KEW H, YONG J. Airline code-share alliances and costs: imposing concavity on translog cost function estimation[J].
Review of Industrial Organization, 2005, 26(4): 461-487.
DOI: 10.1007/s11151-005-0223-6. |
| [15] |
DU Y. Code-sharing in the U. S. airline industry[D]. USA: Oregon State University, 2008
|
| [16] |
IATROU K, ALAMDARI F. The empirical analysis of the impact of alliances on airline operations[J].
Journal of Air Transport Management, 2005, 11(3): 127-134.
DOI: 10.1016/j.jairtraman.2004.07.005. |
| [17] |
王新安, 杨秀云. 航空公司之间的代码共享及其对民航业的影响[J].
兰州大学学报(社会科学版), 2005, 33(1): 99-103.
WANG Xin’an, YANG Xiuyun. Code sharing and the civil aviation industry[J]. Journal of Lanzhou University(Social Sciences), 2005, 33(1): 99-103. DOI: 10.3969/j.issn.1000-2804.2005.01.019. |
| [18] |
罗利, 萧柏春. 收入管理理论的研究现状及发展前景[J].
管理科学学报, 2004, 7(5): 75-83.
LUO Li, XIAO Bochun. Revenue management: state –of-the-art and future prospects[J]. Journal of Management Sciences in China, 2004, 7(5): 75-83. DOI: 10.3321/j.issn:1007-9807.2004.05.011. |
| [19] |
WRIGHT C P, GROENEVELT H, SHUMSKY R A. Dynamic revenue management in airline alliances[J].
Transportation Science, 2010, 44(1): 15-37.
DOI: 10.1287/trsc.1090.0300. |
| [20] |
WYNNE R. From queen airs to RJS: evolution in major-regional airline alliances and code sharing//Handbook of Airline Economics[M]. New York: Aviation Week Group, McGraw-Hill, 1995
|
| [21] |
NETESSINE S, SHUMSKY R A. Revenue management games: horizontal and vertical competition[J].
Management Science, 2005, 51(5): 813-831.
DOI: 10.1287/mnsc.1040.0356. |
| [22] |
VINOD B. Practice papers: alliance revenue management[J].
Journal of Revenue & Pricing Management, 2005, 4(1): 66-82.
|
| [23] |
DE MAN A P, ROIJAKKERS N, DE GRAAUW H. Managing dynamics through robust alliance governance structures: the case of KLM and Northwest Airlines[J].
European Management Journal, 2010, 28(3): 171-181.
DOI: 10.1016/j.emj.2009.11.001. |
| [24] |
GRAF M, KIMMS A. Transfer price optimization for option-based airline alliance revenue management[J].
International Journal of Production Economics, 2013, 145(1): 281-293.
DOI: 10.1016/j.ijpe.2013.04.049. |
| [25] |
TALLURI K, RYZIN G V. Revenue management under a general discrete choice model of consumer behavior[J].
Management Science, 2004, 50(1): 15-33.
DOI: 10.1287/mnsc.1030.0147. |
| [26] |
GOETZ C F, SHAPIRO A H. Strategic alliance as a response to the threat of entry: evidence from airline codesharing[J].
International Journal of Industrial Organization, 2011, 30(6): 735-747.
|
| [27] |
CAVALCANTE C S C. Price effects of airline alliances – design and modeling[J].
Journal of Transport Literature, 2013, 7(2): 253-267.
DOI: 10.1590/S2238-10312013000200013. |
| [28] |
FLORES-FILLOL R. Airline competition and network structure[J].
Transportation Research Part B Methodological, 2009, 43(10): 966-983.
DOI: 10.1016/j.trb.2009.03.002. |
| [29] |
WAN X, ZOU L, DRESNER M. Assessing the price effects of airline alliances on parallel routes[J].
Transportation Research Part E Logistics & Transportation Review, 2009, 45(4): 627-641.
|
| [30] |
李实萍, 崔毅. 风险规避型航空联盟的收益共享机制研究[J].
工业工程, 2014, 17(4): 47-53.
LI Shiping, CUI Yi. Revenue sharing mechanism for risk-averse airline alliances[J]. Industrial Engineering Journal, 2014, 17(4): 47-53. DOI: 10.3969/j.issn.1007-7375.2014.04.009. |
| [31] |
李实萍. 网络结构的不同组合对航空公司竞争的影响研究[J].
科研管理, 2014, 35(10): 57-68.
LI Shiping. The effects of different network structure on airlines competition[J]. Science Research Management, 2014, 35(10): 57-68. |
 2018, Vol. 21
2018, Vol. 21