一直以来,农户都面临着严峻的甚至可能继续激化的价格不确定性。市场价格的频繁波动,使农户的收益受到严重损害。如菜农和果农的滞销困境和牛奶价格波动导致的“倒奶宰牛”现象。因此解决农户面临的价格风险是一个重要问题。“公司+农户”型订单农业的出现在一定程度上可以缓解这种困境。但随着订单农业的发展,实践过程中也暴露出许多问题,使得公司与农户不能长期稳定合作。导致合作关系破裂的原因主要集中为:一是合约违约率居高不下;二是公司和农户之间利润分配不均。据报道,近年来全国包括“公司+农户”形式在内的各种形式订单农业合同违约率超过80%[1]。关于订单农业违约率方面的研究,国外学者Zylbersztajn等[2]2003年对巴西北部1 523户种植番茄的农户进行了实地调研;Tang等[3]研究认为公司通过向农户提供市场价格信息和其他的销售渠道,可以达到双赢;Jorge等[4]认为交易过程中的程序公平能够一定程度地降低农户的违约率;Tang等[5]研究部分保证价(partially-guaranteed-price)合同,这种合同可使双方均受益。国内学者曹艳爱[6]认为市场的不确定性是导致违约率居高不下的一个重要的原因;叶飞等[7-8]研究得出“保底收购,随行就市”无法防止公司在市场行情不好时的机会主义行为,公司存在违约风险,并提出了协调订单农业供应链的契约机制。
关于供应链运作效率的研究,浦徐进等[9]认为应构建多种流通渠道并存的农产品供应链;凌六一等[10]研究了在随机产出与随机需求下不同的风险分担合同。张焕勇等[11]研究认为公司分担农户的部分种植成本,并给予农户合理的补贴,双方效用及供应链的整体效用都会有所提升;Chen等[12]认为信息能够降低市场价格的不确定性。
综上所述,现有文献对于双渠道订单农业供应链合作过程中的违约机理进行专门研究的并不是很多,已有的重点研究主要体现在以下几个方面:1) 从宏观方面对订单农业中的违约问题进行分析并提出对策建议[13-15];2) 用博弈论的方法对订单农业供应链的运作进行定量分析,并提出不同的契约形式来协调供应链[16-19]。基于上述分析,本文试图构建数理模型,定量比较公司与农户在守约和违约两种行为决策下的收益,深入分析在不同模型下的合约设计对于双方行为选择和利润的影响,从而为我国订单农业的可持续发展提出可供借鉴的建议。
1 基本模型的构建 1.1 模型假设本文研究由一个农户和一个公司所组成的两级农产品供应链,其中公司为主导者,农户为跟随者(该农户指某一地域范围内的具有一定规模的种植大户或合作社组织)。在生产季节,公司与农户签订“保底收购,随行就市”合约,规定保底收购价格
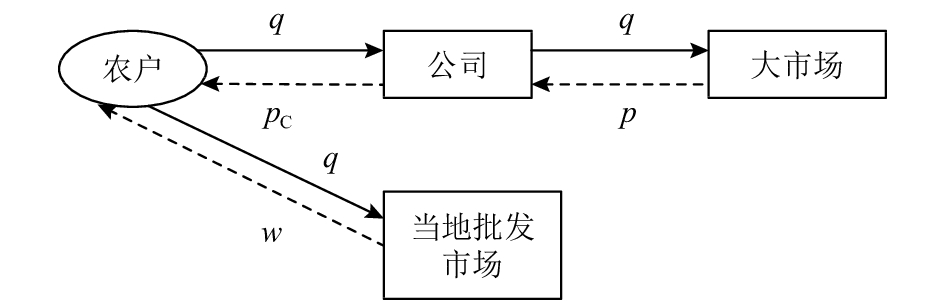
|
图 1 双渠道农产品供应链示意图 Fig. 1 Dual channel agricultural supply chain |
为了建立模型和讨论问题方便,在此提出以下假设。
1) 农户的生产量为
2) 农产品的销售渠道可分为:(1) 通过与公司签订合约到达大市场;(2) 直接卖给当地的批发市场。设大市场的农产品零售价格为
3) 公司与农户都为风险中性的决策个体。
4) 上标“
公司没有与农户签订收购合约,农户和公司只能在当地批发市场出售/收购农产品。此时农户的关于产量
| $\quad\quad E\left( {{\textit{π}} _{\rm{f}}^{\rm{l}}} \right) = \bar w{q^{\rm{l}}} - \left({s_0} + {s_1}{q^{\rm{l}}} + \frac{{{s_2}}}{2}{\left( {{q^{\rm{l}}}} \right)^2}\right){\text{。}}$ | (1) |
由一阶最优条件可以得到,农户的最佳生产量为
| $\quad\quad E\left( {{\textit{π}} _{\rm{f}}^{{\rm{l*}}}} \right) = \frac{{{{\left( {\bar w - {s_1}} \right)}^2}}}{{2{s_2}}} - {s_0}{\text{。}}$ | (2) |
公司的期望利润函数为
| $\quad\quad E\left( {{\textit{π}} _{\rm{s}}^{\rm{l}}} \right) = \left( {\bar p - \bar w} \right){q^{\rm{l}}}{\text{。}}$ | (3) |
将农户的产量
| $\quad\quad E\left( {{\textit{π}} _{\rm{s}}^{{\rm{l*}}}} \right) = \frac{{\left( {\bar p - \bar w} \right)\left( {\bar w - {s_1}} \right)}}{{{s_2}}}{\text{。}}$ | (4) |
在集中决策模式下,整条供应链的期望利润函数为
| $\quad\quad E\left( {{\textit{π}} _{_{{\rm{sc}}}}^{\rm{c}}} \right) = \bar p{q^{\rm{c}}} - {s_0} - {s_1}{q^{\rm{c}}} - \frac{{{s_2}}}{2}{\left( {{q^{\rm{c}}}} \right)^2}{\text{。}}$ | (5) |
根据一阶最优条件可以得到,农产品的最优产量为
| $\quad\quad E\left( {{\textit{π}} _{_{{\rm{sc}}}}^{{\rm{c}}*}} \right){\rm{ = }}\frac{{{{\left( {\bar p - {s_1}} \right)}^2}}}{{2{s_2}}} - {s_0}{\text{。}}$ | (6) |
农户和公司分别追求自身利润的最大化,由于公司是主导方,所以首先由公司根据市场价格
对于给定的收购价格
| $\quad\quad E\left( {{\textit{π}} _{\rm{f}}^{\rm{d}}} \right) = E\left( {\max \left( {w,p_{\rm{C}}^{\rm{d}}} \right)} \right){q^{\rm{d}}} - \left( {{s_0} + {s_1}{q^{\rm{d}}} + \frac{{{s_2}}}{2}{{\left( {{q^{\rm{d}}}} \right)}^2}} \right){\text{。}}$ | (7) |
根据一阶最优条件,可得农产品的最优产量为
| $\quad \quad E\left( {{\textit{π}} _{\rm{f}}^{\rm{d}}} \right) = \frac{{{{\left( {\int_0^{p_{\rm{C}}^{\rm{d}}} {F\left( x \right)} {\rm{d}}x + \bar w - {s_1}} \right)}^2}}}{{2{s_2}}} - {s_0}{\rm{{\text{。}}}}$ | (8) |
公司的期望利润函数为
| $\quad\quad E\left( {{\textit{π}} _{\rm{s}}^{\rm{d}}} \right) = \left( {\bar p - E\left( {\max \left( {w,p_{\rm{C}}^{\rm{d}}} \right)} \right)} \right){q^{\rm{d}}}{\text{。}}$ | (9) |
将农产品的最优产量
| $\begin{split}&\quad\quad E\left( {{\textit{π}} _{\rm{f}}^{\rm{d}}} \right) - E\left( {{\textit{π}} _{\rm{f}}^{\rm{l}}} \right) = \left( {E\left( {\max \left( {w,p_{\rm{C}}^{\rm{d}}} \right)} \right) - \bar w} \right){q^{\rm{d}}} =\\&\left( {\int_{ - \infty }^{p_{\rm{C}}^{\rm{d}}} {F\left( x \right)} {\rm{d}}x} \right){q^{\rm{d}}}{\text{。}}\end{split}$ | (10) |
定理1 只有当
由于只有当
定理2 农户与公司在分散决策模型下签约时,农户的最佳生产量为
从定理2可以看出,在分散决策模式下,公司的最大期望利润是农户最大期望利润的2倍还多。这主要是因为在公司和农户的两级农产品供应链中,公司对于农户而言,实力大、规模大,具有强势的谈判地位,在供应链中占主导地位;而农户只能够根据公司的决策作出反应。同时可以发现,分散决策模式下的供应链整体期望利润少于集中决策下供应链整体利润。这是因为在分散决策模式下,公司和农户分别以自身利润最大化为目标,存在“双边际”效应。
定理3 农户与公司签订“保底收购,随行就市”合约对农户有利,对公司不利,公司存在违约风险。
若农户违约,将签约时的最优产量
对于公司而言,公司守约的最大期望利润为
在分散决策模型下的利润分配,对农户有利,对公司不利,公司存在违约风险,此时供应链不稳定。因此使用Nash构建的纳什协商模型来刻画双方的谈判过程。首先在双方谈判过程中,农户的期望利润为
双方进行纳什协商的决策函数为
| $\quad\quad \mathop {\max }\limits_{p_{\rm{C}}^{\rm{n}}} \left( {E\left( {{\textit{π}} _{\rm{f}}^{\rm{n}}} \right) - {d_{\rm{f}}}} \right)(E\left( {{\textit{π}} _{\rm{s}}^{\rm{n}}} \right) - {d_{\rm{s}}}){\text{。}}$ | (11) |
由式(11)的一阶最优条件可以得到
| $\quad\quad E({\textit{π}} _{\rm{f}}^{{\rm{n}}*}) = \frac{{{{\left( {\bar p - {s_1}} \right)}^2}}}{{4{s_2}}} - \frac{{\left( {\bar w - {s_1}} \right)\left( {2\bar p - 3\bar w + {s_1}} \right)}}{{4{s_2}}} - {s_0},$ |
| $\quad \quad E({\textit{π}} _{\rm{s}}^{{\rm{n}}*}) = \frac{{{{\left( {\bar p - {s_1}} \right)}^2}}}{{4{s_2}}} + \frac{{\left( {\bar w - {s_1}} \right)\left( {2\bar p - 3\bar w + {s_1}} \right)}}{{4{s_2}}},$ |
| $\quad\quad E({\textit{π}} _{{\rm{sc}}}^{{\rm{n}}*}){\rm{ = }}\frac{{{{\left( {\bar p - {s_1}} \right)}^2}}}{{2{s_2}}} - {s_0}{\text{。}}$ |
观察比较
观察比较
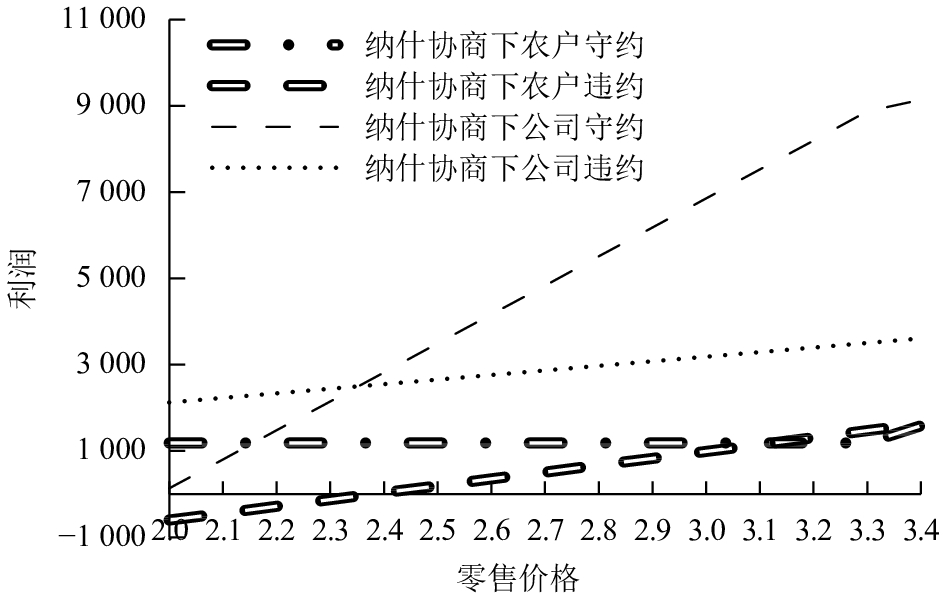
定理4 在纳什协商模型下,农户与公司的利润分配对双方均有利,双方均不会毁约,供应链可以达到稳定。
若农户毁约,将在纳什协商模型下的最优农产品生产量
但是若公司主动违约,农户与公司的合约关系就会破裂。由于此时农户将全部农产品卖给当地批发市场只会赔钱,所以理性的农户选择只在当地市场出售部分商品
所以可以得出结论,在纳什协商模型下的利润分配对于公司和农户均有利,双方均不会主动违约。
表1为集中决策模型、分散决策模型和纳什协商模型的均衡结果。
| 表 1 不同模型下的均衡结果 Tab. 1 Equilibrium results under different models |
为了更清楚地看到不同决策模型下,农户与公司的行为选择,接下来用数值实验来验证上述的分析结果。
1) 2种模型下的合约价格与最优产量的比较。
图2为某农产品的批发价格均值为零售价格的0.5倍时(
2) 2种模型下的利润对比。
以
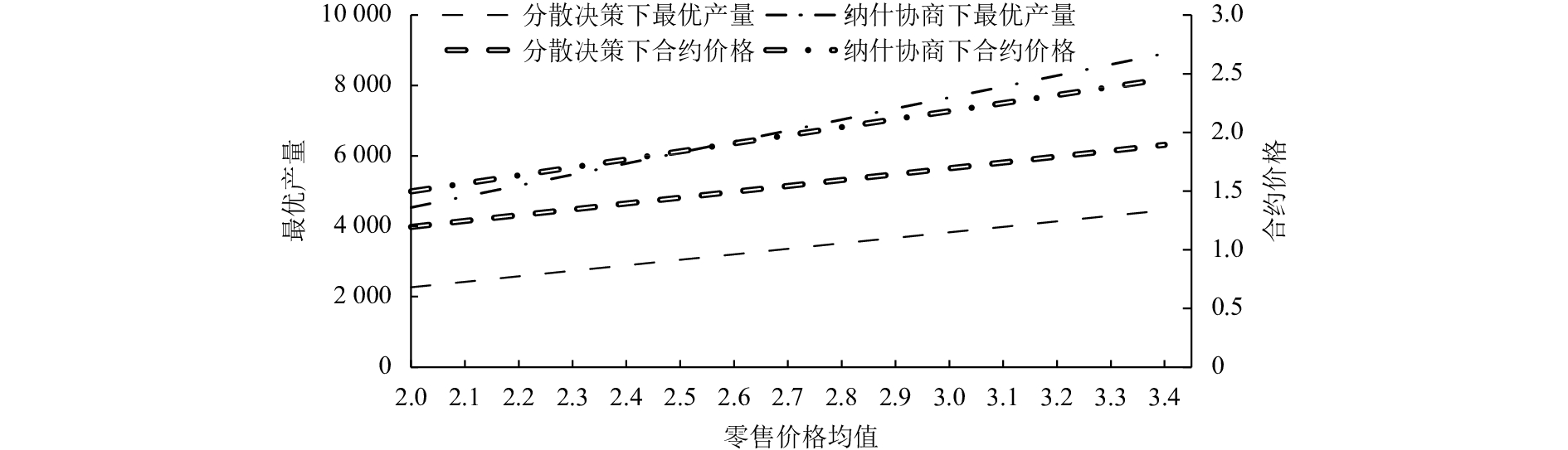
|
图 2 合约价格与最优产量的比较
Fig. 2 The comparison of
|
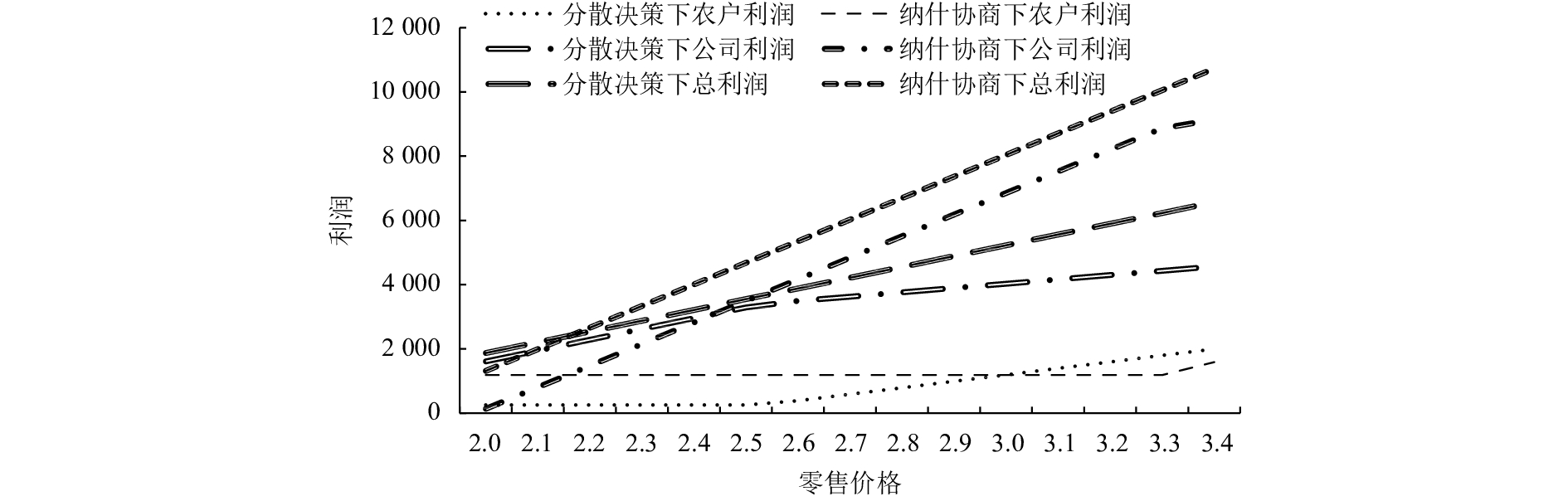
|
图 3 两种模型下的利润对比 Fig. 3 The profit comparison under two models |
3) 违约与守约决策下的利润对比。
图4和图5分别描述了在两种决策模型下,农户和公司分别在守约和违约两种行为下的利润随着零售价格
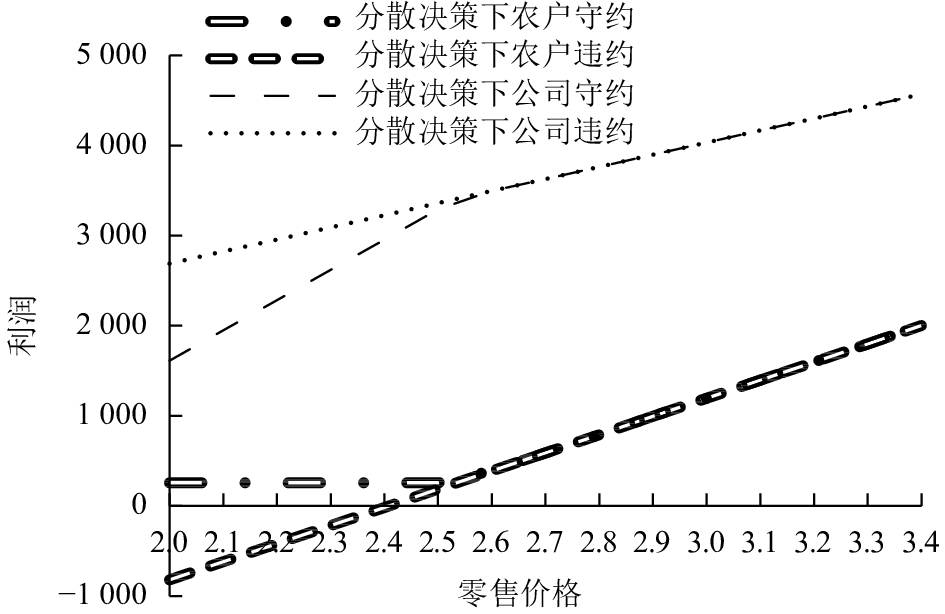
|
图 4 分散决策下守约和违约的利润对比 Fig. 4 Profit comparison under Decentralizing decision model |
|
图 5 纳什协商下守约和违约的利润对比 Fig. 5 Profit comparison under Nash negotiation decision model |
本文考虑了两种农产品销售渠道:一是农户将农产品销售给当地批发市场;二是农户与公司签约,将农产品直接卖给公司。分析了在公司与当地批发市场两种销售渠道同时存在,公司采用“保底收购,随行就市”合约与农户合作的情况下,公司与农户在分散决策和纳什协商模型下的行为选择和利润分配。通过对比,可以得出如下结论:1) 在分散决策模型中,“保底收购,随行就市”的合约对农户来说是有利的,对公司不利,公司存在违约的风险,“公司+农户”的两级供应链整体利润少于集中决策时供应链的利润;2) 纳什协商模型下,农户与公司的利润分配对双方均有利,双方均不会毁约,供应链可以到达稳定状态,同时供应链的整体利润等于集中决策时的供应链利润,可以实现供应链的完美协调。因此,在订单农业的合约设计过程中,公司和农户应进行良性互动和合作,了解农户的收入和成本构成,在考虑双方利润最大化的基础上(而不应以各自利润最大化为目标),公司决定合约价格(保底价格),农户决定种植量。这样可以在一定程度上减少由于市场价格波动而导致的合同违约。
| [1] |
刘凤芹. 不完全合约与履约障碍—以订单农业为例[J].
经济研究, 2003, 568(4): 22-30.
LIU Fengqin. Incomplete contract and the barrier to performance: a case research on the farm produce on order[J]. Economic Research, 2003, 568(4): 22-30. |
| [2] |
ZYLBERSZTAJN D, GUALBERTO A P L, NADALINI L B. Tomatoes and courts: strategy of the agro-industry facing weak contract enforcement[R]. Brazil: School of Economics and Business, University of Sao Paulo, 2003
|
| [3] |
TANG C, SODHI M. Supply-chain research opportunities with the poor as suppliers or distributors in developing countries[J].
Production and Operations Management, 2014, 23(9): 1583-1494.
|
| [4] |
JORGE R, CRISTINA G, DANIEL A, et al. NGOS’ initiatives to enhance social sustainability in the supply chain: poverty alleviation through supplier[J].
Journal of Supply Chain Management, 2016, 52(3): 83-108.
DOI: 10.1111/jscm.2016.52.issue-3. |
| [5] |
TANG C, SODHI M, MARCO F. An analysis of partially-guaranteed-price contracts between farmers and agri-food companies[J].
European Journal of Operational Research, 2016, 254(3): 1063-1073.
DOI: 10.1016/j.ejor.2016.04.038. |
| [6] |
曹艳爱, “公司+农户”模式稳定性研究概述[J]. " 公司+农户”模式稳定性研究概述[J].
广东农业科学, 2013, 40(15): 229-232.
CAO Yanai. Research review on the stability of " company &peasant-household”[J]. Guangdong Agricultural Sciences, 2013, 40(15): 229-232. DOI: 10.3969/j.issn.1004-874X.2013.15.071. |
| [7] |
叶飞, 林强, 莫瑞君. 基于B-S模型的订单农业供应链协调机制研究[J].
管理科学学报, 2012, 15(1): 66-76.
YE Fei, LIN Qiang, MO Ruijun. Contract-farming supply coordination mechanism based on B-S model[J]. Journal of Management Sciences in China, 2012, 15(1): 66-76. DOI: 10.3969/j.issn.1007-9807.2012.01.007. |
| [8] |
叶飞, 林强. " 公司+农户”型订单农业供应链的Nash协商模型[J].
系统工程理论与实践, 2014, 34(7): 1769-1778.
YE Fei, LIN Qiang. Coordination for " company + farmer” contract-farming supply chain under Nash negotiation model[J]. System Engineering Theory and Practice, 2014, 34(7): 1769-1778. |
| [9] |
浦徐进, 金德龙. 生鲜农产品供应链的运作效率比较: 单一" 农超对接”VS. 双渠道[J].
中国管理科学, 2017, 25(1): 98-105.
PU Xujin, JIN Delong. The operational efficiency measurement of agro-food supply chains: the single " farmer-supermarket direct purchase” vs. dual channal[J]. Chinese Journal of Management Science, 2017, 25(1): 98-105. |
| [10] |
凌六一, 胡中菊, 郭晓龙. 随机产出和随机需求下" 农超对接”模式的分析与协调[J].
系统工程, 2011, 29(9): 36-40.
LING Liuyi, HU Zhongju, GUO Xiaolong. Analysis and coordination of " farmer-supermarket docking” mode under stochastic yield and random demand[J]. Systems Engineering, 2011, 29(9): 36-40. DOI: 10.3969/j.issn.1001-2362.2011.09.024. |
| [11] |
张焕勇, 周志鹏, 浦徐进. 农产品供应链视角下的家庭农场销售渠道模式选择[J].
商业研究, 2016, 10(474): 130-137.
ZHANG Huanyong, ZHOU Zhipeng, PU Xujin. The channel-selecting of family farm under agricultural product supply chain[J]. Commercial Research, 2016, 10(474): 130-137. |
| [12] |
CHEN Y, TANG C. The economic value of market information for farmers in developing economics[J].
Production and Operations Management, 2015, 9(24): 1441-1452.
|
| [13] |
焦民赤, 薛兴利. 订单农业中农户违约行为的博弈分析与规避策略[J].
山东社会科学, 2015, 238(6): 122-126.
JIAO Minchi, XUE Xingli. Game analysis and avoidance strategy of farmers’ breach of contract in contract farming[J]. Shandong Social Sciences, 2015, 238(6): 122-126. DOI: 10.3969/j.issn.1003-4145.2015.06.020. |
| [14] |
吴全宏, 陈杰文. 订单农业的发展现状与思考[J].
南方农机, 2017, 48(16): 168-169.
WU Quanhong, CHEN Jiewen. Development status and thinking of order agriculture[J]. South Agricultural Machinery, 2017, 48(16): 168-169. DOI: 10.3969/j.issn.1672-3872.2017.16.154. |
| [15] |
谈冰洁, 徐国虎, 许芳. " 公司+农户”供应链背景下农户公平感知影响因素分析[J].
农村经济与科技, 2015, 361(3): 50-52.
TAN Bingjie, XU Guohu, XU Fang. Influencing factors of farmers’ fairness perception in the context of " company + farmer” supply chain[J]. Rural Economy and Science-Technology, 2015, 361(3): 50-52. DOI: 10.3969/j.issn.1007-7103.2015.03.018. |
| [16] |
浦徐进, 朱秋鹰, 路璐. 参照点效应、公平偏好和" 龙头企业+农户”供应链关系治理[J].
管理工程学报, 2016, 30(2): 116-123.
PU Xujin, ZHU Qiuying, LU Lu. Reference point effect, fairness preference and the relational governance on the supply chain of " leading agricultural enterprises +farmers”[J]. Journal of Industrial Engineering/Engineering Management, 2016, 30(2): 116-123. |
| [17] |
冯春, 王雅婷, 于宝, 等. 农产品供应链渠道利润的分配公平协调机制[J].
系统工程, 2016, 276(12): 103-110.
FENG Chun, WANG Yating, YU Bao, et al. Fair distribution mechanism of channel profit in agri-food supply chain[J]. System Engineering, 2016, 276(12): 103-110. DOI: 10.3969/j.issn.1001-2362.2016.12.068. |
| [18] |
NIU B, JIN D, PU X. Coordination of channel members’ efforts and utilities in contract farming operations[J].
European Journal of Operational Research, 2016, 255(3): 869-883.
DOI: 10.1016/j.ejor.2016.05.064. |
| [19] |
GOU Q, SETHI S, YUE J, et al. Push and pull contracts in a local supply chain with an outside market[J].
Decision Sciences, 2016, 47(6): 1150-1177.
DOI: 10.1111/deci.2016.47.issue-6. |
 2018, Vol. 21
2018, Vol. 21