近年来在我国高铁现代化快速发展的背景下,高铁客运专线的修建以及“四纵四横”快速客运通道的建成使得旅客对高速铁路的需求与服务质量不断提高。这要求我国铁路运营部门充分利用有限的资源,增强与航空等运输方式的竞争力,提高客运量并保证客票收益。
由于目前中央统一管理运价占高铁运价的主要部分,其客票定价体系不能有效适应市场竞争的要求,因此建立反应灵敏、信号准确、运转健康的高铁票价动态调整策略,是目前铁路改革的核心工作之一。
在铁路动态票价调整策略方面,国外研究起步较早,并形成了灵活多样的票价体系。Miller[1]分析了与动态票价相关的马尔科夫决策过程并证明了单位时间内的运输票价存在稳态解等重要的基础性定理。Bharill等[2]通过分析铁路票价和客流间的关系,预测未来的订票需求量及退票数,从而达到提高铁路部门收益的目的。Sidbari等[3]将预售期以天为单位进行离散化,讨论了客票的随机动态启发式算法,利用动态规划的方法对订票需求进行预测,但其短期策略只能保证当前日期受益最大。Feng等[4]研究了一次变更价格问题,通过对价格从较低增加至较高或较高减少至较低的分析,研究了票价的动态变化情况。国内,史峰等[5]结合马氏决策过程和最优化理论研究了我国高铁动态票价理论,并在理论模型的基础上充分考虑了算法复杂度与售票方案的实用性,但该模型只能用于单区段的城际客运专线。朱颖婷[6]基于差别定价的经济学原理,通过理论分析和仿真实验,研究了高铁客运的差别票价和竞争环境下确定高铁客票折扣率的方法,得出票价档数越多获得期望收益越大的结论。钱丙益等[7]根据Bellman原理建立动态规划模型,验证了两个区段客运专线的最优动态票价调整策略的阈值特性。孙熙庆等[8]通过分析铁路运营初期和稳定期进行动态票价控制的方法和步骤,提出了一种动态票价控制及销售策略的二分法方法。整体来看,以往的研究多侧重于从高铁票价与客运需求的角度来研究高铁动态票价问题,缺乏对市场竞争因素的考虑,即使涉及到市场竞争或市场细分的客票定价也没有对席位存量与动态票价的相互影响等问题进行分析。本文将采用动态规划的基本方法,综合考虑旅客购票选择行为、高铁席位存量控制、票价动态变化过程3个方面,确定高铁和航空两者竞争环境下的高铁票价与席位存量的定量关系,最终获得合理实用的高铁票价动态调整策略。
1 票价策略的市场影响因素高铁客运票价的制定是一个复杂过程,需要综合考虑的因素非常多。除了运输成本和政府管制之外,本文基于市场竞争,在动态票价模型的构建过程中主要考虑竞争者因素和旅客购票行为因素[6]。
1.1 竞争者因素由于运输通道内各种运输方式均具有替代性,高铁客运票价必然受到竞争状况的影响。在800~1 500 km的长距离运输市场,高速高铁的主要竞争对手是民航客运。因此了解长距离运输市场,以更加灵活的票价应对市场竞争是本文制定票价策略考虑的因素之一。
1.2 购票行为因素高铁的票价同时还受到旅客选择及购票行为的影响。高铁票价动态调整的目标就是在稳定既有忠诚旅客的同时尽量多地吸引没有出行偏好的旅客。因此,根据历史售票数据准确把握预售期内旅客购票请求到达的规律,有效刻画旅客的购票过程,能为客票精细化配置提供依据。
2 非同质旅客购票效益的表达高铁票价动态调整过程需要考虑的主要竞争者为民航客运。本文假设高铁、航空运营方和出行旅客均为完全理性,运营方完全有能力采取最优定价策略,旅客完全有能力根据运输市场状况作出最优反应,且对于相同OD间的直达客流,其二者运输市场的客运需求为稳定需求。
2.1 旅客购票到达行为的过程描述考虑高铁与相同OD间的航空两种运输方式在预售期
| $ \quad\quad{{\lambda}} = f({\lambda _L},{\lambda _{L - 1}},...,{\lambda _2},{\lambda _1},{\lambda _0}){\text{。}} $ | (1) |
式中,
根据运输市场的市场细分结果,将客运市场潜在购票需求分为3类:高铁忠诚旅客、航空忠诚旅客与带概率选择性旅客。由复合泊松分布的性质可得在周期
| $ \quad\quad\begin{array}{l}{\lambda _t} = \displaystyle\sum\limits_{i = 1}^3 {{\lambda _{it}}} ,\quad t = L,L - 1,...,3,2,1,0 {\text{。}}\end{array} $ | (2) |
式中,
设高铁与航空的票价在周期
| $\quad\quad \begin{array}{l} {P_i}\left( {{p_1}(t),{p_2}(t)} \right){\rm{ = }}\displaystyle\frac{{{\lambda _{it}}^n}}{{n!}}{{\rm{e}}^{ - {\lambda _{it}}}} ; \quad i = 1,2,3,\quad n {\text{≤}} 1 {\text{。}}\end{array} $ | (3) |
带概率选择性旅客除购票行为到达概率外,还存在选择何种客票的选择概率。设该类旅客选择第
| $\quad\quad {U_j} = {\alpha _j} - {\beta _j}{p_j} + {\varepsilon _j},\quad j = 1,2,0{\text{。}} $ | (4) |
式中,
| $\quad\quad {P_{3j}}\left( {{p_1}(t),{p_2}(t)} \right) = \frac{{{{\rm{e}}^{{\alpha _j} - \beta {p_j}}}}}{{1 + \sum\limits_{j = 0}^2 {{{\rm{e}}^{{\alpha _j} - \beta {p_j}}}} }}{\text{。}} $ | (5) |
旅客不购买任何一种运输方式客票的概率为
| $\quad\quad {P_{30}}\left( {{p_1}(t),{p_2}(t)} \right) = \frac{1}{{1 + \sum\limits_{j = 0}^2 {{{\rm{e}}^{{\alpha _j} - \beta {p_j}}}} }}{\text{。}} $ | (6) |
因此,该类型旅客购票行为由购票到达与客票选择的联合概率刻画,如下式所示:
| $ \begin{split}&\quad\quad {P'_{3j}}\left( {{p_1}(t),{p_2}(t)} \right) = {P_3}\left( {{p_1}(t),{p_2}(t)} \right) \times{P_3}_j\left( {{p_1}(t),}\right. \\&\left.{{p_2}(t)} \right),\quad j = 1,2,0{\text{。}} \end{split}$ | (7) |
在周期
| $ \begin{gathered} \quad\quad{R_t} = \left[ {{P_1}\left( {{p_1}(t),{p_2}(t)} \right) + {{P'}_3}\left( {{p_1}(t),{p_2}(t)} \right)} \right] \times {p_1}(t) = \\ \!\!\!\!{\Bigg{(}} {\frac{{{\lambda _{1t}}^n}}{{n!}}{{\rm{e}}^{ - {\lambda _{1t}}}} + \frac{{{\lambda _{3t}}^n}}{{n!}}{{\rm{e}}^{ - {\lambda _{3t}}}} \times \frac{{{{\rm{e}}^{{\alpha _1} - \beta {p_1}}}}}{{1 + \sum\limits_{j = 0}^2 {{{\rm{e}}^{{\alpha _j} - \beta {p_j}}}} }}} {\Bigg{)}} \times {p_1}(t)\quad , \\ \quad n {\text{≤}} 1,\quad t = L,L - 1,...,2,1,0 {\text{。}}\end{gathered} $ | (8) |
考虑高铁席位存量对票价的动态影响。设
| $ \quad\quad\left\{ \begin{array}{l} {z_1} {\text{≤}} {c_1},\quad {z_2} {\text{≤}} {c_2} ;\\ {\left( {{d_1}} \right)_{\min }} {\text{≤}} {p_1} {\text{≤}} {\left( {{d_1}} \right)_{\max }}; \\ {\left( {{d_2}} \right)_{\min }}{\text{≤}} {p_2}{\text{≤}} {\left( {{d_2}} \right)_{\max }} {\text{。}}\end{array} \right. $ | (9) |
当没有旅客购票行为到达时,相邻周期的高铁或航空席位存量关系与期望效益关系为
| $ \quad\quad\left\{ \begin{array}{l} {z_j}(t) = {z_j}(t - 1); \\ {R_t}( {{z_j}} ) = {R_{t - 1}}( {{z_j}}); \\ j = 1,2{\text{。}} \end{array} \right.$ | (10) |
在第
| $\left\{ \begin{array}{l}\quad\quad{{R_{t - 1}}\left( {p,z} \right) = \max }\;\;{\left[ {{P_1}\left( {{p_1}(t),{p_2}(t)} \right)\left[ {{p_1}\left( t \right) + {R_t}\left( {{z_1} - 1,}\right.}\right.} \right.}\\\left.{\left.{{z_2}} \right)} \right] + {{{P'}_{31}}\left( {{p_1}(t),{p_2}(t)} \right)\left[ {{p_1}\left( t \right) + {R_t}\left( {{z_1} - 1,{z_2}} \right)} \right] + }\\{{{P'}_{32}}\left( {{p_1}(t),{p_2}(t)} \right){R_t}\left( {{z_1},{z_2} - 1} \right) + }{\left. {{{P'}_{30}}\left( {{p_1}(t),}\right.}\right.}\\{\left.{\left.{{p_2}(t)} \right){R_t}\left( {{z_1},{z_2}} \right)} \right]}{\text{。}}\\{\rm{s}}.{\rm{t}.}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;\quad\quad\quad(11)\\\quad\quad 0 {\text{≤}} {z_1} {\text{≤}} {c_1};\quad 0 {\text{≤}} {z_2} {\text{≤}} {c_2};\quad {z_1},{z_2} \in {\rm{N}};\\{({d_1})_{\min }} {\text{≤}} {p_1} {\text{≤}} {({d_1})_{\max }};\quad {({d_2})_{\min }} {\text{≤}} {p_2} {\text{≤}} {({d_2})_{\max }};\\ t = L,L - 1,...,2,1,0{\text{。}} \end{array}\right.$ |
对目标函数求导可得
| $ \begin{array}{l} \quad\;\;\displaystyle\frac{{{\rm{d}}{R_{t - 1}}\left( {p,z} \right)}}{{{\rm{d}}t}} = \max {\Bigg{[}} {\lambda _{1t}} \left( {\frac{{{\rm{d}}{p_1}\left( t \right)}}{{{\rm{d}}t}} + {R_{t - 1}}\left( {p,z} \right) - {R_t}\left( {p,z} \right)} \right) + \\ \left. {\lambda _{3t}} \beta \left( {\displaystyle\sum\limits_{j = 0}^2 {\displaystyle\frac{{{\rm{d}}{P_{3j}}\left( {{p_1}(t),{p_2}(t)} \right)}}{{{\rm{d}}t}} \frac{{{\rm{d}}{p_1}\left( t \right)}}{{{\rm{d}}t}}} + {R_{t - 1}}\left( {p,z} \right) - {R_t}\left( {p,z} \right)} \right){\rm{ + }} \right. \\ {\gamma _\lambda } {\Bigg{]}}{\text{。}}\\\end{array} $ | (12) |
其中,
由单位时间
| $ \frac{{{\rm{d}}{R_{t - 1}}\left( {p,z} \right)}}{{{\rm{d}}t}} = \max \;\; \left\{ {\left( {{\lambda _{1t}} + {\lambda _{3t}}\beta } \right) \left[ {{R_{t - 1}}\left( {p,z} \right) - {R_t}\left( {p,z} \right)} \right] + {\gamma _\lambda }} \right\}{\text{。}} $ | (13) |
由Miller的结论:当
| $\quad\quad \frac{{{\rm{d}}{R_{t - 1}}\left( {p,z} \right)}}{{{\rm{d}}s}} = k \left[ {{R_{t - 1}}\left( {p,z} \right) - {R_t}\left( {p,z} \right)} \right] + {\gamma _k}{\text{。}} $ | (14) |
解此线性微分方程得[5]
| $ {R_{t - 1}}\left( {p,z} \right) = \int_0^{\Delta {{t}}_0} {\left[ {k{R_t}\left( {p,z} \right) + {\gamma _k}} \right]{{\rm{e}}^{ - \beta \Delta {{s}}_0}}{\rm{d}}s + {{\rm{e}}^{ - \beta \Delta {{t}}_0}}{R_{t - 1}}\left( {p,z} \right)}{\text{。}} $ | (15) |
当
| $ \quad\quad \frac{{{\rm{d}}{R_{t - 1}}\left( {p,z} \right)}}{{{\rm{d}}s}} = \frac{{{R_{t - 1}}\left( {p,z} \right) - {R_t}\left( {p,z} \right)}}{{\Delta {t_0}}} {\text{。}} $ | (16) |
得到高铁期望收益
| $ \quad\quad {R_{t - 1}}\left( {p,z} \right) - {R_t}\left( {p,z} \right) = \frac{{{\rm{d}}{R_{t - 1}}\left( {p,z} \right)}}{{{\rm{d}}s}}\Delta {t_0} {\text{。}} $ | (17) |
结合式(15)并对式(17)移项可得
| $ \left( {1 \!-\! {{\rm{e}}^{ - \beta \Delta {t_0}}}\Delta {t_0}} \right){R_{t - 1}}\left( {p,z} \right) \!-\! \left( {1 \!+\! k{{\rm{e}}^{ - \beta \Delta {t_0}}}\Delta {t_0}} \right){R_t}\left( {p,z} \right) \!=\! {{\rm{e}}^{ - \beta \Delta {t_0}}}\Delta {t_0}{\text{。}} $ | (19) |
在
| $ \quad\quad{R_{j0}}(z) = 0, $ | (18) |
表示预售期结束,运输产品的残值为0;
利用递推公式(17)和边界条件式(18),选择适当的
本文对某预售期为60 d的京广高铁旅客与相同OD下的航空旅客购票行为进行仿真研究,设高铁初始席位能力为
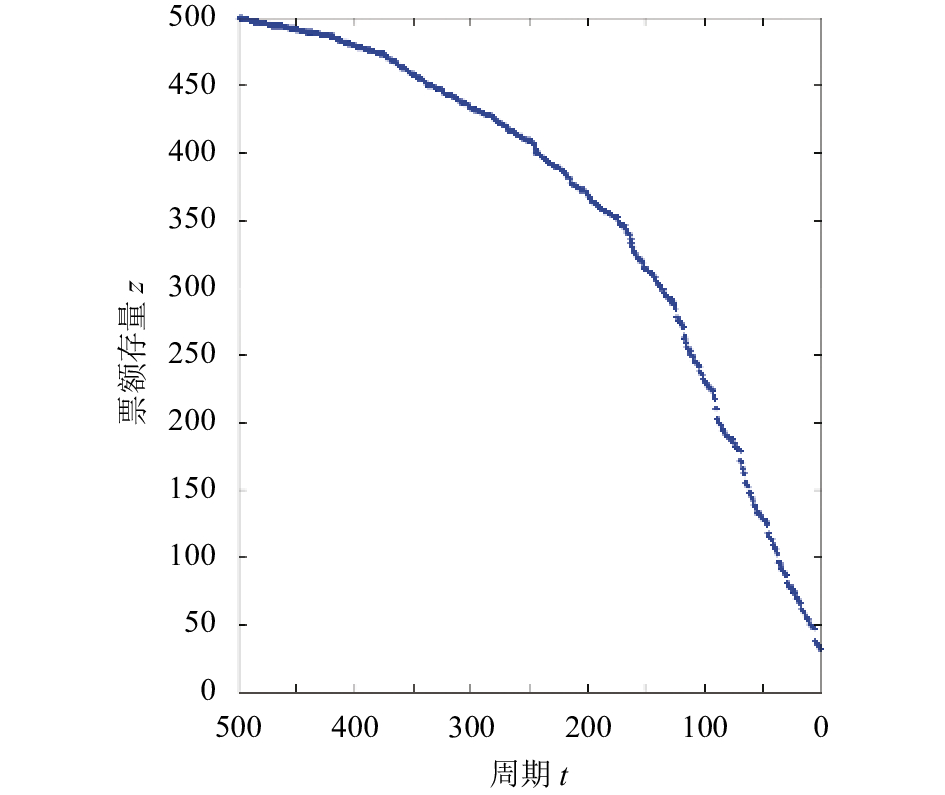
|
图 1 第
|
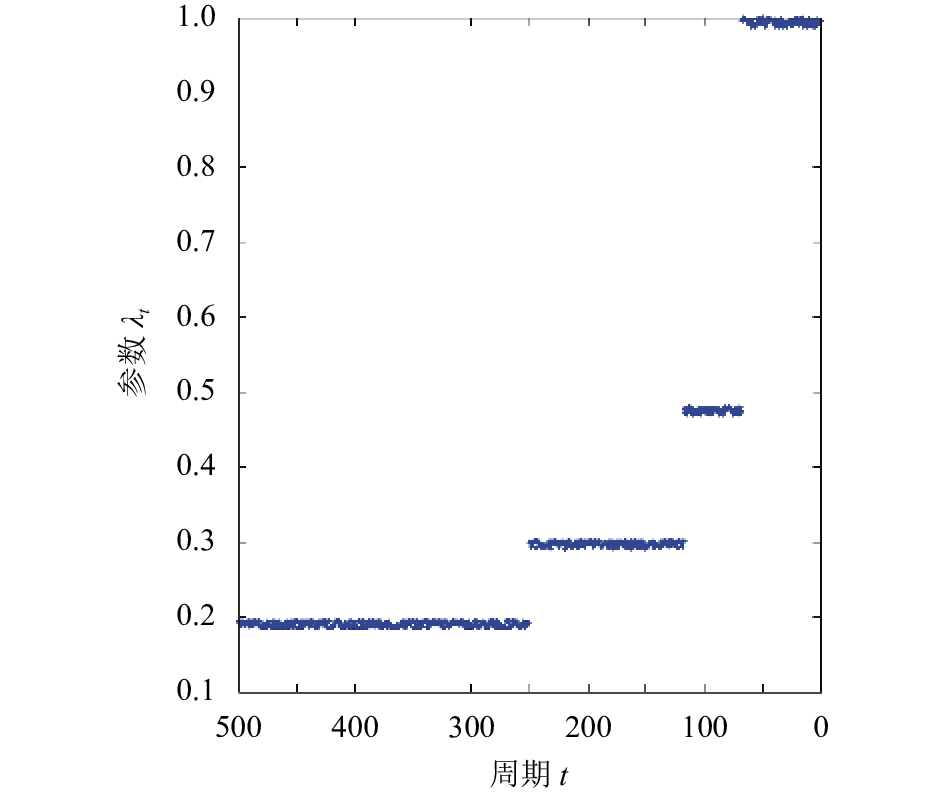
|
图 2 第
|
根据图1、图2的仿真结果,本文将京广高铁预售期按参数
| 表 1 统计京广高铁预售期旅客购票的仿真结果 Tab. 1 Simulation results of passenger ticket purchase during the pre-sale period of Beijing-Guangzhou High-Speed Rail |
根据阶段购票比例和式(2)对预售期内高铁忠诚旅客与带选择概率旅客的购票到达强度
| 表 2 不同类型旅客购票到达强度 Tab. 2 Arriving strength of purchasing ticket of different types of passenger |
将表2参数与
| 表 3 旅客出行效用函数参数标定 Tab. 3 Passenger travel utility function parameter calibration |
分别设定高铁动卧、航空的票价
| $\quad\quad \left\{ \begin{gathered} 900 {\text{≤}}{p_1}(t) {\text{≤}} 1\;200, \\ 1\;000 {\text{≤}} {p_2}(t) {\text{≤}} 1\;500{\text{。}} \end{gathered} \right. $ |
故按照各阶段参数值

|
图 3 各阶段期望收益随票价变动情况 Fig. 3 Expected revenue at each stage varies with fare |
计算得到各阶段最大期望收益分别为112 500元、99 750元、63 000元、161 000元,共计最大期望收益436 250元。对应的高铁最优票价分别为900元、950元、1 000元、920元。
按照上述的求解结果,按各阶段票额起始存量,旅客购票到达强度和持续周期数不同,构建实用的动态票价策略如图4所示。

|
图 4 高铁客票动态调整策略 Fig. 4 High-Speed Rail ticket dynamic adjustment strategy |
其直观解释为:在预售期开始时,京广高铁按900元/张的价格发售125张客票,当到达预售期30 d前进入下一个调整状态,发售950元/张的客票105张,同理在到达预售期14 d前调整客票价格为1 000元/张并发放车票63张,最后当到达预售期8 d前再次调整价格为920元/张并将余票全部放出。注意:1) 当到达预售期价格调整点但还存在票额剩余时,则剩余客票与下一阶段发放的客票同时采用下阶段票价;2) 当在到达预售期价格调整点前客票提前售完,则进入下一阶段价格调整状态并采用该阶段的票额发售量,以此类推直到放空全部客票存量。
5 结论随着我国铁路运营的市场化,高速铁路的动态票价策略对于国家综合运输市场的作用日益凸显。本文在高铁与航空运输的竞争环境下,利用数学方法与仿真手段求解给定票价范围下的最优客票调整策略。较之以往的票价需求弹性分析和静态定价策略,本文考虑了基于旅客概率选择行为的动态票价、席位容量控制策略,更能体现目前高铁在我国综合运输体系下的市场特征。通过仿真京广高铁的旅客购票行为表明,在高铁预售期内分阶段调整相应的票额存量与票价可以保证高铁运营者获得最优期望收益。
本文对旅客购票到达的非齐次泊松过程采用极限条件下的理想假设,对时变非增到达强度以及不同等级客票的差异性特征没有作定量描述。研究到达强度的“时变函数”和制定不同等级票价策略,将是本文进一步的研究方向。
| [1] |
MILLER B L. Finite state continuous time Markov decision process with a finite state planning horizon[J].
SIAM Journal of Control, 1968, 6(2): 266-280.
DOI: 10.1137/0306020. |
| [2] |
BHARILL R Rangaraj. Revenue management in railway operations: a study of the Rajdhani Express, India Railways Rajghani Express[J].
Transportation Research Part A, 2008, 42(9): 1195-1207.
|
| [3] |
SIDBARI S, LIN K , CHELLAPPAN S. Multiproduct revenue management: an empirical study of auto train at Amtrak[J].
Journal of Revenue and Pricing Management, 2008, 7(2): 172-184.
DOI: 10.1057/rpm.2008.9. |
| [4] |
FENG Y, GALLEGO G. Optimal starting times foe end-of-season sales and optimal stopping times for promotional fares[J].
Management Science, 1995, 41(8): 1371-1391.
DOI: 10.1287/mnsc.41.8.1371. |
| [5] |
史峰, 郑国华, 谷强. 铁路客票最优动态票价理论研究[J].
铁道学报, 2002, 24(1): 1-4.
SHI Feng, ZHENG Guohua, GU Qiang. Optimal dynamic pricing of railway passenger ticket[J]. Journal of the China Railway Society, 2002, 24(1): 1-4. DOI: 10.3321/j.issn:1001-8360.2002.01.001. |
| [6] |
朱颖婷.铁路客运票价策略与收益优化研究[D].北京: 中国铁道科学研究院, 2014
ZHU Yingting. Research on pricing and revenue optimization in railway passenger transport[D]. Beijing: China Academy of Railway Sciences Doctoral Dissertation, 2014 |
| [7] |
钱丙益,帅斌,陈崇双,等. 基于旅客保留价格的客运专线票价最优动态调整[J].
计算机应用研究, 2014, 31(9): 2635-2639.
QIAN Bingyi, SHUAI Bin, CHEN Chongshuang, et al. Optimal dynamic price adjustment for dedicated passenger railway line based on passengers’reservation prices[J]. Application Research of Computers, 2014, 31(9): 2635-2639. DOI: 10.3969/j.issn.1001-3695.2014.09.018. |
| [8] |
孙熙庆,孙熙安. 铁路客票动态票价控制及销售策略探讨[J].
铁道运输与经济, 2012, 34(10): 33-36.
SUN Xiqing, SUN Xi’an. Discussion on railway dynamic ticket price control and selling strategies[J]. Railway Transport and Economy, 2012, 34(10): 33-36. DOI: 10.3969/j.issn.1003-1421.2012.10.008. |
| [9] |
何平.数理统计与多元统计[M].成都: 西南交通大学出版社, 2014
|
| [10] |
叶玉玲, 陈鹏超, 程正. 基于双参数的城际旅客出行方式动态仿真方法[J].
同济大学学报(自然科学版), 2015, 43(6): 859-865.
YE Yuling, CHEN Pengchao, CHENG Zheng. Dynamic simulation method for travelling mode choice behavior of itercity passengers based on two parameters[J]. Journal of Tongji Univercity(Natural Science), 2015, 43(6): 859-865. |
 2018, Vol. 21
2018, Vol. 21