随着购买力增强，我国汽车产销已连续8年蝉联全球第一，自主品牌整车企业以其低成本、大批量在中低端市场占有显著优势^[1]。21世纪是质量的世纪，依靠质量取得核心竞争力已成为世界顶级装备制造企业的竞争理念^[2]。诸如西门子、舍弗勒等德国制造在行业内均以高质量享誉世界。质量强国战略驱动自主品牌整车企业开始实施持续质量改进计划，提高国产汽车质量水平。保修与售后服务作为产品质量的有效补充，被各行业所采用以保证产品在役期内的正常使用^[3]。新出台的“三包”政策规定了汽车企业的售后服务范围及对象。消费观的转变敦促汽车消费者不局限于产品基本性能，而开始关注愈多的消费体验和使用经济性，且互联网电子商务模式刺激消费者通过使用者口碑与社会网络宣传进行辅助购买决策。

为指导消费者购买决策，第三方咨询机构诸如汽车之家、JD Power和众调科技等对汽车品牌进行了质量排名，不同学者从不同视角提出汽车质量评价模型，综合评估不同车型的质量性能。

通过汽车可靠性评价及质量评估帮助指导购车消费决策。鹿应荣等^[4]分析了国产汽车的故障规律，通过可靠性建模分析整车可靠性，并通过改善影响整车可靠性的关键因素，提升整车可靠性；宋年秀等^[5]用模糊可靠性建模和综合评价实现对大修汽车可靠性模糊综合评价；王化吉等^[6]强调汽车质量指标的不确定性，并利用模糊层次分析法实现对汽车稳定性的评估，同时强调汽车稳定性在整车质量及消费者购买决策中的重要性。为研究汽车操纵稳定性等主观特性，邢如飞等^[7]利用层次分析法确定定性指标权重，实现对汽车主观特征的评价。模糊理论及主观评价方法能够实现对汽车整车的质量评价，辅助消费者进行购买决策。但除了产品质量，汽车等耐用型产品的售后维修及服务质量也显著影响购车者消费决策，Chang等^[8]通过研究产品质量、售后质量及消费者满意度的交互关系，认为售后服务质量不仅对消费者忠诚度产生积极影响，同时作为产品质量的有效补充，显著影响潜在消费者购买意愿。因此不同学者从售后服务提出服务质量评价模型。陈力华等^[9]强调售后服务对轿车销售的影响，提出基于GAP的服务质量评价模型，指导消费者决策。而影响购车者消费决策的另一因素是经济性，购买成本和燃油经济性作为最重要的组成部分，不仅被汽车之家等实践质量排名列入关键指标，也受到学者理论研究的关注。陈明等^[10]侧重考虑纯电动汽车动力性与经济性的综合评价指标，利用AHP-Entropy方法实现纯电动汽车动力性经济性综合评价的指标的权重计算，以理想解法(TOPSIS)进行排序，建立了纯电动汽车动力性经济性的综合评价模型；何煦等^[11]以动力性和燃油经济性为目标函数，描绘燃油经济性—加速时间曲线，并根据燃油经济性—加速时间曲线来优化动力传动系主减速比，改善动力性和燃油经济性。王献雨等^[12]以质量成本及其构成为主要指标，通过DEA投入产出分析实现对产品质量经济性综合评价；Snieska等^[13]强调不仅传统质量成本要素，质量损失及顾客抱怨等造成的隐形损失也显著影响购买决策。消费者在购车决策时往往关注以较经济的价格购买可靠有保证的车型。上述文献从可靠性、产品质量、售后服务质量及质量成本等方面，构建评价模型，为消费者购车选择提供指导。但忽略消费者购车后使用过程中的经济性问题，且缺乏集成产品质量、服务质量及质量成本综合考虑的质量经济性综合评价研究，缺乏理论评价模型指导购车者在车型选择时提供科学合理指导。

因此，本文集成产品质量和售后服务质量分析汽车质量，引入总拥有成本研究购车经济性，从质量经济性视角，构建基于扩展VIKOR的汽车产品质量经济性综合评价模型，指导消费者购买决策。针对评价指标复杂多样、主观不确定性问题，引入区间数和直觉模糊数等混合指标量化方法处理评价矩阵，并构建基于混合距离的熵权对指标进行赋权，通过满意妥协解法(VIKOR)为决策者提供车型排名，辅助购车者消费决策。

1 汽车产品质量经济性指标体系描述及构建 1.1 质量经济性指标体系

国内自主品牌整车企业经过几十年的发展，逐步开始关注产品质量和顾客满意调研。顾客导向的竞争战略造成质量的最终决定权和话语权转向了消费者，消费者对汽车产品感知质量的认识评判决定了整车的市场价值和品牌形象，如J.D. Power 的PP100指标。当前大多品牌主机厂已形成集研发、设计、生产制造、销售、售后服务、报废等全生命周期活动一体的运作能力。因此整车企业需在全生命周期范围内进行质量改善实践以提升产品质量和顾客满意度。持续质量改善进程(CQIP)成为主机厂研发和品牌建设的重要环节。设计质量是依据市场需求和上一代产品的反应综合得出的。国产汽车质量经济性指标汇总见表1。

1.2 基于粗糙集属性约简的评价指标体系构建

粗糙集 (rough set, RS) 由于其具备处理模糊、不完整信息能力，在首次被波兰大学Parlak教授提出后，在数据挖掘、属性约简、模式识别等领域得到广泛应用。为提升决策效率，基于粗糙集的属性约简常用来删除冗余指标。

定义1 　知识系统KS用一个四元组KS=(U, AA, V, ff)表示。 $U = \{ {\rm{x}}{{\rm{x}}_1},{\rm{x}}{{\rm{x}}_2},...,{\rm{x}}{{\rm{x}}_m}\} $ ^[14]称为论域，为对象的非空有限集；AA=(aa₁, aa₂,..., aa_n)表示属性的非空有限集合，包含条件属性C和决策属性CD。 $V = \mathop \cup \limits_{{\rm{aa}} \in {\rm{AA}}} {V_{{\rm{aa}}}}$ ，V_aa是属性aa的值域； ${\rm{ff}}:U \times {\rm{AA}} \to V$ 为映射函数，它为每个对象的各属性赋值，即 $\forall $ aa $ \in $ AA，xx $ \in $ U，ff(xx, aa) $ \in $ V_aa。

定义2 　对任意属性集 $Z \subset {\rm{AA}}$ ， $\exists $ 对象xx_i, xx_j $ \in $ U，对 $\forall $ z $ \in $ Z，若满足z(xx_i)=z(xx_j)，则称对象对于属性集Z不可分辨，记作IND(Z)；对条件属性a_i $ \in $ AA，若IND(AA)=IND(AA-a_i)^[15]，则称a_i是冗余的，否则称属性a_i为必要的或独立的。

定义3 　若 $Z \subset A$ 是独立且IND(Z)=IND(AA)，则称Z是AA的一个约简，AA的约简即为red(AA)，可知AA的约简并不唯一。AA中所有不可约简的属性集合成为AA的核(core)，记作core(AA)。

选择m个不同汽车品牌车型的购车者历史经验作为决策信息，构架决策表KS=(U, CC∪D, V, ff) ，本文采用Rosetta中的基于遗传属性约间算法SAVGeneticReducer板块实现指标约简，方法实施步骤详见文献[16]。

2 混合评价指标体系量化 2.1 混合型评价指标

汽车的质量经济性不仅可通过主机厂规定的参数反映，也可过使用者的质量反馈对汽车质量经济性作出评估。汽车质量评价信息的模糊不确定性导致前文中所陈述总结的指标类型参差不齐。针对指标含义及收集渠道，将汽车质量经济性指标分为确定型、区间型和模糊型语言变量等3种。

1) 确定型指标。

对于数值型数据，分为效益型指标BT和成本型指标CT，将评价信息按式(1)处理：

$\quad\quad{r_{ij}} = \left\{ \begin{array}{l}\displaystyle\frac{{{u_{ij}}}}{{{{\max }_j}{u_{ij}}}},1 {\text{≤}} i {\text{≤}} m,1 {\text{≤}} j {\text{≤}} n,{u_{ij}} \in {\rm{BT}};\\\displaystyle\frac{{{{\min }_j}{u_{ij}}}}{{{u_{ij}}}},1 {\text{≤}} i {\text{≤}} m,1 {\text{≤}} j {\text{≤}} n,{u_{ij}} \in {\rm{CT}}{\text{。}}\end{array} \right.$

(1)

其中： ${u_{ij}}$ 是确定型评价信息的指标值；m为备选车型个数，n为指标个数。

2) 区间型指标。

区间数是定量数据的模糊性，是对不确定性的数值型评价指标进行处理的一种方法。对不确定性定量数据的处理如下。

区间数值评价值记为 $\left[ {u_{ij}^{\rm{L}},u_{ij}^{\rm{U}}} \right]$ ，经规范化处理后记为 $\left[ {r_{ij}^{\rm{L}},r_{ij}^{\rm{U}}} \right]$ ，其中

$\begin{split}&\quad\quad r_{ij}^{\rm{L}} = \displaystyle\frac{{u_{ij}^{\rm{L}}}}{{{{\max }_j}u_{ij}^{\rm{U}}}},r_{ij}^{\rm{U}} = \displaystyle\frac{{u_{ij}^{\rm{U}}}}{{{{\max }_j}u_{ij}^{\rm{U}}}},1 {\text{≤}} i {\text{≤}} m,1 {\text{≤}} j {\text{≤}} n,\\&\left[ {u_{ij}^{\rm{L}},u_{ij}^{\rm{U}}} \right] \in \rm{BT};\end{split}$

(2)

$\begin{split}&\quad\quad r_{ij}^{\rm{L}} = \displaystyle\frac{{{{\min }_j}u_{ij}^{\rm{L}}}}{{u_{ij}^{\rm{U}}}},r_{ij}^{\rm{U}} = \displaystyle\frac{{{{\min }_j}u_{ij}^{\rm{U}}}}{{u_{ij}^{\rm{L}}}},1 {\text{≤}} i {\text{≤}} m,1 {\text{≤}} j {\text{≤}} n,\\&\left[ {u_{ij}^{\rm{L}},u_{ij}^{\rm{U}}} \right]\in\rm{CT}{\text{。}}\end{split}$

(3)

3) 模糊不确定型指标。

模糊不确定型指标主要存在于使用者对产品的质量评价反馈，由于消费者对产品性能无法准确描述，须用自然语言或语言变量辅助其评价信息的确定。语言变量是决策者用诸如极差、差、中等、好、非常好等定性的语言来描述决策者对性能指标的主观感受。本文中提出的很多指标都为定性指标，导致无法与定量指标放在一起进行处理。因此，本文引入模糊集理论中的直觉模糊数将语言变量转化为直觉模糊数进行处理。下文对直觉模糊数稍作介绍。

定义4 　设 $X$ 为非空论域， $X$ 上的直觉模糊集^[17]定义为

$\quad\quad{\rm{CC}} = \left\{ {\left( {x,{\mu _{\rm{CC}}}(x),{\gamma _{\rm{CC}}}(x)} \right)\left| {x \in \rm{CC}} \right.} \right\}{\text{。}}$

(4)

其中： ${\mu _{\rm{CC}}}(x)$ 为元素 $ x $ 对于集合CC的隶属度函数， ${\mu _{\rm{CC}}}(x):X \to \left[ {0,1} \right],x \in X \to {\mu _{\rm{CC}}}(x) \in \left[ {0,1} \right];$

${\gamma _{\rm{CC}}}(x)$ 为元素 $ x $ 对于集合CC的非隶属度函数， ${\gamma _{\rm{CC}}}(x):X \to \left[ {0,1} \right],x \in X \to {\gamma _{\rm{CC}}}(x) \in \left[ {0,1} \right]$ ;

对于任意 $x \in X,0 {\text{≤}} {\mu _{\rm{CC}}}(x) + {\gamma _{\rm{CC}}}(x) {\text{≤}} 1$ ，则 ${\pi _{\rm{CC}}}(x) = $ $ 1 - {\mu _{\rm{CC}}}(x) - {\gamma _{\rm{CC}}}(x)$ 称作集合CC的犹豫度。

特别地，称 $\alpha = ({\mu _\alpha },{\gamma _\alpha },{{\text{π}} _\alpha })$ 为直觉模糊数。其中： ${\mu _\alpha } \in \left[ {0,1} \right],{\gamma _\alpha } \in \left[ {0,1} \right],{\mu _\alpha } + {\gamma _\alpha } {\text{≤}} 1,{{\text{π}} _\alpha } = 1 - {\mu _\alpha } - {\gamma _\alpha }$ 。

令第l个决策者的权重为 ${\lambda _l}$ ，将多个决策者的信息综合处理，令 $(\mu _{ij}^l,\gamma _{ij}^l,\pi _{ij}^l)$ 为直觉模糊数和语言变量的决策信息，按如下处理^[18]：

$\begin{split}&\quad\quad{r_{ij}} = {\lambda _l}r_{ij}^1 \oplus \cdots \oplus {\lambda _l}r_{ij}^l \oplus \cdots \oplus {\lambda _L}r_{ij}^L =\\&\left(1 - \prod\limits_{l = 1}^L {{{\left( {1 - \mu _{ij}^l} \right)}^{{\lambda _l}}},\prod\limits_{l = 1}^L {{{\left( {\gamma _{ij}^l} \right)}^{{\lambda _l}}},\prod\limits_{l = 1}^L {{{\left( {1 - \mu _{ij}^l} \right)}^{{\lambda _l}}} - \prod\limits_{l = 1}^L {{{\left( {\gamma _{ij}^l} \right)}^{{\lambda _l}}}} } } } \right){\text{。}}\end{split}$

(5)

语言变量与直觉模糊数的转化关系如表2所示。

2.2 基于总拥有成本的经济性指标量化

本文构建的总拥有成本包括购车成本 ${C_{\rm{p}}}$ 、燃油经济性 ${C_{\rm{F}}}$ 、保养费用 ${C_{\rm{m}}}$ 、维修成本 ${C_{\rm{w}}}$ 和隐性损失成本C_h构成，即总拥有成本模型如下所示：

$\quad\quad{\rm{TCO}} = {C_{\rm{p}}} + {C_{\rm{F}}} + {C_{\rm{m}}} + {C_{\rm{w}}} + {C_{\rm{h}}}{\text{。}}$

(6)

1) 购车成本。

指汽车经销商把使用价值让渡给购车者时购车者所耗费的成本。本文汽车购买成本等于购车款、汽车购置税、上牌费与车船使用税之和。总购车成本是定量数据，并且该成本为成本型指标，则总购车成本

$\quad\quad{C_{\rm{p}}} = {C_{\rm{b}}} + {C_{\rm{t}}} + {C_{\rm{l}}} + {\rm{un}} \times {C_{\rm{u}}}{\text{。}}$

(7)

其中：总购车成本为 ${C_{\rm{p}}}$ ，购车成本为 ${C_{\rm{b}}}$ ，汽车购置税为 ${C_{\rm{t}}}$ ，车船使用税 ${C_{\rm{u}}}$ 固定 (420元/a)，un为使用年数，上牌费 ${C_{\rm{l}}}$ 固定(500元)，购置税 ${C_{\rm{t}}}$ =购车款÷(1+17%)×购置税率(7.5%)。

2) 燃油经济性。

燃油经济性指汽车使用过程中的燃油成本。燃油经济性与油耗量息息相关，单位用L/100 km表示，由于官方给出的数据仅供参考，在不同的路况模式下油耗量是不同的，故本文对百公里油耗量处理按照数据统计得来。油耗量为区间型数据，所以燃油经济性也为区间型数据和定量数据，燃油经济性越小越好，故为成本型指标，燃油总成本

$\quad\quad{C_{\rm{F}}} = ({\rm{O}}{{\rm{L}}_{\rm{c}}} \cdot {F_{\rm{m}}} \cdot {C_{{\rm{op}}}})/100{\text{。}}$

(8)

其中：燃油总成本为C_F，油耗量为 ${\rm{O}}{{\rm{L}}_{\rm{c}}}({\rm{L}}/100{\rm{km}})$ ，燃油里程 ${F_{\rm{m}}}({\rm{km}})$ ，平均燃油售价为C_op。

3) 维修成本。

汽车后市场的不规范操作导致实际中汽车维修成本难以统计，为确定对象车型的维修成本，需借助可靠性模型和维修更新模型进行预测。

Step 1　通过对汽车售后数据的分析，得出故障时间的分布函数，本文用指数分布、两参数威布尔分布、三参数威布尔分布、最小极值进行拟合，找出最合适的分布函数。

设T为故障时间的随机变量，t表示时间，则定义故障分布函数为：

$\quad\quad F(t) = P(T {\text{≤}} t){\text{。}}$

(9)

当 $F(t)$ 可微，其概率密度函数的表达式为

$\quad \quad f(t) = {\rm{d}}F(t)/{\rm{d}}t{\text{。}}$

(10)

定义与 $F(t)$ 相关的故障率函数为

$\quad \quad h(t) = f(t)/(1 - F(t)){\text{。}}$

(11)

Step 2　通过更新过程方程^[19]求解所要预测的平均故障次数。

计数过程{ $N(t),t {\text{≥}} 0$ }为普通更新过程，其中 $N(t)$ 为t时刻前发生的故障次数。

$N(t)$ 的期望值表示为 $M(t)$ ，对于 $M(t)$ 的推导过程已有很多文献研究^[14]，这里仅仅给出通过积分方程求解的表达式：

$\quad\quad M(t) = F(t) + \int_0^t {M(t - x)} f(x)\rm{d}x{\text{。}}$

(12)

则称该方程为更新过程方程。

假设本文的故障分布函数是已知的，故障频次的计数过程满足更新过程，故更新过程方程适用。根据威布尔分布的分布函数及其概率密度函数，运用Matlab软件计算在 $t = 6$ 时的平均故障次数 $M(6)$ 。

Step 3　单车平均维修成本

$\quad\quad{C_{\rm{w}}} = M(t) \cdot {\bar c_{\rm{w}}}{\text{。}}$

(13)

其中 ${C_{\rm{w}}}$ 为单车平均维修成本， $M(t)$ 为平均故障次数， ${\bar c_{\rm{w}}}$ 为单次故障的平均维修成本。对于 ${\bar c_{\rm{w}}}$ ，其与样本车的总维修成本 ${\rm{C}}{{\rm{B}}_{\rm{w}}}$ 与样本车的总维修次数 $N$ 相关；样本车的总维修费用等于同一辆车的维修次数和不同车的维修次数之和，令第 $ k $ 辆车的维修次数为pf_k，维修车辆的样本数为mm，则 ${\rm{C}}{{\rm{B}}_{\rm{w}}} = $ $ \displaystyle\sum\limits_{i = 1}^{{\rm{mm}}} {\displaystyle\sum\limits_{k = 1}^{{n_k}} {{\rm{p}}{{\rm{f}}_k}} } $ ；故 ${\bar c_{\rm{w}}} = {\rm{C}}{{\rm{B}}_{\rm{w}}}/N = \displaystyle\sum\limits_{i = 1}^{{\rm{mm}}} {\displaystyle\sum\limits_{k = 1}^{{n_k}} {{\rm{p}}{{\rm{f}}_k}} } /N$ 。也即维修成本模型为 ${C_{\rm{w}}} = M(t) \cdot {\bar c_{\rm{w}}} = M(t) \cdot \displaystyle\sum\limits_{i = 1}^{{\rm{mm}}} {\displaystyle\sum\limits_{k = 1}^{{n_k}} {{\rm{p}}{{\rm{f}}_k}} } /N$ 。

4) 隐形损失成本。

隐性损失成本是基于顾客角度出发的，是顾客因为维修及售后服务过程中造成车辆无法使用所占用的时间成本。隐性成本与维修及售后服务的次数、顾客的重要性，间接与汽车产品本身的质量相关，则每位顾客的平均隐性损失成本(点估计)计算如下：

$\quad\quad {C_{\rm{h}}} = \left(\sum\limits_{i = 1}^n {{T_{{\rm{s}}i}} \cdot } {W_{{\rm{ah}}i}}\right)/n{\text{。}}$

(14)

其中：维修及售后服务的数量为n，第 $ i $ 次维修及售后服务所需要的时间为 ${T_{{\rm{s}}i}}$ ，顾客 $ i $ 的平均时薪为 ${W_{{\rm{ah}}i}}$ 。

2.3 混合指标的欧氏距离公式

由于影响消费者购车的指标形式不同，距离公式也有一定差异，对于量化指标，可以通过差值表征属性值间的距离；对于区间型和直觉模糊数型指标，采用欧氏距离表征不同属性值间的无量纲差距，辅助多属性决策方法FVIKOR的实施。

定义5 　两个区间数 $x = \left[ {{x^{\rm{L}}},{x^{\rm{U}}}} \right],y = \left[ {{y^{\rm{L}}},{y^{\rm{U}}}} \right],$ x与 $y$ 的距离^[20]为

$\quad\quad d(x,y) = \displaystyle\frac{{\sqrt 2 }}{2}\sqrt {{{({x^{\rm{L}}} - {y^{\rm{L}}})}^2} + {{({x^{\rm{U}}} - {y^{\rm{U}}})}^2}} {\text{。}}$

(15)

定义6 　两个直觉模糊数 $\alpha = ({\mu _\alpha },{\gamma _\alpha },{{\text{π}} _\alpha })$ 和 $\beta = ({\mu _\beta },{\gamma _\beta },{{\text{π}} _\beta })$ 之间的距离^[21]为

$\quad\quad d(\alpha ,\beta ) \!=\! \displaystyle\frac{{\sqrt 2 }}{2}\!\!\sqrt {{{({\mu _\alpha } \!-\! {\mu _\beta })}^2} \!+\! {{({\gamma _\alpha } \!\!-\! {\gamma _\beta })}^2} \!+\! {{({{\text{π}} _\alpha } \!-\! {{\text{π}} _\beta })}^2}} {\text{。}}$

(16)

3 基于扩展VIKOR的质量经济性评价模型

模糊VIKOR (FVIKOR)是一种处理含不确定性评价信息的多准则决策方法，能够实现在多个属性约束下对不同待评对象的评价，并确定其综合性能优劣。经典VIKOR的多属性决策是在L_p-Metrix公式基础上发展而来的：

$\begin{split}&\quad\quad{L_{p,i}} = {\left\{ {\sum\limits_{j{\text{ = }}1}^n {{{\left[ {\displaystyle\frac{{{w_j}(f_j^* - {f_{ij}})}}{{f_j^* - f_j^ - }}} \right]}^p}} } \right\}^{1/p}} = \\&{\left\{ {\sum\limits_{j{\text{ = }}1}^n {{{\left[ {{w_j}\displaystyle\frac{{{d_j}(\max ,i)}}{{{d_j}(\max ,\min )}}} \right]}^p}} } \right\}^{1/p}}\!\!\!\!,p \!\in\! [1, \!+\! \infty ),i \!\!=\!\! 1,2,...,m{\text{。}}\end{split}$

(17)

其中： $f_{ij} $ 为评价信息值； $f_j^* = \mathop {\min }\limits_{1 {\text{≤}} i {\text{≤}} m} ({f_{ij}})$ , $f_j^ - = \mathop {\max }\limits_{1 {\text{≤}} i {\text{≤}} m} ({f_{ij}})$ ， ${d_j}(p,q)$ 表示关于j指标的p和q的距离；对象通过群体效用值L_1i(S_i)和个体遗憾值L_∞i(R_i)进行评选排序。

3.1 问题描述

假设有备选的车型A=(A₁,A₂,…,A_i,…,A_m)，影响汽车质量经济性的主要属性集为CC=(CC₁,CC₂,...,CC_j,...,CC_n),n≥2，且指标的重要程度权重向量为w=(w₁,w₂,...w_j,...,w_n)，元素w_j为决策属性j的权重值，x_ij为对象车型i隶属指标j的评价值信息，可以为量化准确数值，区间数或直觉模糊集表述的模糊语言等。

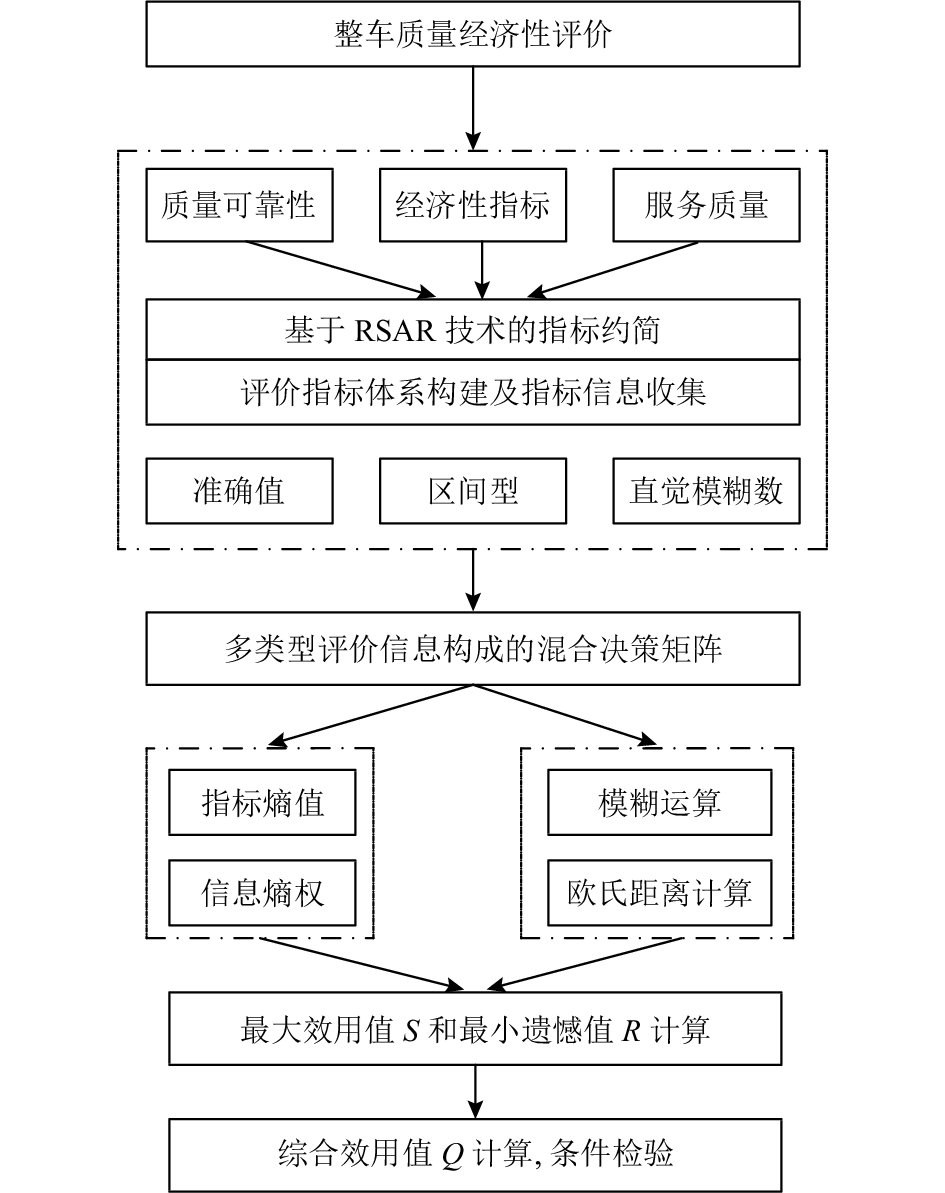
3.2 扩展VIKOR多准则实施步骤

本文基于构建的质量经济性评价指标体系，利用模糊多属性决策方法FVIKOR实现对多指标约束下不同车型的质量经济性评价。针对构建的混合型指标体系特点，提出基于欧氏距离的改进模糊VIKOR决策方法，通过对混合型指标欧氏距离的计算，求解最大效用值、最小遗憾值和综合效用值指标，实现不同车型的质量经济性评价。本文提出的基于欧氏距离的改进模糊VIKOR多属性决策实施流程如图1所示。

Step 1　基于粗糙集属性约简的指标体系构建。采用Rosetta中SAVGeneticReducer板块遗传属性约简算法^[16]，遗传算子设置如下：交叉概率P_c=0.3，变异概率P_m=0.05；初始种群规模M₀=70，最大种群规模M=256；最优解不提高终止迭代次数NN=30。

Step 2　对象车型的信息收集及整理。通过数值型、区间型和语言变量等3种形式描述评价车型隶属混合指标的决策信息，并将语言变量按照表2转化为直觉模糊数进行下一步计算。

Step 3　混合指标信息熵计算，并确定因素权重。

1) 用信息熵计算各决策者权重 ${\lambda _l}$ ，设决策者 ${D_l}$ 的信任函数为 ${B_l}(\delta )$ ，如下式：

$\quad\quad{B_l}(\delta ) = - \displaystyle\frac{1}{{\left(\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\delta _{ij}^l} } \right)\ln \left(\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\delta _{ij}^l} } \right)}},$

(18)

$\quad\quad {\lambda _l} = \displaystyle\frac{{{B_l}(\delta )}}{{\sum\limits_{l = 1}^p {{B_l}(\delta )} }}{\text{。}}$

(19)

其中δ_ij^l为决策者 ${D_l}$ 的评价知识所对应直觉模糊数中的犹豫度值。

2) 计算各指标权重。设各评价指标的权重为 ${\omega } = ({\omega _1},{\omega _2}, \cdots ,{\omega _m})$ ，其中 ${\omega _j} \geqslant 0,j = 1,2, \cdots ,m,\sum\limits_{j = 1}^m {{\omega _j}} = $ 1。各评价准则的均值定义如下：数值型评价值归入 ${I_1}$ ，区间型数值归入 ${I_2}$ ，直觉模糊数型评价值归入 ${I_3}$ 。

$\quad\quad\overline {{\gamma _j}} = ({r_{1j}} \oplus {r_{2j}} \oplus \cdot \cdot \cdot \oplus {r_{ij}} \oplus \cdot \cdot \cdot \oplus {r_{nj}})/n=$

$\left\{ {\begin{array}{l}\displaystyle{\frac{1}{n}\sum\limits_{i = 1}^n {{r_{ij}},{r_{ij}} \in {I_1};} }\\\displaystyle{\left[ {\frac{1}{n}\sum\limits_{i = 1}^n {r_{ij}^L,\frac{1}{n}\sum\limits_{i = 1}^n {r_{ij}^U} } } \right],{r_{ij}} \in {I_2};}\\\displaystyle\begin{array}{l}\left( {1 - \displaystyle\prod\limits_{i = 1}^n {{{\left( {1 - {\mu _{ij}}} \right)}^{\frac{1}{n}}},\displaystyle\prod\limits_{i = 1}^n {{{\left( {{\gamma _{ij}}} \right)}^{\frac{1}{n}}},} } } \displaystyle\prod\limits_{i = 1}^n {{{\left( {1 - {\mu _{ij}}} \right)}^{\frac{1}{n}}} -}\right.\\\displaystyle\left. { {\prod\limits_{i = 1}^n {{{\left( {{\gamma _{ij}}} \right)}^{\frac{1}{n}}}} } } \right),{r_{ij}} \in {I_3}{\text{。}}\end{array}\end{array}} \right.$

(20)

评价指标 ${C_j}$ 的熵值求解如下：

$\;\;{e_j} = - \displaystyle\frac{1}{{\ln (n)}}\sum\limits_{i = 1}^n {\left[ {\displaystyle\frac{{d({r_{ij}},\overline {{\gamma _j}} )}}{{\sum\limits_{i = 1}^n {d({r_{ij}},\overline {{\gamma _j}} )} }}\ln (\displaystyle\frac{{d({r_{ij}},\overline {{\gamma _j}} )}}{{\sum\limits_{i = 1}^n {d({r_{ij}},\overline {{\gamma _j}} )} }})} \right]}{\text{。}}$

(21)

各指标权重为

$\quad\quad{\omega _j} = \displaystyle\frac{{1 - {e_j}}}{{\sum\limits_{q = 1}^m {(1 - {e_q})} }},j = 1,2, \cdot \cdot \cdot ,m{\text{。}}$

(22)

Step 4　确定各属性的理想解f_j^*和负理想解f_j^-。

$\begin{array}{l}\quad\quad f_j^* = (f_1^*,f_2^*, \cdot \cdot \cdot ,f_j^*, \cdot \cdot \cdot ,f_n^*) =\\(\max {r_{i1}},\max {r_{i2}}, \cdot \cdot \cdot ,\max {r_{ij}}, \cdot \cdot \cdot ,\max {r_{in}}),i = 1,2, \cdot \cdot \cdot ,m;\\\quad\quad f_j^ - = (f_1^ - ,f_2^ - , \cdot \cdot \cdot ,f_j^ - , \cdot \cdot \cdot ,f_m^ - ) =\\(\min {r_{i1}},\min {r_{i2}}, \cdot \cdot \cdot ,\min {r_{ij}}, \cdot \cdot \cdot ,\min {r_{in}}),i = 1,2, \cdot \cdot \cdot ,m{\text{。}}\end{array}$

(23)

Step 5　计算每个待评车型的最大群体效用S_i和最小遗憾值R_i。

$\quad\quad {S_i} = \sum\limits_{j = 1}^m {{\omega _j}} \displaystyle\frac{{d(f_j^*,{r_{ij}})}}{{d(f_j^*,f_j^ - )}},{R_i} = \mathop {\max }\limits_j \left[ {{\omega _j}\displaystyle\frac{{d(f_j^*,{r_{ij}})}}{{d(f_j^*,f_j^ - )}}} \right]{\text{。}}$

(24)

其中：S_i代表第i个对象关于准则j的与最优理想值的距离比，R_i表示最小遗憾值。

Step 6　计算各个待评车型的综合效用值Q_i。

$\quad\quad {Q_i} = v\displaystyle\frac{{{S_i} - {S^*}}}{{{S^ - } - {S^*}}} + \left( {1 - v} \right)\displaystyle\frac{{{R_i} - {R^*}}}{{{R^ - } - {R^*}}}{\text{。}}$

(25)

其中： ${S^ - } \!=\! \mathop {\max }\limits_i {S_i}$ , ${S^*} \!=\! \mathop {\min }\limits_i {S_i}$ , ${R^ - } \!=\! \mathop {\max }\limits_i {R_i}$ , ${R^*} \!=\! \mathop {\min }\limits_i {R_i}$ , $v \in \left( {0,1} \right)$ 表示决策者最大群体效用的权重，而(1-v)表示个体遗憾的权重。

Step 7　确定折中满意方案解。分别通过S、R和Q值对评选对象进行排序，得出3组排序结果。按照Q_i值递增得到排序A⁽¹⁾,A⁽²⁾,...,A^(m)。当同时满足以下两个条件时，则最小对象综合效用值Q_i(Q⁽¹⁾)所对应的评价对象A⁽¹⁾将作为折中满意方案解。

条件1(接受优势)：令DQ=1/(m–1)，满足Q(A⁽²⁾)–Q(A⁽¹⁾)≥DQ。

条件2(决策的稳定性)：Q_i值最小对应的评选对象A⁽¹⁾必须与S或R排序规则中的最优评价对象一致，即A⁽¹⁾同时为依据S或R值排序的最优，才能保证决策的稳定性。

如果上述条件不能同时满足，则出现折中满意方案集(即不止有一个满意方案解)，此时分两种情况^[22-23]。

若不满足条件1，则 ${A^{\left( 1 \right)}},{A^{\left( 2 \right)}}, \ldots ,{A^{\left( m \right)}}$ 组成备选折中满意方案集，A^(m)是Q(A^(m))−Q(A⁽¹⁾)＜DQ确定最大化的m值。若不满足条件2，则A⁽¹⁾和A⁽²⁾组成备选折中满意方案集，即可以选择A⁽¹⁾和A⁽²⁾作为满意方案解。

4 案例研究 4.1 案例设置

本文以某汽车电商平台中几款车型排名问题为研究对象，从多属性视角为购车消费者推送车型推荐，主要是针对售价在10万左右的5款运动型多用途汽车(SUV)进行综合排名。通过对决策表的属性约简，构建汽车质量经济性指标体系，调研对象的属性值如表3。通过式(6)~(14)计算成本指标项。

本文所使用的总拥有成本模型是购车者购买汽车及使用过程中发生的成本，同时为了便于定量化对比几款车型的总拥有成本情况，以行驶6年所发生的成本计算，而从售后维修数据的105条数据中，得出汽车平均每天的行驶里程为68.49 km，约合2.5万km/a，故总拥有成本近似为15万km耗费的成本总和。

4.2 计算结果

在案例计算过程中取v=0.5，即最小化个体遗憾值和最大化群体效用权重相等，均为0.5，通过式(18)~(26)，计算各对象车型的最大群体效用 ${S_i}$ 、最小个体遗憾 ${R_i}$ 和综合效用值 ${Q_i}$ 如表4所示。

由 ${Q_i}$ 值增加的方式进行排序，得到结果为 ${A_2},{A_1},{A_5},{A_4},{A_3}$ ，并判别 ${A_2}$ 是否满足最优方案的条件。条件1： $Q({A_2}) - Q({A_1}) = 0.403 {\text{＞}} {\rm{DQ}} = 1/4$ ；条件2： ${A_2}$ 按照S和R的排序结果是最优解。故得出 ${A_2}$ 为在这5款车关于汽车综合质量评价的满意妥协解。

4.3 对比分析

J.D. Power报告调研证明，价格作为购车消费者关注要素之一，往往显著影响其购买决策^[1]。实际消费者在购车过程往往忽视使用成本及隐形损失等经济性要素，往往看重产品质量及购买成本。为此，本文对不考虑运营、使用、隐形损失等成本条件下，基于此模型的车型推荐结果进行对比分析，实施步骤同上文方法，得出各车型的最大效用值S、最小遗憾值R及综合效用值Q，推荐排名如表5所示。

同理，计算结果满足两个验证条件；由Q值降序可知，各车型的推荐结果为 ${A_2},{A_1},{A_4},{A_5},{A_3}$ ，与原有排序 ${A_2},{A_1},{A_5},{A_4},{A_3}$ 存在差异；虽然 ${A_2}$ 仍然作为最有满意妥协解，仍获得优先的购买推荐；但A₄与A₅车型的排名发生了明显变化。这可以说明，在预防性考虑使用、维系等运维成本时，相对于A₄车型，A₅车型并没有显著的竞争力，敦促消费者在购车决策时，充分考虑总拥有成本。

4.4 效用权重灵敏度分析

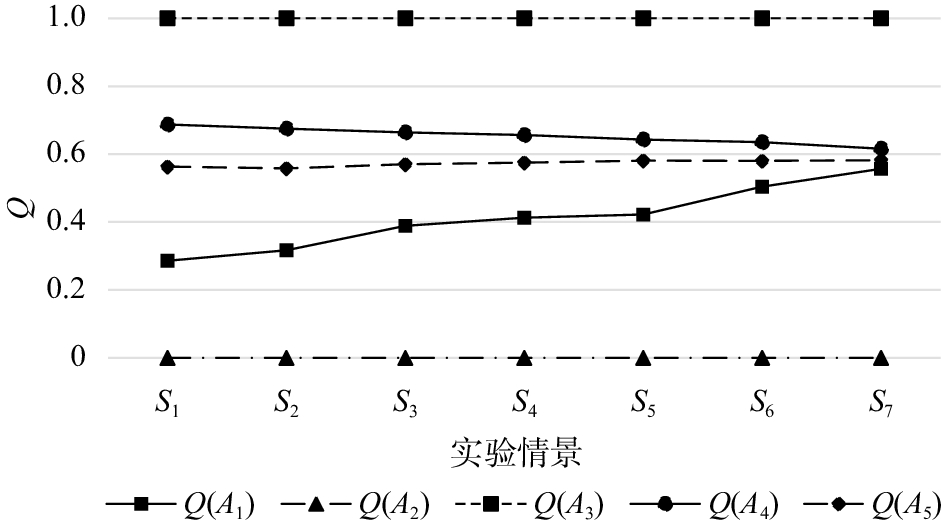
在决策过程中，前文选取效用值权重v=0.5，为验证不同效用权重下各车型推荐排名的鲁棒性，探究不同效用值权重下对象车型的质量经济性排序，通过表6中的7种情景设置，进行灵敏度分析；不同实验情景下，各车型的综合效用值计算结果如图2所示。

通过图2可知，虽然不同实验情景下，各车型的综合效用值有轻微波动，但整体排名仍保持相对稳定的状态，与算例相同，即A₂车型仍然作为最优推荐，故具有较好的鲁棒性。

4.5 指标敏感性分析

本文利用混合指标的欧氏距离量化计算评价矩阵中指标的信息熵权，进而通过VIKOR多准则决策实现对象车型的排名推荐；为研究指标的敏感度，利用扰动分析，研究指标权重波动情况下，各对象车型的质量经济性排名。由于本文涉及指标较多，为简化研究，本文采取对消费者最为关注的二级指标进行扰动性实验，主要包括产品质量权重 ${\tau _1}$ (可靠性CC₁)、动力性能权重 ${\tau _2}$ (动力性CC₂)、安全性能权重 ${\tau _3}$ (安全性CC₃、制动性CC₄、操纵稳定性CC₅)，消费者体验 ${\tau _4}$ (舒适性CC₆、美观性CC₇、服务质量CC₈) 及经济性指标权重 ${\tau _5}$ (购车成本CC₉、燃油经济性CC₁₀、保养费用CC₁₁、维修费用CC₁₂)，其中 $\displaystyle\sum\limits_{i = 1}^5 {{\tau _i} = 1} (i = 1,2,...,5)$ 。

给定一个扰动Δ，初始指标权重τ_i，经过扰动变动后的权重为τ_i'，令τ_i' =Δτ_i，其中0≤τ_i' ≤1，可得0≤Δ≤1/τ_i，而 $\displaystyle\mathop \sum \limits_{i = 1}^5 {\tau _i}\left( {i = 1,2, \ldots ,5} \right)$ ，当控制指标得到扰动影响后，其余指标权重也发生相应扰动变化，记作τ'_n=φτ_n,n≠i, n=1,2,…,5 (φ指相应扰动系数)，且满足

$\quad\quad\tau _i' + \mathop \sum \limits_{n \ne i,n = 1}^5 \tau _n' = 1 \Rightarrow \varDelta {\tau _i} + \varphi \mathop \sum \limits_{n \ne i,n = 1}^5 {\tau _i} = 1{\text{。}}$

(26)

进而得出φ=(1-Δτ_i)/(1-τ_i)，取Δ=2, 1.5, 0.5, 0.25进行20次扰动，得到不同计算结果如表7所示。

由表7中可以得出， ${A_2}$ 车型在20次不同指标权重的变化中有18次的Q值仍然保持最小，占比90%； ${A_3}$ 车型在权重变化过程中的Q值有18次排在最后一位，占比90%；这说明权重变化时，车型 ${A_2}{\text{、}}{A_3}$ 的综合质量排序结果相对稳定，其他车型需要根据对指标的看重情况来优选车型。

增大可靠性指标的权重时，排序结果发生变化， ${A_5}$ 车型排在了 ${A_1}$ 车型的前面说明 ${A_5}$ 的可靠性是要优于 ${A_1}$ 的。在不断增大动力性指标权重时， ${A_4}$ 车型排名靠前，表明 ${A_4}$ 车型在动力性能的表现是要高于 ${A_1}$ 车型，当顾客比较看重动力性能时，可以考虑 ${A_2}{\text{、}}{A_4}$ 车型。当看重安全性能时， ${A_1}$ 车型排在了 ${A_2}$ 车型的前面，说明了 ${A_1}$ 车型综合安全性能是要好于 ${A_2}$ 车型的，才使得其综合排名在第一位。增大顾客感知方面的权重时， ${A_4}$ 车型排在 ${A_1}$ 车型的前面，说明 ${A_4}$ 车型的美观性、舒适性和服务质量综合是要好于 ${A_1}$ 车型的。当减小总拥有成本方面的权重时， ${A_4}$ 车型排在了 ${A_5}$ 车型的前面，表明在不考虑成本的情况下， ${A_4}$ 车型在其他指标方面的表现要好于 ${A_5}$ 车型。

5 结论

针对汽车消费者在购车时面对参差不齐的汽车排名的问题，为帮助汽车消费者选择车型时的购买决策，综合考虑产品质量、售后服务质量和总拥有成本等质量经济性指标，在基于粗糙集属性约简基础上删除冗余指标，并构建基于扩展VIKOR多准则决策的综合评价模型，实现对各对象车型的质量经济性排名，辅助消费者选车时的购买决策。由于集成指标的复杂多样及主观不确定性，引入区间数和直觉模糊数处理主观不确定评价信息，提出基于混合指标的欧氏距离公式，并计算指标权重，通过VIKOR实施步骤计算出满意妥协解，为汽车消费者购买决策提供排名建议。通过案例中灵敏度分析和指标扰动敏感性分析，可知本文方法具有较好的鲁棒性，能够选择具有稳定最佳质量经济性的车型；同时通过是否考虑使用成本前后的对比分析，相比传统关注购买价格和燃油经济性的汽车排名方法，本文方法具有一定的实用性和科学性，帮助购车者理智消费决策。

相比汽车之家、J.D Power、众调科技等汽车排名信息，本文的汽车质量经济性综合评价模型从消费者视角，强调购车者从购买至使用全过程的理智消费，为汽车购买推荐决策提供理论支撑。但随着互联网数据挖掘技术的广泛应用及潜在消费者对车型口碑的重视，如何高效利用冗乱、繁杂的使用评价口碑信息，挖掘有效质量经济性信息，在考虑顾客个性化需求同时，实现车型排名的智能推荐是下一步研究方向。同时依据不同消费群体的消费偏好，在不同消费群体差异化需求下，提供更加准确的评价模型也是笔者进一步需研究的重点。