2. 西安交通大学 管理学院,陕西 西安 710049
2. School of Management, Xi’an Jiaotong University, Xi’an 710049, China
工程项目的支付和进度安排与承包商的收益密切相关。随着较高的利率和昂贵的融资费用,尤其对于资金密集型的项目,如何实现进度与支付的集成优化,使得项目净现值最大化已成为一个更贴近现实的项目调度优化目标[1]。另外在项目实施过程中,保持现金流的动态均衡对项目的成功至关重要。因此通过项目内部调度优化实现现金流动态均衡,并力图实现项目收益的最大化,是具有较高实用价值的研究问题[2]。
以Max-npv作为项目调度优化目标,国内外学者对此进行了深入研究。其中,Doersch等[3]从提高经济效益角度,最早建立了净现值最大化的调度模型。Dayanand等[4]分别从承包商和业主的角度研究了工程款支付时间和进度的安排。李诗娴[5]以净现值最大化为目标,并综合考虑模式选择、支付进度、支付方式等影响净现值的因素,建立了调度优化模型。何小丽[6]对考虑时间转换约束的净现值最大化项目调度问题进行了研究,建立了里程碑事件和相等时间间隔两种支付下的优化模型。何正文等[7]、马志强等[8]以Max-npv为优化目标,以一个真实工程案例为对象,从承包商、业主以及双方联合角度建立了支付进度优化模型,并获得了不同角度下的满意支付进度安排。在考虑承包商和业主交互作用下的项目调度优化方面,何正文等[9]以净现值最大化为目标,构建了由业主和承包商两个子模型构成的项目调度优化模型,对合同双方交互作用下的项目调度优化问题进行了研究。李兰英等[10]从合同双方的双重视角出发,研究了承包商和业主基于合作博弈的多模式Max-npv项目调度优化问题。郑维博等[11]从项目双方的视角出发,研究了融资能力约束下的Max-npv项目调度问题。在随机工期下的项目调度优化方面,郑维博等[12]研究了不确定环境中在可更新资源约束下,活动工期具有随机性的Max-npv项目鲁棒性调度问题。王艳婷等[13]研究了在活动工期随机中断情况下,比较了不同目标、不同资源分配方式及进度生成方式基础上的反映性调度过程,并通过总成本及项目完工时间等指标分析反映性策略对调整过程的影响。
基于上述理论与实际研究现状,本文综合考虑支付进度与现金流动态均衡两方面因素,并以一个实际的房地产项目室外基础设施配套工程为对象,对基于Max-npv的项目进度与支付集成优化问题进行研究。首先介绍工程的背景资料,随后基于承包商角度构建项目进度与支付集成调度优化模型,并选取4种优化方案对模型进行求解,完整呈现不同支付进度下NPV的手算过程与方法,并将理论求解结果与实际情况进行对比分析,找出工程实际进度管理中存在的差距。文中计算方法简便,可操作性强,能为项目在现实中进行支付进度集成优化提供可操作性强的定量化决策方法。
1 案例背景简介新疆维吾尔族自治区鄯善县某房地产项目室外基础设施配套工程(三标段)是由室外道路、给水排水管道、供热管道、消防管道4部分组成,合同总金额594.834 4万元,要求开工日期为2013年6月20日,竣工验收日期为2013年11月15日,工期148 d,最迟完工日期不得超过2013年12月10日。该项目的双代号网络图如图1所示,活动工期以日历天(d)为单位,各活动相关数据见表1。根据项目总工期及网络图可确定网络图中关键活动为:1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-18-32。
| 表 1 某室外基础设施配套工程各活动的工期、挣值及费用 Tab. 1 Duration, earned value, and expenses for activities of an outdoor infrastructure supporting project |

|
图 1 某室外基础设施配套工程双代号网络图 Fig. 1 Double-code network diagram of the outdoor infrastructure supporting project |
项目支付要点如下。
1) 本工程无预付款,承包商需调拨110万元专项资金,作为前期启动和材料周转资金。项目实施过程中,资金使用量不得超过其上限。
2) 业主每月5日支付上月已完工程价款的70%,其余30%在整个项目结束时刻,即最后一次事件进行支付。承包商也是在每月5日向供应商支付各种成本费用,产生负的现金流,即正负现金流都是在每月5日发生。
3) 必须在合同规定的最终日期前完工,竣工验收即为整个项目的终事件,并且业主在此时间点进行竣工结算支付。
4) 关于项目完工日期无奖惩条款。
项目实际执行进度计划的完工日期为2013年12月9日,项目实施过程中最大化资金缺口为103万元,累计净现值429 448元。
2 优化模型构建及求解 2.1 优化模型构建采用基于事件的方法[14]构建净现值最大化优化模型,本项目共31个事件,32个活动。问题界定及各符号定义如下。
令
| $\quad\quad{e_m} = \zeta \sum\limits_{n \in S_m^1} {{c_n}} + \left( {1 - \zeta } \right)\sum\limits_{n \in S_m^2} {{c_n}} ,$ |
| $\quad\quad{v_m} = \sum\limits_{n \in S_m^2} {\mathop \nu \nolimits_n } {\text{。}}$ |
其中,ζ为活动费用在其开始事件和结束事件的分配比例,课题组对ζ分别取值0.3、0.5、0.7,按照项目实际执行情况,进行相应取值下的模型算例测试。结果显示,ζ取0.5时测试结果最接近项目实际情况,故在此确定ζ取值为0.5;
令
在符号定义的基础上,构建某房地产项目室外基础设施配套工程NPV最大化调度优化模型如下。
| $\begin{split}&\quad\quad\displaystyle\max{\rm{NPV }} = \sum\limits_{k = 1}^{31} {\left( {{p_k}\sum\limits_{m = 1}^{31} {{x_{km}}} \sum\limits_{t = {E_m}}^{{L_m}} {{z_{mt}}} \exp ( - \alpha t)} \right)} -\\&\displaystyle\sum\limits_{m = 1}^{31} {\left( {{e_m}\sum\limits_{t = {E_m}}^{{L_m}} {{z_{mt}}} \exp ( - \alpha t)} \right)}{\text{。}} \end{split}$ | (1) |
本工程折现率取值
s.t.
| $\quad\quad\sum\limits_{m = 1}^{31} {{x_{km}}} = 1,k = 1,2, \cdots ,K - 1;$ | (2) |
| $\quad\quad{x_{KM}} = 1;$ | (3) |
| $\quad\quad\sum\limits_{k = 1}^K {{x_{km}}} {\text{≤}} 1,m = 1,2, \cdots ,31;$ | (4) |
| $\quad\quad{e_m} = 0.5\sum\limits_{n \in s_m^1} {{c_n}} + 0.5\sum\limits_{n \in s_m^2} {{c_n}} ,m = 1,2, \cdots ,31;$ | (5) |
| $\quad\quad\sum\limits_{t = {E_m}}^{{L_m}} {{z_{mt}}} = 1,m = 1,2, \cdots ,31;$ | (6) |
| $\quad\quad\sum\limits_{t = {E_g}_{_n}}^{{L_{{g_n}}}} {({Z_{{g_n}}}_tt)} + {d_n} {\text{≤}} \sum\limits_{t = {E_{h_n^{}}}}^{{L_{{h_n}}}} {({Z_{{h_h}t}}t)} ,n = 1,2,\cdots ,32;$ | (7) |
| $\quad\quad\sum\limits_{t = {E_M}}^{{L_M}} {({Z_{{M_t}}}t)} {\text{≤}} 173;$ | (8) |
| $\begin{split}&\displaystyle\quad\quad{p_k} = 0.7\left( {\sum\limits_{m = 1}^{31} {\left( {{v_m}\sum\limits_{t = 0}^{{T_k}} {{z_{mt}}} } \right) - \sum\limits_{m = 1}^{31} {\left( {{v_m}\sum\limits_{t = 0}^{{T_{k - 1}}} {{z_{mt}}} } \right)} } } \right),\\&\displaystyle k = 1,2,\cdots ,K - 1;\end{split}$ | (9) |
| $\quad\quad{p_K} = U - \sum\limits_{k = 1}^{K - 1} {{p_k}} ;$ | (10) |
| $\begin{split}&\displaystyle\quad\quad\sum\limits_{m = 1}^{31} {\left( {{e_m}\sum\limits_{t = 0}^T {{z_{mt}}} } \right)} \!- \!\!\sum\limits_{k = 1}^K {\left( {{p_k}\sum\limits_{m = 1}^{31} {\left( {{x_{km}}\sum\limits_{t = 0}^T {{z_{mt}}} } \right)} } \right)} {\text{≤}} {\rm{ICA}},\\&\displaystyle T = 1,2,\cdots ,173;\end{split}$ | (11) |
| ${x_{km}},{z_{mt}} \in \left\{ {0,1} \right\}{\text{。}}$ | (12) |
其中,
| $\quad\quad{T_k} = \sum\limits_{t = 0}^{173} {\left( {t\sum\limits_{m = 1}^{31} {({x_{km}}{z_{mt}})} } \right)} {\rm{ }},{T_{k - 1}} = \sum\limits_{t = 0}^{173} {\left( {t\sum\limits_{m = 1}^{31} {\left( {{x_{(k - 1)m}}{z_{mt}}} \right)} } \right)} $ |
分别表示第k及k–1次工程款的支付时间。
在上述优化模型中,目标函数式(1)为承包商净现值NPV最大化;约束条件式(2)表示支付在事件点上发生,且每次支付发生时取1,否则取0;式(3)表示最后一次工程款安排在项目的最终事件上支付;式(4)表示每个事件最多只能安排一次支付;式(5)表示事件费用的计算式;式(6)表示事件m发生的时间窗;式(7)表示网络计划中活动的优先关系;式(8)表示项目截止日期的约束;式(9)表示每次支付的支付量;式(10)表示最后一次的支付量;式(11)表示承包商累计费用与累计支付之差不超过其初始可用资金;式(12)表示决策变量的定义域约束。在满足约束条件的前提下,该优化模型通过合理安排事件的实现时间,有效地调整各项费用及各次支付的发生时间,达到项目实施过程中承包商净现值NPV最大化目标。
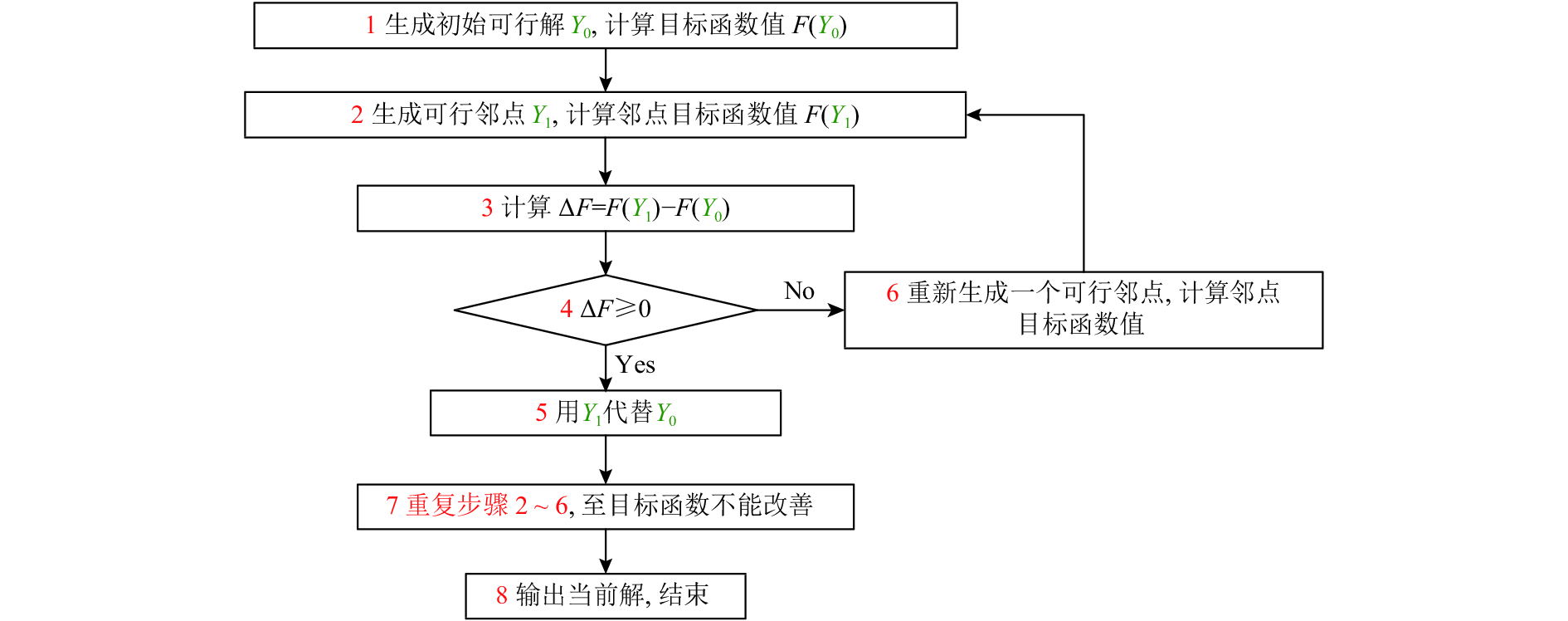
2.2 优化模型的求解流程及过程基于模型理论,建立模型求解流程图如图2所示。
|
图 2 模型求解流程图 Fig. 2 The model solution flow chart |
步骤1 确定满足资金约束和工期约束的初始可行解(按项目实际进度运行),计算其目标函数值F(Y0);
步骤2:任选一个事件,在其开始时间窗内随机变动,生成满足资金约束和工期约束的可行邻点,计算其目标函数值F(Y1);
步骤3 计算可行邻点Y1的目标函数值F(Y1)和初始可行解Y0的目标函数值F(Y0)的差值
步骤4 判断
步骤5 如
步骤6 如
步骤7 重复步骤2~步骤6,直到目标函数值不能改善为止;
步骤8 输出当前满意解,求解结束。
3 求解过程及结果讨论 3.1 初始可行解及目标函数值确定由前述项目网络图、开工日期、最迟完工日期可得到每个事件的开始时间窗。在此以项目实际执行情况作为初始可行解,即关键路径上活动按最早开始时间执行,其他非关键路径上的活动按最晚开始时间执行,得到每个事件的开始时间表如表2所示。
| 表 2 项目实际执行进度下事件的开始时间表 Tab. 2 Starting time schedule of events under actual project progress |
按照项目支付要点及在折现率为0.000 5的条件下,确定出各次支付活动,依据前述优化模型求解原理,手工计算并借助Excel软件得出每次支付的净现值及项目累计净现值如表3所示。
| 表 3 项目实际执行进度下支付活动及净现值 Tab. 3 Payment activity and net present value under actual project progress |
上述结果反映了项目实际执行进度下完工日期为12月9日,累计净现值为429 448元,最大化资金缺口为103万元,虽未超过资金可用量上限,但仍给承包商造成较大的资金压力。
3.2 优化方案可行解及目标函数值确定按照模型求解原理,应在其可行解范围内访问所有邻点,逐一比较,求得最优解。一般借助算法编程完成求解过程。此处采用手工计算借助Execl软件完成,故随机选择4种优化方案,同时考虑以下因素。
优化方案1 活动3位于网络图的关键线路中,属关键活动,且其费用较大。为减轻承包商的前期资金压力,将事件3开始时间由最早开始时间第11 d设定为第25 d,得到可行邻点1。按照网络优先关系得到各事件的开始日期,进而得到优化方案1下各次支付的支付活动及净现值。由于篇幅所限,事件开始时间表未列。各次支付的净现值及项目累计净现值见表4。
| 表 4 优化方案1的支付活动及净现值 Tab. 4 Payment activity and net present value of the optimization Scheme One |
根据净现值计算结果及模型求解流程图步骤3~步骤7,优化方案1净现值大于项目实际进度净现值,项目完工日期为11月29日,比实际进度提前10 d,且最大化资金缺口比项目实际进度资金缺口小,缓解了承包方的资金压力,故用优化方案1代替初始可行解,确定为当前最优解。
优化方案2 活动19位于非关键路径中,且其属非关键路径中工期最长的活动。为使活动19能按支付要点尽早支付,将非关键路径中事件19与20设定按最早开始时间执行,其他非关键路径上活动按最晚开始时间执行,得到可行邻点2。按照网络优先关系得到各事件的开始日期,进而得到优化方案2下各次支付的支付活动及净现值,各次支付的净现值及项目累计净现值见表5。
| 表 5 优化方案2的支付活动及净现值 Tab. 5 Payment activity and net present value of the optimization Scheme Two |
重复步骤3~步骤7,优化方案2的净现值小于当前最优解的净现值,故确定优化方案1仍为当前最优解。
优化方案3 考虑尽早完工,使承包商费用消耗及早得到补偿,故设定优化方案3为所有事件均按最早开始时间执行,得到可行邻点3。按照网络优先关系计算各事件的开始日期,进而得到优化方案3下各次支付的支付活动及净现值,各次支付的净现值及项目累计净现值见表6。
| 表 6 优化方案3的支付活动及净现值 Tab. 6 Payment activity and net present value of the optimization Scheme Three |
重复步骤3~步骤7,优化方案3的净现值大于当前最优解的净现值,故用优化方案3代替优化方案1,确定优化方案3为当前最优解。
优化方案4 关键路径上活动最多,费用消耗最大,考虑到承包商资金压力及资金流均衡,将优化方案4设定为:关键路径上活动12~32按最晚开始时间执行,其他活动按最早开始时间执行,得到可行邻点4。按照网络优先关系计算各事件的开始日期,进而得到优化方案4下各次支付的支付活动及净现值。各次支付的净现值及项目累计净现值见表7。
| 表 7 优化方案4的支付活动及净现值 Tab. 7 Payment activity and net present value of the optimization Scheme Four |
重复步骤3~步骤7,优化方案4的净现值小于当前最优解的净现值,故确定优化方案3仍为当前最优解。优化方案3下各事件的开始时间如表8所示。
| 表 8 优化方案3下各事件的开始时间表 Tab. 8 Starting time schedule of each event in the optimization Scheme Three |
通过上述计算结果可知,项目实际执行情况下与当前最优解下的净现值、项目完工日期及最大化资金缺口如表9所示。由表9可知,当前最优解执行方案与项目实际执行情况相比较,净现值增加76 433元,增加幅度17.8%;项目完工日期提前18 d;最大化资金缺口减少101 595元。
| 表 9 项目实际执行情况与当前最优解各项指标对比 Tab. 9 Comparison between the actual implementation of the project and the current optimal Solution |
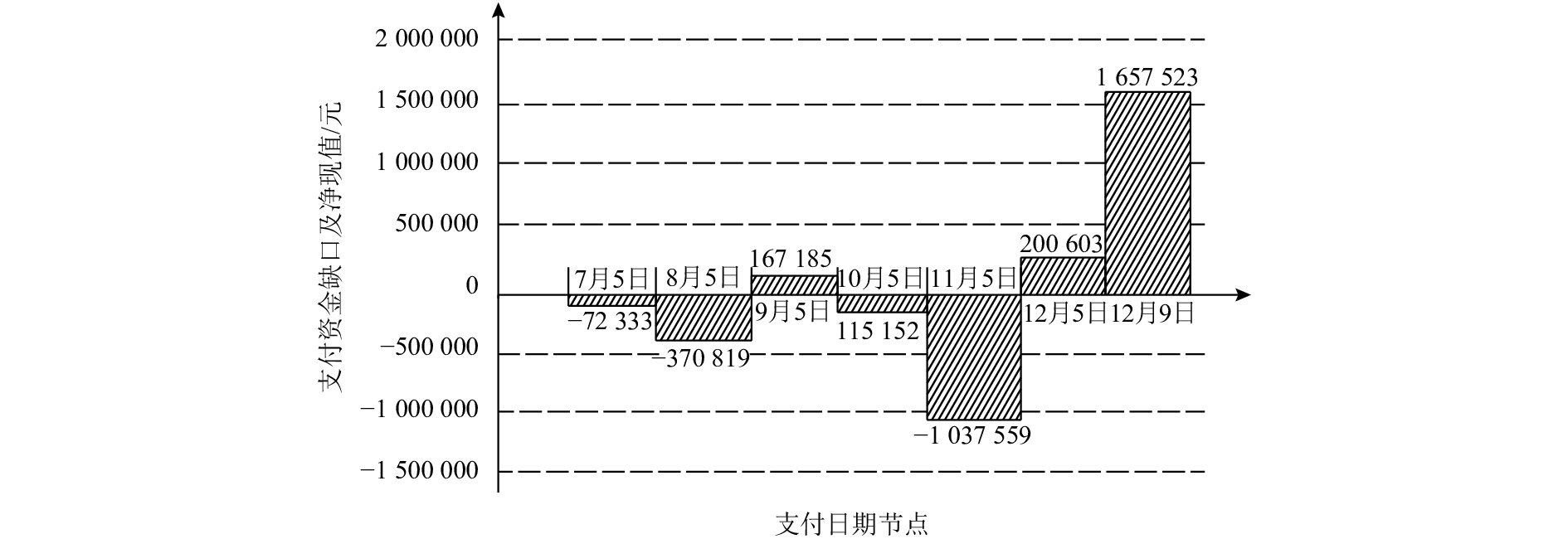
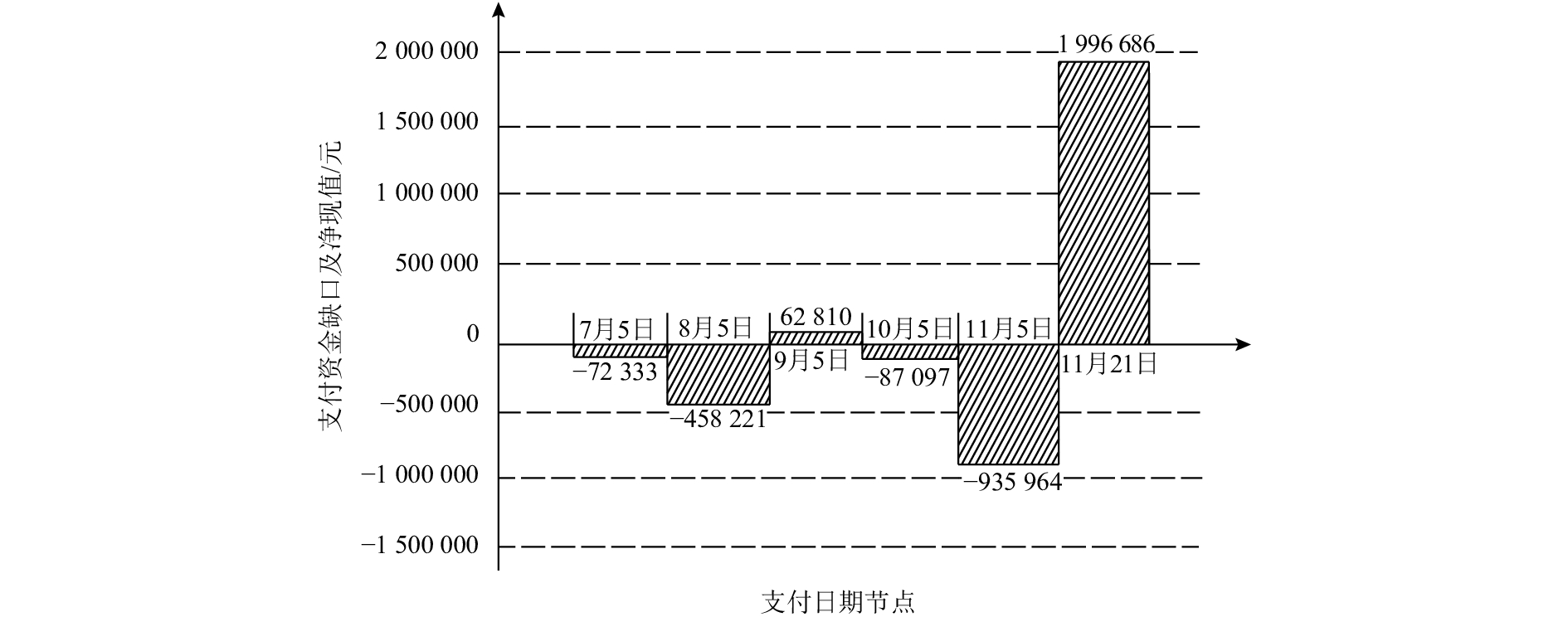
两种执行方案下每次支付资金约束缺口及净现值柱状图如图3、图4所示。
|
图 3 实际执行进度资金支付缺口及净现值 Fig. 3 Funding gap and net present value of the actual execution plan |
|
图 4 优化方案3资金支付缺口及净现值 Fig. 4 Funding gap and net present value of the optimization Scheme Three |
从图中可看出,优化方案3在10月5日、11月5日两次支付净现值资金缺口都比实际执行进度下资金缺口净现值小,下降幅度约10%。而项目实际执行情况之所以出现较大资金缺口,是由于第5次支付活动未包括活动16,而此项活动在第5次支付时已发生费用,且数额较大,费用支出没有及时补偿,造成承包商资金缺口较大。优化方案3通过调整事件开始时间,使得活动16支付与费用同时在竣工结算周期发生,费用支出及时得到补偿,较好地实现了进度与支付的集成优化。
优化方案竣工结算支付发生在11月21日,比实际执行方案结算支付12月9日提前了18 d,累计净现值增加额76 433元,增加幅度17.8%。主要是因为项目进度安排的不同,导致支付次数、竣工结算支付的时点、每次支付的活动数量及费用挣值不同,使得项目累计净现值额度不同。
本文对模型求解采用手工计算、辅助Excel软件完成,故只对4种优化方案进行了求解。为对更多的可行邻点进行搜索,可采用启发式算法[15]等求解,以获得最优可行解。
4 结论通过本文的研究,可以得到如下几点结论。
1) 所有事件在其时间窗内均按最早开始时间执行,能够使项目完工日期提前18 d,最大化资金缺口减少101 595元,承包商净现值收益提升17.8%。
2) 项目实际进度安排虽满足合同工期要求,但未考虑进度与支付的集成优化,未能实现承包商收益最大化,且项目实施过程中资金缺口较大。应通过内部调度优化,尽可能使费用较大的活动费用支出与价款支付在同一支付周期内发生,使得费用支出能够得到及时补偿,实现项目进度与支付的集成优化。
3) 承包商可通过争取提高支付比例、缩短支付时间间隔、延长项目截止日期等措施提高项目净现值收益。
| [1] |
RUSSELL R A. A comparison of heuristics for scheduling project with cash flows and resource restrictions[J].
Management Science, 1986, 32(10): 1291-1300.
DOI: 10.1287/mnsc.32.10.1291. |
| [2] |
何正文,刘人境,胡信布, 等. 现金流平衡约束下的Max-npv项目调度[J].
系统工程理论与实践, 2009, 29(3): 132-140.
HE Zhengwen, LIU Renjing, HU Xinbu, et al. Max-npv project scheduling Problems with cash flow balance constraints[J]. Systems Engineering - Theory & Practice, 2009, 29(3): 132-140. DOI: 10.3321/j.issn:1000-6788.2009.03.019. |
| [3] |
DOERSCH R H, PATTERSON J H. Scheduling a project to maximize its present value: a zero-one programming approach[J].
Management Science, 1977, 23(8): 882-889.
DOI: 10.1287/mnsc.23.8.882. |
| [4] |
DAYANAND N, PADMAM R. Project contracts and payment schedules: the client’s problem[J].
Management Science, 2001, 47(12): 1654-1667.
DOI: 10.1287/mnsc.47.12.1654.10242. |
| [5] |
李诗娴. 基于净现值的资源受限型项目调度问题研究[D]. 天津: 天津大学, 2012
LI Shixian. Research on resource-constrained project scheduling problem based on net present value[D]. Tianjin: Tianjin University, 2012 |
| [6] |
何小丽. 考虑时间转换约束的净现值最大项目进度研究[D]. 郑州: 郑州大学, 2012
HE Xiaoli. Study on maximizing the net present value of the project progress by considering time conversion constraints.[D]. Zhengzhou: Zhengzhou University, 2012 |
| [7] |
何正文,徐渝. 工程项目支付进度优化: 一个案例研究[J].
管理工程学报, 2008, 22(1): 67-71.
HE Zhengwen, Xu Yu. Project payment schedule optimization: a case study[J]. Journal of Management Engineering, 2008, 22(1): 67-71. DOI: 10.3969/j.issn.1004-6062.2008.01.014. |
| [8] |
马志强,何正文,黄昶生. 现金流均衡项目调度优化[J].
工业工程与管理, 2014, 19(3): 109-115.
MA Zhiqiang, HE Zhengwen, HUANG Changsheng. Cash flow balanced project scheduling optimization[J]. Industrial Engineering and Mnagement, 2014, 19(3): 109-115. DOI: 10.3969/j.issn.1007-5429.2014.03.018. |
| [9] |
何正文,刘人境,胡信布. 基于合同双方交互作用的项目调度优化[J].
管理科学学报, 2014, 17(8): 48-58.
HE Zhengwen, LIU Renjing, HU Xinbu. Project scheduling optimization based on interaction between two parties of contracts[J]. Journal of Management Sciences in China, 2014, 17(8): 48-58. |
| [10] |
李兰英, 何正文,刘人境. 合同双方基于合作博弈的Max-npv项目调度优化[J].
工业工程与管理, 2016, 21(5): 42-48.
LI Lanying, HE Zhengwen, LIU Renjing. Multimode max-npv project scheduling optimization of both parties of contract based on cooperative game[J]. Industrial Engineering and Management, 2016, 21(5): 42-48. DOI: 10.3969/j.issn.1007-5429.2016.05.007. |
| [11] |
郑维博,何正文,刘人境. 基于融资能力约束的多模式Max-npv项目调度优化:双重视角[J].
运筹与管理, 2016, 25(1): 25-34.
ZHENG Weibo, HE Zhengwen, LIU Renjing. Financing capacity constraint based multimode max-npv project scheduling optimization from both perspectives of contract[J]. Operations Research and Management Science, 2016, 25(1): 25-34. |
| [12] |
郑维博,何正文,刘人境. 随机工期下基于可更新资源约束的Max-npv项目鲁棒性调度优化[J].
管理工程学报, 2017, 31(4): 186-192.
ZHENG Weibo, HE Zhengwen, LIU Renjing. Renewable resource constraint based max-npv project robust scheduling optimization with stochastic activity duration[J]. Journal of Engineering Management, 2017, 31(4): 186-192. |
| [13] |
王艳婷, 何正文,刘人境. 随机工期下反应性多模式项目调度优化[J].
系统管理学报, 2017, 26(1): 86-93.
WANG Yanting, HE Zhengwen, LIU Renjing. Reactive strategies in the multi-mode project scheduling with stochastic activity durations[J]. Journal of Systems and Management, 2017, 26(1): 86-93. |
| [14] |
ELMAGHRABY S E. Activity nets: a guided tour through some recent developments[J].
European Journal of Operational Research, 1995, 82(3): 383-408.
DOI: 10.1016/0377-2217(94)00184-E. |
| [15] |
熊燕华,沈厚才,周晶,等. 工程项目调度技术研究综述[J].
数学的实践与认识, 2013, 43(21): 1-14.
XIONG Yanhua, SHEN Houcai, ZHOU Jing, et al. Theoretic review of project scheduling technology[J]. Mathematics in Practice and Theory, 2013, 43(21): 1-14. DOI: 10.3969/j.issn.1000-0984.2013.21.001. |
 2018, Vol. 21
2018, Vol. 21