复杂系统由联系广泛紧密网络的各系统单元组成,拥有多层次、多功能的结构,具有“分解性”,动态发展且有一定预测能力[1-3]。飞机、船舶、计算机、汽车、集成电路等均属于具有复杂性、可分性、需求不确定性等特征的复杂系统[4],也属于高端制造业生产的典型产品。经过几十年的高速发展,国内高端制造业的发展虽然取得傲人的成绩,打造了高铁、航母、大飞机等多个有代表性的“中国制造名片”,但与发达国家相比仍有较大差距,存在发展起步晚、大型复杂产品系统集成能力差、生产资料配套能力差导致交付延迟、高端制造产品产能不足等问题[5]。国内高端制造业在追赶国外先进制造业水平,努力实现“中国制造2025”之时,迫切需要能实现复杂系统集成、规范管理生产资料配套并保证如期完成、提高复杂系统制造产能的技术。
模块化生产技术具有减弱系统内部要素间的相互依赖,增强产品灵活性,耗费更低的要素成本,实现更高的产能利用率,降低总成本和风险等多项优势[6],被广泛应用于国内外工业界。20世纪30年代,德国率先将模块化生产方法应用于机床制造业,取得了显著的成果。20世纪90年代,在电子、通信、计算机等行业,模块化技术逐渐取代流水线技术,成为新的主导技术。21世纪,波音构造的系统集成供应链[7]、空客公司的流程式生产[8]、西门子的“数字化企业平台”、库卡机器人、大众汽车制造机器人等,运用模块化技术明确制造流程,在实现工厂、机器、生产资料、人员等多要素高度整合集结的同时,降低生产系统管理和控制决策的复杂性,大幅缩短产品研制时间,快速响应环境变化[9],最终迈向智能制造主导的“工业4.0”时代。
模块化技术作为高效的生产组织模式,被众多学者广泛研究,但相关研究多为模块化技术在发展相对成熟行业的应用,如国内汽车制造业、造船业、铁路运输业[10-12]等;或针对行业发展初期复杂产品制造过程的其他管理层面,如质量控制、创新机制、供应链生产网络、结构设计[13-16]等;或是针对设计阶段或全生命周期,未侧重研究制造过程[17];或只是概念描述,未提供建模分析等具体的实施措施[18-19]。
本文以处于发展初期的复杂产品的制造过程为研究对象,为了满足国内工业界对提高产能及标准化程度的迫切需求,进行模块化建模研究。基于模块化理论、制造工艺、项目管理、最优化理论等方法,构建复杂系统制造模块顺序网络图,并建立制造周期求解模型,最后举出实例,运用优化求解软件cplex得出整个系统制造周期及对应的关键制造路径,并用于制定生产资料准备计划及生产计划。与传统串行生产模式相比,发现模块化技术可更大程度地并行开展整个系统生产准备工作,大大降低生产资料延迟交付的可能性,大幅度缩短制造周期,增强生产计划的可控性,进而验证了模型的有效性、条理性和优越性。模块化技术在复杂系统制造过程中的应用步骤如图1所示。

|
图 1 复杂产品制造过程实施标准化和并行化作业的步骤 Fig. 1 The procedure of implementing standardized and parallelized work for complex system manufacturing process |
为了增强复杂系统制造过程的可预测性、集成性和可控性,提升标准化程度,需将复杂系统根据设计方案、工艺路线、制造周期的可度量性和人机工效学等因素拆分成若干个标准制造模块,使复杂系统制造过程有层次地体现[20],为后续实现生产资料准备按照生产计划节拍提前有序进行及工作最大并行化奠定重要的理论基础。随后,被拆分后的标准制造模块后续还可借助拼组技术按需重新组合,通过接口把各独立且可关联的模块联结为完整的系统,继而完成预设产品的研制和生产[4,21-22]。
|
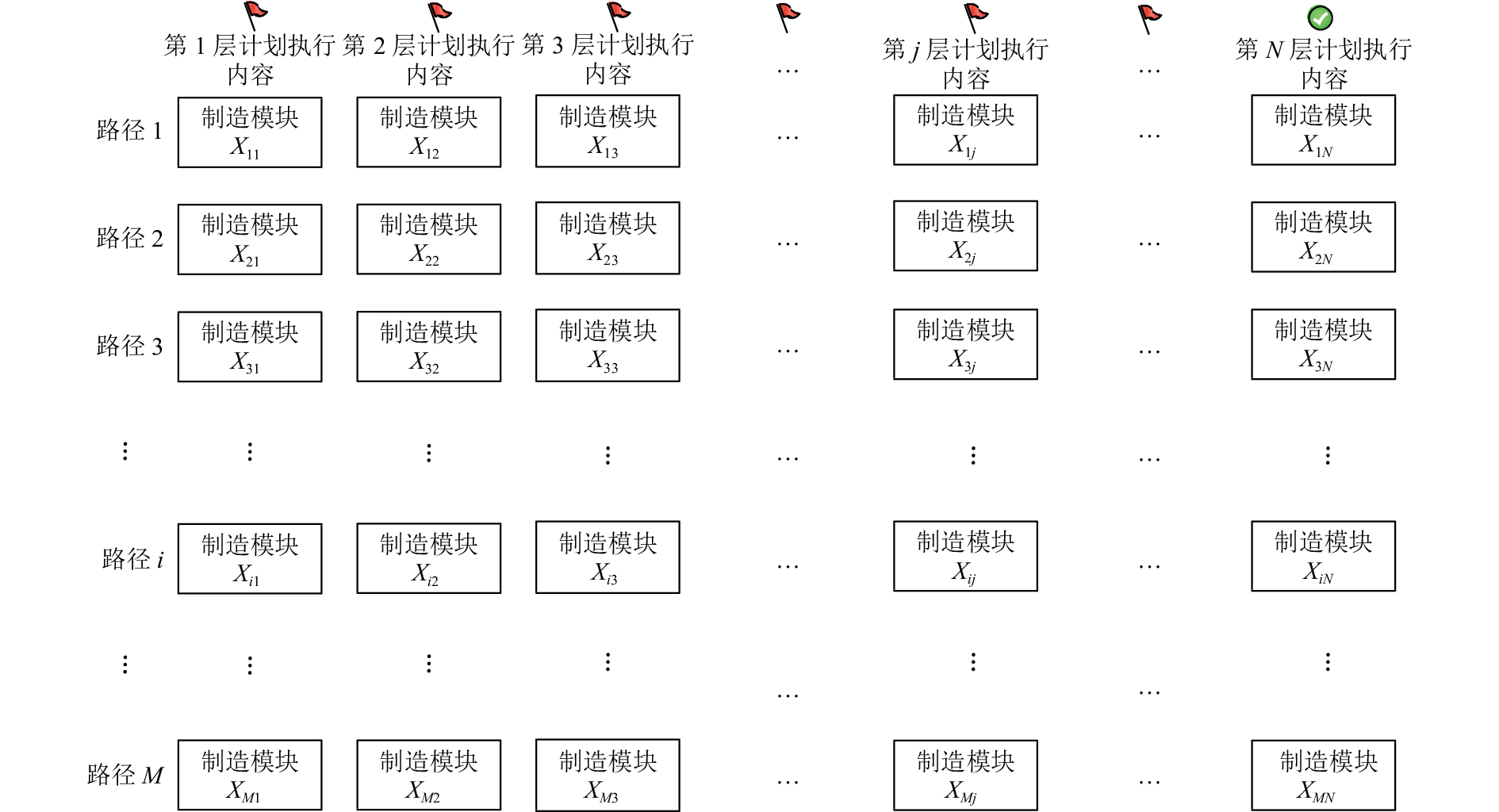
图 2 制造模块阵列图 Fig. 2 Array chart of manufacturing module |
图2将复杂产品的制造过程拆分成若干个标准制造模块,以M行N列的阵列呈现。阵列图中每列的模块代表可以并行执行的模块(第1列~第j列~第N列),每行的模块代表完成产品制造需要完成的制造路径(第1行~第i行~第M行)。不同制造模块间有先后顺序关系,如图3。

|
图 3 任意两制造模块间的关系表示 Fig. 3 Notation of relationship for two manufacturing modules |
图3中,任意两制造模块间先后关系用单向箭头→或空白表示,箭头发出的制造模块表示需先行制造的模块,箭头指向的模块表示需待箭头发出的制造模块完工后才能开始工作的制造模块,空白表示两制造模块相互独立,无先后制造顺序关系。
确定制造模块间先后顺序关系的原则有:1) 为了依据制造模块关系网络图定量确定制造周期,被拆分的制造模块需容易确定完工周期;2) 确定模块间的相互关系时,需在设计方案、工艺方案的基础上考虑人机工效学等其他因素,确保可操作性。设函数
| $\begin{array}{l}Q\left( {{X_{ij}}} \right) \!+\!\! Q\left( {{X_{mn}}} \right) \!=\! \!\left\{ \!\!\!\!\!\!\!\!{\begin{array}{l}\begin{array}{l}2,\;\;{X_{ij}}{\text{与}}{X_{mn}}{\text{有前置或后置}}\\\quad\, {\text{关系}},{\text{同时出现在某路径}};\\1,\;\;{X_{ij}}{\text{与}}{X_{mn}}{\text{两者不能同时}}\\\quad\, {\text{出现在一条路径中}};\end{array}\\\begin{array}{l}{0,\;\;{X_{ij}}{\text{与}}{X_{mn}}{\text{二者相互独立}},}\\\quad\, {{\text{无前后置关系}},{\text{未出现在}}}\\\quad\, {\text{任意一条路径中。}}\end{array}\end{array}} \right.\\Q\left( {{X_{ij}}} \right),\;Q\left( {{X_{mn}}} \right) = \left\{ {0,1} \right\}{\text{且}}n = j + 1{\text{。}}\end{array}$ | (1) |

|
图 4 任意两制造模块间的路径关系 Fig. 4 Notation of path relationship for two manufacturing modules |
式(1)和图4中,分段函数
为了利于将制造模块统一标准化地用公式表示,用分段函数
| $\quad\quad F\left( {{X_{ij}}} \right) = \left\{ {\begin{array}{*{20}{l}}{0,\;\;{\text{实际生产中无该装配顺序对}}}\\\quad\,\, {\text{应的模块}};\\{1,\;\;{\text{实际生产中有某生产模块与}}}\\\quad\,\, {{\text{该位置下的}}{X_{ij}}{\text{唯一对应}}{\text{。}}}\end{array}} \right.$ | (2) |
式(2)中,
设完成模块
| $\quad\quad\sum\limits_{j = 1}^N {\left( {{T_{ij}} + \Delta {T_{ij}}} \right)Q\left( {{X_{ij}}} \right)} F\left( {{X_{ij}}} \right), \;\; i \in \left\{ {1,2,...,M} \right\}{\text{。}}$ | (3) |
如果不能按照模块逻辑关系层级计划如期完成生产资料准备而造成生产资料缺乏、生产停滞等待后的整个模块制造时间,比生产资料准备完善情况的模块制造时间多出的时间如下表示:
| $\eta \left( \% \right) = \frac{{\displaystyle\sum\limits_{j = 1}^N {\left( {{T_{ij}} + \Delta {T_{ij}}} \right)Q\left( {{X_{ij}}} \right)} F\left( {{X_{ij}}} \right)}}{{\displaystyle\sum\limits_{j = 1}^N {{T_{ij}}Q\left( {{X_{ij}}} \right)} F\left( {{X_{ij}}} \right)}} - {\rm{1}},\;\;i \in \left\{ {1,2,...,M} \right\}{\text{。}}$ | (4) |
通过绘制完成的流程图,从宏观上,可直观确定完成每一步最大限度的并行作业包中所包含的所有制造模块;从微观上,可确定每个制造模块受控的前置模块;最终不但可直观观测项目进度,还可直接有目的地专项控制直接影响关键里程碑节点的制造模块周期,达到有效进行项目和生产管控的目标。
2 模块化后的生产计划制定 2.1 基于关键路径法的求解制造周期整数规划建模根据第1节复杂产品制造过程的关系网络图,可求解整个产品制造周期,建立的模型如式(5)~式(9)所示。
| $\max T = \sum\limits_{j = 1}^N {\left( {{T_{ij}} + \Delta {T_{ij}}} \right)Q\left( {{X_{ij}}} \right)} F\left( {{X_{ij}}} \right), \;\; i \in \left\{ {1,2,...,M} \right\}{\text{。}}$ | (5) |
s.t.
| $\quad\quad Q\left( {{X_{ij}}} \right) = \left\{ {0,1} \right\}, \;\; i \in \left\{ {1,2,...,M} \right\},j \in \left\{ {1,2,...,N} \right\};$ | (6) |
| $\quad\quad F\left( {{X_{ij}}} \right) = \left\{ {0,1} \right\}, \;\; i \in \left\{ {1,2,...,M} \right\},j \in \left\{ {1,2,...,N} \right\};$ | (7) |
| $\quad\quad\sum\limits_{i = 1}^M {Q\left( {{X_{ij}}} \right)} = 1, \;\; j \in \left\{ {1,2,...,N} \right\};$ | (8) |
| $\begin{split}&\quad\quad Q\left( {{X_{ij}}} \right) + Q\left( {{X_{mn}}} \right) = \left\{ {0,1} \right\}, n = j + 1,i,\\&m \in \left\{ {1,2,...,M} \right\},j \in \left\{ {1,2,...,N{\rm{ - }}1} \right\},n \in \left\{ {2,3,...,N} \right\}{\text{。}}\end{split}$ | (9) |
式(5)为目标函数,表示以寻找耗费周期最长的制造路径为目标;式(6)为制造模块间相互逻辑关系的函数
复杂系统的模块化生产网络由若干节点组成[18],生产网络中的生产控制节点可通过明确复杂系统制造模块关系网络图及关键制造路径后得出。复杂系统制造模块关系网络图在第1节中构建,关键制造路径由第2.1节求出,然后制定对应的生产资料准备计划,如图5所示。
|
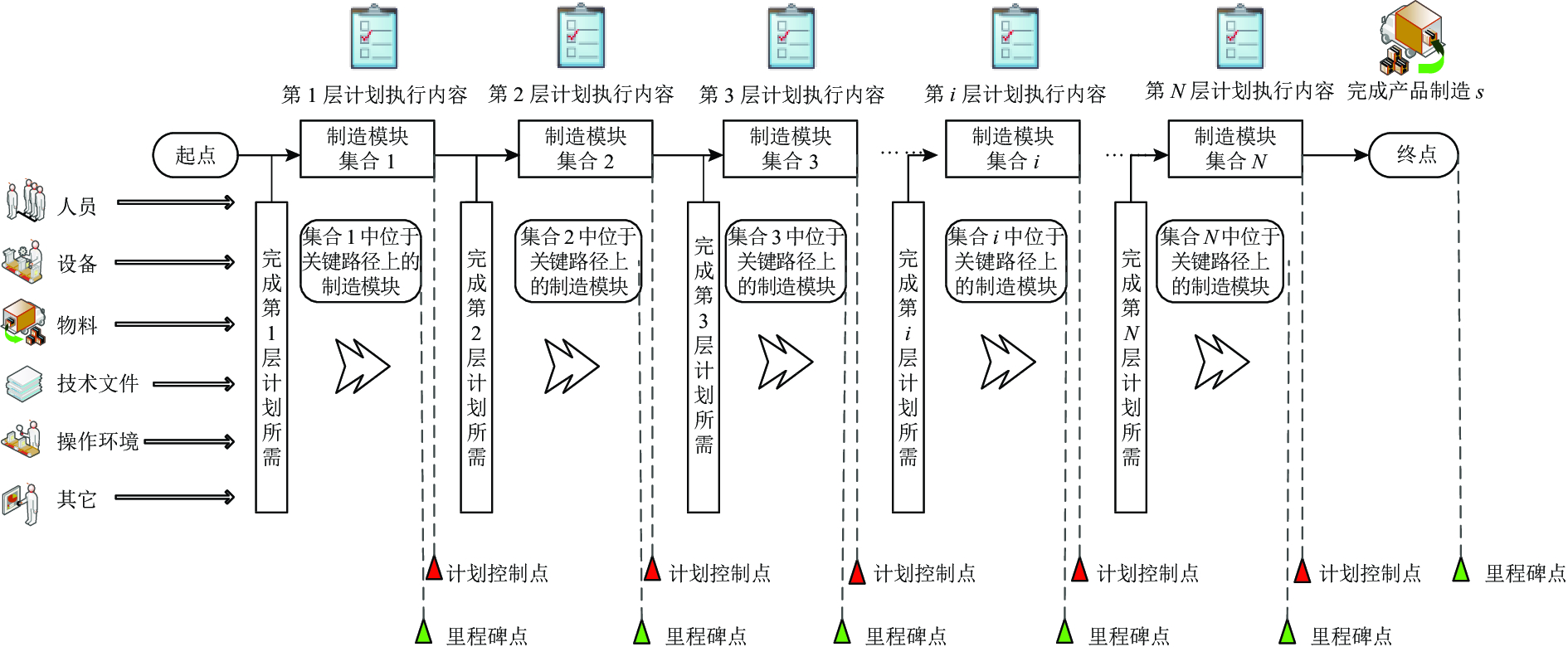
图 5 制造模块化及标准化运用后的生产准备计划及生产计划 Fig. 5 Production preparation plan and production plan after utilizing manufacture modularization and standardization method |
图5中,复杂产品的制造模块及制造顺序确定后,“人、机、料、法、环”等相关的生产准备计划将根据各个层次制造模块的生产计划依次得出。人员指与制造复杂产品工作相关的人员;设备指制造复杂产品过程所需的设备;料指制造复杂产品所使用的化工材料、零部件等;操作环境指完成复杂产品制造所要求的操作环境条件,如温度、湿度等;其他指除“人、机、料、法、环”这五大工业制造管理五要素之外的影响复杂产品制造的因素,如技术准备文件的发放、不合格品的处理流程等。位于关键制造路径上的点直接决定产品制造周期,包含生产计划的里程碑控制点,是控制产品制造周期的重要指标;计划控制点决定每层计划的完成,直接影响后续多层计划的实施,是从宏观上控制产品制造过程逐步推进的指标。
3 案例分析 3.1 分析过程描述假设针对某大型复杂产品制造过程,为了达到更好地控制生产的目标,现欲分解生产系统管理和控制决策的复杂性,增强制造系统的集成性,增加制造过程的标准化程度,提升生产资料配套能力,大幅缩短产品研制时间。已知设计方案、工艺路线、现场操作要求及操作时间,需基于已有的制造信息、图1的流程及第1、2节研究结果确定该复杂产品的制造周期,主要实施步骤如下。
1) 执行图1中第1步,将复杂产品制造过程拆分成可评估制造周期的制造模块,假设得到16个制造模块,用
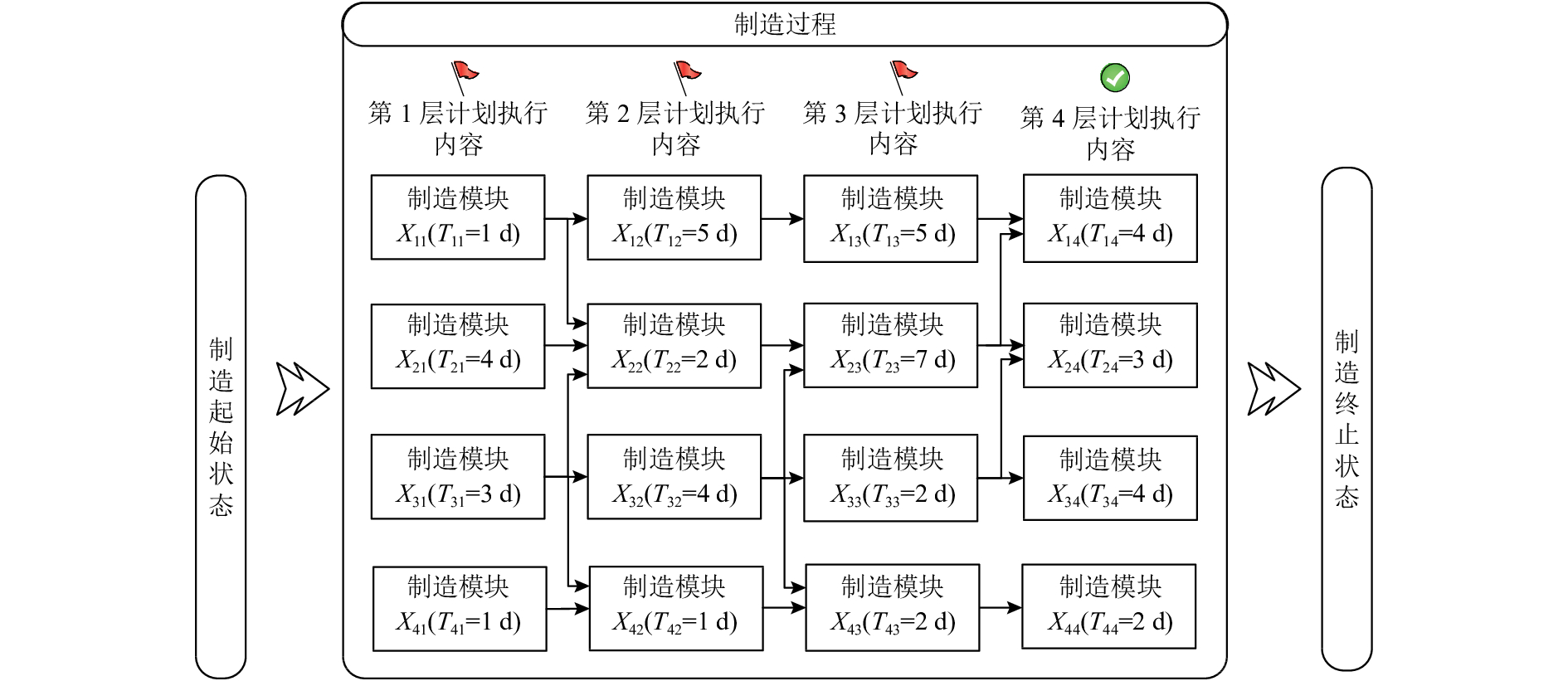
2) 执行图1中第2步,依据工艺技术方案、人机工效学、最大并行化等知识或原则,将复杂产品制造流程用制造模块的网络关系图表示,每个模块的完工周期用天(d)表示,如图6所示。
|
图 6 包含制造周期的产品制造模块关系网络图 Fig. 6 Relation network diagram containing manufacturing cycles of product manufacture modules |
3) 执行图1中第3步,基于图6中制造模块间相互制造顺序关系建立产品制造周期求解模型,并确定关键路径。
| $\begin{split}&\quad\quad\max T = \displaystyle\sum\limits_{j = 1}^5 {\left( {{T_{ij}} + \Delta {T_{ij}}} \right)Q\left( {{X_{ij}}} \right)} F\left( {{X_{ij}}} \right) = \\&\left( {{T_{i1}} + \Delta {T_{i1}}} \right){T_{i1}}Q\left( {{X_{i1}}} \right)F\left( {{X_{i1}}} \right) +\left( {{T_{i2}} + \Delta {T_{i2}}} \right)F\left( {{X_{i2}}} \right)Q\left( {{X_{i2}}} \right) +\\&\left( {{T_{i3}} + \Delta {T_{i3}}} \right)Q\left( {{X_{i3}}} \right)F\left( {{X_{i3}}} \right) + \left( {{T_{i4}} + \Delta {T_{i4}}} \right)Q\left( {{X_{i4}}} \right)F\left( {{X_{i4}}} \right) +\\&\left( {{T_{i5}} + \Delta {T_{i5}}} \right)Q\left( {{X_{i5}}} \right)F\left( {{X_{i5}}} \right),\;i = \left\{ {1,2,3,4} \right\}{\text{。}}\end{split}$ | (10) |
s.t.
| $\quad\quad Q\left( {{X_{ij}}} \right) = \left\{ {0,1} \right\},i,j \in \left\{ {1,2,3,4} \right\};$ | (11) |
| $\quad\quad F\left( {{X_{ij}}} \right) = 1,i,j \in \left\{ {1,2,3,4} \right\};$ | (12) |
| $\quad\quad\Delta {T_{ij}} = 0,i,j \in \left\{ {1,2,3,4} \right\};$ | (13) |
| $\quad\quad\sum\limits_{i = 1}^5 {Q\left( {{X_{ij}}} \right)} = 1,j = \left\{ {1,2,3,4} \right\};$ | (14) |
| $\quad\quad\begin{split}& \{Q\left( {{X_{11}}} \right) + Q\left( {{X_{32}}} \right),Q\left( {{X_{11}}} \right) + Q\left( {{X_{42}}} \right),\\& Q\left( {{X_{21}}} \right) + Q\left( {{X_{12}}} \right),Q\left( {{X_{21}}} \right) + Q\left( {{X_{32}}} \right),\\& Q\left( {{X_{21}}} \right) + Q\left( {{X_{42}}} \right),Q\left( {{X_{31}}} \right) + Q\left( {{X_{12}}} \right),\\& Q\left( {{X_{41}}} \right) + Q\left( {{X_{12}}} \right),Q\left( {{X_{41}}} \right) + Q\left( {{X_{22}}} \right),\\& Q\left( {{X_{41}}} \right) + Q\left( {{X_{32}}} \right),Q\left( {{X_{12}}} \right) + Q\left( {{X_{23}}} \right),\\& Q\left( {{X_{12}}} \right) + Q\left( {{X_{33}}} \right),Q\left( {{X_{12}}} \right) + Q\left( {{X_{43}}} \right),\\& Q\left( {{X_{22}}} \right) + Q\left( {{X_{13}}} \right),Q\left( {{X_{22}}} \right) + Q\left( {{X_{33}}} \right),\\ & Q\left( {{X_{22}}} \right) + Q\left( {{X_{43}}} \right),Q\left( {{X_{32}}} \right) + Q\left( {{X_{13}}} \right),\\& Q\left( {{X_{42}}} \right) + Q\left( {{X_{13}}} \right),Q\left( {{X_{42}}} \right) + Q\left( {{X_{23}}} \right),\\& Q\left( {{X_{42}}} \right) + Q\left( {{X_{33}}} \right),Q\left( {{X_{13}}} \right) + Q\left( {{X_{24}}} \right),\\& Q\left( {{X_{13}}} \right) + Q\left( {{X_{34}}} \right),Q\left( {{X_{13}}} \right) + Q\left( {{X_{44}}} \right),\\& Q\left( {{X_{23}}} \right) + Q\left( {{X_{34}}} \right),Q\left( {{X_{23}}} \right) + Q\left( {{X_{44}}} \right),\\& Q\left( {{X_{33}}} \right) + Q\left( {{X_{14}}} \right),Q\left( {{X_{33}}} \right) + Q\left( {{X_{44}}} \right),\\& {Q\left( {{X_{43}}} \right) + Q\left( {{X_{14}}} \right),Q\left( {{X_{43}}} \right) + Q\left( {{X_{24}}} \right),}\\& { Q\left( {{X_{43}}} \right) + Q\left( {{X_{34}}} \right)}\} = \left\{ {0,1} \right\}{\text{。}}\end{split}$ | (15) |
式(10)为寻找耗时最长制造路径的目标函数,所耗费时长即为完成产品制造所需的最短时间,也即产品制造周期。式(11)与式(12)含义同式(6)和式(7)。式(13)中,由于生产资料准备可根据制造关系网络图按层次提前准备,认为不会出现由于生产资料准备工作层次不清楚导致生产准备工作未能先于制造计划如期完成,进而导致模块
4) 执行图1中第4步,使用数学规划模型求解软件cplex求解第3)中建立的模型,得出整个复杂产品的制造周期,得出关键路径结果为
5) 执行图1中第5步,确定各层级计划对应的“人、机、料、法、环”等生产资料准备计划。假设产品制造计划起始时间为2020-1-1,每项生产资料准备工作耗费时间
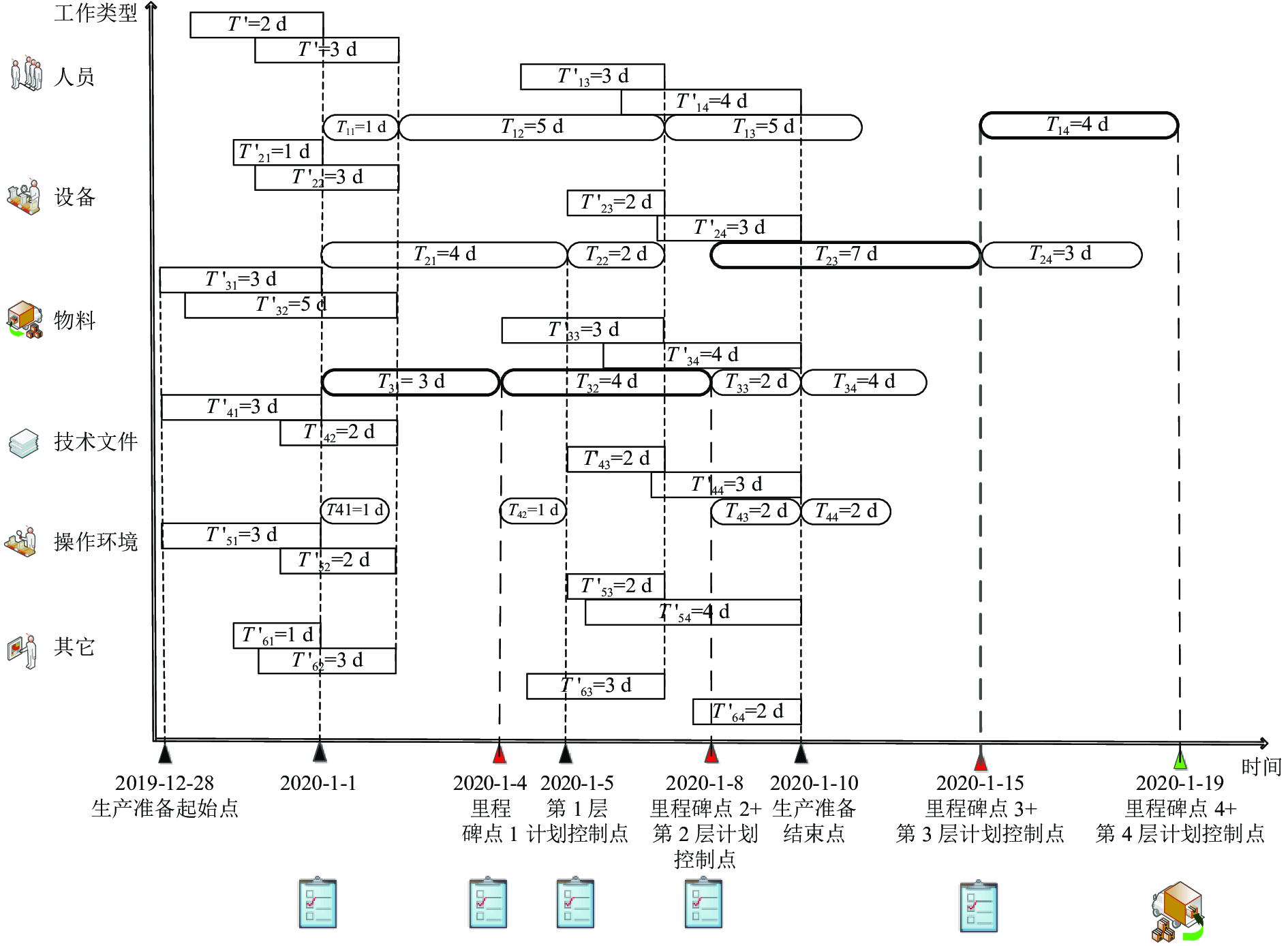
|
图 7 基于模块化的生产资料准备及生产计划示意图 Fig. 7 The schematic diagram of production preparation plan and production plan based on modularization |
图7为根据图6中制造模块的先后逻辑顺序及周期绘制的生产资料准备及生产计划执行图,包含可用于指导生产的主要信息如下。
1) 16个制造模块由4层计划组成(即图6中每列模块,
2) 关键路径上每个模块(即
3) 每一层计划的完成时间点为计划控制点,每到每层计划中耗费时间最长的模块完工后,均应核查该层计划是否完成,例如第1层计划控制点为该层计划中耗费周期最长的模块
4) 部分计划层级中里程碑点与计划控制点是重合的。
5) 生产资料准备也对应于生产计划形成层级模式,每层计划对应的生产资料准备工作需要在每层计划最早开始的模块前完成。例如第2层计划对应的生产资料准备需要在第2层计划开始最早的模块
6) 整个制造项目耗费时间为2020-1-1~2020-1-19,共18 d,生产准备耗费周期为2019-12-28~2020-1-10,共12 d。
3.2 与优化前的效果对比执行图1中第6步,说明采用模块化技术制定生产资料准备计划及生产计划后的效果。
模块化技术采用前,复杂系统制造过程主要存在的问题如下。
1) 无法提前制定对应实际生产节拍和流程的生产资料准备计划,生产资料缺乏现象频繁。由于制造模块间制造先后逻辑顺序不清晰,生产资料准备计划层次性很弱,基本采用使用前才想起准备的方式,生产资料缺乏现象出现频繁。
2) 生产计划反复受制于生产资料缺乏,导致制造周期一再延迟,制造周期的控制力被大大削弱。
3) 无法把每一层级的全部生产模块纳入跟踪范围,实现工作最大并行化,后期制造工作反复受制于前期未完工的工作导致无法开展,形成锁链反应。
4) 难以形成持续改善的固化流程和机制。由于负责每批生产任务的人员不同,其具有的生产经验、操作习惯等个人因素不同,经其管理操作制造的产品质量、制造周期受经验、心情的影响很大,产品的质量、制造周期波动性很大;当经验不能以良好的方式在每批操作人员间全面地传承时,前一批人的制造经验很难完全被后一批人采纳,产品的制造水平又或多或少地重回原点,不能形成较好的持续改善机制。
未采用模块化生产前的生产计划及生产准备情况如图8。

|
图 8 未采用模块化技术时的生产计划 Fig. 8 The production plan without applying modularization techniques |
图8中,在制造模块周期后的条形块
基于模块化技术在降低复杂系统制造难度、标准化制造流程、提高生产效率、缩短生产时间、提高产能、提升高端制造业发展水平的优越性及国内相关研究的匮乏性,为了提高复杂系统的制造效率及标准化程度、缩短制造周期,基于模块化理论、关键路径法、运筹学优化论建立了复杂系统的模块化制造模型并绘出制造模块间的关系网络图,采用优化模型求解软件CPLEX等求解得出关键制造模块路径及整个项目周期,制定生产资料准备计划及生产计划,确保生产资料准备工作有层次性地提前于生产计划完成,避免生产资料准备不完善反复阻碍生产计划的正常执行。与未采用模块化技术前反复出现生产资料缺乏现象的生产系统相比,明显缩短了复杂系统的制造周期。实例证明,模块化技术可使生产资料准备工作最大程度地并行且在制造模块开工前完成,使生产周期比采用前明显缩短,进而使同样时间下产品的生产数量增加,提升产能,验证了模型的有效性、条理性和优越性。
| [1] |
成思危. 复杂性科学探索[M]. 北京: 民主与建设出版社, 1999
|
| [2] |
SIMON H A. The architecture of complexity[J].
Proceeding of the American Philosophical Society, 1962, 106: 467-482.
|
| [3] |
BALDWIN C Y, CLARK K B. Managing in an age of modularity[J].
Harvard Business Review, 1997, 75(5): 84-93.
|
| [4] |
刘欣. 模块化生产网络下中国制造业升级研究[D]. 上海: 上海社会科学院, 2016
LIU Xin. China’s manufacturing industry upgrade under modular production network [D]. Shanghai: Shanghai Academy of Social Sciences, 2016 |
| [5] |
武永娜. 中国高端装备制造业发展研究[D]. 辽宁: 辽宁大学, 2017
WU Yongna. Research on the development of high-end equipment manufacturing industry in China [D]. Liaoning: Liaoning University, 2017 |
| [6] |
STURGEON T J. Modular production networks: a new American model of industrial organization[J].
Industrial and Corporate Change, 2002, 11(3): 451-496.
DOI: 10.1093/icc/11.3.451. |
| [7] |
胡海林. 解码: 波音之道[J].
大飞机, 2013(4): 31-35.
HU Hailin. Decode: Boeing’s approach[J]. Jetlines, 2013(4): 31-35. |
| [8] |
姚鸿翔. 精益生产方式在大型飞机制造中的应用研究[D]. 天津: 天津大学, 2011
YAO Hongxiang. Research on application of lean manufacturing method in large aircraft manufacturing [D]. Tianjin: Tianjin University, 2011 |
| [9] |
李政. 基于波音787的全球供应链战略模式研究[J].
科技促进发展, 2012(5): 97-102.
LI Zheng. Study of global supply chain strategy model basing on Boeing 787[J]. Science & Technology for Development, 2012(5): 97-102. |
| [10] |
钱镇. 汽车制造业模块化供应关系及协调机制研究[D]. 上海: 上海交通大学, 2007(1): 1-50
QIAN Zhen. A research on the modularization supply relationship and collaboration mechanism in automobile industry [D]. Shanghai: Shanghai Jiaotong University, 2007 |
| [11] |
杨国兵. 我国造船业模块化制造网络研究[D]. 哈尔滨: 哈尔滨工程大学, 2010
YANG Guobing. Research on the modular manufacturing networks of shipbuilding industry [D]. Harbin: Harbin Engineering University, 2010 |
| [12] |
齐振法. 我国铁路运输业模块化重组研究[D]. 北京: 北京交通大学, 2010
QI Zhenfa. Research on modular restructuring of Chinese railway transportation [D]. Beijing: Beijing Jiaotong University, 2010 |
| [13] |
黄大莉. 航空装备研制项目的模块化质量控制研究[D]. 南昌: 南昌航空大学, 2017
HUANG Dali. Research on modular quality control of aviation equipment development project [D]. Nanchang: Nanchang Hangkong University, 2017 |
| [14] |
于欢欢. 区域高端装备制造业技术模块化创新机制研究[D]. 哈尔滨: 哈尔滨理工大学, 2017
YU Huanhuan. Research on the technical modular innovation mechanism of regional high-end equipment manufacturing industry [D]. Harbin: Harbin University of Science and Technology, 2017 |
| [15] |
戴爱明, 肖灵机. MILDDC算法及其在飞机模块化生产网络分析中的应用[J].
航空科学技术, 2013(3): 68-71.
DAI Aiming, XIAO Lingji. An algorithm-MILDDC and its applying in airplane modular production networks analyzing[J]. Aeronautical Science & Technology, 2013(3): 68-71. DOI: 10.3969/j.issn.1007-5453.2013.03.021. |
| [16] |
李苏杭, 李铁. 飞机模块化结构平台构造优化方法[J].
江苏航空, 2015(4): 9-12.
LI Suhang, LI Tie. An optimization method of building aircraft modular structure platform[J]. Jiangsu Aviation, 2015(4): 9-12. |
| [17] |
侯卓兵. 面向模块化配置生产的大型飞机装配规划与仿真技术[J].
航空制造技术, 2017(4): 24-30.
HOU Zhuobing. Large aircraft assembly plan and simulation technology for module-based configuration production[J]. Aeronautical Manufacturing Technology, 2017(4): 24-30. |
| [18] |
范林, 王哲. 模块化技术在飞机研制中的应用[J].
航空科学技术, 2010(3): 19-21.
FAN Lin, WANG Zhe. Application of modularization technology at each development stage of aircraft[J]. Aeronautical Science & Technology, 2010(3): 19-21. DOI: 10.3969/j.issn.1007-5453.2010.03.007. |
| [19] |
谢光亚. 基于模块化的大型飞机技术创新路径研究[J].
工业技术经济, 2011(1): 75-79.
XIE Guangya. Research on technological innovation path to large aircraft based on modularity theory[J]. Journal of Industrial Technological Economics, 2011(1): 75-79. DOI: 10.3969/j.issn.1004-910X.2011.01.013. |
| [20] |
王海军, 徐伟, 宋红英, 等. 从内部优化到全局协同: 模块化生产网络构建策略[J].
科技管理研究, 2017(1): 1-5.
WANG Haijun, XU Wei, SONG Hongying et al. From internal optimization to global collaboration: research on the strategies of building modular production networks[J]. Science and Technology Management Research, 2017(1): 1-5. DOI: 10.3969/j.issn.1000-7695.2017.01.001. |
| [21] |
孙晓峰. 模块生产网络研究[J].
中国工业经济, 2005(9): 60-66.
SUN Xiaofeng. Research of modular production network[J]. China Industrial Economy, 2005(9): 60-66. DOI: 10.3969/j.issn.1006-480X.2005.09.008. |
| [22] |
BALACHANDRA R. Modular design and technological innovation: the case of hard disk drives [R]. UC San Diego: Information Storage Industry Center, 2002: 1-4
|
 2018, Vol. 21
2018, Vol. 21