自动化生产中，控制图被广泛应用于过程监控和质量管理中，对于监控生产过程输出数据、提高产品质量起着重要作用^[1]。针对自相关性数据的监控问题，主要有以下两种解决思路。1)结合数据的自相关性调整控制图上下限，直接对原始数据进行监控。Vasilopoulos等^[2]、Yashchin^[3]、Schmid等^[4]、Runger^[5]分别讨论了常规控制图应用于具有自相关性数据时的性质、ARL表现以及修正方法。2)对原始数据建立预测模型，对预测误差进行监控，即残差控制图。Alwan等^[6]、Wardell等^[7]、Runger等^[8-9]、Shu等^[10]分别讨论了使用不同的控制图对预测模型的残差进行监控的效果。随着对自相关控制图应用场景的拓宽，更多不同的研究方向随之出现。针对多变量自相关数据的情境，Huang等^[11]、He等^[12]、Leoni等^[13]提出新的监控模型。针对多阶段及多工序的自相关数据监控问题，Asadzadeh等^[14]、Asgari等^[15]、万松等^[16]进行了讨论研究。张锐等^[17-18]考虑使用集成的方法及联合监控的方式重点对AR(p)模型的自相关过程进行控制管理。

在众多研究方法中，通过拟合时间序列模型对残差进行监控的方法由于操作简便，在实际中应用最为广泛。其中最常采用的模型为自回归滑动平均(ARMA)模型。然而随着生产过程的复杂化，自相关过程模型也变得更加多样，真实模型的未知性，以及历史数据的有限性，导致该方法存在以下问题：1)真实的自相关过程可能并不符合ARMA模型；2)拟合的模型参数不准确；3)拟合模型后得到的残差不服从独立正态分布。若仍采用传统残差控制图进行监控，效果会大打折扣。为了解决这个问题，一些专家提出将非参数检验应用到控制图中，构建出不考虑分布(distribution-free)的控制图^[19-22]。然而理论上，建立控制图时，Phase-I阶段需要大量受控(in control)数据建立统计模型；生产中，受控数据需要通过人工的方式评估并获取。为了尽快将控制图投入使用，减少人工成本，建立控制图时应该尽量减少所需数据。而非参数的不考虑分布型控制图并不适用于这样的实际情境。针对监控自相关过程中涉及到拟合模型的控制方法，控制效果必然都会受到模型参数准确度的影响，Alonso等^[23]、Gapizzi等^[24]、Mancenido等^[25]在考虑模型参数误差的影响下，提出一种基于Sieve Bootstrap的方法,通过对自相关数据建立AR(p)模型，并估计模型参数，对残差建立经验分布函数，重构样本，从而建立控制图。这种方法考虑了模型参数误差的影响，但主要应用于AR(p)模型，对于实际生产中应用更加广泛、更具普适作用的ARMA模型的讨论较少，同时没有具体地讨论模型参数和残差分布的类型对控制效果的影响。

基于Sieve Bootstrap的思路，结合拟合ARMA模型做残差控制图的方法，以及尽可能使用较少的历史数据的需求，本文提出一种针对未知自相关过程的新型Bootstrap控制图的设计方法。并通过蒙特卡洛模拟，分析不同情况下的平均运行链长表现，证明了新方法对于未知的自相关过程监控的普遍适用性和有效性。

1 问题描述

对于一个复杂的生产过程，设备在投入生产初期，产生了一组受控状态下的自相关生产数据 ${\left\{ {{Y_t}} \right\}_{t \in {Z^ + }}}$ 。为了尽可能快速地建立控制图，假设工厂仅在获取当前数据样本后开始构建控制图，数据中的样本个数不少于14个^[26]。一种常使用的方法是利用该组样本数据拟合ARMA模型，再对残差建立控制图。标准的ARMA(p, q)模型为

$\quad\quad{Y_t} = \mathop \sum \limits_{i = 1}^p {\hat \phi _i}{Y_{t - i}} + \mathop \sum \limits_{j = 1}^q {\hat \theta _j}{{\rm{\hat \varepsilon }}_{t - j}}{\text{。}}$

其中 $\hat \phi $ 为自回归系数， $\hat \theta $ 为移动平均系数， ${\hat \varepsilon _t}$ 为残差项， ${\varepsilon _t} \sim N\left( {0,{\sigma ^2}} \right) $ 。

建立残差控制图的具体步骤如下。

1) 给定一组样本生产数据 ${\left\{ {{Y_t}} \right\}_{t \in {Z^ + }}}$ ，其中t=1，2，…，t₀，基于AICC的准则^[27]，选择适合的ARMA(p, q)模型阶数。

2) 利用Yule-Walker方程求解自回归系数 $\hat \phi = $ $ \left( {{{\hat \phi }_1},{{\hat \phi }_2}, \ldots ,{{\hat \phi }_p}} \right)$ 和移动平均系数 $\hat \theta = \left( {{{\hat \theta }_1},{{\hat \theta }_2}, \ldots ,{{\hat \theta }_q}} \right)$ 。

3) 利用一步向前预测的方法计算残差：

$\quad\quad\begin{array}{l}{{\hat Y}_t} = \displaystyle\mathop \sum \limits_{i = 1}^p {{\hat \phi }_i}{Y_{t - i}} + \mathop \sum \limits_{j = 1}^{q - 1} {{\hat \theta }_j}{{\hat \varepsilon }_{t - j}};\\{{\hat \varepsilon }_t} = {Y_t} - {{\hat Y}_t}\;,\;\;{{\hat \varepsilon }_1} = 0{\text{。}}\end{array}$

4) 出界概率设置为α，残差 ${\hat \varepsilon _t}$ 的标准差为σ，Z^p表示在标准正态分布中，使得 $P\left\{ {X {\text{＜}} \lambda } \right\} = p$ 的数λ，即Z^p=λ，则控制上下限为

$\quad\quad\begin{array}{l}{\rm{UCL}} = {Z^{1 - \frac{\alpha }{{{\rm{}}2}}}} \times \sigma ,\\{\rm{LCL}} = {Z^{\frac{\alpha }{2}}} \times \sigma{\text{。}}\end{array}$

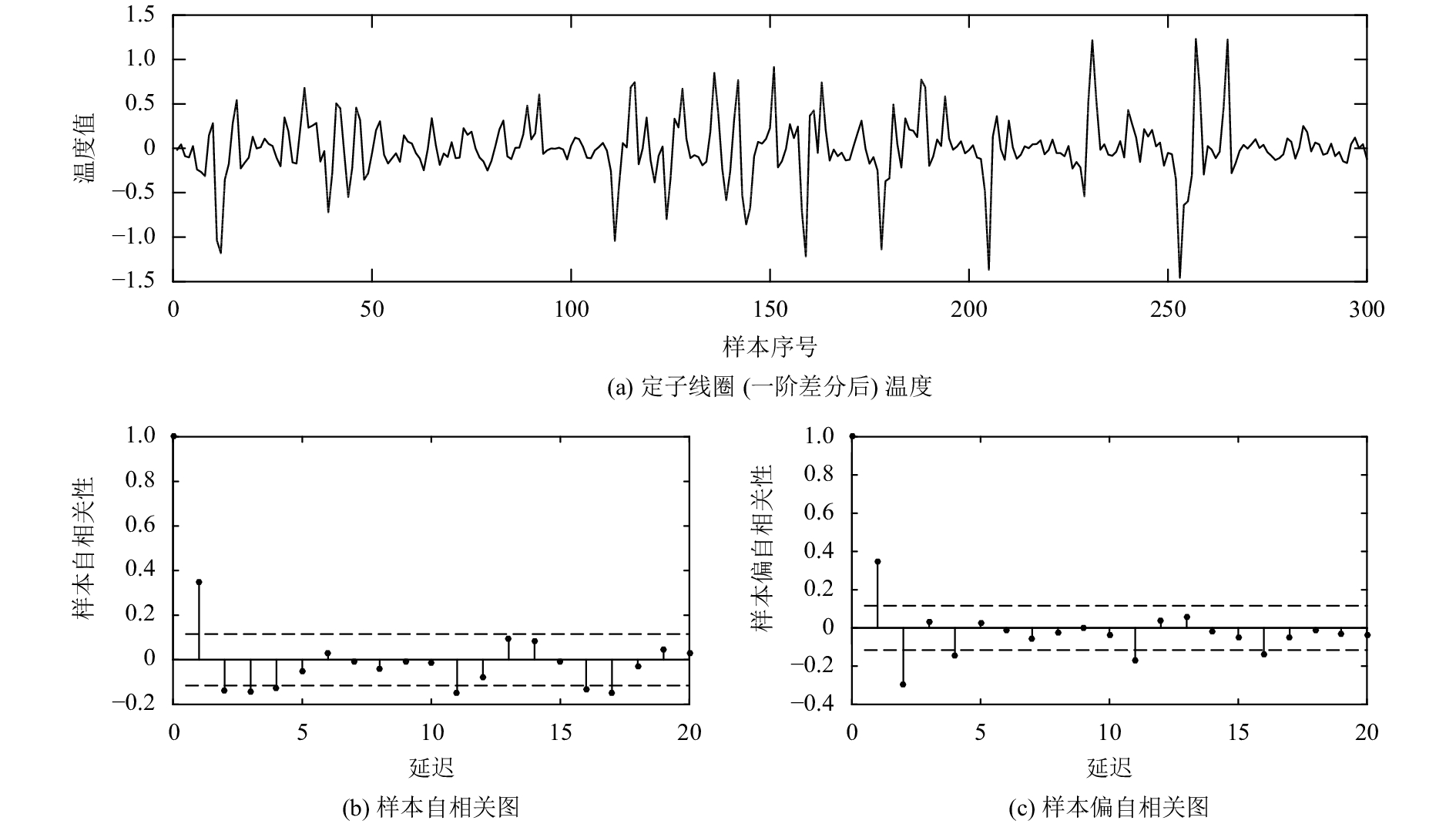
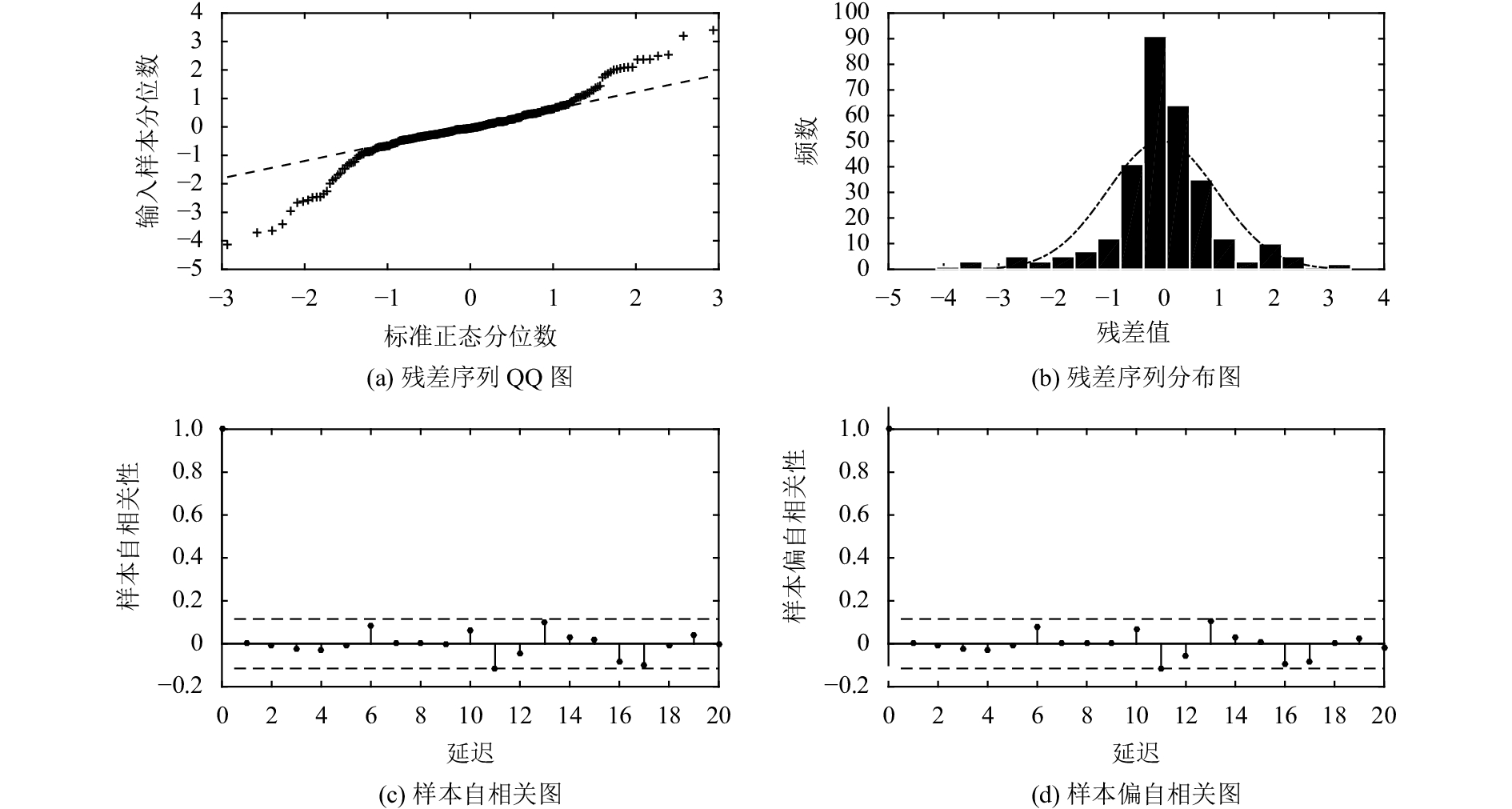
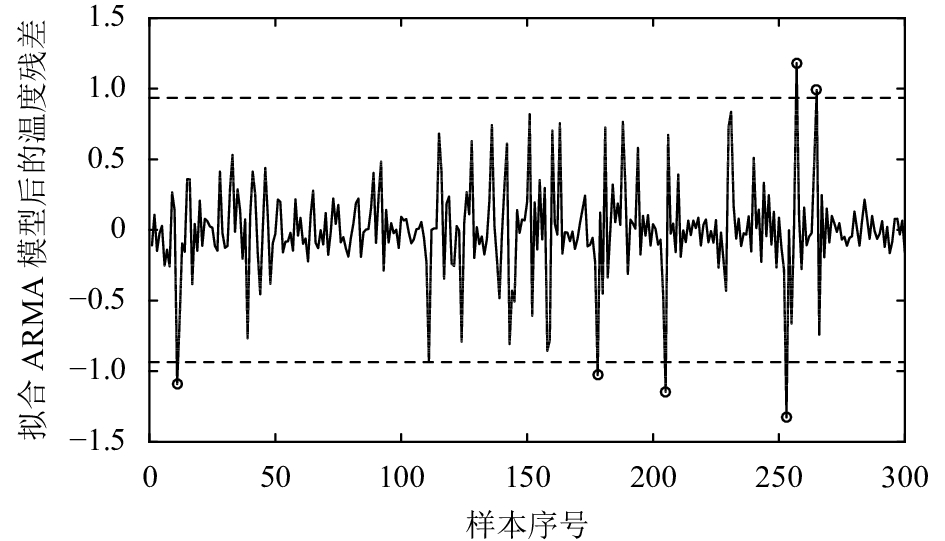
实际上，由于自相关过程的未知性，拟合ARMA(p, q)模型后残差并不一定服从独立正态分布，因此传统的残差控制图控制效果不佳。以监控发电机定子线圈温度为例，已知受控状态下，样本个数为600的定子线圈温度数据，通过一阶差分将定子线圈温度序列平稳化，以前300个点作为已知受控数据构建控制图，并对后300个点进行监控。图1为前300个点的相关性分析，该序列是一条模型未知的自相关序列。对该自相关序列拟合ARMA模型后得到的残差分析结果如图2所示，尽管残差序列的自相关性已经消除，但是残差并不服从正态分布。因此采用传统残差控制图效果不佳。如图3所示，在受控状态下，残差控制图出现频繁的误报警。

2 改进的Bootstrap控制图设计

针对传统残差控制图存在的问题，为未知的自相关过程重新设计控制图。将拟合ARMA模型后的时间序列表达为更加普遍的模型：

$\quad\quad{Y_t} = \mathop \sum \limits_{i = 1}^p {\hat \phi _i}{Y_{t - i}} + \mathop \sum \limits_{j = 1}^q {\hat \theta _j}{\hat \varepsilon _{t - j}}{\text{。}}$

其中ε_t为任意独立分布。

利用已知的受控数据样本拟合ARMA模型后，得到对应的残差序列ε_t。再利用核密度估计的方法估计残差样本ε_t的概率密度函数f(ε)，从而重构残差样本。结合模型表达式，通过递归的方式重构足量的原始样本，最后利用重构的原始样本建立非参数控制图。具体来说，在求出自相关序列的残差以后，接下来的步骤如下。

1) 设置初始平均运行链长ARL₀=L₀，则初始出界概率为 ${\alpha _0} = \displaystyle\frac{1}{{{\rm{AR}}{{\rm{L}}_0}}} = \frac{1}{{{L_0}}}$ 。

2) 估计残差的概率密度函数f(ε)，则f(ε)的非参数核密度估计^[28]为

$\quad\quad\hat f\left( \varepsilon \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \frac{1}{h}k\left( {\frac{{\varepsilon - {\varepsilon _i}}}{h}} \right){\text{。}}$

其中k(·)为核函数，h为窗宽，n为样本容量。

3) 按照概率密度函数 $\hat f\left( \varepsilon \right)$ 重新生成一组独立同分布的残差观测样本 $\varepsilon _t^*$ 。

4) 通过递归的方式，重构原始样本 $Y_t^*$ ，样本个数为s：

$\quad\quad\mathop \sum \limits_{i = 0}^p {\hat \phi _i}Y_{t - i}^{\rm{*}} = - \mathop \sum \limits_{j = 0}^p {\hat \theta _j}\varepsilon _{t - j}^*;\;{\hat \theta _0} = - 1{\text{。}}$

5) 令s=s₁，重复步骤3)、4)，共计m₁次，重构Phase-I阶段所需受控数据集M₁。

6) 令s=s₂，其中 $s_2\gg s_1 $ ，重复步骤3)、4)，共计m₂次，得到检验数据集M₂。

7) 对于数据集M₁，取第i条数据 $Y_{ti}^*$ ，参考步骤2)，得到 $Y_{ti}^*$ 的概率密度函数 ${\hat f_{Y_{ti}^*}}$ ，求解控制上下限(其中， ${\hat f_{Y_{ti}^*}}^p$ 表示 $Y_{ti}^*$ 的概率分布中，使得概率 $P\left\{ {Y_{ti}^* {\text{＜}} \lambda } \right\} = p$ 的数λ，即 ${\hat f_{Y_{ti}^*}}^p = \lambda $ )：

$\quad\quad\begin{array}{l}{\rm{uc}}{{\rm{l}}_i} = {{\hat f}_{Y_{ti}^*}}^{1 - \frac{{{\alpha _0}}}{2}},\\{\rm{lc}}{{\rm{l}}_i} = {{\hat f}_{Y_{ti}^*}}^{\frac{{{\alpha _0}}}{2}}{\text{。}}\end{array}$

8) 步骤7)中，i取值为1，2，3，…，m₁，计算控制上下限均值：

$\quad\quad\begin{array}{l}\overline {{\rm{ucl}}} = \frac{1}{{{m_1}}}\mathop \sum \limits_{i = 1}^{{m_1}} {\rm{uc}}{{\rm{l}}_i},\\\overline {{\rm{lcl}}} = \frac{1}{{{m_1}}}\mathop \sum \limits_{i = 1}^{{m_1}} {\rm{lc}}{{\rm{l}}_i}{\text{。}}\end{array}$

9) 以 $\overline {{\rm{ucl}}} $ 、 $\overline {{\rm{lcl}}} $ 为控制界限，监控检验数据集M₂中的m₂条数据序列，并计算当前平均运行链长ARL_now。

10) 观察当前ARL_now与L₀的差值，调整出界概率α₀，重复步骤7)~9)，直至ARL_now=L₀，此时得到最终的控制上下限，分别记作UCL、LCL。

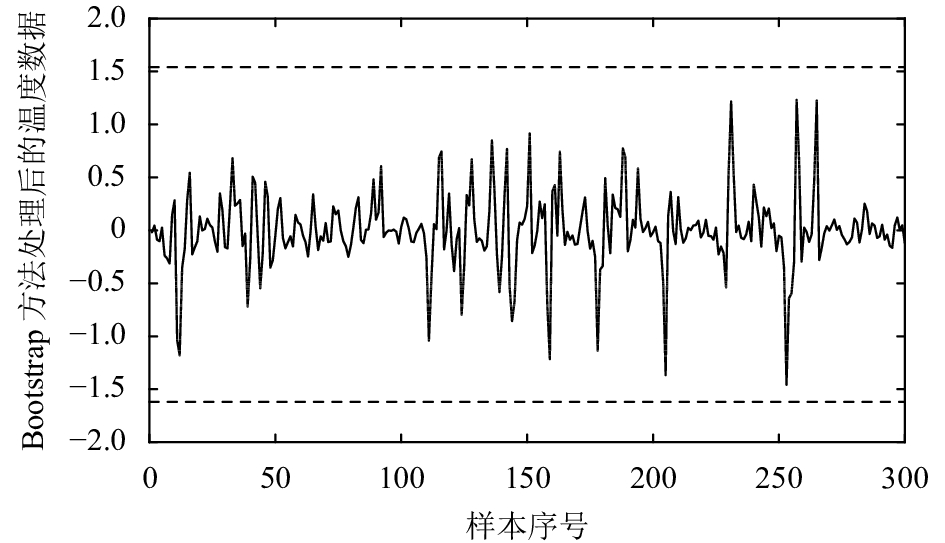
采用改进的Bootstrap方法重新计算第1节中发电机定子线圈温度的控制限，用于监测原始数据，结果如图4所示。在受控状态下，并无误报出现，效果良好。但由于缺乏定子线圈温度失控状态下的数据，无法验证改进的Bootstrap控制图在过程失控时的控制效果。为此，在第3节中，将通过仿真模拟的方式来完成完整的验证。

3 仿真模拟

通过使用蒙特卡洛模拟，在不失一般性的前提下，对数据拟合后符合ARMA(1, 1)模型的自相关数据进行研究，对比两种控制图的实际控制效果。自相关过程模型表示为

$\quad\quad{Y_t} = \phi {Y_{t - 1}} + {\varepsilon _t} + \theta {\varepsilon _{t - 1}},$

其中ε_t~D，D为任意独立分布。

仿真的具体步骤如下。

1) 按照模型 ${Y_t} = \left( {\phi + \delta } \right){Y_{t - 1}} + {\varepsilon _t} + \theta {\varepsilon _{t - 1}}$ ，生成m^*条样本个数为s^*的时间序列集，表示残差ε_t服从D分布，模型参数ϕ发生δ的偏移时的数据集 ${M_\delta }^{\rm{*}}$ ，当δ=0时，数据集 ${M_0}^{\rm{*}}$ 为受控数据集。

2) 按照模型 ${Y_t} = \phi {Y_{t - 1}} + {\varepsilon _t} + \theta {\varepsilon _{t - 1}}$ ，生成一条样本个数为S₀的时间序列,作为获取的第1组受控数据 ${\left\{ {{Y_t}^s} \right\}_{t \in {Z^ + }}}$ ，其中t=1，2，…，S₀，按照第1节中残差控制图的构建步骤1)~3)求其残差序列。

3) 按照第2节中Bootstrap控制图的构建步骤1)~10)，利用上一步所得的残差序列，求取控制限UCL、LCL。

4) 利用控制限UCL、LCL监控数据集 ${M_\delta }^{\rm{*}}$ ，得到相应的平均运行链长进行效果验证。

在模拟过程中，主要考虑4个方面因素的影响。1) ARMA模型的自相关系数的影响：分别取ϕ=0.5和ϕ=0.8。2)模型系数偏移大小δ的影响：相对于原有的自相关系数，偏移后的系数调整量δ为+0.02，+0.04，+0.06，+0.08，+0.1，+0.19。3)选取数据样本个数S₀的影响：S₀分别选取50，70，100，200，300。4)拟合ARMA模型后的残差分布类型D的影响：(1) F分布；(2) 伽马分布；(3) 卡方分布；(4) 正态分布。令各分布均值为0，具体选择的分布参数如表1所示，从表1各分布图形可以看出，4种分布的形状逐渐向正态分布靠近，在下文中，会详细讨论分布的这种变化对控制效果的影响。所有的仿真数据构成如表1所示。

仿真中，初始平均链长设置为ARL₀=100，重构的样本量m^*=3 000，s^*=10 000，s₁=S₀，s₂=10 000。核函数的性能通常是通过渐进积分均方误差度量的。在最小均方误差意义下，Epanechnikov内核是最优的，效率损失也最小^[29]。因此核函数选择Epanechnikov。

4 仿真结果讨论

通过蒙特卡洛模拟分别得到未知自相关过程在受控和失控状态下测得的平均运行链长，记作 IC ARL(ARL in control)和OC ARL(ARL out of control)。下面分别讨论受控和失控状态下的控制图效果。

4.1 受控过程分析(IC ARL)

在初始平均运行链长设置为100的前提下，比较改进的Bootstrap控制图(B图)和传统的残差控制图(R图)在监控受控过程数据时的平均运行链长表现(IC ARL)，结果如表2所示。其中AR和MA分别表示模型的自回归系数和移动平均系数，S₀为所取序列中样本观测点的个数。通过整理表2得到两种控制图受控状态下的整体表现情况，如表3所示。

可以看出，改进的Bootstrap控制图的IC ARL均值可以控制在100左右，且方差很小。而对于传统残差控制图，在分布逐渐变为正态分布的过程中，IC ARL的均值逐渐靠近初始设置值100，但是整体效果依然较差。传统残差控制图的IC ARL均明显低于初始设置值，因此在实际监控中会出现频繁报警的情况，同时传统残差控制图的IC ARL方差极大，说明这种方法在受控状态下的监控效果不稳定。

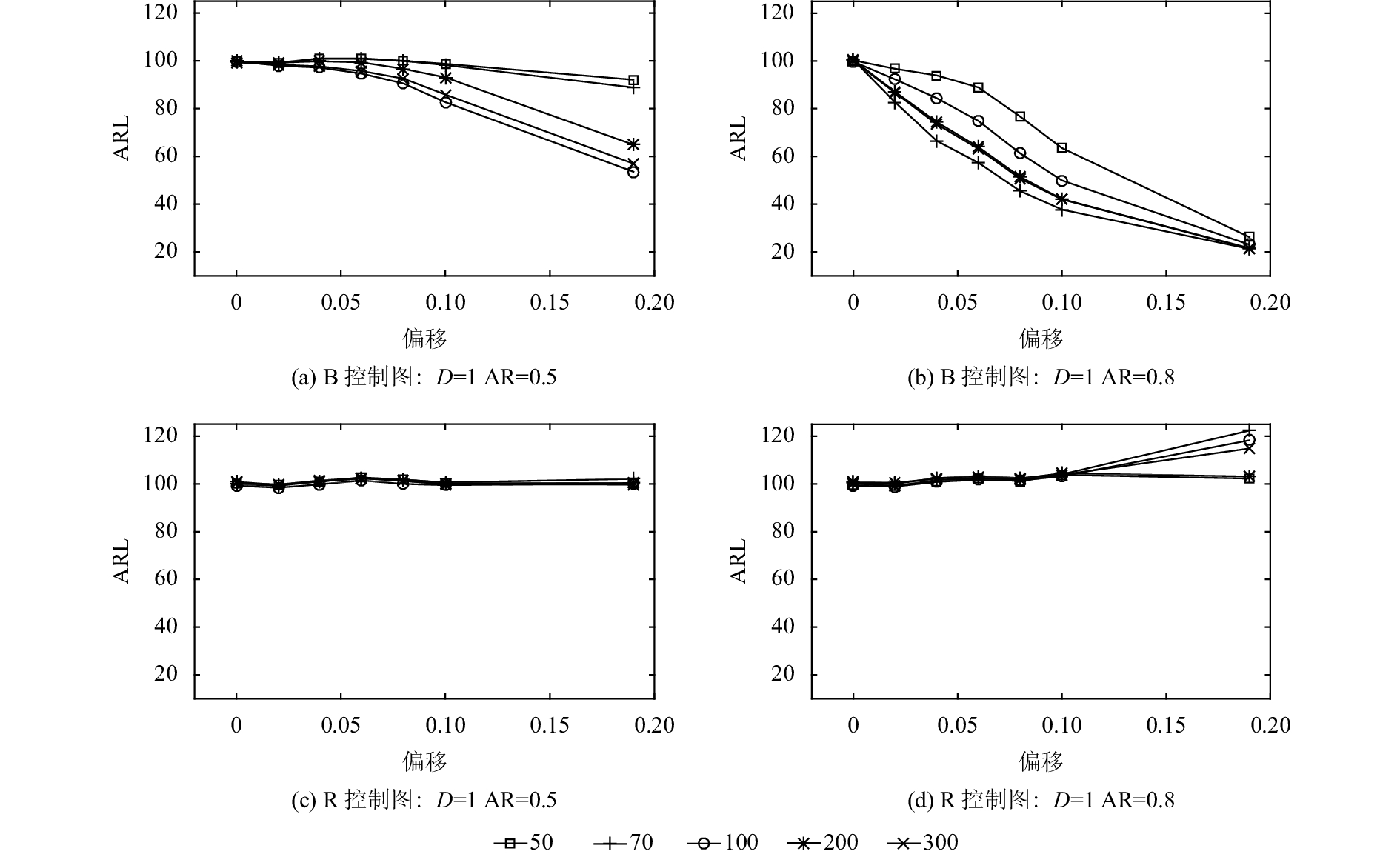
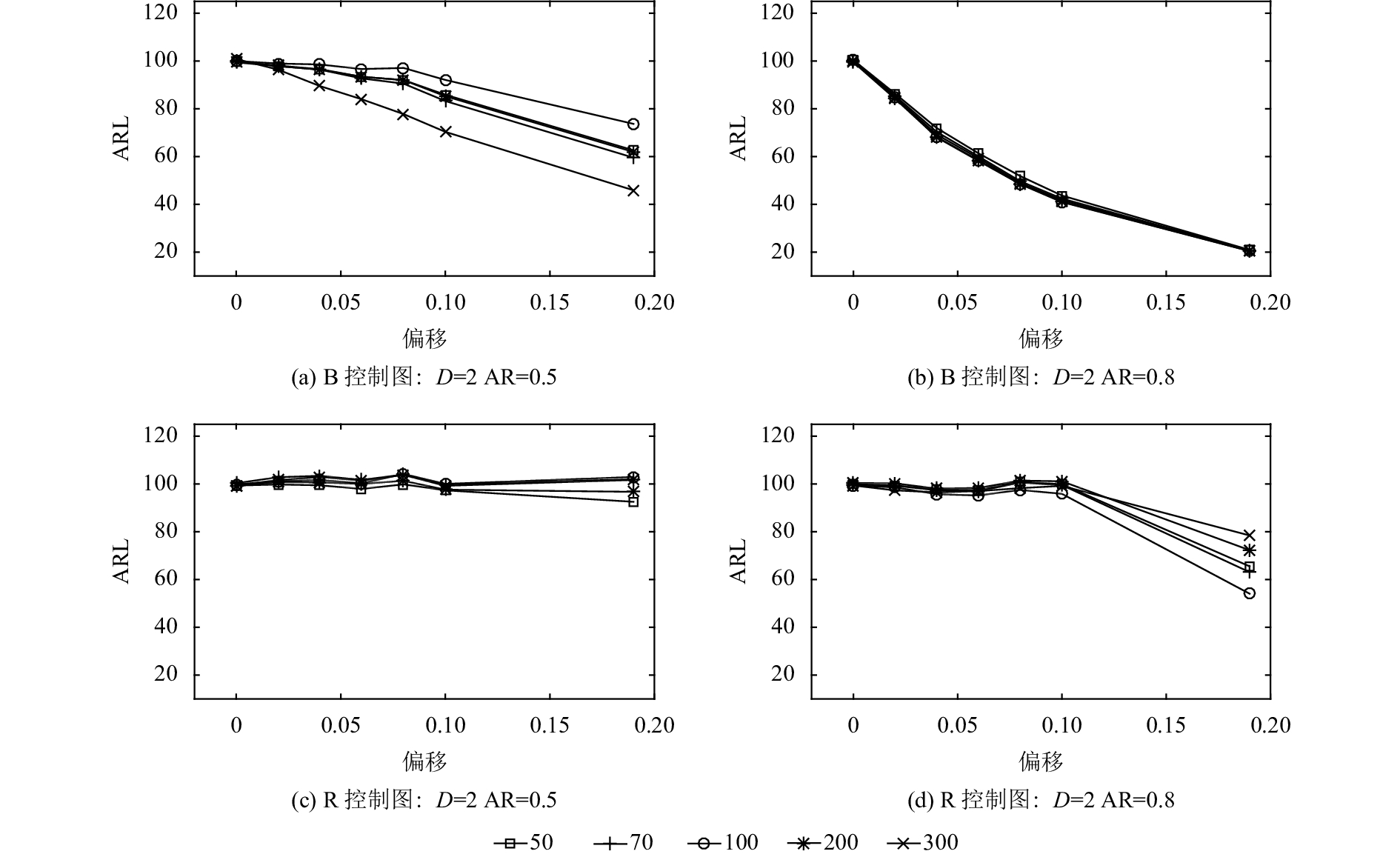
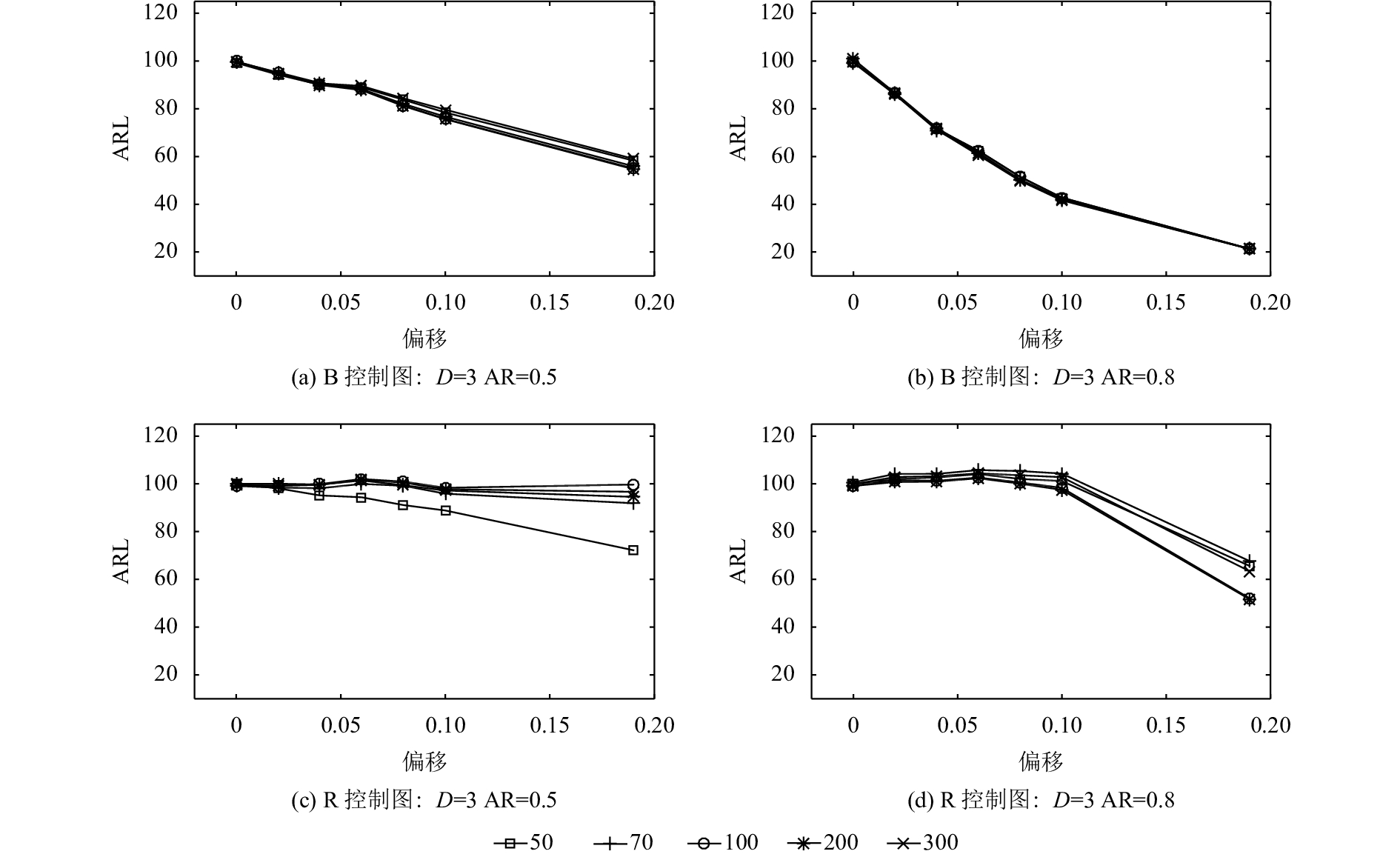
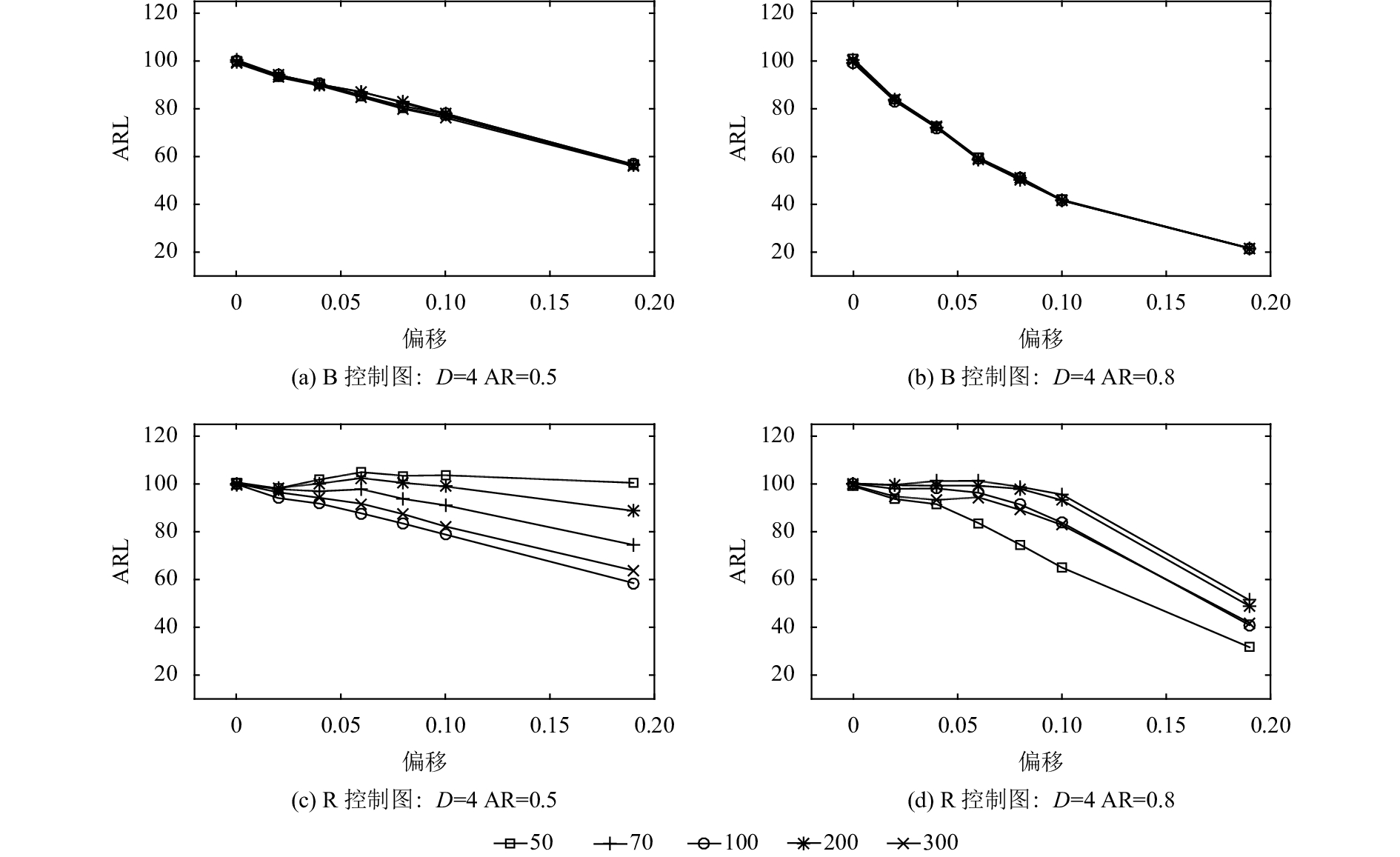
4.2 失控过程分析(OC ARL)

在进行失控过程分析之前，首先通过人工调整传统残差控制图的控制限，将其IC ARL调节到100，再对两种控制图的控制效果进行比较。如表4所示，为输出数据失控的情况下，改进的Bootstrap控制图和传统的残差控制图的OC ARL的具体表现(ARL₀=100)。通过对表格内容进行整理，得到残差为4种不同分布时，ARL随着模型系数、偏移量以及样本个数变化的变化情况，分别如图5~图8所示。其中，B控制图表示基于Bootstrap设计的新控制图，R控制图为残差(residual)控制图；D表示残差分布类型(distribution)：1)F分布F(30, 12)；2)伽马分布G(4, 2)；3)卡方分布χ²(20)；4)正态分布N(0, 1)。例如图5中，B控制图：D=1，AR=0.5表示在改进的Bootstrap控制图的控制下，当残差分布为F分布，AR系数为0.5时，模型系数AR发生不同的偏移时ARL的表现情况，每张小图中的线段对应不同样本个数下的平均运行链长。

根据图5~图8，详细分析第3节提到的4个方面的因素对监控效果的影响。

1) ARMA模型自相关系数的影响。对于改进的Bootstrap控制图而言，自相关系数越大，控制效果越好。具体表现在，相同偏移情况下，自相关系数越大，OC ARL越小，报警越及时；同时随着偏移量的增加，自相关系数越大，OC ARL变化越剧烈，敏感度越高。对于传统的残差控制图而言，在自相关系数较小的时候，OC ARL几乎没有变化，控制图不起作用；在自相关系数较大时，随着残差分布逐渐变为正态分布，控制图的控制效果逐渐转好。在相同的自相关系数下，传统残差控制图的控制效果远不如改进的Bootstrap控制图。

2) 模型系数偏移大小的影响。对于改进的Bootstrap控制图而言，随着模型系数偏移量的增加，OC ARL逐渐减小，符合监控要求，同时变化的幅度较大，能够明显地由OC ARL的变化推测模型系数的改变。而传统残差控制图对模型系数偏移的敏感度远不如改进的Bootstrap控制图，尤其是在残差分布不是正态分布且模型自相关系数较小的情况下，如F分布下，OC ARL几乎不随偏移的改变而改变，甚至出现了大偏移下OC ARL反而增大的情况。因此旧方法的报警频率不能反映出偏移量的改变，甚至会给决策者带来完全相反的错误判断。在相同的偏移大小下，改进的Bootstrap控制图的OC ARL更小，报警更加及时。

3) 选取数据样本个数的影响。对于改进的Bootstrap控制图而言，随着残差分布逐渐接近正态分布，样本个数的影响逐渐变小。这表示，如果所检测的未知过程自相关数据恰好残差分布是满足正态分布的，则监控效果与所选取的数据样本个数无关，减少了控制图的使用限制，即对样本量的选择限制缩小。在残差分布与正态分布差别较大的情况下，尽可能选择较多的样本个数有利于提高控制效果。而传统残差控制图受样本个数的影响较大，不同的样本个数下往往得到不同的平均运行链长。有时样本个数并不总是越大越好，不能据此合理地选择样本个数，同时也无法确定控制图报警的结果是否有效。出现这种情况很大程度上是由于样本个数太少，所抽取的样本对于描述输出数据的整体模型的准确性具有随机性。

4) 残差分布类型的影响。仿真所采用的4种残差分布，其分布形式是逐渐向正态分布接近的。传统残差控制图的设计是基于拟合ARMA模型以后，残差符合正态分布的情况，具有很大的局限性。从图中也可以看出来，在监控未知的自相关过程时，传统的残差控制图在残差非正态分布的情况下几乎不起作用，而改进的Bootstrap控制图在多种分布下都有较好的监控效果。对于实际生产中数据形式未知的情况，新方法的适用范围更广泛，即使是在残差服从正态分布的情况下，传统残差控制图的监控效果也不如改进的Bootstrap控制图。改进后的控制图通过对残差分布做核密度估计，克服了原有方法仅适用于正态分布的局限性，可以对任意分布做合理的估计，并且通过重构原始样本解决了缺乏历史数据的问题。

5 结论

针对未知的自相关过程在监控过程中存在的问题，结合拟合ARMA模型建立控制图的方法，基于Sieve Bootstrap的思路，提出一种改进的Bootstrap控制图。在拟合ARMA模型得到残差以后，通过估计样本残差的密度函数，重构残差从而重构原始样本，一定程度上解决了缺乏历史数据的问题，另一方面也避免了直接将残差作为正态分布处理的误区。通过数值实验，对拟合模型服从ARMA(1，1)，且其残差符合4种不同的分布情况下，进行蒙特卡洛模拟。根据ARL表现，证明了在仅获取一组Phase-I阶段的受控数据情况下，就可以构建有效的Bootstrap控制图，并且取得较好的监控效果。相比于传统的残差控制图，改进后的控制图报警更加准确，适用范围更加普遍，同时操作简便，易于投入实际的生产控制过程中。