智能制造时代的到来,推动了制造业向基于大数据分析与应用基础上的智能转型[1]。如何在满足市场需求的同时,又能有效控制生产成本,提高生产效率是转型的主要目的之一。多产品、多计划期综合生产计划(multi-period and multi-product aggregate production planning, MPMP-APP) 是为完成某项生产任务而制定的中长期生产计划,其编制过程建立在对大数据的分析与应用的基础之上,以总成本最小为目标,实现生产、劳动力和库存水平等变量的最优组合。编制过程中往往涉及的决策变量和相关参数种类多,数量庞大,仅依靠经验排程是很难实现目标最优的。此外,在实际的经营决策中,MPMP-APP往往是多目标决策问题,且某些参数是不确定的。因此,如何统筹兼顾多种目标,在不确定环境下制订出综合最优的计划方案一直受到企业和学术界的重视,也是工业大数据应用的重要课题之一。
在传统的生产计划模型中,以研究确定性的生产计划问题居多,且主要集中在单一目标的优化上。然而在现实世界中,不确定性广泛存在于生产经营活动中,不确定环境下的多目标生产计划问题已成为当前的研究热点[2-6]。依据优化问题中对所出现不确定变量描述方法的不同,不确定APP问题的研究方法主要可分为随机规划和模糊规划两类方法[7],2种方法的主要区别是对不确定性的描述方法不同,随机规划是将随机变量包含在数学规划模型中的理论和方法,而模糊规划则采用模糊集的方法来建立和求解不确定模型。两种方法在解决不确定APP问题中都有广泛的应用。如在随机规划方法中,文献[8]以产品需求、废品数和每班每台机床的可用时间为随机变量,建立了柔性自动化车间随机生产计划与控制的数学模型,并给出了求解该问题的算法;文献[9]提出了一种具有需求为随机变量、多产品多计划期多生产厂址的生产计划问题的随机规划方法,并考虑了订购数量的折扣、提前期和运输成本的关系、缺货惩罚和废物排放等因素。提出的模型首先是一个非线性混合整数规划,通过应用一些理论和数值方法,将其转化为线性混合整数规划实现模型的求解。文献[10]考虑了多产品多计划期生产计划中需求、生产能力、材料供应、加工时间、返工和报废等的不确定性,研究了柔性自动化车间的分层随机生产规划问题,建立了包含需求约束和分段线性目标函数的随机非线性规划模型。为便于求解,首先将模型近似转化为确定性非线性规划模型,并进一步转化为线性规划模型,并采用Karmarkar算法和交互/预测算法实现模型的求解。在模糊规划方法中,文献[11]建立了以单位利润、生产能力以及产品需求为模糊参数的批量生产计划的可信性规划模型,将模糊参数描述为梯形模糊数,并转化为清晰等价形式以进行求解;文献[12]提出了具有模糊需求量和模糊能力约束以及资本水平约束的多产品综合生产计划问题的模糊优化模型及模糊解方法;文献[13]以产品的市场需求和库存成本为模糊变量,提出了一种两阶段多产品多计划期模糊优化方法;文献[14]提出了包含模糊需求与随机生产能力的跨国供应链计划模型,采用等价理论,将模型转化为模糊机会约束规划模型,并利用遗传算法与模糊模拟技术相结合的混合算法进行求解。
虽然上述两类方法能够较好地处理生产系统中的不确定性,但是随机规划建立在不确定参数的概率分布基础上,而模糊规划则需要获取不确定参数的模糊隶属度函数。构造精确的概率分布和模糊隶属度函数需要大量的信息支持,对于很多生产实际问题,由于信息采集技术、人员操作水平的差异或实际条件所限,往往无法获得足够的样本信息。因此,上述两类方法的适用性均存在一定的局限性。区间数优化是一种相对较新的不确定性优化方法[15],它利用区间的上下界来描述参数的不确定性,故在不确定性建模方面体现了很好的方便性和经济性,具有更强的工程应用潜力。
为此,针对传统不确定规划方法在解决多目标、多产品、多计划期、参数不确定APP问题存在的问题,本文提出一种基于区间数的目标规划优化方法,建立了多目标、多产品、多计划期、参数不确定APP问题的区间数目标规划模型,通过引入区间可能度和置信水平,实现将不确定区间模型转化为等价确定模型,在此基础上采用Lingo软件,并编写相应的程序完成对模型的求解。
1 问题描述多目标、多产品、多计划期、参数不确定生产计划问题可描述为:在计划期T内要生产N种不同类型的产品i以满足市场需求,假设计划期t对产品i的需求量是
决策变量如下:
相关参数如下:
上述参数中,上方带“~”字母在本文中假设为区间型不确定参数,其余为确定参数。
1.2 多目标MPMP-APP模型建立以总生产成本最小为目标1,同时为避免开工不足,确保设备充分利用,将目标2设定为最大化机器的累计利用时间,具体模型如下。
| $\begin{split}&\displaystyle\quad\quad\min \;{{\tilde f}_1} = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {\left( {{{\tilde q}_{it}}{Q_{it}} + {{\tilde o}_{it}}{O_{it}} + {{\tilde s}_{it}}{S_{it}}} \right)} }+ \\&\displaystyle \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^N {{{\tilde h}_{it}}{I_{it}}} } + \sum\limits_{t = 1}^T {\left( {\tilde {\rm{h}}{{\rm{r}}_t}{H_t} + {\rm{l}}{{\tilde {\rm{o}}}_t}{L_t} + {{\tilde w}_t}{W_t}} \right)} ,\end{split}$ | (1) |
| $\quad\quad{\max \;{{\tilde f}_2} = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{{\tilde r}_i}({Q_{it}} + {O_{it}})} } }{\text{。}}$ | (2) |
s.t.
| $\quad\quad{{Q_{it}} + {O_{it}} + {S_{it}} + {I_{i(t - 1)}} - {I_{it}} {\text{≥}} {{\tilde D}_{it}},\;\;\forall i,\forall t;}$ | (3) |
| $\quad\quad{\sum\limits_{i = 1}^N {{{\tilde r}_i}({Q_{it}} + {O_{it}}) {\text{≤}} {{\tilde M}_{t\max }},\;\;\forall t;} }$ | (4) |
| $\quad\quad{\sum\limits_{i = 1}^N {{e_i}} {Q_{it}} {\text{≤}} \rho {W_t},\;\;\forall t;}$ | (5) |
| $\quad\quad{\sum\limits_{i = 1}^N {{e_i}} {O_{it}} {\text{≤}} {\lambda _t}\rho {W_t},\;\;\forall t;}$ | (6) |
| $\quad\quad{{W_t} = {W_{t - 1}} + {H_t} - {L_t},\;\;\forall t;}$ | (7) |
| $\quad\quad{{Q_{it}},{O_{it}},{S_{it}},{I_{it}},{H_t},{L_t},{W_t} {\text{≥}} 0,\;\;\forall i,\forall t}{\text{。}}$ | (8) |
式(1)为目标函数1,表示总生产成本,其中,
为便于对区间数约束进行分析和求解,模型中没有考虑库存和违约等约束,并假设区间数仅存在于式(1)~式(4)中,且式(4)两边均包含区间数。
2 基于区间可能度的目标规划方法 2.1 区间数和区间可能度定义1 设R为实数域,对于任意
定义2 设计区间数
可能度反映了两区间数的大小(或优劣)关系,其值一般在0~1之间。对于区间数可能度的构造,国内外学者提出了多种不同的构造方法[18-20]。文献[15, 21]在上述方法的基础上,将区间数
| $\quad\quad\quad\quad\quad{P_{{\rm{(}}\tilde A {\text{≤}} \tilde B{\rm{)}}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}}{0,} & {{A^{\rm{L}}} {\text{≥}} {B^{\rm{R}}};}\\{\displaystyle\frac{1}{2}\cdot\displaystyle\frac{{{B^{\rm{R}}} - {A^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}} \cdot \displaystyle\frac{{{B^{\rm{R}}} - {A^{\rm{L}}}}}{{{B^{\rm{R}}} - {B^{\rm{L}}}}},} & {{B^{\rm{L}}} {\text{≤}} {A^{\rm{L}}} {\text{<}} {B^{\rm{R}}} {\text{≤}} {A^{\rm{R}}};}\\{\displaystyle\frac{{{B^{\rm{L}}} - {A^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}} + \displaystyle\frac{1}{2}\cdot\displaystyle\frac{{{B^{\rm{R}}} - {B^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}},} & {{A^{\rm{L}}} {\text{<}} {B^{\rm{L}}} {\text{<}} {B^{\rm{R}}} {\text{≤}} {A^{\rm{R}}};}\\\!\!\!\begin{array}{l}\displaystyle\frac{{{B^{\rm{L}}} - {A^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}} + \displaystyle\frac{{{A^{\rm{R}}} - {B^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}} \cdot \displaystyle\frac{{{B^{\rm{R}}} - {A^{\rm{R}}}}}{{{B^{\rm{R}}} - {B^{\rm{L}}}}} + \displaystyle\frac{1}{2}\cdot\displaystyle\frac{{{A^{\rm{R}}} - {B^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}} \cdot \displaystyle\frac{{{A^{\rm{R}}} - {B^{\rm{L}}}}}{{{B^{\rm{R}}} - {B^{\rm{L}}}}},\end{array} & {{A^{\rm{L}}} {\text{<}} {B^{\rm{L}}} {\text{≤}} {A^{\rm{R}}} {\text{<}} {B^{\rm{R}}};}\\{\displaystyle\frac{{{B^{\rm{R}}} - {A^{\rm{R}}}}}{{{B^{\rm{R}}} - {B^{\rm{L}}}}} + \displaystyle\frac{1}{2}\cdot \displaystyle\frac{{{A^{\rm{R}}} - {A^{\rm{L}}}}}{{{B^{\rm{R}}} - {B^{\rm{L}}}}},} & {{B^{\rm{L}}} {\text{≤}} {A^{\rm{L}}} {\text{<}} {A^{\rm{R}}} {\text{<}} {B^{\rm{R}}};}\\{1,} & {{A^{\rm{R}}} {\text{<}} {B^{\rm{L}}}{\text{。}}}\end{array}} \right.$ | (9) |
其中,
| $\quad\quad P(\tilde A {\text{≤}} b) = \left\{ {\begin{array}{*{20}{l}} {0,}&{b {\text{≤}} {A^{\rm{L}}};} \\ {\displaystyle\frac{{b - {A^{\rm{L}}}}}{{{A^{\rm{R}}} - {A^{\rm{L}}}}},}&{{A^{\rm{L}}} {\text{<}} b {\text{≤}} {A^{\rm{R}}};} \\ {1,}&{b {\text{>}} {A^{\rm{R}}}{\text{。}}} \end{array}} \right.$ | (10) |
目标规划可视为多目标优化问题的一种特殊的妥协模型,广泛应用于经济建设的各个领域。其目的是最小化目标函数与理想目标的偏差(正偏差或负偏差)。在实际问题中,多个目标之间往往是不相容的。如在MPMP-APP问题中,一个目标是总生产成本最小,另一个目标则要求各个计划期内设备的工作和空闲时间安排合理,即设备的利用率要最大化。因此,目标之间具有不同的优先系数。此外,在目标规划中,约束有两类,一类是对资源有严格约束的,用严格的等式或不等式处理,这类约束称为刚性约束(hard constraint),另一类约束是可以不严格限制的,称为柔性约束(soft constraint)。为便于分析,本文将目标函数(1)、(2),以及约束(3)和约束(4)作为柔性约束,其他约束作为刚性约束。依据区间可能度的定义,MPMP-APP模型可修改为基于区间可能度的MPMP-APP目标规划模型,如下所示。
| $\quad\quad{{\rm{lex}}\min (d_1^ + ,d_2^ - ){\text{。}}}$ | (11) |
s.t.
| $\quad\quad{{P_1}[({f_1}({{x}},{{\xi }}) - d_1^ + ) {\text{≤}} {\rm{Goa}}{{\rm{l}}_1}] {\text{≥}} {\alpha _1}};$ | (12) |
| $\quad\quad{{P_2}[({f_2}({{x}},{{\xi }}) + d_2^ - ) {\text{≥}} {\rm{Goa}}{{\rm{l}}_2}]{\text{≥}} {\alpha _2};}$ | (13) |
| $\quad\quad{{P_{3it}}[{Q_{it}} \!+\! {O_{it}} \!+\! {S_{it}} \!+\! {I_{i(t \!-\! 1)}} \!-\! {I_{it}} {\text{≥}} {{\tilde D}_{it}}] {\text{≥}} {\alpha _{3it}},\forall i,\forall t;}$ | (14) |
| $\quad\quad{{P_{4t}}(\sum\limits_{i = 1}^N {{{\tilde r}_i}({Q_{it}} + {O_{it}}) {\text{≤}} {{\tilde M}_{t\max }}) {\text{≥}} {\alpha _{4t}}} ,\;\;\;\;\forall t;}$ | (15) |
| $\quad\quad{d_1^ + ,d_2^ - {\text{≥}} 0;}$ | (16) |
| $\quad\quad{\text{式}}{\left( {5} \right) {\text{~}} {\text{式}}\left( {8} \right){\text{。}}}$ | (17) |
式中,lexmin表示字典序最小化目标向量;
因为区间目标规划模型中的目标函数和约束函数中含有区间型参数,因此该模型不能直接求解,需要先将模型中不确定约束转换为等价的确定形式。为此,需引入下述定理。
定理1 假设函数
| $\quad\quad f({{x}},{{\xi }} ) = \sum\limits_{k = 1}^m {{h_k}({x_k}){\xi _k}} + {h_0}(x){\text{。}}$ | (18) |
其中,
| $\quad\quad\alpha f{({{x}},{{\xi }})^{\rm{R}}} + (1 - \alpha )f{({{x}},{{\xi }})^{\rm{L}}} {\text{≤}} r{\text{。}}$ | (19) |
其中,
证明:因为
同理,区间可能度
| $\quad\quad(1 - \alpha )f{({{x}},{{\xi }})^{\rm{R}}} + \alpha f{({{x}},{{\xi }})^{\rm{L}}} \geqslant r{\text{。}}$ | (20) |
图1和图2给出了
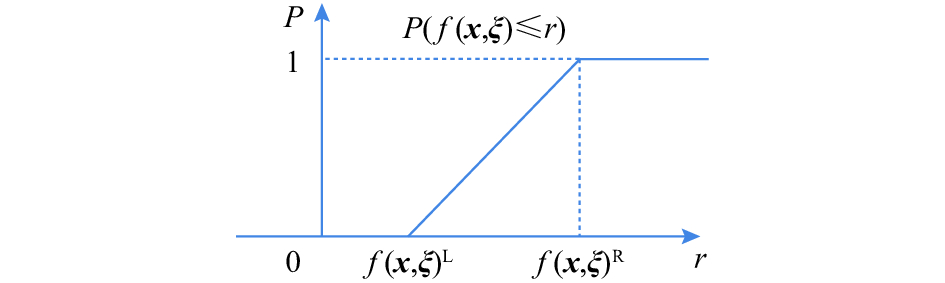
|
图 1 |
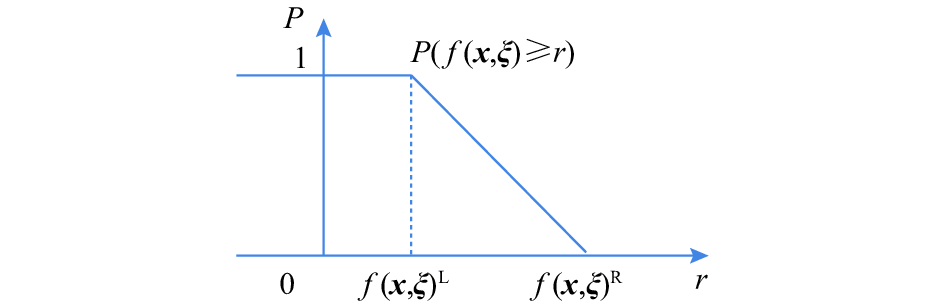
|
图 2 |
根据定理1和式(19),约束(12)可转换为
| $\begin{split} &\quad\quad{P_1}[({f_1}({{x}},{{\xi }}) - d_1^ + ) {\text{≤}} {\rm{Goa}}{{\rm{l}}_1}] {\text{≥}} {\alpha _1} \Rightarrow \\ &{\alpha _1}[{f_1}{({{x}},{{\xi }})^{\rm{R}}} \!-\! d_1^ + ] \!+\! (1 \!-\! {\alpha _1})[({f_1}{({{x}},{{\xi }})^{\rm{L}}} \!-\! d_1^ + )] \!\leqslant\! {\rm{Goa}}{{\rm{l}}_1}{\text{。}}\\ \end{split} $ | (21) |
同理,由定理1和式(20),约束(13)可转换为
| $\begin{split} &\quad\quad{P_2}[({f_2}({{x}},{{\xi }}) + d_2^ - ) {\text{≥}} {\rm{Goa}}{{\rm{l}}_2}] {\text{≥}} {\alpha _2} \Rightarrow \\ &(1 \!-\! {\alpha _2})[{f_2}{({{x}},{{\xi }})^{\rm{R}}} \!+\! d_2^ - ] \!+\! {\alpha _2}[{f_2}{({{x}},{{\xi }})^{\rm{L}}} \!+\! d_2^ - ] {\text{≥}} {\rm{Goa}}{{\rm{l}}_2} {\text{。}}\end{split} $ | (22) |
由定理1和式(19),约束(14)可转换为
| $\begin{split}&\quad\quad{P_{3it}}[{Q_{it}} +\! {O_{it}} +\! {S_{it}} \!+\! {I_{i(t - 1)}} - {I_{it}} {\text{≥}} {{\tilde D}_{it}}] {\text{≥}} {\alpha _{3it}} \Rightarrow \\ &{\alpha _{3it}}D_{it}^{\rm{R}} + (1 - {\alpha _{3it}})D_{it}^{\rm{L}} {\text{≤}} {Q_{it}} + {O_{it}} + {S_{it}} + {I_{i(t - 1)}} - {I_{it}} {\text{。}} \end{split} $ | (23) |
此外,因约束(15)中
经过上述转换,上述区间可能度目标规划模型已转换为等价的确定性模型,对该模型可采用Lingo软件编写程序进行求解。
3 算例分析为便于说明,本文给出一个产品种类N=2、计划期T=4的MPMP-APP区间目标规划计算算例。相关参数见表1~表5。
| 表 1 各计划期需求量 Tab. 1 Demands for different planning period |
| 表 2 各计划期最大人工数和设备能力 Tab. 2 Maximum labor and machine capacity |
| 表 3 成本参数 Tab. 3 Operation cost data |
| 表 4 各计划期劳动力、雇佣、解雇成本 Tab. 4 Labor cost and workforce changing costs |
| 表 5 劳动力和设备的单位消耗工时 Tab. 5 Labor and machine relevant time data |
其他相关参数说明如下。
1) 假设产品1的期初库存为40,产品2的期初库存为20;另外,要求产品1的期末库存为300,产品2的期末库存为200。
2) 设各计划期加班系数均为
3) 假设目标1的期望成本Goal1=320 000,且可能度置信水平为80%,即
4) 假设目标2的期望值为各计划期总生产能力均值的85%,即
| $\quad\quad{\rm{Goa}}{{\rm{l}}_2} = \sum\limits_{t = 1}^T {(M_{t\max }^{\rm{L}} + M_{t\max }^{\rm{R}}) \times 85\% } = 1\;474.75{\text{。}}$ |
且可能度置信水平为80%,即
5) 约束(14)和(15)各计划期的可能度置信水平均为
采用Lingo软件编制相应的程序对上述模型进行求解。优化结果如表6所示。
| 表 6 运行结果Goal1=320 000 Tab. 6 Optimization results when Goal1=320 000 |
结果分析如下。
1) 因目标函数中有不确定的区间型参数存在,因此求解后得到的目标值仍为区间数。优化后总成本
2) 优化后总成本满足
3) 正常上班和加班的累计设备利用时间不能满足
4) 其他刚性约束均严格满足约束要求。
5) 如将目标1的成本期望值由320 000元调整为280 000元,即Goal1=280 000元,其他参数不变,运行结果如表7所示。
| 表 7 运行结果(Goal1=280 000) Tab. 7 Optimization results when Goal1=280 000 |
从表7可以看出,当决策者将成本目标设置为280 000元时,优化后总成本为:
针对多产品多计划期参数不确定的生产计划问题,本文将各计划期的市场需求量、生产成本参数、生产能力、人工工时和机器工时等视为区间数,并根据约束的实际意义和分析的方便,将成本和设备利用目标作为柔性区间约束处理,而数量平衡和生产能力约束作为刚性区间约束处理,建立了基于区间可能度的MPMP-APP问题的目标规划模型。根据区间可能度的序关系,将不确定的区间约束转换为确定约束,最终得到等价的清晰模型。最后采用Lingo软件编写相应程序进行模型求解。该方法能有效解决随机规划和模糊规划需要获取大量样本信息的不足,根据实际情况确定柔性约束和刚性约束,在不确定性生产计划目标规划建模方面体现了很好的方便性和经济性,因此具有较好的工程应用价值。
| [1] |
钟海. 大数据在工业制造业的应用与研究[J].
企业技术开发: 学术版, 2015, 34(5): 104-105.
ZHONG Hai. Application and research of big data in industrial manufacturing[J]. Technological Development of Enterprise, 2015, 34(5): 104-105. |
| [2] |
Liang Tienfu. Fuzzy multi-objective production/distribution planning decisions with multi-product and multi-time period in a supply chain[J].
Computers & Industrial Engineering, 2008, 55(3): 676-94.
|
| [3] |
唐加福, 汪定伟, 许宝栋. 多品种集约生产计划问题的模糊方法[J].
管理科学学报, 2003, 6(1): 44-50.
TANG Jiafu, WANG Dingwei, XU Baodong. Fuzzy modeling approach to aggregate production planning with multi-product[J]. Journal of Management Sciences in China, 2003, 6(1): 44-50. DOI: 10.3321/j.issn:1007-9807.2003.01.007. |
| [4] |
ENTEZAMINIA, Arezoo, HEIDARI Mahdi, RAHMANI Donya. Robust aggregate production planning in a green supply chain under uncertainty considering reverse logistics: a case study[J].
International Journal of Advanced Manufacturing Technology, 2017, 90(5-8): 1507-1528.
DOI: 10.1007/s00170-016-9459-6. |
| [5] |
徐学军, 顾培亮. 随机综合生产计划模型及其求解研究[J].
工业工程, 2001, 4(3): 12-15.
XU Xuejun, GU Peiliang. Study on stochastic aggregate production planning models and solution procedure[J]. Industrial Engineering Journal, 2001, 4(3): 12-15. DOI: 10.3969/j.issn.1007-7375.2001.03.003. |
| [6] |
MULA J, POLER R, GARCIA-SABATER JP, et al. Models for production planning under uncertainty: a review[J].
International Journal of Production Economics, 2006, 103(1): 271-285.
DOI: 10.1016/j.ijpe.2005.09.001. |
| [7] |
彭锦, 刘宝碇. 不确定规划的研究现状及其发展前景[J].
运筹与管理, 2002, 11(2): 1-10.
PENG Jin, LIU Baoding. Uncertain programming: current status and future prospects[J]. Operations Research and Management Science, 2002, 11(2): 1-10. DOI: 10.3969/j.issn.1007-3221.2002.02.001. |
| [8] |
严洪森, 张晓东, 王浩. 满足产品需求条件下的车间最优随机生产计划与控制[J].
中国机械工程, 2002, 13(3): 228-232.
YAN Hongsen, ZHANG Xiaodong, WANG Hao. Optimal stochastic production planning and control for workshops with demand constraints[J]. China Mechanical Engineering, 2002, 13(3): 228-232. DOI: 10.3321/j.issn:1004-132X.2002.03.016. |
| [9] |
Al-E-HASHEM S M J Mirzapour, BABOLI A, SAZVAR Z. A stochastic aggregate production planning model in a green supply chain: considering flexible lead times, nonlinear purchase and shortage cost functions[J].
European Journal of Operational Research, 2013, 230(1): 26-41.
DOI: 10.1016/j.ejor.2013.03.033. |
| [10] |
YAN H S. Hierarchical stochastic production planning with delay interaction[J].
Journal of Optimization Theory and Applications, 2000, 104(3): 659-689.
DOI: 10.1023/A:1004645827172. |
| [11] |
白进达, 曹喆, 张东凯, 等. 模糊批量生产计划问题的可信性规划模型与算法[J].
模糊系统与数学, 2007, 21(2): 113-120.
BAI Jinda, CAO Zhe, ZHANG Dongkai, et al. Credibility programming approach to lot sizing production planning in fuzzy environment[J]. Fuzzy Systems and Mathematics, 2007, 21(2): 113-120. DOI: 10.3969/j.issn.1001-7402.2007.02.018. |
| [12] |
唐加福, 董颖, 刘士新, 等. 模糊需求和模糊能力约束的集约生产计划[J].
控制理论与应用, 2003, 20(6): 894-896.
TANG Jiafu, DONG Ying, LIU Shixin, et al. Aggregate production planning with fuzzy demands and fuzzy capacity[J]. Control theory & Applications, 2003, 20(6): 894-896. |
| [13] |
GUO Q Y. Two-stage fuzzy production planning expected value model and its approximation method[J].
Applied Mathematical Modelling, 2012, 36(6): 2429-2445.
DOI: 10.1016/j.apm.2011.09.001. |
| [14] |
葛健, 李燕风, 夏国平. 不确定环境下跨国供应链生产计划研究[J].
计算机集成制造系统, 2005, 11(8): 1120-1126.
GE Jian, LI Yanfeng, XIA Guoping. Research on global supply chain production planning under uncertain environment[J]. Computer Integrated Manufacturing Systems, 2005, 11(8): 1120-1126. DOI: 10.3969/j.issn.1006-5911.2005.08.014. |
| [15] |
姜潮. 基于区间的不确定性优化理论与算法[D]. 长沙: 湖南大学, 2008
JIANG Chao. Theories and algorithms of uncertain optimization based on interval[D]. Changsha: Hunan University, 2008 |
| [16] |
邱涤珊, 贺川, 朱晓敏. 基于概率可信度的区间数排序方法[J].
控制与决策, 2012, 27(12): 1894-1898.
QIU Dishan, HE Chuan, ZHU Xiaomin. Ranking method research of interval numbers based on probability reliability distribution[J]. Control and Decision, 2012, 27(12): 1894-1898. |
| [17] |
肖峻, 张跃, 付川. 基于可能度的区间数排序方法比较[J].
天津大学学报, 2011, 44(8): 705-711.
XIAO Jun, ZHANG Yue, FU Chuan. Comparison between methods of interval number ranking based on possibility[J]. Journal of Tianjin University, 2011, 44(8): 705-711. DOI: 10.3969/j.issn.0493-2137.2011.08.009. |
| [18] |
张全, 樊治平, 潘德惠. 不确定性多属性决策中区间数的一种排序方法[J].
系统工程理论与实践, 1999(5): 129-133.
ZHANG Quan, FAN Zhiping, PAN Dehui. A ranking approach for interval numbers in uncertain multiple attribute decision making problems[J]. Systems Engineering-Theory & Practice, 1999(5): 129-133. DOI: 10.3321/j.issn:1000-6788.1999.05.025. |
| [19] |
达庆利, 刘新旺. 区间数线性规划及其满意解[J].
系统工程理论与实践, 1999(4): 3-7.
DA Qingli, LIU Xinwang. Interval number linear programming and its satisfactory solution[J]. Systems Engineering-theory & Practice, 1999(4): 3-7. DOI: 10.3321/j.issn:1000-6788.1999.04.002. |
| [20] |
DUBIOS D, PARADE H. Ranking fuzzy numbers in the setting of possibility theory[J].
Information Sciences, 1983, 30(3): 183-224.
DOI: 10.1016/0020-0255(83)90025-7. |
| [21] |
JIANG C, HAN X, LIU G R. A nonlinear interval number programming method for uncertain optimization problems[J].
European Journal of Operational Research, 2008, 188(1): 1-13.
DOI: 10.1016/j.ejor.2007.03.031. |
 2018, Vol. 21
2018, Vol. 21