2. 中国科学院 空间应用工程与技术中心,北京 100094
2. Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China
研发型企业的项目多数不是孤立存在的,而是分成若干子项目或与其他研发项目同时进行,并且研发项目的组合也往往随时间变化。在这种复杂的环境下,该类型企业暴露出诸多问题。由于资源在项目间共享,项目的资源冲突也更加明显,人员负荷不均。当项目进行的不确定性增加和资源的冲突愈加明显时,项目按时交付可能性就随之减小,进而导致企业信誉率的降低和客户群的丧失。研发型企业内设备资源一般比较固定,人力资源是其主要的约束,所以,如何有效地配置动态环境下研发项目的人力资源是一个亟待解决的实际问题。
Blazeiwicz等[1]已经证明资源约束下的项目调度问题为NP-hard问题,无法在多项式时间内得到最优解,所以,近年来的研究也多集中在利用启发式算法求解。在已有的研究中,Alvarez-Valdes等[2]对最大分级位置权重、最多紧后活动等规则等进行了综述与分析,Kolisch R[3-4]分别将最迟完成时间、最坏情形松弛等规则应用于该类问题的求解,取得较好的性能。张连营等[5]将6种常见优先规则预先进行模糊化处理,进而用模糊数的比较方法确定各个工序的优先顺序,然后根据优先顺序对改进后的模糊资源受限多项目调度模型进行调度。启发式规则具有很好的求解效率但是寻优能力差,近年来启发式算法被应用到该类问题中来。Wu等[6]对此问题建模研究,根据学习曲线采用遗传算法求解。王一帆等[7]将模型分解后采用了两阶段算法,部分案例可以达到最优。Goncalves等[8]利用参数化活动进度产生机制,构建了一个新的遗传算法解决该类问题。启发式算法提高了寻优能力,但是其计算效率受问题规模影响大[9]。付芳等[10]采用了基于优先原则的启发式方法给出问题的初始解,再由遗传算法寻优。Anagnostopoulos[11]针对资源均衡配置问题提出了基于模拟退火的超启发式算法,并且还提出了遗传超启发式算法,这些方法在项目管理软件中的使用证明了其有效性。Koulinas[12]使用了基于粒子群算法的超启发式算法求解项目调度问题,该算法中的活动调度采用串行调度生成机制,其活动的优先级由低层的启发式算法修正得来,通过实例测试验证了算法的有效性。
总的来说,针对资源调度问题的研究,已经有了一定的研究成果,但这些搜索算法还是基于某种或者某两种启发式算法的结合解决项目调度时面临的择优问题,超启发式算法的研究相对稀缺。根据不同的优先规则会产生不同的调度方案[13-14],不同的启发式规则下求得的结果差异很大,故本文提出一种基于启发式算法选择启发式规则的超启发式算法,先通过高层启发式策略选择启发式规则,再进一步构造可行解,极大地降低了搜索空间的维度,提高了计算效率,同时保证了解的最优性。本研究理论上为多项目下资源调度问题求解提供了新思路,实践上为更多企业和行业在实施多项目管理时提供理论指导。
1 问题建模 1.1 问题描述研发型企业有多个项目在同时进行,每个项目涉及多个活动,企业为了获取更大的效益,降低总成本,就需要更好地进行项目间的人员调度。本文针对研发型企业中多项目中的人力资源调度问题,建立相应模型。
1.2 问题假设假设只考虑人力资源约束;活动之间只存在“完成—(等待)—开始”的顺序关系,无需额外的准备时间;每个项目开始时间不同,每个项目包括多个活动,且活动间有明确的先后次序;增加某一活动的人数可减少该活动的完成时间;不可预期的项目延误不在考虑范围内。
1.3 模型参数将该问题中的各项活动、相应工作量、人员工资和数量等抽象,定义相应的参数,如表1。模型参数列表中各项目活动的分解及工作量、相关人员的工作量、惩罚费用等认为已知。
| 表 1 模型参数 Tab. 1 Model parameter list |
本文以最小成本为优化目标,包括了人力成本及项目延期惩罚成本。根据以上假设及变量定义,建立模型,描述如下。
1.4.1 变量定义| $\quad\quad{{ {x}}_{{ {k,t}},i,j}} = \left\{ \begin{array}{l}1,{\text{员工}}k {\text{在}}t {\text{时刻在项目}}i {\text{中活动}}j;\\0,{\text{其他。}}\end{array} \right.$ |
| $\quad\quad{{ {L}}_i} = \left\{ \begin{array}{l}1,{\text{项目}}i {\text{的持续时间超过计划工期}};\\0,{\text{其他。}}\end{array} \right.$ |
| $\quad\quad{{ {s}}_{i,j,t}} = \left\{ \begin{array}{l}1,{\text{项目}}i {\text{的活动}}j {\text{在}}t {\text{时刻开始进行}};\\0,{\text{其他。}}\end{array} \right.$ |
| $\quad\quad\min \sum\limits_{{ {k}} = 1}^ {\rm{MR}} {{C_{ {k}}}}\left({\sum\limits_{{ {i}} = 1}^N {\sum\limits_{j = 1}^{{M_i}} {\sum\limits_{{ {t}} = { {1}}}^T {{{ {x}}_{{ {k}},t,i,j}}} } } } \right)+ \sum\limits_{{ {i}} = 1}^N {{\rm{TC}}_i} + \sum\limits_{{ {i}} = 1}^N {{P_i}{L_i}} {\text{。}}$ |
| $ \quad\quad\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{M_I}} {{{ {x}}_{k,i,j,t}}} } {\text{≤}} 1,\forall { {k}},t ;$ | (1) |
| $ \quad\quad\sum\limits_{{ {i}} = { {1}}}^{ {N}} {{{ {x}}_{{ {k,i,j,t}}}}} {\text{≤}} {\rm{MR}},\forall { {t}} ;$ | (2) |
| $\quad\quad\sum\limits_{{ {t}} = { {1}}}^T {{{ {s}}_{i,j,t}}} = 1,\forall i,j;$ | (3) |
| $\quad\quad {{ {s}}_{{ {i,j}} + { {1}}}} {\text{≥}} {{ {f}}_{{ {i,j}}}}{ {,}}\forall {{ {z}}_{i,j}} \in {O_{i,j}};$ | (4) |
| $ \quad\quad{{ {s}}_{i,j}} = \sum\limits_{t = 1}^T {{s_{i,j,t}}} t,\forall i,j ;$ | (5) |
| $ \quad \quad {{ {f}}_{i,j}} = {s_{i,j}} + \sum\limits_{t = { {1}}}^T {{x_{k,i,j,t}}} t,\forall i,j ;$ | (6) |
| $\quad\quad{Q_{{ {i}}.j}} = \sum\limits_{k = 1}^{\rm{MR}} {\sum\limits_{t = 1}^T {{x_{k,i,j,t}}} } {{ {q}}_k},\forall i,j{\text{。}}$ | (7) |
式(1)保证一个员工在同一时间最多只被分配到一个活动中;式(2)保证同一时间各活动中工作的员工数之和不超过可用员工总数量;式(3)表示每项活动必须被完成且只被完成一次;式(4)确保活动被进行的顺序关系,即某一活动的开始时间不得早于所有紧前活动的结束时间;式(5)和式(6)定义了项目中活动的开始时间和结束时间;式(7)保证项目的活动均被完成。
2 蚁群优化的启发式选择算法解决本文提出的人力资源调度问题时,需要为项目中的活动分配人员,也要为人员进行已分配活动的先后排序。由于根据不同的优先规则会产生不同的调度方案,本文采用了启发式选择启发式规则的超启发式算法,即用蚁群算法作为高层搜索策略对低层的启发式规则进行搜索。
2.1 算法流程Step1 初始化所有参数值、信息素矩阵、等待列表等。
Step2 选择规则,每只蚂蚁分别进行启发式规则的选择。
蚂蚁为每个项目活动选择人员分配规则。
蚂蚁为每个人员选择项目活动分配规则。
Step3 构造调度解,根据所选择的规则,独立构造一个可行解,并计算该可行解的目标函数值。
Step4 更新相应的信息素。
Step5 到达预设迭代次数后结束算法。
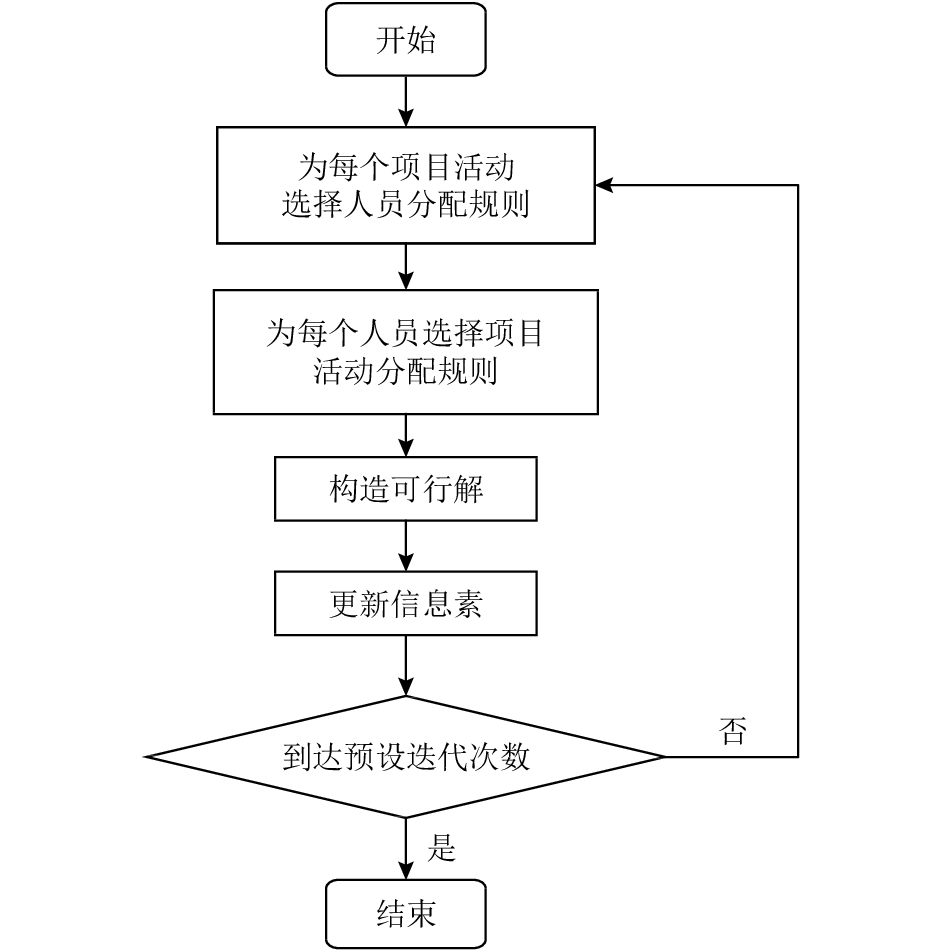
算法流程图如图1。
|
图 1 算法流程 Fig. 1 Algorithm flow chart |
当每个项目开始进行或项目中上一项活动已经完成需要进行下一项活动时,需要为即将进行的项目活动选择人员,由于可用人员并不唯一,故蚂蚁需要选择启发式规则并使用该规则为项目活动选择人员。同样,当几项项目活动都分配给一个人员时,人员也需要决定这几项活动执行的先后顺序,这时同样就要根据启发式规则进行选择。
基于不同的启发式规则,项目活动从人员列表中选择人员,人员从可进行的项目活动中选择活动,从而将部分进度逐步扩展为完全进度。表2、表3为本文采用的启发式规则。
| 表 2 项目活动分配的启发式规则集 Tab. 2 Heuristic rule set for project activity distribution |
| 表 3 人员选择项目活动的启发式规则集 Tab. 3 Heuristic rule set for project activity selection |
项目活动分配的启发式规则信息素结构:为每个项目定义
人员选择项目活动的启发式规则信息素结构:定义
当每个项目开始进行或项目中上一项活动已经完成需要进行下一项活动时,需要为即将进行的项目活动选择人员,由于可用人员并不唯一,故蚂蚁需要选择启发式规则并使用该规则为项目活动选择人员。
当蚂蚁选择启发式规则时,首先根据项目活动分配规则信息素矩阵上的信息素浓度计算每个启发式规则被选中的概率,该概率的计算方式如式(8),基于此概率采用较经典的轮盘赌方式选择一个规则,作为该项目活动的分配规则。
| $\quad\quad P({\gamma _{{ {j}},a}}) = \displaystyle\frac{{{\gamma _{{ {j}},a}}}}{{\sum\limits_{k = 1}^{{K_{ {a}}}} {{\gamma _{{ {j}},k}}} }}{\text{。}}$ | (8) |
由于本文采用的是“启发式选择启发式”的算法,搜索空间并不是调度解而是启发式规则集,故每个项目活动与每个人员的规则确定后,需要进行规则解码。
人员的活动等待列表结构:定义
解的结构:定义
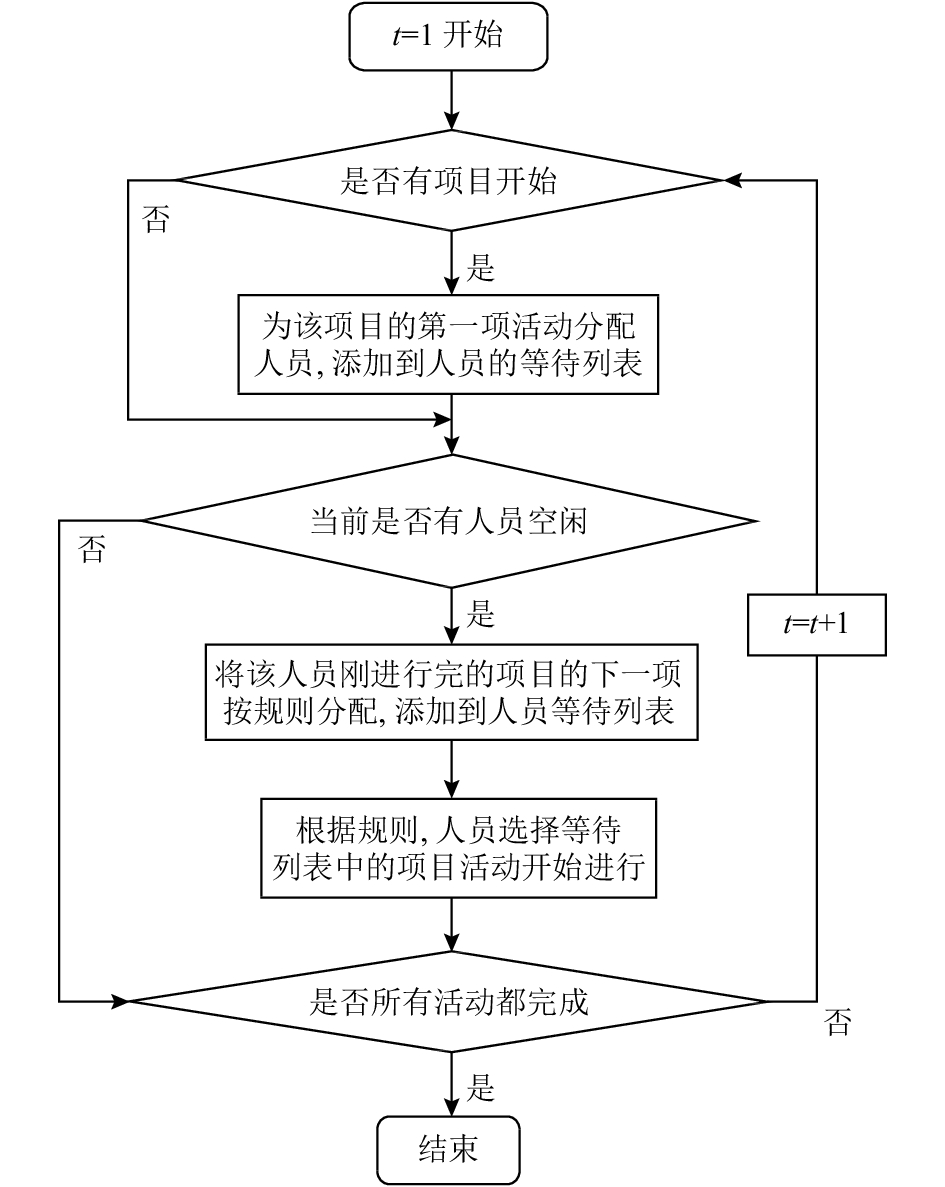
构造可行解的流程图如图2所示。
|
图 2 构造可行解流程图 Fig. 2 Flow chart for feasible solution construction |
每次迭代结束后,更新相应的信息素矩阵。若候选分配规则集中第a个候选规则被选为活动j的分配规则,则信息素更新方式为
| $\quad\quad{\gamma _{{ {j}},a}} = (1 - \rho ) \cdot {\gamma _{{ {j}},a}} + \rho \cdot Q{ {/}}{\rm {sumcost}}{\text{。}}$ | (9) |
式(9)中,
为了验证该算法的性能,本文设计了不同规模的测试问题进行仿真实验。仿真使用MATLAB(R2014a)软件,运行在Core i7,4 GB内存的PC机上。
3.1 测试问题设计通过对Kolisch等[15]的ProGen生成器进行适当调整,生成适应此特定模型的实验数据。其中,活动顺序关系的生成与ProGen一致,各组模型参数都是在给定范围内随机生成(见表4)。测试问题示例如表5。
| 表 4 模型参数生成标准 Tab. 4 Generation standard of model parameter |
| 表 5 测试问题(示例) Tab. 5 Test problems (examples) |
蚁群算法中参数设置对结果的影响比较大,现对于算法中重要的参数信息素挥发强度
|
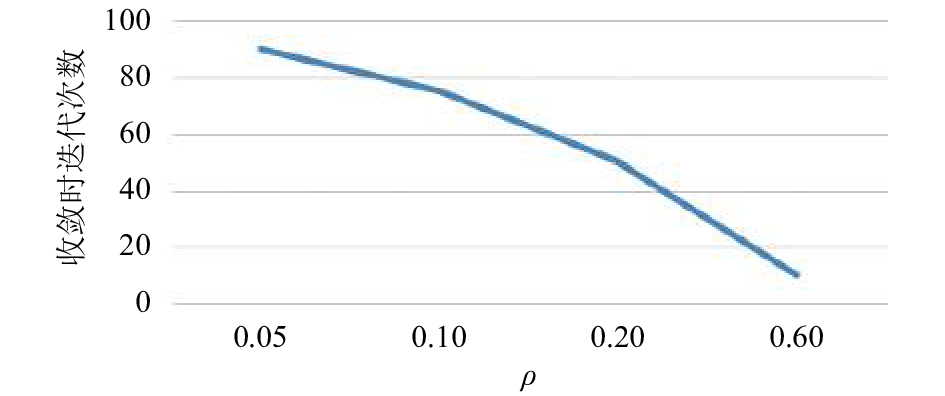
图 3 参数多组取值实验结果 Fig. 3 Experimental results of parameter with multi-group values |
从图3中可以看出,如果信息素挥发强度过大,则会使算法收敛过快,如果信息素挥发强度太小,则每次迭代结果对信息素的正反馈弱,影响算法搜索效率。本文将参数设定为
基于蚁群优化的超启发式算法是用蚁群算法作为高层策略搜索低层启发式规则,进而构造可行解。为了验证算法的有效性,选用同一组数据,分别运行10次,将该算法运行结果与采用文中提到的几种启发式规则的运行结果进行比较。以本文算法作为基准,其他几组所得值与之相除得到相对比例,如表6。
| 表 6 对比实验数据结果 Tab. 6 Comparison of experimental data |
从表6可以看出,使用单一的启发式规则,结果相差很大。组合的启发式规则寻优能力增强,但是会因为特定的规则限制降低了人员利用率,从而使得工期一般较长。本文提出的蚁群优化的超启发式算法由于是多种规则的动态选择与组合,运行时间没有减少但是求得结果更优,整体表现出更好的搜索性能。
4 结语本文将现实问题抽象建模,以考虑项目延期惩罚成本的总成本为目标函数,建立了研发型企业多项目人力资源调度的模型。根据本文的研究问题,通过比较多种高层启发式策略,选择蚁群算法作为高层策略,将文献中广泛使用的多种启发式规则总结,这些启发式规则作为低层被搜索的规则集。本文提出基于蚁群优化的超启发式算法进行求解,将蚁群算法作为高层策略搜索低层启发式规则,设计了信息素结构、信息素更新方法、候选规则集和构造可行解流程等,进一步确定算法求解的总流程。最后通过对实验环境配置和测试问题设计,进行了仿真实验。本文提出的算法由于是多种规则的动态选择与组合,搜索空间变小,表现出较好的搜索性能,实验验证了该算法的有效性。通过本文研究为研发型企业多项目人力资源调度问题提供了新的求解思路与方法,并且为企业实施多项目管理提供有力的理论指导,有利于优化企业内部人力资源的配置。
此类问题的研究还可以进一步深入,可以考虑在人员受限时动态增加所需人员,以及考虑将项目的几项活动组合分配,更贴近实际问题。同时在求解方法上,可以通过动态生成新的启发式规则扩充现有的启发式规则集,提升寻优性能。
| [1] |
BLAZEWICZ J, LENSTRA J K, KAN A H G R. Scheduling subject to resource constraints: classification and complexity[J].
Discrete Applied Mathematics, 1983, 5(1): 11-24.
DOI: 10.1016/0166-218X(83)90012-4. |
| [2] |
ALVAREZ-VALDES R, TAMARIT J M. Heuristic algorithms for resource-constrained project scheduling: a review and an empirical analysis[J].
Advances in project scheduling, 1989, 15(2): 125-134.
|
| [3] |
KOLISCH R. Serial and parallel resource-constrained project scheduling methods revisited: theory and computation[J].
European Journal of Operational Research, 1996, 90(2): 320-333.
DOI: 10.1016/0377-2217(95)00357-6. |
| [4] |
KOLISCH R. Efficient priority rules for the resource-constrained project scheduling problem[J].
Journal of Operations Management, 1996, 14(3): 179-192.
DOI: 10.1016/0272-6963(95)00032-1. |
| [5] |
张连营, 李彦伟, 孙若昕. 基于优先规则的模糊资源受限多项目调度[J].
工业工程, 2014, 17(3): 13-17.
ZHANG Lianying, LI Yanwei, SUN Ruoxin. Fuzzy resource constrained multi-project scheduling based on precedence rules[J]. Industrial Engineering, 2014, 17(3): 13-17. |
| [6] |
WU M C, SUN S H. A project scheduling and staff assignment model considering learning effect[J].
The International Journal of Advanced Manufacturing Technology, 2006, 28(11): 1190-1195.
|
| [7] |
王一帆, 刘士新, 陈迪. 求解多技能人力资源约束的项目调度问题的两阶段算法[J].
东北大学学报(自然科学版), 2014, 35(2): 184-189.
WANG Yifan, LIU Shixin, CHEN Di. The two stage algorithm for solving the project scheduling problem of multi-skilled human resource constraints[J]. Journal of Northeastern University(Natural Science Edition), 2014, 35(2): 184-189. DOI: 10.3969/j.issn.1005-3026.2014.02.008. |
| [8] |
GONÇALVES J F, MENDES J J M, RESENDE M G C. A genetic algorithm for the resource constrained multi-project scheduling problem[J].
European Journal of Operational Research, 2008, 189(3): 1171-1190.
DOI: 10.1016/j.ejor.2006.06.074. |
| [9] |
王乐衡. 考虑多元设备类型的超启发式跨单元调度方法[D]. 北京: 北京理工大学, 2015
WANG Leheng. Hyper-heuristic method cross unit scheduling considering multiple device types[D]. Beijing: Beijing Institute of Technology, 2015 |
| [10] |
付芳, 周泓. 多项目人力资源调度实证研究[J].
管理工程学报, 2011, 25(3): 73-77.
FU Fang, ZHOU Hong. An Empirical Study on multi-project human resource scheduling[J]. Journal of Management Engineering, 2011, 25(3): 73-77. DOI: 10.3969/j.issn.1004-6062.2011.03.013. |
| [11] |
ANAGNOSTOPOULOS K P, KOULINAS G K. A genetic hyperheuristic algorithm for the resource constrained project scheduling problem[C/OL].(2010-07-18). https://ieeexplore.ieee.org/document/55864881
|
| [12] |
KOULINAS G, KOTSIKAS L, ANAGNOSTOPOULOS K. A particle swarm optimization based hyper-heuristic algorithm for the classic resource constrained project scheduling problem[J].
Information Sciences, 2014, 277(2): 680-693.
|
| [13] |
PONSTEEN A, KUSTERS R J. Classification of human- and automated resource allocation approaches in multi-project management[J].
Procedia - Social and Behavioral Sciences, 2015, 194: 165-173.
DOI: 10.1016/j.sbspro.2015.06.130. |
| [14] |
BHASKAR T, PAL M N, PAL A K. A heuristic method for RCPSP with fuzzy activity times[J].
European Journal of Operational Research, 2011, 208(1): 57-66.
DOI: 10.1016/j.ejor.2010.07.021. |
| [15] |
KOLISCH R, SPRECHER A, DREXL A. Characterization and generation of a general class of resource-constrained project scheduling problems[J].
Management Science, 1995, 41(10): 1693-1703.
DOI: 10.1287/mnsc.41.10.1693. |
 2018, Vol. 21
2018, Vol. 21