道路交通网络作为交通运输的基础设施,因突发事故、灾害天气、节日游行或恐怖袭击等原因,容易造成路网中多个重要节点拥堵,而这些拥堵节点可能再次引起路网中其他关联路段或交叉口出现连锁反应,如此便形成级联失效现象。随着社会经济的快速发展与交通需求的迅猛增长,道路交通网络发生级联失效的可能性也越来越大。因此,基于城市复杂网络特性,进行多节点拥堵的道路网级联失效仿真研究,对突发条件下的城市道路交通管理与控制具有重要意义。
目前,关于复杂网络级联失效问题的研究主要集中在3个方面:级联失效模型、级联失效的影响因素以及对级联失效的控制策略。在模型研究方面,经典的容量—负载模型在城市道路交通中应用最广。21世纪初,Motter等[1]最先考虑到电网中节点与负载的线性关系,提出了容量—负载模型(ML模型)。随后Wu等[2]根据道路交通的双层网络特征,在ML模型基础上建立了应用于城市交通网络的级联失效模型。在影响因素方面,Albert等[3]利用随机攻击与蓄意攻击两种方式对无标度网络进行实验,根据网络效率指标的变化,发现路网具有“鲁棒且脆弱”的特性。国内的王正武等[4-5]基于道路交通的级联失效现象改进了路网节点重要度的测算方法,随后采用正交实验法完成了交通网络级联失效的影响源识别。而在控制策略方面,王正武等[6]在城市道路交通网络的双层网络特性基础上,进行了路网级联失效后关闭策略方面的研究。
由于我国对于城市道路网络的级联失效研究才刚刚起步,虽然在级联失效模型与影响因素识别等方面有了初步的成果,但是对突发多节点拥堵时的路网鲁棒性分析,量化多节点失效条件下的路网级联失效特征等方面还有待补充与完善。故本文首先将城市道路网转化为几何拓扑网络,采用2种攻击方式从路网中删除重要节点,通过连通度、圈数率等鲁棒性评价指标衡量路网通行效率,进而获得路网在最不利条件下的最大节点失效比例,再基于双层网络配流模型设计路网拥堵度的计算方法,最后利用Transcad 4.5等仿真软件对成都市某地的中等规模路网进行仿真实验,验证该研究方法的可行性与实用性。
1 城市道路网络特性分析城市道路交通网一般由路段和交叉口2大元素构成,在进行网络特性分析时,常常对这2类元素采用边或节点进行表示。为了能直观反映路网拓扑结构,本文选用原始法抽象现实路网。对于图中要素点、边的特性,主要通过点的度、点或边介数、网络直径、平均路径长度、聚类系数、有效性和网络直径[7]等指标描述。在此,本文仅对与节点相关的“点的度”和“点介数”2个特性指标进行说明。
1.1 路网节点的指标说明 1.1.1 节点度节点度指与节点i相连的边数量。一个节点的度越高说明该点在路网中的重要性越显著。计算公式为
| $\quad\quad {k_i} = \sum\limits_{j \in N} {{e_{ij}}} ,\; i \in N{\text{。}} $ | (1) |
式中,
点介数指整个路网中经过该节点的最短路径的数量比例。该指标可衡量节点在整个路网中的主要程度,对于基于最短路径的交通网络配流具有重要意义。计算公式为
| $\quad\quad {B_n} = \sum\limits_{i {\text{≥}} j} {\frac{{{d_{inj}}}}{{{d_{ij}}}}} ,\; i,j \in N{\text{。}} $ | (2) |
式中,
相较于单一节点拥堵,突发事件由于其范围广、成因复杂与不可预知等特点,更容易在路网造成多处节点并发拥堵。
根据Albert等[3]的研究结果:城市道路网具有一定程度的鲁棒性与耐受性。故本文对城市路网遭受攻击后的网络特性变化进行研究,试从中观层面将多节点拥堵问题转化为对路网的鲁棒性分析。现对节点的攻击方式定义如下[7]。
1) 基于节点度的攻击方式:按照节点度的大小依次删除网络中的节点;
2) 基于节点介数的攻击方式:按照点介数的大小依次删除网络中的节点。
设
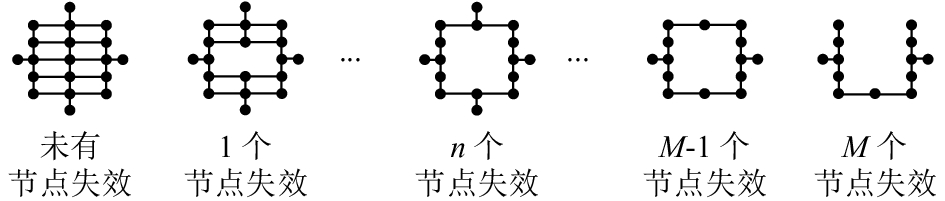
|
图 1 多节点失效后路网拓扑结构变化 Fig. 1 Road network topology changes after multi-node failure |
从图1可以得到,根据节点特性指标(节点度或点介数的大小)对路网进行攻击,得到路网濒临瘫痪的临界条件(最多
节点的突发拥堵具有随机性,当重要程度较低的节点发生拥堵,其对路网影响较小。因此,如果逐次攻击路网中节点度或点介数较大的节点,则该条件下得到的节点失效数
现有的鲁棒性评价指标主要有连通度、最大连通子图的相对大小与圈数率[7]等。
1.3.1 连通度连通度是指路网中实际边数目与原有最大边数目的比值。在网络遭受突发拥堵的攻击时,突发拥堵节点的连通度越大,说明网络攻击导致的该点失效对路网鲁棒性影响也越显著。其计算公式为
| $\quad\quad \gamma = \frac{{|D|}}{{3|{V_d}| - 6}}{\text{。}} $ | (3) |
式中,
最大连通子图是指以最少的边把网络中的所有节点连接起来的子图。其大小等于最大连通子图中节点的数目与网络中节点数目之比,反映了网络在遭受攻击后的破坏程度。其计算公式为
| $\quad\quad S = \frac{{|{V_d}^\prime |}}{{{V_d}}}{\text{。}} $ | (4) |
式中,
圈数是指网络破坏时能提供线路的数量,圈数率是圈数与网络中节点数目的比值。该指标可以衡量城市道路网在遭受突发拥堵的攻击时提供其他替代路线的能力。其中,圈数的计算公式为
| $ \quad\quad\mu = |D| - |{V_d}| + 1{\text{。}} $ | (5) |
圈数率的计算公式为
| $ \quad\quad{\mu ^{\rm{T}}} = \frac{\mu }{{|{V_d}|}}{\text{。}} $ | (6) |
以上3个指标可衡量城市道路网络从一个节点失效逐步到多节点(最多
级联失效(cascading failure)是真实网络中的少数几个节点并发失效导致的连锁反应现象[4]。本文基于城市道路网络鲁棒性分析,筛选出路网重要节点集合,对集合内的节点进行攻击,模拟路网中多节点并发拥堵的情况,再引用双层网络模型刻画城市交通系统的级联失效现象。本文采用的级联失效模型是负荷—容量模型,如图2所示。
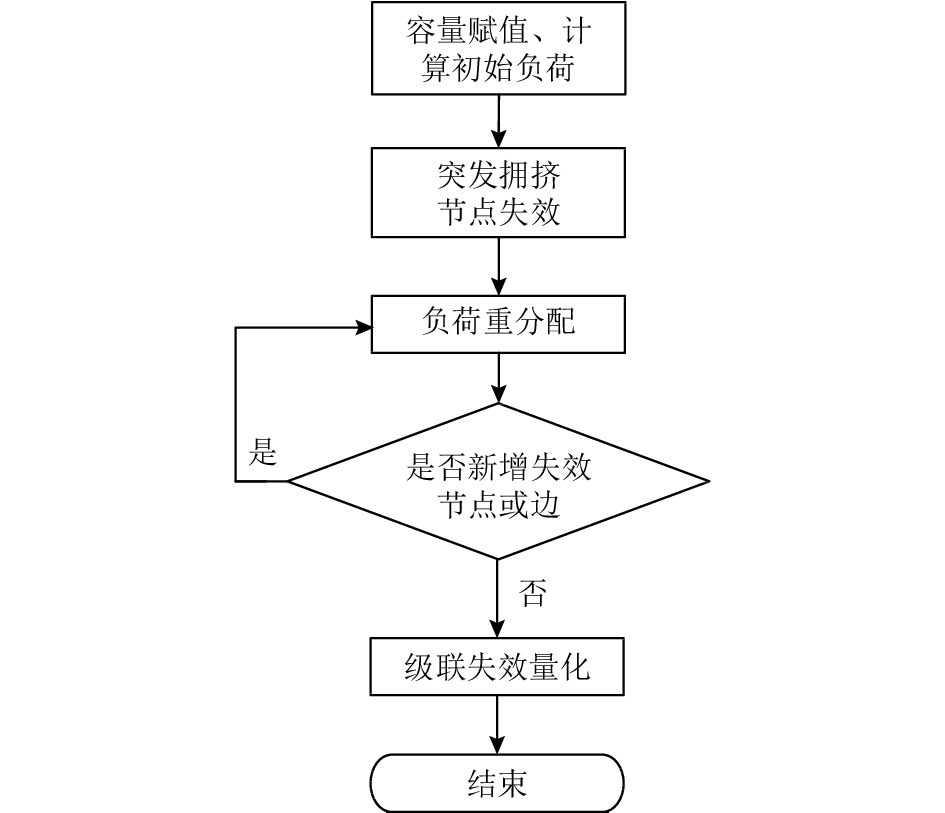
|
图 2 交通网络级联失效模型示意图[4] Fig. 2 Traffic network cascade failure model diagram |
上述模型考虑了道路交通网络所具有的双层网络特性。其中,下层网络为实际路网,节点表示交叉口,边表示路段;上层网络为出行网络,网络节点为交通起讫(OD)点,边表示出行径路选择[7]。
上、下层出行网络相互影响:上层出行网络通过实时的交通分配,决定下层道路网络节点、边的负荷;下层道路网发生相应的阻抗变化,将影响上层出行者的路径选择行为。
故设道路网络
| $\quad\quad M {\text{≤}} n \times \eta {\text{。}} $ | (7) |
利用节点度、点介数等指标对
Step 1 初始化。根据路网情况对
Step 2 道路阻抗集合
| $ \begin{array}{l} \quad\quad{t_{ij}}( x ) = {t_{ij}}( 0 )\left[ {1 + 0.15 {{\left( {\displaystyle\frac{{{q_{ij}}\left( x \right)}}{{{c_{ij}}\left( x \right)}}} \right)}^4}} \right],\\ \quad\quad{t_{ij}} \in T,\;{q_{ij}}\left( x \right) \in Q,\;{c_{ij}}\left( x \right) \in C {\text{。}} \end{array}$ | (8) |
式中,
Step 3 边的容量更新方法为
| $ \quad\quad{c_{ij}}\left( {x + 1} \right) = \left\{ \begin{gathered} {c_{ij}}\left( 0 \right)\frac{{{c_j}\left( x \right)}}{{{q_j}\left( x \right)}},\quad {\text{若}}\;{c_j}\left( x \right) {\text{≤}} {q_j}\left( x \right) ; \\ {c_{ij}}\left( 0 \right),\quad \quad \quad \;\;{\text{其他。}} \hfill \\ \end{gathered} \right. $ | (9) |
Step 4 路网级联失效的量化指标
| $\quad\quad J = \sum\limits_{ij} {{q_{ij}}\left( x \right){t_{ij}}\left( x \right)} /\sum\limits_{ij} {{q_{ij}}\left( 0 \right){t_{ij}}\left( 0 \right)} {\text{。}} $ | (10) |
依据上述算法,在初始配流的基础上,通过删除相应数量的节点,按照式(8)、式(9)更新路段
本文运用Transcad 4.5地理信息系统,构建路网的点层、线层与面层[7],初始化道路基本阻抗和OD流量对,对成都市某地一个包含54个节点、92条边的中等规模路网
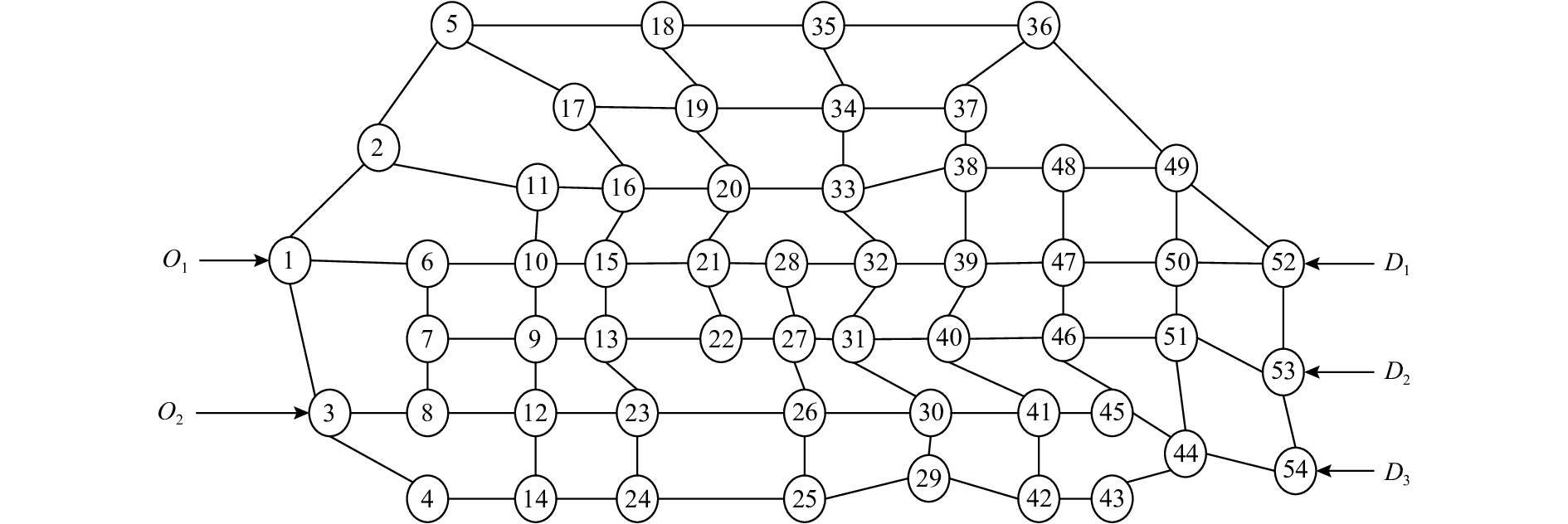
|
图 3 仿真路网几何拓扑结构 Fig. 3 Simulation of road network geometry topology |
首先分析图3中54个节点的路网特性指标:节点度与点介数。利用Matlab 2012a分别按式(1)与式(2)进行计算,其结果如图4所示。
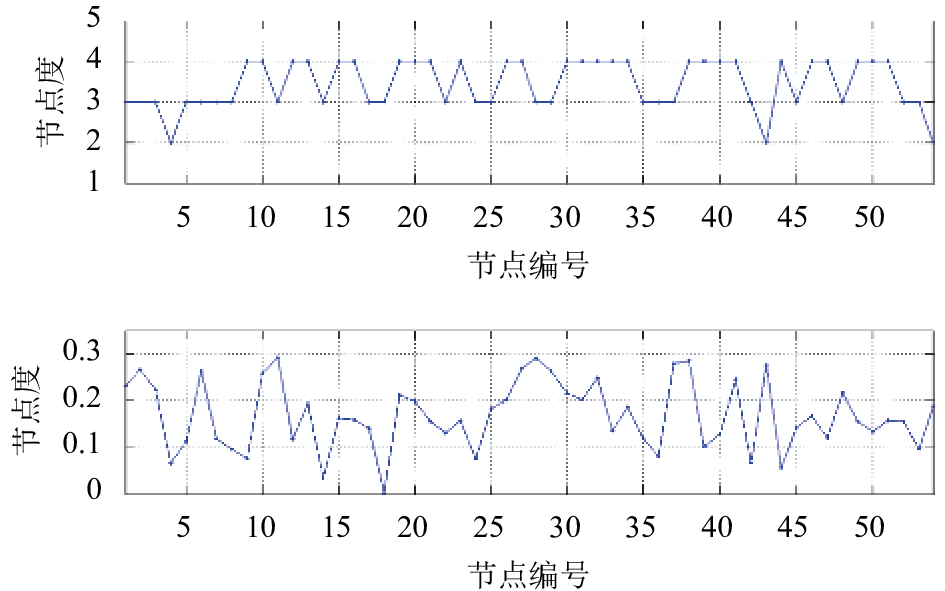
|
图 4 路网中54个节点的路网特性指标 Fig. 4 Road network characteristics of 54 nodes in the road network |
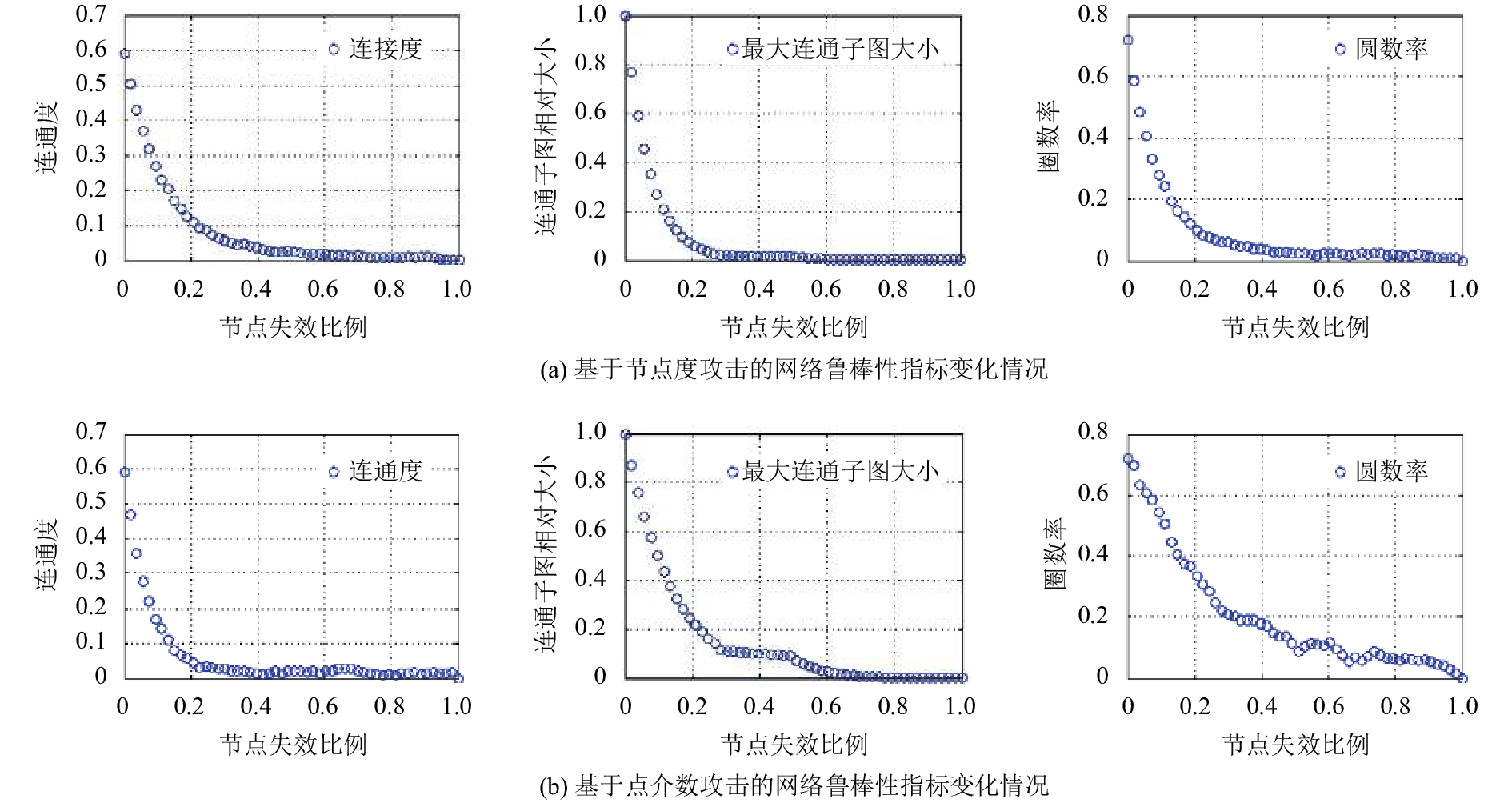
从图4可知,各节点的路网特性指标存在明显不同。本文按两种攻击方式,逐步将节点从路网中删除,并利用Matlab 2012a按照式(3)、式(4)和式(6)分别计算得到仿真路网的连通度、最大连通子图的相对大小和圈数率3项指标的变化情况,如图5所示。
|
图 5 路网鲁棒性指标变化 Fig. 5 Changes in the road network robustness index |
图5(a)为基于节点度大小对节点攻击时,网络鲁棒性指标的变化情况。从图中可以看出,当网络节点失效比例分别达到21.2%、16.8%与20.0%时,3个指标值大小达到原有鲁棒性指标值10%以下,濒临瘫痪状态。故本文综合考虑鲁棒性指标变化情况,取上述3指标节点失效比例的均值[8-9]作为该攻击方式下的节点最大失效比例
图5(b)为点基于介数大小对节点攻击时,网络鲁棒性指标的变化情况。从图中可以看出,当网络节点失效比例分别达到15.7%、26.7%与48.1%时,3个指标值大小达到原有鲁棒性指标值10%以下,濒临瘫痪状态。同理,取上述3指标节点失效比例的均值作为该攻击方式下的节点最大失效比例
综合考虑节点度和点介数这两种攻击方式对仿真路网鲁棒性指标的影响,得到量化路网鲁棒性的最大节点失效比例[8-9]
进一步地,按式(7)可计算出路网允许失效的最大节点数
| $\quad\quad N' = \left\{ {2,4,11,13,26,27,28,30,38,41,45} \right\}{\text{。}} $ |
本文假设仿真道路网络
| $\quad\quad \begin{array}{l} {q_{1 \to 52}} = {q_{1 \to 53}} = {q_{1 \to 54}} = 20\;000\; {\rm{pcu/h}} , \\ {q_{3 \to 52}} = {q_{3 \to 53}} = 15\;000\;{\rm{pcu/h}},\\ {q_{3 \to 54}} = 10\;000\;{\rm{pcu/h}}{\text{。}} \end{array}$ |
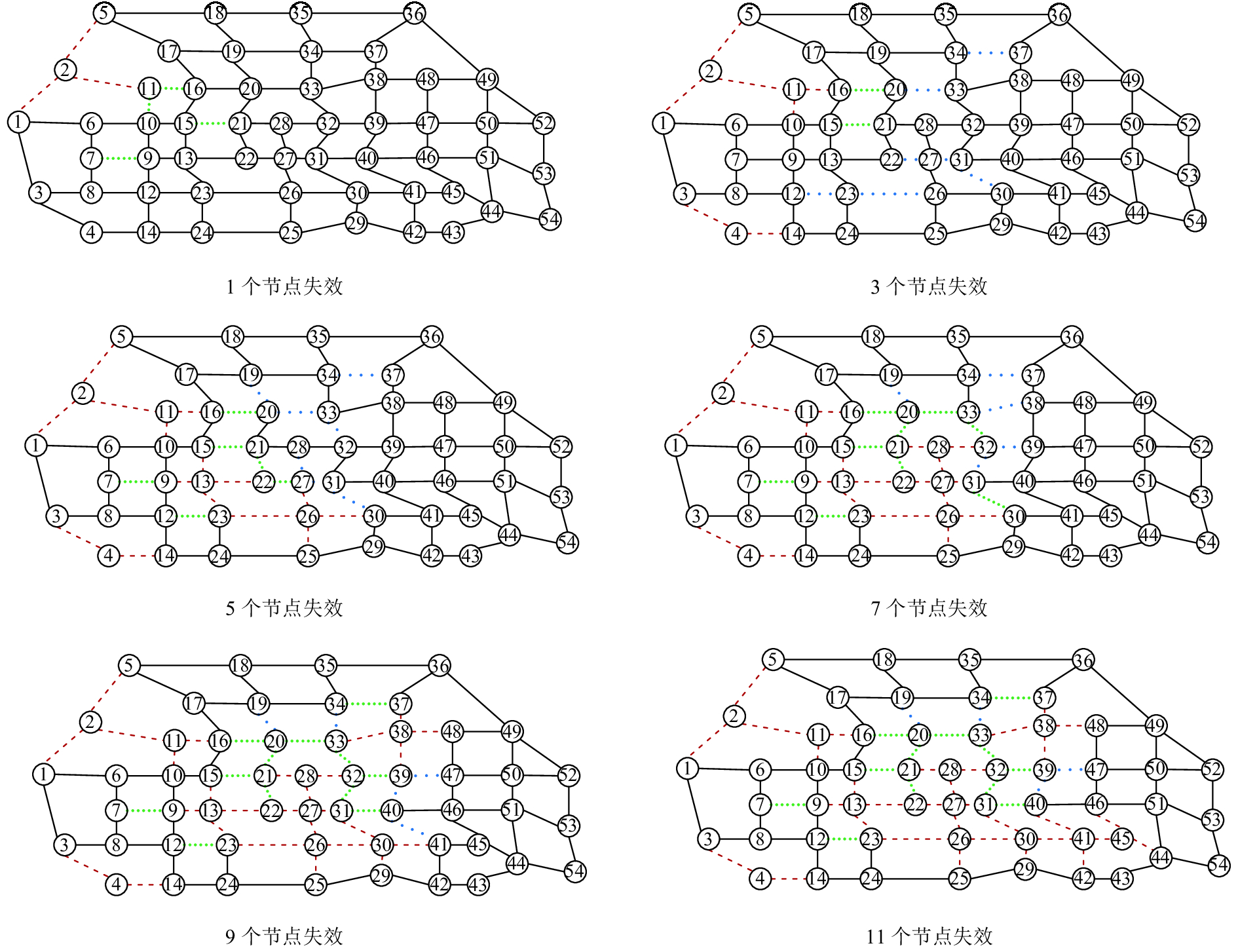
令各边初始流量均为1 064 pcu/h,在Transcad 4.5地理信息系统里,选用UE法完成仿真路网
|
图 6 仿真路网多节点级联失效图 Fig. 6 Cascaded failure diagram of multiple nodes in simulation road network |
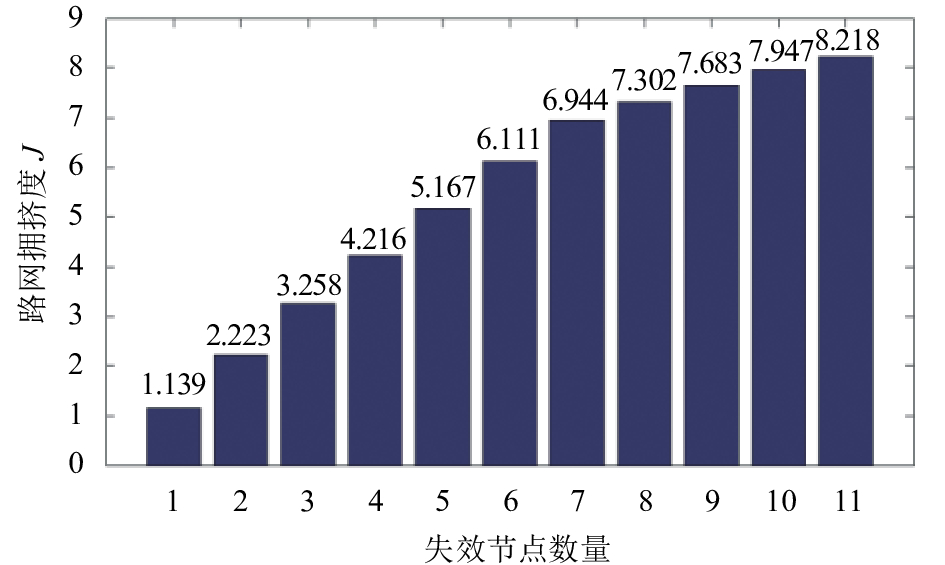
路网拥堵度
|
图 7 多节点失效后的路网拥堵度 Fig. 7 Road network congestion degree after multi-node failure |
从图7可以看出,当失效节点数量在7个以下时,路网级联失效后的拥堵水平变化比较显著,而超过7个节点后,路网的拥堵水平变化趋于稳定。这说明:1) 相比于单一节点拥堵,多节点拥挤导致的级联失效会对路网的通行能力造成更为显著的影响,随着失效节点数目的增加,路网拥挤水平也越高;2) 当路网节点失效数目到达一定数量时,路网整体的拥挤水平趋于稳定,并逐渐到达其鲁棒性的极限,濒于网络瘫痪状态。
4 结语本文基于城市复杂网络分析,构建了多节点并发拥堵条件下的路网级联失效模型并通过计算路网拥堵度完成该情景下的级联失效仿真研究。实验结果表明,多节点拥堵条件下,路网的级联失效现象更为显著;而当节点失效比例到达一定程度时,整个路网将渐渐处于一个临界状态,其拥堵水平趋于稳定。进一步研究工作是:1) 将多节点拥堵扩展到多个节点或路段拥堵的一般情况;2) 分析路网中出行者行为对网络级联失效的影响;3) 研究路网中多节点拥堵引发级联失效后的交通控制策略。
| [1] |
MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[J].
Physical Review E, 2002, 66(6): 065102.
DOI: 10.1103/PhysRevE.66.065102. |
| [2] |
WU Jianjun, GAO Ziyou, and SUN Huijun. Effects of the cascading failures on scale-free traffic networks[J].
PhysicaA, 2007, 378(2): 505-511.
DOI: 10.1016/j.physa.2006.12.003. |
| [3] |
ALBERT R, JEONG H, BARABASI A L. Error and attack tolerance of complex networks[J].
Nature, 2000, 406(6794): 378-382.
DOI: 10.1038/35019019. |
| [4] |
王正武, 况爱武, 王贺杰. 考虑级联失效的交通网络节点重要度测算[J].
公路交通科技, 2012, 29(5): 96-101.
WANG Zhengwu, KUANG Aiwu, WANG Hejie. Calculation of traffic network node importance of cascading failure[J]. Highway Traffic Technology, 2012, 29(5): 96-101. DOI: 10.3969/j.issn.1002-0268.2012.05.016. |
| [5] |
王正武, 陈小兰, 李常乐. 道路交通网络级联失效影响源辨识[J].
中国公路学报, 2015, 28(10): 98-104.
WANG Zhengwu, CHEN Xiaolan, LI Changle. Identifying influence sources of cascading failure for road traffic network[J]. China Journal of Highway and Transport, 2015, 28(10): 98-104. DOI: 10.3969/j.issn.1001-7372.2015.10.013. |
| [6] |
王正武, 王杰, 黄中祥. 控制城市道路交通网络级联失效的关闭策略[J].
系统工程, 2015, 28(10): 98-104.
WANG Zhengwu, WANG Jie, HUANG Zhongxiang. Closing strategies to control cascading failure in urban road traffic networks[J]. System Engineering, 2015, 28(10): 98-104. DOI: 10.3969/j.issn.1001-2362.2015.10.075. |
| [7] |
赵国锋, 苑少伟, 慈玉生. 城市路网的复杂网络特性和鲁棒性研究[J].
公路交通科技, 2016, 33(1): 119-124.
ZHAO Guofeng, YUAN Shaowei, CI Yusheng. Study on complex network characteristics and robustness of urban road network[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 119-124. DOI: 10.3969/j.issn.1002-0268.2016.01.018. |
| [8] |
杨露萍, 钱大琳. 道路交通网络脆弱性研究[J].
交通运输系统工程与信息, 2012, 12(1): 105-110.
YANG Luping, QIAN Dalin. Research on vulnerability of road traffic network[J]. Journal of Transportation Systems Engineering and, 2012, 12(1): 105-110. DOI: 10.3969/j.issn.1009-6744.2012.01.016. |
| [9] |
SCOTT D M, NOVAK D C, AULTMAN-HALL L, et al. Network robustness index: a new method for identifying critical links and evaluating the performance of transportation networks[J].
Journal of Transport Geography, 2006, 14(3): 215-227.
DOI: 10.1016/j.jtrangeo.2005.10.003. |
| [10] |
SULLIVAN J L, NOVAK D C, AULTMAN-HALL L, et al. Identifying critical road segments and measuring system-wide robustness in transportation networks with isolating links: a link-based capacity-reduction approach[J].
Transportation Research Part A, 2010, 44(5): 323-336.
|
| [11] |
D’ESTE G M, TAYLOR M A P. Network vulnerability: an approach to reliability analysis at the level of national strategic transport networks[C]. New York: Pergamon Press, 2003:23-44
|
| [12] |
JENELIUS E, PETERSEN T, MATTSSON L. Importance and exposure in road network vulnerability analysis[J].
Transportation Research Part A, 2006, 40(7): 537-560.
|
| [13] |
吴建军, 高自友. 城市交通复杂性: 复杂网络方法及其应用[M]. 北京: 科学出版社, 2010:24-30
|
| [14] |
陆化普, 黄海军.交通规划理论研究前沿[M]. 北京: 清华大学出版社, 2007
|
 2018, Vol. 21
2018, Vol. 21