2. 宁波大学 附属医院,浙江 宁波 315020
2. The Affiliated Hospital of School of Medicine, Ningbo University, Ningbo 315020, China
突发事件通常会在短时间内为医院带来紧急病人救治需求的激增。医院激增能力(surge capacity)被定义成突发事件发生后,响应这些突然增加的救治需求的能力,不仅包括现有资源能力的充分利用,还包括快速扩充补充资源的能力[1]。针对不同类型公共事件造成的病人救治需求,运用不同的激增能力策略(资源数量、扩充方式等)会对病人和医院产生不同的救护效果和成本效率。在突发事件发生前,做好相关医务人员储备规划工作,是医院应急资源配置研究中不可忽略的一部分。
目前针对医院应急管理中的资源配置研究,国内主要以定性研究为主[2-4],在定量研究方面大部分学者主要通过预测或者计算机仿真的方式进行。Kumar等[5]建立医院病床需求预测模型,并通过这个模型对B2和C级病床进行预测,以此提升了医院病床的使用效率;Liu等[6]利用风险分析的方法,建立了一个基于事件的医院应急需求预测模型;Joshi Amita等[7]基于Arena平台研究了恐怖袭击事件中急诊室面对较多患者时所需要的额外资源数量;Wang等[8]则使用了基于agent 仿真的方法来对大规模伤亡事件的应急医疗响应进行研究,分析了不同应急资源配置对病人总体死亡率的影响;倪玉丽[9]和何国光[10]构建了基于系统动力学的仿真模型,并基于最小化病人死亡率和系统平均逗留时间建立资源分配方案。综合发现,现有应急资源配置研究大多针对事件发生后的应急响应。由于突发公共事件的突发性和紧急性,一旦事件发生,临时响应策略再有效,也只能是将现有资源充分利用,不计成本,临时调配。若能从计划准备层面上就开始统筹优化资源,结合成本和效率长远考虑,会更加科学有价值。进一步考虑储备规划的针对性,应具体分析不同类型及规模的突发公共事件下的医院激增能力储备,才能使应急准备的方案更落地可行。基于此,本文以汶川地震为案例,统计该类规模地震事件下伤患的医疗需求特点,结合文献中某三甲医院接受伤员情况,以此为基础建立医院应急救治离散事件系统仿真模型。特别考虑了在地震这类大规模突发事件下,若伤患因医院无法快速实现激增能力,而导致伤员无法及时救治,造成病人病情加剧的实际情况,在离散事件系统模型上引入了病人病情递进模式,增加了仿真模型的真实性。在该模型基础上,结合某三甲医院现实情况,进行医院储备规划的研究。
1 地震下病人模型研究 1.1 病人源伤情特点分析地震是一类典型的大规模突发事件,通常会为医院带来巨大的紧急伤员救治压力。在相关统计中,地震伤员主要以创伤为主,其中骨折占第一位,软组织损伤占第二位,其余主要是内脏挤压伤等。伤员受伤的部位主要是四肢,头部以及胸部[11]。在伤员伤情严重程度上,周继红等[12]通过统计多家医院伤员数据,得出5 063例汶川地震伤员损伤严重程度AIS(abbreviated injury scale)分值分布,其中AIS评分等级从1至5的伤员分别占比约为37%、33%、28%、1%和1%。
1.2 伤员病情递进的研究通常紧急伤员如果没有得到及时的治疗,会出现病情恶化的情况,且病情越严重,恶化情况往往也越快。因此医院通常会对刚入院的伤员伤情进行快速分诊,以确保紧急度高的伤员能优先治疗。在现阶段医院使用最广泛的评判标准是利用AIS评分确立伤员伤情严重等级。AIS各评分等级与存活概率如表1所示[13](仅考虑身上只有一处受伤时)。
| 表 1 AIS与存活概率关系 Tab. 1 Relationship between AIS and survival probability |
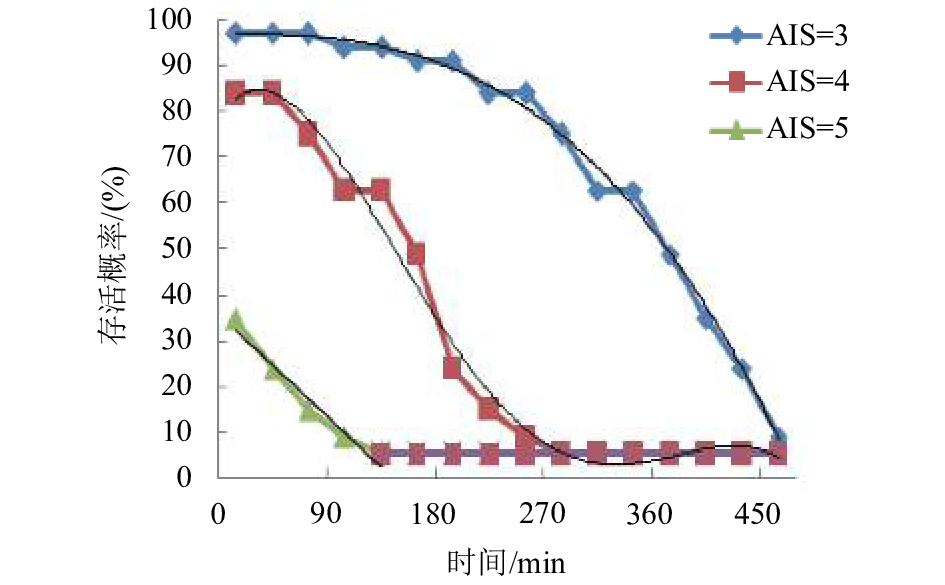
为了能将病人恶化率进行量化分析,Sacco等[14]利用RPM指数确立了各分值与存活概率的关系以及RPM指数恶化的情况。RPM是综合了呼吸频率(respiratory rates),脉搏次数(pulse rate)以及最佳运动反应(best motor response)3项指标得出的一个分值。利用RPM指数的恶化情况,可以得出各AIS评分下其存活概率随时间变化的关系。由于AIS评分为1和2时,恶化情况不明显,AIS=6时,存活概率太低,故本文仅考虑伤员AIS评分为3~5时候的恶化情况。AIS各分值的伤员存活概率随时间恶化曲线如图1所示,AIS分值越高,其恶化速度也越快,其中AIS评分分别为3、4和5的情形下,伤员救助时间不能超过450 min、240 min和120 min,且恶化的速度呈现不同。为了能在后续仿真模型中考虑由于无法及时救治而导致的伤情恶化,通过SPSS分段拟合,确立了各AIS分值下伤员存活概率随时间的拟合函数Y(X)。
|
图 1 AIS各分值的伤员存活概率恶化情况 Fig. 1 Survival Probability of deterioration in different AIS |
| $Y\left( X \right) = \left\{ {\begin{array}{l}\!\!\!\!\!\begin{array}{l}{ - 4.235 \times {{10}^{ - 7}}{x^3}-2.781\times 10^{-4} x^2 +}\\{0.024x+ 96.35,\;\;\;{{x}} \in \left( {0,450} \right);}\end{array}\\{5.2,\;\;\;{{x}} \in \left( {450,\infty } \right){\text{。}}}\end{array}} \right.$ | (1) |
| $ Y(X) = \left\{\begin{array}{l}\!\!\!\!\!\begin{array}{l} - 1.914\times 10^{-8} {x^4} +1.91\times 10^{-5}{x^3} -5.53\times\\ 10^{-3}{x^2} + {0.192x + 82.77},\;\;\;{x \in \left( {0,240} \right);}\end{array}\\5.2,\;\;\;x \in \left( {240,\infty } \right){\text{。}}\end{array} \right.$ | (2) |
| $\quad\quad Y(X) = \left\{ {\begin{array}{l}{ - 0.29x + 33.8,\;\;\;x \in \left( {0,120} \right);}\\{5.2,\;\;\;{{x}} \in \left( {120,\infty } \right){\text{。}}}\end{array}} \right.$ | (3) |
其中,式(1)~(3)分别为AIS等级为3、4和5时,伤员存活概率随时间恶化的拟合函数。可见,初始AIS分值为5时,存活概率随延误时间基本成线性递减趋势,延迟处理超过120 min后无存活几率。随着AIS分值减少(伤情减弱),恶化速度初期较缓,后期加剧。该拟合的存活概率—延迟时间数学模型将引入到仿真模型中的病人模型中。
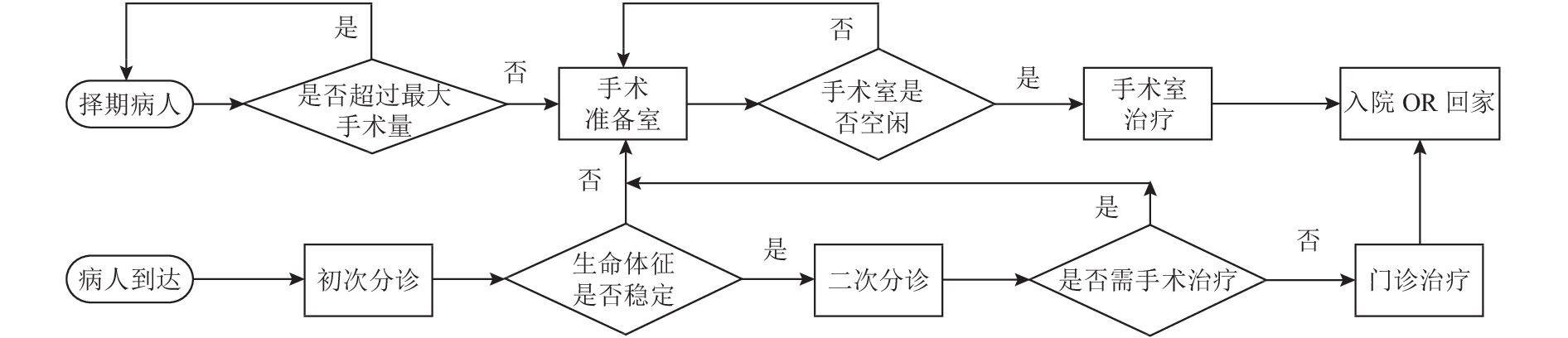
2 基于SIMIO平台的医院应急流程仿真 2.1 医院应急流程当突发事件发生后,伤员陆续到达医院,为了能更有效率地救治伤员,医院会对伤员进行分检处理,其中初次分诊是通过护士判断伤员生命体征是否稳定将伤员实现初次分流,将生命体征不稳定的伤员先进入手术室接受治疗。二次分诊是医生判断伤员需要手术治疗,再将伤员进行一次分流,最终将突发事件伤员分为门诊治疗以及需要手术治疗两部分。当然,日常情况下,医院还有不少择期病人也需要及时治疗,故突发事件伤员分流后治疗工作也需考虑择期病人。由于需要普通门诊的择期病人通常紧急度低,故本文只考虑将择期手术病人源加入整个应急流程中。图2是应急流程图。
|
图 2 医院应对突发事件应急流程 Fig. 2 Hospital emergency process |
SIMIO仿真平台是新一代离散事件系统仿真建模工具,可以更简单直观地对医院应急流程进行建模。在SIMIO工具中,利用Entity描述各类病人类型、利用Source描述各科室的病人源、利用Worker描述医疗流程中各类医务人员;利用Sever描述包含分诊、门诊治疗、手术室等的治疗阶段;利用Path/Timepath描述路线,以及用Sink设置病人进入住院病房或者病人离开医院等。
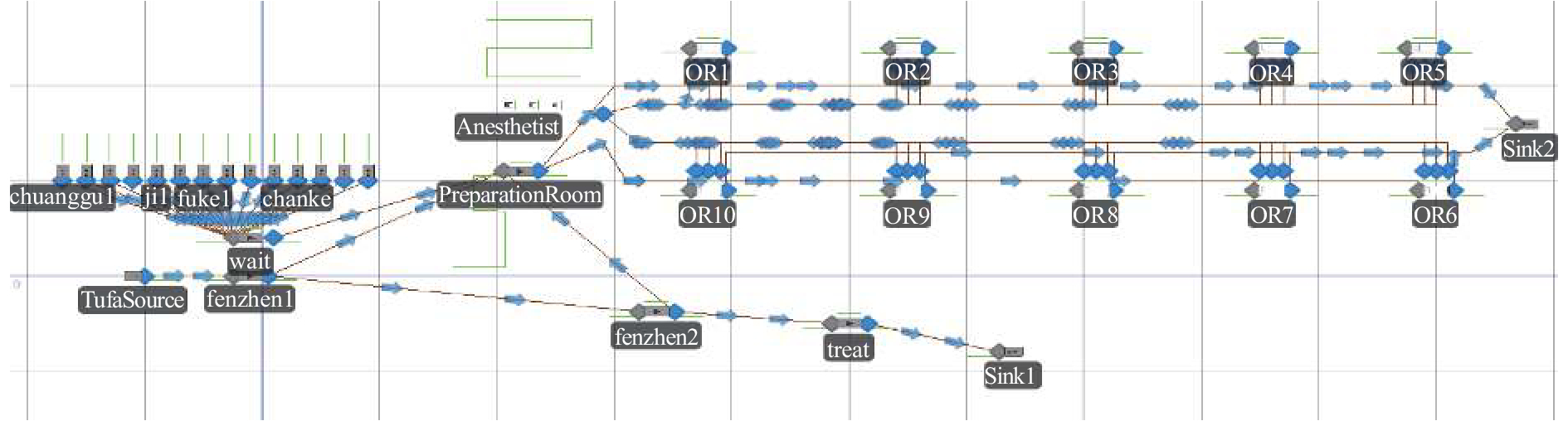
通过上述相关设置,结合图2中医院的应急流程,在SIMIO平台中建立了医院应急流程仿真模型,如图3所示。
|
图 3 医院应急流程仿真模型 Fig. 3 Hospital emergency process simulation model |
该仿真模型中,日常模式下的相关参数数据来自某三甲医院的相关调研,该医院目前创骨科医生共有19人,麻醉师10人,护士20人,手术准备室1间(2床位),手术室10间。常规模式下,该医院每天手术室开放的时间为周一到周五早上8点到下午4点,月手术量大约在950例左右。设置该医院每日最大完成手术量为45,并按照手术时长将择期手术分成小型手术,中型手术,大型手术,特型手术,特大手术5类。突发模式下的伤员数据来源于某三甲医院接受汶川地震伤员的数据[15]。为了简化模型,将突发伤员都考虑成骨科伤员。各治疗阶段的服务时间是和一些医务人员访谈后得出的。由于突发伤员没有具体的手术量数据,故本文设置汶川地震伤员AIS评分≥3的都是手术伤员。AIS评分为4和5的都属于生命体征不稳定的伤员。其余的伤员仅需门诊治疗,并根据AIS评分设置优先级,AIS评分越高优先级越高,突发手术伤员优先于择期手术伤员。各治疗阶段资源分配设置如表2所示。
| 表 2 各治疗阶段资源配置 Tab. 2 Resources allocation in different stages of treatment |
为了确保本模型的有效性,本文将模型运行50次得出各类择期手术病人平均手术用时,与实际统计的各类手术平均用时进行对比,结果如表3所示。
| 表 3 择期手术时间对比 Tab. 3 Selective operation time contrast |
从表3上看,仿真模型多次运行后,各类择期手术时长的仿真数值与实际数值的误差都不大,符合实际。
3 激增能力储备的仿真优化在地震这类型大规模突发事件发生后,激增的伤员给医护人员带来很大工作压力,同时人员的不足也对伤员的及时救治带来限制,造成伤情恶化。本小节将从人员利用和病人等待时间两个角度对激增能力储备进行仿真,提出储备规划方案。
3.1 基于人员利用率的储备规划医务人员利用率是衡量医院管理的一个关键指标,定义为当前医务人员忙碌时间与正常在岗时间(8 h工作)的比率。医务人员利用率高,表明当前医务人员的有效工作时间占比高,人员得以高度利用。然而,医务人员利用率超过100%,意味着医护人员进行加班工作。过多加班,会使得医务人员身体疲惫,降低工作效率,影响救援效果。各类医务人员利用率用
| $\quad\quad{\rm{Average}}(c) = \displaystyle\frac{{\sum\limits_m {T_s^{cm}} }}{{N_s^c \times T_e^c}}{\text{。}}$ | (4) |
其中,
|
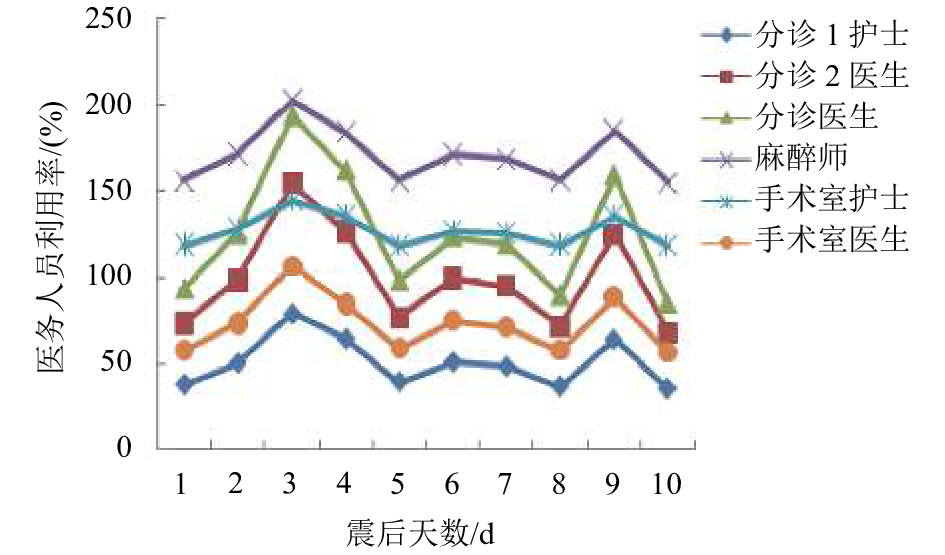
图 4 各医务人员利用率 Fig. 4 Medical staff utilization |
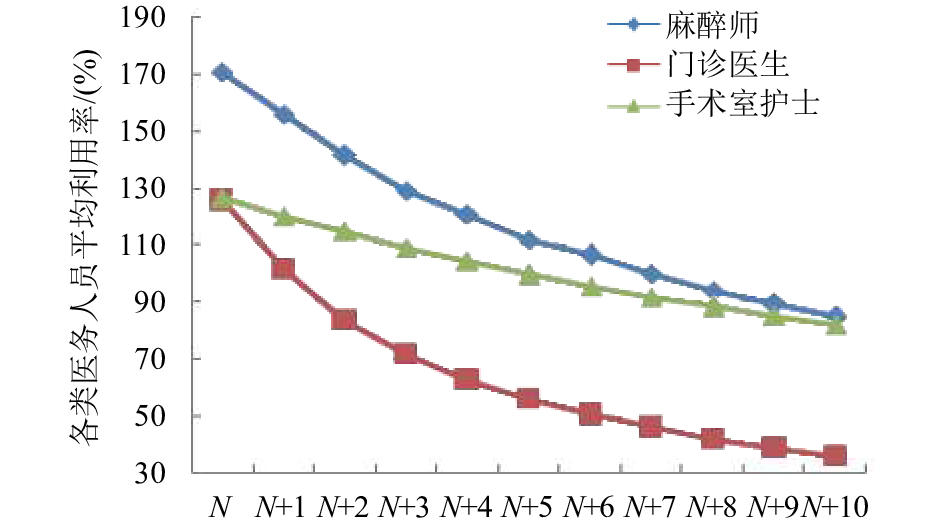
图4可见当前配置下,麻醉师的利用率过高,尤其在伤员到院人数最多的第3天,其利用率超过200%。其余各类人员资源利用率按顺序排列,分别为门诊医生、手术室护士、分诊医生、手术室医生、分诊1护士。根据相关医务人员采访得知,医务人员利用率不宜长时间超过90%。以此为标准,对平均利用率超过90%的医务人员类别进行人员补充规划,设计仿真实验,各方案的人员补充数目从1到10递增,仿真分析得出各类医务人员适宜的补充量(图5)。
|
图 5 各类医务人员数量对其平均利用率的影响 Fig. 5 The effect of the Number of Medical Staff on Utilization |
图5表明,针对目前这样规模的突发事件,该家医院的人员储备方面,麻醉师至少应补充9人,门诊医生至少补充2人,手术室护士则至少补充8人。
3.2 基于病人等待时间的储备规划从病人角度而言,等待时间过长一方面会影响病人的情绪,降低病人满意度,另一方面,过长的等待时间会造成患者病情恶化,增加治疗难度。紧急伤员都需经过一系列的治疗环节,病人在各阶段的等待时间可以用
| $\quad\quad{\rm{WT}}_s^i = {\rm{E}}{{\rm{T}}_s}^i - {\rm{ST}}_s^i{\text{。}}$ | (5) |
其中,
| 表 4 各类伤员在各治疗阶段等待时间 Tab. 4 patients waiting time in different treatment stage |
根据表4的结果,结合上文病人病情递进的研究,设置平均恶化情况和最大恶化情况来说明伤员恶化情况。其中平均恶化情况指的是该类型伤员在平均等待时间内,其存活概率退化情况;最大恶化情况指的是伤员等待时间最大时,其存活概率退化情况。由于实际情况下,AIS评分<3时,病人伤情恶化不明显,本文不予考虑,其他结果如表5所示。
| 表 5 各类伤员恶化情况 Tab. 5 Survival Probability of deterioration in different Patients |
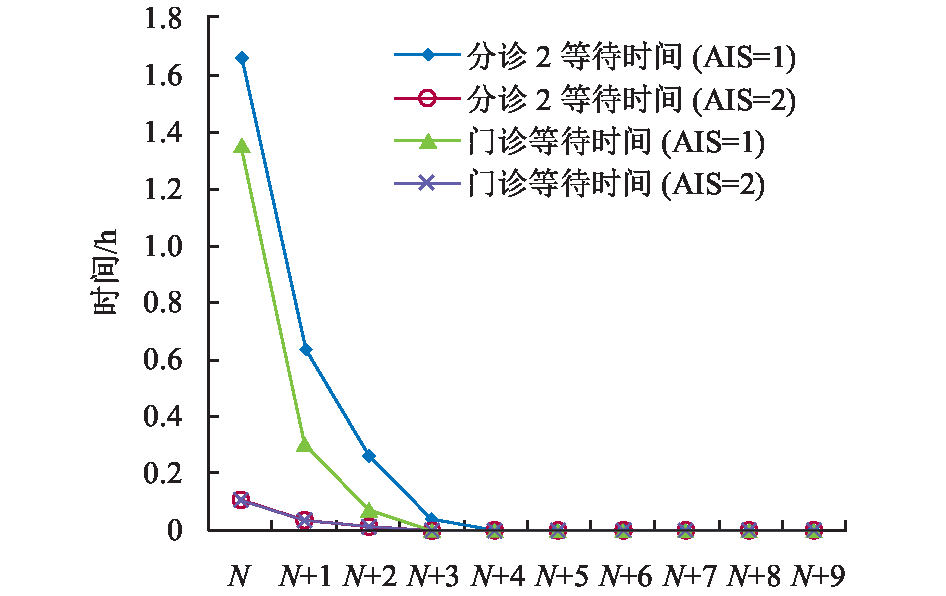
从表4与表5的结果显示,当前资源配置下,仅有分诊1的资源配置能达到快速治疗伤员目标。在病人病情恶化上,大部分伤员恶化情况相对稳定。针对门诊治疗的伤员,通过增加相应的资源数目比较相应情形下病人等待时间的改善效果,结果如图6所示。
|
图 6 医务人员数量对门诊病人等待时间的影响 Fig. 6 The effect of the number of medical staff on waiting time |
图6表明当分诊2的医生数量补充3人就能明显改善伤员在分诊2阶段的等待时间;而门诊医生最多补充3人,能改善伤员在门诊阶段的等待时间。
4 结论医院应急激增能力的量化分析是制定一套合理的应急准备预案的前提,可以使医院应对突发事件的相应措施更加可行高效。在研究类似突发事件对医院影响时,运用系统仿真是一个很好的手段,通过收集各类突发事件下历史病人源信息,建立相应的病人源模型,并结合实际的救助流程,可以对医疗系统建立一套完整的系统仿真,通过历史的相关数据,可以预判不同规模的突发事件下医院的多种人力资源类型的资源配置应该如何补充。本文的研究可以给医院提供一个参考的量化建议,以做出相应的应急预案。
| [1] |
WATSON S K, RUDGE J W, COKER R. Health systems " surge capacity”: state ofthe art and priorities for guture research[J].
The Milbank quarterly, 2013, 91(1): 78-122.
DOI: 10.1111/milq.12003. |
| [2] |
张燕, 马君, 王伟. 突发事件对医院应急管理的影响分析与对策研究[J].
中国卫生产业, 2016, 14(7): 7-9.
ZHANG Yan, MA Jun, WANG Wei. Effect analysis and strategies research on emergent events on hospital emergency management[J]. China Health Industry, 2016, 14(7): 7-9. |
| [3] |
胡万进, 丁森. 科学配置医疗资源提升卫生服务能力[J].
中国医院管理, 2012, 32(1): 11-13.
HU Wanjin, DING Sen. Scientific allocating medical resources and improving health service ability[J]. Chinese Hospital Management, 2012, 32(1): 11-13. |
| [4] |
兰奎旭. 大型公立医院应对突发公共事件应急管理实践[J].
现代医院管理, 2016, 14(4): 61-63.
LAN Kuixu. Emergency, management practice of public accidents in large-scale public hospitals[J]. Modern Hospital Management, 2016, 14(4): 61-63. |
| [5] |
KUMAR A, JIAO R J, SHIM S J. Predicting bed requirement for a hospital using regression models[C]. IEEE International Conference on Industrial Engineering & Engineering Manaagement, 2009: 665-669.
|
| [6] |
LIU Y, CHU C, WANG K. A new heuristic algorithm for the operating room scheduling problem[J].
Computers & Industrial Engineering, 2011, 61(3): 865-871.
|
| [7] |
JOSHI A J. Study on the effect of different arrival patterns on an emergency department’s capacity using discrete event simulation[D]. USA: Kansas State University, 2008.
|
| [8] |
WANG Y, LUANGKESORN K L, SHUMAN L. Modeling emergency medical response to a mass casualty incident using agent based simulation[J].
Socio-Economic Planning Sciences, 2012, 46(4): 281-290.
DOI: 10.1016/j.seps.2012.07.002. |
| [9] |
倪玉丽, 李树刚. 基于仿真分析的医疗应急人力资源配置研究[J].
计算机仿真, 2013, 30(7): 208-213.
NI Yuli, LI Shugang. Research on allocation of medical emergency human resources based on simulation[J]. Computer Simulation, 2013, 30(7): 208-213. |
| [10] |
何国光, 李树刚. 基于系统动力学仿真的医疗资源配置[J].
工业工程, 2016, 19(2): 121-127.
HE Guoguang, LI Shugang. Medical resources allocation based on system dynamics simulation[J]. Industrial Engineering Journal, 2016, 19(2): 121-127. |
| [11] |
王峥. 5.12地震伤情数据库指标体系的研究及伤情规律初步分析[D]. 重庆: 重庆医科大学, 2012.
WANG Zeng. Study on index system of 5.12 earthquake trauma database and initial analyze characteristics of earthquake trauma[D]. Chongqing: ChongQing Medical University, 2012. |
| [12] |
周俊红. 网络版创伤数据库系统v3. 0的研究[J].
中华创伤杂志, 2009, 25(12): 1133-1137.
ZHOU Junhong. Development of trauma database system network version 3.0[J]. Chinese Journalof Trauma, 2009, 25(12): 1133-1137. DOI: 10.3760/cma.j.issn.1001-8050.2009.12.359. |
| [13] |
BAKER S P, O’NEIL B, HADDON W Jr, LONG W B. The injury severity score: a method for describing patients with multiple injuries and evaluating emergency care[J].
Trauma, 1974, 14: 187-96.
DOI: 10.1097/00005373-197403000-00001. |
| [14] |
SACCO W J, NAVIN D M, FIEDLER K E, WADDELL I I, et al. Precise formulation and evidence based application of resource-constrained triage[J].
Academic Emergency Medicine, 2005, 12(8): 759-770.
DOI: 10.1197/j.aem.2005.04.003. |
| [15] |
蒋耀文, 张建成, 钟房, 等. 汶川地震2周2283例急症伤员分检方案的总结与探讨[J].
中国循证医学杂志, 2008, 8(9): 722-725.
JIANG Yaowen, ZHANG Jianchen, ZHONG Fang, et al. Summary of triage after Wenchuan Earthquake in 2 weeks[J]. Chinese Journal of Evidence-Based Medicine, 2008, 8(9): 722-725. DOI: 10.7507/1672-2531.20080163. |
 2018, Vol. 21
2018, Vol. 21

