2. 山东科技大学 矿业工程国家级实验教学示范中心,山东 青岛 266590
2. National Demonstration Center for Experimental Mining Engineering Education, Shandong University of Science and Technology, Qingdao 266590, China
煤炭企业的生产过程中,运输环节是实现产品场地转移必不可少的环节。在现有的运输设备条件下,最大程度地利用现有资源,优化运输系统能力,实现主煤流运输系统效率的提升,是煤炭企业重点关注的问题。系统关键环节的效率决定了系统的整体效率,运输系统的均衡发展能够实现系统的整体效益最优[1],从而实现企业效益的提升。
目前煤炭企业运输系统优化的方法主要采用技术手段对关键点进行优化。车兆学等[2]运用中间迈步式搭桥开拓运输系统的理论,克服了内排时期端帮运输通路压煤问题,减少汽车运距,增加了企业的经济效益。周伟等[3]采用采区间搭桥、反向内排和筑路式组沟开拓运输系统的方式解决了内排空间不均衡的问题,有效减少了运输成本。倪兴华等[4]通过优化矿井开拓布局,改革巷道布置方式,提高了运输系统运输能力。陈虹微等[5]从矿车结构和工况入手,分析了矿车轮对常见故障及原因,提高运输效率。赵红泽等[6]提出采用留沟的方式,减少了综合运距,降低原煤运输成本。以上学者主要从技术角度对煤矿运输系统进行改造。
实际上,运输系统的优化可以通过技术与管理协同优化的方法,根据目前检索到的相关文献,精益管理中人机作业分析、供应链等工具与方法在汽车、空调、电子等行业应用广泛,并取得良好的效果。牛占文等[7-8]以装配车间为研究对象,针对该公司车间布局不合理、人员利用率较低等问题,重新布局车间,运用动作分析原理实现工序活动的标准化,提高了企业效益;并从点、线、面、体角度剖析了精益管理开展的驱动因素,对提高精益创新能力具有一定的指导作用。吉鸿荣[9]认为精益生产已经广泛应用于各行各业,基于精益思想的知识链研究是进行企业优化的重要举措。李军等[10]以华瑞汽车座椅滑轨生产线为研究对象,利用价值流技术发现问题,结合工业工程的方法提高了企业的生产效率。胡适等[11]研究表明精益生产有利于提升汽车制造企业的成本管理水平。
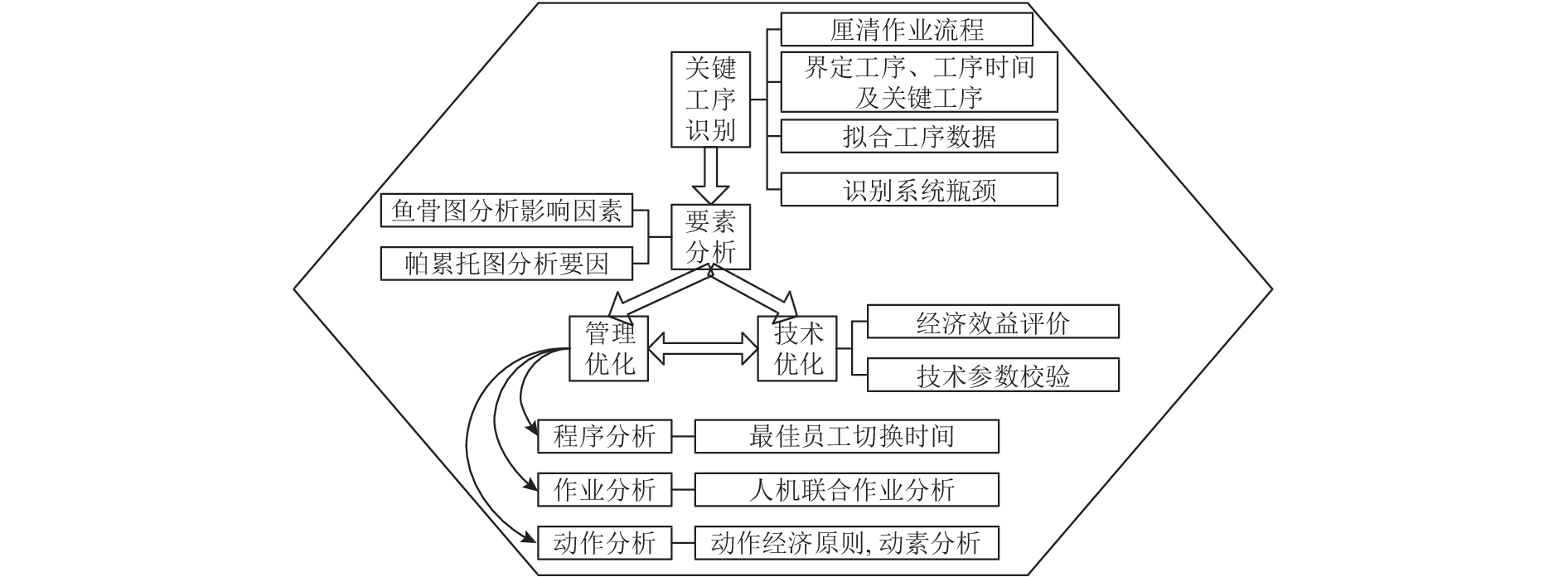
综上所述,在矿山领域,运输系统的优化主要通过技术改造,其周期长、成本高,改造期间对生产影响较为严重,没有充分地考虑系统关键环节对整个系统的效率影响问题。同时,精益管理的工具和方法在汽车、空调、电子等行业应用广泛并取得良好的经济效益。本文研究的意义在于:1) 突破传统的技术角度优化煤矿运输系统带来的周期长、成本高的问题,以系统关键工序的优化为切入点,从精益管理和技术优化相融合的角度优化主煤流运输系统;2) 引入人机作业分析方法,将串行作业改为并行作业,提高作业效率;3) 考虑作业疲劳因素,研究最佳员工切换时间,降低长时间工作导致反应时间增长的影响。本文通过对关键工序实施技术与管理协同优化,进而实现主煤流运输系统效率提升的过程如图1所示。
|
图 1 基于精益管理的利用技术与管理协同优化的方法 Fig. 1 Method of synergistic optimization of technology and management based on lean management |
对煤矿主煤流运输系统进行分析,首先要界定煤矿主煤流运输系统工序和工序时间,才能正确识别关键工序。在机械加工工艺词典中将工序定义为:一个(或一组)工人在一个工作地(如一台机床)对一个(或若干个)劳动对象连续完成的各项生产活动的综合,是组成生产过程的最小单元。与传统制造业相比较,在煤矿主煤流运输系统中,以皮带输送机和主井提升设备的连续运输为主,煤炭在转移过程中始终处于流动状态,本文将煤矿主煤流运输系统工序定义为“在煤矿主煤流运输系统中,员工利用煤炭运输或提升的设备或组合设备完成煤炭转移、处理的过程。”对应于上述工序的定义,本文将煤矿主煤流运输系统的工序时间定义为设备的吨煤运输时间,单位为s·t–1。其公式为
| $\quad\quad P = {\rm{ TY}}/{\rm{SY}}{\text{。}}$ | (1) |
式中,
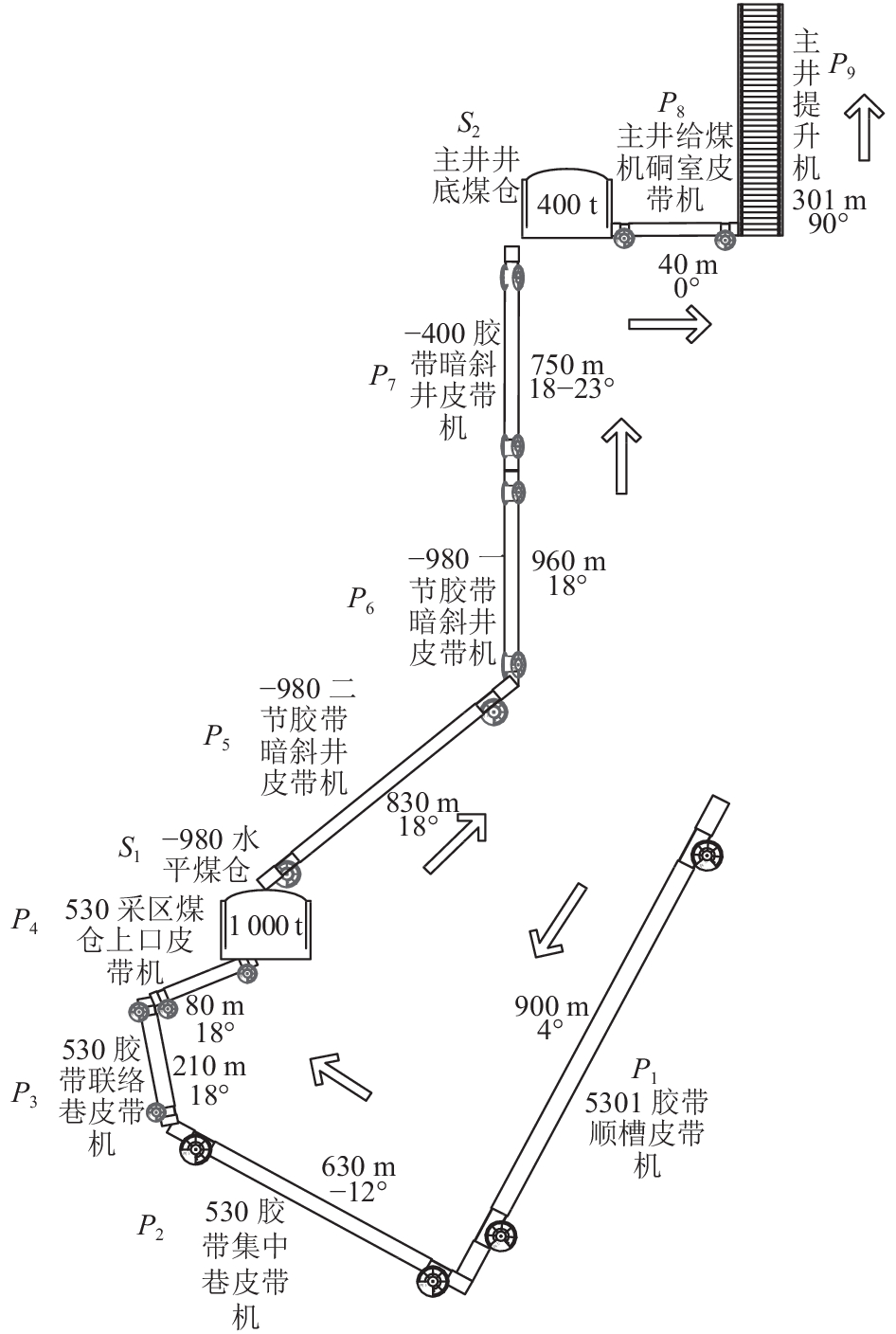
X煤矿主煤流运输系统运输流程如图2所示,主要由5301胶带顺槽皮带机、530胶带集中巷皮带机、530胶带联络巷皮带机、530采区煤仓上口皮带机、–980二节胶带暗斜井皮带机、–980一节胶带暗斜井皮带机、–400胶带暗斜井皮带机、主井给煤机硐室皮带机、主机提升机等设备组成,分别命名为P1、P2、P3、P4、P5、P6、P7、P8和P9。依据工序的定义,可以将X煤矿生产工作面到主井的8条皮带机与主井提升机作为9个工序开展研究。
|
图 2 煤矿主煤流运输系统示意图 Fig. 2 Diagram of main coal transportation system in coal mine |
由于主煤流运输系统的运输量受到瓶颈运输能力的约束,为有效地分析每个工序的时间,均采用设备正常运行时测量的数据,测量每个工序的吨煤运输时间,选取60个有效数据,对数据进行拟合。结果如表1所示。
| 表 1 数据拟合结果 Tab. 1 Data fitting results |
结合对工序及工序时间的界定,参考装配制造业对关键工序的定义[12],本研究定义关键工序为系统中作业时间最长的工序,即系统的瓶颈环节。
节拍的计算:产线上,决定产线作业周期的是最长的工序时间,即节拍。主煤流运输系统受设备运转、配件供应等外界因素的影响,作业时间是波动的。刘俨后等[13]建立了考虑随机性影响因素的模型并求解,发现在相应的完工率条件下,生产节拍和均衡指数均优于忽略随机性影响的模型求解结果。其中,完工率及节拍的定义及计算公式如下。
定义1 标准正态分布
定义2 在生产线中,保证所有节拍在概率
选取完工率
| $\quad\quad{t_o} = \max ({\mu _{{i}}} + 0.25{\sigma _i}){\text{。}}$ | (2) |
式中,
各工序时间计算公式为
| $\quad\quad{t_i} = {\mu _i} + 0.25{\sigma _i}{\text{。}}$ | (3) |
计算各工序时间,结果如表2所示
| 表 2 各工序时间 Tab. 2 The process time |
通过计算得到P9为最长的工序时间,即
一般采用平衡率
| $\quad\quad W = \sum\limits_{i = 1}^n {{t_i} {s_i}/{t_0}\times m} ,$ | (4) |
| $\quad\quad{W_s} = 1 - W{\text{。}}$ | (5) |
平滑性指数计算公式为
| $\quad\quad {\rm{SI}} = \sqrt[{}]{{\frac{{\sum\limits_{i = 1}^n {{{({t_0} - {t_i})}^2}} }}{m}}}{\text{。}}$ | (6) |
式中,
主煤流运输系统损失率较高,其原因在于主煤流运输系统节拍
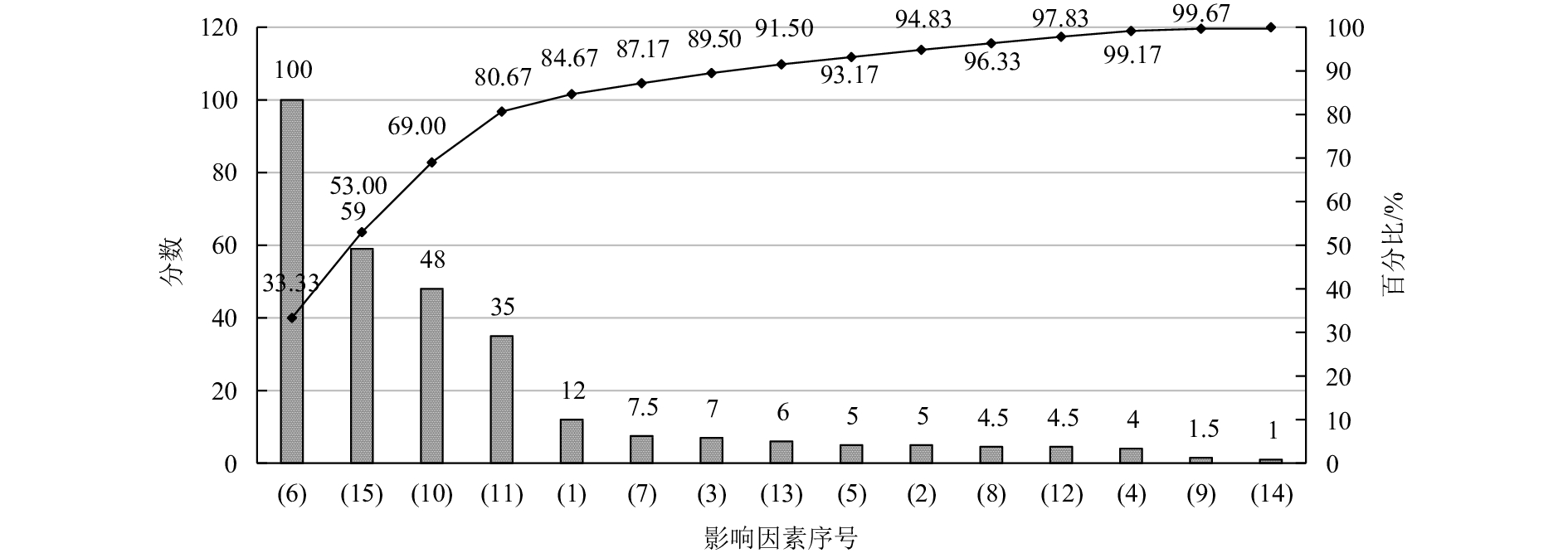
鱼骨图被作为持续改进的工具,可以用来分析关键问题的潜在因素[15]。发现主井是主煤流运输系统的关键工序之后,运用鱼骨图分析该瓶颈产生的原因,共有15种要素,分别是:1) 员工责任心不强;2) 绞车司机能力差;3) 设备故障;4) 设备设计不合理;5) 设备润滑不到位;6) 箕斗过小;7) 点检不到位;8) 配件更换不及时;9) 配件供应不及时;10) 员工作业不统一;11) 一人多职,主绞车司机同时负责打电话;12) 现场物品摆放不整齐;13) 环境嘈杂,影响工作情绪;14) 标识不清;15) 工人作业反应具有较高的时差。对上述15种因素,组织全矿主煤流运输系统技术人员进行定性评分,遵循80/20原则,统计出前20%的因素作为关键因素,实施重点优化。关键因素评价组分为三个小组,其中领导层小组10名、管理中层小组20名和现场工作人员小组50名。每人从15个因素中选取自己认为导致主井能力较低的3个关键因素,3个评分小组的权重
|
图 3 关键影响因素帕累托图 Fig. 3 Pareto chart of key factors |
根据帕累托原则占80%的影响因素为:主井箕斗过小;工人作业反应具有较高的时差;员工作业动作不统一;一人多职,主绞车司机同时负责打电话。本文着重优化上述4个影响因素。
2.2 主煤流运输系统技术优化针对主井箕斗过小的问题,采取技术优化的方法进行优化。在该过程中,涉及经济效益评价与技术参数校验两方面的问题。煤矿工程技术人员以分析结果为依据,选取了6 t箕斗更换为8 t箕斗的技术方案。技术优化结果表明,相比6 t箕斗,优化后的主井每天的提升能力提高629.23 t,是原有能力的133.3%。该技术优化方案,是在对原有井筒不进行大规模技术改造,充分利用现有设备,同时保证设备安全运行的前提下,能够实现的最优方案。
2.3 主煤流运输系统管理优化箕斗过小的问题解决之后,“工人作业反应具有较高的时差”、“员工作业动作不统一”和“一人多职,主绞车司机同时负责打电话”3个影响因素可以通过人机联合作业分析图进行分析,探寻优化的途径。
1) 人机联合作业现状。
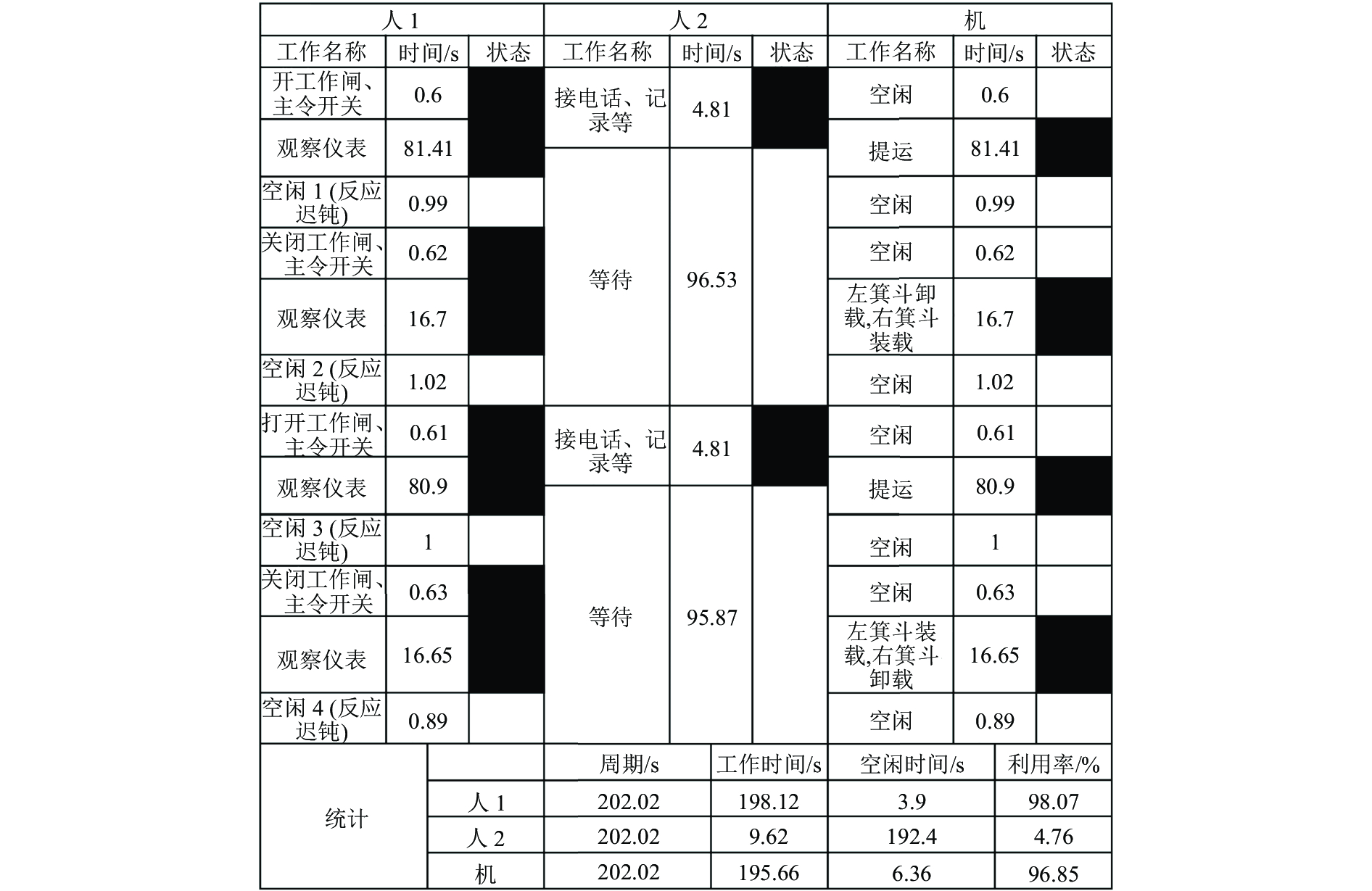
主井提升采用8 h每班,每班次2人的方式进行工作,每人连续操作设备4 h。在此期间,另一人不直接参与设备操作工作。制作箕斗更换之后的人机联合作业分析图,如图4所示。

|
图 4 优化前人机作业图 Fig. 4 Man - machine operation map that before optimization |
从人机作业图中分析可以得出以下结论。
①在主井装载、提升、卸载的过程中,主井绞车司机需要实时观察,机器工作时间暂时已不存在优化空间。
②接电话、记录等作业为串行作业,“一人多职,主绞车司机同时负责打电话”,接电话、记录的时间可以优化。两个人同时作业,一个人操作主井绞车、另一个人接电话和记录,将串行作业改为并行作业,提高作业效率。
③人的开工作闸、主令开关的操作,可以进行优化。通过拍摄的视频,发现“员工作业动作不统一”,不同的司机操作的方式是不一样的,效率有明显差别,存在优化的空间。
④空闲1(反应迟钝)、空闲2(反应迟钝)空闲3(反应迟钝)和空闲4(反应迟钝)数值较高,表明“工人作业反应具有较高的时差”,工人的操作反应时间随着工作时间的增长而增长,这和员工的疲劳程度有着密切的关系。
机器运行方面暂时不能调节以外,将接电话、记录等串行作业改为并行作业,每循环可以降低作业时间9.62 s。本文针对③和④两个方面进行详细的论述。
2) 主井司机操作动作规范的优化。
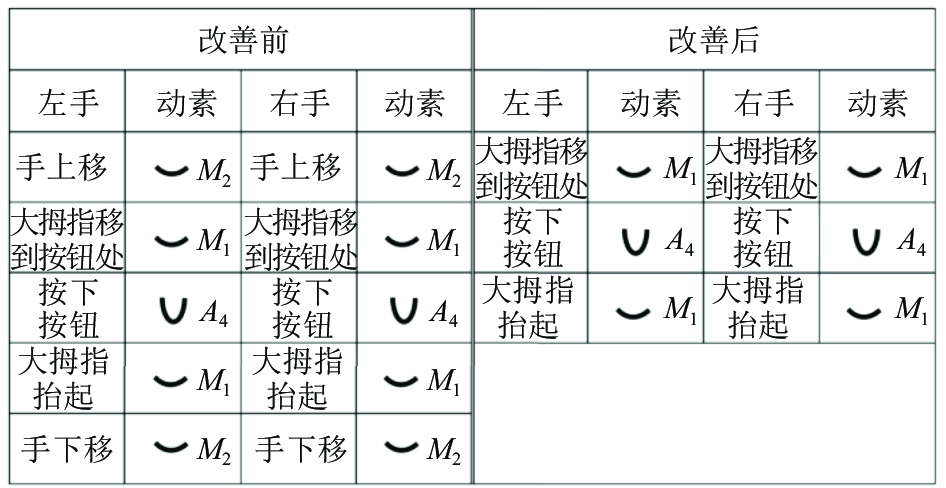
员工作业动作不统一,导致效率存在较大差异。对员工的双手进行定点摄影,以动作经济原则为指导,优化员工工作过程中的动作可以提高效率。针对现场员工的操作,依据动作经济基本原则中的第一个原则——减少动作数,取消不必要的动作,对现场工人的操作进行了定点摄影。采用动作研究方法,结合动素分析,优化作业动作,并与现场绞车司机进行探讨。在作业规程的基础上,规范了操作方法,将司机的操作姿势进行标准化,如图5所示。
|
图 5 绞车司机动作优化 Fig. 5 Action optimization of winch driver |
图5中,优化前动素为M2M1A4M1M2,共10 MOD,通常认为熟练MOD值为0.1s[16],可知,图5中的员工操作时间符合MOD法测定的结果。对图5中改善前的动素进行分析,可以发现,主井司机在操作扳手时,手上移和手下移两个动素属于无效动素,应当消除。优化后动素变为M1A4M1,每次可以缩短4 MOD的作业时间,每个循环可以缩短16 MOD,即1.6 s。
3) 司机反应时间的优化。
采用现场司机连续工作4 h中的64个有效循环数据,分别统计空闲1、空闲2、空闲3和空闲4的时间。统计结果显示,主井绞车司机随着工作时间的增长,由反应时间导致的空闲时间,由起初的1.5 s左右逐渐增长到了3 s左右,可见,长时间工作导致人的效率降低非常明显。实施快速换模来缩短预置时间是精益管理能够开展的关键因素之一[17],可以减少产品切换耗时,提高生产效率。本文采取快速换模的思想,实现快速切换两位绞车司机,减少因为长时间工作疲劳导致的作业时间增长,假设司机换模状态恢复如初,求解员工切换的时间间隔。
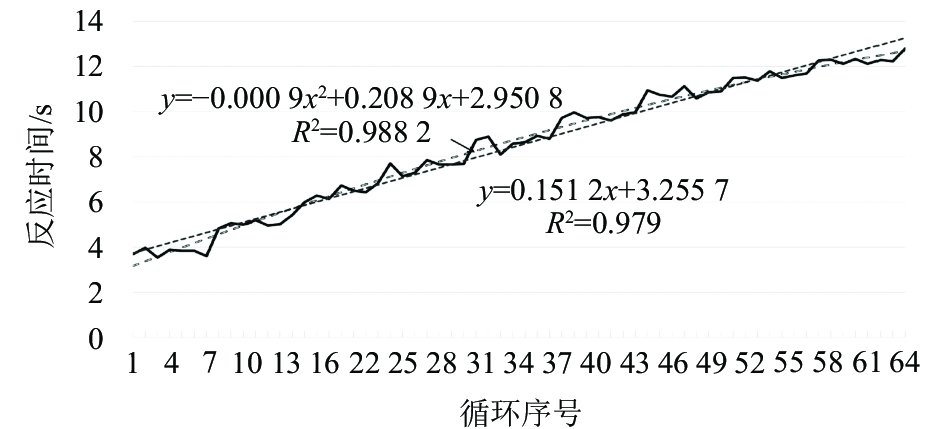
统计每个循环的总体空闲时间,拟合趋势线,如图6所示,二次趋势线效果优于一次趋势线,
| $\quad\quad y = - 0.000 \; 9{x^2} + 0.208 \; 9x + 2.950 \; 8{\text{。}}$ | (7) |
式中,
| $\quad\quad{\rm{max\;SN}} = {\rm{TT}}/{\rm{PT}}{\text{。}}$ | (8) |
| ${\rm{s.t}}.\left\{ {\begin{array}{*{20}{l}}{{\rm{TT}} = T \times N + {T_Q} + {T_S},}\\{{\rm{NT}} \!=\! T \times n \!-\! \left( {{T_{X1}} \!+\! {T_{X2}} \!+\! {T_{X3}} \!+\! {T_{X4}}} \right) \times n \!+\! \sum\limits_{x = 1}^n {y \!+\! {T_Q} \!+\! T} ,}\\{{\rm{PT}} = {\rm{NT}}/n,}\\{y = - 0.000\;9{x^2} + 0.208\;9x + 2.950\;8,}\\{n = 1,2,3, \cdots ,64},\\{x = 1,2,3, \cdots ,n}{\text{。}}\end{array}} \right.$ |
式中,TT为64个连续循环的总时间;
|
图 6 每循环反应时间趋势图 Fig. 6 Each cycle reaction time trend graph |
|
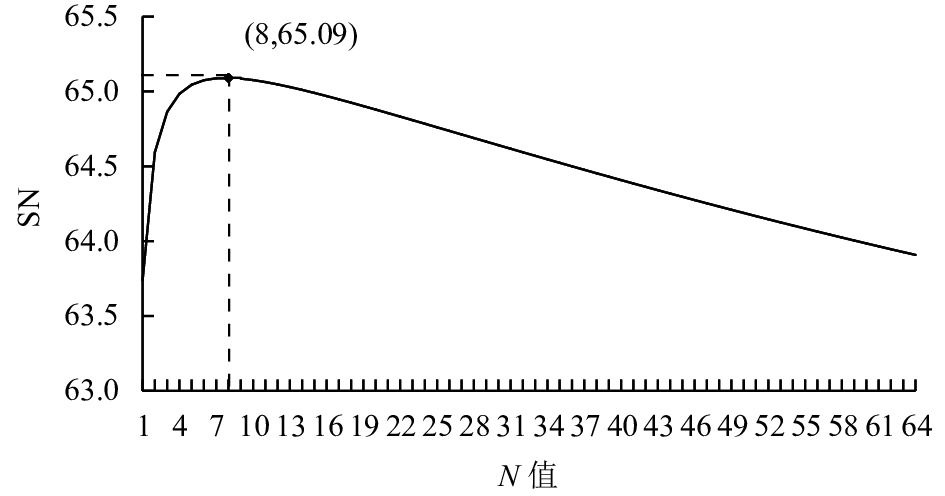
图 7 解的变化曲线 Fig. 7 Solution of the curve |
图7中所示,SN只有一个极值点,也是最大值点,其值为65.09,最佳切换循环间隔
计算节约时间的计算公式为
| $\quad\quad{T_J} = {\rm{PT}} \times \left( {{\rm{S}}{{\rm{N}}_{\max }} - N} \right) \times 2{\text{。}}$ | (9) |
式中,
绘制改进后的人机作业分析图。采用多次测量员工工作0.5 h的反应时间的均值数据,如表3所示,可知每个循环可以节约4.6 s。人机作业分析图如图8所示。
根据上述优化结果,假设在各个工序时间标准差不发生变化的情况下,计算节拍时间,节拍时间的计算依据吨煤计算公式为
| $\quad\quad{t_0} = {t_z}/d + 0.25{\sigma _i}{\text{。}}$ | (10) |
式中,
通过式(4)~(6)计算得出优化后的主煤流运输系统平衡率
| 表 3 优化前后空闲时间对比 Tab. 3 Free time comparison table that Optimize before and after |
|
图 8 优化后人机作业图 Fig. 8 Man - machine operation map that after optimization |
优化之后,主煤流运输系统平衡率比优化之前提高了9.52%,主煤流运输系统的平滑性指数缩小至6.83,生产线节拍降低至12.72 s,降低了24.06%。同时,主井绞车司机的工作时间利用率提高了1.97%,主井提升设备的利用率提高了7.03%,主煤流运输系统的负荷更加趋于平衡,箕斗实施技术优化之后,提升循环周期由初始200.96 s提升至217.84 s,实施管理优化之后,提升周期降为202.02 s,按每天有效工作时间为14 h计算,对应的提升勾数和提升量分别为502勾,463勾,500勾和3 009.55 t,3 701.80 t,3 991.68 t。通过优化可以多提升煤炭982.13 t。可知在实施技术优化之后,提升周期变长,但是提升煤炭的数量大幅度上升,在技术优化的基础上,通过管理优化,进一步优化了作业流程,可以多提升37勾,提高了作业效率。
4 结论本研究通过对X煤矿主煤流运输系统关键工序技术与管理的协同优化,实现了系统整体效率的提升。在界定了主煤流运输系统工序时间及关键工序的基础上,同时考虑了作业时间受随机性因素影响,拟合现场数据确定节拍,识别关键工序;使用帕累托图分析瓶颈主要影响因素,利用人机联合作业图确定消除瓶颈的有效途径;通过采用串行作业改为并行作业、动作经济原则优化动作、改变员工更换频次的手段提高工作效率,提出关于最佳切换循环间隔n的目标函数,并求解出最佳切换时间,每循环作业时间缩短15.82 s。案例分析的结果表明,该方法应用之后,煤矿每天多提升煤炭982.13 t,在实施技术优化之后,提升周期变长,但是提升煤炭的数量大幅度上升,在技术优化的基础之后,通过管理优化,进一步优化了作业流程,可以多提升37勾。本文应用的优化方法避免大规模技术改造带来的周期长,成本高的问题,充分地利用了现有装备条件。对煤矿领域开展主煤流运输系统优化具有一定的借鉴意义。
| [1] |
张生瑞, 严宝杰. 交通运输系统协调发展的理论分析[J].
长安大学学报(自然科学版), 2002, 02: 51-53.
ZHANG Shengrui, YAN Baojie. Analysis of the transportation system coordination[J]. Journal of Chang′an University (Natural Science Edition), 2002, 02: 51-53. |
| [2] |
车兆学. 安家岭露天煤矿内排开拓运输系统优化[J].
采矿与安全工程学报, 2007, 04: 494-497+501.
CHE Zhaoxue. Optimization of Internal Dumping Development Haulage System in An Jialing Surface Coal Mine[J]. Journal of Mining & Safety Engineering, 2007, 04: 494-497+501. DOI: 10.3969/j.issn.1673-3363.2007.04.026. |
| [3] |
周伟, 才庆祥, 谢廷堃, 尚涛, 徐志远. 大型近水平露天煤矿转向期间开拓运输系统优化研究[J].
采矿与安全工程学报, 2008, 04: 404-408.
ZHOU Wei , CAI Qingxiang, XIE Tingkun. Optimization of In-Pit development transport system during transitional period in large open pit mine with flat coal deposit[J]. Journal of Mining & Safe ty Engineering, 2008, 04: 404-408. DOI: 10.3969/j.issn.1673-3363.2008.04.006. |
| [4] |
倪兴华. 安全高效矿井辅助运输关键技术研究与应用[J].
煤炭学报, 2010, 11: 1909-1915.
NI Xinghua. Research and application of key technology for safety and high efficient mine auxiliary transportation[J]. JOURNAL OF CHINA COAL SOCIETY, 2010, 11: 1909-1915. |
| [5] |
陈虹微, 王荣杰. 矿车轮对密封与润滑分析及改进[J].
润滑与密封, 2006, 06: 181-182.
CHEN Hongwei, WANG Rongjie. Analysis and improvement of sealing and lubrication of wheel wheelsets[J]. LUBRICAT ION ENGINEERING, 2006, 06: 181-182. |
| [6] |
赵红泽, 张瑞新, 秦建明, 甄选. 安家岭露天煤矿运煤卡车通道水平优化研究[J].
中国矿业大学学报, 2011, 06: 917-921.
ZHAO Hongze, ZHANG Ruixin, QIN Jianming. Optimization of the trench level for the coal truck of an internal waste dump at the An Jialing surface mine[J]. Journal of China University of Mining & Technology, 2011, 06: 917-921. |
| [7] |
牛占文, 荆树伟, 杨福东. 基于精益管理的制造型企业管理创新驱动因素分析——四家企业的案例研究[J].
科学学与科学技术管理, 2015, 07: 116-126.
NIU Zhanwen, JING Shuwei, YANG Fudong. An analysis of driving factors of the management innovation of manufacturing enterprises based on lean management: case studies of four enterprises[J]. Science of Science and Management of S. & T., 2015, 07: 116-126. |
| [8] |
牛占文, 吴秀婷, 岳楼. 基于精益生产的某离合器公司装配车间优化[J].
工业工程与管理, 2015, 02: 1-6+32.
NIU Zhanwen, WU Xiuting, YUE Lou. Optimization of assembly shop of clutch enterprise based on lean production[J]. Industrial Engineering and Management, 2015, 02: 1-6+32. |
| [9] |
吉鸿荣. 基于精益思想的企业内部知识链模型优化[J].
科技进步与对策, 2012(02): 141-144.
JI Hongrong. Knowledge chain model optimization of inner enterprise based on lean thinking[J]. Science&Technology Progress and Policy, 2012(02): 141-144. |
| [10] |
李军, 徐明强. 基于价值流的汽车座椅滑轨生产线分析与改善[J].
工业工程与管理, 2008, 01: 122-126.
LI Jun , XU Mingqiang, Analysis and improvement of a slippery track production line based on the value flowized[J]. Analysis and improvement of a slippery track production line based on the value flowized[J]. Industrial Engineering and Management, 2008, 01: 122-126. DOI: 10.3969/j.issn.1007-5429.2008.01.024. |
| [11] |
胡适, 蔡厚清. 精益生产成本管理模式在我国汽车企业的运用及优化[J].
科技进步与对策, 2010(16): 78-81.
Hu Shi, CAI Houqing. The application and optimization of cost management model of lean production in automotive firms[J]. Science&Technology Progress and Policy, 2010(16): 78-81. |
| [12] |
陈佳祺, 郭为忠. 基于生产线仿真分析的关键工位诊断与改进设计[J].
机械设计与研究, 2017, 33(1): 83-86.
CHEN Jiaqi, GUO Weizhong. Modification design research and diagnosis of key processs based on simulation analysis[J]. Machine Design and Research, 2017, 33(1): 83-86. |
| [13] |
刘俨后, 左敦稳, 张丹. 随机作业时间的装配线平衡问题[J].
计算机集成制造系统, 2014, 06: 1372-1378.
LIU Yanhou, ZUO Dunwen, ZHANG Dan. Assembly line balancing with stochastic operation times[J]. Computer Integrated Manufacturing Systems, 2014, 06: 1372-1378. |
| [14] |
文龙. C企业液晶屏生产线平衡改善研究[D].成都: 西南交通大学, 2013.
WEN Long. The balance improvement research of C enterprise's LCD screen assembly line[D]. Chengdu: Southwest Jiaotong University,2013. |
| [15] |
HEKMATPANAH M. The application of cause and effect diagram in sepahan oil company[J].
World Academy of Science, Engineering and Technology, 2011, 78: 537-541.
|
| [16] |
易树平, 郭伏主编.基础工业工程[M]. 北京: 机械工业出版社, 2006.
|
| [17] |
ALMOMANI M A, ALADEEMY M, ABDELHADI A, et al. A proposed approach for setup time reduction through integrating conventional SMED method with multiple criteria decision-making techniques[J].
Computers & Industrial Engineering, 2013, 66(2): 461-469.
|
 2018, Vol. 21
2018, Vol. 21

