应急物资具有时间紧急、时变性强、经济性弱和资源有限等特点。如何通过量化手段对应急问题进行分析和优化，是学术界备受关注的研究课题^[1]。

目前对应急物流运输优化的研究主要集中在3方面。1) 以运输成本最小化为目标的救援物资配送问题。如：Rathi等^[2]研究了时间窗约束下，多物流网络下的应急救援物资的配置问题。2) 以运输时间最短为优化目标的问题，如：Özdamar等^[3]研究了以运输成本最小化为目标的应急物流运输模型。阎俊爱等^[4]构建了非常规突发事件救援物资输送动态模型，以车辆配送时间最小为目标。3) 考虑多目标情景优化研究，如：李双琳等^[5]以应急物资配送总时间最短和受灾点应急物资未满足的总损失最小为目标，构建了应急物资需求模糊情境下的选址与运输多式联运配置优化模型。Fontem等^[6]以救灾物资总价值最大化和配送时间最小化为目标，构建了应急情况下的随机车辆路径模型。

此外，一些学者还关注了应急资源公平性问题。Tzeng等^[7]为保证应急物资分配的公平性，把物资分配满意度作为模型的一个目标函数。陈莹珍等^[8]提出了基于公平原则的应急物资分配模型。而基于物联网的智能系统的发展使实时交通信息的可获性变得容易，已有学者对此问题予以研究。如Liebig等^[9]研究了实时交通预测下的动态路线规划问题，并证实了所提模型的有效性。

目前对应急物流运输的研究多是从配送时间最小化、灾后损失最小化、社会效益最大化等角度展开，但仍存在一些不足：1) 缺少对实时交通信息下的应急配送问题研究；2) 对应急情况下多级多源配送体系的研究较少；3) 现有文献对应急资源分配的公平性问题已有关注，但将有限资源分配公平性纳入到实时交通信息等复杂情景下的研究还很鲜见。基于此，本文针对城市应急物流配送问题，考虑救灾需求点物资配送可由配送中心和转运中心多源满足的情况，在实时交通信息下，以救灾时间最小和资源分配公平性最大为目标建立模型，并设计使用混合遗传算法对其进行求解。

1 问题描述与假设条件 1.1 问题描述

灾后应急物资配送是在有限的资源约束下，充分考虑交通状况等实时信息，在最短的时间，以公平性最优和受灾群众满意度最大为目标，完成配送中心和转运中心到受灾需求点的物资配置问题。

$K = \{ 1, 2, \cdots, {k^{\max }}\} $ 表示配送中心集合，任一配送中心 $k \in K$ ； $J = \{ 1, 2, \cdots, j, \cdots, {j^{\max }}\} $ 表示转运中心集合，任一转运中心 $j \in J$ ； $I = \{ 1, 2, \cdots, i, \cdots {i^{\max }}\} $ 表示救灾需求点集合，任一需求点 $i \in I$ 。配送中心和需求点的位置已知，候选转运中心备择，从配送中心/转运中心到需求点的交通状况不同。

1.2 研究假设

1) 受灾点所需的救援物资 ${g_{i\;}}$ 已知且有限，车辆到达受灾点的卸货时间 $t_i^{{{unload}}}$ 已知。

2) 运输车辆车型一致，每辆车的最大载重量为 ${{ca}}{{{p}}^{\max }}$ ，任意受灾需求点可由一辆车满足，且不考虑车辆回程的问题。

3) 配送中心/转运中心/受灾需求点到受灾需求点之间的运输路线并非完全保持畅通，随时可能发生道路塌陷等意外。实时交通状况系数为 $\varphi $ 。如果道路通畅， $\varphi {{ = }}1$ ；如果道路无法通行，则 $\varphi \to \infty $ ，并随拥堵程度增加而增加。

2 城市应急物流多源配送优化模型 2.1 符号说明

$ {{M}} $ 表示救援车辆集合， $ {{M}} = \{ 1, 2, \cdots, m, \cdots, $ $ {m^{\max }}\} $ ，m表示其中的任意一辆车；

${t_{ijkm}}$ 为车辆 $ m $ 从配送中心 $ k $ 经转运中心 $ j $ 到达受灾需求点 $ i $ 的时间；

${t_{ikm}}$ 为车辆 $m$ 从配送中心 $k$ 直达受灾需求点 $i$ 的时间；

${d_{in}}$ 为受灾需求点 $ i $ 到配送中心或转运中心 $ n $ 的距离， $ n \in J \cup K $ ；

${d_{jk}}$ 为转运中心 $j$ 到配送中心 $k$ 的距离；

${c_i}$ 为受灾需求点 $i$ 的物资需求量；

${o_{ke}}$ 为由配送中心 $k$ 发出的物资总量， $e \in J \cup I$ ；

${w_j}$ 为备选转运中心 $j$ 救灾时间窗内的最大吞吐量；

${T_i}$ 为物资运送至受灾需求点 $i$ 的时间；

$V$ 为每辆车的最大平均速度；

${{T}}{{{W}}_i}$ 为受灾需求点 $i$ 的车辆最迟到达时间；

${\varphi _{en}}$ 为点 $ e $ 到点 $ n $ 道路通行状况对救援车辆速度的影响系数， $n \in J \cup K$ ， $e \in I \cup J$ ，是一个动态变化的参数；

${q_{ijk}}$ 为经配送中心 $k$ 和转运中心 $j$ 到达受灾需求点 $i$ 的物资数量；

${x_j} = \left\{ \begin{array}{l}1, \;\;\;\;\text{转运中心}j\text{被选中};\\0, \;\;\;\;\text{否则}{\text{。}}\end{array} \right.$

${y_{in}} = \left\{ \begin{array}{l}1, \;\;\;\;\text{需求点}i\text{的配送由}n \text{满足},\;n \in J \cup K;\\0, \;\;\;\;\text{否则}{\text{。}}\end{array} \right.$

2.2 模型构建

$\min\;{Z_1} \!=\! \sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{\mathop {k \in K}\limits_{n \in (J \cup K)} } {\sum\limits_{m \in M} {(({t_{jkm}} \!+\! {t_{ijm}}){x_j} \!+\! {t_{ikm}}){y_{in}} \!+\! t_i^{{{unload}}}} } } }, $

(1)

$\quad\quad\min\;{Z_2} = \sum\limits_{k \in K} {\sum\limits_{j \in J} {{q_{ijk}}/{c_i}}{\text{。}}} $

(2)

$\displaystyle\begin{array}{l}{{s}}{{.t}}{{.}}\\\quad\!\!\quad\displaystyle\sum\limits_{i \in I} {\displaystyle\sum\limits_{j \in J} {\displaystyle\sum\limits_{k \in K} {{q_{ijk}}} } } = \sum\limits_{k \in K} {\displaystyle\sum\limits_{e \in (J \cup I)} {{o_{ke}}} } ;\end{array}$

(3)

$\quad\quad{t_{en}} = {d_{en}}{x_j}/V{\varphi _{en}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} e \in (I \cup J), n \in (J \cup K);$

(4)

$\quad\quad\sum\limits_{i \in I} {\sum\limits_{k \in K} {{q_{ijk}}} {\text{≤}} {w_j}}, j \in J;$

(5)

$\quad\quad\begin{array}{l}{T_i} \!=\! \displaystyle\sum\limits_{k \in K} {\sum\limits_{j \in J} {\sum\limits_{m \in M} {({t_{kjm}} \!+\! {t_{ijm}}){x_j} \!+\! {t_{ikm}}} } }, i \in I, m \in M;\end{array}$

(6)

$\quad\quad{T_i} {\text{≤}} {{T}}{{{W}}_i}, i \in I;$

(7)

$\quad\quad\sum\limits_{i \in I} {\sum\limits_{j \in J} {\sum\limits_{k \in K} {{q_{ijkm}}} } } {\text{≤}} {{ca}}{{{p}}^{\max }}, m \in M;$

(8)

$\quad\quad\sum\limits_{j \in J} {\sum\limits_{k \in K} {{q_{ijk}}} } {\text{≤}} {c_i}, i \in I;$

(9)

$\quad\quad\sum\limits_{n \in J \cup K} {{y_{in}}} = 1, i \in I;$

(10)

$\quad\quad{y_{ij}} {\text{≤}} {x_j}, i \in I, j \in J;$

(11)

$\quad\quad{q_{ijk}} {\text{≥}} 0, i \in I, j \in J, k \in K;$

(12)

$\quad\quad\!\!\!\!\begin{array}{l}{x_j} \in \{ 0, 1\}, {y_{in}} \in \{ 0, 1\}, i \in I, j \in J;\\n \in J \cup K{\text{。}}\end{array}$

(13)

其中，式(1)表示应急救援物资到达受灾需求点的最短时间；式(2)表示所有受灾需求点 $i$ 的最小满足率最大；式(3)表示从配送中心发出的物资总量与到达受灾需求点的物资总量相等；式(4)表示配送中心、转运中心、受灾需求点间的物资运输时间；式(5)表示备选转运中心规定时间窗内的吞吐量约束；式(6)表示受灾需求点接受完物资的时刻；式(7)表示任意受灾需求点 $i$ 的物资应在规定时间窗内到达；式(8)表示任意运输车辆不能超载；式(9)表示受灾需求点 $i$ 接收到的物资不超过其实际需求量，这是基于应急救援过程中供小于求假设提出的；式(10)表示配送中心和转运中心有且只有一个点为受灾需求点提供物资；式(11)表示只有开放的转运中心才能为受灾需求点提供物资救援活动；式(12)为非负约束；式(13)为0-1约束。

考虑实时交通信息的动态性，将任意旅行过程划分为 $H$ 个时间段，为 $T = {T^1}, {T^2}, \cdots {T^H}$ ，任意时间段 ${T^h}$ 上存在一个恒定的旅行速度 ${v^h} \geqslant 0$ ，且 ${T^h} = [{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ^h}, {\bar t^h}]$ ，对于任意从节点 $ n $ 开往节点 $ e $ 的车辆，始发时间为 $ {t_n} $ 的旅行速度可表示为 ${v_{ne}}({t_n}) = \{ v_{ne}^1({t_n}), \cdots,$ $ v_{ne}^h({t_n}), \cdots, v_{ne}^H({t_n}), \} $ ， $ v_{ij}^1({t_i}) $ 表示从客户 $ i $ 处的始发速度， $ v_{ne}^H({t_n}) $ 表示到达节点 $ e $ 的速度，而这一段旅行上经历的速度变化为 $ H + 1 $ 次，在每个速度间隔内的旅行距离为 $ {D_{ne}}({t_n}) = \{ d_{ne}^1, \cdots, $ $d_{ne}^h, \cdots, d_{ne}^H\}$ ，故 $ {\varphi _{ne}} = \{ \varphi _{ne}^1, \ldots $ $ \varphi _{ne}^h, \cdots \varphi _{ne}^H\} $ 。

3 模型求解 3.1 编码和种群初始化

针对本文的模型，提出以禁忌搜索算法为局部搜索方法，嵌入遗传算法的混合遗传算法，见图1。

令算法的群体规模为 $ N $ ，终止进化代数为 ${{Maxgen}}$ ，交叉概率为 ${p_{{c}}}$ ，变异概率为 ${p_{{m}}}$ 。本算法的核心思想是在满足仓容量和车辆装载的限制下，随机选择若干物资供给点(配送中心/转运中心)，并把受灾需求点分配给送达时间最短的仓库，该方法有利于在备选转运中心确定前产生较高效的配路径，同时保证种群的多样性。

3.2 适应度函数

首先将时间最小转化为最大，结合配送公平性最大，代入目标函数，然后把约束条件转换成惩罚函数，累加后取倒数生成适应度函数 $f(x)$ ，令目标1转化为最大后的函数为 ${z^{_1}}$ ，目标2为 ${z^2}$ ，两个目标的权重系数分别为 ${\omega _1}$ 和 ${\omega _2}$ ， $ {\omega _1} $ + $ {\omega _2} $ =1。约束惩罚函数为 $ R $ ， $ R = \displaystyle\sum\limits_{i \in I} {{k_i}{r_i}} $ ， $ {r_i} $ 表示每一项约束的约束溢出， $ {k_i} $ 表示每项约束溢出系数，即

$\quad\quad f(x) = \frac{1}{{{\omega _1}{z^1} + {\omega _2}{z^2} + \displaystyle\sum\limits_{i \in I} {{k_i}{r_i}} }}{\text{。}} $

(14)

3.3 遗传操作

1)选择算子。

为能够获得较优的目标解，在选择操作中，要对种群中的个体进行排序，因为适应度函数 $f(x)$ 是最小值，考虑按照支配系数和个体适应度联合对种群中的个体进行排序，具体规则如下。

(1) 当 $f({x_i}) \leqslant f({x_j})$ 时， ${x_i}$ 是当前运算 ${x_j}$ 的非占优解(支配解)，即 ${x_i}$ 可以支配 ${x_j}$ 。

(2) 定义种群中可以支配 ${x_j}$ 的个体数量为 $ g $ ， ${x_j}$ 的支配系数为 $ g $ ；若 ${x_j}$ 是此时整个种群的非占优解，则 $ g = 0 $ 。

(3) 假设两个目标的权重系数分别为 ${\omega _1}$ 和 ${\omega _2}$ ，则个体 ${x_j}$ 的适应度值为 $f({x_j}) = {\omega _1}{f^1}({x_j}) + {\omega _2}{f^2}({x_j})$ 。

因此选择过程可以从父代种群随机选择两个个体，若支配程度不同，则选择非占优解进行复制，否则通过小生镜法选择较小的小生镜个体进行复制^[10]。

2) 交叉操作。

本文结合禁忌搜索算法，设计混合遗传算法的交叉操作。遗传禁忌算法的交叉操作方式如下。

根据交叉概率 ${p_{ c}}$ 随机选择两个父代染色体( ${v_i}$ , ${v_j}$ )，对于第 $t$ 代种群，假设每代中父代的父代染色体 $ v $ 的价值为 ${w_t}(v)$ ，每个个体的交叉概率为 $ p_{{c}}^k(t) $ ，两个父代染色体 ${v_i}$ 和 ${v_j}$ 交叉操作为

$\quad\quad{w_{t + 1}}({v_i}, {v_j}) = ({w_t}({v_i}) + {w_t}({v_j}))/2{\text{。}} $

(15)

对第 $ t $ 代基因概率的修正公式为

$\quad\quad{p_{{c}}}(t + 1) = \exp \left[\frac{{{w_t}(v) - {w_{t + 1}}({v_i}, {v_j})}}{{{w_t}(v)}}\right].{p_{ c}}(t){\text{。}} $

(16)

其中，任一 ${p_{{c}}} \in (0, 1)$ 。同时，此交叉操作是自适应搜索，有利于算法搜索的有效性。

3) 变异操作。

变异过程可分解为路径变异操作和选址变异操作。

(1) 车辆路径变异中，把染色体中的转运中心点去除，使用 $2 - {{opt}}$ 变换对受灾需求点序列的子路径进行反转并重新排序。

(2) 转运中心选址的染色体变异中，在满足相关的车辆容量、仓容量约束前提下，以变异概率 ${p_{ m}}$ 将受灾需求点序列分配给一个备选转运中心，直到所有受灾需求点都有转运中心或配送中心对其进行救灾物品配送。

3.4 终止条件

达到遗传算法终止进化代数为 ${{Maxgen}}$ ，或符合最优解跳出条件，终止操作，输出计算结果。

4 算例分析

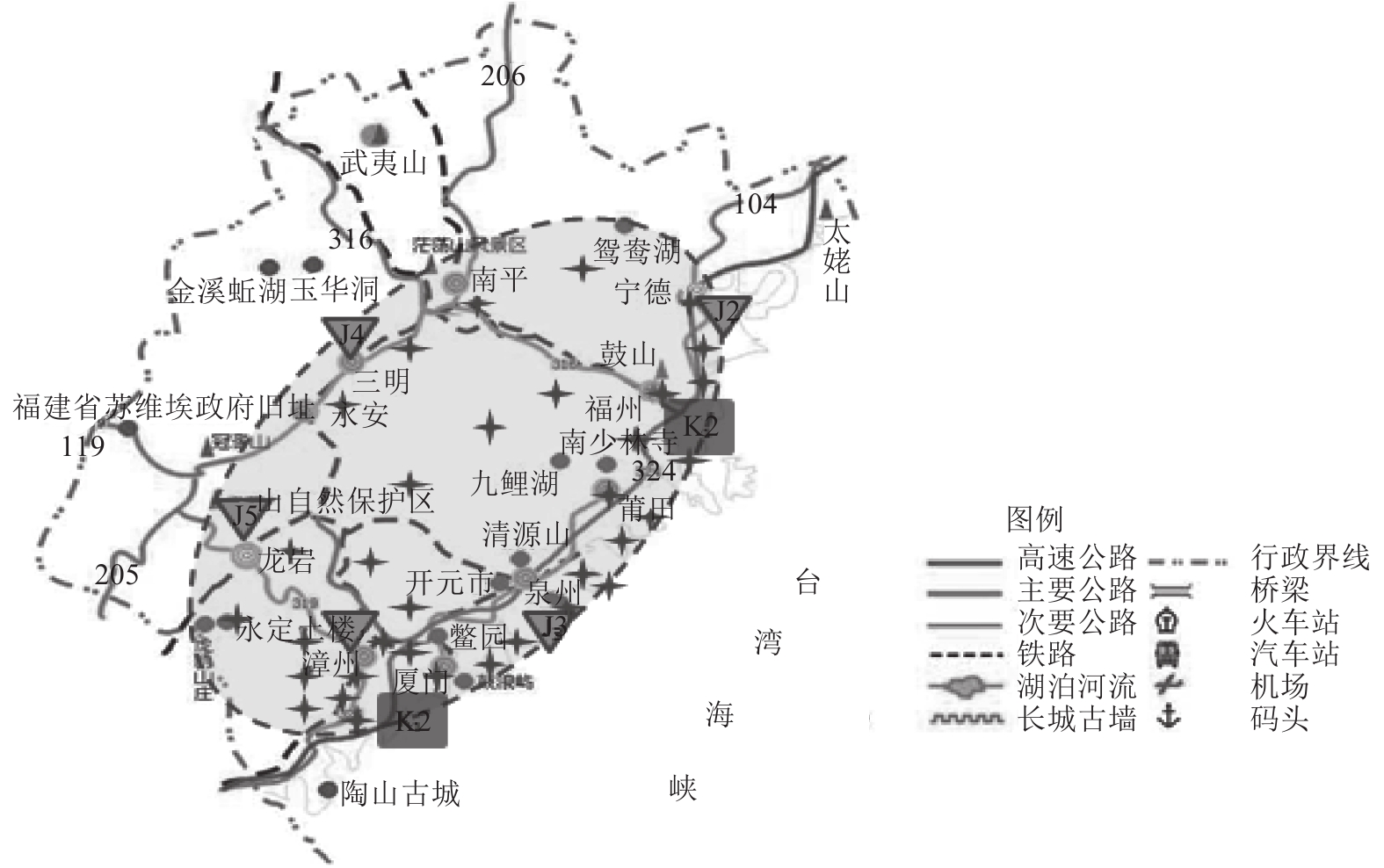
本节以2016年第14号台风“莫兰蒂”登陆福建省后的洪涝灾害应急救援为例。考虑资源的可得性和交通便利性，设厦门和福州为配送中心，漳州、泉州、宁德、三明和龙岩为备选转运中心，受灾需求点包括厦门、漳州、泉州、福州、三明、龙岩、宁德、莆田、南平及平潭综合实验区各县市，图2中的十字星表示受灾需求点。为方便表示，假设34个受灾需求点每个需求点的需求量服从均值为500的随机分布。配送中心A(厦门)、B(福州)的救援能力设为无限，转运中心a(漳州)、b(泉州)、c(宁德)、d(三明)和e(龙岩)，救援能力分别为6 000，6 000，5 500，7 000，5 000。路网信息由实时的地理信息平台提供，这里每3 min更新一次，并在每次更新后重新计算判断行驶路径。车辆的最大载重量为50，救援车辆的正常行驶速度为60 km/h，假设车辆供给能力完全。配送中心、转运中心以及受灾点坐标如表1所示(由于配送中心、转运中心均为受灾点，故将配送中心、转运中心统编为受灾点编号1，2，…，34)。灾区初始化各道路属性对车辆行驶速度的影响系数如表2~3所示。每个受灾点的卸货时间为0.1 h。

参数设置为：N=80，Maxgen=500，p_c=0.95，p_m=0.01。算法运行时间为512 s。图3为算法的收敛图。优化的最优配送时间为0.56×10⁶ s，最小满足度达93.62%，选择的备选转运中心是漳州、泉州、龙岩。

为说明实时交通信息相对于传统静态情景下的改进，对其结果进行比较(表4)。

从表4可见，传统静态情景下的车辆数和旅行距离都较小，但耗费的旅行时间和救灾满意度远低于实时交通信息下的结果。可见，在面临应急救援时，本文考虑实时交通信息更新的理论模型具有很强的优越性。

表4中动静态结果的差异主要是由道路车速影响系数引起的，为进一步分析传统静态情况和实时动态交通信息下道路通行状况对旅行时间的影响，本文研究了动静两种情景下速度影响系数对救援时间的影响(图4)。从图4中可以看出，速度影响系数越小，道路越不通畅，所花费的时间就越长。但随着系数的减小，在实时交通信息情景下花费运送时间远远低于传统静态情景。

5 结束语

本文针对灾后的物资调配问题，结合受灾区域道路受阻等特点，在实时交通信息下，以救灾时间最小和资源分配公平性最大为目标建立模型。并根据模型的特点设计了混合遗传算法对问题进行求解，最后以台风“莫兰蒂”登陆福建省后导致的洪涝灾后的物资救援过程为例，构建了数值算例。研究结果表明，实时交通信息的更新对缩短救灾时间和提高受灾需求点满足水平有极其重要的改善。但本文的研究未考虑多品种产品的区分，也未考虑随着灾后时间的推移，受灾需求点物资需求的动态改变。这些问题将是进一步研究的方向。