在知识经济时代的背景下,知识成为保持供应链企业核心竞争力和维持可持续发展的源泉[1]。供应链蕴藏着丰富的异质知识资源,共享知识资源可以节约知识获取和再利用成本,提高供应链的整体知识存量和知识创新水平,提升各成员企业的经营能力和运作效率,进而提高成员企业和供应链绩效和竞争优势[2]。但由于知识的不可编码和复杂性以及知识共享过程中存在许多固有的障碍因素[3],使得供应链成员企业在没有激励的情形下主动共享知识的现象较少发生。此外,知识本身又难以度量其外部特性[4],造成知识共享努力水平难以被精确监测,成员企业在知识共享活动中易出现“搭便车”现象,影响了供应链的运作效率,破坏了供应链的协调性[5]。因此在不对称信息条件下供应链核心企业如何设计激励机制促进供应链知识共享,一直是学者们关注的热点。当前,国内外学者对知识共享激励开展了广泛研究。Siemen[6]认为激励可以增加团队知识共享行为;Zhang[7]指出物质激励可以促进知识共享的进行;Choi[8]认为相较于技术支持手段,薪酬激励更能促进知识共享。Xie等[9]通过整合经济、社会、心理方面的理论,构建并测试了基于多理论和多因素视角的知识共享激励机制理论框架。Nan等[10]将知识按照其无形性进行分类,在不对称信息条件下,构建了共享不同类型知识的激励模型。杨湘浩等[11]运用委托代理理论研究了企业隐形知识共享激励问题,指出对称信息下企业隐形知识共享努力水平能实现帕累托最优,而非对称信息下无法实现。樊斌等[12]研究了具有不同风险偏好的企业员工的知识共享激励措施。Wang等[13]考虑知识互补性,在委托代理理论框架下,分别设计了代理人风险中性和规避型的激励契约。Liu等[14]基于知识互补性和知识整合能力相结合的视角,提出了电子商务服务供应链的知识共享激励模型。安小风[15]提出了基于个人、企业、组织3个层次的供应链知识共享空间模型,并针对不同的层次提出了对应的激励措施和建议。
这些研究仅限于通过激励来诱导知识共享活动的进行,未涉及将激励与监督机制相结合的研究。而已有的实证研究表明,以产出为标准的薪酬激励并不能防止代理人的不作为或自利行为,应对代理人实施监督[16]。一些学者研究了知识共享激励与监督相结合的机制。Nesheim等[17]认为监督机制有利于知识共享活动的发生。来尧静[18]运用博弈论研究了知识共享的博弈,发现无激励时团队成员陷入“囚徒困境”,反之则有益于知识共享,且企业观测和监督力度越大顾客越容易参加知识共享。魏道江等[19]提出一种基于知识接受者评价模式的知识共享激励机制,该机制的核心是组织将知识共享产出的分配权转移给知识接受者,通过知识接受者对知识转移效果的评价实现间接监督知识共享过程的目的。马轶德等[5]将监控信号和激励机制共同纳入到供应链报酬契约设计中,探讨了监督机制对契约设计的合理性和降低供应链道德风险的作用。
但上述研究都是在“理性经济人”的假设基础上进行的。近年来,“理性经济人”的假设受到越来越多的质疑,现实中人们不仅关注自身收益,还关注他人收益,也关注收益分配公平问题。并且,实验经济学的研究表明,一些社会偏好,尤其是公平偏好具有重要经济意义,在许多情境下,公平偏好影响人们的行为[20]。目前,国内外已有部分文献将公平偏好植入到知识共享激励研究中。胡新平等[21]将创新知识产权引入到研发团队员工知识共享激励模型中,分析了不同公平偏好心理对业绩激励和创新知识产权激励的影响。施建刚等[22]运用委托代理理论研究了具有横向公平偏好的项目团队成员知识共享激励问题,发现横向公平偏好在不同的知识共享风险成本下对个体激励和团队激励的影响具有复杂性。他们的研究重点是公平偏好对知识共享激励效果的影响,未考虑对激励与监督相结合机制的作用。而且现有知识共享激励与监督相结合的文献多是对监督作用的认可,缺乏量化的监督模型。笔者尚未检索到将公平偏好与专门针对供应链这种形式的知识共享激励与监督机制相结合的研究。
鉴于上述分析,本文在委托代理理论的框架下,引入核心企业对成员企业的监督函数,并将公平偏好与供应链知识共享激励与监督问题相结合,探讨成员企业公平偏好、核心企业监督水平、激励系数、奖惩系数等的相互关系。
1 问题描述与假设借鉴已有成果[12, 22-23],假设由一个核心企业和两个同质的成员企业构成的供应链,同时两个成员企业之间具有横向公平偏好,设计考虑核心企业对成员企业的监督以及成员企业彼此间的横向公平偏好心理的收益共享契约,如图1所示。虽然在供应链中确实存在上下游企业之间利益比较的纵向公平偏好,但同级成员企业收益比较的横向公平偏好更具普遍性[22]。此时核心企业主要是根据成员企业的公平偏好心理和观测到的知识共享努力水平,实施适当的激励和监督措施,促使成员企业选择对核心企业最有利的行动,达到核心企业效用最大化的目标。成员企业是根据核心企业提供的契约,决定是否接收,及如果接收应采用的最优努力水平。
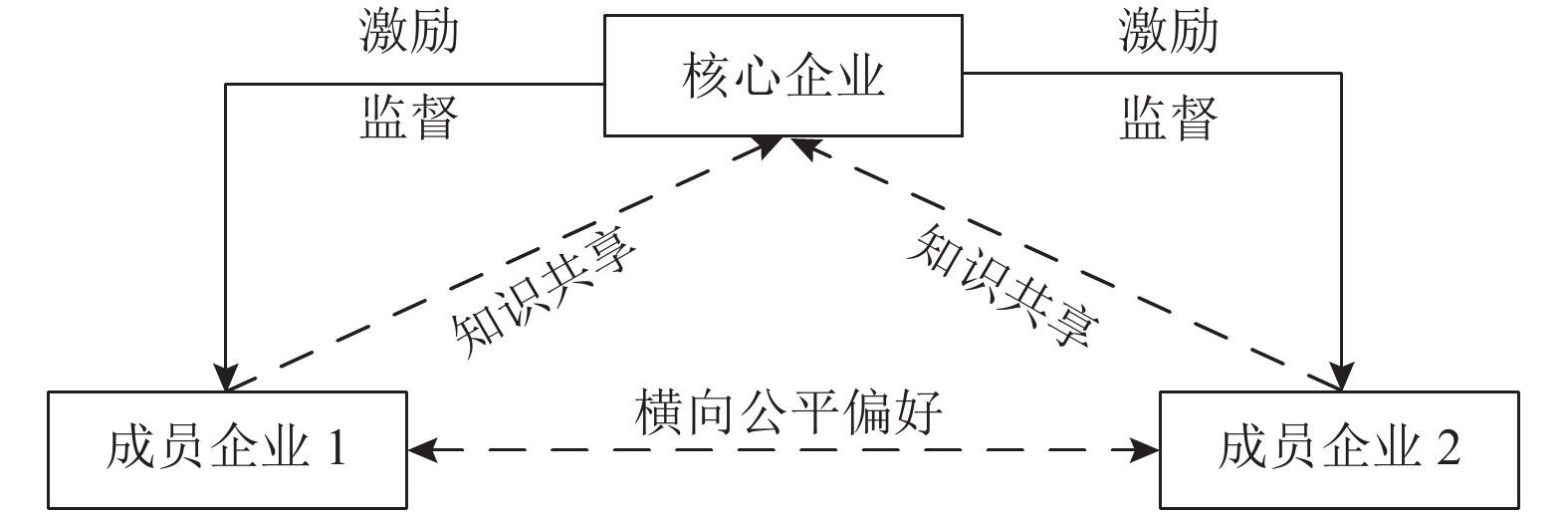
|
图 1 考虑横向公平偏好的供应链知识共享激励与监督 Fig. 1 Considering the horizontal fairness preference for supply chain knowledge sharing incentives and supervision |
在本模型中,将供应链中的核心企业看作是委托人,成员企业看作是代理人。为了简化上述问题,给出如下基本假设。
1) 考虑由1个核心企业(M)和2个同质成员企业
2) 用一维决策变量
3) 成员企业同核心企业进行知识共享时需要花费一定的成本。为了简化模型,暂不考虑外生变量对知识共享成本的影响,成员企业知识共享成本函数为:
4) 核心企业为了更有效地推动知识共享活动的发生,需将激励与监督机制相整合,考虑引入核心企业对成员企业的监督函数,即核心企业根据观测到成员企业参与知识共享活动所付出的努力水平来实施奖惩。成员企业的努力水平必须达到
5) 为了提高成员企业进行知识共享的积极性,核心企业需要给成员企业提供一定的激励合同。线性激励合同能实现激励合约最优化,且目前研究中多采用线性激励[22-24],这里也采用该形式,具体如下:
6) 当具有横向公平偏好的成员企业进行知识共享时,成员企业的实际净收益除了包括自身所得的随机净收益以外,还包括相互之间绝对收益比较的部分。根据FS公平偏好模型[22, 25],假定公平偏好效用
所以供应链中的成员企业的实际收益为
| ${\omega _i} = {s_i} - {c_i} + {U_i} = a + \beta ({\lambda _i}{e_i} + {\varepsilon _i}) + \eta ({e_i} + {\theta _i} - m) - \frac{{b{e_i}^2}}{2} + {U_i}{\text{。}}$ | (1) |
因为成员企业为风险规避性,根据Hsu[26]结论,成员企业风险成本为
| $\quad\quad\left\{ \begin{array}{l}\omega _1' \!\!=\! a \!+\! \beta [{\lambda _1}{e_1} \!+\! k({\lambda _1}{e_1} \!-\! {\lambda _2}{e_2})] + \eta ({e_1} \!-\! m) + \\[8pt]\quad k\eta ({e_1} - {e_2}) - \displaystyle\frac{{b{e_1}^2}}{2} - \displaystyle\frac{{\rho ({\beta ^2}{\sigma ^2} + {\eta ^2}({\delta ^2}{{ - }}\xi ))}}{2},\\[8pt]{\omega _2}' \!\!=\! a \!+\! \beta [{\lambda _2}{e_2} \!+\! k({\lambda _2}{e_2} \!-\! {\lambda _1}{e_1})] \!+\! \eta ({e_2} \!-\! m) + \\[8pt]\quad k\eta ({e_2} - {e_1}) - \displaystyle\frac{{b{e_2}^2}}{2} - \displaystyle\frac{{\rho ({\beta ^2}{\sigma ^2} + {\eta ^2}({\delta ^2}{{ - }}\xi ))}}{2}{\text{。}}\end{array} \right.$ | (2) |
核心企业的实际收益为
| $\begin{split} &\quad\quad \varphi = {\pi _1} + {\pi _2} - {s_1} - {s_2} - {d_1} - {d_2} = - 2a + \left( {1 - \beta } \right) \left( {{\lambda _1}{e_1}\!+\! }\right.\\[2pt] &\left.{ {\lambda _2}{e_2} \!+\! {\varepsilon _1} \!+\! {\varepsilon _2}} \right) \!-\! \eta ({e_1} \!+\! {e_2} \!+\! {\theta _1} \!+\! {\theta _2} \!-\! 2m) \!-\! \phi {\xi ^2}{\text{。}}\quad\quad\;\;\;\;\;\;\;\;\;\;\;(3)\end{split}$ |
核心企业为风险中性,期望效益与期望效用等价:
| $E(\varphi ) \!= \! - 2a + \left( {1 \!-\! \beta } \right)\left( {{\lambda _1}{e_1} \!+\! {\lambda _2}{e_2}} \right) -\eta ({e_1} \!+\! {e_2}\! -\! 2m) \!-\! \phi {\xi ^2}{\text{。}}$ | (4) |
令
| $\quad\quad \left\{ \begin{array}{l}a + \beta [{\lambda _1}{e_1} + k({\lambda _1}{e_1} - {\lambda _2}{e_2})] + \eta ({e_1} - m) +\\[10pt]\;\;\; k\eta ({e_1} \!-\! {e_2}) \!-\!\! \displaystyle\frac{{b{e_1}^2}}{2} \!\!-\!\! \displaystyle\frac{{\rho ({\beta ^2}{\sigma ^2} \!+\! {\eta ^2}({\delta ^2}{{ - }}\xi ))}}{2} \!{\text{≥}} \overline {{\omega _1}} ,\\[10pt]a + \beta [{\lambda _2}{e_2} + k({\lambda _2}{e_2} - {\lambda _1}{e_1})] + \eta ({e_2} - m) +\\[10pt]\;\;\; k\eta ({e_2}\! - \!{e_1}) \!-\!\! \displaystyle\frac{{b{e_2}^2}}{2} \!\!-\!\! \displaystyle\frac{{\rho ({\beta ^2}{\sigma ^2} \!+\! {\eta ^2}({\delta ^2}{{ \!-\! }}\xi ))}}{2}\! {\text{≥}} {\overline {\omega _2}}{\text{。}}\end{array} \right.$ | (5) |
在成员企业同核心企业知识共享时,成员企业同核心企业存在信息不对称情况。成员企业利用自己的信息优势,选择一个低知识共享努力水平,最大化自己的确定性等价收益,而核心企业受制于监督成本不可能完全观测到成员企业努力水平。因此成员企业还需满足激励相容约束,即等价于最大化式(2)。这样,考虑公平偏好的供应链知识共享激励监督机制的设计实际上就是求解下列最优化的问题,确定e1,e2,β,η值。
| $\quad\quad \mathop {\max }\limits_{{e_1},{e_2},\beta ,\eta } E(\varphi ){\text{。}}$ | (6) |
| $\quad\quad {{s}}.{{t}}.\left\{ \begin{array}{l}\left( {{{IR}}} \right):{\omega _i}' {\text{≥}} \overline {{\omega _i}} ;\\[5pt]\left( {{{IC}}} \right):{e_i} \in \arg \max\;{\omega _i}'{\text{。}}\end{array} \right.$ | (7) |
首先由激励约束条件(IC)可求得成员企业
| $\quad\quad \left\{ \begin{array}{l}e_1^* = \displaystyle\frac{{(\beta {\lambda _1} + \eta )(1 + k)}}{b},\\[8pt]e_2^* = \displaystyle\frac{{(\beta {\lambda _2} + \eta )(1 + k)}}{b}{\text{。}}\end{array} \right.$ | (8) |
| $\left\{ \begin{array}{l}E(\varphi ) =\displaystyle\frac{{{\lambda _1}(1 + k)(\beta {\lambda _1} + \eta )}}{b} + \displaystyle\frac{{{\lambda _2}(1 + k)(\beta {\lambda _2} + \eta )}}{b} - \\[12pt]\;\;\;\displaystyle\frac{{{{(\beta {\lambda _1} + \eta )}^2}{{(1 + k)}^2}}}{{2b}} - \displaystyle\frac{{{{(\beta {\lambda _2} + \eta )}^2}{{(1 + k)}^2}}}{{2b}} -\\[12pt]\;\;\;\;\rho ({\beta ^2}{\sigma ^2} + {\eta ^2}({\delta ^2}{{ - }}\xi )) -\overline {{\omega _2}} - \overline {{\omega _1}} - \phi {\xi ^2},\\[12pt]\displaystyle\frac{{\partial E(\varphi )}}{{\partial \beta }} = \displaystyle\frac{{{\lambda _1}^2(1 + k)}}{b} + \displaystyle\frac{{{\lambda _2}^2(1 + k)}}{b} - \\[12pt]\;\;\;\;\displaystyle\frac{{(\beta {\lambda _1} \!+\! \eta ){{(1 \!+\! k)}^2}{\lambda _1}}}{b} \!-\! \displaystyle\frac{{(\beta {\lambda _2} \!+\! \eta ){{(1 \!+\! k)}^2}{\lambda _2}}}{b} \!-\! 2\rho \beta {\sigma ^2},\\[12pt]\displaystyle\frac{{{\partial ^2}E(\varphi )}}{{\partial {\beta ^2}}} \!=\! - \displaystyle\frac{{{\lambda _1}^2{{(1 \!+\! k)}^2}}}{b} \!-\! \displaystyle\frac{{{\lambda _2}^2{{(1 \!+\! k)}^2}}}{b} \!-\! 2\rho {\sigma ^2}{\text{<}} 0{\text{。}}\end{array} \right.$ | (9) |
可知目标函数存在最大值,令供应链知识共享激励监督一阶条件
| $\quad\quad{\beta ^{{*}}}{{ = }}\frac{{({\lambda _1}^2{{ + }}{\lambda _2}^2)(1 + k) - \eta ({\lambda _1} + {\lambda _2}){{(1 + k)}^2}}}{{2b\rho {\sigma ^2} + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}}}{\text{。}}$ | (10) |
同理,可得
| $\quad\quad{\eta ^{{*}}}{{ = }}\frac{{({\lambda _1}{{ + }}{\lambda _2})(1 + k) - \beta ({\lambda _1} + {\lambda _2}){{(1 + k)}^2}}}{{2b\rho ({\delta ^2} - \xi ) + 2{{(1 + k)}^2}}}{\text{。}}$ | (11) |
联立式(10)和式(11),可得:
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad{\beta ^{{*}}}{{ = }}\frac{{2b\rho ({\delta ^2} - \xi )({\lambda _1}^2{{ + }}{\lambda _2}^2)(1 + k){{ + }}{{({\lambda _1}{{ - }}{\lambda _2})}^2}{{(1 + k)}^3}}}{{[2b\rho {\sigma ^2} + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}][2b\rho ({\delta ^2} - \xi ) + 2{{(1 + k)}^2}] - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4}}},$ | (12) |
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad{\eta ^{{*}}}{{ = }}\frac{{2b\rho {\sigma ^2}({\lambda _1}{{ + }}{\lambda _2})(1 + k)}}{{[2b\rho {\sigma ^2} + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}][2b\rho ({\delta ^2} - \xi ) + 2{{(1 + k)}^2}] - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4}}}{\text{。}}$ | (13) |
将
| $\quad\quad\quad\quad\quad\quad\quad\left\{ \begin{array}{l} e_1^* = \displaystyle\frac{{[{\lambda _1}(2b\rho ({\delta ^2} - \xi )({\lambda _1}^2{{ + }}{\lambda _2}^2)(1 + k){{ + }}{{({\lambda _1}{{ - }}{\lambda _2})}^2}{{(1 + k)}^3}{{) + }}2b\rho {\sigma ^2}({\lambda _1}{{ + }}{\lambda _2})(1 + k)](1 + k)}}{{b[(2b\rho {\sigma ^2} + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2})(2b\rho ({\delta ^2} - \xi ) + 2{{(1 + k)}^2}) - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4})]}}, \\[14pt] e_2^* = \displaystyle\frac{{[{\lambda _2}(2b\rho ({\delta ^2} - \xi )({\lambda _1}^2{{ + }}{\lambda _2}^2)(1 + k){{ + }}{{({\lambda _1}{{ - }}{\lambda _2})}^2}{{(1 + k)}^3}{{) + }}2b\rho {\sigma ^2}({\lambda _1}{{ + }}{\lambda _2})(1 + k)](1 + k)}}{{b[(2b\rho {\sigma ^2} + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2})(2b\rho ({\delta ^2} - \xi ) + 2{{(1 + k)}^2}) - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4})]}} {\text{。}} \\ \end{array} \right.$ | (14) |
结论1 在供应链知识共享激励与监督均衡状态下,成员企业的横向公平偏好影响核心企业对其奖惩系数,且横向公平偏好对最优奖惩系数的影响具有多样性。当
设
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\frac{{\partial {\eta ^{{*}}}}}{{\partial k}}{{ = }}\frac{{A({\lambda _1}{{ + }}{\lambda _2})[AB - (2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B){{(1 + k)}^2} - 3{{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}}{{[A + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}][B + 2{{(1 + k)}^2}] - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4}}}{\text{。}}$ | (15) |
当
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \left\{ \begin{array}{l} {(1 + k)^2} {\text{<}} \displaystyle\frac{{AB}}{{2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B}}, \;\;\; \displaystyle\frac{{\partial {\eta ^{{*}}}}}{{\partial k}} {\text{>}} 0 ; \\[18pt] {(1 + k)^2} = \displaystyle\frac{{AB}}{{2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B}}, \;\;\; \displaystyle\frac{{\partial {\eta ^{{*}}}}}{{\partial k}} = 0 ;\\[18pt] {(1 + k)^2} {\text{>}} \displaystyle\frac{{AB}}{{2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B}}, \;\;\; \displaystyle\frac{{\partial {\eta ^{{*}}}}}{{\partial k}} {\text{<}} 0{\text{。}}\end{array} \right.$ | (16) |
当
| $\quad\quad\quad\quad\quad\quad\quad\quad \left\{ \begin{array}{l} {(1 + k)^2} {\text{<}} \displaystyle\frac{{ - (2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B) + \sqrt {{{(2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B)}^2} + 12AB{{({\lambda _1} - {\lambda _2})}^2}} }}{{6{{({\lambda _1} - {\lambda _2})}^2}}}, \;\;\; \displaystyle\frac{{\partial {\eta ^{{*}}}}}{{\partial k}} {\text{>}} 0 ; \\[18pt] {(1 + k)^2} = \displaystyle\frac{{ - (2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B) + \sqrt {{{(2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B)}^2} + 12AB{{({\lambda _1} - {\lambda _2})}^2}} }}{{6{{({\lambda _1} - {\lambda _2})}^2}}}, \;\;\; \displaystyle\frac{{\partial {\eta ^{{*}}}}}{{\partial k}} = 0 ; \\[18pt] {(1 + k)^2} {\text{>}} \displaystyle\frac{{ - (2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B) + \sqrt {{{(2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B)}^2} + 12AB{{({\lambda _1} - {\lambda _2})}^2}} }}{{6{{({\lambda _1} - {\lambda _2})}^2}}}, \;\;\; \displaystyle\frac{{\partial {\eta ^{{*}}}}}{{\partial k}} {\text{<}} 0 {\text{。}} \\ \end{array} \right.$ | (17) |
结论2 成员企业的横向公平并不一定与激励正相关,成员企业的横向公平偏好对激励系数的影响还取决于成员企业的风险成本、成员企业知识共享产出系数、核心企业的监督水平的交互作用。当公平偏好小于上述三者交互作用的影响程度时,激励系数随着成员企业公平偏好的增加而降低,当公平偏好大于上述三者交互作用的影响程度时,激励系数随着成员企业公平偏好的增加而增加。
由式(10)可知
| $\quad\quad\quad\quad\quad\quad\quad\quad\begin{split} & \displaystyle\frac{{\partial {\beta ^{{*}}}}}{{\partial k}}{{ = }}\frac{{A{B^2}({\lambda _1}^2{{ + }}{\lambda _2}^2) - 2AB({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} - {B^2}{{({\lambda _1}^2{{ + }}{\lambda _2}^2)}^2}{{(1 + k)}^2}}}{{[A + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}][B + 2{{(1 + k)}^2}] - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4}}} + \\[8pt] &\displaystyle\frac{{ - 2B({\lambda _1}^2{{ + }}{\lambda _2}^2){{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4} + 2A{{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4} - {{({\lambda _1} - {\lambda _2})}^4}{{(1 + k)}^6}}}{{[A + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}][B + 2{{(1 + k)}^2}] - {{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^4}}} {\text{。}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{split}$ | (18) |
当
| $\quad\quad\left\{ \begin{array}{l} {(1 + k)^2} {\text{<}} \displaystyle\frac{{AB}}{{2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B}}, \;\;\; \displaystyle\frac{{\partial {\beta ^{{*}}}}}{{\partial k}} {\text{>}} 0 ; \\[15pt] {(1 + k)^2} = \displaystyle\frac{{AB}}{{2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B}}, \;\;\; \displaystyle\frac{{\partial {\beta ^{{*}}}}}{{\partial k}} = 0 ; \\[15pt] {(1 + k)^2} {\text{>}} \displaystyle\frac{{AB}}{{2A + ({\lambda _1}^2{{ + }}{\lambda _2}^2)B}}, \;\;\; \displaystyle\frac{{\partial {\beta ^{{*}}}}}{{\partial k}} {\text{<}} 0 {\text{。}} \\ [15pt]\end{array} \right.$ | (19) |
当
结论3 成员企业的知识共享努力水平随着其公平偏好强度的增加而增加,即公平偏好感强的企业具有更高的努力水平。
式(14)等价于:
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\left\{ \begin{array}{l} e_1^* = \displaystyle\frac{{{\lambda _1}}}{b} + \displaystyle\frac{{A({\lambda _2} - {\lambda _1}){{(1 + k)}^2} - {\lambda _1}AB}}{{b[AB + B({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} + 2A{{(1 + k)}^2} + {{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}} , \\[15pt] e_2^* = \displaystyle\frac{{{\lambda _2}}}{b} + \displaystyle\frac{{A({\lambda _1} - {\lambda _2}){{(1 + k)}^2} - {\lambda _2}AB}}{{b[AB + B({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} + 2A{{(1 + k)}^2} + {{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}} {\text{。}} \\ \end{array} \right.$ | (20) |
由上式可知:
结论4 成员企业的知识共享努力水平随着核心企业监督水平的提升而提升。
对式(14)求关于
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\left\{ \begin{array}{l} \displaystyle\frac{{\partial e_1^*}}{{\partial \xi }} = \displaystyle\frac{{2\rho {\lambda _1}A{{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4} + 4\rho {\lambda _1}{A^2}{{(1 + k)}^2}}}{{b{{[AB + B({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} + 2A{{(1 + k)}^2} + {{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}^2}}} {\text{>}} 0 , \\[15pt] \displaystyle\frac{{\partial e_2^*}}{{\partial \xi }} = \displaystyle\frac{{2\rho {\lambda _2}A{{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4} + 4\rho {\lambda _2}{A^2}{{(1 + k)}^2}}}{{b{{[AB + B({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} + 2A{{(1 + k)}^2} + {{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}^2}}} {\text{>}} 0 {\text{。}} \\ \end{array} \right.$ | (21) |
由上式可知核心企业监督水平提高,成员企业的知识共享努力水平也会提升,即监督机制能有效抑制供应链中成员企业偷懒的问题,这与实际相符。核心企业监督水平越高,其对成员企业的知识共享努力水平的信息越了解,成员企业“搭便车”等机会主义行为被发现的概率就越高,面临被惩罚的损失,成员企业会提高自己的努力水平。
结论5 随着核心企业监督水平的提升,其会增加对成员企业的奖惩比例,相应地降低产出分配比例。
对式(12)、式(13)求关于
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\frac{{\partial {\beta ^{{*}}}}}{{\partial \xi }}{{ = }}\frac{{ - 2b\rho A{{({\lambda _1} + {\lambda _2})}^2}{{(1 + k)}^3}}}{{{{[AB + B({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} + 2A{{(1 + k)}^2} + {{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}^2}}} {\text{<}} 0,$ | (22) |
| $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\frac{{\partial {\eta ^{{*}}}}}{{\partial \xi }}{{ = }}\frac{{{A^2}({\lambda _1}{{ + }}{\lambda _2})(1 + k)}}{{{{[AB + B({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2} + 2A{{(1 + k)}^2} + {{({\lambda _1} - {\lambda _2})}^2}{{(1 + k)}^4}]}^2}}} {\text{>}} 0{\text{。}}$ | (23) |
这是个显而易见的结果,如果核心企业的监督只是流于形式,其不能很好地掌握成员企业的努力水平信息,通过奖惩函数来激励成员企业的力水平具有很大的误差性,核心企业会倾向于根据知识共享产出来激励成员企业;反之,当核心企业监督水平较高时,其对成员企业的努力水平信息能够准确观测,所以选择更能反映成员企业努力水平的奖惩激励来诱使成员企业进行知识共享活动,相应地降低产出激励的比例。
结论6 激励与监督都可以促使成员企业努力共享知识,两者可以作为促进知识共享的互补手段。
对式(10)求导,得
| $\quad\quad\displaystyle\frac{{\partial {\beta ^*}}}{{\partial {\eta ^*}}} = \displaystyle\frac{{ - ({\lambda _1} + {\lambda _2}){{(1 + k)}^2}}}{{2b\rho {\sigma ^2} + ({\lambda _1}^2{{ + }}{\lambda _2}^2){{(1 + k)}^2}}} {\text{<}} 0{\text{。}}$ | (24) |
可知
为了进一步阐述模型的有效性和实际运用价值,给出相应的数值算例并对其进行分析。为了简化分析,假设
| 表 1 不同偏好强度和监督水平的数值计算表 Tab. 1 Numerical calculation of different preference intensity and supervisory level |
表1显示公平偏好强度和监督水平共同影响成员企业知识共享努力水平,核心企业的奖惩系数和激励系数。核心企业提高自己的监督水平和选择较高横向公平偏好感的成员企业有助于知识共享的进行。
5 结论为了推动供应链知识共享活动的进行及防范共享过程中可能出现的道德风险,本文构建了供应链知识共享激励与监督模型,并将公平偏好理论植入到该模型中,探讨成员企业公平偏好心理对供应链知识共享激励与监督效果的影响。研究结果表明:激励和监督机制是影响成员企业知识共享努力水平的重要因素,两者可以作为互补手段来促进供应链知识共享的进行,选择合适的奖惩系数和激励系数能够促进成员企业更加努力地共享知识;奖惩系数和激励系数是由核心企业的监督精度与成员企业的风险偏好强度共同决定;成员企业知识共享努力水平随着其公平偏好的强度增加而增加,随着核心企业监督精度的提升而增加;随着核心企业监督水平的提升,核心企业对成员企业的努力水平更加了解,从而核心企业给成员企业的报酬支付契约中会增加奖惩的比例,降低产出分成的比例。
根据本文研究结论,提出如下建议。1) 建立有效的激励与监督机制。在组织方面以核心企业为主导,成员企业参与,核心企业实施激励与监督;在分配方面坚持收益共享,风险共担,做到促进公平,实现效率;在监督方面,严格惩罚,防止机会主义。2) 充分利用成员企业的公平偏好心理。在合作企业选择上适当挑选具有高公平偏好感的成员企业;在契约设计上综合考虑公平偏好与监督精度、风险成本、知识共享产出系数的交互作用,选择合适的奖惩系数和激励系数,最大限度地调动成员企业积极性。
| [1] |
PATON R A, MCLAUGHLIN S. Services innovation: knowledge transfer and the supply chain[J].
European Management Journal, 2008, 26(2): 77-83.
DOI: 10.1016/j.emj.2008.01.004. |
| [2] |
翁莉, 仲伟俊, 鲁芳. 供应链知识共享的决策行为及影响因素研究[J].
管理学报, 2009, 6(12): 1648-1652.
WENG Li, ZHONG Weijun, LU Fang. Study on decision-making behavior and influencing factors of knowledge sharing in supply chain[J]. Chinese Journal of Management, 2009, 6(12): 1648-1652. DOI: 10.3969/j.issn.1672-884X.2009.12.015. |
| [3] |
RAZMERITA L, KIRCHNER K, NIELSEN P. What factors influence knowledge sharing in organizations? A social dilemma perspective of social media communication[J].
Journal of Knowledge Management, 2016, 20(6): 1225-1246.
DOI: 10.1108/JKM-03-2016-0112. |
| [4] |
MA W W K, CHAN A. Knowledge sharing and social media: altruism, perceived online attachment motivation, and perceived online relationship commitment[J].
Computers in Human Behavior, 2014, 39: 51-58.
DOI: 10.1016/j.chb.2014.06.015. |
| [5] |
马轶德, 张旭梅, 陈伟. 考虑监控信号的供应链知识共享激励机制研究[J].
管理学报, 2012, 9(12): 1838-1841.
MA Yide, ZHANG Xumei, CHEN Wei. Incentive mechanism for knowledge sharing considering monitorin signal[J]. Chinese Journal of Management, 2012, 9(12): 1838-1841. |
| [6] |
SIEMSEN E, BALASUBRAMANIAN S, ROTH A V. Incentives that induce task-related effort, helping, and knowledge sharing in workgroups[J].
Management Science, 2007, 53(10): 1533-1550.
DOI: 10.1287/mnsc.1070.0714. |
| [7] |
ZHANG L, ZHANG Z. The effects of incentive mechanism on knowledge management performance in China: the moderating role of knowledge attributes[J].
Project Management Journal, 2014, 45(2): 34-47.
DOI: 10.1002/pmj.21403. |
| [8] |
CHOI S Y, KANG Y S, LEE H. The effects of socio-technical enablers on knowledge sharing: an exploratory examination[J].
Journal of Information Science, 2008, 34(5): 742-754.
DOI: 10.1177/0165551507087710. |
| [9] |
XIE H, LIU C. Incentive mechanism of employees knowledge sharing based on multi-theory perspective[J].
R&D Management, 2014, 2: 5.
|
| [10] |
NAN N. A principal-agent model for incentive design in knowledge sharing[J].
Journal of Knowledge Management, 2008, 12(3): 101-113.
DOI: 10.1108/13673270810875895. |
| [11] |
杨湘浩, 刘云. 企业隐性知识共享激励机制研究[J].
中国管理科学, 2012(s1): 80-83.
YANG Xianghao, LIU Yun. Incentive mechanism research on tacit knowledge sharing with in the enterprise[J]. Chinese Journal of Management Science, 2012(s1): 80-83. |
| [12] |
樊斌, 鞠晓峰. 不完全信息条件下知识共享激励机制研究[J].
科学学研究, 2009, 27(9): 1365-1369.
FAN Bin, JU Xiaofeng. A research on incentive mechanism of knowledge sharing under incomplete information[J]. Studies in Science of Science, 2009, 27(9): 1365-1369. |
| [13] |
WANG M, SHAO C. Special knowledge sharing incentive mechanism for two clients with complementary knowledge: a principal-agent perspective[J].
Expert Systems with Applications, 2012, 39(3): 3153-3161.
DOI: 10.1016/j.eswa.2011.09.001. |
| [14] |
LIU Z, SHANG J, LAI M. Incentive mechanism for knowledge sharing in E-commerce service supply chain: complementarity, integration and risk attitude[J].
Journal of Electronic Commerce Research, 2015, 16(3): 175-193.
|
| [15] |
安小风, 张旭梅, 张玉蓉. 基于供应链知识共享层次的激励机制研究[J].
科技管理研究, 2007, 27(2): 189-191.
AN Xiaofeng, ZHANG Xumei, ZHANG Yurong. Research on incentive mechanism based on knowledge sharing level of supply chain[J]. Science and Technology Management Research, 2007, 27(2): 189-191. |
| [16] |
武开, 张慧颖. 委托代理关系下监督强度与激励机制设计[J].
系统工程, 2016(7): 68-72.
WU Kai, ZHANG Huiying. Supervisory intensity and incentive mechanism based on principal-agency relationship[J]. Systems Engineering, 2016(7): 68-72. |
| [17] |
NESHEIM T, GRESSGÅRD L J. Knowledge sharing in a complex organization: antecedents and safety effects[J].
Safety Science, 2014, 62(62): 28-36.
|
| [18] |
来尧静, 宋秀林, 姚山季. 顾客参与企业产品创新过程中的知识共享博弈分析[J].
南京工业大学学报(社会科学版), 2015, 14(3): 112-117.
LAI Yaojing, SONG Xiulin, YAO Shanji. Game analysis of knowledge sharing in customer participation into enterprise product innovation[J]. Journal of Nanjing Tech University (Social Science Edition), 2015, 14(3): 112-117. |
| [19] |
魏道江, 李慧民, 康承业. 组织内部知识共享激励机制研究——基于知识接受者评价模式[J].
科学学与科学技术管理, 2014, 35(7): 23-30.
WEI Daojiang, LI Huiming1, KANG Chengye. A research on incentive mechanism of knowledge sharing within the organization: a model based on the evaluation of knowledge recipient[J]. Science of Science and Management of S & T, 2014, 35(7): 23-30. |
| [20] |
DANA J, WEBER R A, KUANG J X. Exploiting moral wiggle room: experiments demonstrating an illusory preference for fairness[J].
Economic Theory, 2007, 33(1): 67-80.
DOI: 10.1007/s00199-006-0153-z. |
| [21] |
胡新平, 胡明清, 邓腾腾. 基于公平偏好的研发团队知识共享激励机制研究[J].
商业研究, 2013(10): 82-87.
DOI: 10.3969/j.issn.1001-148X.2013.10.013. |
| [22] |
施建刚, 林陵娜, 唐代中. 考虑横向公平偏好的项目团队成员知识共享激励研究[J].
运筹与管理, 2015, 24(6): 242-250.
SHI Jiangang, LIN Lingna, TANG Daizhong. Study on knowledge sharing incentive within project team based onhorizontal fairness preference[J]. Operations Research and Management Science, 2015, 24(6): 242-250. |
| [23] |
陈克贵, 黄敏, 王兴伟. 双重信息不对称下虚拟企业监督策略[J].
控制与决策, 2013(9): 1288-1293.
CHEN Kegui, HUANG Min, WANG Xingwei. Monitoring strategies of virtual enterprise under dual information asymmetry[J]. Control and Decision, 2013(9): 1288-1293. |
| [24] |
袁茂, 雷勇, 蒲勇健. 基于公平偏好理论的激励机制与代理成本分析[J].
管理工程学报, 2011, 25(2): 82-86.
YUAN Mao, LEI Yong, PU Yongjian. Incentive mechanisms and analysis of agency cost based on fairness theory[J]. Journal of Industrial Engineering and Engineering Management, 2011, 25(2): 82-86. |
| [25] |
FEHR E, SCHMIDT K M. A theory of fairness, competition, and cooperation[J].
Quarterly Journal of Economics, 2001, 114(5): 817-868.
|
| [26] |
HSU I C. Enhancing employee tendencies to share knowledge-case studies of nine companies in Taiwan[J].
International Journal of Information Management, 2006, 26(4): 326-338.
DOI: 10.1016/j.ijinfomgt.2006.03.001. |
 2018, Vol. 21
2018, Vol. 21