顺应“绿色经济”时代要求，废旧产品的回收再利用受到越来越多国家和企业的重视，生活中最常见的回收再利用产品有经过再制造的再制造品和翻新处理的二手产品^[1]。新产品、再制造品和二手产品同时存在既可以满足异质性消费群体的需求又可以最大限度地挖掘市场潜力。

废旧产品回收再利用已成为国内外学者关注的焦点问题。孙浩等^[2]基于产品差异建立了集中式和分散式再制造闭环供应链的决策模型，表明分散决策下存在双重边际效应，最后提出收益共享契约实现闭环供应链的协调。王文宾等^[3]研究了奖惩机制下闭环供应链的协调，得到基于回收率的奖惩机制能够提高回收率。王建明^[4]研究了制造商通过专利授权第三方从事回收再制造活动，结果表明消费者对再制造品的接受程度会影响供应链各方决策及利润，采用收益共享–费用分担契约实现了分散决策下闭环供应链系统的协调。随着异质性消费群体需求越来越多，消费者对不同产品的接受度也备受关注。但斌等^[5]考虑消费者对新产品和再制造品的评价不同，研究了再制造品对新产品市场的影响，建议加强环保宣传，提高消费者对再制造品的认可。徐峰等^[6]也考虑了消费者对新产品和再制造品的不同支付意愿，建立了差别定价模型，探讨了差别定价对回收率和利润的影响。

上述文献主要对涉及新产品和再制造品的闭环供应链协调机制及接受度的研究，忽略了市场中同时存在二手产品的情形，另有一些文献考虑增加了二手产品的问题。Kogan^[7]研究了经销商从事废旧产品回收翻新活动，分析了二手产品对闭环供应链各成员利润的影响。高攀等^[8]分析了可能存在新产品、再制造品、翻新产品不同市场情形的形成条件及需求函数，讨论了再制造品、二手产品的差别定价策略和对新产品市场的影响，之后又进一步研究了专利保护下二手产品的闭环供应链竞争策略问题^[9]。Vorasayan等^[10]研究了翻新产品最优回收比例，得出制造商从事翻新活动能提高其利润。周海霞等^[11]对集成供应链中同时存在新产品、再制造品、二手产品进行了差别定价研究，表明3种产品形式存在的集成供应链系统更符合实际情况。许茂增等^[12]考虑消费者偏好，研究从事再制造和经销二手产品与否的生产决策和差别定价问题。以上考虑了二手产品的文献主要对同种不同形式产品差别定价策略方面的讨论，缺乏进一步协调机制的研究。

本文在文献[8]的研究基础上，针对市场中同时存在新产品、再制造品、二手产品的情形，考虑消费者对3种产品的接受程度不同，建立了集中和分散决策下闭环供应链差别定价模型。讨论消费者接受程度对闭环供应链上各节点企业及系统利润的影响；然后设计了收益共享-费用分担契约，对市场中同时存在三类产品的闭环供应链进行协调，优化分散决策下闭环供应链效率，提高供应链上各成员及系统利润。

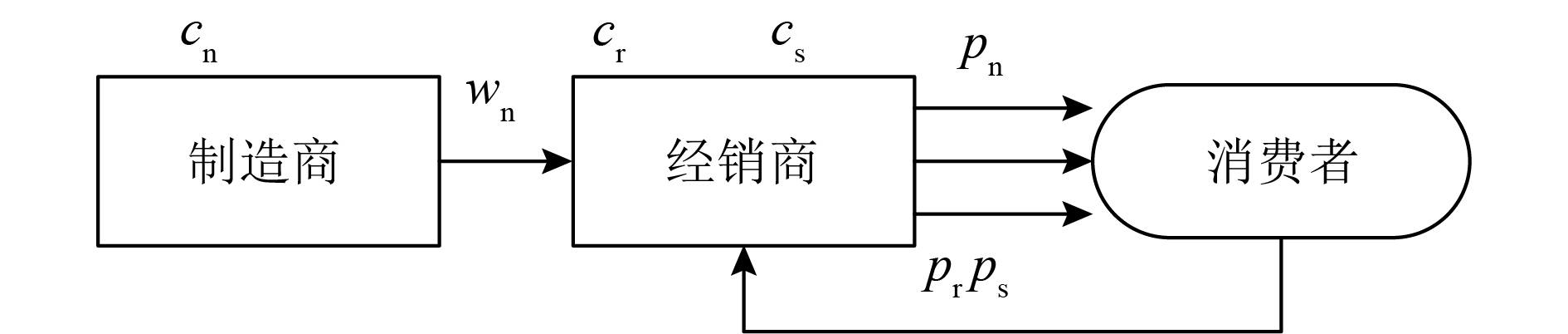
1 问题描述与假设

本文研究由制造商、经销商和消费者构成的再制造闭环供应链。考虑消费者接受度对市场进行细分，讨论集中(C)、分散(D)、协调(S)模型下的差别定价与协调策略。其中制造商是领导者，经销商为跟随者，制造商只生产新产品批发给经销商，经销商将新产品销售给消费者，同时从事废旧产品的回收再制造和翻新处理活动，并将它们以再制造品和二手产品销售给消费者。新产品、再制造品、二手产品均由经销商采取差别定价进行区别销售，模型结构如图1所示。

出于研究问题的需要，给出以下假设和符号说明。

1) 制造商生产新产品的单位成本c_n，经销商对废旧产品回收再制造的单位成本为c_r，翻新处理的单位成本c_s(再制造和翻新处理成本均包含回收成本)，且c_n＞c_r＞c_s。

2) 制造商制定的新产品批发价格为w_n，经销商对新产品、再制造品、二手产品采取差别定价策略，零售价格分别为p_n、p_r、p_s，满足p_n＞p_r＞p_s。

3) 参考文献[8，13]可知市场潜在规模为Q，消费者对新产品的支付意愿为a_n，相对于新产品，消费者对再制造品的支付意愿为 ${a_{{r}}} = \alpha {a_{{n}}}$ ，对二手产品的支付意愿为 ${a_{{s}}} = \beta {a_{{n}}}$ ，其中， ${a_{{n}}} \in [0,Q]$ 且 $0 {\text{＜}} \beta {\text{＜}} \alpha {\text{＜}} 1$ ， $\alpha $ 、 $\beta $ 分别表示相对于新产品消费者对再制造品和二手产品的接受程度(简称再制造品接受度和二手产品接受度)。由此可知，消费者购买新产品、再制造品、二手产品的效用函数分别为 ${u_{{n}}} = {a_{{n}}} - {p_{{n}}}$ ， ${u_{{r}}} = {a_{{r}}} - {p_{{r}}}$ ， ${u_{{s}}} = {a_{{s}}} - {p_{{s}}}$ 。根据文献[8]的计算结果，市场中同时存在新产品、再制造品、二手产品时各自的需求函数分别为
　　 ${D_{{n}}} = Q - \displaystyle\frac{{{p_{{n}}} - {p_{{r}}}}}{{1 - \alpha }}$ ，
　　 ${D_{{r}}} = \displaystyle\frac{{{p_{{n}}} - {p_{{r}}}}}{{1 - \alpha }} - \displaystyle\frac{{{p_{{r}}} - {p_{{s}}}}}{{\alpha - \beta }}$ ，
　　 ${D_{{s}}} = \displaystyle\frac{{\beta {p_{{r}}} - \alpha {p_{{s}}}}}{{\beta (\alpha - \beta )}}$ 。

2 集中决策

集中式决策指制造商、经销商共同决定新产品、再制造品、二手产品的批发价格w_n和零售价格p_n、p_r、p_s。制造商和经销商形成一个“超组织”，以闭环供应链整体利润最大为原则进行决策。集中决策是全局最优决策，为分散式供应链的协调提供基准，该问题建模如下。

$\begin{split} &\quad\quad{\pi _{{c}}} = \left( {{p_{{n}}} - {c_{{n}}}} \right){D_{{n}}} + \left( {{p_{{r}}} - {c_{{r}}}} \right){D_{{r}}} + \left( {{p_{{s}}} - {c_{{s}}}} \right){D_{{s}}} =\\[3pt] &\left( {{p_{{n}}} - {c_{{n}}}} \right)\left( {Q - \displaystyle\frac{{{p_{{n}}} - {p_{{r}}}}}{{1 - \alpha }}} \right) +\left( {{p_{{r}}} \!-\! {c_{{r}}}} \right)\left( {\displaystyle\frac{{{p_{{n}}}\! -\! {p_{{r}}}}}{{1 - \alpha }}\! -\! \displaystyle\frac{{{p_{{r}}} \!-\! {p_{{s}}}}}{{\alpha - \beta }}} \right) +\\[3pt] &\left( {{p_{{s}}} \!-\! {c_{{s}}}} \right)\left( {\displaystyle\frac{{\beta {p_{{r}}} - \alpha {p_{{s}}}}}{{\beta (\alpha - \beta )}}} \right){\text{。}}\end{split} $

(1)

对式(1)求关于p_n、p_r、p_s的一阶偏导等于0，联立方程得：

$\quad\quad\left\{ \begin{array}{l} p_{{n}}^* = \displaystyle\frac{{Q + {c_{{n}}}}}{2}, \\[10pt] p_{{r}}^* = \displaystyle\frac{{\alpha Q + {c_{{r}}}}}{2}, \\[10pt] p_{{s}}^* = \displaystyle\frac{{\beta Q + {c_{{s}}}}}{2}{\text{。}}\end{array} \right.$

(2)

将式(2)代入需求函数可得：

$\quad\quad\left\{ \begin{array}{l} D_{{n}}^* = \displaystyle\frac{{\left( {1 - \alpha } \right)Q - {c_{{n}}} + {c_{{r}}}}}{{2\left( {1 - \alpha } \right)}}, \\[13pt] D_{{r}}^* = \displaystyle\frac{{\left( {\alpha - \beta } \right){c_{{n}}} - \left( {1 - \beta } \right){c_{{r}}} + \left( {1 - \alpha } \right){c_{{s}}}}}{{2\left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}, \\[13pt] D_{{s}}^* = \displaystyle\frac{{\beta {c_{{r}}} - \alpha {c_{{s}}}}}{{2\beta \left( {\alpha - \beta } \right)}}{\text{。}} \\\end{array} \right.$

(3)

将式(2)、(3)代入式(1)求得集中决策下的最优利润为

$\pi _{{c}}^* = \displaystyle\frac{{A\left( {Q - 2{c_{{n}}}} \right) + B\left( {{c_{{n}}} - 2{c_{{r}}}} \right) + \beta \left( {1 - \beta } \right){c_{{r}}}^2 + C\left( {\alpha {c_{{s}}} - 2\beta {c_{{r}}}} \right)}}{{4\beta \left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}{\text{。}} $

(4)

其中， $A \!=\! \beta Q\left( {1 \!-\! \alpha } \right)\left( {\alpha \!-\! \beta } \right)$ , $B \!=\! \beta {c_{{n}}}\left( {\alpha \!-\! \beta } \right)$ , $C \!=\! \left( {1\!-\! \alpha } \right){c_{{s}}}$ 。

结论1 　在集中决策下，再制造品和二手产品的销售价格分别随再制造品接受度和二手产品接受度的升高而增大。

证明：对式(2)中 $p_{{r}}^*$ 、 $p_{{s}}^*$ 求关于消费者接受度 $\alpha $ 、 $\;\beta $ 的偏导有 $\displaystyle\frac{{\partial p_{{r}}^*}}{{\partial \alpha }} = \displaystyle\frac{Q}{2} {\text{＞}} 0$ ， $\displaystyle\frac{{\partial p_{{s}}^*}}{{\partial \beta }} = \displaystyle\frac{Q}{2} {\text{＞}} 0$ ，再制造品和二手产品的销售价格分别为各自接受度的增函数。

结论1说明，当消费者对再制造品和二手产品的接受度升高时，相对于新产品，消费者对再制造品和二手产品的支付意愿增加，故经销再制造品和二手产品的企业可通过加强宣传，提高消费者环保意识，提升消费者对再制造品和二手产品的认可度。

推论1 　再制造品、二手产品的接受度 $\alpha $ 、 $\beta $ 须满足如下关系^[8]：　　 $\displaystyle\frac{{{c_{{r}}}}}{{{c_{{n}}}}} {\text{＜}} \alpha {\text{＜}} 1 - \displaystyle\frac{{{c_{{n}}} \!-\! {c_{{r}}}}}{Q}$ ， $\displaystyle\frac{{\alpha {c_{{s}}}}}{{{c_{{r}}}}} {\text{＜}} \beta {\text{＜}} $ $\displaystyle\frac{{\alpha {c_{{n}}} \!-\! {c_{{r}}} \!+v \left( {1 \!-\! \alpha } \right){c_{{s}}}}}{{{c_{{n}}} - {c_{{r}}}}}$ 。

3 分散决策

分散决策时，制造商为领导者，经销商为跟随者，两者进行Stackelberg博弈，得出Stackelberg均衡。双方均以各自收益最大进行决策，制造商预先确定新产品批发价w_n，经销商根据新产品批发价确定新产品、再制造品和二手产品的零售价，分别表示为p_n、p_r、p_s。在该模型下，利润函数如下。

制造商利润函数为

$\quad\quad\pi _{{m}}^{{D}} = \left( {{w_{{n}}} - {c_{{n}}}} \right){D_{{n}}} = \left( {{w_{{n}}} - {c_{{n}}}} \right)\left( {Q - \displaystyle\frac{{{p_{{n}}} - {p_{{r}}}}}{{1 - \alpha }}} \right){\text{。}}$

(5)

经销商利润函数为

$\begin{split} &\quad\quad \pi _{{r}}^{{D}} = \left( {{p_{{n}}} - {w_{{n}}}} \right){D_{{n}}} + \left( {{p_{{r}}} - {c_{{r}}}} \right){D_{{r}}} + \left( {{p_{{s}}} - {c_{{s}}}} \right){D_{{s}}}= \\ &\left( {{p_{{n}}} \!-\! {w_{{n}}}} \right)\left( {Q \!-\! \displaystyle\frac{{{p_{{n}}} \!-\! {p_{{r}}}}}{{1 \!-\! \alpha }}} \right) \!+\!\left( {{p_{{r}}} \!-\! {c_{{r}}}} \right)\left( {\displaystyle\frac{{{p_{{n}}} \!-\! {p_{{r}}}}}{{1 - \alpha }} \!-\! \displaystyle\frac{{{p_{{r}}} \!-\! {p_{{s}}}}}{{\alpha \!-\! \beta }}} \right) \!+ \\ &\left( {{p_{{s}}} \!-\! {c_{{s}}}} \right)\left( {\displaystyle\frac{{\beta {p_{{r}}} \!-\! \alpha {p_{{s}}}}}{{\beta (\alpha \!-\! \beta )}}} \right){\text{。}} \end{split} $

(6)

通过主从对策原理，对式(5)、(6)求解，得到分散式下新产品最优批发价格 $w_{{n}}^{**}$ 和新产品、再制造品、二手产品的最优零售价格 $p_{{n}}^{**}$ 、 $p_{{r}}^{**}$ 、 $p_{{s}}^{**}$ ，分别为：

$\quad\quad w_{{n}}^{**} = \displaystyle\frac{{\left( {1 - \alpha } \right)Q + {c_{{n}}} + {c_{{r}}}}}{2};$

(7)

$\quad\quad\left\{ \begin{array}{l} p_{{n}}^{**} = \displaystyle\frac{{\left( {3 - \alpha } \right)Q + {c_{{n}}} + {c_{{r}}}}}{4}, \\[9pt] p_{{r}}^{**} = \displaystyle\frac{{\alpha Q + {c_{{r}}}}}{2}, \\[9pt] p_{{s}}^{**} = \displaystyle\frac{{\beta Q + {c_{{s}}}}}{2}{\text{。}}\end{array} \right.$

(8)

将式(7)、(8)代入需求函数得：

$\left\{ \begin{array}{l} D_{{n}}^{**} = \displaystyle\frac{{\left( {1 - \alpha } \right)Q - {c_{{n}}} + {c_{{r}}}}}{{4\left( {1 - \alpha } \right)}}, \\[10pt] D_{{r}}^{**} = \displaystyle\frac{Q}{4} + \displaystyle\frac{{{c_{{n}}}}}{{4\left( {1 - \alpha } \right)}} + \displaystyle\frac{{{c_{{s}}}}}{{2\left( {\alpha - \beta } \right)}} + \displaystyle\frac{{\left( {\alpha + \beta - 2} \right){c_{{r}}}}}{{4\left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}, \\[10pt] D_{{s}}^{**} = \displaystyle\frac{{\beta {c_{{r}}} - \alpha {c_{{s}}}}}{{2\beta \left( {\alpha - \beta } \right)}}{\text{。}} \end{array} \right.$

(9)

再将式(7)~(9)代入式(5)和式(6)，即可得到分散式下经销商、制造商的最优利润及分散式闭环供应链系统总利润，分别为：

$\quad\quad\quad\quad\quad\quad\quad\quad\left\{ \begin{array}{l} \pi _{{m}}^{**} = \displaystyle\frac{{{{\left( {\left( {1 - \alpha } \right)Q - {c_{{n}}} + {c_{{r}}}} \right)}^2}}}{{8\left( {1 - \alpha } \right)}}, \\[10pt] \pi _{{r}}^{**} = \displaystyle\frac{{A\left( {\left( {3\alpha + 1} \right)Q - 2{c_{{n}}} - 6{c_{{r}}}} \right) + B\left( {{c_{{n}}} - 2{c_{{r}}}} \right) + 4C\left( {\alpha {c_{{s}}} - 2\beta {c_{{r}}}} \right) - \beta \left( {3\alpha + \beta - 4} \right){c_{{r}}}^2}}{{16\beta \left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}, \\[10pt] {\pi ^{**}} = \displaystyle\frac{{A\left( {\left( {3 + \alpha } \right)Q - 6{c_{{n}}} - 2{c_{{r}}}} \right) + 3B\left( {{c_{{n}}} - 2{c_{{r}}}} \right) + 4C\left( {\alpha {c_{{s}}} - 2\beta {c_{{r}}}} \right) + \beta \left( {4 - \alpha - 3\beta } \right){c_{{r}}}^2}}{{16\beta \left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}{\text{。}} \\ \end{array} \right.$

(10)

其中， $A \!=\! \beta Q\left( {1 \!-\! \alpha } \right)\left( {\alpha \!-\! \beta } \right)$ ， $B \!=\! \beta {c_{{n}}}\left( {\alpha \!-\! \beta } \right)$ ， $C \!=\! \left( {1 \!-\! \alpha } \right){c_{{s}}}$ 。

结论2 　新产品的最优批发价 $w_{{n}}^{**}$ 和零售价 $p_{{n}}^{**}$ 为再制造品接受度 $\alpha $ 的减函数，而再制造品的最优零售价 $p_{{r}}^{**}$ 和二手产品最优零售价 $p_{{s}}^{**}$ 分别为各自消费者接受度的增函数。

证明：根据 $\displaystyle\frac{{\partial w_{{n}}^{**}}}{{\partial \alpha }} \!=\! - \displaystyle\frac{Q}{2} {\text{＜}} 0$ , $\displaystyle\frac{{\partial p_{{n}}^{**}}}{{\partial \alpha }} \!=\! - \displaystyle\frac{Q}{4} {\text{＜}} 0$ , $\displaystyle\frac{{\partial p_{{r}}^{**}}}{{\partial \alpha }} \!=$ $ \displaystyle\frac{Q}{2} {\text{＞}} 0$ , $\displaystyle\frac{{\partial p_{{s}}^{**}}}{{\partial \beta }} = \displaystyle\frac{Q}{2} {\text{＞}} 0$ ，容易证明出结论2成立。

结论2说明再制造品接受度对新产品产生负相关的影响，而二手产品接受度变化对新产品没有直接影响。

结论3 　1) $p_{{n}}^* {\text{＜}} p_{{n}}^{**}$ ；2) $p_{{r}}^* \!=\! p_{{r}}^{**}$ ；3) $p_{{s}}^* \!=\! p_{{s}}^{**}$ ；4) $\pi _{{c}}^* - $ $\left( {\pi _{{m}}^{**} + \pi _{{r}}^{**}} \right) = \displaystyle\frac{1}{2}\pi _{{m}}^{**}$ 。

证明：由新产品批发价高于生产成本，即w_n＞c_n，可推出 $\displaystyle\frac{{(1 - \alpha )Q - {c_{{n}}} + {c_{{r}}}}}{2} {\text{＞}} 0$ ，比较 $p_{{n}}^*$ 和 $p_{{n}}^{**}$ 得 $p_{{n}}^{**} - p_{{n}}^* = \displaystyle\frac{{\left( {1 - \alpha } \right)Q - {c_{{n}}} + {c_{{r}}}}}{4} {\text{＞}} 0$ ，由式(4)、(10)，即比较集中和分散决策最优利润为　　 $\pi _{{c}}^* - {\pi ^{**}} = $ $\displaystyle\frac{{{{\left( {\left( {1 - \alpha } \right)Q - {c_{{n}}} + {c_{{r}}}} \right)}^2}}}{{16(1 - \alpha )}} {\text{＞}} 0$ 。

结论3说明，与集中决策相比，分散决策的新产品销售价较高，闭环供应链系统总利润较低。因分散决策存在双重边际效应，造成系统效率降低。可见从消费者福利(消费者以更高价购买产品)和闭环供应链整体利润来看，分散式决策都不是一种理想决策。

4 收益共享-费用分担协调契约

从上述比较分析可知，分散决策会造成闭环供应链系统利润损失，主要原因在于制造商、经销商各自以其利润最大化进行独立决策，双方目标产生冲突。为缓解可能发生的目标冲突，本文参考文献[14]提出收益共享–费用分担契约对分散式闭环供应链进行协调。具体操作如下。

制造商共享 $\varphi \left( {{p_{{n}}}{D_{{n}}} + {p_{{r}}}{D_{{r}}} + {p_{{s}}}{D_{{s}}}} \right)$ 的销售收入，并为每单位再制造品和二手产品分担f和γ的回收费用(f，γ>0)；经销商共享 $(1 - \varphi )\left( {{p_{{n}}}{D_{{n}}} + {p_{{r}}}{D_{{r}}} + {p_{{s}}}{D_{{s}}}} \right)$ 的销售收入，其中， $\varphi \in \left( {0,1} \right)$ 是制造商和经销商约定的收益分享比例。

制造商利润函数为：

$\pi _{{m}}^{{s}}= \varphi ({p_{{n}}}{D_{{n}}} \!+\! {p_{{r}}}{D_{{r}}} + {p_{{s}}}{D_{{s}}}) \!+\! ({w_{{n}}} - {c_{{n}}}){D_{{n}}} - f{D_{{r}}} - \gamma {D_{{s}}}{\text{。}} $

(11)

经销商利润函数为

$ \pi _{{r}}^{{s}} \!=\! \left( {1 \!-\! \varphi } \right)({p_{{n}}}{D_{{n}}} \!+\! {p_{{r}}}{D_{{r}}} \!+\! {p_{{s}}}{D_{{s}}}) - {w_{{n}}}{D_{{n}}} \!-\! \left( {f \!-\! {c_{{r}}}} \right){D_{{r}}} \!-\! \left( {\gamma \!-\! {c_{{s}}}} \right){D_{{s}}}{\text{。}} $

(12)

求式(12)的一阶条件得：

$\quad\quad\left\{ \begin{array}{l} p_{{n}}^{{s}} = \displaystyle\frac{{(1 - \varphi )Q + {w_{{n}}}}}{{2(1 - \varphi )}}, \\[9pt] p_{{r}}^{{s}} = \displaystyle\frac{{(1 - \varphi )\alpha Q + {c_{{r}}} - f}}{{2(1 - \varphi )}}, \\[9pt] p_{{s}}^{{s}} = \displaystyle\frac{{(1 - \varphi )\beta Q + {c_{{s}}} - \gamma }}{{2(1 - \varphi )}}{\text{。}} \\ \end{array} \right.$

(13)

若要使该协调契约下闭环供应链整体利润达到集中式水平，则须满足 $p_{{n}}^{{s}} \!=\! p_{{n}}^*$ ， $p_{{r}}^{{s}} \!=\! p_{{r}}^*$ ， $p_{{s}}^{{s}} \!=\! p_{{s}}^*$ ，即：

$\quad\quad \left\{ \begin{array}{l} \displaystyle\frac{{(1 - \varphi )Q + {w_{{n}}}}}{{2(1 - \varphi )}} = \displaystyle\frac{{Q + {c_{{n}}}}}{2}, \\[9pt] \displaystyle\frac{{(1 - \varphi )\alpha Q + {c_{{r}}} - f}}{{2(1 - \varphi )}} = \displaystyle\frac{{\alpha Q + {c_{{r}}}}}{2}, \\[9pt] \displaystyle\frac{{(1 - \varphi )\beta Q + {c_{{s}}} - \gamma }}{{2(1 - \varphi )}} = \displaystyle\frac{{\beta Q + {c_{{s}}}}}{2}{\text{。}}\end{array} \right.$

(14)

解式(14)可得：

解式(14)可得：　　 $w_{{n}}^{{s}} = (1 - \varphi ){c_{{n}}}$ ， $f = \varphi {c_{{r}}}$ ， $\gamma = \varphi {c_{{s}}}$ 。

在此协调契约下求得制造商和经销商的最优利润为

$\quad\quad\quad\quad\quad\quad\quad\quad\left\{ \begin{array}{l} \pi _{{m}}^{{s}}= \varphi \left( {\displaystyle\frac{{A\left( {Q - 2{c_{{n}}}} \right) + B\left( {{c_{{n}}} - 2{c_{{r}}}} \right) + \beta \left( {1 - \beta } \right){c_{{r}}}^2 + C\left( {\alpha - 2\beta {c_{{r}}}} \right)}}{{4\beta \left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}} \right) = \varphi \pi _{{c}}^*, \\[9pt] \pi _{{r}}^{{s}} = \left( {1 - \varphi } \right)\left( {\displaystyle\frac{{A\left( {Q - 2{c_{{n}}}} \right) + B\left( {{c_{{n}}} - 2{c_{{r}}}} \right) + \beta \left( {1 - \beta } \right){c_{{r}}}^2 + C\left( {\alpha - 2\beta {c_{{r}}}} \right)}}{{4\beta \left( {1 - \alpha } \right)\left( {\alpha - \beta } \right)}}} \right) = \left( {1 - \varphi } \right)\pi _{{c}}^*{\text{。}} \\ \end{array} \right.$

(15)

要谈判双方都接受此契约，需满足 $\pi _{{m}}^{{s}}{\text{＞}} \pi _{{m}}^{**}$ ， $\pi _{{r}}^{{s}} {\text{＞}} $ $\pi _{{r}}^{**}$ ，即实现帕累托改进。比较式(10)和式(15)易求得比例分享参数 $\varphi $ 的取值范围 $\displaystyle\frac{X}{{2S}} {\text{＜}} \varphi {\text{＜}} \displaystyle\frac{{3X}}{{4S}}$ ， $\varphi $ 的具体取值则由制造商和经销商谈判来决定。其中， $S = A\left( {Q \!- 2{c_{{n}}}} \right) + B\left( {{c_{{n}}} \!- 2{c_{{r}}}} \right) + \beta \left( {1 \!- \beta } \right){c_{{r}}}^2 \!+C\left( {\alpha {c_{{s}}} -\! 2\beta {c_{{r}}}} \right)$ ， $X \!= \beta \left( {\alpha \! - \beta } \right){\left( {\left( {1 \!- \alpha } \right)Q \!- {c_{{n}}} \!+ {c_{{r}}}} \right)^2}$ ， $A \!= \beta Q\left( {1 \!- \alpha } \right)\left( {\alpha \! - \beta } \right)$ ， $B = \beta {c_{{n}}}\left( {\alpha - \beta } \right)$ ， $C = \left( {1 - \alpha } \right){c_{{s}}}$ 。

结论4 　1) $w_{{n}}^{{s}} {\text{＜}} w_{{n}}^*$ ， $p_{{n}}^{{s}} {\text{＜}} p_{{n}}^{**}$ ， $\pi _{{m}}^{{s}}{\text{＞}} \pi _{{m}}^{**}$ ， $\pi _{{r}}^{{s}} {\text{＞}} \pi _{{r}}^{**}$ ， $\pi ^{{s}} {\text{＞}} \pi^{**}$ 。

2) 当( $w_{{n}}^{{s}}$ ，f，γ)=( $(1 - \varphi ){c_{{n}}}$ ， $\varphi {c_{{r}}}$ ， $\varphi {c_{{s}}}$ )，且 $\varphi $ ∈ $\left( {\displaystyle\frac{X}{{2S}},\displaystyle\frac{{3X}}{{4S}}} \right)$ 时，实现闭环供应链的协调。

结论4说明，与未协调的分散决策相比，当闭环供应链实现协调时，制造商因分享更多收益制定的新产品批发价格降低，相应地经销商制定的新产品零售价格降低，则新产品销售量增加；协调之后双方利润均高于分散决策的利润，即合则两利，闭环供应链总利润与集中决策时一致。由此表明，通过实施收益共享–费用分担契约达到了闭环供应链整体最优，实现了分散决策闭环供应链协调。

5 算例分析 5.1 消费者接受度对两种模式利润的影响

为了更直观地了解消费者对再制造品和二手产品接受度 $\alpha $ 、 $\beta $ 的变化对闭环供应链上参与各方利润的影响，本节通过数值算例，利用matlab进行相关仿真分析。参考文献[8]设Q=2 000，c_n=500,c_r=300,c_s=200,结合推论1中 $\alpha $ 、 $\beta $ 取值范围和数值假设，可算得 $0.6 {\text{＜}} \alpha {\text{＜}} 0.9$ ， $0.4 {\text{＜}} \beta {\text{＜}} 0.85$ 。下面分3种情况进行讨论：1) 当取 $\beta = 0.6$ 时，进一步算得 $\alpha \in \left( {0.73,0.90} \right)$ ，此时各方利润随再制造品接受度 $\alpha $ 的变化情况如图2；2) 取 $\alpha = 0.8$ ，可算得 $\beta \in \left( {0.53,0.70} \right)$ ，各方利润受二手产品接受度 $\beta $ 的变化趋势如图3所示；3) 闭环供应链各方利润随 $\alpha $ 、 $\beta $ 同时变化情况如图4所示。

从图2~4可以看出如下结果。

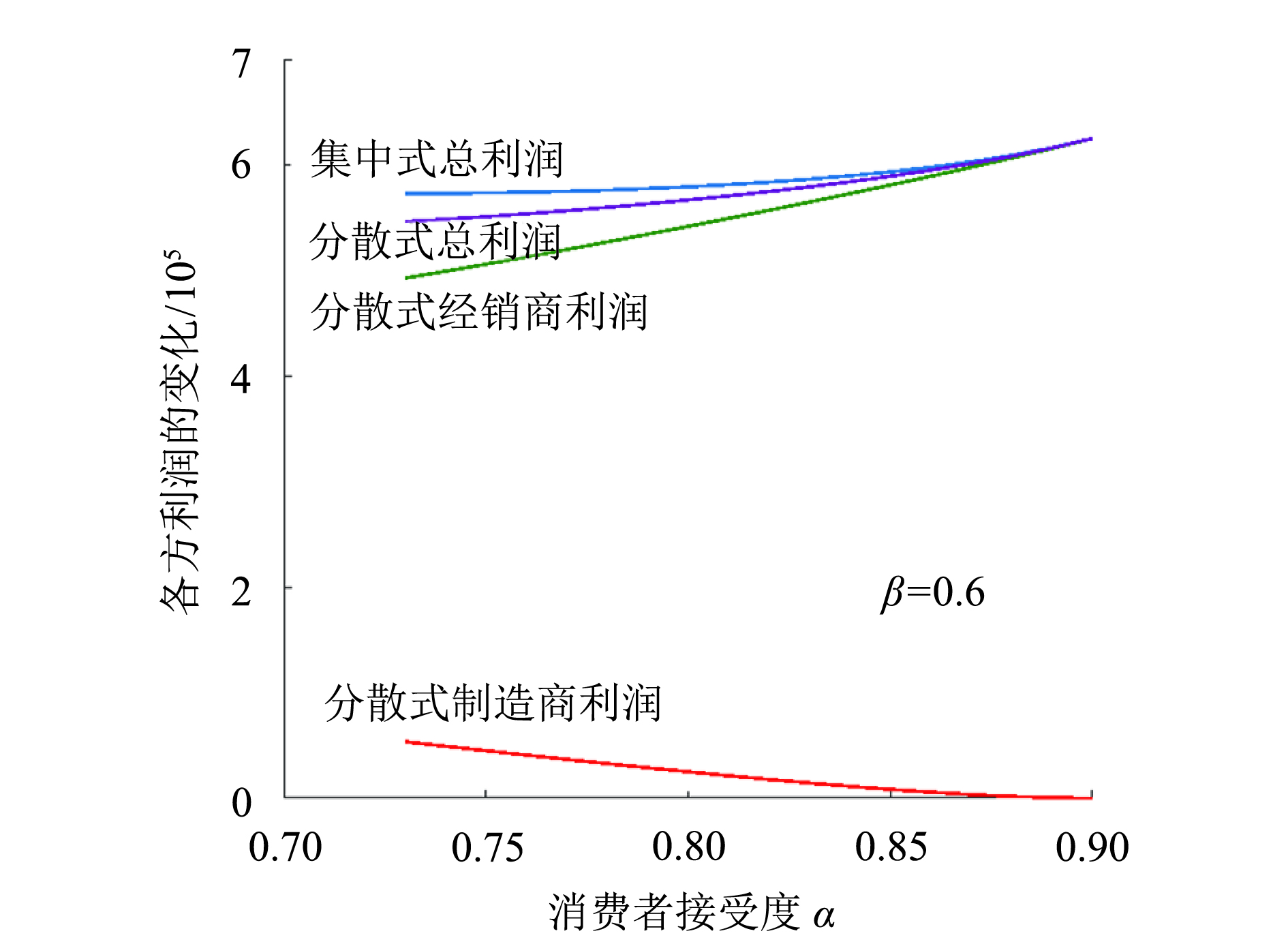
1) 由图2分析可知，集中式总利润、分散式总利润、分散式经销商利润会随着再制造品接受度 $\alpha $ 增大而增大，而制造商利润会随之减小。由于制造商只生产经营新产品，说明再制造品接受度的变化对新产品产生负相关的影响。

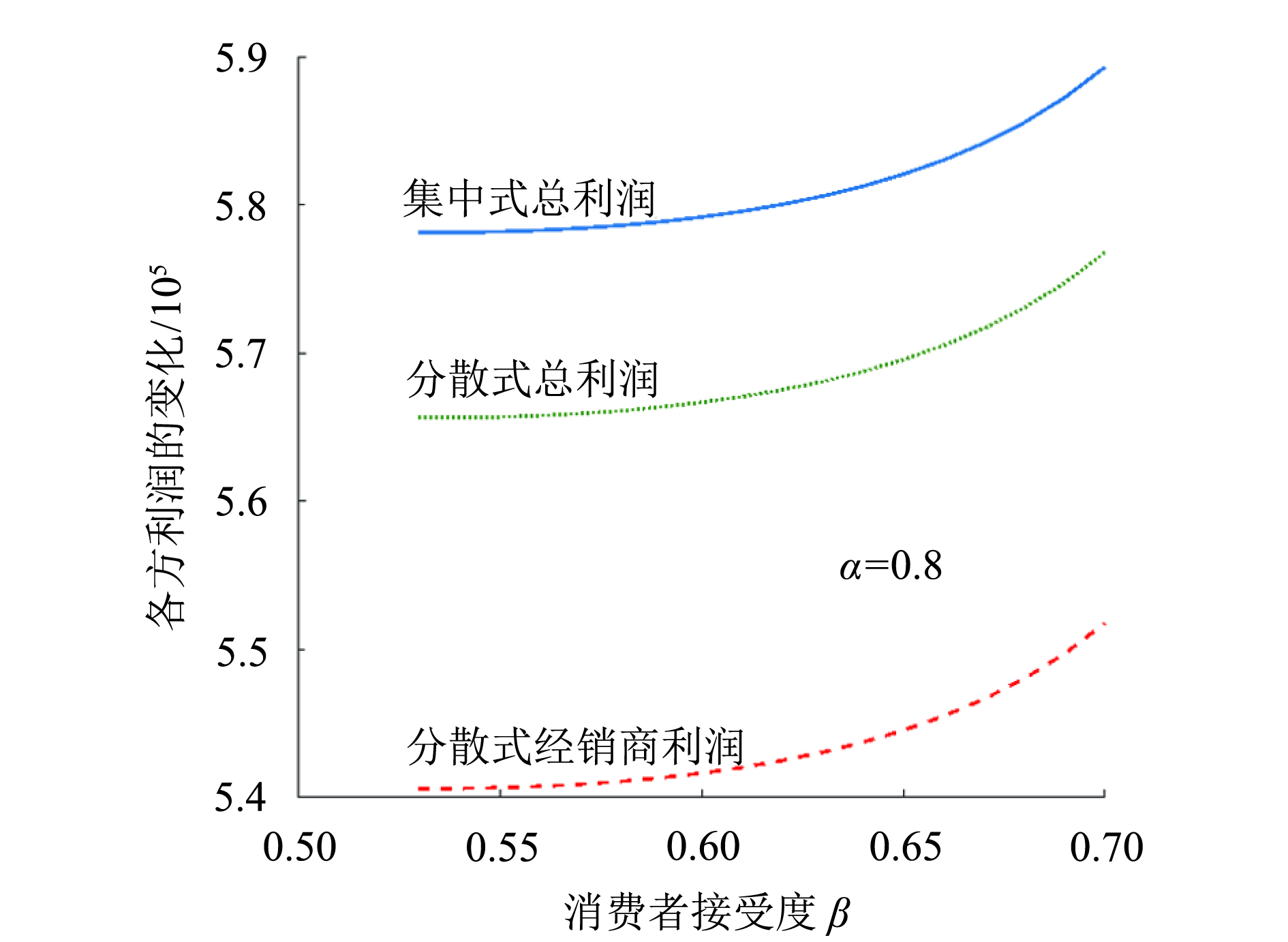
2) 由图3可知，集中式总利润、分散式总利润、分散式经销商利润随二手产品接受度 $\beta $ 的增大而增大，而制造商利润不受 $\beta $ 的影响，说明二手产品接受度对新产品没有直接影响。

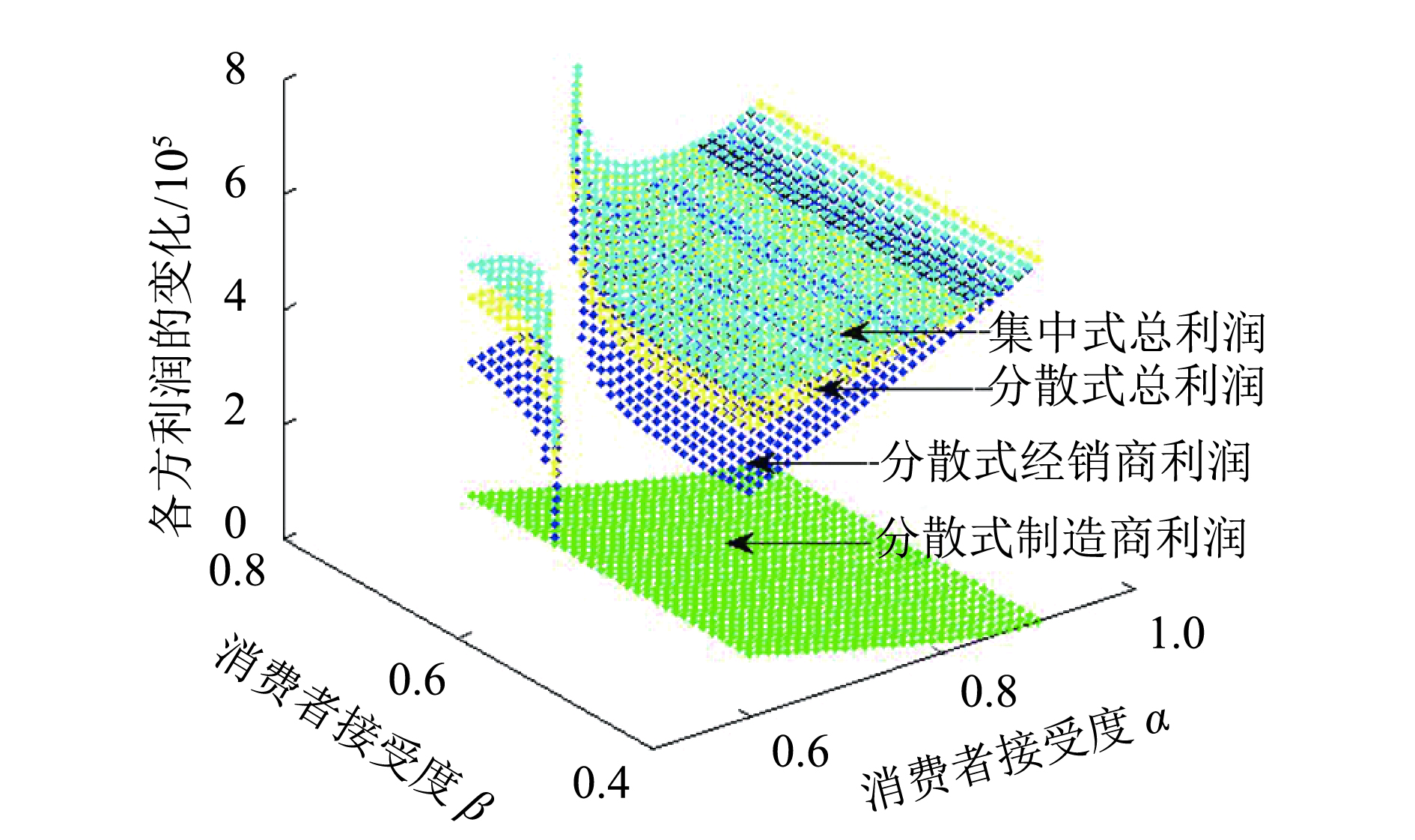
3) 由图4的仿真结果可看出，双方及系统利润随 $\alpha $ 、 $\beta $ 增加而增加。

5.2 比例分享参数对协调均衡结果的影响

在收益共享–费用分担契约下，取 $\alpha = 0.8$ ， $\beta = 0.6$ ，结合结论4和上述相关数值假设可得 $\varphi \in \left( {0.043\;2,0.064\;7} \right)$ ，则分享比例参数对该协调机制下各决策变量和利润的影响情况如表1所示。

从表1可知，在协调契约( $w_{{n}}^{{s}}$ ，f，γ)=( $(1 - \varphi ){c_{{n}}}$ ， $\varphi {c_{{r}}}$ ， $\varphi {c_{{s}}}$ )下，新产品批发价格 ${w^{{s}}}$ 随着分享比例参数 $\varphi $ 的增大而减小，而制造商分担的回收费用f、γ随之增大；制造商利润随分享参数 $\varphi $ 增大而增加，经销商利润则随之减少。其中， $\varphi $ 的具体取值则由双方地位和谈判能力来决定；协调后闭环供应链总利润与集中式时相同，实现了分散式闭环供应链的协调。可见，比例分享参数 $\varphi $ 决定着各方的利润，故各企业应该加强自身实力，提升企业地位，增强谈判能力，获取更多利润。

6 结束语

本文考虑消费者异质性需求，针对市场中同时存在新产品、再制造品、二手产品的情况，讨论消费者对3种产品的不同接受度对集中和分散模式下最优定价策略和最大利润的影响，并对2种模式的最优结果进行比较分析，发现分散决策导致双重边际效应，降低了供应链系统利润；然后通过设计收益共享–费用分担契约对分散决策的闭环供应链进行协调，使得闭环供应链系统总利润达到集中决策水平，制造商和经销商利润得到了Pareto改进，实现分散决策下闭环供应链的完美协调。最后运用数值仿真分析，验证了上述理论的正确性和协调机制的有效性。

本文研究的是信息对称下单个制造商和经销商组成的闭环供应链，而实际环境中信息很难完全对称，且存在竞争对手，因此可以考虑进一步研究竞争环境下非对称信息的闭环供应链协调。