随着客户定制越来越广泛,由此带来的订单个性化、到达时间的随机性、工件加工工期的不确定性和个性化质量不稳定引起的返修率等不断冲击着制造系统的性能。这些随机不确定因素究竟对制造过程有哪些影响?怎样才能够规避?这些都是很多制造企业所关心的问题。
国内外研究者对机器人单元的研究角度和侧重点各不同,但大多基于确定性模型。如文献[1]应用禁止区间法,建立无等待多机器人单元调度的数学模型;文献[2]构建了一种Job Shop类型机器人单元调度模型,提出混沌量子粒子群算法用于模型求解;文献[3]描述一类带输入输出缓冲的无限等待机器人单元调度模型;文献[4]中描述了一类具有成对任务特征的单机无等待机器人制造单元调度问题;文献[5]研究了一种利用双爪机器人进行多类型零件调度的问题;文献[6]描述了一类具有时间窗口约束的集束型半导体装备制造系统调度问题;文献[7] 考虑机器人运输时间,在一个调度周期内,找到任务和机器的最优加工次序,使得机器人制造单元单位时间的产出最大化;文献[8] 针对带有时间窗约束的多循环flow-shop类型机器人制造单元调度问题提出了一种混合整数规划算法;文献[9] 提出了一种基于优化的启发式规则方法求解机器人制造单元调度问题。随着个性化定制和智能制造的发展,制造系统具有智能的同时,将面临更多随机不确定因素,因此对机器人单元在随机生产环境下的研究更具有明确的实际意义。
本文以一典型的机器人制造单元为研究对象,采用eM-Plant仿真软件对该机器人制造单元进行分析和仿真研究,针对由于机器人制造单元中性能参数的随机性而导致的系统性能下降,提出改善方法,进而有效地减小随机性带来的影响,提高系统性能。
1 问题的描述本文主要对一个典型的机器人制造单元进行研究。该机器人单元由若干相同工作站、输入输出缓冲区、三坐标测量机和一个由计算机控制的物料运输机器人等设施组成,如图1。机器人沿环形轨道行走,各设施间的物料运输任务由机器人执行。该机器人单元批量生产若干不同类型的工件,工件按先来先服务规则进入输入缓冲区等待机器人取走;单元中有且仅有一个机器人,机器人在同一时刻只能搬运一个工件;每台工作站均可参与各类工件的加工,一个工件不能同时在两台或多台工作站上加工,一台工作站不能同时加工两个或以上工件;工件加工完成后,由机器人取走运往三坐标测量机;三坐标测量机测量工件是否合格,将合格品运往输出缓冲区,不合格品运往加工站重新加工;工作站与三坐标测量机之间没有设置缓冲区。

|
图 1 机器人制造单元 Fig. 1 Robotic manufacturing cell |
整个仿真模型的流程如下所述:
1) 机器人单元获得订单后,工件从输入缓冲区被运送至任何一台空闲的加工站进行加工;
2) 工件完工后被运到三坐标测量机测量。三坐标测量机若检测出不合格品,工件回工作站重新加工;
3) 测量合格后工件被搬运至输出缓冲区,加工结束;
该机器人单元的物料搬运任务由机器人承担。由此形成订单产生-加工-测量-完成的一个完整的流程。
2.2 仿真模型实现图2是在eM-Plant仿真平台建立的机器人制造单元仿真模型原型。模型分为5大模块,其中:
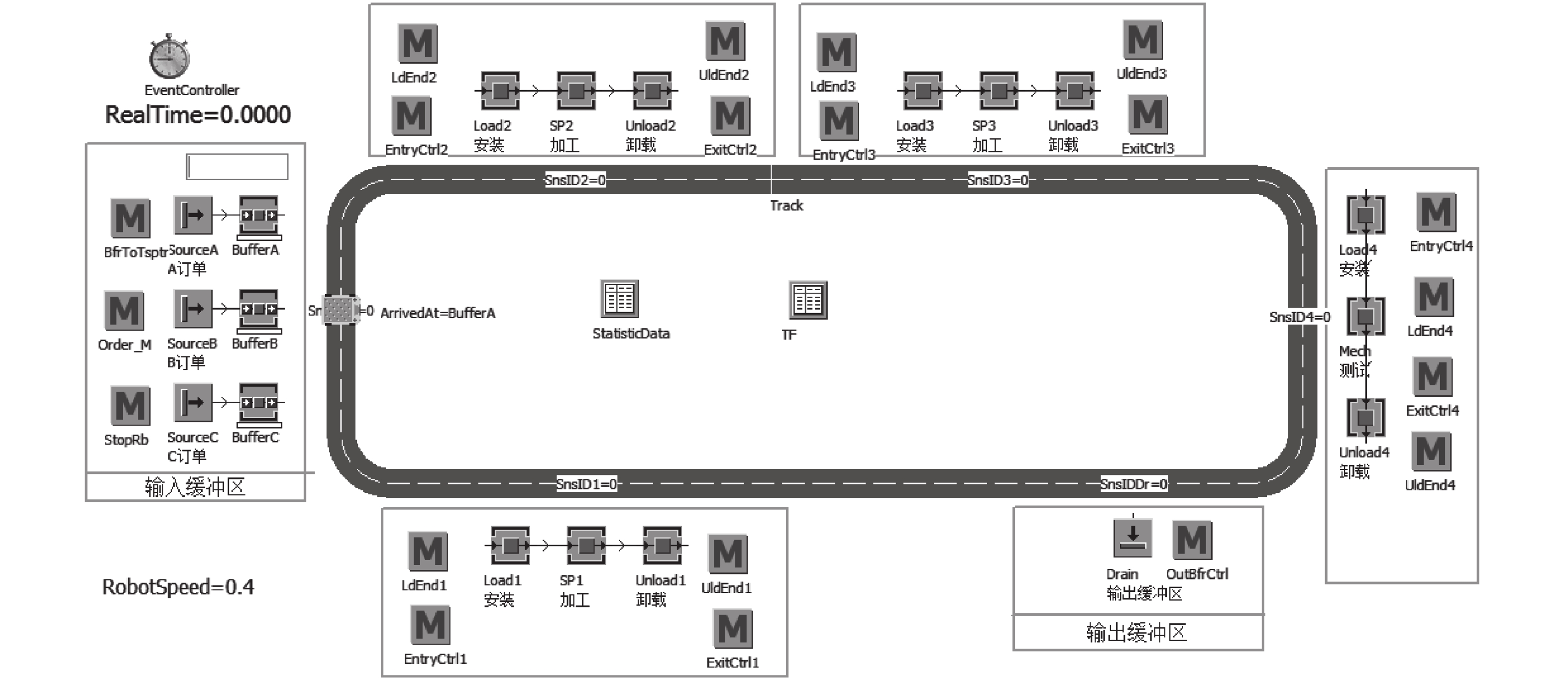
|
图 2 机器人制造单元仿真模型原型 Fig. 2 Simulation prototype of robotic manufacturing cell |
a) 输入缓冲区模块:若干不同类型订单进入机器人单元的入口;
b) 输出缓冲区模块:订单生产完成离开机器人单元的出口,订单进出缓冲区服从先来先处理规则;
c) 工作站模块:加工工件的主要场所,该模块包含若干台加工站;
d) 三坐标测量机模块:工件在工作站加工结束后,进入此模块检测加工是否合格;
e) 机器人模块:搬运工件,以及工件的安装和卸载。
该机器人单元仿真模型原型加工若干种不同类型工件,为多工件类型机器人单元。文献[10]研究了两台机多工件类型的柔性机器人制造单元调度问题。工件加工完成后机器人必须立即把工件搬运至下一工序,称为无等待类型机器人单元。根据工件在工作站上的等待时间不同,可将机器人制造单元分为: 无限等待、有限等待以及无等待类型。文献[11]将上述3种类型分别称为无限处理时间窗、处理时间窗以及零处理时间窗,并进行了详细分析。该多工件类型无等待机器人制造单元的参数表如表1所示。
| 表 1 机器人单元参数表 Tab. 1 the parameters of robotic cell |
本文利用eM-Plant离散系统仿真软件对上述机器人单元的生产流程进行仿真,分析在机器人单元中某些因素如订单到达时间、加工合格率、工件加工时间等在随机环境下对系统性能的影响,探索提高系统性能的方法,减小随机性因素的影响。
3.1 机器人制造单元的仿真实验本文为机器人制造单元建立计算机仿真模型,分别围绕订单到达时间、工件加工时间、测量合格率等随机性因素展开若干实验,实验设计如表2所示。
| 表 2 仿真实验设计 Tab. 2 Experiment design of simulation |
经过仿真实验设计,利用eM-Plant软件对机器人制造单元模型进行若干仿真实验。仿真结束后,得出机器人制造单元的仿真数据,包括订单拒绝率、设备利用率、产品产出率及平均生产周期等。根据仿真输出数据,分析某一因素的随机性对机器人单元性能产生的影响,探索提高系统性能的方法,减小随机性因素的影响。
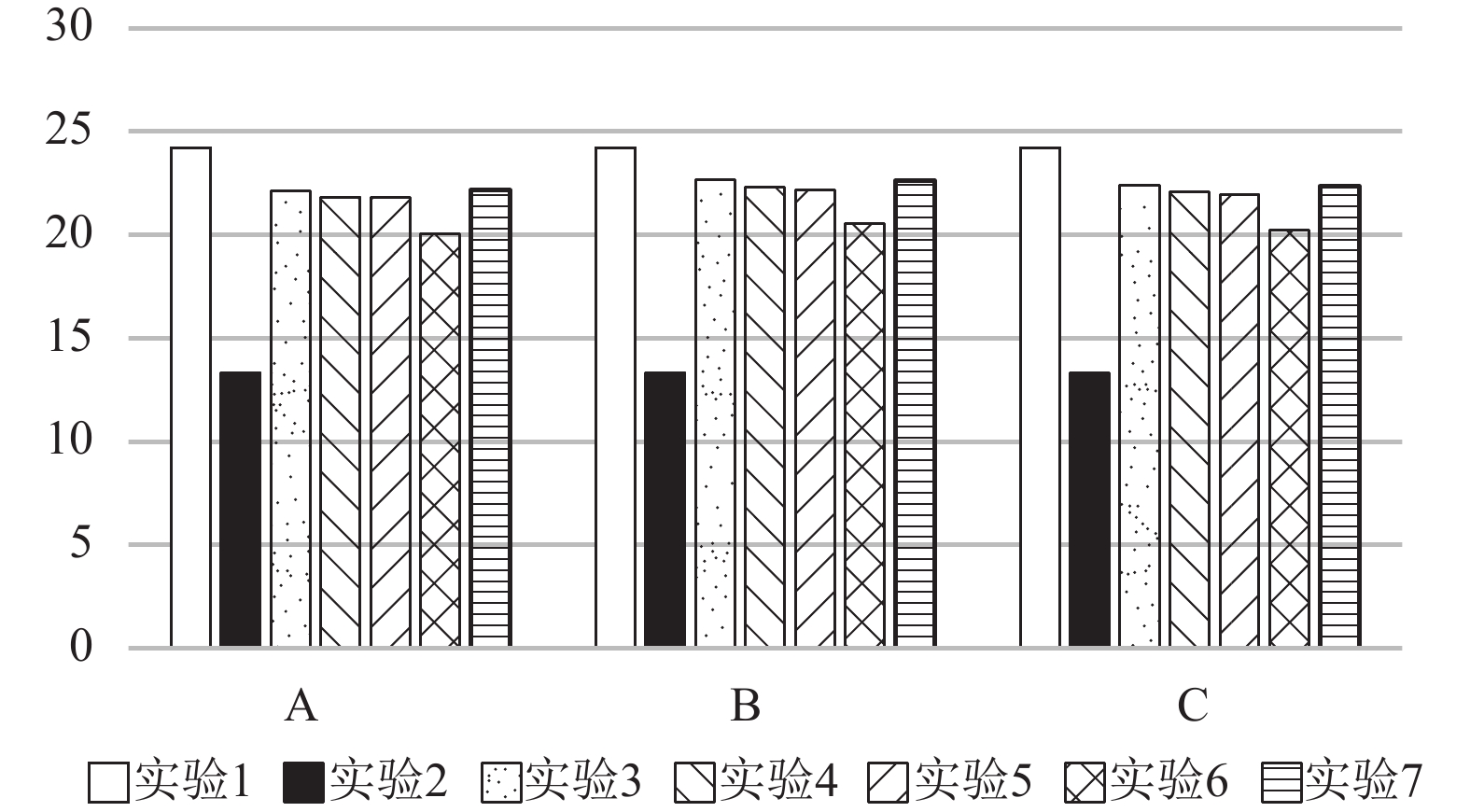
图3~图6分别是通过仿真实验得出的设备利用率、产品产出率、订单拒绝率以及产品平均生产周期。由于实验1中各项参数是完全确定的,因此机器人单元产能平衡,订单拒绝率为零。
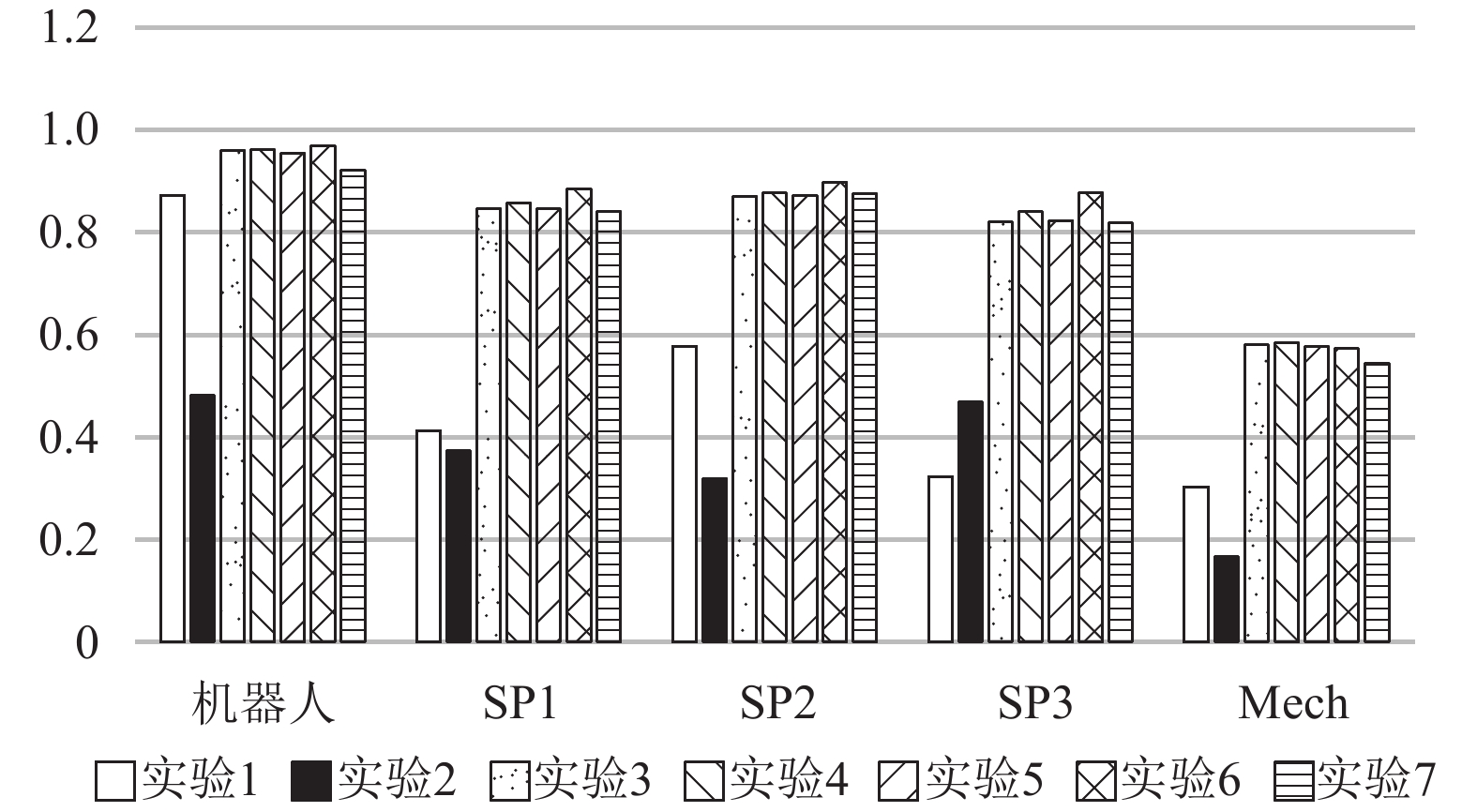
|
图 3 设备利用率 Fig. 3 Utilization of equipment |
|
图 4 产品产出率 Fig. 4 Throughtput of product |
在实验1基础上,实验2中订单到达时间服从负指数分布。
从图3、图4可知当订单到达时间服从负指数分布(实验2)时,设备利用率、产品产出率均比确定的订单到达时间(实验1)低,这是因为实验2不确定的工件到达时间导致设备利用率降低和订单无法及时处理。这也是实验2订单拒绝数远远高于实验1的原因,见图5。
图6中,实验2产品生产周期远大于实验1,这是因为机器人在某特定时间地点以及服务的对象(产品)都是确定的,订单到达的不确定性导致某些订单等待时间过长,拖长产品的生产周期。
3.2.2 调度策略的影响分析实验3改变机器人单元调度策略,该实验中模型为无限等待类型机器人单元,指工件加工完可等待机器人运走,等待时间与机器人状态、速度及位置等因素有关;并且在入口设置一个缓冲区。
根据实验3的结果可知订单拒绝率由0.4485降到0.0735(图5),设备利用率增高一倍以上(图3),产品产出率明显增高(图4)。可见无限等待类型机器人单元能减小不确定的订单到达时间带来的影响。
而由于工件在新增设的输入缓冲区中排队等待加工,产品平均生产周期比实验2有所变长(图6)。
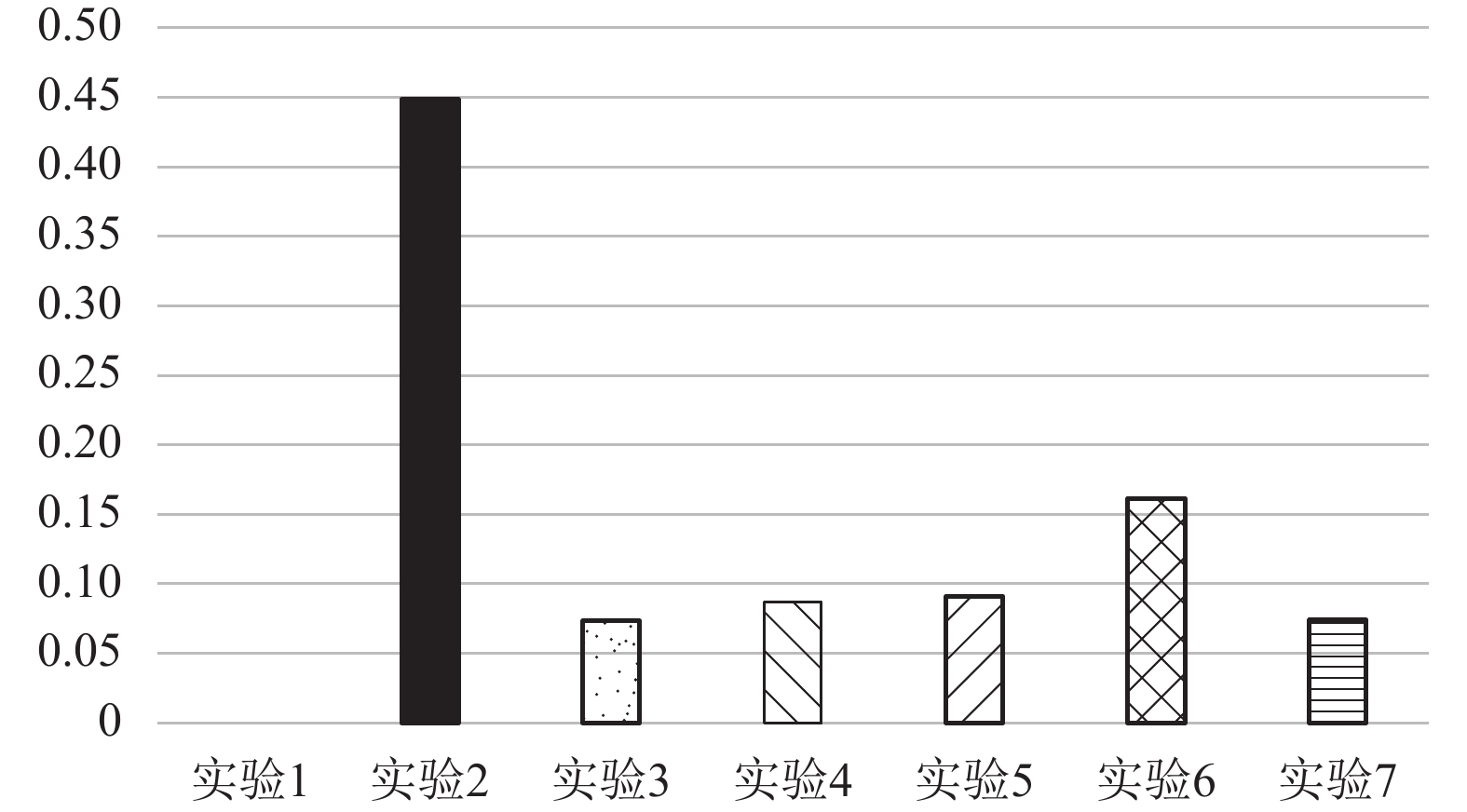
|
图 5 订单拒绝率 Fig. 5 Reject rate of orders |
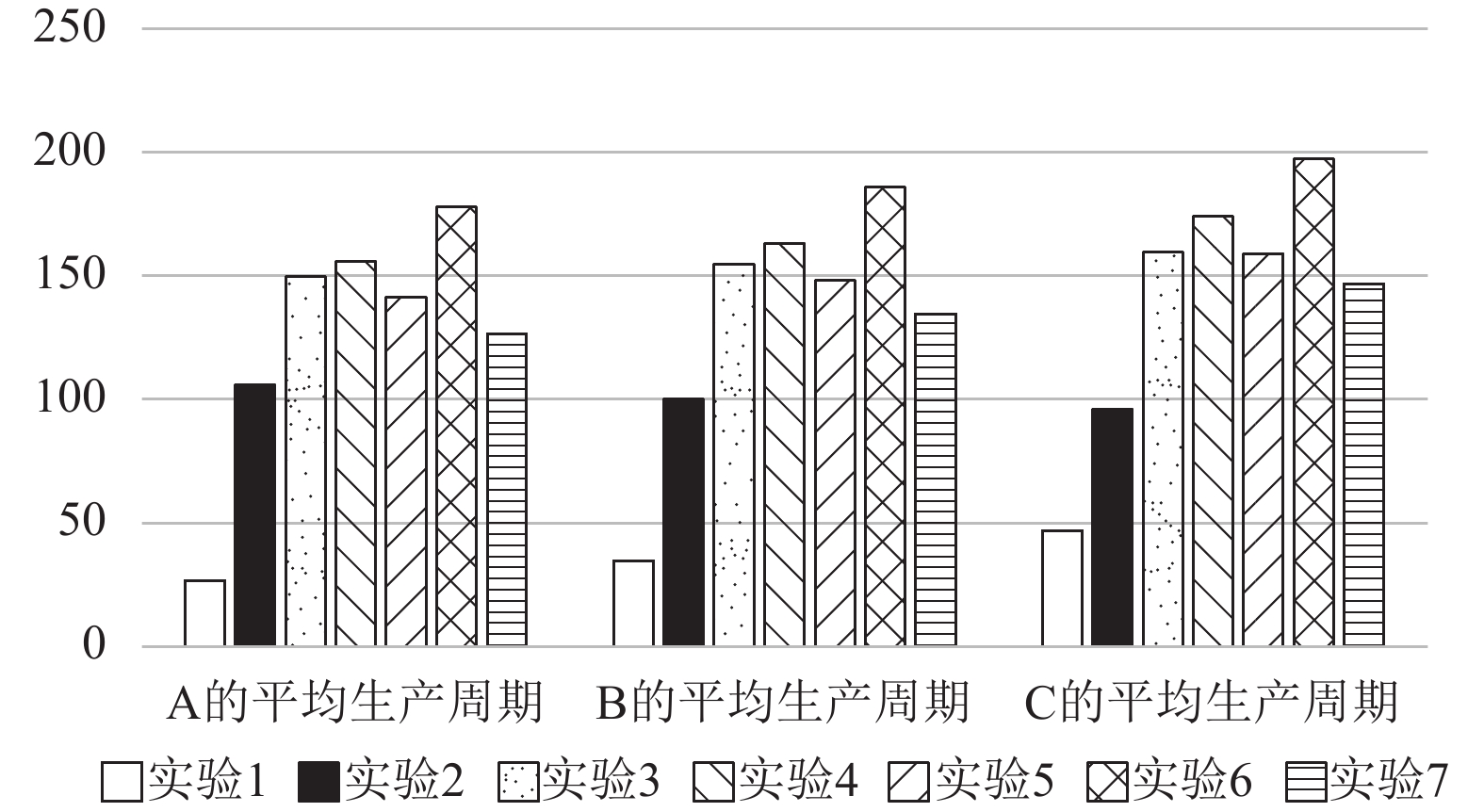
|
图 6 产品平均生产周期 Fig. 6 Mean production cycle |
实验4中工件的加工时间服从负指数分布,工件的安装、卸载以及搬运时间服从正态分布。
对比实验3、4的仿真结果,加工时间的不确定性对订单拒绝率与设备利用率的影响不明显。由于工件的安装卸载以及搬运时间只是对机器人单元内部的流程产生影响,并不会影响外部订单的接收;而且在机器人单元内部,该不确定时间从总体上说不会对设备的利用率产生影响。
工件的安装卸载及搬运时间的不确定性使得工件在加工前后的时间也具有不确定性,缓冲区工件被运走的时间也具有随机性,延长了产品的平均生产周期,而产品的平均生产周期延长必然降低产品产出率。
3.2.4 缓冲区容量的影响分析在实验4基础上,实验5改变输入缓冲区的容量,通过仿真找出合适的容量提高机器人单元性能。
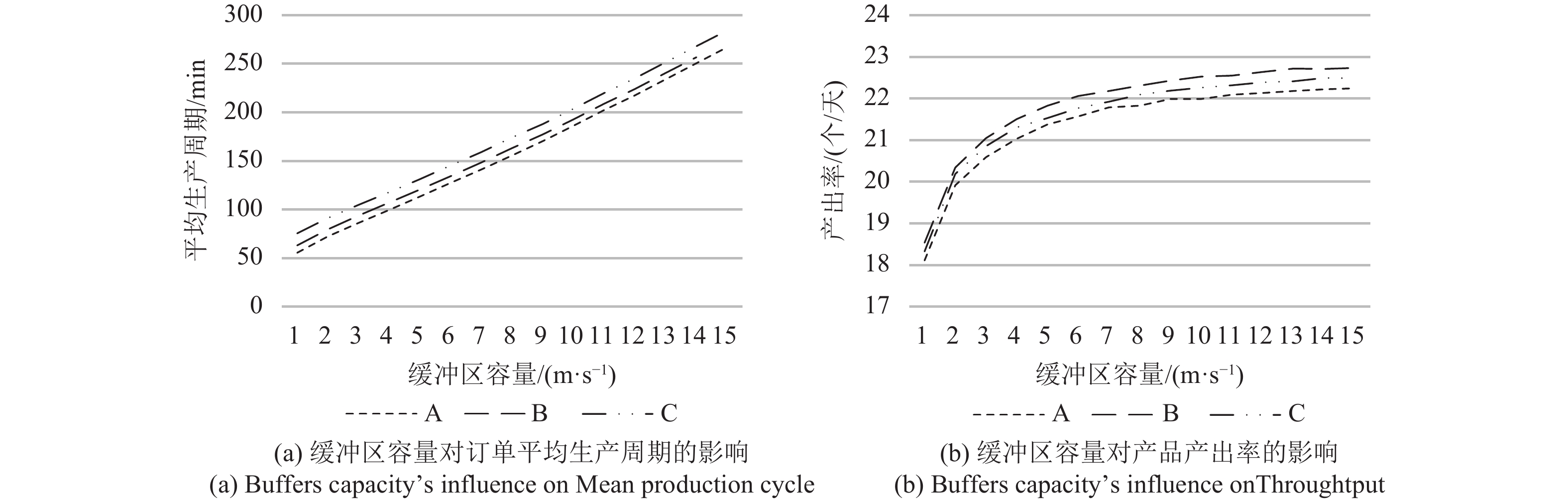
图7(a)、(b)分别表示订单平均生产周期、产品产出率与缓冲区容量的关系。考虑到订单拒绝率及缓冲区容量越少成本越低,而且设备利用率在缓冲区容量值为7~10之间时受影响不大,则容量为7比较合适。
|
图 7 缓冲区容量对性能指标的影响 Fig. 7 Buffers capacity’s influence on capacity index |
当容量为7时,订单拒绝率比容量为8时提高0.45%(图5);设备利用率降低但不明显(图3);产品产出率有所降低(图4),伴随订单拒绝率升高而降低;产品平均生产周期减少(图6),缓冲区容量小,订单平均等待时间则减小。从实验5可知,缓冲区容量的变化会引起产品产出率与平均生产周期的变化。
3.2.5 工件检测合格率的影响分析加工过程可能产生次品,需要三坐标测量机测量是否合格,不合格品将返回重新加工。实验6加入测量合格率,某工件首次加工测量合格率为90%,次品第2、3次加工后测量合格率分别为95%,99%。
当加入测量合格率因素时,机器人单元订单拒绝率提高7.03%达到16.15%(图5),是因为工件在机器人单元中平均加工时间延长,缓冲区容量不足以接收更多订单;产品产出率随着订单拒绝率增加而降低(图4);工件在机器人单元中占用设备时间长,设备利用率升高(图3),产品的平均生产周期也增加(图6)。
3.2.6 机器人速度的影响分析实验6产品的生产周期变长,订单拒绝率、产品产出率表现也比较差。观察eM-Plant仿真动画,发现工件加工完成后往往需要等待机器人取走,机器人位置及速度是影响工件等待时间的因素之一。实验7通过提高机器人的速度,减少机器人行走到目的地的时间。
图8(a)(b)(c)(d)分别表示了机器人速度对订单拒绝率、产品产出率、产品平均生产周期以及设备利用率的影响。考虑到资源的利用效率,把机器人速度提高到0.7 m/s。仿真结果显示提高机器人速度,产品的平均生产周期明显缩短,订单拒绝率与产品产出率的表现明显变好。
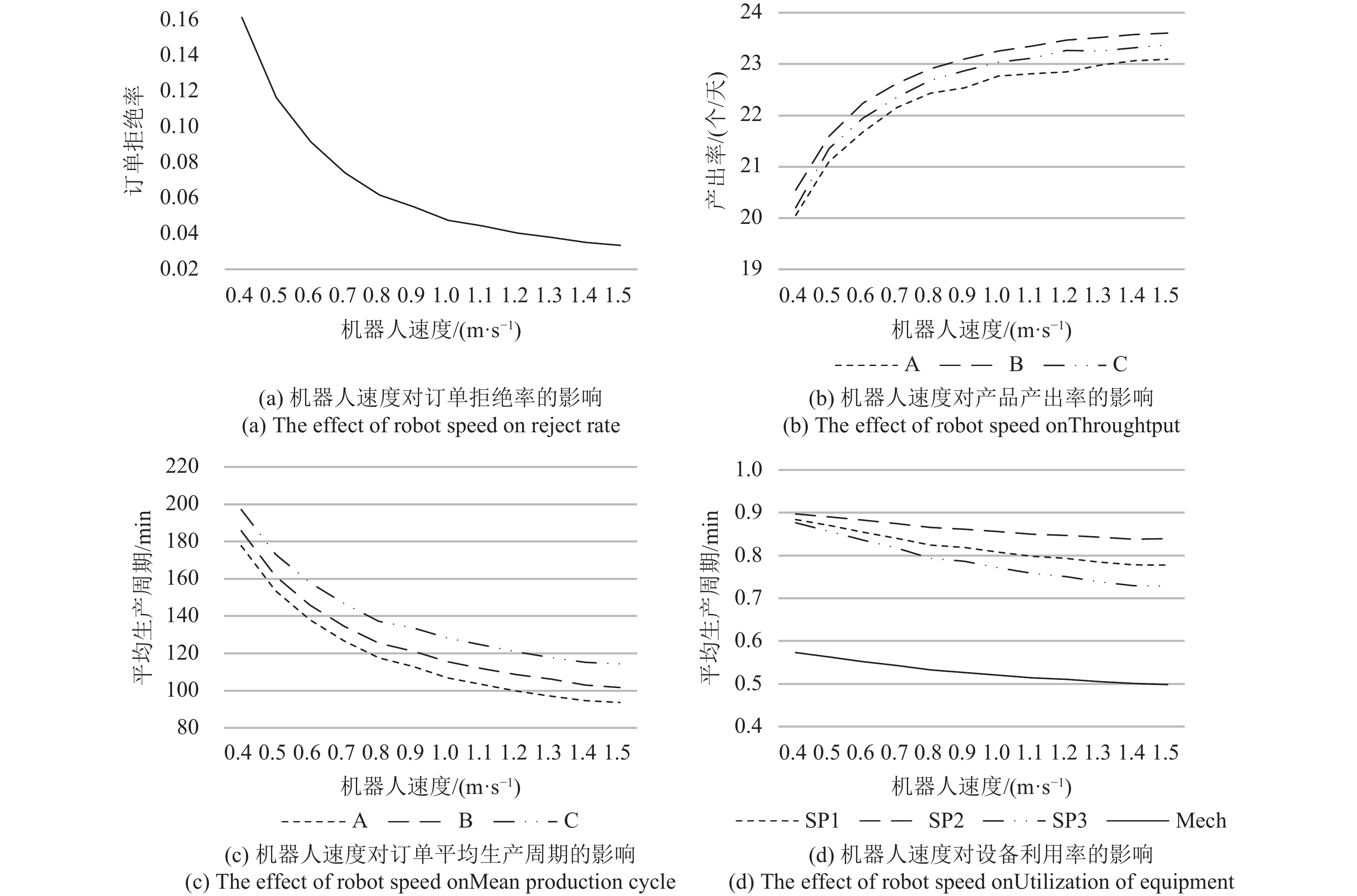
|
图 8 机器人速度对性能指标的影响 Fig. 8 Robot’s speed’s influence on capacity index |
本文在eM-Plant仿真平台上根据若干不同情形对机器人单元实施一系列仿真实验,探索工件到达时间等参数的随机性对系统性能的影响。仿真结果表明,系统性能参数的随机性可能降低机器人单元的性能,而增设缓冲区容量为7的输入缓冲区、设置成无限等待类型的机器人单元、机器人速度提高到0.7 m/s则能够减小随机性对系统性能的影响。改进后的机器人单元产出率有所降低,平均生产周期有所延长,但提高了资源利用率,也大大减小了随机性带来的影响,可以说改进后的机器人单元是有效的。
当确定性系统某一参数发生随机性变化,往往会导致机器人单元的系统性能下降,但系统某一参数或策略的改变可能减小随机性带来的影响。本文以某典型的机器人制造单元为例,设计和实施了一系列仿真实验,结果表明工件到达时间、加工时间以及检测合格率等性能参数的随机性将会降低系统性能。而通过改变输入缓冲区容量、优化调度策略以及提高机器人速度等方法,能够有效地提高随机环境下的系统性能,即可通过调整配置参数提高具有不确定环节的机器人制造单元的系统性能指标。
| [1] |
车阿大, 王远. 无等待多机器人制造单元调度模型和算法研究[J].
计算机集成制造系统, 2008, 14(3): 525-534.
CHE Ada, WANG Yuan. Scheduling model and its algorithm for no-wait robotic cell with multiple robots[J]. Computer Integr ated Manufacturing Systems, 2008, 14(3): 525-534. |
| [2] |
张沙清, 杨海东, 赵洁. 柔性JobShop类型机器人制造单元调度研究[J].
计算机技术与发展, 2015, 25(5): 68-73.
ZHANG Shaqing, YANG Haidong, ZHAO Jie. Research on flexible job shop scheduling problem of robotic manufacturing cell[J]. Computer Technology and Development, 2015, 25(5): 68-73. |
| [3] |
Drobouchevitch I G, GEISMAR H N, SRISKANDARAJAH C. Throughput optimization in robotic cells with input and output machine buffers: a comparative study of two key models[J].
European Journal of Operational Research, 2010, 206(3): 623-633.
DOI: 10.1016/j.ejor.2010.03.002. |
| [4] |
BRAUNER N, FINKE G, LEHOUX L V. Scheduling of coupled tasks and one-machine no-wait robotic cells[J].
Computers & Operations Research, 2009, 36(2): 301-307.
|
| [5] |
SRISKANDARAJAH C, DROBOUCHEVITCH I G, SETHI S. Scheduling multiple parts in a robotic cell served by a dual gripper robot[J].
Operations Research, 2003, 52(1): 65-82.
|
| [6] |
KIM J H, LEE T E. Schedulability analysis of time-constrained cluster tools with bounded time variation by an extended Petri net[J].
IEEE Trans on Automation Science and Engineering, 2008, 5(3): 490-503.
DOI: 10.1109/TASE.2007.912716. |
| [7] |
GEISMAR H N, SRISKANDARAJAH C, RAMANAN N. Increasing throughput for robotic cells with parallel machines and multiple robots[J].
IEEE Transactions on Automation Science and Engineering, 2004, 1(1): 84-89.
DOI: 10.1109/TASE.2004.829430. |
| [8] |
ZHOU Zhen, CHE Ada, YAN Pengyu. A mixed integer programming approach for multicyclic robotic flowshop scheduling with time window constraints[J].
Applied Mathematical Modeling, 2011, 36(8): 3612-3629.
|
| [9] |
JACQUES C, MOHAMED H, MOHAMED K. An optimization-based heuristic for the robotic cell problem[J].
European Journal of Operational Research, 2010, 202(3): 636-645.
DOI: 10.1016/j.ejor.2009.06.035. |
| [10] |
BATUR D G, KARASAN O E, AKTURK M S. Multiple part-type scheduling in flexible robotic cells[J].
International Journal of Production Economics, 2012, 135(2): 726-740.
DOI: 10.1016/j.ijpe.2011.10.006. |
| [11] |
CRAMA Y, KATS V, KLUNDERT J V. Cyclic scheduling in robotic flowshops[J].
Annals of Operations Research, 2000(96): 97-124.
|
 2017, Vol. 20
2017, Vol. 20