分销网络设计(distribution network design, DND)问题是供应链管理中的战略性问题。根据企业不同的需求，一个设计良好的分销网络可以有效降低企业成本，否则，将会使企业蒙受重大损失。分销网络的优化问题就是确定供应商、分销中心的最优位置及最优数量，在最大程度满足顾客需求和保证服务水平的同时还能使得系统运营成本最低。

2006年，Miranda等^[1]对有容量约束和不确定环境下的分销网络设计中的库存—定位问题进行了研究。2009年，Sourirajan 等^[2]提出了考虑安全库存和单周期的两阶段的分销网络设计模型。以上分销网络设计的文献中都暗含着一个假设条件，即供应链外部都是安全的，只考虑了常规成本项。与此同时，随着供应链面临的不确定因素越来越多，风险因素对总成本及供应链全局的影响也作为非常规成本被考虑到分销网络的设计当中，并渐成主流。李志等^[3]假设分销网络的设施周围有固定风险源，固定风险源可能带来中断风险，以惩罚成本表示中断风险损害程度的大小，设计遗传算法进行求解，证明在分销网络设计之初就考虑中断风险的影响可以降低中断发生时的应急成本，从而减小系统总成本。Baghalian等^[4]开发了一种基于路径的分销网络优化模型以应对失效风险和需求波动并存的分销网络优化问题。马卫民等^[5]研究了包含供应点、中转点、需求点三级分销网络设计，同时又考虑了供应端和需求端的不确定性，即有中断风险，结合p-鲁棒模型提出一个新混合整数规划模型。

对转运策略进行的研究无论国内还是国外均有很多，如Rudi等^[6]、Lee等^[7]、邵静等^[8]。鉴于转运能显著降低分销系统的总成本，有研究者就把转运考虑到了仓库的选址过程中。Rosales等^[9]对分销网络设计中的零售商进行横向转运和中央仓库配货进行了比较研究，通过比较发现横向转运在大范围的数值研究中的表现超过中央仓库的配货。王超峰等^[10]研究了维修备件仓库的选址—库存问题，同时在研究中又考虑了缺货下的横向调度，得出横向调度可以降低备件仓库库存的结论。姜燕宁等^[11]在库存—选址问题研究中考虑了横向转运和中心化存储，并且建立了中心仓库时间、成本与地理位置的关系式，真正考虑了选址因素的影响。Farahani等^[12]对以往学者们的供应链中库存选址问题的研究做了一个回顾。基于传统选址决策的单目标模型，Ahmadi等^[13]在他们的研究中开发了一个带有横向转运和运量限制并同时考虑了成本和服务水平的双目标模型，为选址研究开辟了新方向。以上文献在选址研究中有的只是考虑了中断风险或失灵事件的影响，有的只是考虑了转运。陶瑾等^[14] 在弹性分销网络优化中同时考虑了失效风险和转运，但在该研究中转运被当作中断风险发生后补救市场的一种手段，没有把转运当作一种降低系统总成本的工具；Michael等^[15]通过考虑转运研究了供应链的敏捷性，并分析了供应链的敏捷性和分销中心选址的分布关系。以往有关转运的分销网络设计的研究并没有把转运当作一项日常成本研究其对分销中心选址的影响，也即没有真正在分销网络设计中考虑转运的因素。本文将在考虑空间位置的基础上分析在分销网络设计阶段就考虑转运会如何改变分销网络的结构和网络成本。在选址的过程中，总会有一些位置虽然理论上是最佳的选址地点，但是却因为某些环境或人文因素而不适合设置分销中心(比如频发水患的河道旁，还有易引发泥石流的山体旁等可能引起分销中心供货中断的地方)，需要把这些地方作为能引起中断风险的风险源考虑进分销网络设计当中。

1 问题描述与符号定义 1.1 问题描述

企业的销售网络一般包括供应商、分销中心、零售商和客户3个层级(图1)。本文研究的分销网络设计分为两层级，网络内有1个供应商G，n个候选分销中心j， J = { 1 , 2 , 3 … … n } , ∀ j , k ∈ J ，m个零售商 i ， I = { 1 , 2 , 3 … … m } , ∀ i ∈ I 。零售商需求相互独立，等同于客户需求且服从正态分布 N ( μ i , σ i 2 ) ，那么分销中心的需求服从正态分布 N ( μ j , σ j 2 ) 且等于指派给它的零售商的需求总和。分销中心有订单到达且货物充足时则由分销中心安排发货及时满足。若分销中心缺货，则由其他库存比较富余的分销中心对缺货的分销中心进行转运补货，进而满足零售商需求。在与零售商和候选分销中心同一分区内存在有风险源 v ，风险源固定且只有一个，当分销中心中断时功能全部丧失且存货不再存在，市场份额全部消失。一般情况下，假设候选分销中心的风险概率与其和风险源的距离呈负相关关系，即离风险源越远中断风险越小。所有候选分销中心均在中断风险之下。

综上所述，该问题属于一个考虑安全库存，库存成本、随机需求、中断风险和库存共享的分销网络设计问题。该分销网络要解决的问题是：1) 确定分销中心的最佳位置及最优数量；2) 确定分销中心和零售商之间的指派关系；3) 确定分销中心的最佳库存定至点。

1.2 假设条件

1) 本文研究单一产品的系统，每个零售商或分销中心的需求随机、独立且服从正态分布，需求均值和方差已知。

2) 供应商、候选分销中心和每个零售商的位置既定，每一个分销中心 j 有订货提前期 L 。

3) 各分销中心采取 ( s , S ) 连续库存策略，以满足零售商的需求。其中 s 表示分销中心的订货点，包括订货提前期内的客户需求。

4) 分销中心可以向多个零售商配送货物，但每个零售商只能由一个分销中心供货。

5) 转运只在分销中心间进行，且分销中心到零售商的配送和分销中心间的转运均为瞬时完成。

6) 有转运请求时只有存货量超过自己订货点的分销中心才会响应。

7) 转运的货物先经由需求的分销中心，再由该分销中心配送。

1.3 参数符号定义

根据以上假设，模型所需的参数符号定义如下。

μ i 为零售商i的需求均值；

σ i 2 为零售商i的需求方差；

μ j 为分销中心j的需求均值；

σ j 2 为分销中心j的需求方差；

L 为分销中心j的提前期；

T 为年平均天数；

t j 为分销中心j相近两次订货的间隔天数；

g j 为分销中心j的建设成本年折旧成本；

c i j 为分销中心j到零售商i的单位距离运输成本；

c j 为供应商到分销中心j的单位距离运输成本；

tc k j 为分销中心j到分销中心k的单位距离转运成本；

h 为分销中心j的单位库存持有成本；

b 为分销中心j的订货成本；

l 为单位缺货成本；

ε k j 为分销中心j转运至分销中心k的数量；

S j 为分销中心j的库存定至点；

s j 为分销中心j的订货点；

ss j 为分销中心j的安全库存量；

Q j 为分销中心j的订货量；

B j 为分销中心j的缺货量期望值；

R j 为有转运请求时，分销中心j的库存剩余量；

q k 为分销中心k缺货量的期望值；

d j 为供应商到分销中心j之间的距离；

d j v 为风险源v与分销中心j之间的距离；

d k j 为分销中心k与j之间的距离；

d i j 为分销中心j到零售商i之间的距离；

Ω j 为分销中心j中断的惩罚因子；

K 为分销中心的库存水平安全系数；

v 为非常规突发事件的风险源集合；

∂ v 为风险情景的敏感系数，0≤ ∂ v ≤1；

β 为距离敏感系数；

p j 为分销中心j中断风险。

有以下决策变量。

X j ：{0,1}，在j处设立分销中心为1，否则为0；

Y i j ：{0,1}，把零售商i指派给分销中心j时为1，否则为0。

2 模型建立

系统总费用主要包括分销中心选址固定费用的年摊销费用C₁，分销中心的订货费用C₂，供应商向分销中心的配送费用C₃、分销中心向零售商的配送费用C₄、分销中心的库存存储费用C₅、缺货成本C₆、分销中心间转运运输费用C₇、转运后的费用节省C₈以及中断预期惩罚成本C₉。

1) 选址固定费用的年摊销费用。

C 1 = ∑ ​ j = 1 n g j X j 。

(1)

2) 分销中心的订货费用。

安 全 库 存 : ss j = K L σ j ;

(2)

订 货 量 : Q j = S j − ss j ;

(3)

订 货 点 : s j = L μ j + ss j 。

(4)

两次订货的间隔天数：

t j = Q j / μ j = ( S j − K L σ j ) / μ j ;

(5)

C 2 = ∑ ​ j = 1 n T b μ j ( S j − K L σ j ) 。

(6)

3) 供应商到分销中心的配送费用。

假设零售商的需求量服从正态分布 N ( μ i , σ i 2 ) ，且零售商需求相互独立，则分销中心的需求量为 N ( μ j , σ i 2 ) ，其中 μ j = ∑ i = 1 m μ i Y i j ， σ j 2 = ∑ i = 1 m σ i 2 Y i j 。

从供应商到分销中心的运输费用为

C 3 = ∑ j = 1 n T d j c j μ j X j 。

(7)

4) 分销中心到零售商的配送费用。

C 4 = ∑ i = 1 m ∑ j = 1 n T d i j c i j μ i Y i j 。

(8)

5) 分销中心的库存存储费用 。

C 5 = ∑ j = 1 n h T ( S j + K L σ j 2 ) 。

(9)

从式(8)可以看出，S_j并不是越大越好，一是要考虑零售商的需求，再者就是S_j越大，库存费用也越高。

6) 缺货成本。

缺货成本是指分销中心没能满足零售商的需求时分销中心的机会成本。设 f j ( x ) 为分销中心j的需求的概率密度函数， F j ( x ) 为分销中心j的需求的分布函数，则分销中心j在销售周期内缺货量的期望值为

E ( B j ) = ∫ + ∞ R j ( x − s j ) f j ( x ) d x = λ ( k ) L σ j 。

其中 λ ( k ) = K T ( K ) + Γ ( K ) − K ,

Γ ( K ) = ∫ K − ∞ Γ ( x ) d x , Γ ( x ) = 1 2 π e − x 2 2 , f j ( x ) = 1 2 π L σ j e − ( x − L μ j ) 2 2 L σ j 。

(10)

因此，分销中心j期末的缺货成本为

C 6 = ∑ ​ j = 1 n T l B j μ j ( S j − K L σ j ) 。

(11)

7) 转运运输费用。

假设某一分销中心k发生缺货，则首先向距离其最近的分销中心申请转运，最近的不能满足请求，则向次近的分销中心申请，以此类推。只有满足条件 R j ​ ​ ​ ＞ s j 且 tc k j d k j ＜ h + l 的分销中心j才能为分销中心k转运，若不满足转运条件，则允许缺货。分销中心j向分销中心k的转运量为

ε k j = min ( ( R j − s j ) + , ( s k − R k ) + ) 。

(12)

其中分销中心k的总转入量满足条件 ∑ j = 1 j ≠ k n ε k j = ( s k − R k ) + ，分销中心j的总转出量满足条件 ∑ j = 1 j ≠ k n ε k j = ( R j − s j ) + 。总转运费用为

C 7 = ∑ ​ j = 1 n ∑ ​ k = 1 k ≠ j n T d k j tc k j ε k j μ k ( S k − K L σ k ) 。

(13)

8) 转运后的费用节省。

当转运发生后，转出的分销中心会减少库存持有成本，转入的分销中心会减少缺货成本，所以减少成本的公式如下：

C 8 = ∑ ​ j = 1 n ∑ ​ k = 1 k ≠ j n T ε k j μ j ( h + l ) ( S j − K L σ j ) 。

(14)

9) 中断预期惩罚成本。

风险源v引起设施j中断事件p_j是风险源与分销中心间距离d_jv的减函数，借鉴李志等^[3]所作研究，分销中心的p_j可表示为

p j = ∂ v e − β d j v

(15)

∂ v 是风险系数，其取值为(0,1)，取决于风险源的类型、强度、规模等因素，表示中断风险不是大概率事件。 β 是距离的敏感系数。 Ω j 是中断发生后的惩罚成本，包括设施本身的固定设施损失，同时也包括货物损失以及由此引发的需求的损失。因此，中断预期惩罚成本可以表示为

C 9 = ∑ i = 1 m ∑ j = 1 n Ω j p j μ i Y i j 。

(16)

建立的目标函数如下。

min tc = C 1 ​ + C 2 + C 3 ​ + C 4 ​ + C 5 ​ + C 6 ​ + C 7 ​ − C 8 ​ + C 9 。

(17)

s.t

μ j = ∑ ​ i = 1 m μ i Y i j , ∀ i ∈ I , j ∈ J ;

(18)

σ j 2 = ∑ i = 1 m σ i 2 Y i j , ∀ i ∈ I , j ∈ J ;

(19)

s j = L μ j + ss j , ∀ j ∈ J ;

(20)

E ( B j ) = ∫ R j + ∞ ( x − R j ) f j ( x ) d x = λ ( k ) L σ j ；

(21)

ε k j ​ = ​ min ​ ( ( R j ​ − ​ s j ) + ​ , ( s k ​ − ​ R k ) + ) , ∀ j , k ​ ∈ ​ J ;

(22)

l + h ＞ d k j tc k j , ∀ j , k ∈ J ;

(23)

∑ j = 1 j ≠ k n ε k j = ( R j − s j ) + , ∀ k , j ∈ J ;

(24)

∑ j = 1 j ≠ k n ε k j = ( s k − R k ) + , ∀ k , j ∈ J ;

(25)

p j = ∂ v e − β d j v , ∀ j ∈ J ;

(26)

∑ j = 1 n Y i j = 1 , ∀ i ∈ I , j ∈ J ;

(27)

X j ∈ { 0 , 1 } , ∀ j ∈ J ;

(28)

Y i j ∈ { 0 , 1 } , ∀ i ∈ I , j ∈ J 。

(29)

目标函数(17)表示使系统总成本最小；约束式(18)、(19)分别表示分销中心的日需求均值和方差；式(20)表示分销中心j的订货点约束；式(21)表示分销中心j的缺货量的期望值；式(22)表示从分销中心j到k的转运量约束；式(23)保证了转运是有利可图的；式(24)和式(25)分别表示对转出量和转入量的约束；式(26)表示分销中心j的中断风险；式(27)表示每个零售商只能由一个分销中心配货；式(28)、式(29)为0-1整数约束。另外，系统所有参数均大于等于 0。

3 模型求解

本文提出的非线性0-1整数规划模型属于NP-难问题，其求解需要通过启发式算法实现。在以往的模型求解中，遗传算法表现出了良好的鲁棒性和收敛性，具有成熟的解题经验。因此，本文模型选用遗传算法进行求解，并设计求解步骤如下。

步骤1 　染色体编码。假如有n个候选分销中心和m个零售商，则让每个染色体的长度为m，即有m个基因，代表m个零售商。然后让每个基因在[1, n]之间产生一个随机数，来表示指派关系，数字n代表选择第n个候选分销中心。这样，染色体上出现的数字的种类就代表着选择的分销中心的个数。例如，有10个零售商由5个候选分销中心指派。如图2所示，选择了2，4，5三个候选分销中心，且零售商1，2，9，10由分销中心2提供服务，零售商3，4，5由分销中心4提供服务，零售商6，7，8由分销中心5提供服务。

步骤2 　产生初始种群。依照步骤1中的个体产生办法，初始种群规模为100。

步骤3 　计算适应度。染色体在遗传的时候选择的是最大适应度，而文章模型的求解结果是最小值，设染色体r的目标值为 Z r ，则其适应度为 1 / Z r 。

步骤4 　选择算子。选择是建立在适应度函数的评估基础上的，并且符合于优胜劣汰、适者生存这一自然规律。本文选择轮盘赌法和精英策略结合的方法来提高收敛速度。

步骤5 　交叉与变异。本文选择一点交叉和变异。

步骤6 　算法终止。当算法迭代次数达到最大时终止算法并输出计算结果。

4 数值仿真

为了验证模型及算法的有效性，应用Matlab进行仿真分析。假设1个供应商，1个风险源，10个候选分销中心，20个零售商随机分布在一个100×100的坐标平面内。 T = 1 ， L = 1 ， h = 7 ， c j = 1 ， c i j = 1元， tc i j = 2 ， b = 200 ， l = 500 。此外， K = 1.96 (95%的置信概率)^[16]， ∂ v = 0.05 ， β = 0.000 2 ， Ω j = 10 000 ^[17-19]。风险源坐标(29,49)，供应商坐标(95,95)。候选分销中心和零售商的基本信息如表1和表2所示，分布图如图3所示。

4.1 结果分析

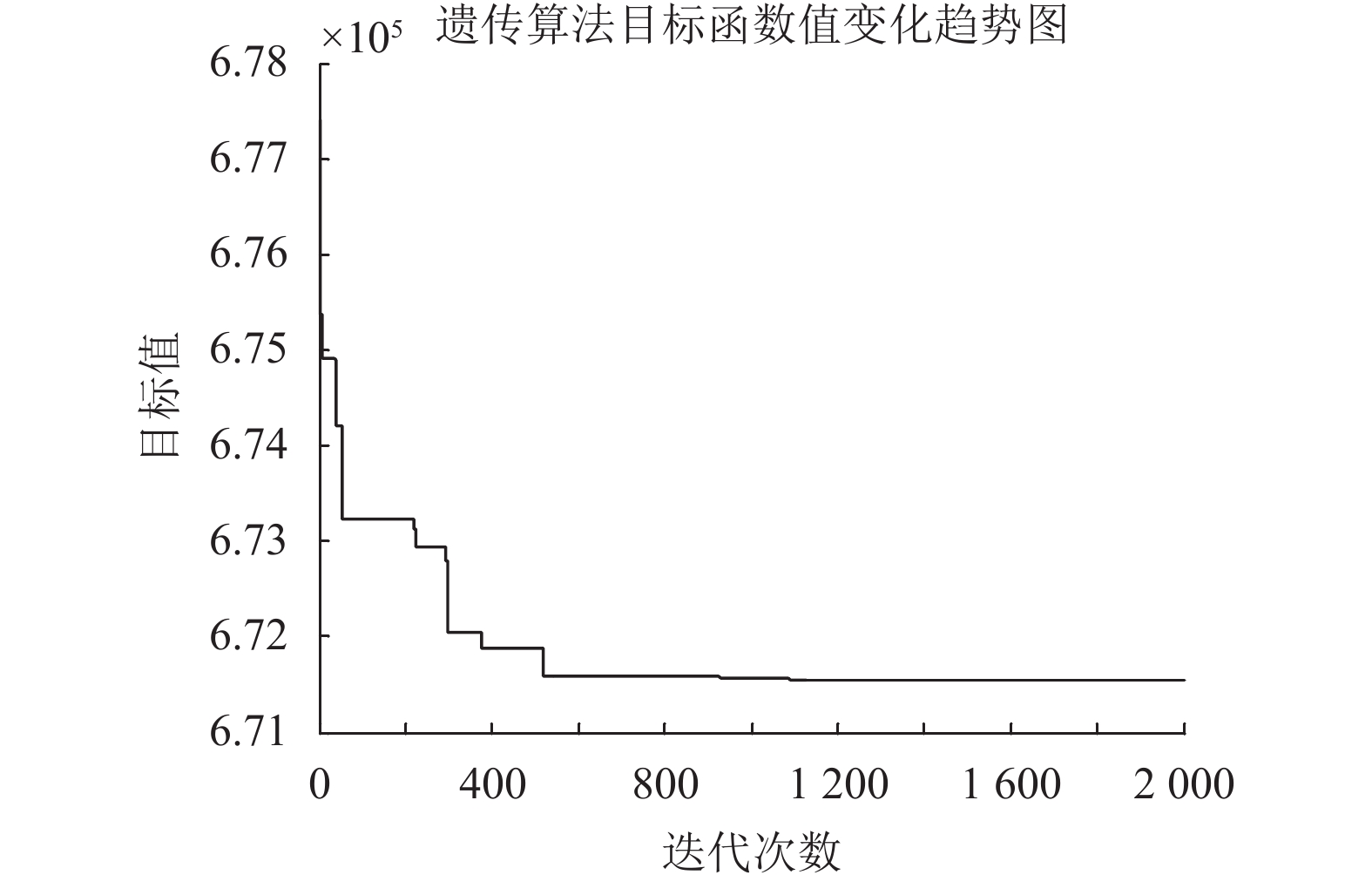
遗传算法的仿真参数设置为，种群规模100，最大迭代次数2 000，交叉概率0.9，变异概率0.2^[20]。设定同时考虑中断风险和转运的选址方案为方案1,不考虑转运和中断风险的方案为方案2、只考虑转运的方案为方案3，只考虑中断风险的选址方案为方案4。得到方案1(即本文模型)结果目标值为671 545.39元，此时分销中心的选择为[0,1,1,0,1,0,1,1,1,1]，指派关系为[7,8,2,5,10,8,7, 10,2,9,3,10,10,10,8,10,10,8,2,8]，选定分销中心的库存定点依次为78，36，30，55，145，25和217。遗传算法的收敛走势图如图4所示，可以发现遗传算法求解此类问题时能够在短时间内有效收敛，得到有效解。为了更进一步检验算法的效率，本文又选取了模拟退火算法和粒子群算法两种经典启发式算法对问题求解并对3种算法结果进行了对比。结果表明，在计算效率方面3种算法中遗传算法效率最高，粒子群算法次之，模拟退火算法效率最低；而在计算精度方面遗传算法和模拟退火算法精度相当，粒子群算法最差(见表3)，故而文章设计的遗传算法性能较好，适用于求解本文模型。

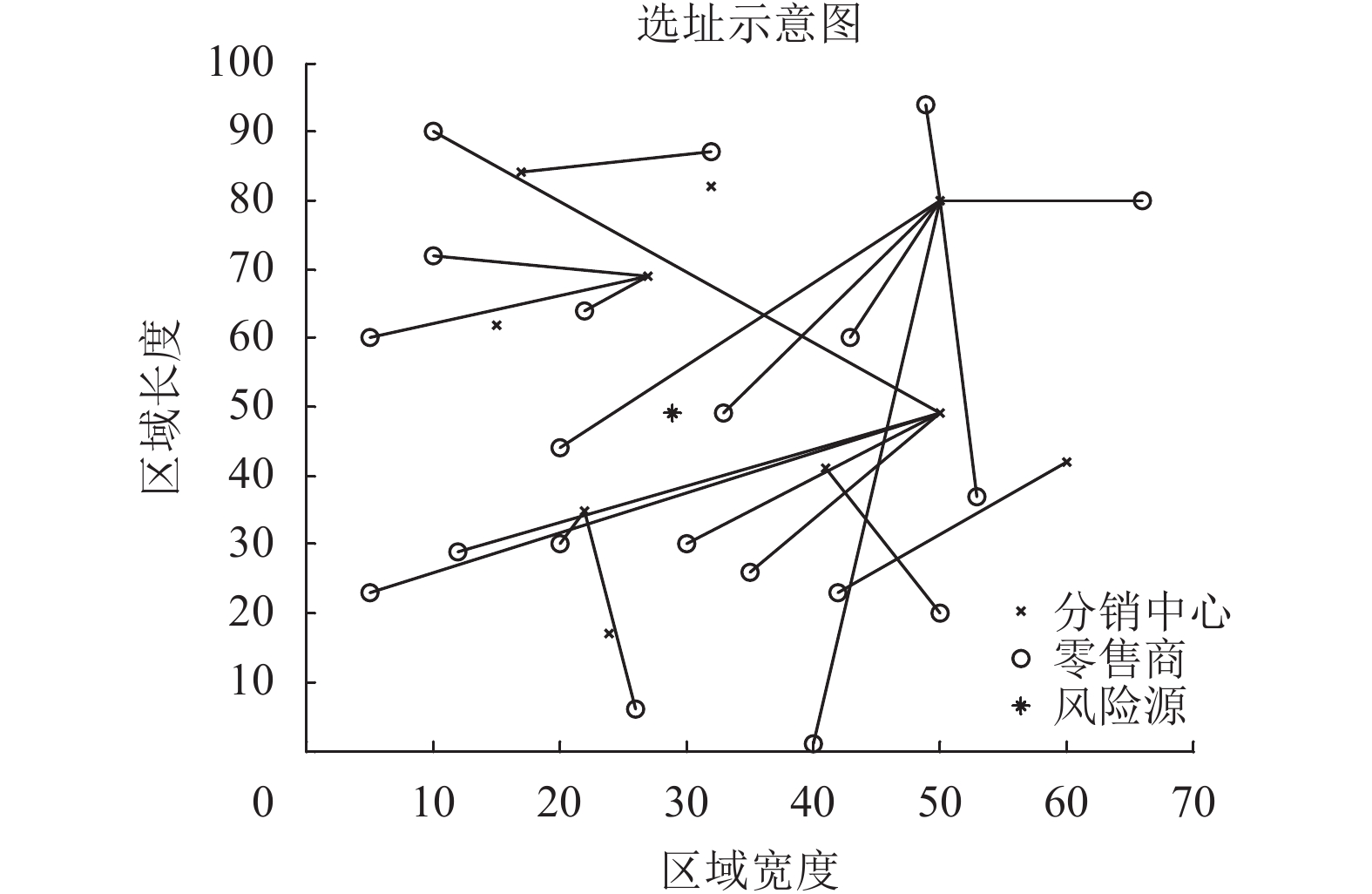
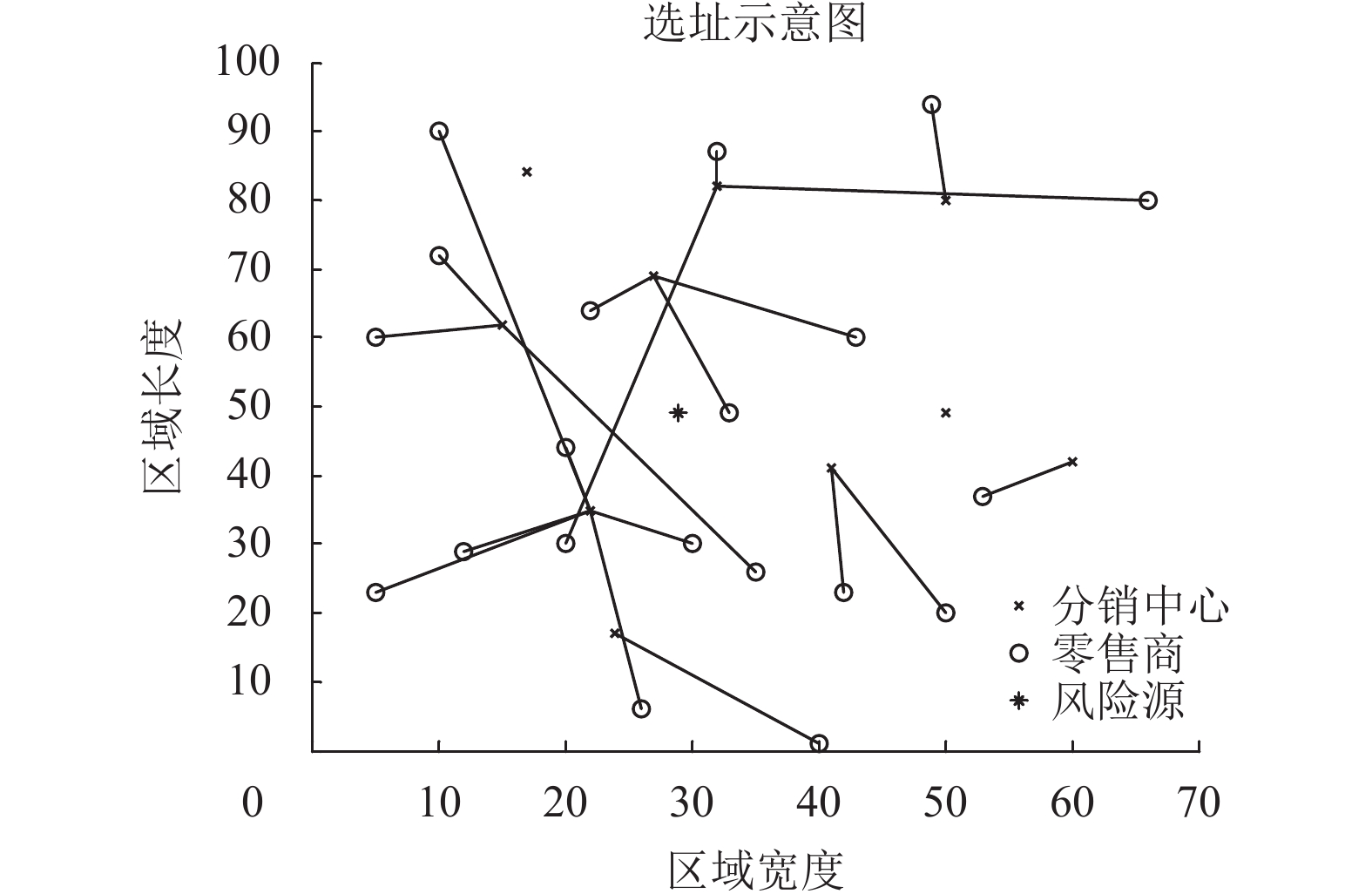
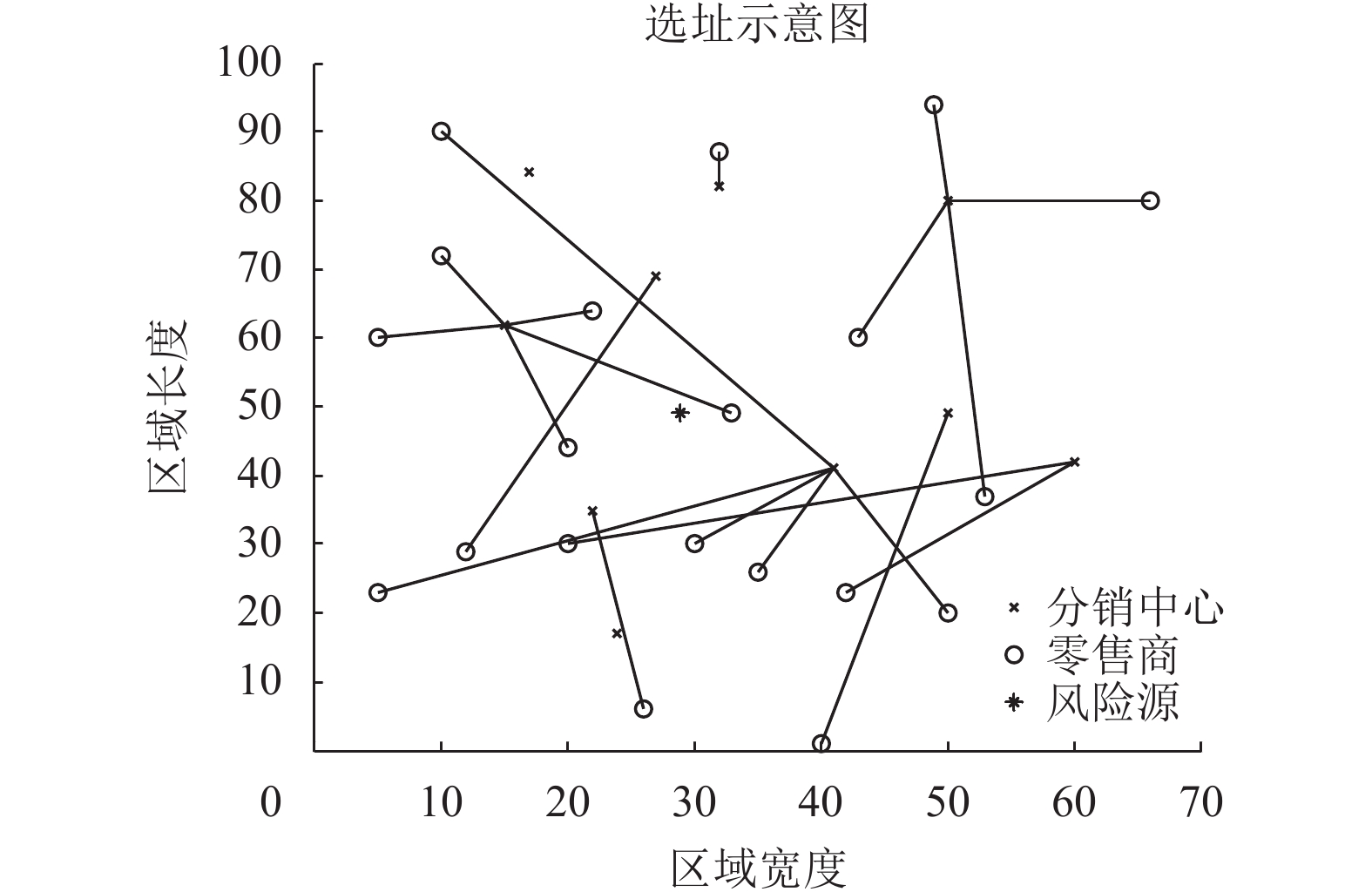
方案1的选址示意图如图5所示。为进一步分析转运对选址分布的影响以及转运与中断风险共同作用对选址的影响，对后3个方案进行仿真(如图6、7、8所示)。得到方案2目标值为481 232.38元，选址结果为[1,1,1,1,1,1,1,0,0,1],指派关系为[6,7, 2,5,2,7,7,1,4,6,5,3,7,10,7,2,6,4,4,7]；方案3目标值为457 479.07元，选址结果为[0,1,1,1,1,1,1,1,0,1],指派关系为[3,5,4,5,8,2,7,8,4,6,3,10,4,10,5,4,10,5,4,5]；方案4目标值723 436.55元，选址结果为[1,1,1, 1,0,0,0,1,1,1],指派关系为[4,2,4,3,8,2,1,1,9, 9,8,3,4,9,4,8,10,3,4,8]。

比较4种方案的平均目标值和最小目标值发现，方案3成本最低，方案2次之，方案1成本再次之，方案4成本最高。比较图4、图5、图6和图7发现，方案2和方案4的选址结果中没有考虑进转运的因素，在选址上偏向于中心化分布，即分销中心选在其所分配的零售商中间，这样做的好处是可以减少配送费用，降低运营成本。

再分析与方案2对应的方案3，以及与方案4对应的方案1发现，考虑进转运因素后，选择的分销中心更集中，零售商的指派也更加集中，并且方案3的最优目标值比方案2减少23 753.31元的支出，支出减少近4.91%，方案1的最优目标值比方案4减少51 891.16元的支出，支出减少7.17%，成本节省效果显著，说明了在分销网络设计之初就考虑进转运因素可以实现成本节约，提高系统总收益。

方案2和方案3中没有考虑中断风险的影响，从其分布示意图中可以看出，选择的分销中心分布比较靠近坐标系中心。但是比较方案2对应的方案4和方案3对应的方案1发现，考虑中断风险影响后的分销中心选址偏向于距离风险源更远的地方，且距离风险源较远的分销中心指派的零售商更多，订货量更大。这是比较容易理解的。某些分销中心距离风险源较近，但是其负责配送的零售商少，订购量和库存量也就少，即使发生中断，其损失也比较少。在方案2和方案3现有选址结果的基础上重新考虑进中断风险，发现其预期成本分别为784 751.33元和727 644.71元，分别比方案4和方案1多支出了8.48%和8.35%。因此在分销网络设计阶段就考虑进中断风险并进行规避是十分必要的，可以显著降低应急发生成本。

方案2和方案3重新考虑进中断风险得到的预期成本，再与方案1和方案4进行比较，发现方案1的成本是最低的，说明在分销网络设计阶段考虑进中断风险和转运因素，不仅统一了分销网络设计的战略和战术两个层面，而且两者对降低分销网络的总成本都能起到积极作用，能够有效降低日常运营成本和分销网络的应急发生成本。

4.2 灵敏度分析

为了进一步分析转运和中断风险对分销网络设计的综合影响效果，以下对方案4和方案1中的中断风险进行灵敏度分析。

分别在当前各候选分销中心中断风险的基础上缩放0.2、0.5、1、2、5、10、100倍，得到方案4和方案1的分析结果如表4所示。由表4可知，首先，中断风险越大惩罚成本越高，系统的应急成本也越高，再一次说明了在分销网络设计之初就考虑中断风险并采取规避措施的重要性；其次，中断风险下考虑转运的目标值相比不考虑转运的目标值的减少比例随着中断缩放倍数的增大而减小，说明一定概率的中断风险下，转运可以有效降低系统总成本，而当放大倍数过大的时候，转运对系统总成本的影响逐渐降低，这是因为中断风险过大的时候，中断惩罚成本在总成本中占据了主导地位，转运所起到的作用就越来越小。

5 结论

本文考虑了一个由单一供应商、多个分销中心和多个零售商组成的分销系统，系统中供应商和零售商的位置、候选分销中心的位置以及零售商的需求分布均为已知，并假设分销中心采取(s, S)库存盘点策略。针对上述系统单一产品、单一周期的情况，问题中又综合考虑中断风险和横向转运，构建了非线性0-1整数规划模型，最后设计了遗传算法并用Matlab进行求解。通过仿真，得到的结论和启示如下。

1) 转运因素对选址的影响是分销中心间的选择更加集中。验证了在分销网络设计阶段就考虑转运的影响可以显著降低整个网络的运营成本，提高系统总收益。

2) 中断风险会使分销中心距离风险源的平均距离增加，且零售商更集中分配给距离风险源较远的分销中心，这使得中断发生的概率更低，且中断发生时的应急发生成本更小，因此在分销网络设计阶段有必要考虑中断风险。

3) 转运的积极作用对风险概率的变化敏感。在对分销网络进行设计时，无论考虑和不考虑中断风险，考虑转运都会使得分销网络更优，且同时考虑中断风险和转运可以降低分销网络日常运营成本和应急发生成本，使得分销网络成本达到最优。但是随着中断风险的增大，转运对分销网络的积极作用会逐渐变小。

4) 鉴于中断风险发生概率小，且转运对于增加系统收益和降低成本都有积极影响，因此在分销网络设计阶段可以着重考虑转运。为配合转运，可以在距离风险源较近的地方选择中断后惩罚成本小的分销中心投入运营，以降低转运成本和配送成本。

本文忽略了分销中心的容量限制，且没有考虑中断发生后转运能起到的作用，未来的研究可以在这些方面进行进一步的探索。