架空输电线路是电网的重要设备，其运行状态对整个电力系统稳定起着决定性的影响。随着电网规模的持续扩大，电网设备的状态检修工作也随之深入，而状态评价正是状态检修管理机制的基础与核心。要对架空输电线路做出继续运行、实施监控或停役检修等决策，必须准确可信地估计或预测架空输电线路的运行状态^[1-3]。

文献[4]提出了基于贝叶斯网络的架空输电线路评价模型，文中各指标故障概率套用国家电网公司110~500 kV架空输电线路评价标准得出。文献[5]通过Delphi法求得架空输电线路状态量权重系数，对输电线路运行状态进行评价，并未讨论主观因素对权重的影响。文献[6]采用蒙特卡洛法对架空输电线路运行状态进行分析研究，文中利用抽取随机数使得该方法所得分析结果具有不确定性。

本文根据架空输电线路的组织架构，结合架空输电线路的常见故障，建立了架空输电线路的评价指标体系，通过相对劣化度概念对架空输电线路实际运行数据进行归一化处理，并对运行状态进行等级划分；针对架空输电线路指标的不确定性，引入集对分析法，建立了架空输电线路各指标的联系度表达式；结合层次分析法与熵权法，最终得到各指标的组合权重，从而对架空输电线路各部件与架空输电线路整体运行状态做出评价。

1 架空输电线路评价体系与等级的建立 1.1 架空输电线路评价体系

架空输电线路主要由基础、杆塔、导地线、绝缘子、金具、接地装置、附属设施以及通道等8个部件构成。结合文献[7-8]对架空输电线路常见故障进行分析，得出架空输电线路评价指标体系如表1所示。

1.2 评价指标相对劣化的度确定

架空输电线路的指标参数主要通过人工定期巡视、检测、试验或通过在线监测装置2种方式获得。根据指标的特点，采用适当的方法得到评价指标的参数：对于绝缘子零值情况，导线的弧垂偏差等随环境状况和运行状况不断变化的指标，根据相关技术要求^[9]，通过安装在线监测装置获得；对于金具锈蚀、附属设施运行情况等需要人为主观判断，或短时间内不会发生突变而影响架空输电线路运行情况的，则可通过人工巡视、检测和试验获得。

由表1所列评价指标可知，架空输电线路评价指标种类众多，各指标的数量级、单位量纲均不相同。本文运用计算相对劣化度^[10]的方法，通过描述各指标的实际状态对良好状态的偏离度，从而将众多指标纳入统一评价。

对于定量指标的相对劣化度计算可分为效益型与成本型，效益型指标即指标数值越大，其运行状态越好，计算公式为

g ( x ) = { 0 , x ＜ a ; x − a b − a , a ≤ x ≤ b ； 1 , x > b 。

(1)

成本型指标即指标数值越小，其运行状态越好，计算公式为

g ( x ) = { 1 , x ＜ a ; b − x b − a , a ≤ x ≤ b ; 0 , x ＞ b 。

(2)

式中，x为指标的实际数值；g(x)为指标状态量的相对劣化度；b为指标评价上限值；a为指标评价下限值。

对于定性指标量可结合相对劣化度的方法，采用专家评分的方式，打分范围取[0, 1]，且运行状态越好，分值越大越靠近1。

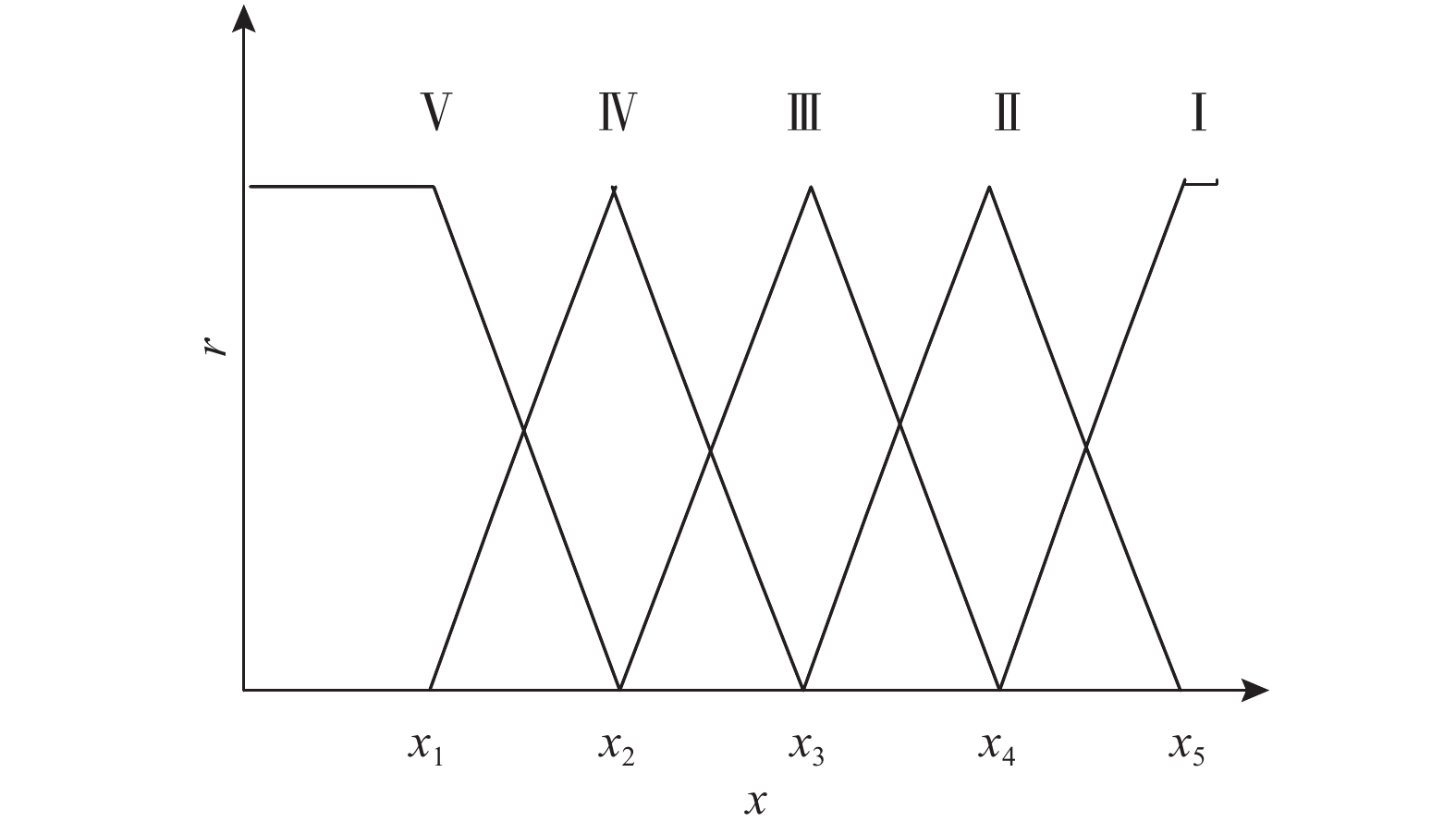
1.3 评价等级及隶属度函数的确定

本文将指标状态划分为5个状态等级^[10]，即I良好(v₁)、II正常(v₂)、III注意(v₃)、IV异常(v₄)、V重大异常(v₅) ，并根据相对劣化度式(1) 式(2)归一化结果，采用三角形和半梯形结合的方式得出指标对5级状态的隶属度函数，如图1所示。

状态等级I(v₁)隶属度函数

r 1 = { 0 , ( x − x 4 ) / ( x 5 − x 4 ) 1 , , x ＜ x 4 ; x 4 ≤ x ≤ x 5 ; x ＞ x 5 。

(3)

状态等级II(v₂)隶属度函数

r 2 = { ( x − x 3 ) / ( x 4 − x 3 ) , ( x 5 − x ) / ( x 5 − x 4 ) , 0 , x 3 ≤ x ≤ x 4 ; x 4 ≤ x ≤ x 5 ; x ＜ x 3 或 x ＞ x 4 。

(4)

状态等级III(v₃)隶属度函数

r 3 = { ( x − x 2 ) / ( x 3 − x 2 ) , ( x 4 − x ) / ( x 4 − x 3 ) , 0 , x 2 ≤ x ≤ x 3 ; x 3 ≤ x ≤ x 4 ; x ＜ x 3 或 x ＞ x 4 。

(5)

状态等级IV(v₄)隶属度函数

r 4 = { ( x − x 1 ) / ( x 2 − x 1 ) , ( x 3 − x ) / ( x 3 − x 2 ) , 0 , x 1 ≤ x ≤ x 2 ; x 2 ≤ x ≤ x 3 ; x ＜ x 1 或 x ＞ x 3 。

(6)

状态等级V(v₅)隶属度函数

r 5 = { 1 , ( x 2 − x ) / ( x 2 − x 1 ) , 0 , x ＜ x 1 ; x 1 ≤ x ≤ x 2 ; x ＞ x 2 。

(7)

式中，r_i(i=1, 2, 3, 4, 5)为5个等级的隶属度函数；x_i(i=1, 2, 3, 4, 5)为各等级的模糊分界。各状态评价等级对应的状态描述^[10]如表2所示。

2 集对分析方法

集对分析法是针对具体问题，根据同一、差异和对立三分原理，引入联系度概念，从而刻画三方面之间的相互关系，对系统展开定量分析。集对分析法在变压器、电能质量等电力系统的状态评价以及其他领域的指标评价中已有了广泛的应用^[11-14] 。

联系度是集对分析的重要数学工具，是集对分析的关键所在，其实质上是对研究对象做“系统性”考察结果的一种描述.其中同一度和对立度的描述相对确定，而差异度根据不同的具体情况，会有不同的描述结果，体现出评价系统具有的不确定性。

2.1 评价指标联系度函数的确定

对于给定集合U与V其联系度定义为

μ ( U , V ) = S N + F N i + P N j 。

(8)

式中，S为具有同一性的特性数；F为具有差异性的特性数；P为具有对立性的特性数，且S+F+P=N；i为不确定的差异度系数，其取值范围为(–1, 1)；j为对立度系数，其值通常取–1。

令同一度a=S/N，差异度 b=F/N，对立度c=P/N，则式(8)其表达式变换为

μ ( U , V ) = a + b i + c j 。

(9)

式中，a、b、c∈[0, 1]且a+b+c=1。

式(9)是对研究对象进行一分为三的一种刻画，但这仍显得过于粗糙，若将联系度根据不同情况继续分析和扩展，则可用对bi项扩展后的多元联系度来反映。

μ ( U , V ) = a + b 1 i 1 + b 2 i 2 + ⋅ ⋅ ⋅ b N − 2 i N − 2 + c j 。

(10)

且式(10)满足

a + ∑ i = 1 N − 2 b i + c = 1 。

(11)

在本文中，通过指标与等级I良好(v₁)的联系度μ_pn来对架空输电线路指标进行评价，因指标分为5个评价等级，则其联系度函数可扩展为

μ p n = a + b 1 i 1 + b 2 i 2 + b 3 i 3 + c j 。

(12)

式中，若指标对5个状态评价等级的隶属度分别为r₁、r₂、r₃、r₄、r₅，则联系度函数中同一度用指标对等级良好(v₁)的隶属度描述，即a=r₁；对立度用指标对等级重大异常(v₅)的隶属度描述，即c=r₅；差异度b₁定义为偏同差异度系数，可用指标对等级正常(v₂)的隶属度描述，即b₁=r₂；差异度b₂定义为中差异度用指标对等级注意(v₃)的隶属度来描述，即b₂=r₃；差异度b₂定义为偏反差异度用指标对等级异常(v₄)的隶属度来描述，即b₃=r₄。

相应的联系度函数表达式可构建为

μ p n = { 1 + 0 i 1 + 0 i 2 + 0 i 3 ​ + 0 j , r 1 + r 2 i 1 + 0 i 2 + 0 i 3 ​ + 0 j , 0 + r 2 i 1 + r 3 i 2 + 0 i 3 ​ + 0 j , 0 + 0 i 1 + r 3 i 2 + r 4 i 3 ​ + 0 j , 0 + 0 i 1 + 0 i 2 + r 4 i 3 ​ + r 5 j , 0 + 0 i 1 + 0 i 2 + 0 i 3 ​ + 1 j , x ≥ x 5 ; x 4 ≤ x ＜ x 5 ; x 3 ≤ x ＜ x 4 ; x 2 ≤ x ＜ x 3 ; x 1 ≤ x ＜ x 2 ; x ＜ x 1 。

(13)

2.2 联系度系数的确定

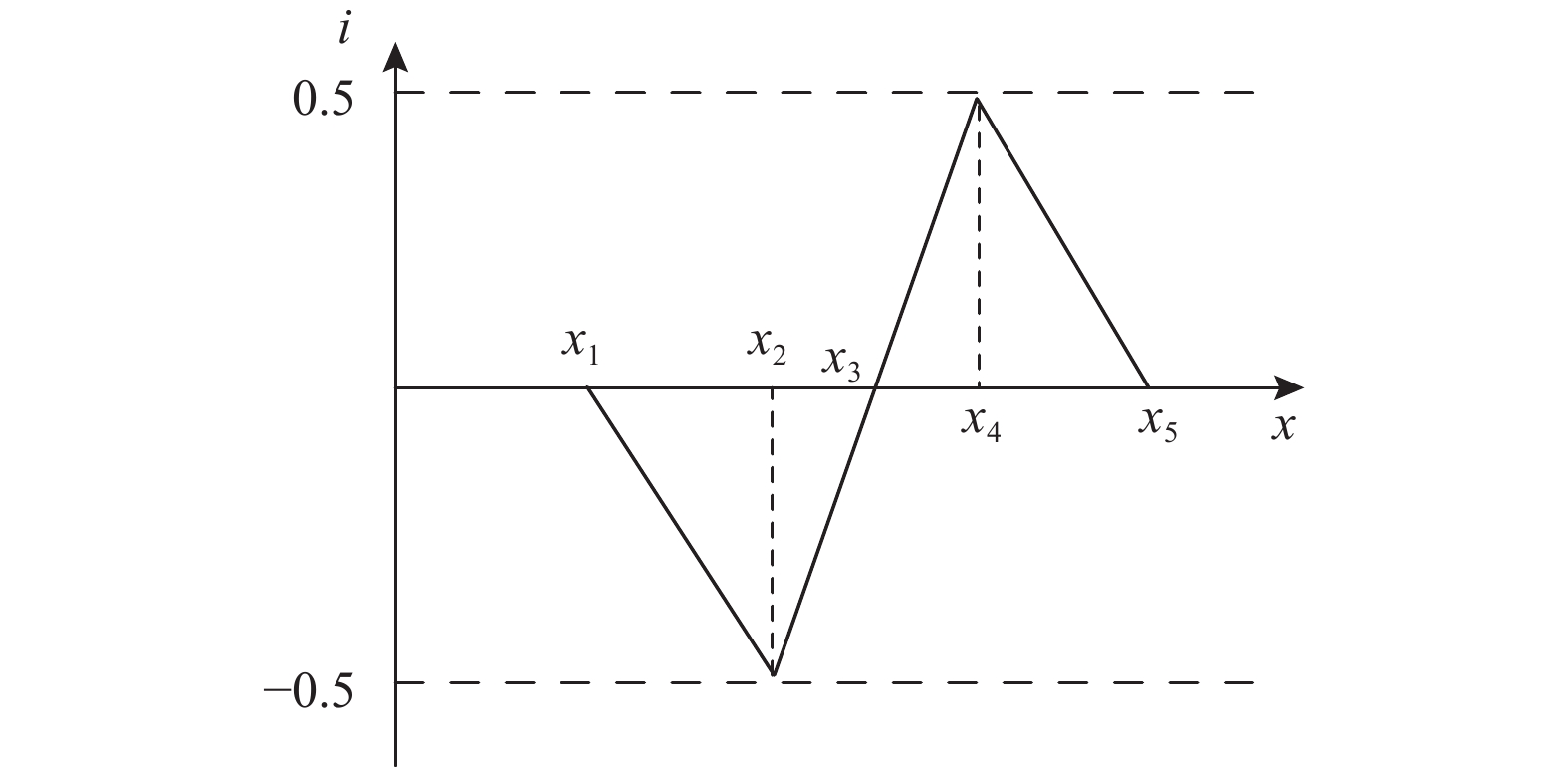
联系度是集对分析的重要数学工具，其实质上是对研究对象 “系统性”考察结果的一种描述，在联系度函数构建完成后，通过对差异度系数i和对立度系数j进行具体量化分析，代入式(13)，得到具体数值，称为联系数。由上文分析可知对立度系数 j=–1，而差异度系数i的分析刻画是集对分析的关键，本文将通过分段三角模糊数来刻画差异度系数，如图2所示。

将等级界限值x₄和x₃、x₂处的差异度系数分别取作i₁=0.5、i₂=0、i₃= –0.5，则其他指标值对应的差异度系数可按三角模糊函数求得：

i 1 = { x 5 − x 2 ( x 5 − x 4 ) , x 4 ＜ x ＜ x 5 ; x − x 3 2 ( x 4 − x 3 ) , x 3 ＜ x ＜ x 4 ; 0 , 其 他 。

(14)

i 2 = { x − x 3 2 ( x 4 − x 3 ) , x 3 ＜ x ＜ x 4 ; − x 3 − x 2 ( x 3 − x 2 ) , x 2 ＜ x ＜ x 3 ; 0 , 其 他 。

(15)

i 3 = { − x 3 − x 2 ( x 3 − x 2 ) , x 2 ＜ x ＜ x 3 ; − x 3 − x 2 ( x 2 − x 1 ) , x 1 ＜ x ＜ x 2 ; 0 , 其 他 。

(16)

将求得的差异度系数代入式(13)即可得出该指标的联系数μ_pn^[15-16]。

3 架空输电线路指标权重确定

通过集对分析可对某一指标运行状态进行评估，而若需要对架空输电线路部件进行分析评价，还需要进一步求解各个指标的权重。

本文首先采用层次分析法求取指标主观权重，通过指标之间的专家比较评判得到判断矩阵Y，求解判断矩阵Y的最大特征根λ_max与其特征向量ξ，并进行一致性检验后，可对特征向量ξ进行归一化处理得向量γ=(γ₁,…, γ_n)，即为求得的主观权重向量。

通过层次分析法确定评价指标的权重时，可能会由于主观人为因素而形成偏差，为尽量减少指标权重计算中主观因素的干扰，本文引入熵权法对主观权重进行修正^[17]。熵的概念是用来表示系统的混乱程度。在信息论中熵引申表示为系统的不确定程度，信息熵值越小，则信息的确定性越大，可靠性越高，相应的权重参数越大。某部件下n个指标，对于评价等级V={v₁, v₂, v₃, v₄, v₅}，按照式(3)~(7)，计算各指标对应于不同状态等级的隶属度值，得到模糊评判矩阵为

R = [ R 1 R 2 ⋯ R n ] = [ r 11 r 12 r 13 r 14 r 15 r 21 r 22 r 23 r 24 r 25 ⋯ ⋯ ⋯ ⋯ ⋯ r n 1 r n 2 r n 3 r n 4 r n 5 ] 。

(17)

式中，R为模糊评判矩阵；r_ij为第i个指标对v_j的隶属关系，表示状态量的隶属度。

本文以式(17)模糊评判矩阵R为研究对象，求得各个指标的信息熵值为

e i = − ( ∑ j = 1 4 r i j ln r i j ) / ln 4 。

(18)

通过信息熵值，可求得指标状态量的熵权值为

ε i = 1 − e i n − ∑ i = 1 n e i i = 1 , 2 , n 。

(19)

由此可得经熵权修正后的指标权重为

ω i = γ i ε i σ ∑ i = 1 n γ i ε i σ 。

(20)

式中，ω_i为指标修正后的组合权重；γ_i为层次分析法求得权重；ε_i为熵权法求得的修正系数；σ为变权系数，根据文献[17]分析，取σ=0.1。

4 架空输电线路评价综合评价 4.1 架空输电线路各部件的评价

架空输电线路共有8个部件，每个部件下都有若干指标。根据第2节所述内容，求得各指标等级标准的联系数μ_pn。根据第3节所述方法求得指标权重ω_n，计算该部件相应的综合联系数μ_pn，以评定等级。相应的计算模型为

μ p = ∑ n = 1 N ω n μ p n 。

(21)

本文指标状态为5级，则其指标评价的数学模型为

m p = 3 − 2 μ p 。

(22)

式中，计算结果m_p的具体数值即为该部件对应评价等级。特别的，若某一部件下任一指标联系数μ_pn=–1，无论其他指标评价结果如何，则该部件的评价等级即为V重大异常(v₅)。

4.2 架空输电线路整体的评价

根据文献[8]，各个部件的状态评价权重如表3所示。

架空输电线路整体评价数学模型为

M = ∑ p = 1 8 ω p m p 。

(23)

式中，与各部件评价相类似，M的具体数值即为对应的评价等级,若某一部件在评价中评价等级为重大异常V(v₅)，则该段线路的评价等级即为重大异常V(v₅)。

5 实例分析

本文以集对分析方法对某市公司下辖的A线、B线、C线3条110kV线路某段运行状态进行评价，并结合线路的实际运行情况与评价结果比对分析。

5.1 架空输电线路部件状态评价

以部件导地线的状态评价为例，导地线断股情况、导线运行温度、导线接续处电阻、导线弧垂偏差4个指标集合为U={u₁, u₂, u₃, u₄}，3条实际线路的导地线指标运行情况如表4所示。

1)根据文献[7]，其中导线标弧偏差的评价上下限制为6%和1.5%，则其归一化函数为

g ( x ) = { 0 , x ＜ 1.5 ; 6 − x 6 − 1.5 , 1.5 ≤ x ≤ 6 ; 1 , x ＞ 6 。

A线实测值归一化后为g(x)=5/9，根据式(3)~(7)可得指标对隶属度向量：

r=(0, 0.5, 0.5, 0)。

根据式(13)~(16)可得其差异度系数，求解联系数得

μ_p4=0+0.5×0.25+0.5×0.25+0+0=0.25。

同理可得其他3项指标的联系数为

μ_p1=0.375，μ_p2=1，μ_p3=0.25。

2)根据第2节所述方法，分别求取4个指标权重。层次分析法得到的权重向量为

γ=(0.532, 0.098, 0.185, 0.185)，

熵权法求得的修正系数为

ε=(0.233, 0.359, 0.204, 0.204)，

则其组合权重为

ω=(0.532, 0.102, 0.183, 0.183)。

3)可得其综合联系数为

μ p = ∑ n = 1 4 ω n μ p n = 0.393 。

可知其评价等级为

m_p=3–2μ_p=2.214。

即A线该段线路指标导地线的评价等级为II正常(v₂)和III注意(v₃)之间。同理可求得B线及C线导地线指标评价等级，如表5所示。

B线该段线路导地线评价等级为I良好(v₁)和II正常(v₂)之间，而C线该段线路导地线因弧垂偏差过大，评价等级为V重大异常(v₅)。

5.2 架空输电线路整体评价

利用上述方法可对架空输电线路基础、杆塔、导地线、绝缘子、金具、接地装置、附属设施以及通道等8个指标单元分别进行分析。根据表所提供权重及式(23)对3条线路运行状态整体进行评价，计算结果如表6所示。

A线评价等级为II正常(v₂)和III注意(v₃)之间；B线评价等级为I良好(v₁)和II正常(v₂)之间；C线因导指标线弧垂联系数μ_pn= –1，则C线该段线路状态评价等级为V重大异常(v₅)。

5.3 评价结果分析

实际中，A线为投运时间超30年线路，是单电源供电线路，为供电公司重点运维线路，所以虽然运行年限久，其依然能保证正常运行，但其线路部件整体已呈老化趋势，检修次数安排较多，符合本文II正常(v₂)和III注意(v₃)之间的评价。

B线为投运10年以内线路，其整体运行状态良，日常维护情况良好，符合本文评价结果状态等级I良好(v₅)和II正常(v₅)之间。

C线为近期投运线路，构建良好，但线路因为外部因素致弧垂已不满足要求，需对该段线路立即安排检修，与评价结果一致。

6 结语

本文参照架空输电线路相关规程，结合对各线路评价指标的归一化处理方法，针对架空输电线路状态信息的模糊性和不确定性，提出了采用集对分析法，从同一度、差异度以及对立度等三方面处理架空输电线路的不确定信息，并构建了架空输电线路各指标以及整体评价体系。在评价指标计算中，采用层次分析法与熵权法的结合方式，实现了各指标权重的合理分配。实际运行线路的分析结果表明，基于集对分析法的架空输电线路状态评价结论可靠，具有良好的实用性。