2. 南京工业大学 经济与管理学院,江苏 南京 210094;
3. 西南交通大学 土木工程学院,四川 成都 610031
2. Economy and Management School, Nanjing Tech University, Nanjing 210094, China;
3. College of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
地面交通负荷过大所带来的交通拥堵、尾气污染已经成为世界各大中型城市所面临的亟待解决的问题。以地铁、轻轨为代表的城市轨道交通系统因为具有大规模的旅客输送能力,运输速度稳定,受地面交通干扰小,耗能低且使用能源清洁等优势,逐渐成为现代城市交通发展的主流与方向。值得注意的是,北京、上海、广州、南京等城市的地铁交通系统已经从单线运营进入了网络化运营时代,规划重点也应从线路设计转向网络规划设计。因而,运用复杂网络理论去分析地铁网络的拓扑结构具有较高的理论与实践价值,一方面结构分析是性能分析的基础;另一方面优化网络结构有利于资源配置优化与风险管理的加强。
Watts等[1]于1998年发表的《小世界网络群体动力学》与Barabasi等[2]1999年发表的《随机网络的标度》引发了研究网络结构的热潮。Wu等[3]研究发现北京地铁网络节点度分布的值为2.24,验证了其无标度性。Angeloudis等[4]针对当时世界上最大的20个城市的地铁网络进行拓扑分析,发现大多数地铁网络具备高联通性与无标度特性。Derrible等[5]同样试图从复杂网络特征入手对世界上19个国家和地区的地铁网络进行分析并提取出拓扑特征。Cai等[6]通过构建拓扑模型来衡量城市轨道交通网络的易损性。王燚等[7]构建SpaceL与SpaceP拓扑结构模型对上海地铁的复杂网络特征进行分析,得出其具有小世界特性和无标度特性。张晋等[8]针对北京市地铁实际网络及运营关系网络分别构建SpaceL与SpaceP拓扑结构模型,得出其节点度指数分别为4.1与4.2,符合幂律分布,网络平均距离分别为15.26与2.68,聚类系数达到0.94,同样符合小世界特性。刘志谦等[9]构建了广州地铁SpaceL拓扑结构模型,发现其表现出随机网络特征。李朴等[10]构架了SpaceL拓扑结构模型,对北京、上海、广州地铁网络的连通性作了对比分析。可见从复杂网络特征入手分析提取地铁网络的拓扑特征是研究地铁网络性能有效途径。
南京地铁自2005年1号线建成运营到2016年已有共计6条线路运营通车,2021年预计将增加到13条线路。但目前关于南京地铁的研究尚集中于单条线路,从全局视角出发对其网络结构及性能分析稍显不足;其次,缺乏将南京地铁实际运营网络与规划运营网络的比较研究,因此规划部门无法从网络整体性能出发对规划站点的设置提出逆向考证;最后,严格采用小世界特性的图论指标会因为忽视地铁网络的平面特性而产生判断的偏差。
本文拟针对南京地铁2016年实际运营网络及2021年规划运营网络分别构建SpaceL拓扑结构模型,并应用节点度及其分布、平均最短距离及其分布、采用联通度指标替代集聚系数,并增加介数指标对其无标度特性及小世界特性进行分析比较,从而通过掌握拓扑结构特性更好地研究其网络性能,进而为规划站点的设置提出逆向考证。
1 地铁网络SpaceL拓扑模型构建与指标选择 1.1 地铁网络拓扑模型构建地铁网络是由地铁站点与轨道交通线路相互连接,并由换乘关系形成某种约束从而相互衔接的网络,因而可将其抽象为由一系列顶点V与链L构成的图G。令G=(V,L),G可以是无向图,即顶点间的衔接没有先后顺序;也可以是有向图,即每条链都规定有起点与终点;同时可以表示为等价图,即假设每条链的长度相等。也可给链赋予不同意义的权值,表示为非等价图。无论构造成上述哪类抽象图,其图中的要素都必须和实际的交通网络呈现出必要的对应关系。图G中的顶点V代表地铁运营网络中的站点,根据功能不同将其分为3类:F代表换乘站,H代表起点站和终点站,M代表中间站,即顶点V可表示为集合V{VF,VH,VM};链L代表地铁站点间的轨道交通线路,若图G中有N个顶点,链可表示为N×N的矩阵{Lij}。
1.2 地铁网络拓扑指标选择无标度特性(scale-free property)与小世界效应(small-world effect)是衡量复杂网络结构的重要指标,也是进行网络性能分析的基础。
无标度特性指网络的节点度分布呈现出幂律分布的规律,少数hub顶点具有较大的节点度,在整个网络中起着重要的作用,因此准确找到这些hub顶点并掌握其演变机理对进一步把握地铁网络性能至关重要。本文采用节点度及其分布衡量地铁网络的无标度特性。
小世界效应,其满足条件为网络具有较高的集聚系数(clustering coefficient)及较小的网络平均最短距离。然而,由于地铁网络的平面特性,集聚系数Ci并不适用于具有平面特性的地铁运营拓扑网络[4]。针对地铁运营网络特点,Garrison等[11]提出应用联通度概念去衡量地铁网络的发展程度,联通度是表达网络整体特征的拓扑指标,通过衡量实际链与潜在链的比例来表达网络的发展程度,其发展程度越高,网络平均最短距离会越短,网络整体的便捷性会越高。综上,本文应用下述两条规则衡量地铁网络是否具备小世界性:1)网络平均最短距离小于顶点数的对数,即
如果以ki表示抽象网络中顶点的节点度(node degree),则ki指与顶点i直接相连的链的数目。在有向网络中,节点度又可分为出度kout和入度kin。出度是指由该顶点指向其它顶点的链的数目,入度是指由其它顶点指向该顶点的链的数目,顶点i总的节点度则可表示为ki=kin+kout。节点度反映了某顶点在网络中与其它顶点联系的强弱,也可以表征该顶点在网络中的重要程度,节点度越大代表该顶点越重要。
|
|
(1) |
式中,Tij表达顶点i,j之间的连接情况,有链相连则Tij=1;无链相连则Tij=0。
然而,交通网络中每一个顶点的节点度只是代表了该顶点的局域属性,对整体网络而言,更有意义的是分析节点度的整体特性,即节点度分布P(k)。节点度分布可以表达抽象图最基本的拓扑特征。一般情况下,规则网络的P(k)呈现出单峰的Delta分布,随机网络的P(k)在远离峰值处以指数分布快速下降。而介于二者之间的一类网络其
图论中将等价网络两顶点间的最短距离定义为连接二者最少链的数目;将加权网络两顶点间的最短距离定义为连接二者的最短路径,最短路径可由最短旅行时间、最小旅行费用、最小旅行距离等及它们的加权值来表达。网络的平均最短距离(average shortest-path length)则是所有顶点对之间最短距离的平均值,计算方法为
|
|
(2) |
其中,dij为顶点i,j间的最短距离;
联通度(degree of connectivity)是表达网络整体特征的拓扑指标,通过衡量实际链与潜在链的比例来表达网络的发展程度,二者比值越高表示网络成熟度越高,计算公式为
|
|
(3) |
其中,LG为图G的实际链数;LmaxG为图G的最大可能链数;N是图G的顶点数。
2 南京地铁运营网络SpaceL拓扑结构模型 2.1 2016年南京地铁实际运营网络SpaceL拓扑图2016年南京地铁有L1、L2、L3、L10、S1、S8 共6条运营线路,共计113个站点,其中7个换乘站;以H表示起点站与终点站,F表示换乘站,暂将中间站忽略;若某站点既为换乘站也同为起迄点站则以换乘站表示,如南京南站既是L1与L3的换乘站,同时也是S1的起点站,表示为F5,如图1所示。
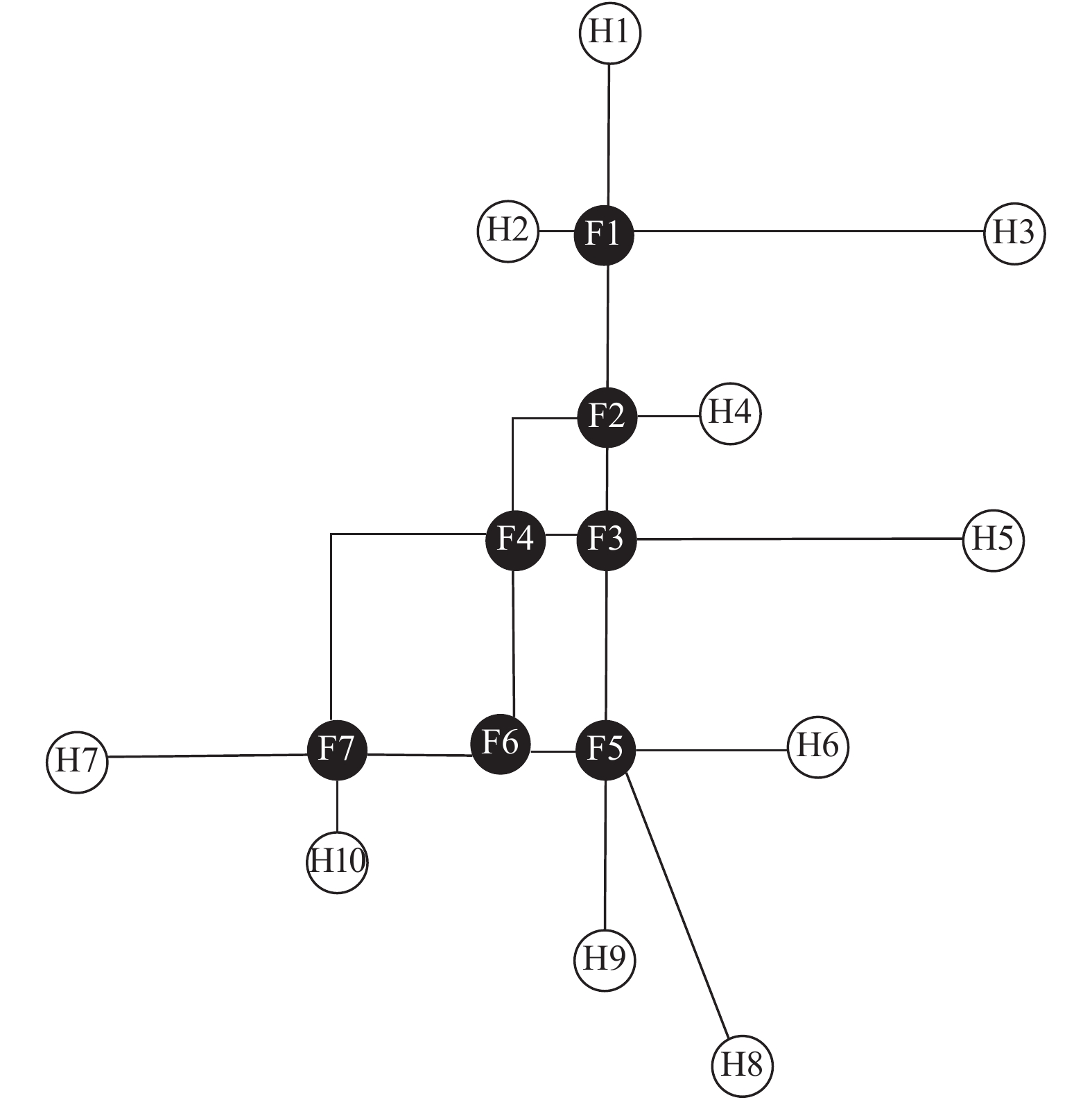
|
图 1 南京地铁网络2016拓扑结构图 Fig. 1 Topology network of 2016 Nanjing metro |
2021年南京地铁规划运营L1、L2、L3、L4、L5、L6、L7、L9、L10、L11、S1、S3、S8 等包括3条城际线在内的13条运营线路,共计241个站点,包括43个换乘站。如图2所示,较之2016年的地铁网络,覆盖区域面积增大,网络复杂程度提高,并且形成多个环状回路结构。
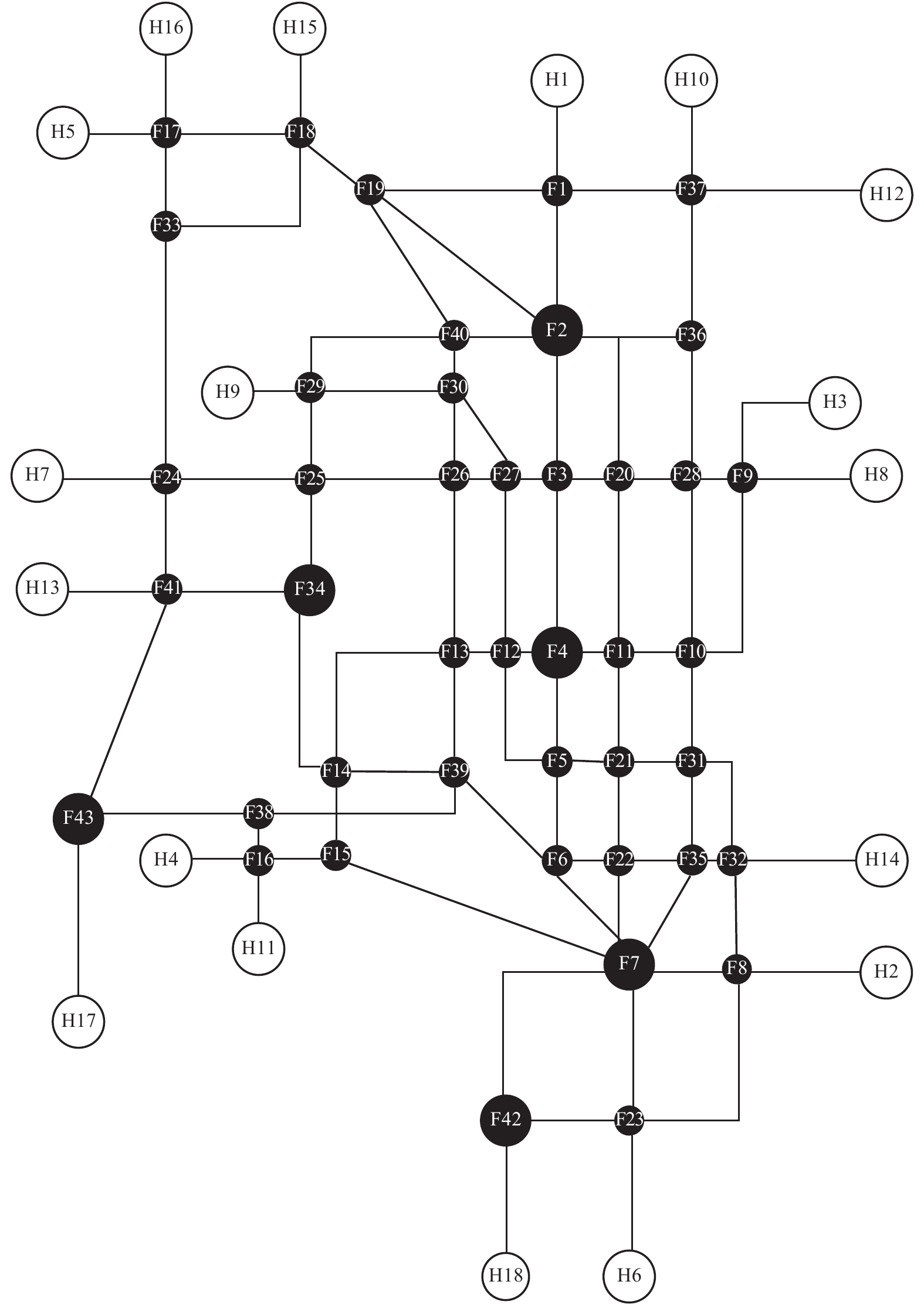
|
图 2 南京地铁网络2021拓扑结构图 Fig. 2 Topology Network of 2021 Nanjing Metro |
对于公共交通系统,研究通过某顶点的线路数目更具实践意义,因此针对地铁网络的平面特性,将通过某站点的线路数目作为该站点的节点度。
南京地铁2016年运营网络共有站点113个,包括中间站96个,其节点度均为1;单一起点站与终点站10个,其节点度亦均为1;共有换乘站7个,其节点度分别为kF1=2(泰冯路站),kF2=2(南京站),kF3=2(大行宫站),kF4=2(新街口站),kF5=3(南京南站),kF6=2(安德门站),kF7=2(元通站);平均节点度
南京地铁2021年规划运营网络共有站点241个,包括中间站180个,其节点度均为1;单一起点站与终点站18个,其节点度亦均为1;共有换乘站43个,除kF2=3(南京站),kF7=5(南京南站)外其余换乘站节点度为2;平均节点度
从表1和图3可直观地看出,在南京地铁网络2016年与2021年的抽象图中,有2条拓扑线路经过的概率较仅有1条线路通过的概率均快速下降,比率分别为94.3%、79.3%,可见2021年较2016年下降趋势明显缓和,这是由于新线路带来的大量换乘站的出现;有3条及更多拓扑线路经过的概率下降速率进一步放缓,分别为0.008 8与0.0041;说明无论是2016年还是2021年的地铁网络节点度分布均初步具有幂律分布的特性。因为拟合点数较少,为避免残差过大,本文运用最小二乘法(OLS)对统计数据进行非线性回归拟合[12],并对得到的幂律函数的一般形式f(x)=axb(x为自变量,a与b为正常数)参数进行检验,结果如表2所示。
| 表 1 南京地铁网络节点度分析数据 Tab. 1 Node degree analysis on Nanjing metro network |
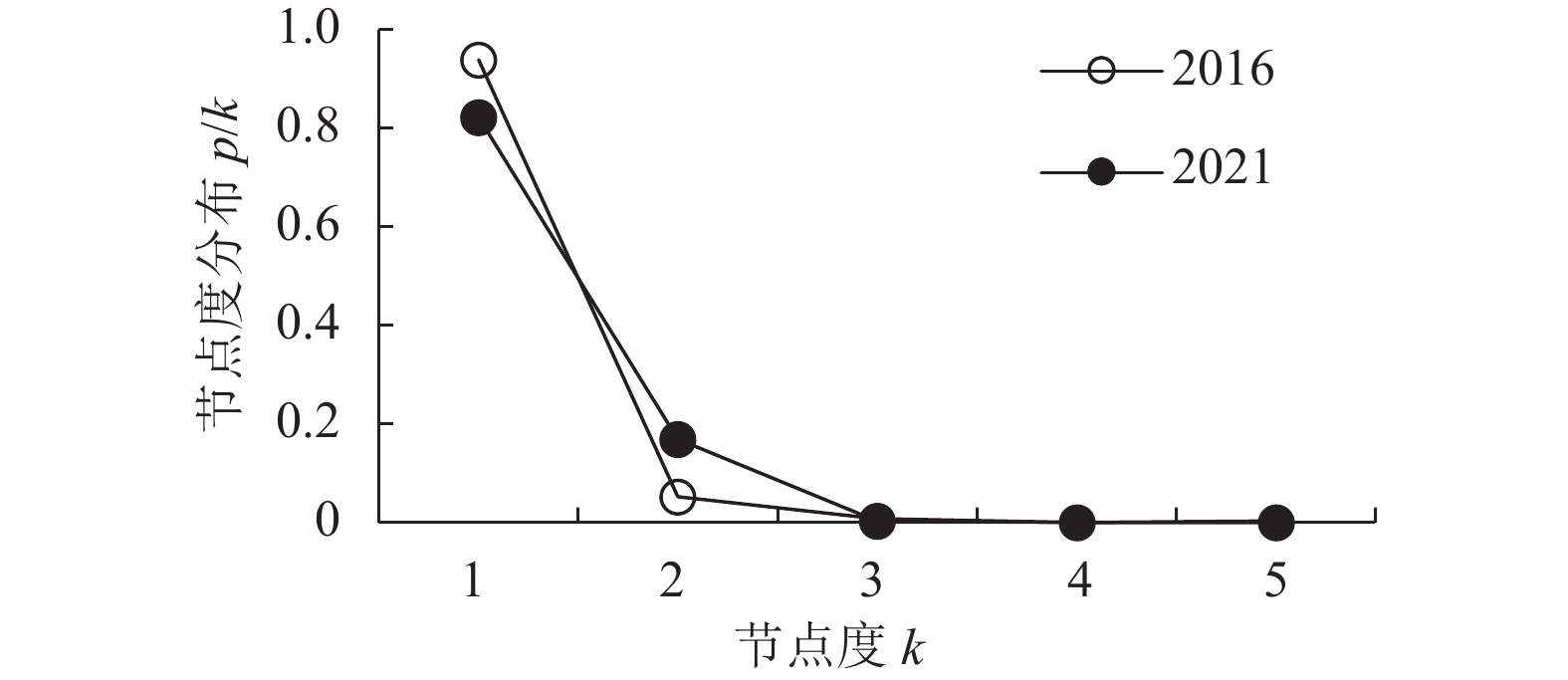
|
图 3 地铁网络节点度分布折线图 Fig. 3 Node Degree Broken Line Graph of Nanjing Metro |
| 表 2 拟合回归参数及检验结果 Tab. 2 Fitting parameters of regression function and testing result |
表2中的参数b等价于–λ,λ值越小,曲线越平缓,幂律尾部特征表现越明显;R2为拟合优度系数;SSE(sum of squares for error)为残差平方和。从检验结果看,南京地铁网络节点度分布基本符合幂律分布。
从上述研究结果可得,首先,2016年与2021年的南京地铁网络均具有无标度特性,其顶点的节点度差异性很大,少量顶点具有较大的节点度。如果将节点度大于2的顶点视为重要节点,在包括113个顶点的2016年南京地铁网络中只有7个为重要节点;2021年的地铁网络共有241个顶点,重要节点亦仅有43个。其次,无标度网络具有较高的容错性,但对基于节点度值高的hub点进行蓄意攻击防范力较差。南京地铁网络重要节点的数量从2016年的7个增加到2021年的43个,一方面重要节点增加,因此需要重点预防与保护的任务加大;另一方面因为替代路径增多,南京地铁网络应对随机故障的鲁棒性增强。
3.2 平均最短距离如图4所示,2016年南京地铁网络平均最短距离为15.29站,说明在各站点客流量相同的前提下,选择地铁出行平均需要经过近15站;2021年平均最短平均距离为13.16站,同样在各站点客流量相同的前提下,选择地铁出行平均缩短为13站。
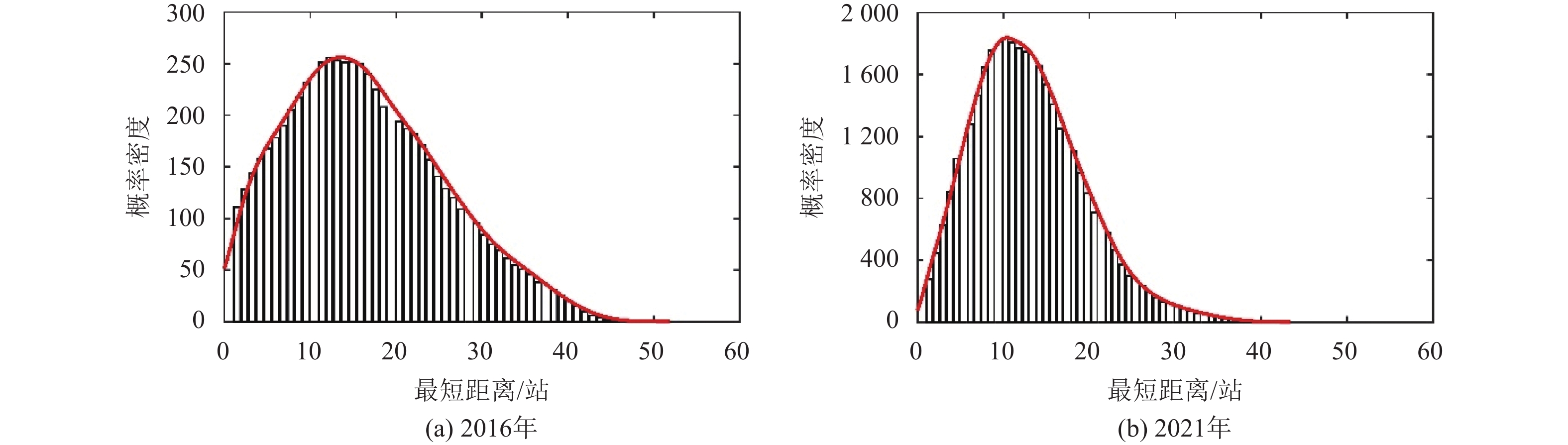
|
图 4 南京地铁网络最短距离分布对比图 Fig. 4 Shortest-path length comparison diagram of Nanjing metro network |
网络中最长的一条最短路径被称为网络直径。有趣的是,2016年与2021年南京地铁网络直径均是从金牛湖站到药科大学站,2016年的地铁网络经由S8-L3-L1共计44站,即网络直径为44;2021年的地铁网络则经由S8-L3-L9-L6-L5-L1,网络直径为41。在网络规模不同的前提下,具有相同起讫点的网络直径减少。
2021年南京地铁网络覆盖区域面积远大于2016年,在网络规模明显扩大的背景下,2021年南京地铁网络平均最短距离缩小,具有相同起讫点的网络直径减小清楚地说明地铁网络通达性提高,便捷程度增加。因此,可以肯定2021年后选择地铁出行的客流量必定大幅增加,新增站点的容量需要合理扩大;这也说明2016年与2021年的地铁网络处于不同的发展阶段。
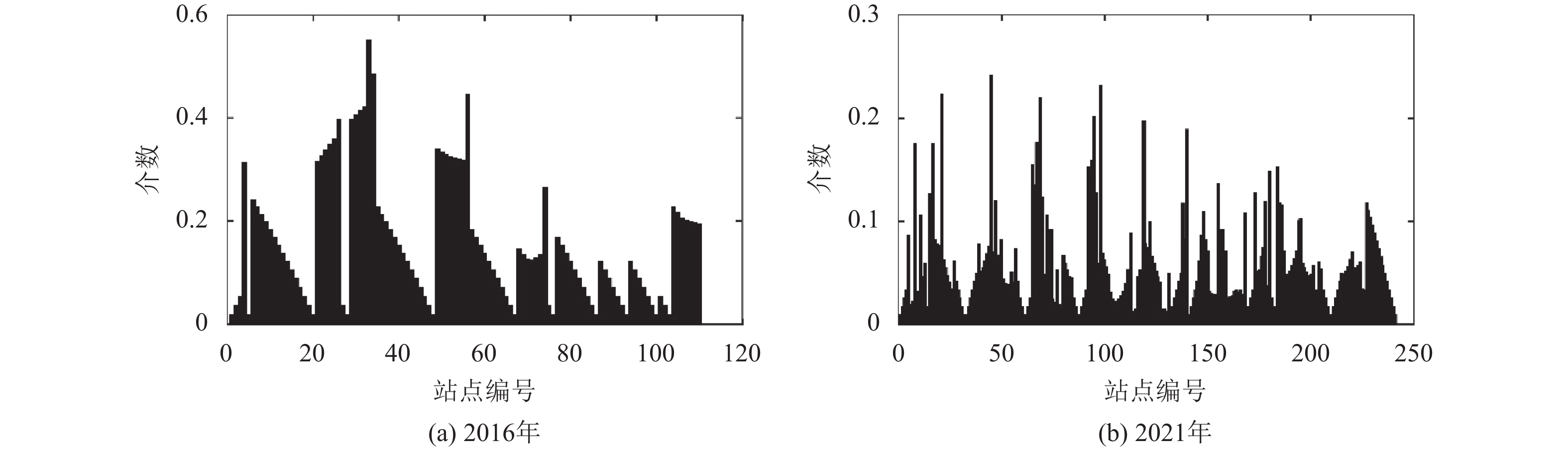
3.3 介数在分析南京地铁网络的平均最短距离的基础上,本文计算了所有站点的介数指标(betweenness),如图5所示,并分别将排名前10位的站点在表3中列出。由此,可以预测出当某站点因故关闭,整体网络中会有多少条最短路径受到影响,并籍此衡量网络的可靠性、易损性,进而预测灾害的危害结果。同时,也可以直观地反映站点的重要程度。
|
图 5 南京地铁网络站点介数 Fig. 5 Betweenness of Nanjing metro network |
由表3与图5可以看出:2021年规划线路中各站点的介数水平较2016年明显下降。这是由于新建线路增加了网络的冗余度,降低了网络运行对于某个站点的依赖程度;非换乘站也可能是重要站点,部分中间站由于位于频率最高的最短路径上因此排名靠前。
| 表 3 最短路径上的高频率站点top10及其介数1) Tab. 3 Top 10 stations and their betweenness with highest frequency on the shortest-paths |
根据式(3)计算得到南京地铁网络的联通度数据,如表4所示。可以看出:1) 南京地铁网络的联通度不高,均不足0.4,即网络的实际边数远少于潜在边数,距离成熟的地铁网络(其联通度值趋近于0.66)还有一定距离,但2021年的地铁网络联通度较2016年的有所提高;2) 无论是2016年还是2021年的南京地铁网络,其网络平均最短距离均大于ln|N|,尚不具备小世界网络特征。
| 表 4 南京地铁网络小世界指标对比分析 Tab. 4 Contrastive analysis on small-world network indexes of Nanjing metro network |
小世界网络的重要特征之一为在既有顶点数目不变的情况下,可通过优化网络结构提高网络的连通性与便捷性。因此后续地铁网络建设除了注重整条线路的增加,也应加强已有站点间的联系,缩短已有站点间的平均最短距离,提高地铁网络整体的连通性、便捷性。
4 结束语本文针对南京地铁2016年实际运营网络及2021年规划运营网络分别构建SpaceL拓扑结构模型,并根据地铁网络的平面特征,应用节点度及其分布、网络平均最短距离及其分布、网络直径,及联通度指标对其无标度特性及小世界特性进行分析比较,对进一步研究南京地铁网络鲁棒性、易损性、可恢复性进而优化其资源配置、加强风险管理具有重要意义。并得到以下结论。
1) 2016年与2021年南京地铁运营网络均具有无标度特性,节点度指数分别为4.2与3.7,其中2021年地铁网络“肥尾”特征更明显,且hub点发生较大变化;如果将节点度大于2的顶点视为重要节点,南京地铁网络重要节点的数量从2016年的7个增加到2021年的43个,一方面重要节点增加,因此需要重点预防与保护的任务加大;另一方面因为替代路径增多,南京地铁网络应对随机故障的鲁棒性增强。
2) 2021年南京地铁网络覆盖区域面积远大于2016年,在网络规模显著扩大的背景下,南京地铁网络平均最短距离从2016年的15站减少到2021年的13站,加上具有相同起讫点的网络直径减小清楚地说明地铁网络通达性提高,便捷程度增加。因此,可以肯定2021年后选择地铁出行的客流量必定大幅增加,新增站点的容量需要合理扩大;这也说明2016年与2021的地铁网络处于不同的发展阶段。
3) 2021年较2016年地铁运营网络联通度有所提高,但均不到0.4,且网络平均最短距离都大于其网络顶点数目的对数,因此尚不具备小世界网络的特征。后续除了注重新增线路,也应加强已有站点间的连接。
4) 基于不同衡量指标下重要站点的排名不一致。以介数为标准的重要度排序中,节点度最高的南京南站没有排名第一,最被熟知的新街口站排名也不靠前,其介数分别只有31.0%与6.2%。其主要原因为:1) 网络平均最短距离的计算是对所有O-D对最短路径求平均值,即假设乘客均是理性的且会自动选择最少站数进行路径规划;2) 节点度与介数均是网络的拓扑结构指标,表达地铁网络本身的固有静态属性,并未考虑客流量的大小,这与人们的基于流量的主观印象是有本质区别的。
这也为本文的深入研究提出了方向:首先,准确识别一个网络的关键站点,有必要将网络本身的静态结构与代表动态结构的流量因素综合考虑,单纯考虑任一方面都是不够的;其次,衡量地铁网络的发展程度时,需将覆盖区域面积加以考虑,单纯考虑联通度值大小不够准确。
| [1] |
WATTS D J, STROGATZ S H. Collective dynamics of small world networks[J].
Nature, 1998, 393: 440-442.
DOI: 10.1038/30918. |
| [2] |
BARABASI A, ALBERT R. Emergence of scaling in random networks[J].
Science, 1999, 286(5439): 509-512.
DOI: 10.1126/science.286.5439.509. |
| [3] |
WU J, GAO Z, SUN H. Urban transit system as a scale-free network[J].
Modern Physics Letter B, 2004, 18(19/20): 1043-1049.
|
| [4] |
ANGELOUDIS P, FISK D. Large subway systems as complex networks[J].
Physica A Statistical Mechanics & Its Application, 2006, 367: 553-558.
|
| [5] |
DERRIBLE S, KENNEDY C. The complexity and robustness of metro networks[J].
Physica A Statistical Mechanics & Its Application, 2010, 389(17): 3678-3691.
|
| [6] |
CAI H, ZHU J, YANG C. Vulnerability analysis of metro network incorporating flow impact and capacity constraint after a disaster[J].
Journal of Urban Planning & Development, 2017, 143(2): 1-10.
|
| [7] |
王燚, 杨超. 上海市轨道交通网络的复杂网络特性研究[J].
城市轨道交通研究, 2009, 12(2): 33-36.
WANG Y, YANG C. Characteristics of the complex network in Shanghai urban rail transit[J]. Urban Mass Transit, 2009, 12(2): 33-36. |
| [8] |
张晋, 梁青槐, 贺晓彤. 北京市地铁网络拓扑结构复杂性研究[J].
北京交通大学学报, 2013, 37(6): 78-84.
ZHANG J, LIANG Q H, HE X B. Study on the complexity of Beijing metro network[J]. Journal of Beijing Jiaotong University, 2013, 37(6): 78-84. |
| [9] |
刘志谦, 宋瑞. 基于复杂网络理论的广州轨道交通网络可靠性研究[J].
交通运输系统工程与信息, 2010, 10(5): 194-200.
LIU Z Q, SONG R. Reliability analysis of Guangzhou rail transit with complex network theory[J]. Journal of transportation systems engineering and information technology, 2010, 10(5): 194-200. |
| [10] |
李朴, 武子晗. 基于复杂网络理论的城市轨道交通网络结构特性[J].
都市快轨交通, 2014, 27(5): 35-38.
LI P, WU Z H. Structure characteristics of urban rail transit network based on complex network theory[J]. Urban Rapid Rail Transit, 2014, 27(5): 35-38. |
| [11] |
GARRISON W L, MARBLE D F. The structure of transportation networks[J].
Transportation Command, 1962, 62-ii: 73-88.
|
| [12] |
王志如, 梁作论, 李启明. 地铁网络无标度特性分析[J].
东南大学学报(自然科学版), 2013, 43(4): 895-899.
WANG Z R, LIANG Z L, LI Q M. Scale-free analysis of subway network[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(4): 895-899. DOI: 10.3969/j.issn.1001-0505.2013.04.041. |
 2017, Vol. 20
2017, Vol. 20