近年来，全球气候变暖趋势进一步加剧，已经成为21世纪人类社会所面临的最严峻的挑战之一。从1997年12月签订《京都议定书》开始，到2016年9月杭州的G20峰会，低碳经济的发展趋势、国际日益严格的环保法规使得各国政府不得不开始反思经济增长方式，开始寻找积极有效地减少碳排放量的措施。

碳税作为一种成本低、效果明显的经济手段已被美国、加拿大等国家采纳。碳税是指针对碳排放量所征收的税，是根据每吨二氧化碳排放量征收的。碳税最早源于1990年的芬兰，此后瑞典、挪威、荷兰等国也相继开始征收碳税^[1]。一直以来供应链减排和碳税征收都是许多学者持续关注的问题。

大部分学者认为征收碳税是一个效果较明显的手段。朱永彬等^[2]分析发现，引入碳税能有效促进各部门减排和降低高碳含量的能源产品的需求。Goulder等^[3]和Buonanno等^[4]认为，碳税会激励企业进行减排研发和技术改进。李剑等^[5]通过研究表明，碳税政策的实施对于供应链成本和碳排放的冲击效果明显。Wissema等^[6]分析了碳税和能源税对爱尔兰经济的影响，发现碳税会显著地改变生产及消费模式，使其向新能源以及低碳能源转变，比单一的能源税带来更大的减排效果。付丽苹等^[7]研究表明，政府设计科学合理的碳税税率可实现高碳行业碳排放总量得以控制的效果，同时增强了高碳企业实施碳减排的内在动力，激发其积极主动向低碳转型。

同时碳税征收手段的引入可以在一定程度上指导政府企业决策的制定。Misiolek^[8]分析了如何借碳税手段找到垄断企业的最优资源配制决策。熊中楷等^[9]论证企业以降低制造商的单位碳排放量为目标，政府应该针对清洁型制造商提高碳税，针对污染型制造商降低碳税。王坤等^[10]分析表明政府征收差异碳税的决策有利于增强减排企业的市场竞争力，激励其进一步加大减排的投入，提高净化率。

有关碳税征收模式模型建立方面的研究，多数学者集中在非合作博弈数学模型来分析。程永伟等^[11]指出，向制造商征税并降低零售商销售相关产品增值税的减排模式减排效果最佳，对经济的负作用最小。Benjaafar等^[12]分析了碳限额、碳交易、碳税和供应链成员合作对碳排放的影响。骆瑞玲等^[13]针对单制造商和单零售商组成的供应链，构建了集中式决策、分散式决策和供应链成员协同决策的博弈模型，探讨了消费者碳足迹敏感系数、碳限额及碳减排成本系数对供应链成员最优决策及减排效果的影响。张汉江等^[14]用数值分析法证明了制定合理碳税税率不仅促使最优减排量达到最大值，并且有利于供应链合作减排研发。马秋卓等^[15]建立了以政府为领导者，垄断企业为跟随者的关于碳排放量与碳税决策的斯坦克尔伯格博弈模型。企业会根据不同的碳税水平实施不同的碳排放策略，以求得自身收益最大化。而政府在预计到企业的碳排放量后，会制定相应的碳税税率，使得总福利最大化。

上述文献主要侧重于论证碳税的制定有利于碳排放量的控制和企业相应的决策制定，而对于碳税政策制定后，制造商、零售商等供应链上的参与企业如何在相互博弈中进行决策以及因碳税的征收而合作的供应链上的企业之间如何将新合作背景下的合作利润进行合理分配的问题的关注较少。因此在低碳经济发展的要求下，政府对制造商征收碳税，制造商投入研发成本减少碳排放，降低产品含碳量。本文用合作博弈的思想，研究在低碳经济发展的要求下，以单制造商、单零售商的二级供应链为研究对象，建立制造商单方面决策模型和制造商、零售商共同博弈合作决策模型，并利用合作博弈经典的Shapley值分配法来对供应链上合作企业的收益进行合理公平地分配，最后得出了不管是从制造商的减排效果还是从零售商制造商的最终受益来说，供应链的各参与者共同合作决策的优势远远大于单独决策的结论。

1 问题说明 1.1 符号说明

${C_{\rm{R}}},{C_{\rm{M}}}$ 分别表示零售商、制造商单位生产成本；P_R为零售商提供给消费者的单位售价；P_M为制造商提供给零售商的单位售价；t为政府征收的碳税税率；Q为零售商的订货量，即零售商的销售量； $\varepsilon $ 为制造商减排研发的投资系数； ${\varPi _{\rm{R}}},{\varPi _{\rm{M}}}$ 分别表示零售商、制造商的利润；其中 ${P_{\rm{R}}} = \alpha - \beta Q - r({e_0} - e)$ ，在此 $\alpha $ 是常数， $\beta $ 为产品需求价格弹性系数；e₀为制造商减排研发前的碳排放量，e为经减排研发后，减掉的碳排放量，即 ${e_0} - e$ 是经减排研发后，制造商的碳排放量；r为消费者的环保意识对产品价格的反映系数，即消费者在一定范围内愿意以适度的高价来购买含碳量低的产品。

Taylor^[16]指出，产品的价格受供求关系影响围绕着产品价值上下波动。当产品数量过多时，产品的价格就会相应地降低，反之亦然。同时产品含碳量的减少需要各方投入一定的研发减排成本。一般来说，产品减排的程度越大，碳排放量越低，所需的减排成本越大，从而反映在产品价格就会相应越高。

不过有许多学者研究发现，有一定环保意识的消费者在一定范围内愿意以适度的高价来购买含碳量低的产品。庞晶等^[17]指出消费者有一定的环保意识，知道低碳产品的重要性后，这些消费者就会愿意为低碳产品支付较高的价格，选择更多低碳产品。周应恒等^[18]基于南京城市消费者的调查数据，发现消费者对低碳农产品的支付意愿较高。据英国RSA保险集团2009年底发布的《可持续商业发展全球态度报告》显示，已经有60%受访的中国消费者表示倾向于购买低碳排放汽车。该报告根据对全球九大市场消费者调查发现，中国消费者愿意为环保产品和服务支付5%~10%的额外费用。

1.2 收益函数说明

首先考虑零售商的收益，其收益是指单位产品收益与销售量的乘积。因此对于零售商来说，其收益

$\quad\quad {\varPi _{\rm{R}}} = Q[\alpha - \beta Q - r({e_0} - e) - {P_{\rm{M}}} - {C_{\rm{R}}}]{\text{。}}$

(1)

式中，Q为零售商的订货量； $\alpha - \beta Q - r({e_0} - e)$ 为零售商的售价P_R；P_M为制造商提供给零售商的单位售价；C_R为零售商的单位生产成本。

其次，考虑供应商的收益，设其收益

$\quad\quad {\varPi _{\rm{M}}} = Q[{P_{\rm{M}}} - {C_{\rm{M}}} - t({e_0} - e)] - \frac{1}{2}\varepsilon {e^2}{\text{。}}$

(2)

式中，Q为来自零售商的订货量，即销售量；C_M为制造商的单位生产成本； $t({e_0} - e)$ 为政府对制造商征收的碳税；根据经典模型标准假设(研发成果与研发投入成二次关系)，在本文中单位产品的碳减排量e即为减排研发的成果，即 $\frac{1}{2}\varepsilon {e^2}$ 表示制造商在低碳环境下所投入的低碳减排研发成本， $\varepsilon $ 为制造商减排研发的投资系数。

1.3 收益分配Shapley值法说明

建立合作联盟的目的是获得更多利润，而如何把利润合理公平地分配到每一个参与者是保证合作联盟稳定持久的关键一步。合作联盟中最经典的分配方法是Shapley所提出的根据参与者对联盟边际贡献的大小来进行分配的Shapley法。它是用于解决多人合作对策问题的一种数学方法，主要集中应用在合作收益在各合作方之间的分配。Shapley值实现的是根据每个合作成员对该合作联盟的贡献大小来考虑分配量，突出反映了各个成员在合作中的重要性。它实现了联盟总体收益在各参与者之间公平有效的分配。Shapley提出，合理的分配方案应该满足对称性、有效性、哑元性、可加性4个公理^[19]，而Shapley值法利用公理化的方法得到合作博弈的唯一解。

通常用 $(N,v)$ 来表示一个博弈，其中 $N = \{ 1,2 \cdots n\} $ 是参与者的集合 $(n {\text{≥}} 2)$ ，任意的子集 $S \subseteq N$ 表示一个合作联盟；v是定义在N上的特征函数并且 $v(\phi ) = 0$ ; 对于任意的 $S \subseteq N$ ， $v(S)$ 表示联盟S获得的收益；如果对于任意的 $S,S' \subseteq N$ 并且 $S \cap S' = \phi $ ，有 $v(S \cup S') {\text{≥}} $ $ v(S) + v(S')$ ，则v是超可加的。这就体现了合作的意义，体现了人多力量大的思想，就意味着 $v(N)$ 是最大的合作收益。

设 $\varPhi (v) = ({\varphi _1}(v),{\varphi _2}(v) \cdots {\varphi _n}(v))$ 是合作时最大收益的分配， ${\varphi _i}(v)$ 表示参与者i从合作的最大收益 $v(N)$ 中获得分配，则满足 $\displaystyle\sum\limits_{i = 1}^n {{\varphi _i} = v(N)} $ ，即各参与者分配的收益之和等于大联盟N的收益，保证大联盟N的有效性；且满足 $\displaystyle\sum\limits_{i \in S,S \subset N} {{\varphi _i} {\text{≥}} v(S)} $ ，即各参与者在大联盟中获得的分配收益大于参与者单干或参与者自己形成小联盟的分配收益，各参与者具有群体理性，没有离开大联盟的动机，因此保证了大联盟N的稳定性。

因此，在合作N下，用Shapley值法确定的各参与者所分配的利益为

$\quad\quad {\varphi _i}(v) = \!\!\!\!\!\! \!\! \sum\limits_{i \in S,S \subset N}\!\! {\frac{{(\left| N \right| - \left| S \right|)!(|S| - 1)!}}{{|N|!}}(v(S) - v(S\backslash \{ i\} ))} {\text{。}}\!\!$

(3)

式中，|S|为子集S中元素的个数， $v(S) - v(S\backslash \{ i\} )$ 为参与者i对联盟S的边际贡献的大小。

2 模型建立 2.1 单方面决策模型

单方面决策模型的决策过程是：企业之间没有合作意识，站在自己效益最大化的角度来决策；政府对制造商征收碳税，提高了制造商的生产成本，相对应地供给零售商的产品价格就会上涨；零售商的进价提高，必然在销售价格上有所体现，加之消费者对低碳产品越来越高的偏好意识，让零售商不得不合理谨慎安排产品的订货量。零售商根据自己收益最大化的实际情况，先给出相应的订货量，然后制造商再根据低碳发展要求和企业利润角度来作出相应的决策执行。

因此对式(1)求关于Q的导数，并令 $\displaystyle\frac{{\partial {\varPi _{\rm{R}}}}}{{\partial Q}} = 0$ ，得零售商利润最大时对应订货量

$\quad\quad {Q_1} = \frac{{\alpha - r({e_0} - e) - {P_{\rm{M}}} - {C_{\rm{R}}}}}{{2\beta }}{\text{。}}$

(4)

将式(4)代入式(2)，并对式(2)求关于e和P_M的导数，并令 $\displaystyle\frac{{\partial {\varPi _{\rm{M}}}}}{{\partial e}} = 0,\displaystyle\frac{{\partial {\varPi _{\rm{M}}}}}{{\partial {P_{\rm{M}}}}} = 0$ ，可得制造商利润最大时对应的减排量e₁和制造商售价P_M1分别为

$\left\{ {\begin{array}{*{20}{c}}{{e_1} = \displaystyle\frac{{(r - t){P_{\rm{M}}} + t\alpha - r{C_{\rm{M}}} - t{C_{\rm{R}}} - 2rt{e_0}}}{{2\beta \varepsilon - 2rt}},}\\\!\!\!\!\!\! {{P_{{\rm{M}}1}} = \displaystyle\frac{{\alpha + (t - r)({e_0} - e) + {C_{\rm{M}}} - {C_{\rm{R}}}}}{2}{\text{。}}}\end{array}} \right.$

(5)

结合式(4)可以得到当制造商利润最大时，减排量e₁，制造商售价P_M1满足：

${e_1} = \frac{{(r + t)[\alpha - (r + t){e_0} - {C_{\rm{M}}} - {C_{\rm{R}}}]}}{{4\beta \varepsilon - {{(r + t)}^2}}},$

(6)

$\begin{split}& {P_{M1}} = \\ & \frac{{(\alpha + {C_{\rm{M}}} - {C_{\rm{R}}})(4\beta \varepsilon - 4rt) \!+\! (t - r)[4\beta \varepsilon {e_0} \!-\! 2(t - r)(\alpha - {C_{\rm{R}}})]}}{{8\beta \varepsilon \!-\! 2{{(r + t)}^2}}}{\text{。}}\end{split}$

(7)

因此可得出零售商利润最大时对应的订货量Q₁满足

${Q_1} \!=\! \frac{{\alpha - r({e_0} - {e_1}) - {P_{{\rm{M}}1}} - {C_{\rm{R}}}}}{{2\beta }} \!=\! \frac{{\varepsilon [\alpha - {C_{\rm{R}}} - {C_{\rm{M}}} - (r + t){e_0}]}}{{4\beta \varepsilon - {{(r + t)}^2}}}{\text{。}}$

(8)

将式(6)~式(8)代入式(1)~式(2)可得零售商、制造商最优的利润 $\varPi _{\rm{R}}^{\rm{*}},\varPi _{\rm{M}}^{\rm{*}}$ 。

2.2 协同合作决策模型

政府征收碳税会促使制造商进行减排研发，降低单位产品的碳排放量。而对于零售商来说，消费者日益提高的环保意识，使得低碳产品更受欢迎，更能带来利润。因此低碳产品成为整条供应链中的需求，政府对制造商征收碳税，增加了整条供应链的成本，具有合作意识的供应链参与企业通过合作来简化供应链流程，降低冗杂流程的成本浪费，将这些成本浪费转化为低碳减排成本，提供给消费者更具价格优势和环境友好的产品，从而提高整条供应链的竞争力。站在合作供应链收益最大的角度来对产品的订货量、价格以及含碳量进行决策，最后再通过合理公平的方式将供应链的总体收益分配到每一个参与企业，收益分配的合理公平性保证每一个合作参与企业都更愿意留在联盟中参与合作。

设 ${\varPi _{\rm{RM}}}$ 为零售商和制造商合作后的利润，双方合作后，零售商向制造商支付的单位产品费用P_M就成为合作联盟内部的资金改变，不会影响到联盟的总收益。然后对式(1)零售商的利润函数，式(2)制造商的利润函数处理得到

${\varPi _{{\rm{RM}}}} = Q[\alpha - \beta Q - (r + t)({e_0} - e) - {C_{\rm{R}}} - {C_{\rm{M}}}] - \frac{1}{2}\varepsilon {e^2}{\text{。}}$

(9)

对式(9)求关于e和Q的导数，并令 $\displaystyle\frac{{\partial {\varPi _{{\rm{RM}}}}}}{{\partial e}} = 0,$ $\displaystyle\frac{{\partial {\varPi _{{\rm{RM}}}}}}{{\partial Q}} = 0$ ，可得合作联盟利润最大时对应的减排量e₂和订货量Q₂为

$\left\{ {\begin{array}{*{20}{c}}{{e_2} = \displaystyle\frac{{(r + t)[\alpha - (r + t){e_0} - {C_{\rm{M}}} - {C_{\rm{R}}}]}}{{2\beta \varepsilon - {{(r + t)}^2}}},}\\{{Q_2} = \displaystyle\frac{{\varepsilon [\alpha - {C_{\rm{R}}} - {C_{\rm{M}}} - (r + t){e_0}]}}{{2\beta \varepsilon - {{(r + t)}^2}}}{\text{。}}}\end{array}} \right.$

(10)

建立合作联盟的目的是获得更多利润，而利润合理公平分配到每一个参与者是保证合作稳定持久发展的一个关键因素。本文利用合作联盟中最经典的Shapley法来进行利润的分配。

3 结果分析

结论1　零售商和制造商合作决策的情况下更有利于制造商降低碳排量。即合作情况下，制造商碳减排量要大于单独决策时的碳减排量，即 ${e_2} {\text{＞}} {e_1}$ 。说明零售商和制造商之间的合作可以使减排效果更加显著，因此在政府对制造商征收碳税的前提下，应当鼓励供应链中的参与者注重合作，建立合作联盟来共同决策。

证明　通过观察式(6)和式(10)，可以很容易观察到：

$ \begin{split}& \quad\quad {e_2} = \frac{{(r + t)[\alpha - (r + t){e_0} - {C_{\rm{M}}} - {C_{\rm{R}}}]}}{{2\beta \varepsilon - {{(r + t)}^2}}}{\text{＞}}\\& {e_1} = \frac{{(r + t)[\alpha - (r + t){e_0} - {C_{\rm{M}}} - {C_{\rm{R}}}]}}{{4\beta \varepsilon - {{(r + t)}^2}}}{\text{。}}\end{split}$

结论2　合作决策的情况下零售商的订货量要大于两者单独决策时的订货量。即合作情况下，零售商的订货量大于单独决策时零售商的订货量，即 ${Q_2}{\text{＞}} {Q_1}$ 。说明零售商和制造商之间的合作使得消费者对低碳产品的需求有一定幅度的增大。

证明　跟结论1相同，通过观察式(8)和式(10)就可得证。

结论3　合作决策的情况下零售商和制造商合作所获得的总收益要大于两者单独决策时的总收益，即 ${\varPi _{{\rm{RM}}}} {\text{＞}} \varPi _{\rm{R}}^{\rm{*}} + \varPi _{\rm{M}}^{\rm{*}}$ 。这也体现了合作的意义，合作可以带来“1+1＞2”的效果。

证明　两者单独决策时总收益为

$\begin{split}& \quad\quad {\varPi _{\rm{R}}} + {\varPi _{\rm{M}}} = Q[\alpha - \beta Q - r({e_0} - e) - P_{\rm{M}}^{} - {C_{\rm{R}}}] + \\ & Q[{P_{\rm{M}}} - {C_{\rm{M}}} - t({e_0} - e)] - \frac{1}{2}\varepsilon {e^2} = Q[\alpha - \beta Q - \\& (r + t)({e_0} - e) -{C_{\rm{R}}} - {C_{\rm{M}}}] - \frac{1}{2}\varepsilon {e^2}{\text{。}}\end{split}$

(11)

可以看出式(9)和式(11)是一样的函数，即零售商和制造商合作决策的情况就是对式(11)进行处理得到的。通过分析得: 当 $Q {\text{＜}} {Q_2}$ 时，式(11)单调递增; 当 $Q {\text{＞}} {Q_2}$ 时，式(11)单调递减; 当 $Q = {Q_2}$ 时，式(11)达到最优。

由命题2可得 ${Q_1}{\text{＜}} {Q_2}$ ，即处于式(11)单调递增的区间内，故零售商和制造商合作决策的情况下两者所获得的总收益要大于两者单独决策时的总收益。

结论4　合作决策的情况下零售商和制造商依照Shapley值法分配得到的收益大于两者单独决策时分别获得的收益。即 ${\varphi _{\rm{R}}} > \varPi _{\rm{R}}^{\rm{*}},{\varphi _{\rm{M}}} > \varPi {}_{\rm{M}}^{\rm{*}}$ ，各参与者在合作联盟中得到了比单干更多的收益，这就保证了合作联盟的参与者没有离开联盟的动机，从而保证了联盟的稳定性。

证明　在文中可以得到， $v(\{ R\} ) = \varPi _{\rm{R}}^{\rm{*}},v(\{ M\} ) = \varPi _{\rm{M}}^{\rm{*}},$ $v(\{ {\rm{RM}}\} ) = {\varPi _{{\rm{RM}}}} $ 。

根据式(3)可以得到，零售商R在两者合作中分配得到的收益

$\begin{split}& \quad\quad {\varphi _{\rm{R}}} = \frac{1}{2}[v(\{ {\rm{R}}\} ) - v(\phi )] + \frac{1}{2}[v(\{ {\rm{RM}}\} ) - v(\{ {\rm{M}}\} )] = \\ & \frac{1}{2}[v(\{ {\rm{RM}}\} ) + v(\{ {\rm{R}}\} ) - v(\{ {\rm{M}}\} )],\end{split}$

即 ${\varphi _{\rm{R}}} = \displaystyle\frac{1}{2}({\varPi _{{\rm{RM}}}} + \varPi _{\rm{R}}^{\rm{*}} - \varPi _{\rm{M}}^{\rm{*}})$ 。零售商和制造商单独决策时，根据2.1节可得，零售商获得的最大收益为 $\varPi _{\rm{R}}^{\rm{*}}$ ，则 ${\varphi _{\rm{R}}} - \varPi _{\rm{R}}^{\rm{*}} = \displaystyle\frac{1}{2}({\varPi _{{\rm{RM}}}} + \varPi _{\rm{R}}^{\rm{*}} - \varPi _{\rm{M}}^{\rm{*}}) - \varPi _{\rm{R}}^{\rm{*}} = \displaystyle\frac{1}{2}({\varPi _{{\rm{RM}}}} - \varPi _{\rm{R}}^{\rm{*}} - \varPi _{\rm{M}}^{\rm{*}})$ ，根据结论3，可得 ${\varPi _{{\rm{RM}}}}{\text{＞}} \varPi _{\rm{R}}^{\rm{*}} + \varPi _{\rm{M}}^{\rm{*}}$ ，故可得 ${\varphi _{\rm{R}}} {\text{＞}} \varPi _{\rm{R}}^{\rm{*}}{\rm{,}}$ 同理可得 ${\varphi _{\rm{M}}} {\text{＞}} \varPi {}_{\rm{M}}^{\rm{*}}$ 。

4 算例分析

利用Matlab 7.0作为计算工具对各个公式进行求解，为了更好地说明政府碳税、消费者环保意识对最优减排量的影响，结合已有的研究，对相应参数作如下设定：

$\quad {C_{\rm{R}}} = 10,{C_{\rm{M}}} = 22,{e_0} = 2.3,\varepsilon = 3\;800,\alpha = 900,\beta = 6,r = 5{\text{。}}$

合作决策和单独决策时碳税率t的影响分析见表1、表2。

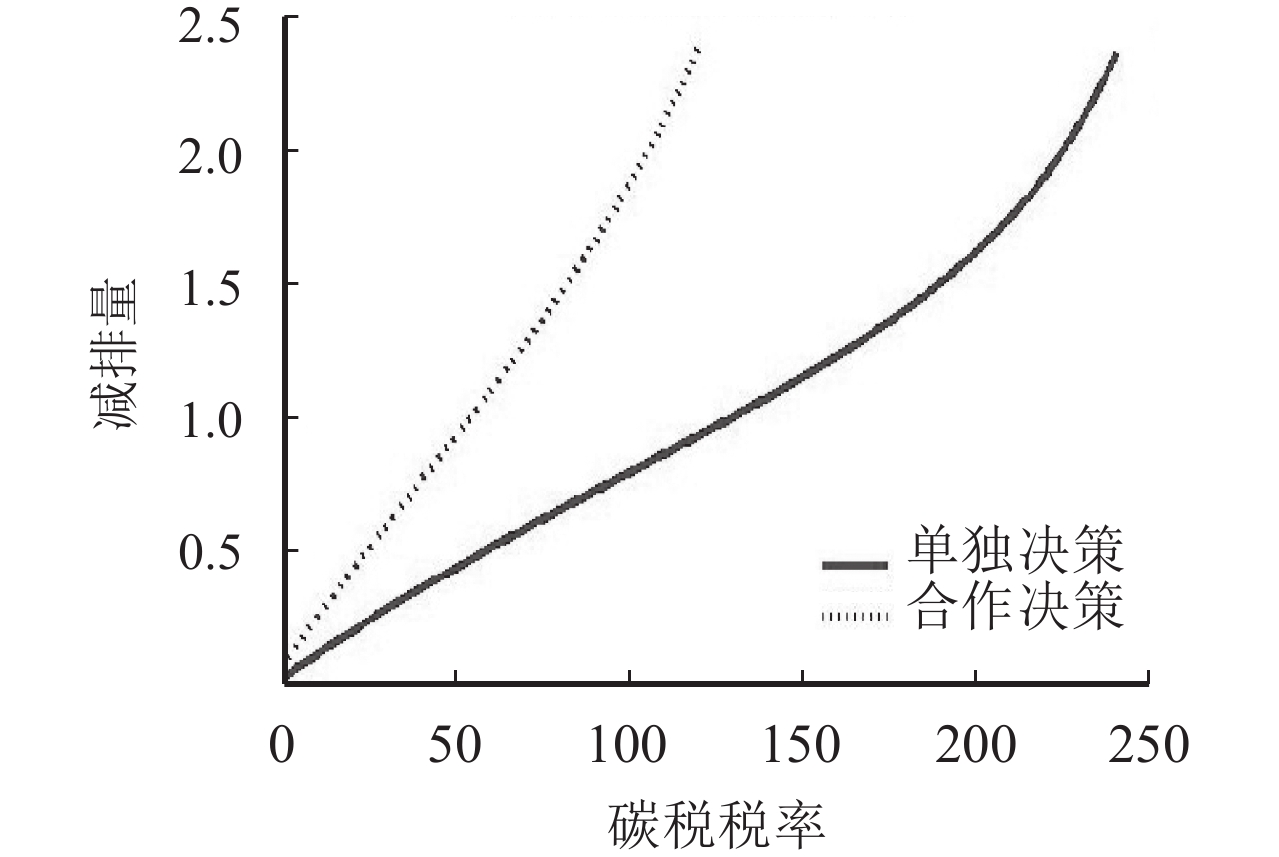
通过图1可以看出，合作之后，制造商的减排量对碳税的敏感度有很明显的提高。碳税在一定范围内提高一单位，制造商的减排量会相应地提高，但制造商所能承担的最大碳税水平有所下降。例如在此文中：单独决策时，碳税税率达到240时，才会达到制造商所能接受的最大碳税水平；而在合作决策中，这一最大碳税水平在碳税税率为120时就已经达到。说明在不同的情况下，碳税税率的制定水平不能一成不变。在合作的情况下，政府可以通过制定较低的碳税税率来达到较高的减排量。征收碳税税率标准的制定要结合供应链的实际情况。若供应链中的参与者普遍都能够积极合作协同决策，那么碳税水平就可以适当地下调；反之，碳税水平应当适当上调。同时，碳税水平制定的标准不能太低也不能太高，太低会达不到制约制造商减排的目的，太高会使得碳税失去对制造商的约束。

同时消费者的环保意识也在迫使着制造商进行积极地减排研发。通过图1可以看出，不管是单独决策模型还是合作决策模型，即使政府碳税税率为0，制造商也是有相应的减排量。这说明日益提高的消费者环保意识对于环境的改善有一定的正面影响作用，让市场上的低碳产品开始受欢迎，有较高环保意识的消费者愿意在一定范围内以一定的高价来购买低碳的产品。

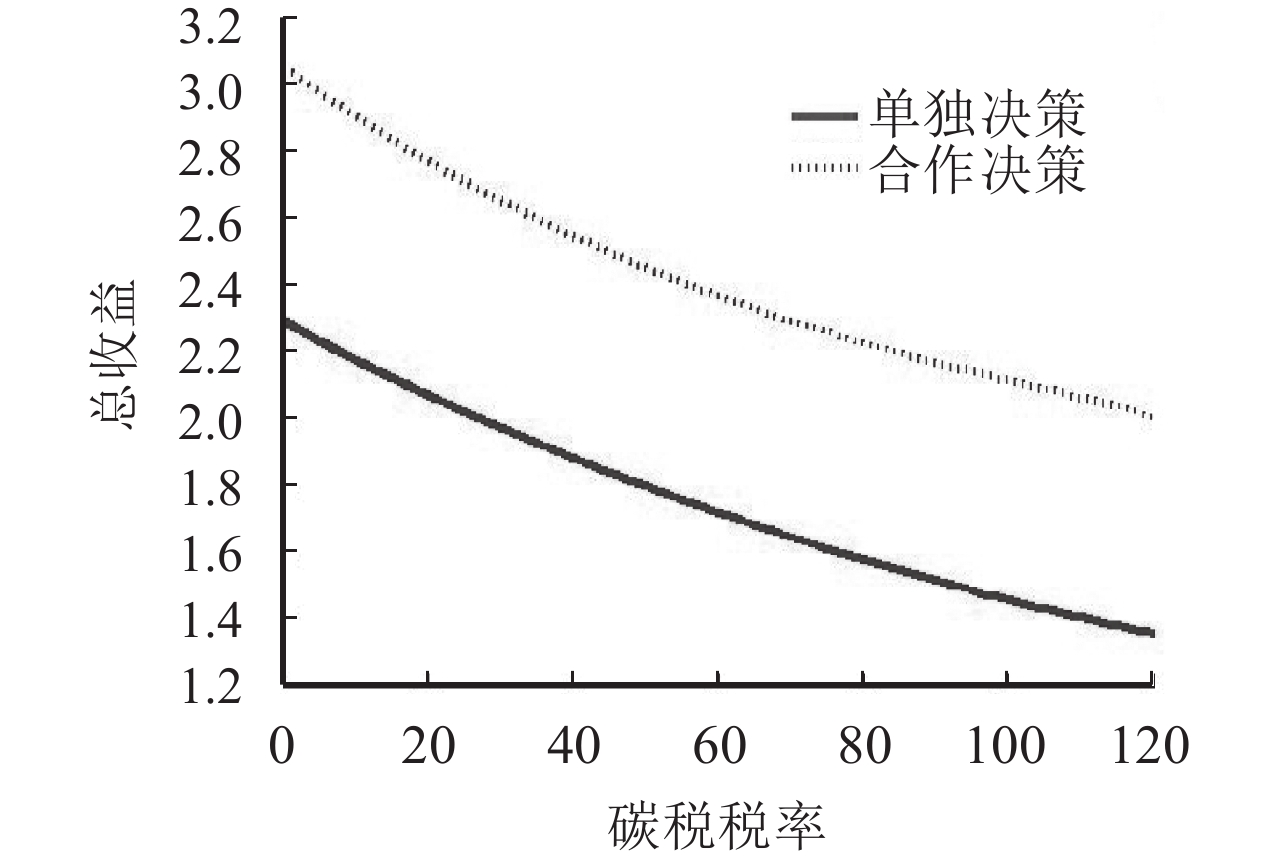
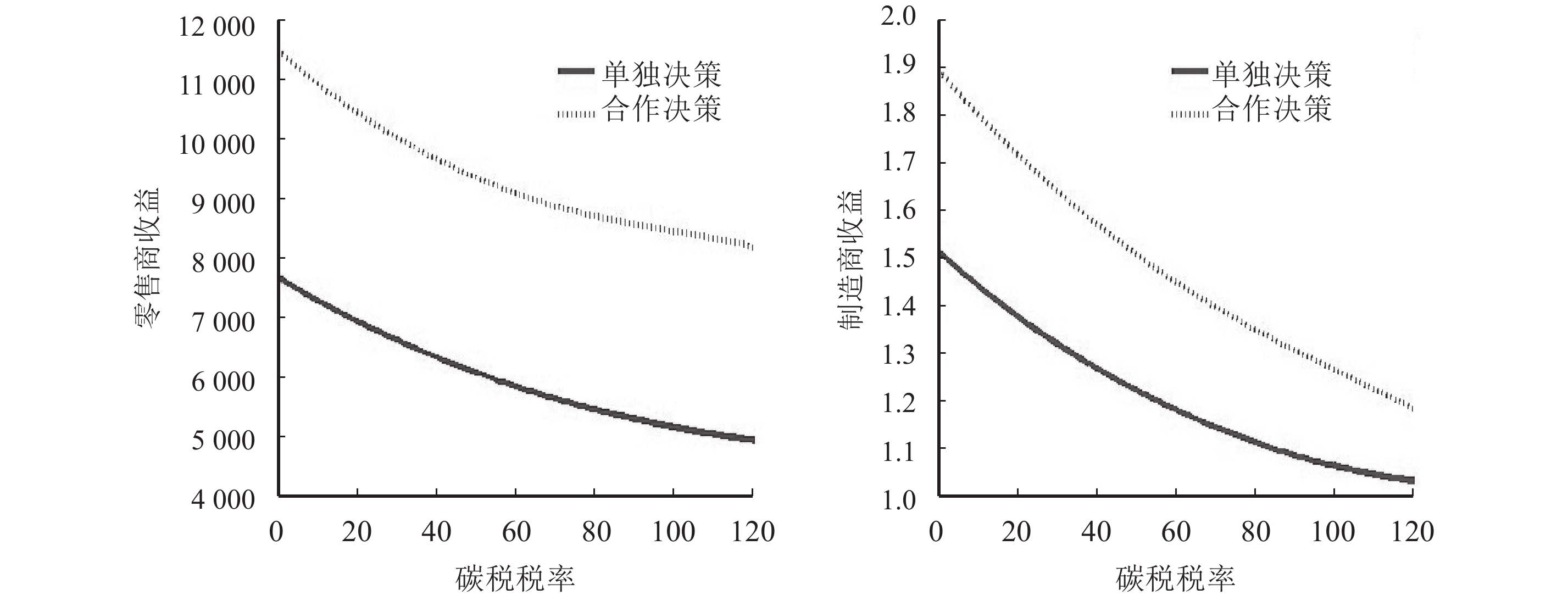
通过图1~3，经过对比可以明显看出不管是从制造商的减排效果还是零售商制造商的最终受益来说，供应链的参与者合作起来共同决策的优势远远大于单独决策的优势。图2可以说明供应链的参与者建立合作联盟是有一定意义的，通过合作产生了额外的收益，这部分收益就保证了合作的有效性；图3中表明不管是零售商还是制造商都可以从合作联盟的总收益分配中获得高于原本单独决策时的收益，这就保证了合作参与者的合作积极性，也体现了合作参与者的合作理性，参与者在这种情况下都不愿意打破合作联盟，从而保证了合作联盟的稳定性。

5 结束语

在低碳经济发展的趋势下，本文研究建立制造商单方面决策模型和制造商、零售商共同合作协同决策模型，利用合作博弈经典的Shapley值分配法作为工具，得出不管是从减排效果还是从各企业的最终受益来说，供应链的各参与者合作起来共同决策的优势远远大于单独决策的结论。

此外本文在模型建立过程中没有考虑参与成员建立合作联盟时的合作建立成本，合作前对合作企业的安全风险评估等都需要成本，因此考虑合作成本在内的情景也是值得探讨的问题。同时，消费者的环保意识对产品的偏好程度问题上可以深入研究，本文是假设产品的定价未超过消费者的承受范围的，若高出消费者的承受范围，那么消费者的环保意识就会失效，因此分析消费者环保意识可以承担的最大的产品价格，如何给环保产品定价等问题也是值得研究学习的一个方向。