预防性维修下装备二维保修策略优化模型

引用本文

程中华, 杨志远, 杨红兵. 预防性维修下装备二维保修策略优化模型[J]. 工业工程, 2017, 20(4): 79-86. DOI: 10.3969/j.issn.1007-7375.e15-0555.

CHENG Zhonghua, YANG Zhiyuan, YANG Hongbing. An Optimization Model for Two-Dimensional Warranty Policy of Equipment under Preventive Maintenance[J]. Industrial Engineering Journal, 2017, 20(4): 79-86. DOI: 10.3969/j.issn.1007-7375.e15-0555. 复制到剪切板

基金项目:

国家社会科学基金资助项目(14GJ003-135)；国家自然科学基金资助项目(70971135)

作者简介:

程中华(1972-)，男，河南省人，教授，主要研究方向为装备保障理论与技术。

文章历史

收稿日期：2015-11-21
网络出版时间：2017-07-01

Contents Abstract Full text Figures/Tables PDF

预防性维修下装备二维保修策略优化模型

程中华¹, 杨志远¹, 杨红兵²

1. 军械工程学院装备指挥与管理系，河北石家庄 050003;
2. 73158部队，福建厦门 361021

收稿日期：2015-11-21; 网络出版时间：2017-07-01

基金项目：国家社会科学基金资助项目(14GJ003-135)；国家自然科学基金资助项目(70971135)

作者简介：程中华(1972-)，男，河南省人，教授，主要研究方向为装备保障理论与技术。

摘要: 装备保修是装备售后服务的主要内容，合理的保修策略不仅能够降低承制方保修成本，而且能够提高装备可用度。针对在装备售后服务中控制保修成本和保证可用度的问题，在不完全预防性维修下，采用加速失效时间(AFT)模型描述装备故障率，构建了装备二维保修成本和可用度模型并给出了有效解法。在此基础上，权衡军地双方利益，以保修期内费效比最小为优化目标，得到最优预防性维修间隔期。对不同保修期限下最优费效比值进行回归分析，在控制保修成本、保证装备可用度的前提下，得到柔性保修策略方案。最后，通过算例验证了模型的有效性。

关键词: 二维保修预防性维修费效比加速失效时间

An Optimization Model for Two-Dimensional Warranty Policy of Equipment under Preventive Maintenance

CHENG Zhonghua¹, YANG Zhiyuan¹, YANG Hongbing²

1. Department of Equipment Command and Management, Ordnance Engineering College, Shijiazhuang 050003, China;
2. 73158 Troops, Xiamen 361021, China

Abstract: Warranty is the primary coverage of equipment after-sale service, and reasonable warranty servicing strategy has significant impact on manufacturer′s warranty cost and the product availability. A two-dimensional warranty cost and availability model is developed under preventive maintenance and the solving process proposed, where the function of failure rate is given by accelerated failure time (AFT) model. By modeling the warranty cost and product availability, the optimum warranty servicing strategy is derived to minimize the cost-effect ratio. Then, regression analysis with optimal cost-effect under different warranty regions is used to derive the flexibility warranty servicing strategy. Finally, a numerical illustration is given to examine the validity of the model.

Key words: two-dimensional warranty preventive maintenance cost-effective ratio accelerated failure time (AFT)

装备保修是承制单位在装备购置后在规定责任期限内对其进行维修、更换等相关活动的总称。合理的装备保修策略不仅可以降低承制方的保修成本，也能在装备列装部队初期，部队未形成保障能力的情况下提高装备可用度。由于部队装备的特殊属性，承制方和装备管理部门在制定保修策略时，应权衡承制方和军方的利益，在控制承制方保修成本的同时提高装备的可用度，以满足部队对装备战备完好性的需求。

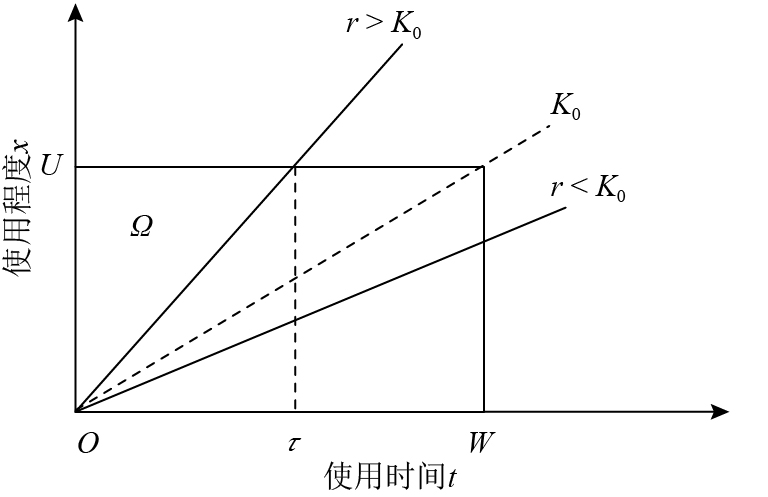
保修策略(warranty policy)又称保证策略，根据保修期测度维度不同可划分为一维、二维及多维保修策略^[1]。其中，二维保修策略是指采用两个维度来确定保修期，通常采用使用时间和使用程度两个指标，比较典型的是汽车保修期，通常采用时间和里程两个维度确定。典型的二维保修区域如图1所示，其中K₀=U/W，可以认为是保修区域的形状参数。使用率R=U(t)/t，其中U(t)表示在使用时间为t时的使用程度值。在实际中，装备使用率受装备的实际使用环境和任务环境等因素的影响会有所差异，所以总体上装备使用率R可以用概率分布函数描述^[2]。r表示随机变量R的取值，即装备使用率的具体值。

近年来，国内外学者在不同维修策略基础上建立了二维保修成本优化模型。Iskandar等^[3]在最小维修和故障更换两种维修方式组合下，以保修成本最小为目标，得到了最优的保修服务提供方案；Iskandar等^[4]和Yun等^[5]考虑在特定区域内采取不完全修复性维修的情况下，建立了二维保修成本模型；Jack等^[6]和于俭等^[7]运用加速失效时间(accelerated failure time，AFT)模型建立了在最小维修和不完全维修组合策略下的二维产品保修成本模型。

图 1 不同使用率下二维保修区域 Fig. 1 Two-dimensional warranty region under different usage rate

以上研究均只考虑保修成本和修复性维修策略，而预防性维修往往能够降低保修成本，提高产品可用度^[8]。目前，对保修期内预防性维修的研究主要集中在一维保修策略。Chun^[9]在设计产品保修时较早引入定期预防性维修；Jack等^[10]研究了在保修期内实施序贯不完全预防性维修的保修成本问题；Yeh等^[11]和姜国等^[12]分别在预防性更换和预防性维修策略下建立了产品保修成本模型。虽然以上研究取得了一定成果，但它们大多只以保修成本为优化目标，而对于一些特殊产品如部队装备，由于军方对装备战备完好性的要求，所以可用度也是一项重要指标；将预防性维修引入二维保修策略进行建模分析的研究也较少，而实际中预防性维修对双方往往都是有利的。

本文基于AFT模型，构建了预防性维修策略下装备二维保修费用和可用度模型，并提出了有效解法。综合考虑军地双方利益，以装备保修期内费效比最小为优化目标，得到具有柔性的最优保修策略方案，在降低保修成本的同时，保证装备可用度。

1 二维保修策略优化模型 1.1 模型假设

1) 装备保修期是由使用时间和使用程度两个度量指标共同确定的二维区域。

2) 装备在保修区域Ω内由承制方采用定期预防性维修策略，对装备故障采用最小维修(即“修复如旧”)，在保修期内，由承制方承担维修费用(free repair warranty)。每次预防性维修后故障率介于“恢复如新”和“恢复如旧”之间，即不完全维修。

3) 预防性维修间隔期采用时间为度量单位。

4) 装备具有老化特性，故障率随时间增加而增加。

5) 装备每次修复性维修所需费用及时间是固定的，不随保修次数、时间而变化。

6) 预防性维修费用和所需时间只与改善因子有关，不随保修次数、时间而变化。

7) 只考虑与维修有关的费用和停机时间。

8) 装备故障模式为单一故障，不考虑多重故障。

1.2 符号说明

为了便于模型构建，对模型中的常用符号设置如下：

W, U分别为保修时间及使用程度；

R为装备使用率(随机变量)；

r₀为设计使用率；

Δ_j为第j次预防性维修改善因子；

T为预防性维修间隔期；

n为装备预防性维修次数；

C_d为单位时间的平均停机损失；

T_p，C_p分别为单次预防性维修所需时间及总费用；

T_f，C_f分别为单次修复性维修所需时间及总费用；

g(r)，G(r)分别为使用率概率密度函数及分布函数；

$f_{0} (t; α_{0})$ ， $F_{0} (t; α_{0})$ 分别为设计使用率下装备故障密度函数及累计故障分布函数；

$f (t; α (r))$ ， $F (t; α (r))$ 分别为使用率为r时装备故障密度函数及累计故障分布函数；

$h (t; α (r))$ 为使用率为r时装备的故障率(故障强度)函数；

$h_{i} (t; α (r))$ 为第i个预防性维修间隔期内装备故障率函数；

EC(T, W, U)为期望保修成本；

EA(T, W, U)为保修期内装备期望可用度；

V(T, W, U)为保修期内费效比。

1.3 AFT模型

在二维保修策略下，装备的故障率同时受使用时间和使用程度的影响。本文采用文献[6]中提出的AFT模型得到装备故障率函数，在使用率为r时装备累计故障分布函数可表示为

F (t; α (r), β) = F_{0} (t; α_{0} {(\frac{r_{0}}{r})}^{γ}, β) 。

(1)

其中，α₀和β分别表示设计使用率下故障分布的尺度参数和形状参数，γ为AFT模型参数。由式(1)容易得到在使用率为r时，形状参数不变，尺度参数变为

α (r) = α_{0} {(\frac{r_{0}}{r})}^{γ} 。

(2)

由于形状参数不变，所以在以下表达式中省略。由此，使用率为r时装备的故障率函数可表示为

h (t; α (r)) = \frac{f (t; α (r))}{\bar{F} (t; α (r))} 。

(3)

在本文中，不完全预防性维修对装备故障率函数的影响采用虚拟工龄法^[13]进行描述。在虚拟工龄法中，令∆_j为第j次预防性维修改善因子，则在第i个预防性维修间隔期内，装备故障率函数可表示为

h_{i} (t; α (r)) = h (t - \sum_{j = 1}^{i - 1} Δ_{j} T; α (r)) 。

(4)

1.4 费用模型

如图1所示，根据装备的使用率和保修区域Ω的形状参数对比关系，在计算装备的保修成本时，可以分为r≤K₀和r>K₀两种情况。

每次预防性维修和修复性维修总费用包括维修费用和停机损失，可表示为：

\begin{array}{l} C_{p} = C_{pr} + C_{d} T_{p}, \\ C_{f} = C_{fr} + C_{d} T_{f} 。 \end{array}

其中，C_pr和C_fr分别表示每次预防性维修和修复性维修费用。

下面，将分别在以上两种情况下对保修成本进行建模分析。

1.4.1 r≤K₀的情况

当r≤K₀时，由图1可知，装备会在时间W处超出保修区域。保修成本 $E C_{r}^{1} (T, W)$ 可以表示为

\begin{matrix} {EC}_{r}^{1} (T, W) = \\ n C_{p} + \sum_{i = 1}^{n} {EC}_{f i | r} (T) + {EC}_{f | r} (W - n (T + T_{p})) 。 \end{matrix}

(5)

其中，nC_p表示保修期内预防性维修总费用， $n = int [W / (T + T_{p})]$ ，表示预防性维修次数； ${EC}_{f i | r} (T)$ 表示在使用率为r时，第i个间隔期内故障最小维修费用期望值； ${EC}_{f | r} (W - n (T + T_{p}))$ 表示 $[n (T + T_{p}), W]$ 时间内故障最小维修费用期望值。

在保修期内对于装备故障均采用最小维修，而最小维修的特性是一个非齐次泊松过程^[14]。装备在第i个预防性维修间隔期内的故障率函数可由式(4)得到，因此，在第i个预防性维修间隔期内装备出现故障的期望次数可表示为

{EN}_{f i | r} (T) = \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t 。

(6)

由此，在第i个预防性维修间隔期内的装备最小维修费用期望值可表示为

{EC}_{f i | r} (T) = {EN}_{f i | r} (T) C_{f} = \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t C_{f} 。

(7)

同理，在保修期结束前， $[n (T + T_{p}), W]$ 时间段内发生故障的平均次数可表示为

{EN}_{f | r} (n + 1) = \int_{n (T + T_{p})}^{W} h_{(n + 1)} (t; α (r)) d t 。

(8)

相应地，在 $[n (T + T_{p}), W]$ 时间段内装备修复性维修费用期望值可表示为

{EC}_{f | r} (W - n (T + T_{p})) = {EN}_{f | r} (n + 1) C_{f} 。

(9)

综上所述，将式(6)~(9)代入式(5)中，即可得到在r≤K₀时，装备在不完全预防性维修策略下保修成本为

\begin{matrix} {EC}_{r}^{1} (T, W) = int [W / (T + T_{p})] C_{p} + \\ \sum_{i = 1}^{n} \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t C_{f} + \int_{n (T + T_{p})}^{W} h_{(n + 1)} (t; α (r)) d t C_{f} 。 \end{matrix}

(10)

1.4.2 r>K₀的情况

同样，当r>K₀时，由图1可知装备会在时间τ处超出保修区域，即由于使用率过高，装备在使用时间限制W之前超出了使用程度限制U。容易得到在使用率为r时，τ的表达式为

τ = U / r 。

当r>K₀时，装备保修成本的表达式与r≤K₀时形式相同，只需将式(5)中的W用τ替换即可，其余符号含义不变。由此，在这种情况下，装备保修成本可表示为

\begin{matrix} {EC}_{r}^{2} (T, τ) = int [τ / (T + T_{p})] C_{p} + \\ \sum_{i = 1}^{n} \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t C_{f} + \int_{n (T + T_{p})}^{τ} h_{(n + 1)} (t; α (r)) d t C_{f} 。 \end{matrix}

(11)

在实际应用中，使用率随机变量R的分布可由装备或相似装备的实际使用情况数据或承担任务情况统计分析得到。综合考虑以上两种情况，假设使用率R的分布函数为G(r)，装备期望保修成本可表示为

\begin{matrix} EC (T, W, U) = \\ \int_{0}^{K_{0}} {EC}_{r}^{1} (T, W) d G (r) + \int_{K_{0}}^{\infty} {EC}_{r}^{2} (T, τ) d G (r) 。 \end{matrix}

(12)

1.5 可用度模型

与计算保修成本类似，在建立装备在保修期内的可用度模型时，也需要分为r≤K₀和r>K₀两种情况。

下面，对这两种情况下装备可用度分别进行建模分析。

1.5.1 r≤K₀的情况

与费用模型中相对应的情况类似，装备会在时间W处超出保修范围。此时，保修期内的期望停机时间 ${ED}_{r}^{1} (T, W)$ 与 ${EC}_{r}^{1} (T, W)$ 具有类似的表示，只需用T_p，T_f代替C_p，C_f，即可得到在预防性维修间隔期为T的维修策略下，保修期内装备的期望停机时间

\begin{matrix} {ED}_{r}^{1} (T, W) = \\ n T_{p} + \sum_{i = 1}^{n} {ET}_{f i | r} (T) + {ET}_{f | r} (W - n (T + T_{p})) 。 \end{matrix}

(13)

其中，nT_p表示保修期内由于预防性维修所导致的停工时间； ${ET}_{f i | r} (T)$ 表示在使用率为r时，在第i个间隔期内由修复性维修所导致的停机时间期望值； ${ET}_{f | r} (W - n (T + T_{p}))$ 表示 $[n (T + T_{p}), W]$ 时间内修复性维修所导致的停机时间期望值。

与保修费用模型类似，相应的故障停机时间表达式如下：

{ET}_{f i | r} (T) = {EN}_{f i | r} (T) T_{f} = \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t T_{f},

(14)

{ET}_{f | r} (W - n (T + T_{p})) = {EN}_{f | r} (n + 1) T_{f} 。

(15)

将式(14)、式(15)代入式(13)中，即可得到保修期内装备期望停机时间表达式：

\begin{matrix} {ED}_{r}^{1} (T, W) = int [W / (T + T_{p})] T_{p} + \\ \sum_{i = 1}^{n} \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t T_{f} + \int_{n (T + T_{p})}^{W} h_{(n + 1)} (t; α (r)) d t T_{f} 。 \end{matrix}

(16)

由此，可以得到r≤K₀时，装备在预防性维修策略下保修期内的期望可用度表达式：

\begin{matrix} {EA}_{r}^{1} (T, W) = 1 - {ED}_{r}^{1} (T, W) / W = \\ 1 - \frac{1}{W} [\begin{matrix} int [\frac{W}{(T + T_{p})}] T_{p} \\ + \sum_{i = 1}^{n} \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t T_{f} \\ + \int_{n (T + T_{p})}^{W} h_{(n + 1)} (t; α (r)) d t T_{f} \end{matrix}] 。 \end{matrix}

(17)

1.5.2 r>K₀的情况

与相应的保修费用模型相似，当r>K₀时，装备在时间τ处超出保修范围。将式(17)中的W用τ代替，即可得到相应的装备期望可用度表达式：

\begin{matrix} {EA}_{r}^{2} (T, τ) = 1 - {ED}_{r}^{2} (T, τ) / τ = \\ 1 - \frac{1}{τ} [\begin{matrix} int [\frac{τ}{(T + T_{p})}] T_{p} \\ + \sum_{i = 1}^{n} \int_{(i - 1) (T + T_{p})}^{i T + (i - 1) T_{p}} h_{i} (t; α (r)) d t T_{f} \\ + \int_{n (T + T_{p})}^{τ} h_{(n + 1)} (t; α (r)) d t T_{f} \end{matrix}] 。 \end{matrix}

(18)

其中， ${ED}_{r}^{2} (T, τ)$ 表示在r>K₀下，装备在保修期内的期望停机时间。

与保修成本模型类似，综合考虑以上两种情况，假设使用率R的分布函数为G(r)，装备在保修期内的期望可用度可表示为

\begin{matrix} EA (T, W, U) = \\ \int_{0}^{K_{0}} {EA}_{r}^{1} (T, W) d G (r) + \int_{K_{0}}^{\infty} {EA}_{r}^{2} (T, τ) d G (r) 。 \end{matrix}

(19)

2 二维保修策略优化模型解析

可以看出，文中构建的装备保修成本与可用度模型结构较为复杂，且具有非线性、非连续的特性，很难得到解析结果。所以，本文中利用Matlab编程工具求解模型的数值解，在此基础上对模型进行优化。在工程应用中，数值优化结果可以为制定装备保修策略提供科学支撑。

当r≤K₀时，由于装备保修时间不会随使用率变化而变化，恒为W，所以当预防性维修间隔期T确定时，保修期内预防性维修次数n也可以确定。因此， ${EA}_{r}^{1} (T, W)$ 和 ${EC}_{r}^{1} (T, W)$ 的值相对容易计算。

当r>K₀，此时τ=U/r，因此对应的预防性维修次数n随着r的值是不断变化的。在这种情况下，在给定R分布的情况下，编程求解 ${EC}_{r}^{2} (T, τ)$ 和 ${EA}_{r}^{2} (T, τ)$ 往往会出现溢出错误等问题。为此，本文采用以下的近似算法计算 ${EC}_{r}^{2} (T, τ)$ 和 ${EA}_{r}^{2} (T, τ)$ 的值^[15]，在此基础上，最终得到装备保修成本与可用度的数值。

令装备使用率最大值为R_U(R_U≥K₀)，之后将区间[K₀，R_U]划分成长度相同的M个子区间，一般M越大，计算结果越精确，同时计算的复杂度越高。M个子区间分别表示为 $[r_{i - 1}, r_{i})$ ，i=1, 2, …, M，则

r_{i} = K_{0} + i \times \frac{R_{U} - K_{0}}{M}, i = 1, 2, \dots, M

(20)

其中r₀=K₀。

每个区间 $[r_{i - 1}, r_{i})$ 内所对应的平均使用率可表示为

\bar{r_{i}} = \int_{r_{i - 1}}^{r_{i}} \frac{s g (s)}{G (r_{i}) - G (r_{i - 1})} d s 。

(21)

其中，s表示每个区间内使用率变化值；g(s)表示使用率分布概率密度函数。

此外，装备使用率在第i个使用率子区间内的概率

P_{i} = G (r_{i}) - G (r_{i - 1}) 。

(22)

所以，在区间 $[r_{i - 1}, r_{i})$ 内，可以近似地认为装备在时间点 $τ_{i} = U / \bar{r_{i}}$ 超出保修范围。那么 ${EC}_{r}^{2} (T, τ)$ 和 ${EA}_{r}^{2} (T, τ)$ 可以近似表示为：

\int_{K_{0}}^{\infty} {EC}_{r}^{2} (T, τ) d G (r) = \sum_{i = 1}^{M} P_{i} {EC}_{r}^{2} (T, τ_{i}) ，

(23)

\int_{K_{0}}^{\infty} {EA}_{r}^{2} (T, τ) d G (r) = \sum_{i = 1}^{M} P_{i} {EA}_{r}^{2} (T, τ_{i}) 。

(24)

因此，采用以上方法可以得到在预防性维修策略下二维保修成本EC(T, W, U)和可用度EA(T, W, U)的数值。

装备可用度是装备战备完好性的重要指标，一般来说，提高装备在保修期内的可用度意味着承制方保修成本的增加。因此，在双方制定保修策略时，单纯强调保修费用或装备可用度都是片面的，只有控制保修费用和保证可用度才是科学的方法。为此，引入保修期内费效比函数V(T, W, U)对模型进行费效比分析，作为优化装备二维保修策略的重要依据。费效比函数

\begin{matrix} V (T, W, U) = \frac{EC (T, W, U)}{EA (T, W, U)} = \\ \frac{\int_{0}^{K_{0}} {EC}_{r}^{1} (T, W) d G (r) + \sum_{i = 1}^{M} P_{i} {EC}_{r}^{2} (T, τ_{i})}{\int_{0}^{K_{0}} {EA}_{r}^{1} (T, W) d G (r) + \sum_{i = 1}^{M} P_{i} {EA}_{r}^{2} (T, τ_{i})} 。 \end{matrix}

(25)

由式(25)给出的保修期内费效比最小为目标，优化得到最优预防性维修间隔期，此时可以在控制保修成本的同时，保证装备可用度。通过分析得到的保修成本、可用度等数据，可以为装备保修策略的制定提供科学依据。

基于式(25)可以计算得到不同保修区域(W, U)下最优的费效比V_min(W, U)数值，但是由于式(25)结构比较复杂且存在非连续函数关系，难以得到(W, U)和V_min(W, U)的直接关系。假设两者之间存在以下的函数关系：

V_{min} (W, U) = f (W, U) 。

如果得到函数关系的表达式，那么只要给定保修区域(W, U)，就能够直接得到对应的最小保修费效比值，降低了计算复杂度，并且可以为保修策略制定提供数据支撑。在此基础上，可以综合考虑装备保修成本和可用度，针对装备不同使用和任务情况提供更加灵活的装备保修策略。可以看出，精确的函数关系 f 很难得到甚至对于大多数情况是不存在的，此时，可基于上面计算的结果数据采用回归拟合模型得到近似函数关系，在满足一定精确性的前提下即可在工程实际中应用。

3 算例分析 3.1 问题描述

本文以某型轮式装备产品为例对所建模型进行分析，承制方为该产品提供二维保修服务，保修期测度为使用时间和里程，保修期内的维修费用由承制方承担。综合考虑军地双方利益，为降低保修成本及提高装备可用度，承制方在保修期内采用定期预防性维修策略，对于保修期内的装备故障采用最小维修方式进行修复。

假设该产品初始确定的保修期限为W=2 a，U=10 万km。产品在设计使用率下的累积故障分布函数服从威布尔分布，如下所示：

F_{0} (t; α_{0}) = 1 - e^{- {(t / α_{0})}^{β}} 。

其中，α₀=0.5，β=1.5。

则在产品使用率为r时，累计故障分布函数为

F (t; α (r)) = 1 - e^{- {(r / r_{0})}^{γ β} {(t / α_{0})}^{β}} 。

此时，产品的故障率函数可表示为

h (t; α (r)) = \frac{f (t; α (r))}{\bar{F} (t; α (r))} = \frac{β}{α_{0}^{β}} {(\frac{r}{r_{0}})}^{γ β} t^{β - 1} 。

产品使用率的分布可以通过实际使用数据统计分析得到，为方便分析，假设产品使用率服从以下均匀分布：R~Uniform[1, 11]。

对模型中其它一些参数的设定值如表1所示。

表 1 相关参数设置 Tab. 1 The values of relevant parameters

为方便计算描述，在以下分析中设置时间单位统一为年(a)；里程单位为万km；费用单位为百元，不再统一标明。

3.2 问题求解与分析

结合第2节的分析，模型很难求得解析解。因此，在不同的保修期限制下，令预防性维修间隔期T以步长0.05在[0.1, 2]区间内取值，并计算对应的保修成本、可用度以及费效比值，通过比较进而确定最优的预防性维修间隔期。

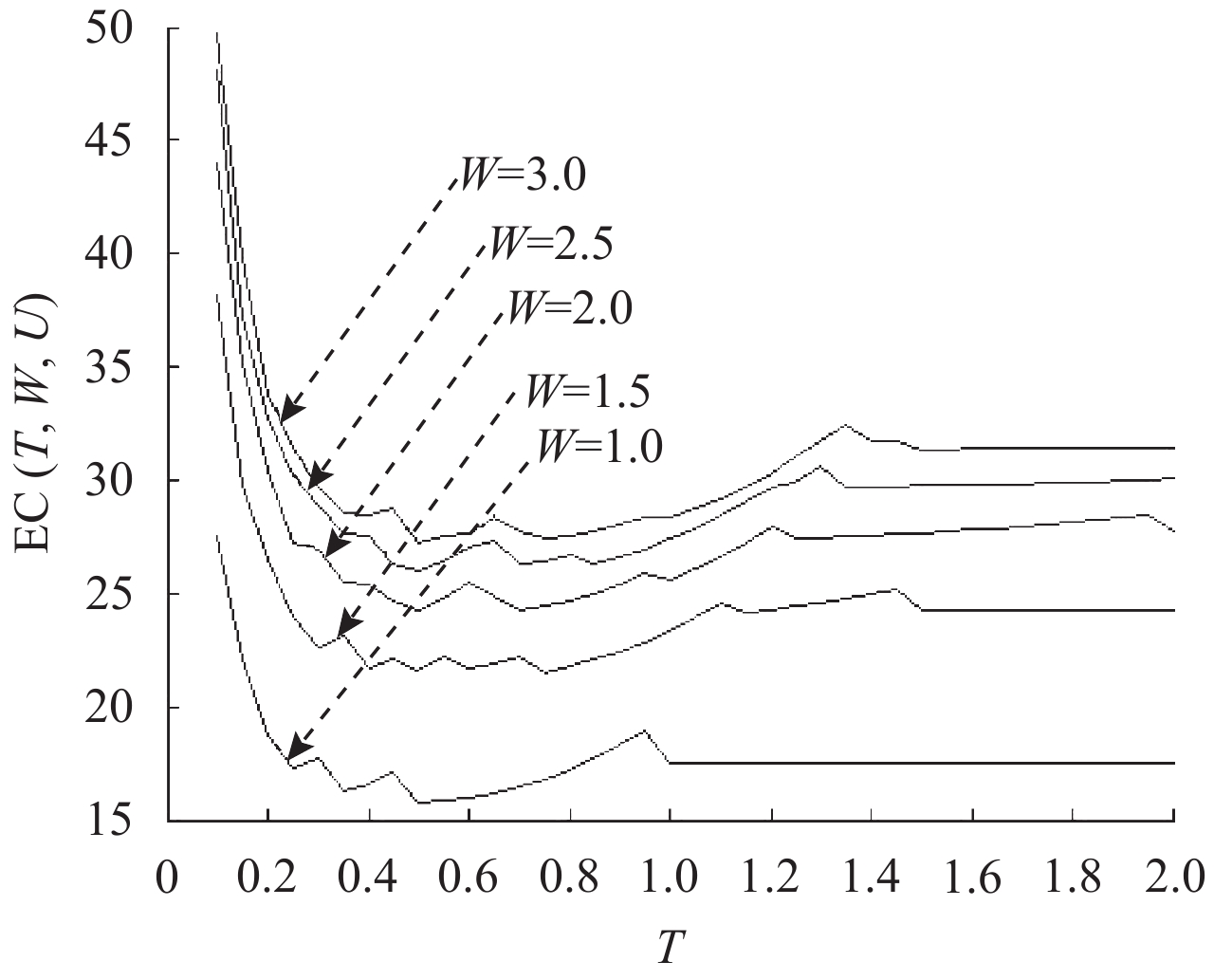
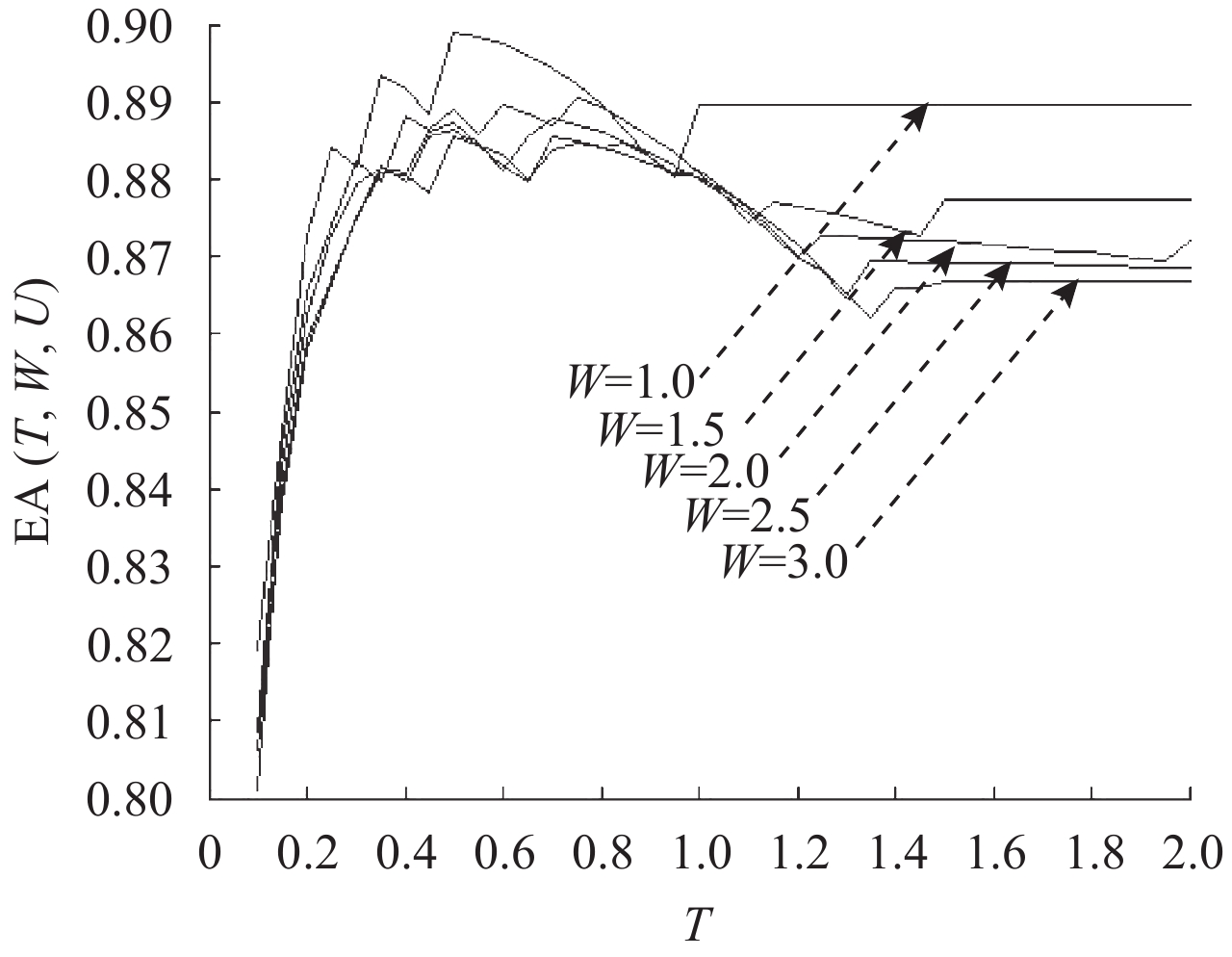
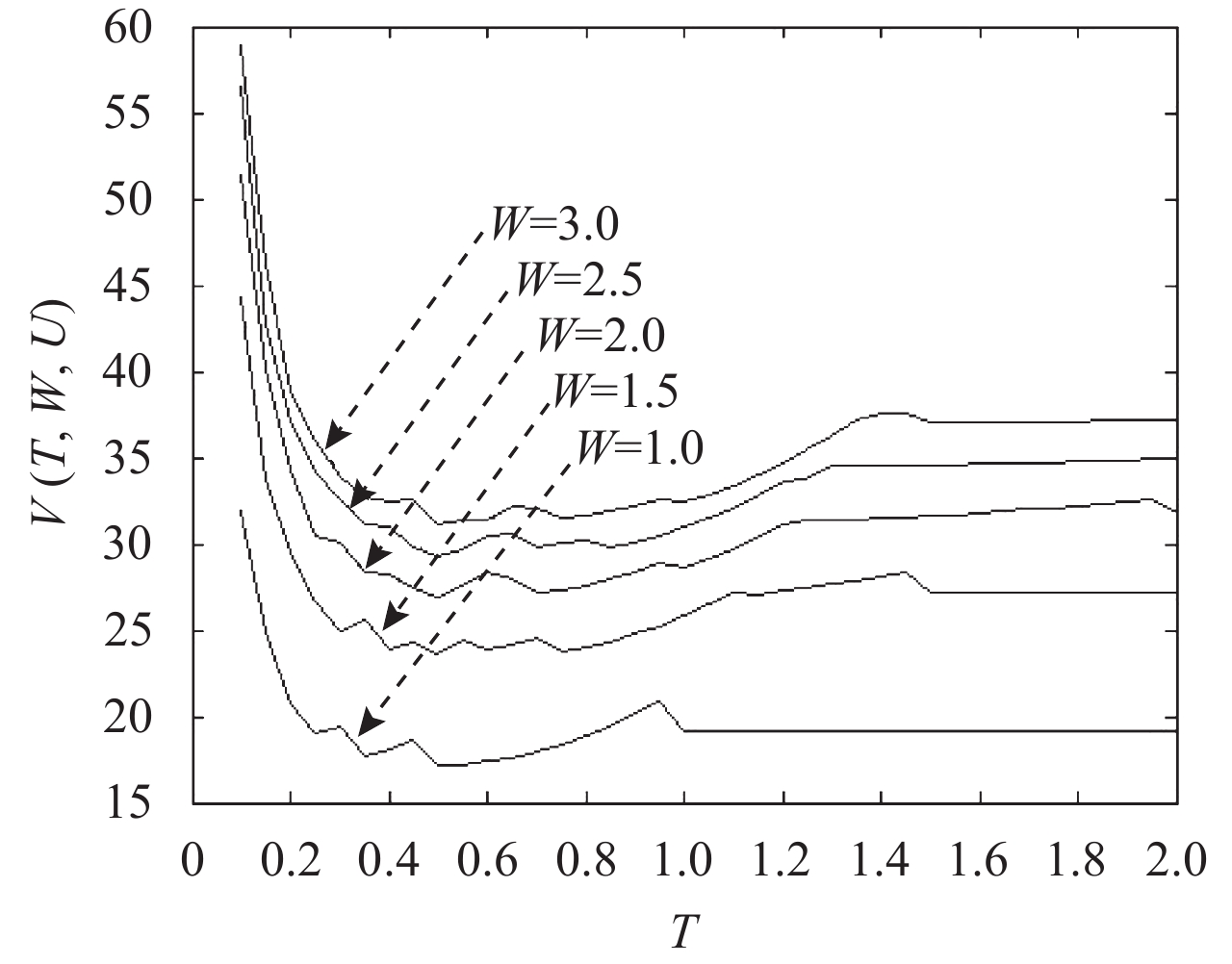
在给定保修期限的基础上，运用文中给出的数值算法可得到不同预防性维修间隔期所对应的保修成本、产品可用度以及费效比值。图2~图4分别表示在产品保修时间为1，1.5，2，2.5，3 a，保修里程为10 万km下，不同预防性维修间隔期所对应的保修成本、产品可用度及费效比变化情况，曲线上的跳跃点是由维修间隔期的突变所引起。

图 2 不同维修间隔期下保修成本变化情况 Fig. 2 Variation trend of warranty cost

图 3 不同维修间隔期下可用度变化情况 Fig. 3 Variation trend of availability

由图2和图3容易看出，当U和T一定时，随着保修期限时间W的延长，保修成本会随之增加，而相应的产品可用度降低；在保修期内，随着预防性维修间隔期T的增加，保修成本C值先降低后上升，存在特定的T值使得保修成本达到最低；相应地，也存在使得产品可用度最高的预防性维修间隔期值。

图 4 不同维修间隔期下费效比变化情况 Fig. 4 Variation trend of cost-effectiveness

由图4可以看出在不同保修期限下随着T的变化存在最优的费效比，使得保修费用和可用度得到权衡优化。表2列举了几种不同保修期限下对应的优化结果。

当W=2，U=10时，假设在保修期内只采用修复性维修，即预防性维修间隔期T大于保修时间W，其所对应的保修成本、可用度以及费效比数据如下：

C=27.77，A=0.868 2，V=31.98。

表 2 不同保修期限对应优化方案 Tab. 2 The corresponding optimization project under various warranty expiration

通过对表2中的数据进行分析，可以得到以下结论。

1) 对比只采用修复性维修的保修策略和方案8的优化结果数据，采用不完全预防性维修策略的方案8可使保修成本降低12.68%，可用度提高了2.27%，在提高可用度的同时控制了保修成本，充分验证了保修策略的优越性和科学性。

2) 通过比较表2中的费效比数据，在保证初始费效比(即只采用修复性维修的费效比)的前提下，如果在保修期内采用不完全预防性维修策略，保修期限可延长至W=3，U=10或者W=2，U=11.5；如果在控制保修成本不提高的前提下，保修期限同样可延长至W=3，U=10或者W=2，U=11.5。

3) 表2中保修成本、可用度、费效比等结果数据可以为装备使用方及承制方制定科学的保修策略提供参考，以保证军地双方利益。

3.3 柔性保修策略

由表2中费效比的变化可以看出最优费效比的值随着W、U的增加而上升，具有一定的相关性，结合在第2节中的分析，下面在不同的保修期限下运用上文的方法对保修期内最优费效比值进行计算，表3给出了60组不同(W, U)组合下的最优费效比值。

基于表3中所给出的数据，运用回归方法分析描述(W, U)和V_min(W, U)之间的函数关系。本文中使用1stOpt (FirstOptimization)软件对表3中数据进行曲线拟合，通过对比，二次多项式回归模型拟合效果较好，回归函数如下：

\begin{matrix} V_{min} (W, U) = 3.284 4 W + 1.049 2 U + \\ 1.215 2 W U - 0.063 5 U^{2} - 2.102 3 W^{2} 。 \end{matrix}

(26)

相关系数为99.51%，卡方系数为2.446 3。

由上面给出的显著性检验结果可以看出，拟合精度较高，可以用来估计不同保修期限下的最优费效比值。由式(26)可以看出，W每增加1 a，费效比上升(3.284 4+1.215 2U–4.204 6W)，图5和图6分别表示用回归函数得到的不同(W, U)值下最优费效比变化情况及等费效比曲线。

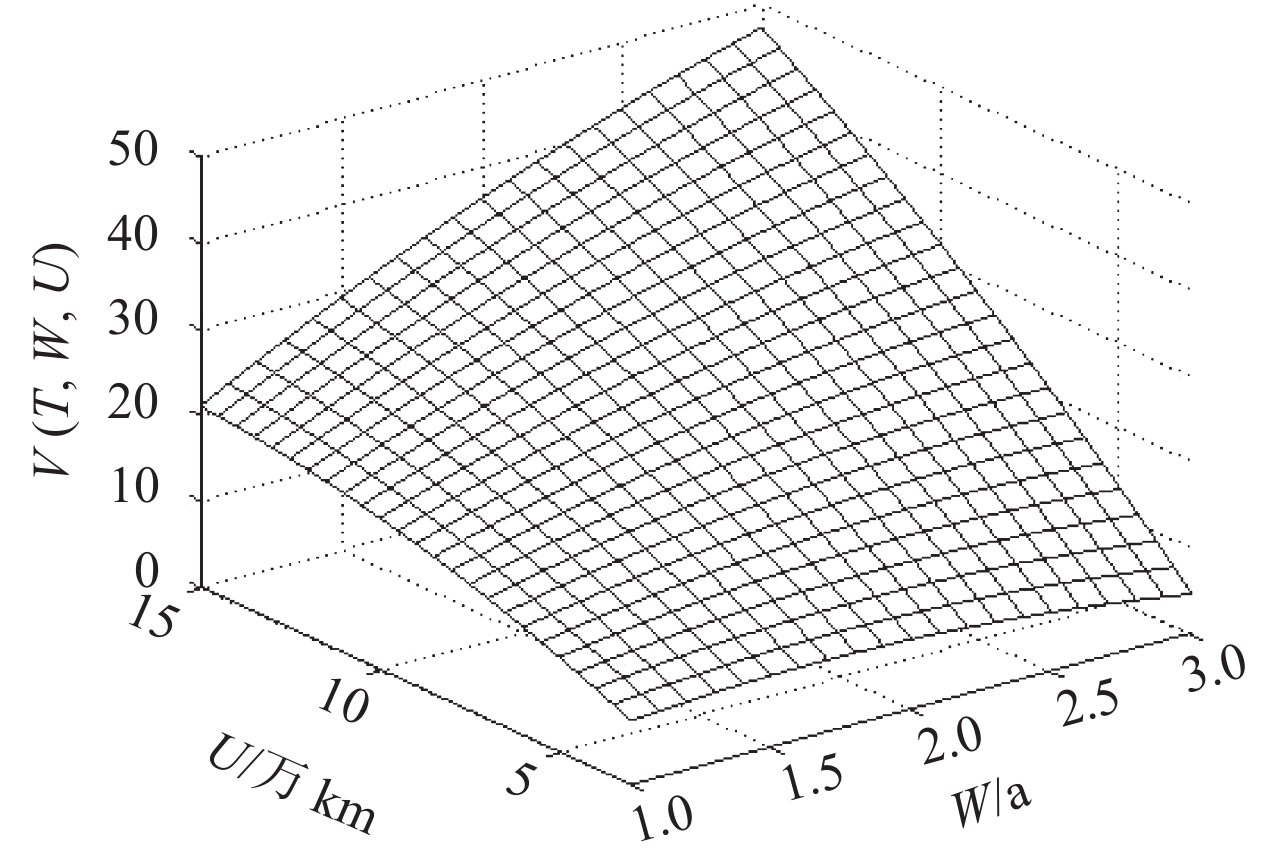
图 5 不同保修期限下最优费效比变化情况 Fig. 5 Variation trend of optimization cost-effectiveness under various warranty region

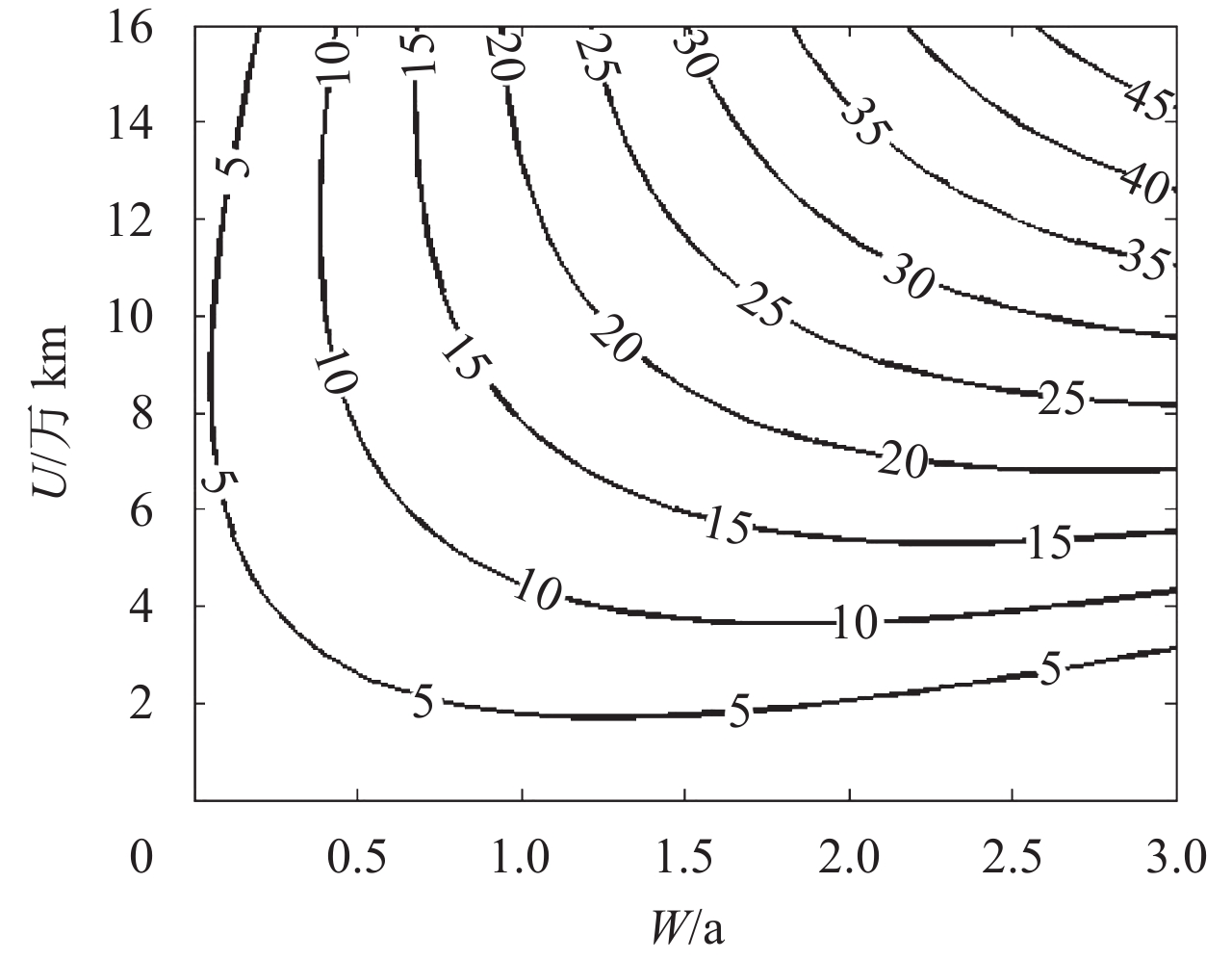
图 6 等费效比曲线 Fig. 6 The isoline of cost-effectiveness

由图5和图6可以看出，在给定(W, U)值的情况下，可以运用回归函数直接得到最优的费效比值，极大降低了计算复杂度；根据等费效比曲线，可以在降低保修成本、提高可用度的前提下，提供更加灵活的保修期方案供军地双方选择。如当V_min(W, U)=25时，由相应的等费效比曲线可得到不同的(W, U)组合，在这些保修期策略下最优费效比均为25，军方和承制方可根据装备任务情况等因素进行选择，结合本文所构建的二维保修策略优化模型可以得到对应的最优预防性维修间隔期。

表 3 不同保修期限下最优费效比 Tab. 3 The corresponding optimization cost-effectiveness under various warranty expiration

4 结束语

针对承制方控制保修成本和军方对装备可用度要求较高的问题，构建了装备二维保修成本和可用度模型，以保修期内费效比最小为优化目标，得到了不同二维保修期限下对应的最优预防性维修间隔期，并提拱了柔性保修策略方案，综合考虑军地双方利益，在降低装备保修成本的同时，提高产品可用度，为科学保修策略方案的制定提供了依据。

参考文献

[1]	MINJAE P, HOANG P. A new warranty policy with failure times and warranty servicing times[J]. IEEE Trans. on Reliability, 2012, 61(3): 822-831. DOI: 10.1109/TR.2012.2208298.
[2]	VARNOSAFADERANI S, CHUKOVA S. A two-dimensional warranty servicing strategy based on reduction in product failure intensity[J]. Computers and Mathematics with Applications, 2012(63): 201-213.
[3]	ISKANDAR B P, MURTHY D N P. Repair-replace strategies for two-dimensional warranty policies[J]. Mathematical and Computer Modelling, 2003(38): 1233-1241.
[4]	ISKANDAR B P, MURTHY D N P, Jack N. A new repair–replace strategy for items sold with a two-dimensional warranty[J]. Computers and Operations Research, 2005, 32(3): 669-682. DOI: 10.1016/j.cor.2003.08.011.
[5]	YUN W Y, KANG K M. Imperfect repair policies under two-dimensional warranty[J]. Proc. of the Institution of Mechanical Engineers, 2007, 221(4): 239-247.
[6]	JACK N, ISKANDAR B P, MURTHY D N P. A repair–replace strategy based on usage rate for items sold with a two-dimensional warranty[J]. Reliability Engineering and System Safety, 2009(94): 611-617.
[7]	于俭, 毛春苗. 不完全维修的二维产品保证成本[J]. 工业工程与管理, 2010, 15(4): 57-61. YU J, MAO C M. Research on the cost of two dimensional product warranty based on imperfect repair[J]. Industrial Engineering and Management, 2010, 15(4): 57-61.
[8]	SOUMAYA B, ANIS C, NIDHAL R. A decision model for adopting an extended warranty under different maintenance policies[J]. International Journal of Production Economics, 2012(135): 840-849.
[9]	CHUN Y H. Optimal number of periodic preventive maintenance operations under warranty[J]. Reliability Engineering and System Safety, 1992, 37(3): 223-225. DOI: 10.1016/0951-8320(92)90127-7.
[10]	JACK N, MURTHY D N P. A new preventive maintenance strategy for items sold under warranty[J]. Journal of Management Mathematics, 2002(13): 121-129.
[11]	YEH R H, LO H C. Optimal preventive maintenance warranty policy for repairable products[J]. European Journal of Operational Research, 2001, 134(1): 59-69. DOI: 10.1016/S0377-2217(00)00238-1.
[12]	姜国, 胡飞. 带保修期产品的预防维修建模分析[J]. 数学杂志, 2009, 29(4): 546-550. JIANG G, HU F. An optimal preventive maintenance policy for product sold with warranty[J]. Journal of Mathematics, 2009, 29(4): 546-550.
[13]	DOYEN L, GAUDOIN O. Classes of imperfect repair models based on reduction of failure intensity or virtual age[J]. Reliability Engineering and System Safety, 2004, 84(1): 45-46. DOI: 10.1016/S0951-8320(03)00173-X.
[14]	SHAFIEE M, CHUKOVA S. Maintenance models in warranty: a literature review[J]. European Journal of Operational Research, 2013(229): 561-572.
[15]	SHAHANAGHI K, NOOROSSANA R, HEYDARI M. Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts[J]. Engineering Failure Analysis, 2013(28): 90-102.