目前超过30%的全球经济活动基于项目形式进行[1]。企业在项目管理方面的竞争不断增加,项目团队需要在计划工期内和一定预算下交付高质量的项目。而在变化迅速的市场中,项目受到各种各样的限制,如资源稀缺、网络复杂性和各种不确定性约束[2],项目管理越来越具有挑战性。
传统的项目进度管理方法有关键路径法(CPM)、计划评审技术(PERT)。关键路径法出现于20世纪50年代,该方法在有向的项目网络图中识别出耗时最长的一条路线作为关键路径。在工序工期确定的情况下,关键路径法已经被证明是有效的项目管理方法,在现实项目实施中得到了广泛的应用[3-4]。计划评审技术在基本原理上与关键路径法相似,该方法采用最短估计时间、最可能估计时间和最长估计时间来确定工序工期[5]。资源稀缺项目调度是项目管理领域最复杂的问题之一。针对该问题,传统的项目进度管理方法如关键路径法、计划评审技术等方法很难满足资源冲突下的管理需要。面对这些挑战,Goldratt将约束理论引入项目管理,提出了关键链法(CCPM)[6]。
关键链法的主要优点在于对工期、逻辑关系和资源约束的整合,利用聚合缓冲区和一系列缓冲区监控等方法来应对项目中的不确定性因素。关键链法与传统方法(关键路径法和计划评审技术)相比,能够显著缩短工期[7]。此外关键链法已经在制造和服务行业的生产系统中实现了实际应用[8-9]。不论是关键路径法还是关键链法,均认为项目的工序工期是确定的,但是在实际中,通常很难精确估计工序工期。随着理论研究的深入,关键链法有许多改进和扩展。Long等[10]用模糊数来设置项目缓冲区,提出了模糊关键链法,用来处理在资源约束和不确定环境下的项目进度管理。随着灰色系统理论的发展,高朋等[11]结合灰色系统思想,研究了灰色关键链调度方法,改进了关键链中缓冲时间的选择方法。工期不确定情况下的关键链方法研究集中于关键链的识别和缓冲区设置,缺少有效的工期风险评估方法。
工期风险在项目中普遍存在。工程建设项目由于具有规模大、工期长、资源消耗多等特点,在项目实施过程中存在各种不确定因素,时常发生工期延误。因此,消除和有效控制项目工期风险就显得十分重要。本文在灰色关键链方法的理论背景下,引入适合贫信息聚类评估的三角白化权函数的灰色聚类评估模型[12],对工程项目进行工期风险评估,根据评估结果对后续工作提出指导性建议,有助于提高管理层在项目进度方面的管理效率。
1 基础理论背景 1.1 关键链法的基本思想Goldratt首次将约束理论引入项目管理领域,提出关键链法(critical chain project method,CCPM)。该方法在关键路径法的基础上发展而来。关键链法不仅考虑到工序间的逻辑关系,而且考虑到项目实施过程中人的行为因素,解决了传统进度管理方法无法解决的并行工序资源冲突的问题。
关键链基本思想是:首先以每个工序持续时间的50%作为工期估计,考虑工序间的资源约束对工序重新排序,确定关键链。之后通过缓冲区的设置和管理来消除项目不确定因素对工期的影响。缓冲区主要分为3类:项目缓冲区(PB)、输入缓冲区(FB)和资源缓冲区(RB),其中项目缓冲区设置在关键链的尾部,用来吸收关键链的不确定性;输入缓冲区设置在非关键链和关键链的交汇处,防止非关键链工序的延期对关键链造成影响;资源缓冲区是资源准备过程的预留时间,不加入到项目的各项链中。
1.2 基于中心点三角白化权函数的灰色评估模型的基本思想本文采用基于中心点三角白化权函数对项目工期风险进行灰色评估。灰色聚类是根据灰色关联矩阵或灰数的白化权函数将一些观测指标或观测对象划分成若干个可定义类别的方法[13]。由于项目实施的独特性,对于这种缺乏历史数据的对象,本文采取基于中心点三角白化权函数的灰色评估模型[14]进行评估,确定工期不确定因素影响对工期的影响程度,从而进行工期风险评估。
基于中心点三角白化权函数的灰色评估模型的具体计算步骤如下[14]。
第1步 根据评估要求确定的灰类数s,分别定义灰类
第2步 将灰类向不同方向进行延拓,考虑增加0灰类和s+1灰类,并确定其中心点
|
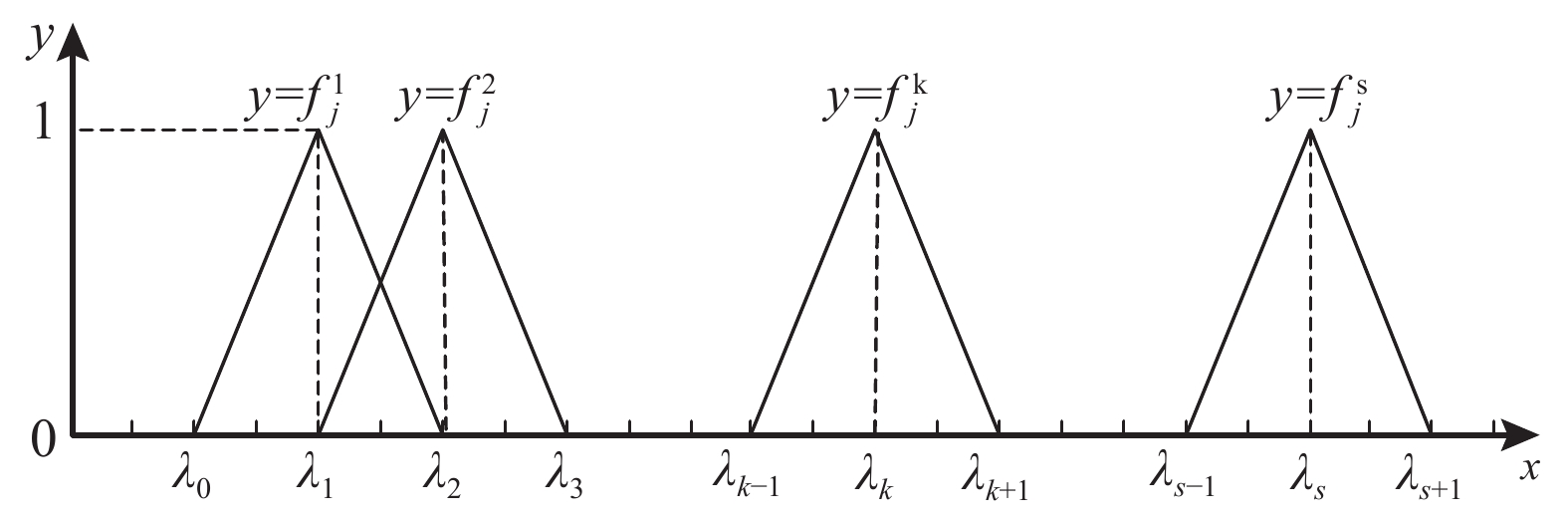
图 1 中心点三角白化权函数 Fig. 1 Center-point triangular whitenization weight function |
对于指标j的一个观测值x,可由式(1)计算出其属于灰类
|
$\quad\quad f_j^k\left( x \right) = \left\{ \begin{array}{l}0,{\rm{ }} x \notin [{\lambda _{k - 1}},{\lambda _{k + 1}}];\\[8pt]\displaystyle\frac{{x - {\lambda _{k - 1}}}}{{{\lambda _k} - {\lambda _{k - 1}}}},{\rm{ }}x \in \left( {{\lambda _{k - 1}}} \right.,\left. {{\lambda _k}} \right];\\[15pt]\displaystyle\frac{{{\lambda _{k + 1}} - x}}{{{\lambda _{k + 1}} - {\lambda _k}}},{\rm{ }}x \in ({\lambda _k},{\lambda _{k + 1}}){\text{。}}\end{array} \right.$
|
(1) |
第3步 计算对象
|
$\quad\quad \sigma _i^k = \sum\limits_{j = 1}^m {f_j^k({x_{ij}}) \cdot {\eta _j}} {\text{。}}$
|
(2) |
其中,
第4步 由
在灰色关键链法中不再认为工序工期是确定的。对于工序A,假设工序工期服从典型白化权函数
|
$\quad\quad {f_A}\left( t \right) = \left\{ \begin{array}{l}0,{\rm{ }} x \notin [c,d];\\[8pt]\displaystyle\frac{{t - c}}{{a - c}},{\rm{ }}x \in [c,a);\\[13pt]1,{\rm{ }}x \in [a,b);\\[8pt]\displaystyle\frac{{d - t}}{{d - b}},{\rm{ }}x \in [b,d]{\text{。}}\end{array} \right.$
|
(3) |
对于给定的工序可以利用一致指数进行工序工期的灰色估计[15],可认为当一致指数为95%时的灰色估计工期为高符合工期,并以高符合工期的一半作为期望工期。
|
${\rm{AI}}(A',A) = \left\{ \begin{array}{l}0,{\rm{ }} {t^{\rm{h}}} {\text{≤}} c;\\[8pt]\displaystyle\frac{{{{({t^{\rm{h}}} - c)}^2}}}{{(a - c)(b + d - c - a)}},{\rm{ }} {t^{\rm{h}}} \in (c,a];\\[13pt]\displaystyle\frac{{(2{t^{\rm{h}}} - c - a)}}{{(b + d - c - a)}},{\rm{ }}{t^{\rm{h}}} \in (a,b];\\[13pt]1 - \displaystyle\frac{{{{(d - {t^{\rm{h}}})}^2}}}{{(d - b)(b + d - c - a)}},{\rm{ }}{t^{\rm{h}}} \in (b,d];\\[10pt]1,{\rm{ }}{t^{\rm{h}}} {\text{≥}} d{\text{。}}\end{array} \right.$
|
(4) |
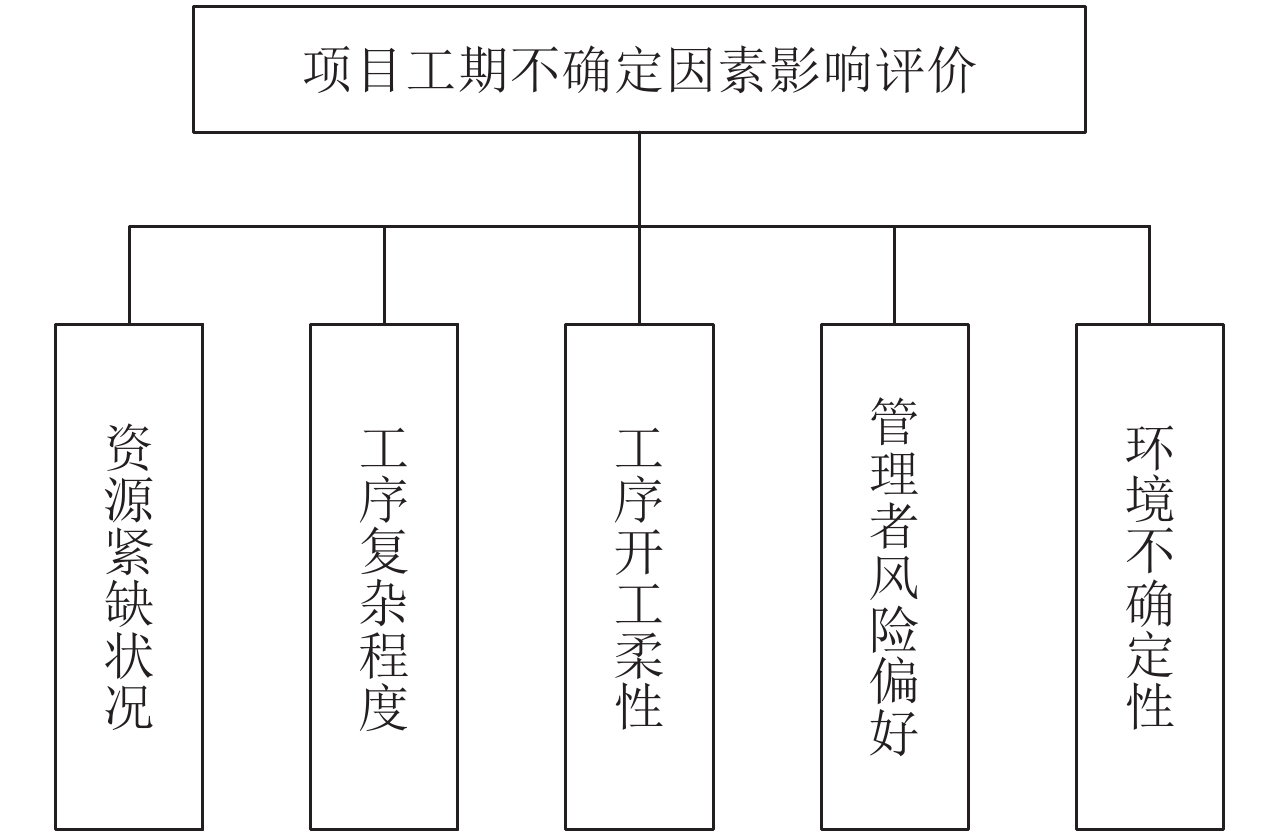
本小节介绍影响进度的不确定性因素。项目实施环境是一个由人因、社会、经济组成的复杂的多因素系统。根据项目实施环境的特点,建立如下评价指标体系(图2)。目标层为项目工期不确定因素影响评价(X),准则层包括:资源紧缺状况RF(i)、工序复杂程度CF(i)、工序开工柔性OF(i)、管理者风险偏好rF(i)和环境不确定性EU(i)。
|
图 2 项目工期不确定因素评价指标体系 Fig. 2 Evaluation index system of uncertainty factors in project duration |
1) RF(i)资源紧缺状况。
项目中出现多个工序共享某种相同的资源时,由于资源的稀缺性,工序之间会出现竞争现象。当资源的使用量接近可用资源量时,项目会受到资源稀缺和延迟的影响。资源稀缺可能源于一系列因素,例如供应不足,库存管理不善[16]。引入资源紧缺指数来反映资源紧缺情况所带来的不确定性,资源紧缺指数RF(i)表示为
|
$\quad\quad {\rm{RF}}(i) = \max \left\{ {\sum\limits_{q = 1}^n {\frac{{{r_t}(i,q)}}{{{\rm{Ra}}{{\rm{v}}_t}(q)}}} } \right\}\text{。}$
|
(5) |
其中,
2) CF(i)工序复杂程度。
项目中的工序复杂程度也称为链路复杂度,由通过工序i的最长链路和工序i的位置共同确定[17]。工序i的前置任务越多,该工序更可能受到前置活动延迟的影响,不确定性程度就越大。引入链路复杂度来反映工序复杂程度,则工序复杂度CF(i)表示为
|
$\quad\quad {\rm{CF}}(i) = \frac{{{m_i}}}{{{L_i}}}{\text{。}}$
|
(6) |
其中,Li表示通过工序i的最长链路上的工序数;mi代表工序i在该最长链路上的位序。为了保证项目按时完工,需要对工序复杂程度高的工序设置更大缓冲区。
3) OF(i)工序开工柔性。
工序开工柔性程度是指允许工序开工的时间窗口大小[18]。在关键链理论中可认为紧后工序会在紧前工序结束的瞬间就开工。但是在实际项目中该条件往往很难满足。这是因为在包含多个连续工序的项目中存在着级联效应,一个工序的延迟会转移到紧后工序,从而使项目的总体工期延迟[19]。然而当紧前工序提前完工时,如果没有到达紧后工序的规定开工时间,就会造成资源闲置。根据允许工序开工的时间窗口大小,在这里分为开工柔性大和开工柔性小。开工柔性大是指紧后工序会在紧前工序结束的瞬间就开工;开工柔性小是指紧前工序即使提前完工,紧后工序也不能立刻开工,需等到计划开工时间,此时需要适当增大缓冲区大小。
在这里引入工序开工柔性指数OF(i),并赋值1.1、1分别表示工序开工柔性大和工序开工柔性小。
4) rF(i)管理者风险偏好。
实际上,对于同一个项目的实施,管理者对项目的风险评估是不同的。从而,管理者的风险偏好会影响项目实施的不确定性。例如,当管理者属于风险规避型时,为了保证项目的完工率,此时会设置更大的缓冲区。假设工序工期服从正态分布,引入风险调整系数反映风险偏好,则风险偏好rF(i)表示为
|
$\quad\quad{\rm{rF}}(i) = \frac{{{z_\varepsilon }}}{2}{\text{。}}$
|
(7) |
其中,
5) EU(i)环境不确定性。
除了上述提到的4种不确定因素,项目实施过程中环境的变化也会对工期产生影响,例如合同风险、供应链稳定性等项目特定因素;自然灾害等非项目特定因素;以及宏观经济因素等。针对项目的环境不确定性因素,可以采取PEST分析方法评价其影响。PEST分析模型是一种分析企业宏观环境的有效工具方法,通过对政治、经济、社会和技术这4个因素进行分析,可以把握整个组织的环境状况[20]。引入环境不确定系数EU(i)反映环境不确定性,环境影响可分为3类:影响较小、影响一般和影响严重。采用专家打分的方法,确定工序i的环境影响程度,并用1、3、5分别赋值予以量化。
2.2.3 项目工期不确定因素权重设置本文采取优先关系比较法进行项目工期不确定因素的权重设置。由于工序的独特性,需要针对每个工序进行权重设置,但对于工序数量多的项目,如此操作过于繁琐,可操作性不强。对于上述问题本文分层进行权重设置,一个完整的房建工程项目主要分为3个阶段:施工准备与基础工程阶段;主体工程与装饰工程阶段;安装工程和调试验收阶段。因此依据每个阶段特色设计三阶段权重体系。
优先关系比较法与层次分析法类似,层次分析法中专家依靠判断矩阵评分表对各因素的相对重要程度进行打分,构建各因素指标权重判断矩阵,从而计算出各因素的权重值。优先关系比较法按照互补性原则,将各因素的相对重要程度进行量化,此方法原理清晰、计算快捷,可以为项目管理者提供比较科学的决策依据。
假设系统决策集为
对于系统决策集中的决策逐个两两比较,量化决策di对于系统D的相对重要性。建立二元对比优先矩阵:
|
$\quad\quad {R} = \left[ {\begin{array}{*{20}{c}}{{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}}\\{{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}}\\ \vdots & \vdots & & \vdots \\{{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nn}}}\end{array}} \right]{\text{。}}$
|
其中,rij仅在0,0.5,1中取值。当di比dj重要时rij取1,反之rij取0;当di和dj同等重要时rij取0.5;
|
$\quad\quad {r_i} = \sum\limits_{j = 1}^n {{r_{ij}},\;i{\rm{ = 1,2,}} \cdots {\rm{,}}n;\;j{\rm{ = }}} {\rm{1,2,}} \cdots {\rm{,}}n{\text{。}}$
|
(8) |
最后对ri进行归一化,从而得到决策di的权向量
|
$\begin{split}& \qquad {\bar w} = \left( {{w_1},{w_2}, \cdots ,{w_n}} \right)= \\ & \left( {{r_1}\Biggr/\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{r_{ij}},} } {r_2}\Biggr/\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{r_{ij}},} } \cdots ,{r_n}\Biggr/\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{r_{ij}}} } } \right){\text{。}}\end{split}$
|
(9) |
步骤1 按照关键链法的基本思想,首先对工序的工期进行灰色估计,之后解决资源冲突,从而确定关键链。
步骤2 对项目工期不确定因素进行评估,得到每个工序的不确定因素特征值,并设置不确定因素权重。
步骤3 基于中心点三角白化权函数的灰色评估模型进行项目工期风险评估:
1)按照评估要求,划分灰类,本文将评估结果划分为“影响不大”、“一般影响”、“较大影响”、“严重影响”4个灰类。为便于综合评价,首先将各指标分值转化为百分制。然后取每类区间中点作为各灰类代表
2)将灰类向两个方向延拓,考虑增加“弱影响”灰类和“很严重影响”灰类,并确定灰类代表
3)分别计算每个工序中工期不确定因素对于4个灰类的隶属度,利用式(2)求得该工序工期不确定因素的综合聚类系数。
4)由
为了说明所提方法项目工期风险评估的计算过程,本文选取铁道·京广家园(郑州材料厂住宅)工程建设项目进行案例分析。
由于工程建设项目自身特点,劳动力使用十分密集,在整个施工过程中常常出现人力资源冲突,因此本文主要从人力资源角度考虑资源约束。根据工程结构特点和涉及专业工种情况,将管理人员和施工作业人员分为4类资源。R1为管理人员;R2为专业化强的技术工种;R3为普通技术工种;R4为非技术工种。4种人力资源平均日可用量为R =
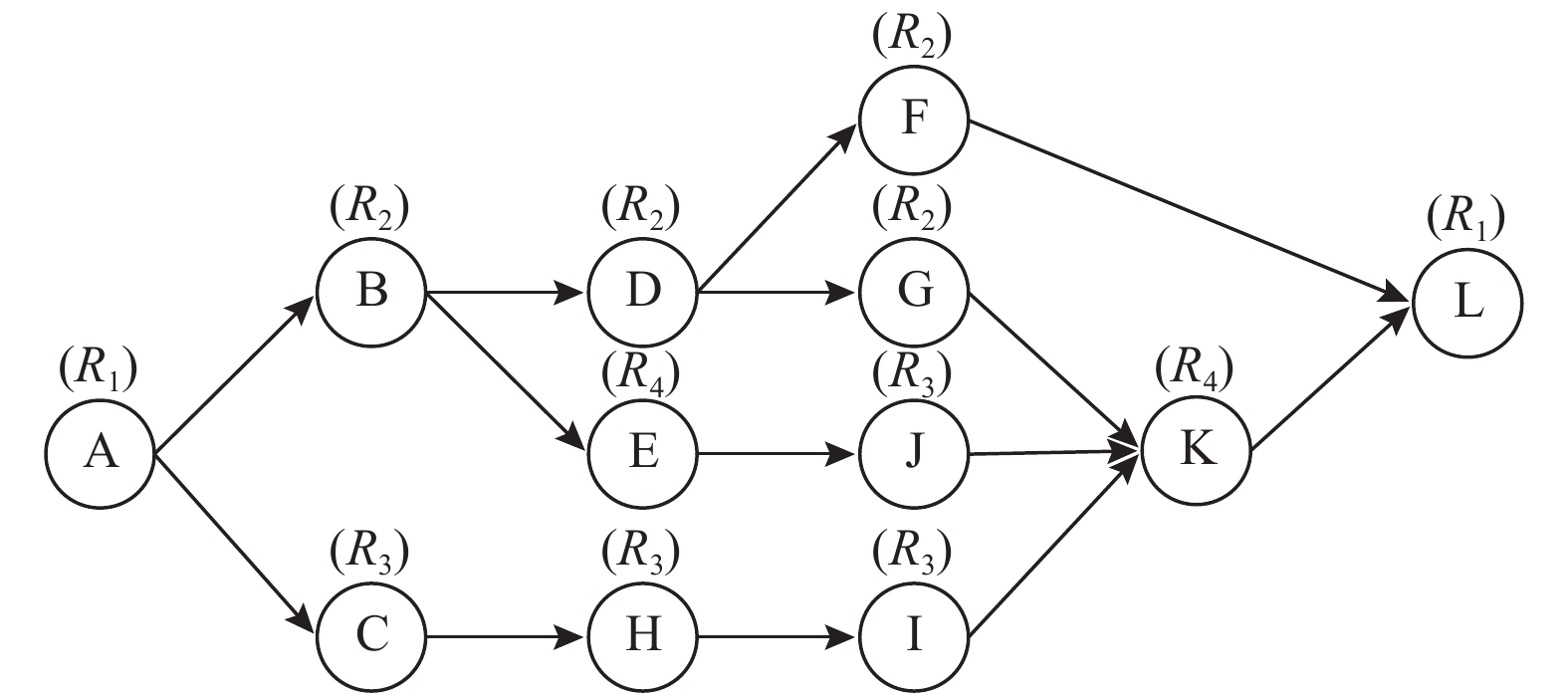
如图3所示,该案例包括12项工序,其中B、D、F、G工序需要共同资源R2,C、H、I、J工序需要共同资源R3,项目基本信息如表1。
| 表 1 项目工作分解 Tab. 1 Project work breakdown |
|
图 3 案例项目单代号网络计划 Fig. 3 Single code network plan of case project |
步骤1 首先进行工序工期的灰色估计, 确定关键链。在一致性指数为95%水平下,计算各工序的高符合工期,并取高符合工期的一半作为修正工期,见表1。
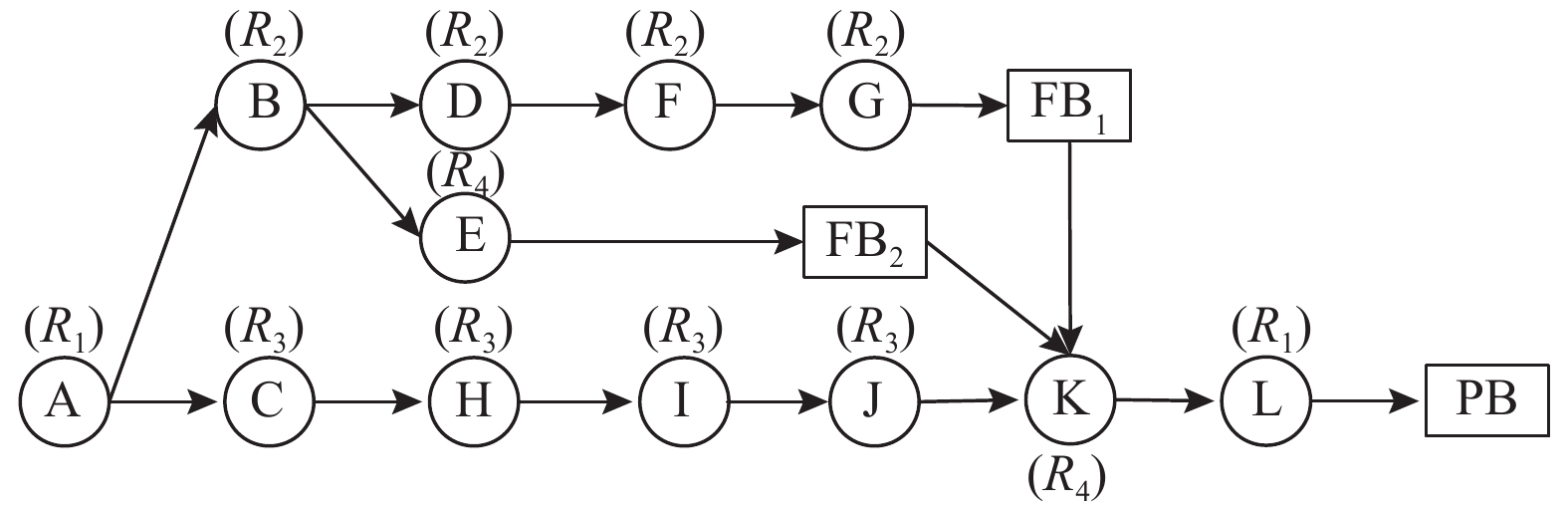
由于B、D、F、G工序需要共同资源R2,C、H、I、J工序需要共同资源R3,消除资源冲突后,确定关键链为
|
图 4 案例项目关键链进度计划图 Fig. 4 Case project critical chain schedule |
步骤2 项目工期不确定评估。按照2.2节内容建立项目工期不确定因素评价指标体系,根据项目相关信息计算各指标数值见表2。各阶段的二元对比矩阵及工期不确定因素权重见表3~5。
| 表 2 各类指数数值 Tab. 2 Various index values |
| 表 3 施工准备与基础工程阶段二元对比矩阵及权重 Tab. 3 Binary contrast matrix and weight of construction preparation and basic engineering |
| 表 4 主体工程与装饰工程阶段二元对比矩阵及权重 Tab. 4 Binary contrast matrix and weight of main engineering and decoration engineering |
| 表 5 安装工程和调试验收阶段二元对比矩阵及权重 Tab. 5 Binary contrast matrix and weight of installation engineering and commissioning phase |
在施工准备与基础工程阶段:
步骤3 项目工期风险评估。为便于综合评价,首先将各工期不确定因素影响值做无量纲化处理,修正边界指数数值,并转化为百分制。
| 表 6 指数修正数值 Tab. 6 Index correction values |
1)由于表6中风险值在10~98分,故可以将指标取值范围确定为[10, 98]。按照评估要求,本文将评估结果划分为“较弱影响”、“一般影响”、“较大影响”、“严重影响”4个灰类,分别对应灰区间为[10, 30),[30, 60),[60, 80),[80, 98),以各灰区间中点作为各灰类的中心点:
|
$\quad\quad {\lambda _1} = 20,{\lambda _2} = 45,{\lambda _3} = 70,{\lambda _4} = 89{\text{。}}$
|
2)将灰类向两个方向延拓,考虑增加“弱影响”灰类和“很严重影响”灰类,并确定灰类代表
此时得到工期不确定性因素关于4种灰类的三角白化权函数如下。
|
$\begin{array}{l} f_j^1\left( x \right) \!=\!\! \left\{ \!\!\!\! \begin{array}{l}0,{\rm{ }}x \notin [0,45];\\[8pt]\displaystyle\frac{x}{{20}},{\rm{ }}x \in (0,20];\\[10pt]\displaystyle\frac{{45 - x}}{{25}},{\rm{ }}x \in (20,45){\text{。}}\end{array} \right.\!\!\!\!\!\!\!\!\!\!\!\! f_j^2\left( x \right) \!=\!\! \left\{\!\!\!\! \begin{array}{l}0,{\rm{ }} x \notin [20,70];\\[10pt]\displaystyle\frac{{x - 20}}{{25}},{\rm{ }}x \in (20,45];\\[10pt]\displaystyle\frac{{70 - x}}{{25}},{\rm{ }}x \in (45,70){\text{。}}\end{array} \right.\end{array}$
|
|
$\begin{array}{l}\!\!\!\! f_j^3\left( x \right) \!=\!\! \left\{\!\!\!\! \begin{array}{l}0,{\rm{ }} x \notin [45,89];\\[10pt]\displaystyle\frac{{x - 45}}{{25}},{\rm{ }}x \in (45,70];\\[13pt]\displaystyle\frac{{89 - x}}{{19}},{\rm{ }}x \in (70,89){\text{。}}\end{array} \right.\!\!\!\!\!\!\!\!\!\!\!\!\! f_j^4\left( x \right) \!=\!\! \left\{\!\!\!\! \begin{array}{l}0,{\rm{ }} x \notin [70,100];\\[10pt]\displaystyle\frac{{x - 70}}{{19}},{\rm{ }}x \in (70,89];\\[10pt]\!\!\!\! \displaystyle\frac{{100 - x}}{{11}},{\rm{ }}x \in (89,100){\text{。}}\end{array} \right.\end{array}$
|
3)分别计算每个工序中工期不确定因素对于4个灰类的隶属度,并求得该不确定因素的综合聚类系数。
下面以施工准备与基础工程阶段的A工序和主体工程与装饰工程阶段的F工序为例进行说明。
工序A属于施工准备与基础工程阶段,选取权重
| 表 7 工序A工期不确定因素的综合聚类系数 Tab. 7 Comprehensive clustering coefficient of uncertain factors in A process |
| 表 8 工序F工期不确定因素的综合聚类系数 Tab. 8 Comprehensive clustering coefficient of uncertain factors in F process |
4)判断工序i的不确定因素属于哪种灰类。属于较弱影响灰类的工序有A、H;属于一般影响灰类的工序有I;属于较大影响灰类的工序有B、C、G、J;属于严重影响灰类的工序有D、E、F、K、L。由以上分析可知,项目管理者在优化项目工期时需关注处于严重影响灰类中的工序,例如对于工序F,增加工期风险的因素主要是资源紧缺状况和管理者风险偏好,有针对性地监督这些风险因素可以有效降低工期延误风险。
4 结语有效地评价、掌控工期风险对于项目进度管理具有重要的现实意义。本文先在灰色关键链思想下对工序工期进行灰色估计,找出关键链,然后结合工程建设项目的实际情况,确定项目工期不确定因素特性值。之后引入基于中心点三角白化权函数的灰色评估方法。该评估方法综合考虑多种影响工期的不确定因素,以综合聚类系数划分不同灰类,进行工期风险评估,为项目进度管理的后续工作提供有益的参考。
| [1] |
CHURCHWELL C D. Handbook of project-based management: leading strategic organizations by J. Rodney Turner[J].
Journal of Business & Finance Librarianship, 2015, 20(3): 246-248.
|
| [2] |
HU X, Cui N, Demeulemeester E. Incorporation of activity sensitivity measures into buffer management to manage project schedule risk[J].
European Journal of Operational Research, 2015, 249(2): 717-727.
|
| [3] |
孟丽丽, 路春光, 朱昌健, 等. 项目管理技术在钢铁企业大修项目中的应用案例[J].
工业工程, 2010, 13(3): 89-94.
MENG Lili, LU Chunguang, ZHU Changjian. Application of project management to equipment overhaul in a steel enterprise[J]. Industrial Engineering Journal, 2010, 13(3): 89-94. |
| [4] |
慕光宇, 李莉, 张文孝, 等. 基于CPM和挣值法的船舶建造项目进度控制的研究[J].
科技管理研究, 2011, 31(7): 206-208.
MU Guangyu, LI Li, ZHANG Wenxiao. Research on the progress management in shipbuilding project based on CPM and earned value method[J]. Science and Technology Management Research, 2011, 31(7): 206-208. |
| [5] |
刘庆. 计划评审技术在工程项目管理中的应用[J].
工程建设与设计, 2005(2): 61-62.
LIU Qing. Application of program evaluation review technique on project management of engineering[J]. Construction & Design for Project, 2005(2): 61-62. |
| [6] |
GOLDRATT E M. Critical chain[M]. Great Barrington: The North River Press, 1997: 110-121.
|
| [7] |
闫文周, 任格叶. 关键链的随机性及其在建筑工程项目进度中的应用[J].
工业工程, 2014, 17(6): 111-114.
YAN Wenzhou, REN Geye. The randomness of the critical chain and its application in the progress of construction project[J]. Industrial Engineering Journal, 2014, 17(6): 111-114. |
| [8] |
UMBLE M, UMBLE E J. Utilizing buffer management to improve performance in a health care environment[J].
European Journal of Operational Research, 2006, 174(2): 1060-1075.
DOI: 10.1016/j.ejor.2005.02.059. |
| [9] |
KUO T C, CHANG S H, HUANG S N. Due-date performance improvement using TOC’s aggregated time buffer method at a wafer fabrication factory[J].
Expert Systems with Applications, 2009, 36(2): 1783-1792.
DOI: 10.1016/j.eswa.2007.12.038. |
| [10] |
LONG L D, OHSATO A. Fuzzy critical chain method for project scheduling under resource constraints and uncertainty[J].
International Journal of Project Management, 2008, 26(6): 688-698.
DOI: 10.1016/j.ijproman.2007.09.012. |
| [11] |
高朋, 冯俊文. 基于灰色关键链的项目进度管理方法及应用[J].
工业工程与管理, 2009, 14(3): 55-59.
GAO Peng, FENG Junwen. A grey critical chain approach for schedule management and its application[J]. Industrial Engineering and Management, 2009, 14(3): 55-59. |
| [12] |
刘思峰, 方志耕, 杨英杰. 两阶段灰色综合测度决策模型与三角白化权函数的改进[J].
控制与决策, 2014, 29(7): 1232-1238.
LIU Sifeng, FANG Zhigeng, YANG Yingjie. Two stages decision model with grey synthetic measure and a betterment of triangular whitenization weight function[J]. Control and Decision, 2014, 29(7): 1232-1238. |
| [13] |
刘思峰, 党耀国, 方志耕. 灰色系统理论及其应用[M]. 3版. 北京: 科学出版社, 2007: 99.
|
| [14] |
刘思峰, 谢乃明. 基于改进三角白化权函数的灰评估新方法[J].
系统工程学报, 2011, 26(2): 244-250.
LIU Sifeng, XIE Naiming. New grey evaluation method based on reformative triangular whitenization weight function[J]. Journal of Systems Engineering, 2011, 26(2): 244-250. |
| [15] |
王凯, 袁永博, 丁乐. 基于模糊关键链法工程项目缓冲区的确定[J].
建筑经济, 2009(s1): 76-79.
WANG Kai, YUAN Yongbo, DING Le. Determination of project project buffer based on fuzzy critical chain method[J]. Construction Economy, 2009(s1): 76-79. |
| [16] |
MA G, WANG A, LI N. Improved critical chain project management framework for scheduling construction projects[J].
Journal of Construction Engineering & Management, 2014, 140(12): 04014055-1.
|
| [17] |
TUKEL O I, ROM W O, EKSIOGLU S D. An investigation of buffer sizing techniques in critical chain scheduling[J].
European Journal of Operational Research, 2006, 172(2): 401-416.
DOI: 10.1016/j.ejor.2004.10.019. |
| [18] |
杨立熙, 李世其, 黄夏宝, 等. 属性相关的关键链计划缓冲设置方法[J].
工业工程与管理, 2009, 14(1): 11-14.
YANG Lixi, LI Shiqi, HUANG Xiabao. A buffer sizing approach in critical chain scheduling with attributes dependent[J]. Industrial Engineering and Management, 2009, 14(1): 11-14. |
| [19] |
杨雪松, 胡昊. 基于关键链方法的多项目管理[J].
工业工程与管理, 2005, 10(2): 48-52.
YANG Xuesong, HU Hao. Mult-project management based on critical chain method[J]. Industrial Engineering and Management, 2005, 10(2): 48-52. |
| [20] |
李芳健, 王家骥, 王培席, 等. 我国全科医学教育的PEST分析及策略选择[J].
中国全科医学, 2013, 16(1): 69-71.
LI Fangjian, WANG Jiaji, WANG Peixi. PEST analysis and strategy selection of general practice education in china[J]. Chinese General Practice, 2013, 16(1): 69-71. |
 2017, Vol. 20
2017, Vol. 20