手术排程旨在以特定的排程法则确定排程周期内各例手术进行的时间和地点,并安排相应医护人员及医疗设备。在满足人员、时间和空间等资源约束下如何安排各例手术,使得医生完成手术的工作时间、患者的等待时间和手术室的安排调度等方面均达到最佳状态,得到了学术界和医务工作者的普遍关注。在因医疗资源短缺而引发的医患矛盾日渐突出且手术收入成为医院主要收入的背景下,科学高效地进行手术排程,不仅有助于医院增加收入,减少成本和改善服务,也可以使得医患关系更加和谐。
Pham等[1]将手术排程问题视为类多模式加工车间的生产调度问题(MMBJS),在进行了理论分析后构建了混合整数线性规划模型,并采用商用求解器CPLEX进行求解;Lamiri等[2]以最小化手术成本和患者的等待时间作为优化目标,采用数学规划方法对多目标手术排程问题进行了有效研究;Heydari等[3]将紧急手术作为手术排程过程中需要考虑的对象,建立相应的数学模型并提出保持手术排程方案鲁棒性和稳定性的求解方法。
上述已有的数学规划方法可以在同时考虑众多资源约束的情况下,较好地刻画出手术排程问题的复杂性。但由于手术排程问题通常是NP难问题,上述精确型算法很难快速有效地进行求解[4]。因此,近年来众多研究者开始将思路转向运用进化算法和排序理论来解决该问题。例如Hsu等[5]采用禁忌搜索算法有效减少了麻醉复苏室护士的需求数量并使得手术结束时间提前;Roland等[6]提出针对门诊手术排程问题的遗传算法,以确定病人的手术日期、手术室和手术开始时间等;朱悦等[7]提出了手术中医疗团队间准备时间的概念,并运用恶化效应理论,构建了最小化手术完成时间的手术排程模型。
进一步分析可以发现,上述研究通常以提升医生和患者满意度为目标,采用将启发式算法和多目标优化理论相结合的方式来进行手术排程问题求解,在提升算法收敛速度和避免陷入局部最优方面进行了较大改进。然而在问题的关注视角上尚存在改进的空间,比如目前已有研究大多在优化医患满意度的过程中将开启的手术室数量设为定值而非决策变量,忽视了减少开启手术室的数量可以帮助医院节省可观的手术成本这一重要影响因素[8]。因此,本文将在上述研究的基础上,充分考虑开启手术室数量对降低医院手术成本的影响,进行多资源约束下考虑医患满意度和手术成本的多目标手术排程优化模型构建,并提出改进的NSGA-III算法进行不同规模手术排程问题的优化求解。
1 多目标手术排程问题描述及模型构建手术排程如果调度安排过于紧凑将导致医护人员工作疲劳,而如果调度安排过于松散将造成手术室闲置,这些都会影响到医院的运作管理质量与服务水平。一方面手术室成本是手术成本的重要部分[9];另一方面医护人员和患者的满意度分别与完成所有手术过程的总时长和平均时长有关[4]。本文从医院、医生和病人3个角度综合考虑,针对待安排的手术集合,开展最小化完成所有手术过程的总时长、平均时长以及开启手术室数量的多目标手术排程问题研究,从而为构造有效的科室手术排程系统提供支撑。
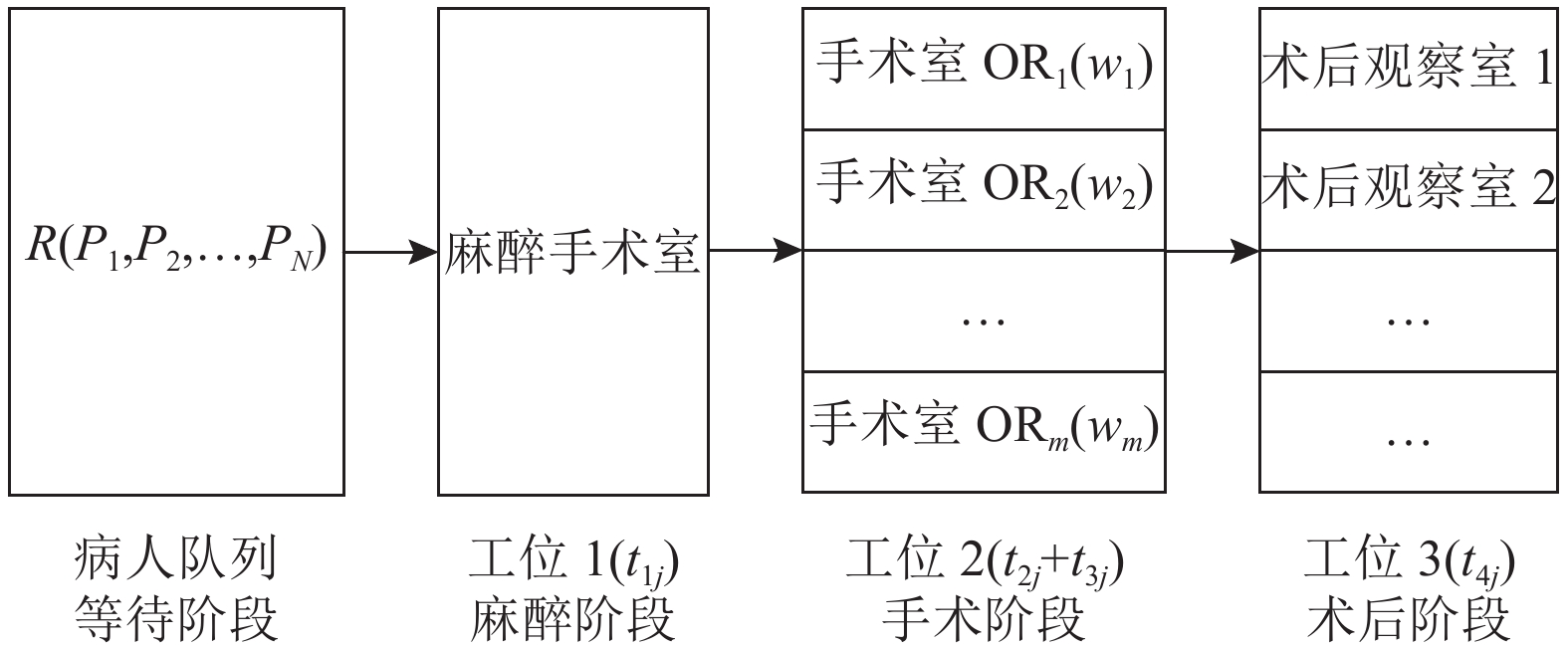
1.1 问题描述手术过程通常分为等待、麻醉、手术和术后观察4个阶段[10]。其中手术阶段包括术前准备和手术2个过程。病情不同的患者麻醉、术前准备、手术和术后观察所用时间各不相同,病人的术前准备时间也会由于所安排手术室前一场手术类型的不同而存在差异,各手术阶段之间没有空闲,且手术过程不允许中断。多数医院以科室为单位进行手术排程,各科室拥有独立的麻醉室和手术室供该科室进行手术,手术过程如图1所示,对于其中涉及的各手术阶段进行如下定义。
a) 等待阶段。本文针对住院病人进行手术排程方法研究,病人服从科室的安排进行手术。若手术日内有N位患者需进行手术,则构成任务集合P={P1, P2, …, PN}。手术顺序R为P中所有元素的一个排列,显然R包含N!种情形。病人在病房等候通知进行手术,等待时间为系统开始手术至该患者开始手术所用的时间。
b) 麻醉阶段。手术排程系统包含一间能满足所有患者麻醉需求的麻醉术间,麻醉手术室每时只能对一位手术患者进行麻醉,定义对患者Pj进行麻醉的时间为t1j。
|
图 1 病人手术过程流程 Fig. 1 The flow chart of surgery for patients |
c) 手术阶段。假定科室手术排程系统包含M间手术室,每间手术室均配备医疗器械和可用的医疗资源以适用于该科室各类型患者的手术,辅助人员能协助主刀医生进行不同类型的手术,主刀医生不能同时进行两例以上手术,同一手术室内不能同时进行一台以上的手术。设调度方案中开启手术室的数量为m,开启手术室的集合为记为OR={OR1, OR2, …, ORm}。定义患者Pj的手术类型为Tj,术前的准备时间为t2j,手术持续时间为t3j,设手术室ORi在开始第一例手术之前的等待时间为wi。患者在麻醉完成后,选择编号最小的可用空闲手术室进行手术;若此时所有手术室均占用,则选择最早可用手术室进行手术。
d) 术后观察:科室手术排程系统包含一定数量的术后观察室。定义患者Pj术后观察所用时间为t4j。
1.2 多目标手术排程问题模型构建基于上述手术排程问题描述,其决策变量包括是否安排患者Pj在手术室ORi的倒数第k个手术室进行手术的变量xjik和开启手术室数量m,具体定义如下。
|
$\begin{array}{l}{x_{jik}} = \left\{\!\!\!\!\!\! {\begin{array}{*{20}{c}}{1,\;{\text{病人}}{P_j}{\text{在手术室}}{\rm{O}}{{\rm{R}}_i}{\text{倒数第}}k{\text{个做手术}};\;\;\;}\\[8pt]{\begin{array}{*{20}{c}}{0,\;{\text{否则}};\forall j \in P;\forall i \in {\rm{OR}};\forall k {\text{≤}} N{\text{。}}\qquad \qquad}\end{array}}\end{array}} \right.\\[8pt]m \in \left\{ {f\left| {f \in N + ,f {\text{≤}} M} \right. } \right\}{\text{。}}\end{array}$
|
于是可构建如下手术排程问题模型。
|
$\quad\quad \min \;\left( {{G_1},{G_2},{G_3}} \right){\text{。}}$
|
((1)) |
|
$\quad\quad{G_1} = \mathop {{\rm{max}}} \limits_{i {\text{≤}} m} \; \left\{ {{w_i} + \sum\limits_{j = 1}^N {\sum\limits_{k = {\rm{1}}}^N {({t_{2j}} + {t_{3j}} + {t_{4j}}) \cdot {x_{jik}}} } } \right\},$
|
((2)) |
|
$\quad\quad G_2{\rm{ = }}\frac{1}{N} \cdot \sum\limits_{i = 1}^m {\left\{ \begin{array}{l}{k_{\max }}({x_{jik}} = 1) \cdot {w_i} + \\\sum\limits_{j = 1}^N {\sum\limits_{k = {\rm{1}}}^N {(t{}_{2j} + {t_{3j}} + {t_{4j}}) \cdot k \cdot {x_{jik}}} } \end{array} \right\}} ,$
|
((3)) |
|
$\quad\quad {G_3} = m,$
|
((4)) |
|
$\quad\quad {w_i} = \sum\limits_{x = 1}^i {{R_x}{t_{1j}}} \;\;\;\forall i {\text{≤}} m{\text{。}}$
|
((5)) |
其中,Rxt 1j表示队列R中第x位病人的麻醉时间;式(1)表示目标函数;式(2)~(4)分别表示完成所有手术过程的最长时间(G1)、平均时间(G2)以及开启的手术室数量(G3);式(5)表示手术室ORi等待时间wi的计算方式。
约束条件如式(6)~(10)所示。
|
$\quad\quad \sum\limits_{i = 1}^m {\sum\limits_{k = 1}^N {{x_{jik}} = 1} } ,\;\;\;\forall j {\text{≤}} N;$
|
(6) |
|
$\quad\quad \sum\limits_{j {\text{≤}} N} {{x_{jik}} {\text{≤}} 1} ,\;\;\;\forall i {\text{≤}} m,\forall k {\text{≤}} N;$
|
(7) |
|
$\quad\quad {x_{jik}} \cdot \sum\limits_{l = k}^N {\sum\limits_{h = 1}^N {{x_{ihl}} = {x_{jik}} \cdot k,\;\;} } \forall i {\text{≤}} m,\forall j {\text{≤}} N,\forall k {\text{≤}} N;$
|
(8) |
|
$\quad\quad {t_{2j}} \in [P],\;\;\;\forall j {\text{≤}} N;$
|
(9) |
|
$\quad\quad {t_{4j}} \in [O],\;\;\;\forall j {\text{≤}} N{\text{。}}$
|
(10) |
上述约束式中i、j、k、h均为正整数,其中约束式(6)表示患者手术过程需要经历a)、b)、c)、d) 4个阶段;约束式(7)表示同一个手术室不能同时进行多台手术;约束式(8)表示同一手术室内的两台手术之间没有空闲时间;式(9)和(10)给出了每位患者术前准备时间和术后观察时间的取值约束,其中[P]对应术前准备时间二维表,[O]对应术后观察时间表。
2 基于INSGA-III的手术排程问题求解非支配排序遗传算法常用于优化医院医疗资源的分配[11]。本文提出改进的非支配排序遗传算法(INSGA-III)以解决多目标手术排程问题:将全局优化能力较强的自适应机制引入INSGA-III的交叉和变异操作,有效避免其陷入局部最优,进而大幅提高全局优化和局部搜索的能力及效率;采取作用于选择阶段的种群染色体唯一策略(PCUP)和改进的三维空间中Pareto前沿面上的个体拥挤距离计算算子,以提升种群的多样性;将精英策略和锦标赛选择机制等成熟有效的策略运用到INSGA-III中,以加快算法的收敛速度。
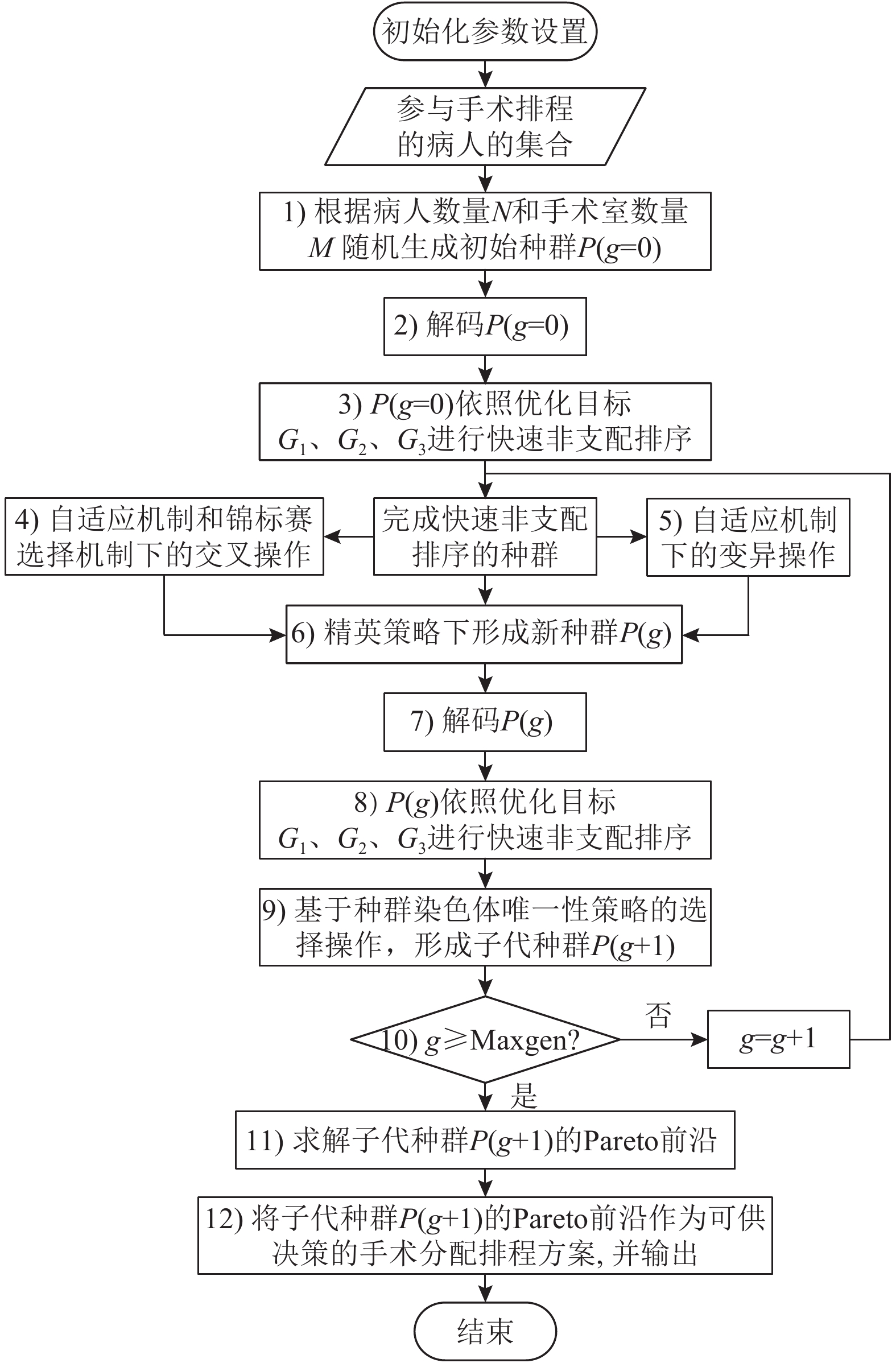
对于本文提出的多资源约束下的手术排程问题,排程可行方案的数量最多可达M×N!个。为了有效权衡问题模型中考虑到的3个目标函数,本文对其同时进行优化,所设计的算法最终输出进化迭代后得到的非支配解以供管理者根据偏好进行决策。INSGA-III算法的流程框架如图2所示,具体步骤说明如下。
|
图 2 算法总体框架 Fig. 2 The overall framework of the algorithm |
Step1 设置进化代数计数器g=0,根据手术室数量M和患者数量N,按设计的编码方式随机产生数量为Popsize的初始种群P(g=0)。
Step2 对初始种群P(g=0)的染色体进行解码。
Step3 对初始种群P(g=0)进行快速非支配排序。
Step4 对完成非支配排序的种群执行交叉操作。
Step5 对完成非支配排序的种群执行变异操作。
Step6 执行精英策略,将交叉和变异操作后形成的新个体与原有种群融合成一个新的种群P(Com)。
Step7 对新种群P(Com)染色体进行解码。
Step8 对新种群P(Com)进行快速非支配排序。
Step9 执行种群染色体唯一策略(PCUP),在P(Com)中选择出数量为环境最大容纳量(Popsize)的个体形成子代种群P(g+1)。
Step10 判断代数计数器g是否达到最大代数(Maxgen),如果是,则转向Step11;否则,g=g+1,重复执行Step4~Step10。
Step11 求解最终种群的Pareto前沿面对应的解集。
Step12 将非支配解作为决策参考方案输出。
上述各步骤中的细节将在下文进行详细阐述。
2.1 染色体编码设计对于排序寻优问题,采用1~N的整数序列编码具有天然优势。依据手术排程问题需确定患者手术顺序的特点,INSGA-Ⅲ以{m, 1~N的整数序列}作为个体染色体,其中,m代表开启手术室数量;1~N整数序列代表编号为1~N的患者的手术顺序R。采用这种编码方式可为后续交叉和变异算子的操作带来便捷,染色体结构及各基因代表的含义如图3所示。解码操作则是根据染色体中的基因,读取或计算得到个体的xjik和对应优化目标值,分别为t1、t2和m。

|
图 3 染色体编码示意图 Fig. 3 An illustration of chromosome coding |
非支配排序算子用于区别种群中个体的优劣从而对其进行排序,执行过程由以下3部分组成。
1) 求解种群中所有的非支配解,指定这些个体的非劣等级为1;从种群中移除这些个体,对剩余种群求所有非支配解,指定非劣等级为2;重复上述步骤直到种群中所有个体的非劣等级都被确定。
2) 对非劣等级相同的个体,计算个体基于小生境尺寸的拥挤距离,拥挤距离越大说明该点附近越稀疏,被给予的生存几率就越大,从而使种群保持多样性,保证算法收敛到一个均匀分布的Pareto曲面[12]。
3) 按照非劣等级越小非支配排序越靠前和非劣等级相同时拥挤距离越大非支配排序越靠前的原则,确定种群的非支配排序。
计算拥挤距离的具体过程是:将非支配解向3个坐标轴上投影;分别计算3个投影点的拥挤距离,拥有最大或最小的目标函数值的投影点的拥挤距离为1,其他投影点计算基于小生境尺寸的拥挤距离;个体的拥挤距离为3个投影点的拥挤距离之和,设定坐标轴上值相同的投影点具有相同拥挤距离。某级非支配解中第q个染色体的拥挤距离CDq可按下式计算。
|
$\begin{array}{l}\qquad {\rm{C}}{{\rm{D}}_q} = \displaystyle\sum\limits_{s = 1}^3 {d_s^q} {\text{。}}\\d_s^q = \left\{ \begin{array}{l}1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;G{}_s(q) = G_s^{\min }{\rm{||}}G{}_s(q) = G_s^{\max };\\[7pt]\displaystyle\frac{{G{}_s(q + 1) - G{}_s(q - 1)}}{{(G_s^{\max } - G_s^{\min }) \cdot n}},G{}_s(q) \ne G_s^{\min },G{}_s(q) \ne G_s^{\max }{\text{。}}\end{array} \right.\end{array}$
|
(11) |
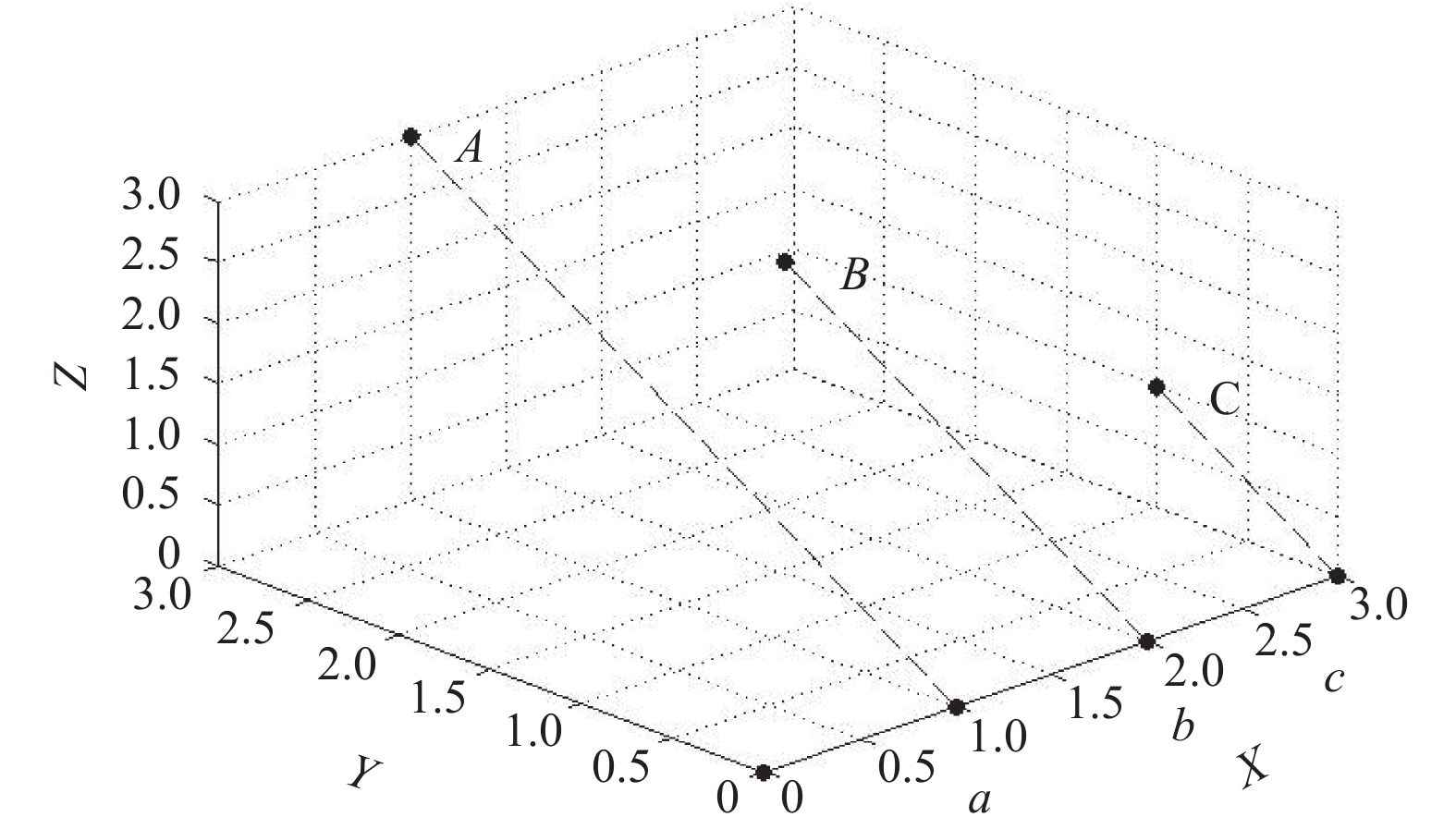
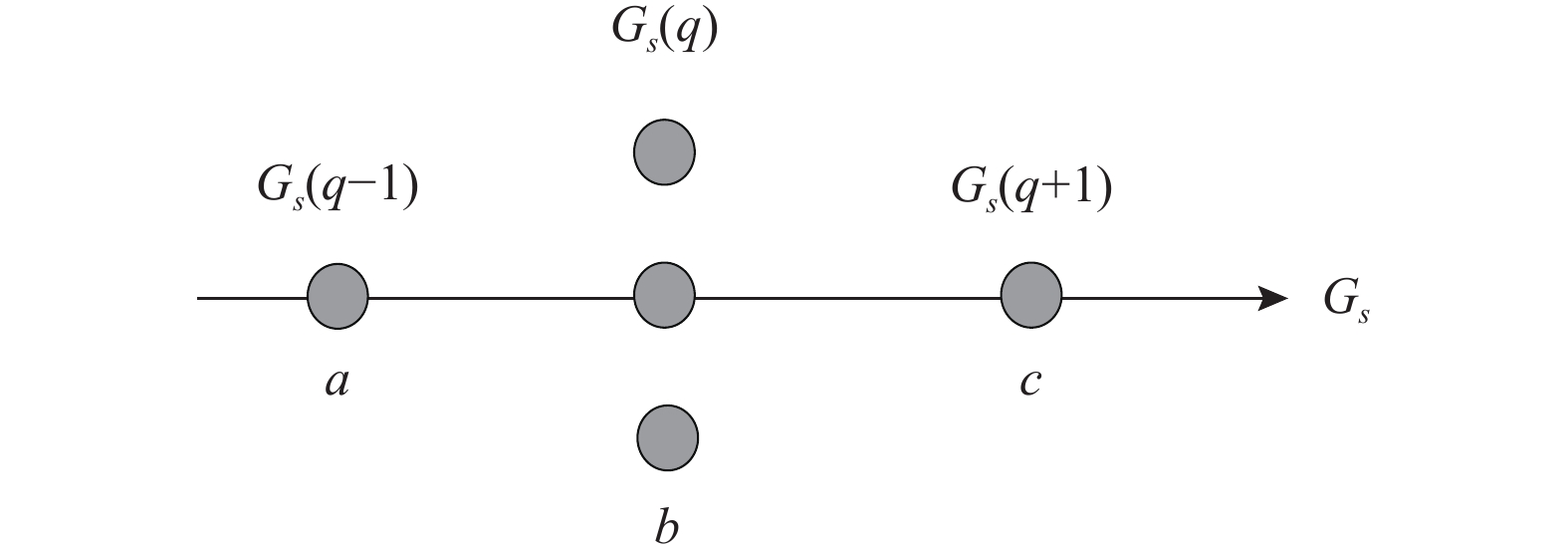
式(11)中,Gs为第s个目标函数;Gs(q)为染色体q在坐标轴上的投影点;n为坐标轴上值等于Gs(q)的投影点的个数;Gs(q-1)是坐标轴上距离Gs(q)最近且目标函数值比Gs(q)小的投影点;Gs(q+1)是坐标轴上距离Gs(q)最近且目标函数值比Gs(q)大的投影点。INSGA-III中拥挤距离计算如图4和图5所示。
|
图 4 空间点向坐标轴投影示意图 Fig. 4 An illustration of spatial points being projected to the axis |
|
图 5 投影点的拥挤距离计算示意图 Fig. 5 An illustration of crowded distance calculation for the projection point |
图4中个体A、B和C处于同一级Pareto前沿面中,将A、B和C分别向3个坐标轴做投影。图5显示的是计算投影点基于小生境的拥挤距离的示意图。
2.3 交叉和变异算子交叉和变异算子用于对父代种群的染色体进行小规模的变动,以寻求种群在目标函数上的突破。
1) 交叉算子。
为模拟生物进化过程中的交配环节,将交叉算子作用于已经完成非支配排序的种群。种群进行交叉时将采用锦标赛选择机制,交叉过的个体不再重复交叉。交叉操作后形成两个新个体,将父代基因有保留地继承下来,达到了染色体小范围突变的效果。父体和母体的染色体交叉具体过程为:随机产生两个不同的病人编号范围内的整数基因,记为g1和g2;保持父体基因序列中g1和g2的位置和顺序不变,其他位置用母体中除去g1和g2之外的基因依次填补,同时交换父体和母体的第1个基因,再用同样的方式操作母体便得到2个全新的后代。
2) 变异算子。
为模拟生物进化过程中个体基因变异,将变异算子作用于群体。有变异资格的父代经过变异操作后形成了全新的子代,并将父代的基因有保留地继承了下来,达到了染色体小范围突变的效果。基因变异具体过程为:随机选取2个不同的有效范围内的整数基因,记为g3和g4;保持染色体中第1个基因不变,交换g3和g4这2个变异基因在染色体中的位置,便形成一个新个体。
2.4 选择算子和自适应机制1) 选择算子。
选择算子用于挑选种群中优秀的个体进入下一代。选择算子是保证INSGA-Ⅲ顺利进行并使最后的非支配解集具有说服力的关键。若选择算子使种群数量持续上升,这将降低算法的运行速度和可行性;若选择算子使种群数量越来越少,虽然算法的运行速度得到了提升,但种群数量过少会导致最后的非支配解集缺乏说服力。选择算子的具体操作细节如下。
(1) 选择算子采用精英策略,即保留父代中的优良个体直接进入子代。采用的方法是将完整的父代和子代融合成一个大种群,根据对合并后的大种群进行非支配排序的结果,依照非支配排序结果越好的个体被优先选取的原则,产生下一代的种群。
(2) 为了增强种群分布多样性,算法中采用了种群染色体唯一策略(population chromosome unique policy, PCUP),即种群中拥有完全相同染色体的个体在选择过程中最多只有一个能被选择进入下一代。
(3) 设定环境最大容纳量为Popsize,当种群数量大于Popsize时,选择非支配排序结果的前Popsize个个体进入下一代,否则保持当前个体数量。
2) 自适应机制。
考虑到算法迭代到一定次数后易陷入局部最优,在保证非支配排序较优的个体以较高的概率进行交叉和变异的同时,还需要提高排序结果较差的个体进行交叉和变异操作的概率。因此,针对种群的非支配排序情况,随着算法迭代过程的进行,需要以一定的概率对个体自适应地进行交叉和变异操作,如式(12)和(13)所示。
|
${\text{交叉}}:\;\;p = \left\{ {\begin{array}{*{20}{c}}{{k_1} \times {{({\rm{Popnum}} - {\rm{ns}})} / {{\rm{Popnum}}}},\;\;\;{\rm{ns}} < K;}\!\!\!\!\! \\[5pt]\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{p_1},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ns}} {\text{≥}} K{\text{且}}g {\text{≥}} G{\text{。}}}\end{array}} \right.$
|
(12) |
|
${\text{变异}}:\;\;p = \left\{ {\begin{array}{*{20}{c}}{{k_2} \times {{({\rm{Popnum}} - {\rm{ns}})} / {{\rm{Popnum}}}},\;\;{\rm{ns}} < K;}\!\!\!\!\! \\[5pt]\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{p_2},\quad\quad\quad\quad\quad {\rm{ns}} {\text{≥}} K{\text{且}}g {\text{≥}}G.}\end{array}} \right.$
|
(13) |
其中,Popnum为当前种群的个体数量;ns为个体在种群中的非支配排序序数;K为非支配排序常量;g为进化代数变量;G为进化代数常量;p1、p2为概率常量,k1、k2为概率系数常量。
群体P(g)经过上述算子后得到下一代群体P(g+1)。
3 仿真实验及分析 3.1 实验设计为验证所提算法的有效性,针对某三甲医院外科某日手术排程问题,运用本文所提出的方法进行模型构建和求解。具体手术相关信息如表1~表3所示。表1为患者手术信息。表2所列数据是根据医院历史手术时间数据库,并结合患者病情、医生意见以及统计学知识综合得到的术前准备时间二维表[P],可根据每场手术的前序手术类型确定其术前准备时间,其中Tnext表示下一场手术类型,Tprevious表示上一场手术类型,该科室共能处理7种类型的手术。表3是与病人手术类型有关的术后观察所用时间表。
| 表 1 患者手术信息 Tab. 1 Surgery information of patients |
| 表 2 术前准备时间二维表[P] Tab. 2 [P]: Two-dimensional table of preoperative preparation time |
| 表 3 术后观察时间表[O] Tab. 3 [O]: Postoperative observation time information |
为了使算法性能达到最优,数值实验中对所涉及参数进行了调优,确定具体取值:最大进化代数Maxgen为300,当前环境最大容纳个体数量Popsize为200,交叉率计算参数k1为0.65,变异率计算参数k2为0.65,进化代数常量G为200,非支配排序常量K为150,概率常量p1为0.5、p2为0.5,手术室数量M为12。多次运行后得到的较优仿真结果如图6和图7所示。
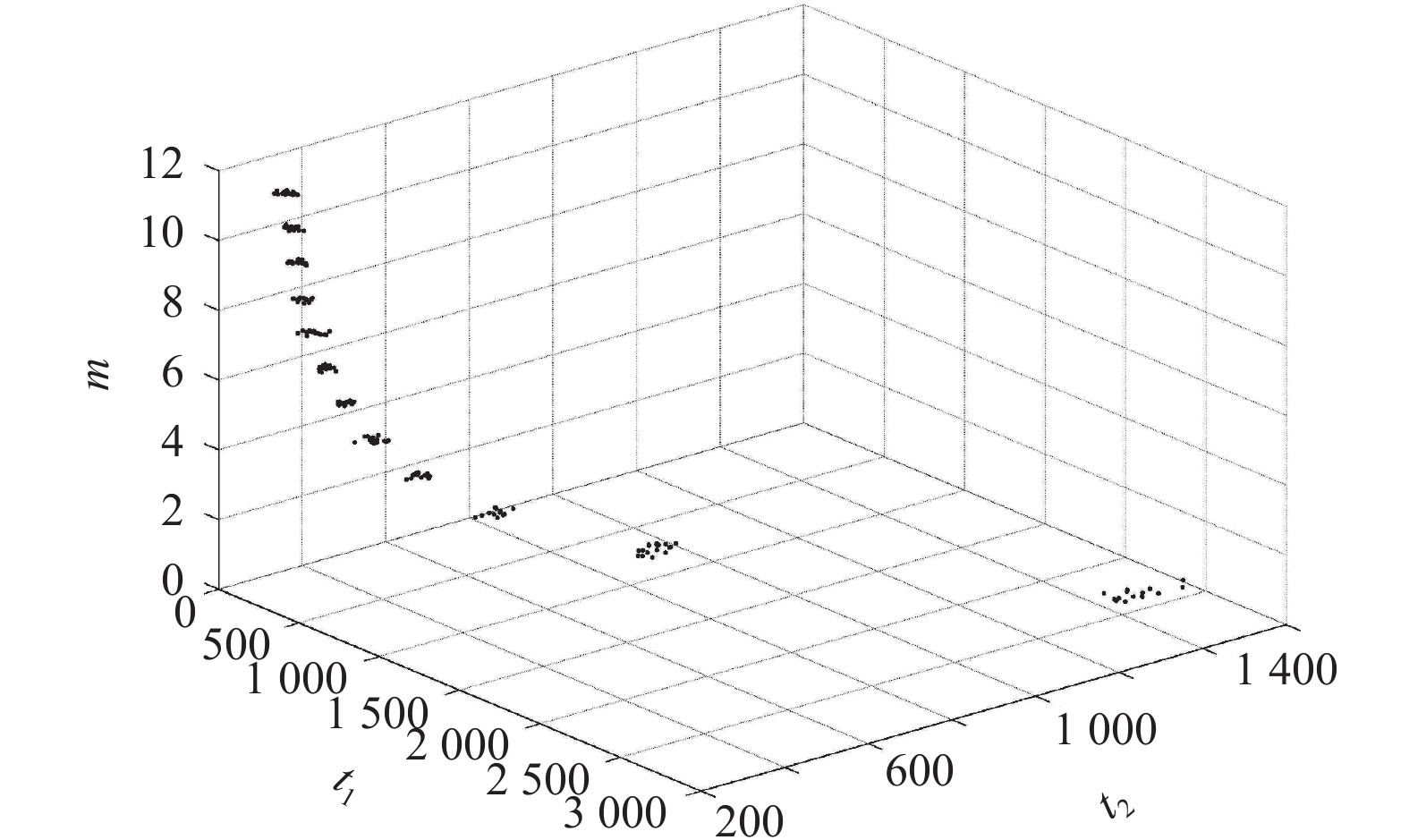
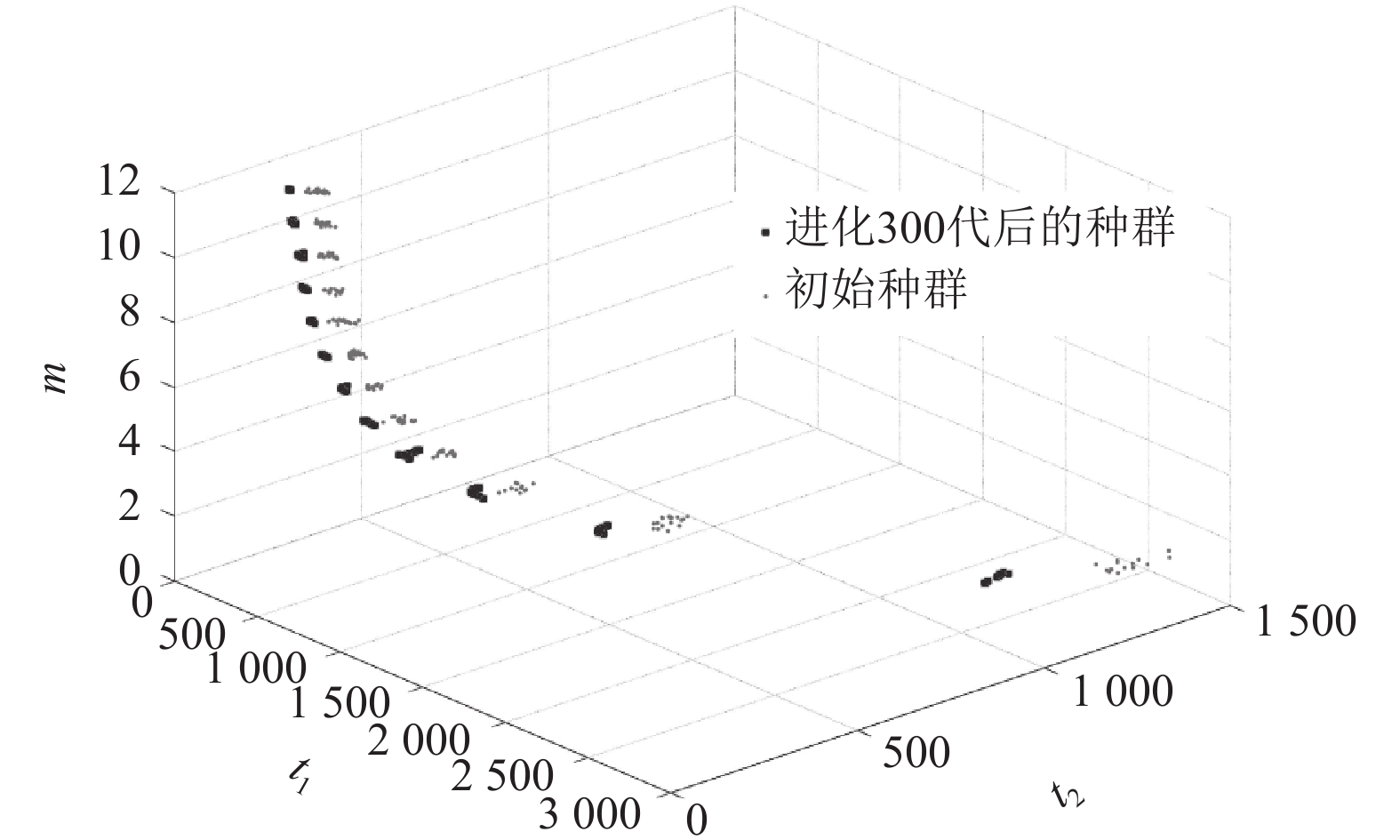
图6所示为依据病人手术信息和手术室数量随机生成的初始种群P(g=0),可以看出完成所有手术过程最长时间t1和平均时间t2随着开启的手术室数量m的增加而呈现减少的趋势,由此验证了开启更多手术室能减少医护人员的工作时间和病人的等待时间,提升了医患满意度但同时增加了手术成本;图7展示的是初始种群多次进化300代之后出现的最优结果,与初始种群对比分析可知,进化后的种群与初始种群同样较为均匀地分布在每一层上,进化后的种群在每一层上的目标函数值t1和t2较初始种群得到了更好的优化结果,大幅降低了完成手术过程的总时间和平均时间。调度管理者可以权衡目标函数值t1、t2和m并在多次进化后的种群中选择非支配解作为手术排程方案。同开启全部手术室的手术排程方式(m=M)相比,实验结果得到的开启最少数量手术室的手术排程方案可以有效地为医院节省手术成本。
|
图 6 初始种群P(g=0) Fig. 6 Initial population P(g=0) |
|
图 7 初始种群P(g=0)及其进化300代之后的种群P(g=300) Fig. 7 Initial population and evolution after 300 generations |
1)算法收敛性分析。
世代距离(GD)对应解空间中真正的Pareto前沿(PFtrue)和一个已知的Pareto前沿(PFknown)之间的距离,常被用来衡量遗传算法的收敛性,其度量公式如下:
|
$\quad\quad{\rm{GD}} = {\left( {\frac{1}{u}\sum\limits_{v = 1}^u {d_v^2} } \right)^{\frac{1}{2}}}{\text{。}}$
|
(14) |
其中,u是PFknown中成员数目;dv是目标空间中成员v和它最近的PFtrue中的成员之间的欧氏距离;GD值越小表明已知的Pareto前沿越接近真实的Pareto前沿,算法的收敛性越好[13]。
表4中给出了使用INSGA-III与传统的NSGA-III 2种方法下的3组实验数据,每组实验分别运行50次。从计算结果可以看出,使用INSGA-III方法优化后的种群GD值不同程度地小于使用传统NSGA-III方法优化得到的种群GD值,可知INSGA-III算法收敛性优于传统NSGA-III。同时,3组实验中的GD值变异系数表明INSGA-III的计算结果具有良好的稳定性。
| 表 4 不同方法和规模下种群的GD值对比 Tab. 4 Comparison of GD values for different methods and populations |
2)种群多样性分析。
由于父代种群的多样性直接影响到子代种群的多样性,而种群多样性高的算法有利于避免计算结果陷入局部最优。此外,Pareto前沿的多样性直接关系到决策集的范围,而决策集范围越广表明解决问题时的灵活性越高,因此验证算法效果时有必要对种群多样性进行分析。为了提高种群多样性,本文所提的INSGA-III方法采取了种群染色体唯一策略(PCUP)并且改进了传统NSGA-III的拥挤距离计算算子。在基于相同的交叉和变异算子以及初始种群数量的情况下,比较执行PCUP的种群Pareto前沿和不执行PCUP的种群Pareto前沿。
HyperVolume(HV)值是Pareto前沿与参考点所围成的面积,HVR是相对同一参考点的Pareto前沿HV值与最大的HV值的比率,HVR值的计算公式如式(15)所示,HVR越大表明Pareto前沿的多样性越好[14]。
|
$\qquad{\rm{HVR}} = \frac{{{\rm{HV}}(W)}}{{{\rm{HV}}({W_{\max }})}}{\text{。}}$
|
(15) |
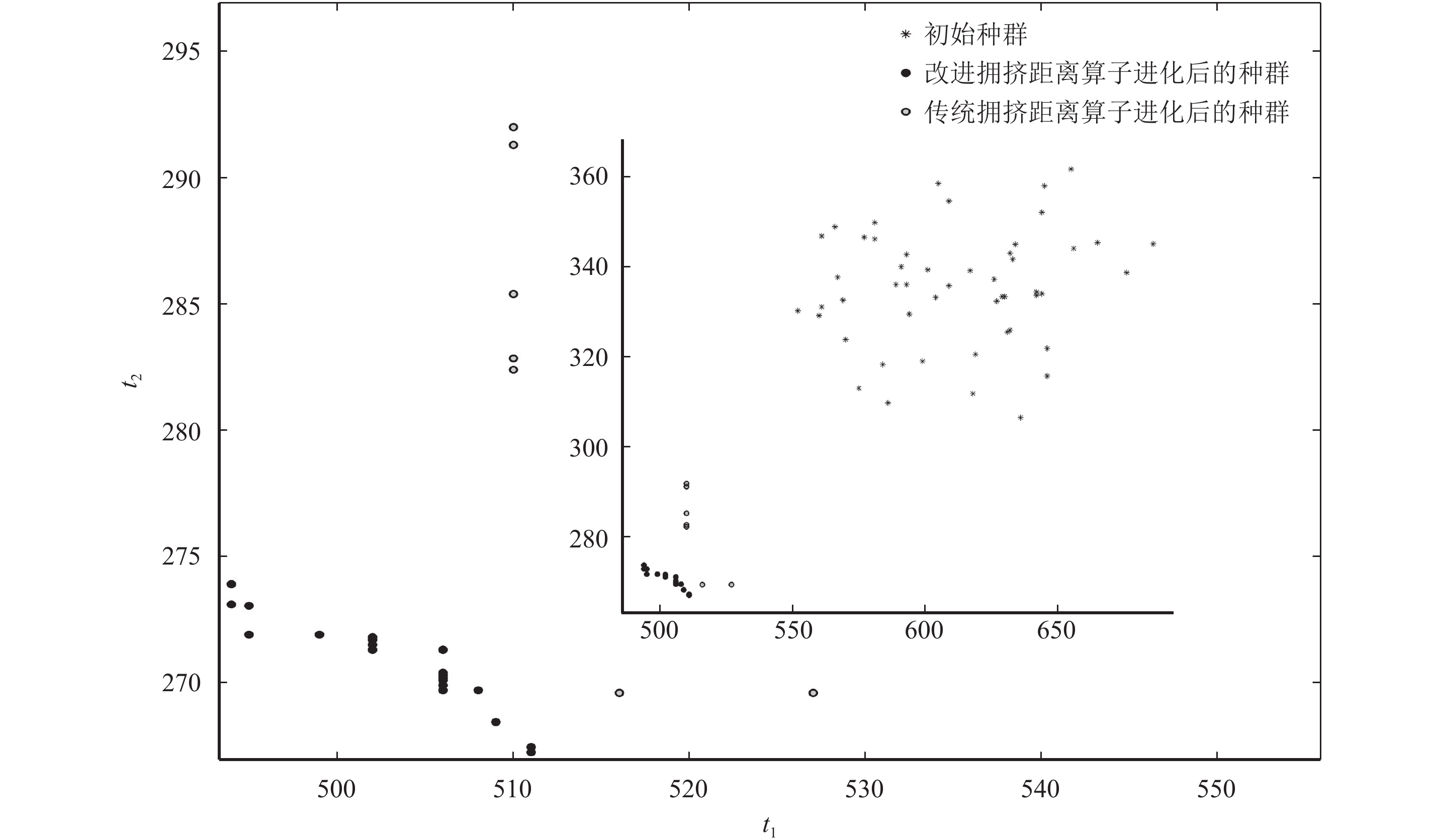
分别设置开启手术室数量(m)和患者数量(N)不同的3组算例,每组连续计算50次得到的结果如表5所示:当Popsize充分大且相同时,各组算例中执行PCUP的种群Pareto前沿上染色体不同的个体数(N1)和目标函数值不同的个体数(N2)均不同程度地多于不执行PCUP的种群Pareto前沿的相应指标;并且,执行PUCP的种群Pareto前沿的HVR平均值明显高于不执行PUCP的种群Pareto前沿。以上实验结果表明执行PCUP提高了种群多样性,避免了算法陷入局部最优。另外,图8所示是采用不同拥挤距离计算算子进行二维目标优化后的种群对比图,与传统NSGA-III中拥挤距离计算算子相比,改进的拥挤距离计算算子使得进化后的种群在目标空间中分布更加分散,体现出更高的种群多样性。
| 表 5 执行PCUP和未执行PCUP的Pareto前沿性能指标对比 Tab. 5 Comparison of Pareto front performance while using PCUP and not |
|
图 8 2种不同拥挤距离计算算子下的种群局部放大图 Fig. 8 Population magnification under two different crowded distance calculators |
手术室调度问题是当代医疗运作管理中的一类非常重要的资源调度问题。本文在考虑时间、人员、空间等相关医疗资源约束的前提下,建立了以提升医患满意度与降低运作成本为目标的手术排程问题优化模型,并设计了INSGA-III算法进行问题求解。该算法中引入了自适应机制和精英策略,以及改进的拥挤距离算子和种群染色体唯一策略。数值实验中通过对某三甲医院某日的手术安排进行排程,验证了所提出的多资源约束下考虑医患满意度和手术成本的手术排程方法的可行性和有效性。
本文接下来将从以下方面对研究工作进行拓展,其中包括引入数据分析技术进行数据驱动下的医疗手术排程方法研究;探索排程方法在面对紧急情况时再调度的能力;考虑手术过程中普遍存在的不确定因素,进行动态手术排程方法研究。
| [1] |
PHAM D N, KLINKERT A. Surgical case scheduling as a generalized job shop scheduling problem[J].
European Journal of Operational Research, 2008, 185(3): 1011-1025.
DOI: 10.1016/j.ejor.2006.03.059. |
| [2] |
LAMIRI M, XIE X, DOLGUI A. A stochastic model for operating room planning with elective and emergency demand for surgery[J].
European Journal of Operational Research, 2008, 185(3): 1026-1037.
DOI: 10.1016/j.ejor.2006.02.057. |
| [3] |
HEYDARI M, SOUDI A. Predictive/reactive planning and scheduling of a surgical suite with emergency patient arrival[J].
Journal of medical systems, 2016, 40(1): 1-9.
DOI: 10.1007/s10916-015-0365-5. |
| [4] |
SAMUDRA M, VAN RIET C, DEMEULEMEESTER E. Scheduling operating rooms: achievements, challenges and pitfalls[J].
Journal of Scheduling, 2016, 19(5): 493-525.
DOI: 10.1007/s10951-016-0489-6. |
| [5] |
HSU V N, DE MATTA R, LEE C Y. Scheduling patients in an ambulatory surgical center[J].
Naval Research Logistics, 2003, 50(3): 218-238.
DOI: 10.1002/(ISSN)1520-6750. |
| [6] |
ROLAND B, DI MARTINELLY C, RIANE F. Scheduling an operating theatre under human resource constraints[J].
Computers & Industrial Engineering, 2010, 58(2): 212-220.
|
| [7] |
朱悦, 张玉林, 宋旼珊. 考虑手术间及医疗团队间准备时间的手术分配排程[J].
东南大学学报 (自然科学版), 2015, 45(6): 1218-1222.
ZHU Yue, ZHANG Yulin, SONG Minshan. Surgical scheduling considering setup time between surgeries and setup time between surgical teams[J]. Journal of Southeast University (Natural Science Edition), 2015, 45(6): 1218-1222. |
| [8] |
HEALTH CARE FINANCIAL MANAGEMENT ASSOCIATION. Achieving operating room efficiency through process integration[R/OL]. (2003-03). https://www.ncbi.nlm.nih.gov/pubmed/12793445.
|
| [9] |
LI F, GUPTA D, POTTHOFF S. Improving operating room schedules[J].
Health Care Management Science, 2016, 19(3): 261-278.
DOI: 10.1007/s10729-015-9318-2. |
| [10] |
LEBOWITZ P. Schedule the short procedure first to improve or efficiency[J].
AORN Journal, 2003, 78(4): 657-659.
|
| [11] |
WANG D, LIU F, YIN Y. Prioritized surgery scheduling in face of surgeon tiredness and fixed off-duty period[J].
Journal of Combinatorial Optimization, 2015, 30(4): 967-981.
DOI: 10.1007/s10878-015-9846-1. |
| [12] |
邓富民, 梁学栋, 刘爱军, 等. 多资源约束下改进NSGA-II算法的手术调度[J].
系统工程理论与实践, 2012, 32(6): 1337-1345.
DENG Fumin, LIANG Xuedong, LIU Aijun. Surgical operation scheduling with mufti-resource constrained based on the improved NSGA-II algorithm[J]. System Engineering Theory and Practice, 2012, 32(6): 1337-1345. DOI: 10.12011/1000-6788(2012)6-1337. |
| [13] |
DONOHO D L. For most large underdetermined systems of linear equations the minimal L1-norm solution is also the sparsest solution[J].
Communications on Pure and Applied Mathematics, 2006, 59(6): 797-829.
DOI: 10.1002/(ISSN)1097-0312. |
| [14] |
WAGNER F, KLÖPPER B, ISHIKAWA F, et al. Towards robust service compositions in the context of functionally diverse services[C/OL]. (2012-04-16). http://dl.acm.org/citation.cfm?id=2187966.
|
 2017, Vol. 20
2017, Vol. 20