随着互联网的普及,越来越多的人选择网上购物和电子商务模式进行交易,快递物流行业也因此飞速发展。快递车辆作为物流企业管理系统中的关键要素,其优化调度显得至关重要。通过制定科学合理的快递车辆调度方案,能够有效地达到提升客户满意度,降低企业运输成本等目的,从而提高企业市场竞争力。
目前,大量学者针对快递车辆的优化调度问题,主要从节约运输成本、提高算法效率等方面进行深入研究,已取得较多研究成果[1-5]。Chang等[1]提出了一种多目标分散搜索框架,为快递物流企业提供了降低运输成本、提高服务水平的决策依据;Janssens等[2]将服务对象划分为不同的区域,并在每个区域设置仓库,进而简化车辆调度问题;Damon等[5]考虑物流系统中有多个仓库的情况,建立了整数规划模型,并通过实例验证其研究能够缩短运输距离。
上述文献都对快递车辆优化调度问题作了非常有意义的探索。但是快递物流系统是一个典型的基于人的服务系统,包含了客户、物流企业管理者、配送人员等多个行为主体。企业除了考虑降低成本之外,更应关注人的因素。目前从客户为行为主体的角度考虑的研究相对较少[6-9]。于宝琴等[6]结合物流服务理论与系统动力学理论,以物流服务质量下配送及时率为附属变量,建立系统动力学模型;McNabb等[7]考虑交货时间窗,建立基于蚁群算法的快递车辆调度模型,达到了减小客户等待时间的目的;Salani等[9]考虑客户满意时间窗及车辆容量限制,构建了以最小化运输成本为目标函数的混合整数规划模型。以上研究都提到,在快件物品运输中,要关注快件到达的时效性,即送达时间最好在客户满意的时间窗之内,但是受个人偏好(如心理期盼程度)、时间安排等因素影响,每个人对期望服务时间窗表现出个体差异,不同客户对等待时间的感知也不尽相同。
基于此,本文将从客户为行为主体的角度出发,结合现实情境及认知心理学分析客户对等待时间的感知,并在前景理论中融入模糊理论,构建客户等待时间感知满意度函数,完善快递车辆调度模型;最后采用参数设置简单、调度运算性能较高的模拟植物生长算法对快递车辆进行调度,以达到提高客户满意度和降低运输成本的目的。
1 基于客户等待时间感知分析的满意度函数构建客户是需求主体,具有各自的行为,且个体差异较为明显,因此对等待时间的感知很大程度上是不一样的。结合现实情境及认知心理学分析客户对等待时间的感知,能够在构建满意度函数方面产生一定意义。通过调查发现,目前大部分网购物流模式为:客户下单—商家出货—配送中心1……配送中心n—客户点(例如菜鸟驿站)—客户,本文正是基于与客户密切相关的“配送中心n—客户点”这一环节来展开研究。
1.1 客户等待时间感知分析1) 等待时间越短越满意。
物品到达客户点后,客户会根据自身情况选择取件时间,通常配送车辆越早将物品送到客户点,客户等待时间越短,便拥有较多的时间进行协调。例如上班族希望在上班时间内尽快收到取件通知,而不希望下班回家后才收到,因为这样可以提早安排亲人代取或者在回家路上顺道取物品,避免折返。
2) 临界值不同。
每位客户具有不同的个人偏好,因此客户期望服务时间窗和容忍服务时间窗的临界值存在差异。例如,从心理期盼程度来看,客户对物品的喜欢程度越高,心理期盼就越强,更希望快递物品尽快达到,此时客户期望、容忍服务时间窗较早;物品越贵重,客户更希望它越快送达,省去途中丢失或损坏的担忧,但同时又担忧太快会损坏物品,在这种情况下,客户的风险偏好不同,期望、容忍服务时间窗也不同。
3) 非线性。
客户每接受一次取件服务,便会对等待时间进行感知,从而产生对本次服务的满意度。通过调查发现,客户满意度随等待时间的变化不是完全线性,而是非线性曲线。
4) 边际递减。
等待时间越长,客户感知越麻木,满意度体现为边际递减。
5) 损失规避。
满意度值为正表示满意,为负表示不满意,两者在相同等待时间取值区间内,客户不满意较满意的感知更为敏感,客户更讨厌损失。
1.2 构建客户等待时间感知满意度函数通过以上分析可知,客户对等待时间的感知个体差异较大,且感知是人的主观感受和认知的结果,是基于人的非完全理性[10]。客户作为行为主体,其基本行为特征表现为有限理性。Kahneman等[11-12]提出的前景理论涉及行为科学和心理学,能够很好地描述客户对等待时间感知的有限理性行为。但它是一种描述性模式的决策分析模型,缺少数学理论的支撑,不能对行为的不确定性进行度量。模糊理论能够对人行为的不确定性进行数学性地刻画,但不能准确地描述人的行为特征。基于此,本文试图在前景理论中融入模糊理论,以前景理论中的价值函数对客户感知满意度曲线进行刻画,然后采用模糊隶属度函数进行量化处理,从而构建客户等待时间感知满意度函数。
1) 基于前景理论的价值函数。
等待时间作为客户的关注点,每个客户都会对其产生一个主观感受的满意度或价值,用前景理论来描述人对损失和收获的不同敏感程度,价值函数模型为:
|
$\quad\quad v\left( x \right) = \left\{ \begin{array}{l}{\left( x \right)^\alpha },\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm if}\;x {\text{≥}} 0;\\ - \lambda \cdot {\left( { - x} \right)^\beta },\;\;\;\;\;{\rm if}\;x {\text{<}} 0{\text{。}}\end{array} \right.$
|
(1) |
其中,α表示收益系数,β表示损失系数,它们能够显示价值幂函数的凹凸程度;α,β<1表示客户对待收益和损失是边际递减的;系数λ>1表示客户对待损失比收益更敏感,更不希望出现损失。其曲线如图1所示。
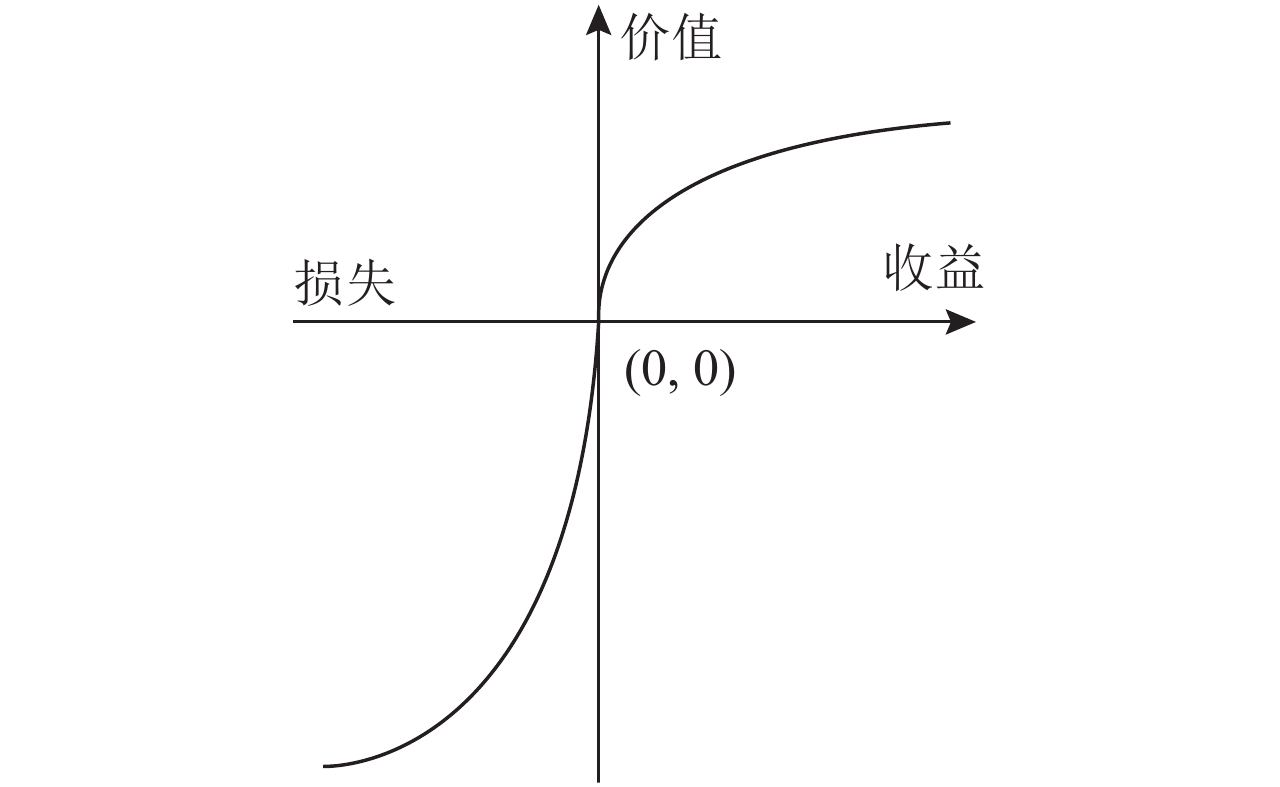
|
图 1 价值函数曲线 Fig. 1 The value function curve |
2) 选择参考点。
参考点的选取是前景理论的核心:一方面,前景理论用价值函数值表示客户主观感受的价值,在客户决策的初始阶段会选择一个参考点,通常将价值为0的点作为参考点,后果值的盈亏变化都是相对于这个参考点而言;另一方面,选取的基准比较对象(即参考点)不同,同样的等待时间对于不同客户的感知也不一样,因此需要在模型中体现个性化差异(个人偏好)。
结合实际,当实际等待时间处于客户容忍服务时间窗之内时,客户满意度为收益;当实际等待时间处于容忍服务时间窗之外时,满意度为损失。因此,本文将参考点定义为客户容忍的最晚服务时间
3) 确定客户感知满意度函数。
结合现实情景及前景理论中的价值函数来刻画客户对等待时间的感知为:每个客户对等待时间感知的界定有两个基本时间窗,心理最期望的服务时间窗
与此同时,客户对事件的感知是模糊的,例如:实际等待时间、时间临界值等。因此,为量化客户的实际心理感知,本文采用模糊理论中对时间模糊化处理的方法来刻画,并定义感知满意度函数(y轴)为客户实际等待时间(x轴)的模糊隶属度函数,为方便度量,令隶属度为1。得到客户对等待时间的感知满意度函数,以及满意度曲线(图2中,
|
$S(d_i^e) = \left\{ \begin{array}{l}1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\,\;{\rm if}\;d_i^e \in [{\rm ET}_i^e,{\rm LT}_i^e);\\[8pt]{\left(\displaystyle\frac{{{\rm ELT}_i^e - d_i^e}}{{{\rm ELT}_i^e - {\rm LT}_i^e}}\right)^\alpha },\;\;\;\,\,\;\;\;\;\;\;{\rm if}\;d_i^e \in [{\rm LT}_i^e,{\rm ELT}_i^e);\\[10pt]0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\;\;\;\;\;{\rm if}\;d_i^e = {\rm ELT}_i^e;\\[8pt] - \lambda {\left(\displaystyle\frac{{d_i^e - {\rm ELT}_i^e}}{{{T_2} - {\rm ELT}_i^e}}\right)^\beta, }\;\;\;\;\;\;\;{\rm if}\;d_i^e \in ({\rm ELT}_i^e,{T_2}]{\text{。}}\end{array} \right.$
|
(2) |
其中,
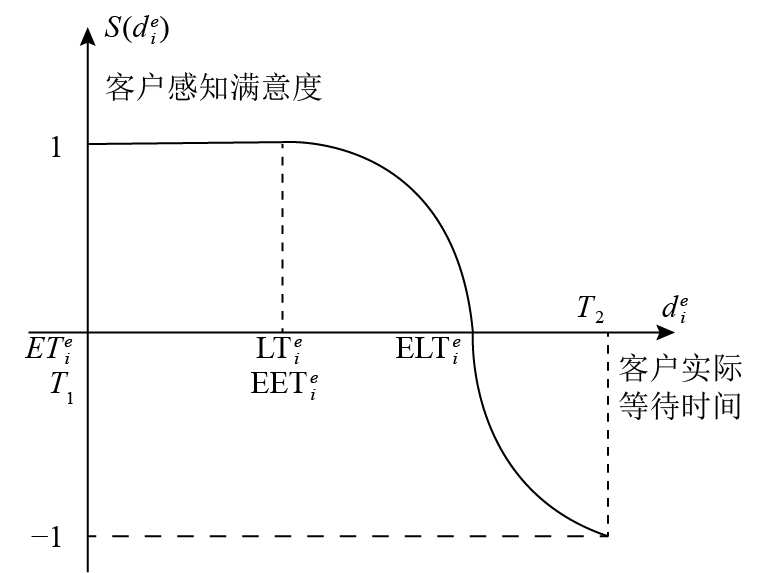
|
图 2 客户等待时间感知满意度曲线 Fig. 2 The agents’ perception satisfaction curve toward waiting time |
快递公司从一个配送中心向若干个客户点配送快递,配送中心拥有若干辆快递车辆。车辆以配送中心作为路程起点,将装载的快件运送到指定客户点,并揽收退回或寄出的快件后,回到配送中心。运用调度知识,“零件”为快递车辆,“机器”为各个客户点,各个客户点的快件配送任务看作“零件”经过预定路线在“机器”上加工。因此,可将快递车辆调度问题描述为加工车间调度问题。
2.1.2 任务特征和约束(β域)快递车辆从配送中心出发,对客户点服务完后,必须返回配送中心;为保证成本,每辆车装载的快件不止满足一个客户点,可以为一条路线上的多个客户点配送,同时为保证配送准确性,每个客户点的快件只能由一辆车配送;由于每辆车具有一定的容量限制,因此所服务的客户点快件数之和不能超过它的载重;车辆到达客户点的时间、客户的容忍时间在客户点的工作时间窗之内。
2.1.3 调度目标(γ域)快递物流系统是一个典型的基于人的服务系统,需要考虑客户的因素,以最大化平均等待时间感知满意度
m表示将服务的客户点总数,i,i*表示任意一个客户点,取值范围i,i*∈[0, m],其中i=0表示配送中心;n表示接受任务的车辆总数,j表示任意一辆快递车辆,取值范围j∈[1, n];
|
$\begin{array}{l}\qquad {x_{i{i^*}j}} = \left\{ \begin{array}{l}1,\;\;\;\;\;{\text{车辆}}j{\text{从客户点}}i{\text{开向客户点}}{i^*};\\0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{其他}}{\text{。}}\end{array} \right.\\ \qquad {y_{ij}} = \left\{ \begin{array}{l}1,\;\;\;\;\;\;{\text{客户点}}i{\text{由车辆}}j{\text{服务}};\\0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{其他}}{\text{。}}\end{array} \right.\end{array}$
|
假设1:快递车辆在运行线路上的行驶速度处处相等;
假设2:快递车辆的规格和型号相同,装载能力相同;
假设3:每个客户点具有相同的最早最晚工作时间窗;
假设4:客户收到取件通知后,可选择当天去取件或不取,这两种情况下客户的感知满意度是相同的。
2.4 模型建立综上所述,建立快递车辆的调度数学模型如下。
|
$\quad\quad \max \;{\theta _1}\overline S (d_i^e) - {\theta _2}s,$
|
(3) |
|
$\quad\quad \overline S (d_i^e) = \sum\limits_{i = 1}^m {\sum\limits_{e = 1}^{q_i^1} {S(d_i^e)} } \times {(\sum\limits_{i = 1}^m {q_i^1} )^{ - 1}},$
|
(4) |
|
$\quad\quad s = \sum\limits_{i = 0}^m {\sum\limits_{{i^{\rm{*}}} = 0}^m {\sum\limits_{j = 1}^n {{s_{i{i'}}}} } } {x_{i{i^{\rm{*}}}j}}{\text{。}}$
|
(5) |
|
$\quad\quad {\rm s.t.}\;\sum\limits_{j = 1}^n {{y_{0j}}} = n;$
|
(6) |
|
$\quad\quad \sum\limits_{i = 1}^m {{x_{i0j}}} = 1,\;\;\;\;j \in \left[ {1,\;n} \right];$
|
(7) |
|
$\quad\quad \sum\limits_{j = 1}^n {{y_{ij}}} = 1,\;\;\;\;i \in \left[ {1,\;m} \right];$
|
(8) |
|
$\quad\quad \sum\limits_{i = 1}^m {q_i^1{y_{ij}}} {\text{≤}} Q,\;\;\;\;j \in \left[ {1,\;n} \right];$
|
(9) |
|
$\quad\quad {T_1} {\text{≤}} {r_{ij}},{\rm ELT}_i^e {\text{≤}} {T_2};$
|
(10) |
|
$\sum\limits_{j = 1}^n\! {\sum\limits_{i = 0}^m \!\!{{x_{i{i^*}j}}} } \left[{r_{ij}} + (q_i^1 + q_i^2)t + {t_0} \!\!+\! \frac{{{s_{i{i^*}}}}}{v}\right]\!\! = {r_{{i^*}j}},\;{i^*} \!\!\in [1,m];$
|
(11) |
|
$\quad\quad d_i^e = {r_{ij}} \theta, \;\;\;\;\;i \in [1,m];j \in [1,n];e \in [1,q_i^1];$
|
(12) |
|
$\quad\quad {x_{i{i^{\rm{*}}}j}} = {\rm{\{ 0,1\} }},\;\;\;\;\;\;\;i,{i^*} \in [0,m];j \in [1,n];$
|
(13) |
|
$\quad\quad{y_{ij}} = \{ 0,1\}, \;\;\;\;\;\;\;\;i \in [0,m];j \in [1,n]{\text{。}}$
|
(14) |
模型中,式(3)为目标函数,式(4)确定客户平均等待时间感知满意度,式(5)确定总运输里程。式(6)~式(10)为约束条件,其中,式(6)限制每辆车只能将配送中心作为出发点;式(7)限制车辆将快件配送完后,必须回到配送中心;式(8)限制每个客户点只能由一辆车服务,且所有客户点的配送需求都能被满足;式(9)限制每辆车所服务的客户点快件数之和不超过载重;式(10)限制车辆到达客户点的时间、客户容忍时间在客户点工作时间窗之内;式(11)定量化车辆j到达客户点i*的时间;式(12)确定客户点i上第e位客户的实际等待时间;式(13)~(14)为决策变量取值。
3 调度算法设计模拟植物生长算法(PGSA)是源于大自然植物生长机理,所产生的一种仿生类智能搜索算法。相较于传统的遗传算法(GA)、粒子群算法(PSO)、模拟退火算法(SA),其优点在于运行它所需设定的参数较少,寻找解时具有较好的全局搜索性能以及较好的收敛性、精确度。它将调度问题规划模型的可行域当作植物在生长过程中的生长环境,通过对当前调度可行解(植物生长点)施加选择、生长等一系列操作,从而产生新的可行解,并逐步向最优解转变。目前,该算法主要用于工程技术领域[13-14],在交通运输网络布局以及车辆调度领域运用较少[15]。算法设计步骤如下。
Step1:确定初始生长点集。初始生长点即树根,用于模拟植物生长的位置点。为满足约束条件(6)~(10),采用如下编码方式:首先将m个数字(客户点)随机排列,然后在满足载容量、时间窗约束条件下,将0插入随机排列的数字中,从而形成多个闭合的配送路径。例如:码串“0, 3, 5, 2, 0, 6, 4, 0, 1, 8, 0, 7, 9, 0”表示有9个客户点,4辆车完成任务,每辆车的配送路径分别为“0, 3, 5, 2, 0”、“0, 6, 4, 0”、“0, 1, 8, 0”、“0, 7, 9, 0”。按照此种方式,产生30组排列数字,得到初始生长点集合
Step2:计算目标函数值。在生长点集之中,dk表示任意生长点,求
Step3:计算各生长点的形态素浓度。形态素浓度用于确定植物系统现有生长点集合中进行优先生长的点,并确保现有生长点最终向最优生长点蔓延。结合问题目标,生长点dk所对应形态素浓度Dk的计算方式为
|
$\quad\quad {D_k} = \frac{{f({d_k})}}{{\sum {f({d_k})} }}{\text{。}}$
|
(15) |
在多个生长点所构成的可行解集之中,令每个生长点所对应的形态素浓度值的总和为1,即
Step4:寻找优先生长点。计算机产生[0, 1]的随机数α,α落入形态素浓度在[0, 1]概率空间模型的某一空间内,所对应的生长点就能够优先生长,从而选出本次迭代的生长点。
Step5:求出新的生长点。在外界环境刺激(光照) 下,优先生长点通过系统生长,不断产生新的生长点。对优先生长点进行2N次邻域搜索,剔除重复、不满足载容量、时间窗约束条件的新生长点。
Step6:保留最好的生长点。计算新生长点的目标函数值,将其与f(x0)进行比较,如果函数值小于f(x0),则剔除这个新生长点;如果函数值大于f(x0),则保留,并入待生长点集。与此同时,在新生长点中选出具有最大目标函数值的点,与fmax(xmax)进行比较,若这个值大于fmax(xmax),则置换xmax和fmax(xmax);若这个值小于fmax(xmax),则保留原来的最优值。
Step7:重复上述步骤Step3~Step6,直到没有新的生长点产生或达到迭代次数,输出最优解。
4 实例仿真为验证模型及算法的有效性,以成都市某快递物流公司为例进行实例仿真。配送中心的地理坐标为(44,25),调查区域内共有12个客户点,用欧氏距离表示客户点之间的距离,已知各客户点的需求量、揽收量,客户点详细信息见表1;客户点的最早最晚工作时间窗为[9:00-19:00],以min换算为[0, 600];客户点i第e位客户的时间窗表示为
为了进一步分析模拟植物生长算法的性能,将其与节约里程算法进行比较(节约里程算法普遍用于车辆配送路径问题求解[16])。采用Matlab软件编程实现上述两种算法,在Samsung主频1000 MHz的硬件平台下运行,得到快递车辆调度方案(表2)。
| 表 1 客户点详细信息 Tab. 1 The details of agents |
| 表 2 快递车辆调度方案 Tab. 2 The delivery vehicle scheduling |
表2比较了模拟植物生长算法和节约里程算法的调度方案。可以看出,两者的车辆总数相同,通过节约里程算法求解得到的方案目标函数值为-0.434 2,模拟植物生长算法较之而言增加0.287 6,验证了模型及算法的有效性。结果表明,采用合理的快递车辆调度方案,能够较好地实现客户及物流企业利益的均衡优化。
5 结论快递车辆的优化调度能够很好地提升客户满意度,降低企业运输成本,保证多方面利益。目前大多数研究主要以降低运输成本为目标对调度问题进行建模,并采用运算性能较高的智能算法求解,从而得到快递车辆调度方案。本文从客户为行为主体的角度出发,结合现实情境及认知心理学分析客户对等待时间的感知,并构建客户感知满意度函数完善调度模型。通过模拟植物生长算法求解结果表明,研究能够实现客户及物流企业利益的均衡优化。在此基础上,如何在模型中反映现实生活中的不确定因素(如客户需求量及时间变动),以及实现客户、物流企业、配送人员三者间需求及利益的交互协调调度,将是下一步需要研究的课题。
| [1] |
CHANG T S, YEN H M. City-courier routing and scheduling problems[J].
European Journal of Operational Research, 2012, 223(2): 489-498.
DOI: 10.1016/j.ejor.2012.06.007. |
| [2] |
JANSSENS J, SÖRENSEN K, CATTRYSSE D. Multi-objective microzone-based vehicle routing for courier companies: From tactical to operational planning[J].
European Journal of Operational Research, 2015, 242(1): 222-231.
DOI: 10.1016/j.ejor.2014.09.026. |
| [3] |
侯玲娟, 周泓. 基于离散差分进化算法的随机车辆路径问题[J].
工业工程, 2014, 17(3): 101-107.
HOU Lingjuan, ZHOU Hong. A novel discrete differential evolution algorithm for stochastic VRPSPD[J]. Industrial Engineering Journal, 2014, 17(3): 101-107. |
| [4] |
AVCI M, SEYDA T. An adaptive local search algorithm for vehicle routing problem with simultaneous and mixed pickups and deliveries[J].
Computers & Industrial Engineering, 2015, 83(3): 15-29.
|
| [5] |
GULCZYNSKI D, GOLDEN B, WASIL E. The multi-depot split delivery vehicle routing problem: an integer programming-based heuristic, new test problems, and computational results[J].
Computers & Industrial Engineering, 2011, 61(3): 794-804.
|
| [6] |
于宝琴, 武淑萍, 杜广伟. 网购快递物流服务系统测评的枝模型仿真[J].
中国管理科学, 2014, 22(12): 72-78.
YU Baoqing, WU Shuping, DU Guangwei. Branch model simulation for express logistics system evaluation under online shopping[J]. Chinese Journal of Management Science, 2014, 22(12): 72-78. |
| [7] |
MCNABB M E, WEIR J D, HILL R R. Testing local search move operators on the vehicle routing problem with split deliveries and time windows[J].
Computers & Operations Research, 2015, 56(6): 93-109.
|
| [8] |
LIN C K Y. A vehicle routing problem with pickup and delivery time windows, and coordination of transportable resources[J].
Computers & Operations Research, 2011, 38(11): 1596-1609.
|
| [9] |
SALANI M, VACCA I. Branch and price for the vehicle routing problem with discrete split deliveries and time windows[J].
European Journal of Operational Research, 2011, 213(3): 470-477.
DOI: 10.1016/j.ejor.2011.03.023. |
| [10] |
CHOPRA S, LOVEJOY W, YANO C. Five decades of operations management and the prospects ahead[J].
Management Science, 2004, 50(1): 8-14.
DOI: 10.1287/mnsc.1030.0189. |
| [11] |
KAHNEMAN D, TVERSKY A. Prospect theory: an analysis of decision under risk[J].
Econometrica, 1979, 47(2): 263-291.
DOI: 10.2307/1914185. |
| [12] |
KAHNEMAN D, TVERSKY A. Choices, values, and frames [M]. New York: Cambridge University Press, 2000.
|
| [13] |
CAI W, YANG W W, CHEN X Q. A global optimization algorithm based on plant growth theory: plant growth optimization[J].
Intelligent Computation Technology and Automation, 2008, 1(11): 1194-1199.
|
| [14] |
WANG C H, CHENG H Z H. Transmission network optimal planning based on plant growth simulation algorithm[J].
European Transactions on Electrical Power, 2009, 19(2): 291-301.
DOI: 10.1002/etep.v19:2. |
| [15] |
曹庆奎, 刘新雨, 任向阳. 基于模拟植物生长算法的车辆调度问题[J].
系统工程理论与实践, 2015, 35(6): 1449-1456.
CAO Qingkun, LIU Xinyu, REN Xiangyang. Vehicle scheduling problem based on plant growth simulation algorithm[J]. Systems Engineering--Theory & Practice, 2015, 35(6): 1449-1456. DOI: 10.12011/1000-6788(2015)6-1449. |
| [16] |
陈刚, 张锦, 彭永涛. 震后应急物资敏捷保障体系模型及算法[J].
自然灾害学报, 2013, 22(3): 47-53.
CHEN Gang, ZHANG Jin, PENG Yongtao. Agile security system model and algorithm for post-earthquake urgent relief provisions[J]. Journal of Natural Disasters, 2013, 22(3): 47-53. |
 2017, Vol. 20
2017, Vol. 20

