2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China
随着城市人口增长,城市交通拥堵问题日益严重,构建合理的公共交通系统,倡导公交出行成为缓解这一问题的有效手段。合理的公交线网设计是构建有效公交系统的关键部分,如何根据公交出行需求设计相应的公交线网成为了交通研究热点。
早在1967年,Lampkin等[1]就对公交线路设计进行了相关研究,他们将问题分为公交线网设计和发车频率设计两个部分,首先设计公交线网然后设计发车频率,其优化目标是在不降低公交服务水平的基础上减少车辆配备。Newell[2]和Salzborn[3]基于乘客的角度,在给定的公交资源条件下通过优化发车频率使乘客出行时间最小化。早期的研究都是基于单条线路或小规模路网的路网设计,模型较为简单,且缺乏模型算法研究,很难运用到实际的公交线网设计中。相比于国外,国内对于公交线网研究起步较晚,最早王炜[4]提出了实用的“逐条布设,优化成网的公交线网规划方法”。张杰林等[5]提出了城市常规公交线网的“一路一线”布局构想。
文献[6-15]从线网层面,探究了公交线网设计的问题。这些研究集中在运用智能算法解决公交线网设计的问题上,如文献[6-7]构建了公交线网优化模型,并讨论了公交线网设计问题本身的复杂性:当公交线网从线路层面上升至网络层面之后,由于线路之间的相关特性,传统的解析式算法很难应用于该问题的求解,特别是网络规划过大时,传统的算法无法得到有效解。针对网络层面的求解问题,文献[8-15]均提出了相应的智能算法,利用其迭代优化的特性,实现了公交线网模型的求解。总的来说,这些研究对公交线网及发车频率都采用分阶段优化方法,没有考虑两者之间的相关关系,以及公交线网及发车频率的同步优化。
公交线网求解算法研究可以分为两个阶段,早期由于线网设计多是基于单线路或小规模路网,考虑因素较少,模型较为简单,主要采用传统的最优方法求解[1-3]。随着研究的问题规模扩大,模型越来越复杂,传统的最优化方法计算量过大,有时甚至无法求解,采用智能算法求解模型成为了主流趋势[10-12]。但这些研究没有考虑线网与发车频率之间的关系,特别是对于如何利用两者关系,改进算法,提高算法效率还缺乏相关研究。
通过上述对公交线网相关研究的回顾,可以发现,现有的研究主要基于乘客和运营商的角度考虑公交线网的设计问题,主要分阶段对公交线网及发车频率进行优化,没有深入考虑公交线网及发车频率之间的相关关系。从现有的研究来看,依据乘客视角进行公交线网规划的主要目标是使乘客出行时间最小化,包括乘客从出发地到达起始站点的时间、等待时间、换乘时间、在车旅行时间和从目的站点到达终点的时间。依据公交运营商的角度进行公交线网规划的主要目标是使运营成本降到最低,运营成本涉及多个方面,包括车辆配置成本、人员配置成本、管理调度成本、燃油消耗成本等。由于两者追求的目标相互矛盾,从管理层面主要是协调两者之间的矛盾。因此,基于乘客视角所构建的模型主要是以给定的公交资源配置条件下,如何使乘客出行时间最小化;基于运营层面的视角所构建的模型主要是在给定的服务水平条件下,如何使总运营成本最小化;基于管理层面视角所构建的模型通常是双目标同时优化。
依据本文主要针对的是已经确定站点布局以及给定的车辆配备条件下的公交线网布设优化问题,涉及到的主要是乘客等待时间、在车旅途时间,以及车辆配备,构建以乘客等待时间和在车旅途时间最小化为目标,以车辆配置数量为约束条件的混合整数规划的公交线网优化模型,实现公交线网及发车频率的同步优化,同时,深入分析公交线网及发车频率的相关关系,对算法进行改进,提高算法的执行效率。
1 模型构建公交线网及线网发车频率同步优化问题是公交线网优化和发车频率优化问题的组合问题,目的是为了获取规划区域最佳线网布局及与线网中每条线路相匹配的线路发车频率。根据相关研究,模型假设及模型建立如下。
1.1 模型假设1) 乘客采用公交出行时选择换乘最少,出行时间最短的公交线路;
2) 乘客选择第一辆能够满足其出行需求的公交车辆;
3) 乘客的公交出行OD(起终点间的交通出行量)已知;
4) 规划区域的站点布局,及规划线路数量、车辆配置总量已知;
5) 假设乘客客流随机到达,乘客的平均等待时间为发车间隔的0.5倍;
6) 假设站点间的运行时间已知且为固定值。
1.2 公交线网及发车频率同步优化模型构建依据公交线网优化相关研究分析,构建在给定的公交资源的条件下,以出行时间最小化为目标的公交优化模型,模型及相关说明如下。
|
$\quad\quad\begin{split}{\min } \ {Z = \displaystyle\sum\limits_{o \in {D_o}} {\sum\limits_{d \in {D_d}} {{D_{od}}({T_{od}} + {W_{od}})} } }\text{。}\end{split}$
|
(1) |
|
${T_{od}}{\rm{ = }}\frac{{\sum\limits_{l \in {L_s}} {{\rm{RT}}_{od}^l} {f_l}T_{od}^l + 1}}{{{\rm{N}}{{\rm{R}}_{od}} + \sum\limits_{l \in {L_s}} {{\rm{RT}}_{od}^l{f_l}} }}(1 - {\rm{N}}{{\rm{R}}_{od}}) + \left( {\frac{{\sum\limits_{l \in {L_s}} {{\rm{RT}}_{ok}^l} {f_l}T_{ok}^l + 1}}{{\sum\limits_{l \in {L_s}} {{\rm{RT}}_{ok}^l{f_l}} }} + } \right.{\rm{ }}\left. {\frac{{\sum\limits_{l \in {L_s}} {{\rm{RT}}_{kd}^l} {f_l}T_{kd}^l + 1}}{{\sum\limits_{l \in {L_s}} {{\rm{RT}}_{kd}^l{f_l}} }}} \right){\rm{N}}{{\rm{R}}_{od}}$
|
(2) |
|
$\begin{split}\quad\quad{T_{ik}^l = {c_{ik}}{x_{ikl}} + \sum\limits_{j \in {L_o} \cup {L_m},j \ne i \cap j \ne k} {{x_{ijl}}{\rm{RT}}_{jk}^l} (T_{jk}^l + {c_{ij}} + s)}, \\ i \in {L_o} \cup {L_m},k \in {L_d} \cup {L_m},k \ne i,l = 1, \cdots, L\text{。}\end{split}$
|
(3) |
|
$\begin{split}\quad\quad{{\rm{RT}}_{ik}^l }= & {{x_{ikl}} + \sum\limits_{j \in {L_o} \cup {L_m},j \ne i,j \ne k} {{x_{ijl}}} {\rm{RT}}_{jk}^l}, \\ & {i \in }{L_o} \cup {L_m},k \in {L_m},k \ne i,l = 1, \cdots, L\text{。}\end{split}$
|
(4) |
|
$\begin{split}\quad\quad{{{\rm{NR}}_{od}} = \displaystyle\prod\limits_{l = 1}^L {(1 - {\rm{RT}}_{od}^l} )}, {o \in} {L_o}, \end{split}d \in {L_d}\text{。}$
|
(5) |
|
$\quad\quad\begin{split}& {\rm{s.t}}\\& {\sum\limits_{n \in {L_o}} {{x_{nml}}} = 1}, {l = 1, \cdot \cdot \cdot ,}L\end{split}\text{;}$
|
(6) |
|
$\quad\quad\begin{split}{\displaystyle\sum\limits_{n \in {L_d}} {{x_{nml}}} = 1}, {l = 1}\end{split}, \cdot \cdot \cdot ,L\text{;}$
|
(7) |
|
$\begin{split}\quad\quad{\displaystyle\sum\limits_{n \in {L_o} \cup {L_m}} {{x_{nml}} {\text{≤}} 1} }, {l = 1}\end{split}, \cdots, L\text{;}$
|
(8) |
|
$\begin{split}\quad\quad{\displaystyle\sum\limits_{m \in {L_d} \cup {L_m}} {{x_{nml}} {\text{≤}} 1} }, {l = 1}\end{split}, \cdot \cdot \cdot ,L\text{;}$
|
(9) |
|
$\quad\quad{{x_{nml}} {\text{≤}} {S_{\max }}}, {n \in {L_o}} \cup {L_m},m \in {L_m} \cup {L_d}\text{;}$
|
(10) |
|
$\quad\quad\sum\limits_{l = 1}^L {2{f_l}{T_l}} {\text{≤}} B\text{;}$
|
(11) |
|
$\quad\quad\begin{split}{{f_{\min }} {\text{≤}} {f_l}}, {l = 1, \cdot \cdot \cdot }\end{split},L\text{;}$
|
(12) |
|
$\quad\quad\sum\limits_{n \in {L_o} \cup {L_m}} {\sum\limits_{m \in {L_d} \cup {L_m}} {{x_{nml}}} } {\text{≤}} {N_{\max }}\text{。}$
|
(13) |
变量符号说明。
1) 集合。
Do为公交出行需求起始站点集合;
Dd为公交出行需求终点站点集合;
Dod为从起始站点o到达终点站点d的公交出行客流量;
Lo为线路起始站点集合;
Ld为线路终点站点集合;
Lm为线路中间站点集合;
Ls为公交线网线路集合;
2) 上下标。
l表示标号为l的公交线路。
3) 变量。
已知常量:
s为车辆在站点的平均停靠时间;
L为线网总线路总条数;
B为线网总配备的车辆总数;
fmin为线路最小发车频率;
Nmax为线路中站点数量最大值;
Smax为相邻站点的站点距离最大值;
中间变量:
Tod为站点o到站点d的平均在车旅行时间;
Wod为站点o到站点d的平均等待时间;
决策变量:
fl为线路l的发车频率;
目标函数:
Z为公交线网乘客总的出行时间,即模型的目标函数。
模型说明:式(1)为目标函数,为最小化所有乘客出行时间;式(2)为从站点o到站点d的平均出行时间,其中第1部分分项为从站点o到站点d直达的平均出行时间,第2部分分项为从站点o到站点d换乘的平均出行时间;式(3)为通过线路l从站点o到站点k的出行时间;式(4)是定义
根据对公交线网求解的算法研究,本文针对该问题设计相应的遗传算法。不同于以往的算法,本文根据该问题的特点对算法进行了改进,提出公交线网客流换乘比例检验方法,以此减少对不可行解的计算,提高算法的执行效率。
公交线网优化的目标函数是乘客出行时间最小化,出行时间分为在车旅行时间和等待时间。而在设计的算法中,适应度通常用来反映解的好坏,一般的优化问题都以目标函数适应度函数作为适应度函数,但在公交线网设计中,目标函数包含在车旅行时间以及等待时间,涉及到线网设计和发车频率设计两个阶段。如果以目标函数作为适应度函数就需要对所有公交线网进行发车频率的分配,但这种求解方式会增加一些本身不可行解的计算量。因此针对该问题,合理的适应度函数以及相应算法的改进,能够有效地增加求解速度,提高算法效率。
本文的改进策略是首先对线网结构计算客流换乘比例值,记为Lc,评价线网结构优劣。对于线网客流换乘高于换乘比例下界值
|
$ \quad\quad {\rm{Lc}} = \frac{{\displaystyle\sum\limits_{o \in {D_o}} {\displaystyle\sum\limits_{d \in {D_d}} {{D_{od}}} } (1 - {{\rm{NR}}_{od}})}}{{\displaystyle\sum\limits_{o \in {D_o}} {\displaystyle\sum\limits_{d \in {D_d}} {{D_{od}}} } }}\text{。}$
|
(14) |
Step1 数据输入:通过前期工作确定规划区域站点Lo,Ld,Lm,线路条数L,站点间最短出行时间
Step2 初始线网产生:依据约束条件(6)~(10)及Step1的数据输入,产生初始线网。
Step3 线网客流换乘比例判断:依据式(14)对公交线网客流换乘比例进行判断,将公交线网分为满足下界和不满足下界的公交线网。
Step4 分配及优化发车频率:
1)对于线网客流换乘比例Lc<
2)根据式(1)计算分配了发车频率的线网的目标函数;
3)对发车频率进行局部优化得到该线网的最佳发车频率方案,具体发车频率局部优化方案参照文献[8]。
Step5 判断算法是否停止:对算法的停止条件进行判断,如果满足算法停止条件则停止计算,并输出线网及相应发车频率的设计方案,如果没有满足算法停止条件则转至下一步。
Step6 依据选择规则和设定的交叉变异概率, 选择公交线网进行相关的交叉变异操作, 得到与原种群规模一致的新的公交线网。
Step7 对公交线网子代及其父代按目标函数值大小进行排序, 取目标函数值小的作为新的种群, 并转至Step3。
需要说明的是,本文所针对的问题是单条线路可以覆盖的中小城市的公交线网规划。在这种规模的网络中,换乘比例过高将导致网络结构不合理,因此在算法设计层面不适用于大规模网络及城乡通道性客流较多的公交线网规划。
3 算例分析1)算例条件说明。
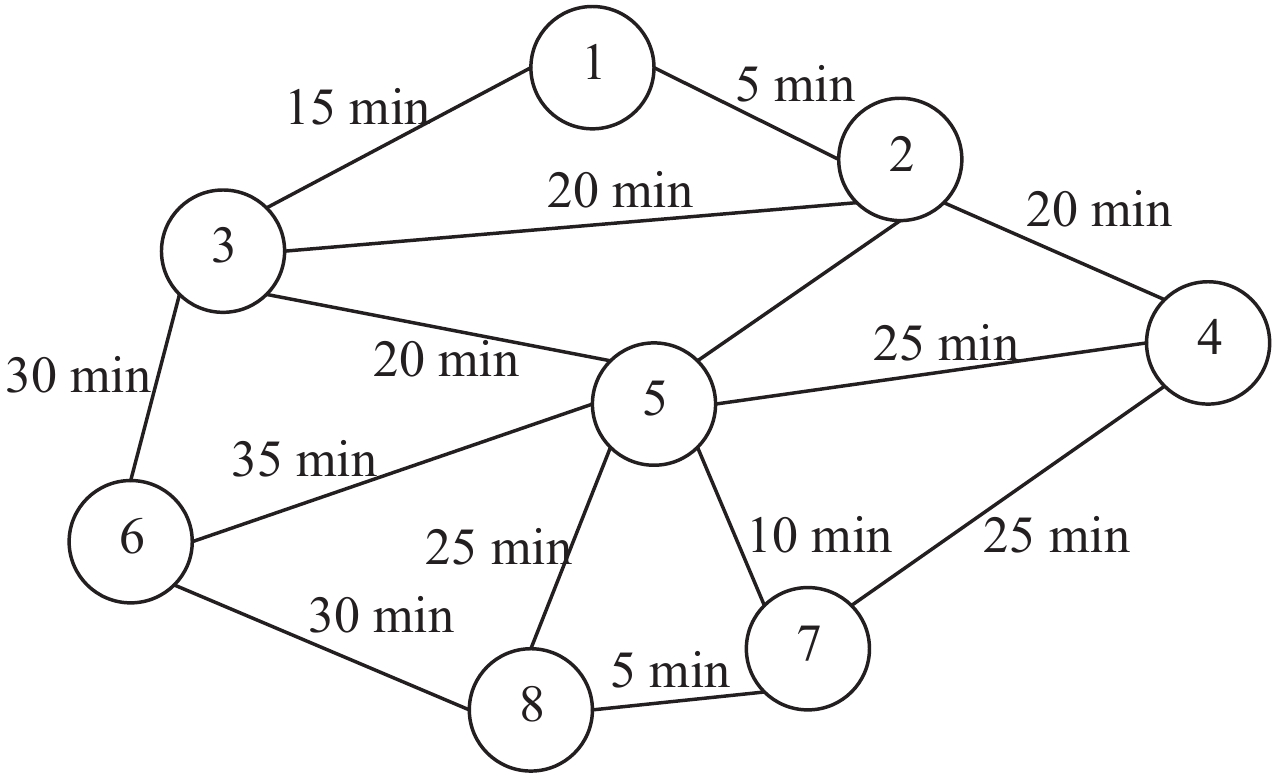
该方法将应用至一个如图1所示包含8个节点线网的站点及道路布局图,其中站点间的运行时间以及站点间客流OD如表1所示,该算例与文献[6]一致。在设计线网时,本算例根据文献[6]的相关研究,规划线路数量为6条,单条线路配备车辆数最少为12辆最多为40辆,每条线路最少站点数为3,最大站点数为4,整个线网车辆配备总数量不超过146辆。
|
图 1 算例站点及道路布局图 Fig. 1 Layout of stations and routes for the case |
| 表 1 OD矩阵表 Tab. 1 Table of OD matrix |
需要说明的是,虽然引用案例选取的是包含8个站点、6条规划线路和146辆车辆的小规模网络进行验证,但涉及到了全部的公交线网规划因素,在对于中小型城市实际较大的网络中,应用该模型和算法也可以得到相应的优化结论。不过随着网络规模的扩大,将会导致算法计算时间的增加。
2)将算例的已知条件代入至本文构建的公交线网优化模型,并采用Matlab语言编写相关遗传算法程序实现对模型的求解。通过数据实验,对
(1) 对
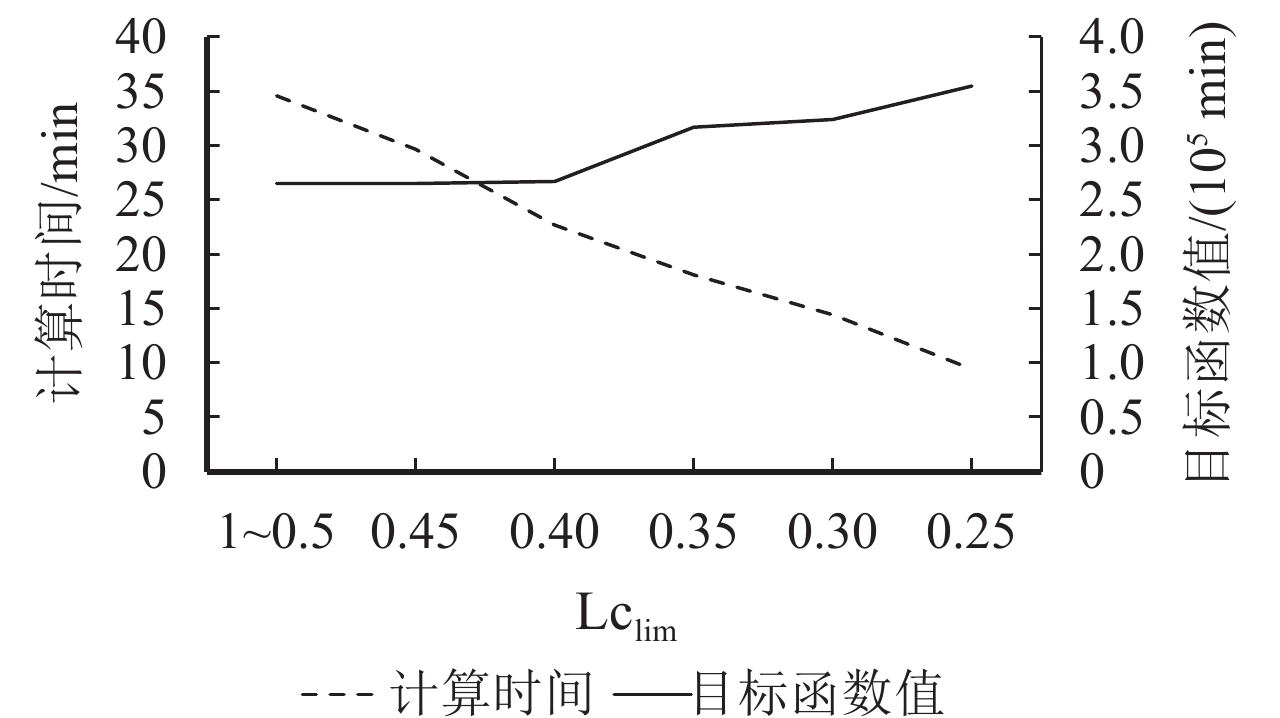
对参数
|
图 2
|
通过灵敏度分析可知如下结果。
① 随着
② 随着
③ 在区间1~0.5时计算时间均为34.58 min说明,初始化线网的客流换乘比例Lc均小于0.5,换乘比例下界值
④ 在灵敏度分析图中,换乘比例最小取值为0.25,这是因为当
通过对
(2)通过对
| 表 2 线路及发车频率优化结果 Tab. 2 The optimized results of lines and frequencies |
1)本文建立了公交线网优化的混合整数规划模型,可以实现公交线网及相应的发车频率同步优化。并针对该问题设计了改进遗传算法,通过设计客流换乘比例下界值
2)在实际中小城市公交线网优化及规划过程中,该方法可以对现有的公交线网结构作出相应的评价,并在此基础上,对公交线网结构优化提出相应基于乘客出行时间最小化视角的的线网及发车频率设计方案。
| [1] |
LAMPKIN W, SAALMANS P D. The design of routes, service frequencies, and schedules for a municipal bus undertaking: a case study[J].
OR, 1967, 18(4): 375-397.
DOI: 10.2307/3007688. |
| [2] |
NEWELL G F. Dispatching policies for a transportation route[J].
Transportation Science, 1971, 5(1): 91-105.
DOI: 10.1287/trsc.5.1.91. |
| [3] |
SALZBORN F J M. Optimum bus scheduling[J].
Transportation Science, 1972, 6(2): 137-148.
DOI: 10.1287/trsc.6.2.137. |
| [4] |
王炜. 实用公交线网规划方法研究[J].
东南大学学报(自然科学版), 1990, 20(4): 81-88.
WANG Wei. Research on bus-route network planning[J]. Journal of Southeast University (Natural Science Edition), 1990, 20(4): 81-88. |
| [5] |
张杰林, 王炜, 陈学武. 城市常规公交线网的" 一路一线”布局构想[J].
交通运输工程与信息学报, 2010, 8(1): 96-102.
ZHANG Jielin, WANG Wei, CHEN Xuewu. Consideration of " one road one route” bus line networks layout[J]. Journal of Transportation Engineering and Information, 2010, 8(1): 96-102. |
| [6] |
BAAJ M H, MAHMASSANI H S. An AI-based approach for transit route system planning and design[J].
Journal of advanced transportation, 1991, 25(2): 187-209.
DOI: 10.1002/atr.v25:2. |
| [7] |
SHIH M C, MAHMASSANI H, BAAJ M. Trip assignment model for timed-transfer transit systems[J].
Transportation Research Record: Journal of the Transportation Research Board, 1997, 1571: 24-30.
DOI: 10.3141/1571-04. |
| [8] |
CEDER A. Public transit planning and operation: theory, modeling and practice[M]. London: Elsevier, Butterworth-Heinemann, 2007.
|
| [9] |
Szeto W Y, Wu Y. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong[J].
European Journal of Operational Research, 2011, 209(2): 141-155.
DOI: 10.1016/j.ejor.2010.08.020. |
| [10] |
Verbas İ Ö, Mahmassani H S. Exploring trade-offs in frequency allocation in a transit network using bus route patterns: Methodology and application to large-scale urban systems[J].
Transportation Research Part B: Methodological, 2015, 81(1): 577-595.
|
| [11] |
Baaj M H, Mahmassani H S. Hybrid route generation heuristic algorithm for the design of transit networks[J].
Transportation Research Part C: Emerging Technologies, 1995, 3(1): 31-50.
DOI: 10.1016/0968-090X(94)00011-S. |
| [12] |
Martínez H, Mauttone A, Urquhart M E. Frequency optimization in public transportation systems: Formulation and metaheuristic approach[J].
European Journal of Operational Research, 2014, 236(1): 27-36.
DOI: 10.1016/j.ejor.2013.11.007. |
| [13] |
Wu J, Song R, Wang Y. Modeling the Coordinated Operation between Bus Rapid Transit and Bus[J].
Mathematical Problems in Engineering, 2015, 21(1): 1-7.
|
| [14] |
蒋阳升, 罗孝羚. 考虑首末站约束和站间客流强度的公交线网优化[J].
长安大学学报(自然科学版), 2017, 37(01): 106-111.
Jiang Yangsheng, Luo Xiaoling. Optimization of public transit network considering initial and terminal stations location requirements and passenger flow intensity[J]. Journal of Chang’an University (Natural Science Edition), 2017, 37(01): 106-111. |
| [15] |
徐光明, 史峰, 罗湘, 等. 基于策略均衡分配的公交线网规划优化方法[J].
交通运输系统工程与信息, 2015, 15(3): 140-145.
XU Guangming, SHI Feng, LUO Xiang. Method of public transit network planning based on strategy equilibrium transit assignment[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(3): 140-145. |
 2017, Vol. 20
2017, Vol. 20