随着互联网经济的飞速发展,网络购物已越来越普及,进而推动了配送业的迅猛发展。由于物流的最终用户例如企业、商店和个人等绝大多数集中在城市,在整个物流的环节中,城市配送成为最后一个环节,也是物流业务好坏评价最重要的体现;同时上下班高峰期、天气变化和突发事故等因素在很大程度上影响着城市配送的时效性。在实际路网中,车辆出发时间、路段的行驶速度和行驶时间总是处于不断变化中[1],从而形成了时间依赖型车辆调度问题(time dependent vehicle routing problem, TDVRP)。时间依赖型车辆调度问题主要研究路段行程时间随出发时间变化的路网环境下,如何安排车辆配送路线,以达到路程最短、费用最少、时间最少或使用车辆最少等优化目标。
目前TDVRP问题已受到国内外学者的广泛关注。20世纪90年代,Malandraki等[2]就提出了时间依赖性车辆路径问题,并建立了旅行时间函数模型,但其没有考虑先进先出原则(first in first out, FIFO)。Ichoua等[3]将先进先出准则引入TDVRP问题中,采用速度时间依赖函数表示动态路网,采用改进并行禁忌搜索算法,求解了带时间窗TDVRP问题。Haghani等[4]使用遗传算法求解TDVRP,对比了精确算法和遗传算法的求解结果。Chen等[5]建立了具有时间窗TDVRP问题的混合整数规划模型,并设计了该问题的启发式算法。Lecluyse等[6]通过构建具有时空性质的一致性网络求解时间依赖性车辆路径问题,在路网中设置拥挤范围圈确定旅行时间的变化范围。李春霞等[7]将动态车辆调度问题置于时间依赖网络,建立了包括车辆固定成本费用、路阻费用和违反时间窗约束费用在内的广义费用最小化数学模型,并采用改进的蚁群算法进行优化求解。穆东等[1]根据TDVRP的特性,对经典的串行模拟退火算法进行改进,提出并行模拟退火算法,并进行了测试。Tas等[8]研究了一个具有软时间窗的时间依赖车辆路径问题,并将问题分为两类,分别设计了禁忌搜索算法和自适应大邻域搜索算法。李宇飞[9]在充分考虑战时军事配送影响因素的情况下,建立了基于时间依赖网络的军事配送网络路径优化模型,提出了考虑等待风险的时间依赖网络最短时算法以及考虑等待风险的时间依赖网络综合最优算法。Rincon-Garcia等[10]考虑交通拥堵对配送时间的影响,设计了一种混合元启发式算法求解带硬时间窗的时变车辆路径问题。Alinaghian等[11]介绍了二维装载时变车辆路径问题,并建立了双目标数学规划模型。提出的模型满足先进先出准则,基于非支配排序局部搜索方法设计了模型的求解算法。Huang 等[12]将时间依赖性的车辆路径问题看作一个路径选择的综合决策问题,基于路径灵活性研究了确定和随机交通条件下TDVRP问题。
从相关研究来看,现有的TDVRP问题优化主要体现在路程最短、费用最少及使用车辆最少等方面的优化。多数研究采用多目标数学规划模型进行TDVRP问题描述,计算方法上大部分采用启发式智能算法。在借鉴国内外相关研究的基础上,本文综合考虑上述因素,以总配送时间、使用车辆数最小及客户满意度最大为目标,考虑路段行程时间的时间依赖性,建立多目标时间依赖网络的城市物流车辆调度模型,采用遗传算法对该问题进行求解。
1 问题描述与建模 1.1 符号说明本文研究的是软时间窗TDVRP问题,变量和参数符号按如下定义。
i=0为物流配送中心;
时间依赖网络的表示主要是路段行驶时间的表示。城市物流配送一般是分区域进行,因此本研究只考虑最多跨两个时间段的情况。假设车辆在s时刻从顾客i出发,如果能在同一时间段l内到达j,则到达顾客j的时刻为
设
|
$\begin{split}& \qquad {t_j} = s + t_{ij}^{sl} + t_{ij}^{ll + 1}\! =s + \! {B_l} - s \! +\! \left(1 \! - \! \displaystyle\frac{{{B_l} - s}} {{t_{ij}^l}}\right)t_{ij}^{l + \! 1} \!=\\& \! t_{ij}^{l + 1} \!+ s \displaystyle\frac{{t_{ij}^{l + \! 1}}}{{t_{ij}^l}}s \! + \left(1 - \frac{{t_{ij}^{l + \! 1}}}{{t_{ij}^l}}\right){B_l}{\text{。}}\!\!\!\!\!\end{split}$
|
((1)) |
由式(l)可知,到达顾客j的时刻tj为从顾客i出发时刻s的增函数,因此满足先进先出原则。
1.3 软时间窗口的处理对于软时间窗而言,若车辆晚于bi到达顾客i,顾客在等待过程中会对配送服务产生不满;若早于ai到达顾客i,配送员可能需要等待顾客从而产生等待费用,同时也可能打乱顾客的时间安排而对配送服务产生不满。这里设计一种价值函数来表示顾客对服务产生的不满意程度,价值函数值越大,表示顾客对服务产生的满意度越大。本文设计的顾客对服务时刻价值函数如下:
|
$V({t_i}) = - {\lambda _1}\max \; {({a_i} - {t_i},0)^\alpha } + (- {\lambda _2})\max \; {({t_i} - {b_i},0)^\beta }{\text{。}}$
|
((2)) |
式中,
如果车辆在时间窗口之前到达,配送员可能需要等待顾客,因此,在顾客i处的停留时间为顾客i的交货服务时间与等待时间之和。由于等待时间存在着较大的随机性,这里采用一个比例系数p进行处理,即在顾客i处的停留时间表示为
|
$\quad\quad {\rm{T}}{{\rm{S}}_i} + p\max ({a_i} - {t_i},0){\text{。}}$
|
((3)) |
对车辆k,其服务的顾客数由决策向量Y确定,为
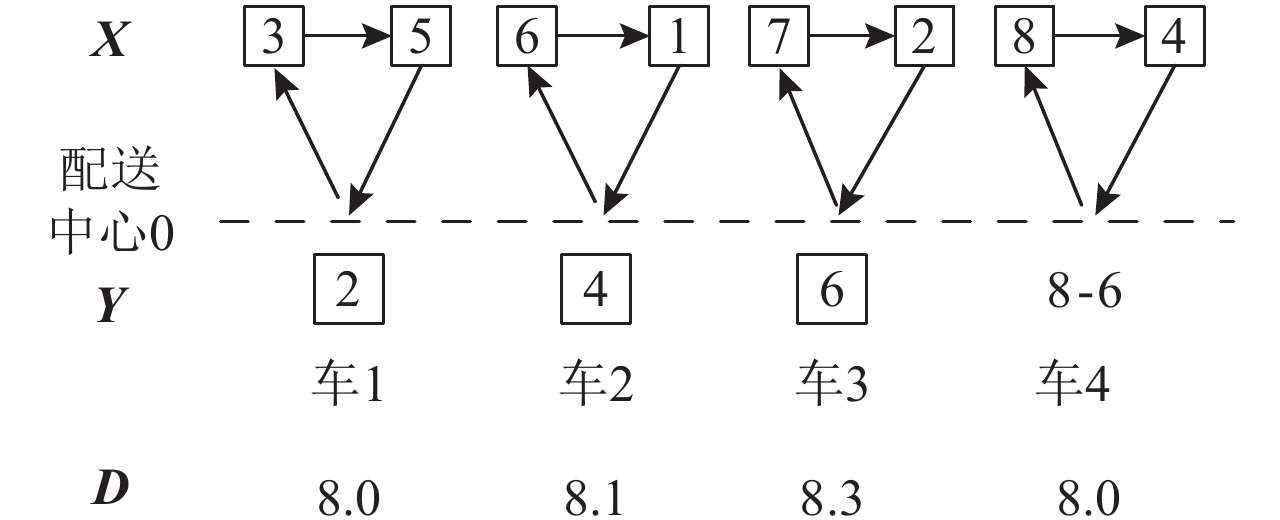
|
图 1 配送方案示意图 Fig. 1 Example for distribution scheme |
根据式(1),则车辆k到达
|
${t_{{x_i}}} = \left\{ \begin{array}{l}{d_k} + {t_{0{x_i}}},i = {y_{k - 1}} + 1;\\[10pt]{t_{{x_{i - 1}}}} + {\rm{T}}{{\rm{S}}_{{x_{i - 1}}}} + p\max \; ({a_{{x_{i - 1}}}} - {t_{{x_{i - 1}}}},0) + \;{t_{{x_{i - 1}}{x_i}}},\\ [10pt]{y_{k - 1}} + 2 {\text{≤}} i {\text{≤}} {y_k}{\text{。}}\end{array} \right.$
|
((4)) |
式中
根据1.2节的分析,车辆从配送中心至第1个顾客间的行驶时间
|
${t_{0{x_i}}} = \left\{ {\begin{array}{*{20}{l}}{t_{0{x_i}}^l,}&\!\!\!{{B_{l - 1}} {\text{≤}} {d_k} {\text{<}} {B_l} - t_{0{x_i}}^l;}\!\!\!\! \\{t_{0{x_i}}^{l + 1} + \left(1 - \displaystyle\frac{{t_{0{x_i}}^{l + 1}}}{{t_{0{x_i}}^l}}\right)\left({B_l} - {d_k}\right),}&\!\!\!{{B_l} - t_{0{x_i}}^l {\text{≤}} {d_k} {\text{<}}{B_l}{\text{。}}}\end{array}} \right.$
|
(5) |
同理,第
|
${t_{{x_{i - 1}}{x_i}}} = \left\{\!\!\!{\begin{array}{*{20}{l}}{t_{{x_{i - 1}}{x_i}}^l,}\\[8pt]{{B_{l \! - \! 1}} {\text{≤}} {t_{{x_{i \! - \! 1}}}} \! + \! {\rm{T}}{{\rm{S}}_{{x_{i \! - \! 1}}}} \! + \! p\max \; ({a_{{x_{i \! - \! 1}}}} \! - \! {t_{{x_{i - 1}}}},0) {\text{<}} {B_l} \! - \! t_{{x_{i \! - \! 1}}{x_i}}^l;}\\[10pt]t_{{x_{i - 1}}{x_i}}^{l + 1} + \left( {1 - \displaystyle\frac{{t_{{x_{i - 1}}{x_i}}^{l + 1}}}{{t_{{x_{i - 1}}{x_i}}^l}}} \right) \times ( {{B_l} - {t_{{x_{i - 1}}}} - {\rm{T}}{{\rm{S}}_{{x_{i - 1}}}}} - \\p\max \; ({a_{{x_{i - 1}}}} - {t_{{x_{i - 1}}}},0) ),\\[10pt]{B_l} - t_{{x_{i \! - \! 1}}{x_i}}^l {\text{≤}}{t_{{x_{i \! - \! 1}}}} \! + \! {\rm{T}}{{\rm{S}}_{{x_{i \! - \! 1}}}} \! + \! p\max \; ({a_{{x_{i - 1}}}} \! - \! {t_{{x_{i \! - \! 1}}}},0) {\text{<}} {B_l}{\text{。}}\end{array}} \right.$
|
(6) |
车辆从最后一个顾客返回配送中心的行驶时间
|
${t_{{x_i}0}} = \left\{\!\! {\begin{array}{*{20}{l}}{t_{{x_i}0}^l,}\\[7pt] \! {{B_{l - 1}} {\text{≤}} {t_{{x_i}}} + {\rm{T}}{{\rm{S}}_{{x_i}}} + p\max \; ({a_{{x_i}}} - {t_{{x_i}}},0) {\text{<}} {B_l} \! - \! t_{{x_i}0}^l;}\!\!\! \\[7pt]t_{{x_i}0}^{l + 1} + \left(1 - \displaystyle\frac{{t_{{x_i}0}^{l + 1}}}{{t_{{x_i}0}^l}}\right) \times ({B_l} - {t_{{x_i}}} - {\rm{T}}{{\rm{S}}_{{x_i}}} - \\[15pt]p \max \; ({a_{{x_i}}} - {t_{{x_i}}},0)),\\ [7pt] {{B_l} - t_{0{x_i}}^l {\text{≤}} {t_{{x_i}}} + {\rm{T}}{{\rm{S}}_{{x_i}}} + p\max \; ({a_{{x_i}}} - {t_{{x_i}}},0){\text{<}} {B_l}{\text{。}}}\!\!\!\!\! \end{array}} \right.$
|
(7) |
从顾客角度出发,建模时考虑最大化顾客的满意程度,即所有顾客的价值函数值最大:
|
$\max {z_1} \! = \!\! \sum\limits_{i = 1}^n {\left[ { \! - \! {\lambda _1}\! \max \; {{({a_i} \! - \! {t_i},0)}^\alpha } \! + \! (\! - \! {\lambda _2})\! \max \; {{({t_i} \! - \! {b_i},0)}^\beta }} \right]}{\text{。}}\!\!\!\!\!\!\!\!\!\!\! $
|
(8) |
从物流公司角度出发,建模时考虑最小化配送车辆数和最小化总配送时间。令
|
$\quad\quad \min {z_2} = \sum\limits_{k = 1}^m {{u_k}} {\text{。}}$
|
(9) |
目标函数3:最小化总配送时间,令
|
$\begin{split}& \quad\quad {\rm{t}}{{\rm{r}}_k} = {t_{0x}}_{_{{y_{k - 1}}} \! + \! 1} + \! \! \sum\limits_{j = {y_{k - 1}} + 1}^{{y_k} - 1} {{t_{{x_j}{x_{j + 1}}}}} + {t_{{x_{{y_k}}}0}} \! + \! \! \! \sum\limits_{j = {y_{k - 1}} \! + \! 1}^{{y_k}} ({t_{{x_j}{x_{j + 1}}}} + \!\!\!\! \\ & {\rm{T}}{{\rm{S}}_{{x_j}}} + p\max \; ({a_{{x_j}}} - {t_{{x_j}}},0) ) {\text{。}}\end{split}$
|
(10) |
那么,最小化为总配送时间:
|
$\quad\quad \min {z_3} = \sum\limits_{k = 1}^m {{\rm{t}}{{\rm{r}}_k}} {\text{。}}$
|
(11) |
根据上述分析,构建多目标时间依赖网络车辆调度模型如下。
|
$\begin{array}{l}\min z = \left( { - {z_1},{z_2},{z_3}} \right){\text{。}}\\[10pt]{\rm{s}}{\rm{.t}}.\left\{ {\begin{array}{*{20}{l}}{\displaystyle\sum\limits_{j = {y_{k - 1}} + 1}^{{y_k}} {{q_{{x_j}}}{\text{≤}}{Q_k}} ,k = 1,2,L,m;}&\quad\ (12)\\[20pt]{1{\text{≤}} {x_i} {\text{≤}}n,i = 1,2,L,n;}&\quad\ (13)\\[13pt]{{x_i} \ne {x_j},i \ne j,i,j = 1,2,L,n;}&\quad\ (14)\\[13pt]{0 {\text{≤}} {y_1} {\text{≤}} {y_2} {\text{≤}} L {\text{≤}} {y_{m - 1}} {\text{≤}} n;}&\quad\ (15)\\[13pt]{{x_i},{y_k}\,{\text{为整数}},i = 1,2,L,n,k = 1,2,L,m - 1;}&\quad\ (16)\\[15pt]{{u_k} = \left\{ \begin{array}{l}\begin{array}{*{20}{c}}\!\!\!\! {1,}&{{y_k} {\text{>}} {y_{k - 1}},}\qquad\end{array}\\[13pt]\begin{array}{*{20}{c}}\!\!\!\! {0,}&{{y_k} = {y_{k - 1}},}\qquad\end{array}\end{array} \right.\;\;k = 1,2,L,m;}&\quad\ (17)\\[16pt]{{\rm{t}}{{\rm{r}}_k} = \left\{ {\begin{array}{*{20}{l}}{0,}&{{y_k} = {y_{k - 1}},}\\[13pt]{{\text{式}}(9),}&{{y_k} {\text{>}} {y_{k - 1}},}\end{array}k = 1,2,L,m;} \right.}&\quad\ (18)\\[15pt]{{\text{式}}\,(4),(5)\,,\,(6)\,,\,(7)\,,\;\;\,l \in L{\text{。}}}&{}\end{array}} \right.\end{array}$
|
其中,约束条件(12)表示车辆能力约束,式(13)及(14)表示顾客决策向量约束,式(15)表示车辆服务顾客数约束,式(17)表示车辆是否被使用,式(18)表示车辆配送时间,式(4)描述车辆到达顾客的时刻, 式(5)~(7)表示时间依赖的车辆行驶时间。
2 模型求解算法设计本文采用了顾客、车辆及发车时刻3个向量作为决策变量,同时决策向量X和Y均为整数,有利于遗传算法染色体的编码实现,因而本文借鉴文献[13]的编码方式设计了求解时间依赖的城市物流车辆优化调度问题的遗传算法。
2.1 染色体编码设计及产生染色体
基因
在初始种群产生的过程中,基因x不需要特殊处理,而基因y确定的顾客数不合适会违反约束条件(12),因此在产生y时需要进行控制,具体方法如下。
Step1 令i=1,k=1,num=0,q=0。
Step2 如果i等于n,或者k等于m,则终止;否则,令
Step3 如果
对于基因d,车辆k从配送中心的发车时间最早为配送中心开始上班的时刻,一般不能晚于第一个顾客
1)选择操作。
采用保存最佳个体和适应度比例相结合的选择策略。将每代群体中的
2)基因交叉。
除排在第一位的最优个体外,对其余的
3)基因变异。
对群体中,除排在第一位的最优个体外,其余的
对于基因x,在1和n之间随机产生两个变异位置n1和n2,并对序列
终止采用目标值变化控制准则,当连续G代个体最优目标函数值不发生变化时,终止算法。另外,为了防止出现早熟现象,随着遗传进程对Pc和Pm的值进行调整。
3 算例分析设配送公司有一个配送中心和20名客户
|
表 1 客户需求qi及时间窗口
|
| 表 2 配送中心及客户间3个时间段的行驶时间 Tab. 2 The travel time between distribution center and customers |
终止条件G=3 000,初始群体
| 表 3 遗传算法结果 Tab. 3 The result of genetic algorithm |
在不同的时间段相同路段的行驶时间可能会发生变化,利用时间依赖网络能更好地刻画实际城市物流车辆调度的特征。在借鉴国内外相关研究的基础上,本文综合采用跨越时间段比例的方法来确定路段行驶时间,该方法满足先进先出原则。另外,本文设计了一种价值函数来衡量顾客对服务的满意程度。在分析时间依赖网络中车辆行驶时间的基础上,综合考虑顾客及物流公司两个方面,建立多目标时间依赖网络城市物流车辆调度模型,模型采用顾客、车辆及发车时刻3个向量作为决策变量,使得决策变量的数量大大下降,同时决策向量X和Y均为整数,有利于遗传算法染色体的编码实现。最后,本文设计了遗传算法对该模型进行求解,并进行了算例研究。算例分析表明本模型在城市物流车辆调度方面是合理可行的,设计的算法求解时间依赖网络物流车辆调度问题是有效的。但本文只研究了分时段车辆行驶时间依赖性,而现实中,城市道路的行驶时间是动态变化的,如何进一步利用城市交通的动态信息,研究时变条件下城市物流车辆的柔性优化调度,是今后进一步研究的内容。

|
图 2 车辆行驶路线及时间 Fig. 2 The result of vehicle route |
| [1] |
穆东, 王超, 王胜春, 等. 基于并行模拟退火算法求解时间依赖型车辆路径问题[J].
计算机集成制造系统, 2015, 21(6): 1626-1636.
MU Dong, WANG Chao, WANG Shengchun. Solving TDVRP based on parallel-simulated annealing algorithm[J]. Computer Integrated Manufacturing Systems, 2015, 21(6): 1626-1636. |
| [2] |
MALANDRAKI C, DASKIN M S. Time dependent vehicle routing problems: formulations, properties and heuristic algorithms[J].
Transportation Science, 1992, 26(3): 185-200.
DOI: 10.1287/trsc.26.3.185. |
| [3] |
ICHOUA S, GENDREAU M, POTVIN J Y. Vehicle dispatching with time-dependent travel times[J].
European Journal of Operational Research, 2003, 144(2): 379-396.
DOI: 10.1016/S0377-2217(02)00147-9. |
| [4] |
HAGHANI A, JUNG S. A dynamic vehicle routing problem with time-dependent travel times[J].
Computers & Operations Research, 2005, 32(11): 2959-2986.
|
| [5] |
CHEN H K, HSUEH C F, CHANG M S. The real-time time-dependent vehicle routing problem[J].
Transportation Research Part E Logistics & Transportation Review, 2006, 42(5): 383-408.
|
| [6] |
LECLUYSE C, SÖRENSEN K, PEREMANS H. A network-consistent time-dependent travel time layer for routing optimization problems[J].
European Journal of Operational Research, 2013, 226(3): 395-413.
DOI: 10.1016/j.ejor.2012.11.043. |
| [7] |
李春霞, 张思林, 庞明宝. 基于时间依赖网络的车辆调度问题研究[J].
交通科技, 2011, 244(1): 104-107.
LI Chunxia, ZHANG Silin, PANG Mingbao. Study of vehicle scheduling problem in time-dependent[J]. Transportation Science & Technology, 2011, 244(1): 104-107. |
| [8] |
TAS D, DELLAERT N, VAN WOENSEL T. The time-dependent vehicle routing problem with soft time windows and stochastic travel times[J].
Transportation Research Part C Emerging Technologies, 2014, 48: 66-83.
DOI: 10.1016/j.trc.2014.08.007. |
| [9] |
李宇飞. 基于时间依赖网络的军事物流配送路径优化问题研究[D]. 北京: 北京交通大学, 2016.
LI Yufei. Research on military logistics distribution routing optimization based on time dependent network[D]. Beijing: Beijing Jiaotong University, 2016. |
| [10] |
RINCON-GARCIA N, WATERSON B, CHERRETT T. A hybrid metaheuristic for the time-dependent vehicle routing problem with hard time windows[J].
International Journal of Industrial Engineering Computations, 2016, 8(1): 141-160.
|
| [11] |
ALINAGHIAN M, ZAMANLOU K, SABBAGH M S. A bi-objective mathematical model for two-dimensional loading time-dependent vehicle routing problem[J/OL]. (2017-02-08). https://link.springer.com/article/10.1057/s41274-016-0151-x.
|
| [12] |
HUANG Y X, ZHAO L, VAN WOENSEL T. Time-dependent vehicle routing problem with path flexibility[J].
Transportation Research Part B Methodological, 2017, 95: 169-195.
DOI: 10.1016/j.trb.2016.10.013. |
| [13] |
杨信丰, 杨庆丰. 随机车辆路径问题的模型及其算法[J].
交通运输系统工程与信息, 2006, 6(4): 75-80.
YANG Xinfeng, YANG Qingfeng. Model and algorithm of vehicle routing problem with stochastic travel time[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6(4): 75-80. |
 2017, Vol. 20
2017, Vol. 20