航空公司通过直销和中介代理商(简称“中介”)销售机票,已成为航空公司机票销售的重要方式。这种机票销售双渠道供应链模式往往以航空公司为主导,以收益分享契约为载体,由航空公司决定收益分享比例[1]。随着“互联网+”时代的到来,由于利益分配不合理,现在航空公司越来越倾向于以直销模式来代替中介。如2016年初,国航等5家航空公司先后宣布国际及地区客票代理费降至为零,并加强直销力度[2]。与传统的双渠道供应链模式相比,直销的优势在于减少了供应链环节,能够依据销售状态及时调整价格;其劣势在于不能有效地获取市场信息,使航空公司直接处于激烈的市场竞争中。特别是在乘客具有策略等待行为的情况下,乘客容易获取航空公司的定价信息,形成理性预期从而选择购买时机,导致航空公司的收益损失。因此,在乘客具有策略行为的情况下,直销模式能否经得住市场竞争的考验,双渠道供应链模式与直销模式相比孰优孰劣,值得深入研究。
基于上述背景,本文在传统航空公司销售渠道的基础上,构建了由中介决定收益分享比例双渠道供应链模式(简称“中介主导的供应链模式”),研究了在供大于求的情况下,航空公司在竞争市场上的供应链协调,并与直销模式相比较,分析该模式对航空公司收益的影响。
本文的研究主要集中在零售商主导的供应链协调和运营管理中策略乘客行为两个方面。以往研究由零售商决定收益分享比例的收益分享契约下供应链协调问题中,往往都认为市场上只存在短视顾客。比如:Cachon等[3]通过分析零售商决定收益分享比例的收益分享契约对供应链协调的影响,发现制定契约后的监督管理成本会比较高,但通过恰当的设计,收益分享契约依然可以实现供应链的协调。张贵磊等[4]构建了供应链和零售商的Stackelberg利润分配博弈模型,引入收益分享契约作为利润再分配的手段,分别分析了供应链主导型和零售商主导型供应链的利润分配情况。Liu等[5]研究了在政府价格管制下通过零售商主导的收益分享契约实现供应链协调。短视顾客不能有效地刻画顾客购买行为,因为策略顾客会选择合适的购物时机,使得自身效用最大化,从而影响零售商以至于生产商的决策。所以近几年在运营管理下的顾客策略行为的研究已成为热点,比如Besanko等[6]首次在垄断厂商跨期定价中考虑顾客的策略行为,分析厂商和策略顾客间的博弈,研究显示如果厂商在跨期定价中忽视顾客的策略行为,会减少约20%的收益。Anderson等[7]考虑了等待至最后时刻或者航空公司重新开放低价舱位时购买机票的行为对收益管理带来的影响,指出应该将乘客的策略行为考虑到收益管理的动态定价决策之中。Liu等[8]研究零售商通过价格承诺和定量配给来减少顾客的策略行为,实现零售商利润最大化。Jerath等[9]考虑厂商面对策略顾客购买行为时,引入模糊销售机制分析理性预期均衡问题,结果表明模糊销售机制能缓解收益管理中顾客策略行为的影响。Prasad等[10]在航空公司机票销售实践中考虑了策略乘客的存在,并引入机票绑定和预留机票定价机制来缓解策略行为的影响。Yan等[11]针对易逝品的顾客策略行为,提出PM(posterior price matching)和DPM(delay posterior price matc- hing)两种定价策略,并给出了两种定价策略的适用情况。这些文献都以价格为变量,探究在乘客策略行为下航空公司价格体系的调整,但是传统运营管理乘客策略行为的研究,没有站在供应链的角度考虑。
也有文献将供应链协调和策略乘客相结合,比如杨道箭等[12]同时考虑顾客策略行为与风险偏好,分析收益分享契约,研究供应链绩效。Su等[13]基于消费者策略行为,在报童模型的基础上分析了理性预期均衡问题,从多角度阐述了该行为对供应链绩效的影响并提出供应链协调策略。Yang等[14]研究在顾客策略行为下,快速反应对供应链绩效的影响。研究结果表明,若快速反应的额外成本较低, 则快速反应在集中式供应链比分散式供应链更有价值。但是这些文献都以供应商为主导并且没有在竞争环境下考虑供应链协调问题。
不同于上述模型,本文构建了由中介主导的机票销售双渠道供应链模式。考虑双航班竞争下面向乘客策略等待行为的供应链协调,并与传统航空公司主导的双渠道供应链模式以及直销模式的收益进行比较,分析了该供应链的有效性。
1 模型假设考虑竞争环境下由中介主导的供应链模式,将销售周期划分为2个周期。在第1周期,由航空公司直接向乘客销售机票;第2周期,将剩余的机票委托中介进行销售,由中介决定机票价格和收益分享比例。该销售供应链模式已应用于国外航空实践中,比如维珍澳洲航空公司和Kayak网站。在销售淡季,在大部分时期由维珍澳洲航空公司直接向乘客销售机票;在临近飞机起飞前,由Kayak网站进行销售,航空直销渠道停止供应机票[15]。该销售供应链模式如图1所示。
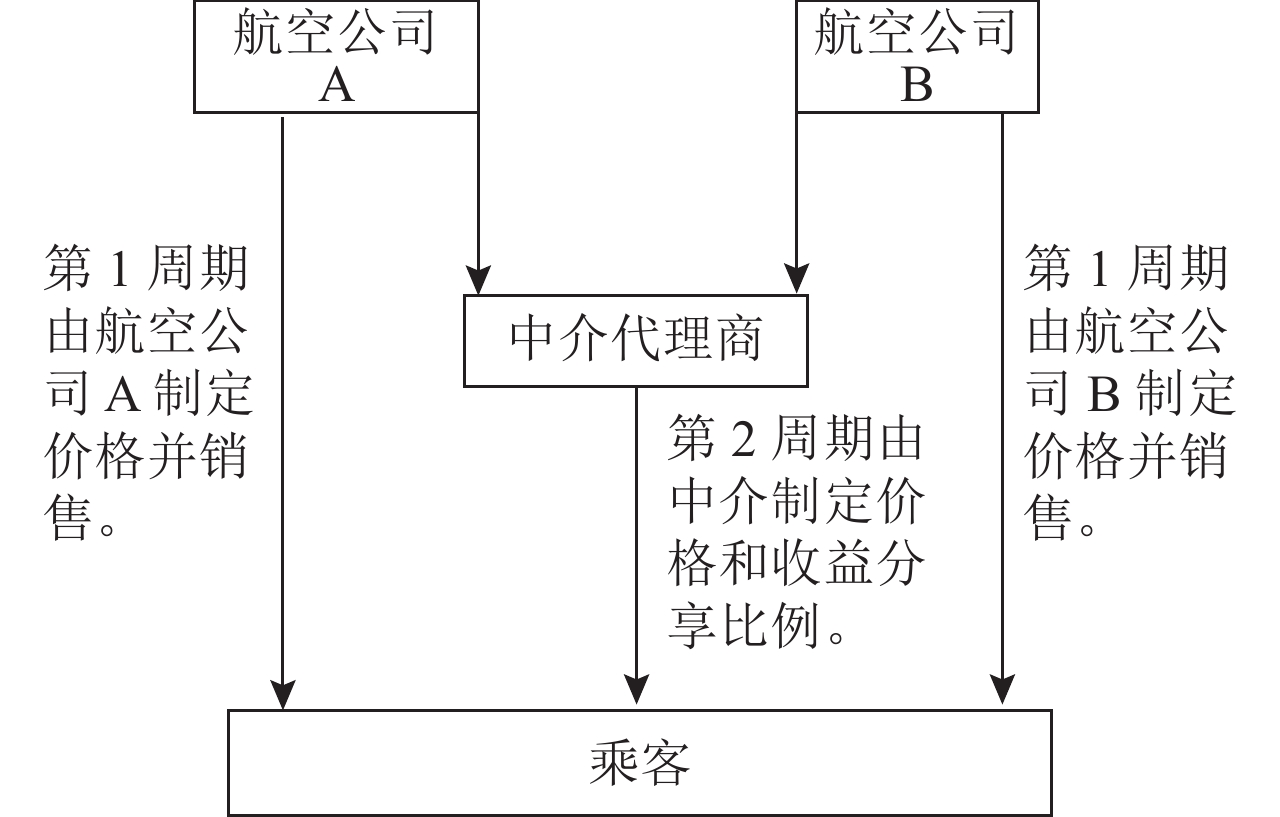
|
图 1 航空公司和中介的销售供应链 Fig. 1 The airline supply chain with the intermediary agent |
假定两家竞争的航空公司A和B需要销售的机票数量均为
本文采用Hotelling模型来刻画乘客的支付意愿,如图2所示。假定A、B分别位于长度为1的Hotelling线的两端,乘客均匀分布在线上,在线上任意一点x值越大,表示对A的偏好越大。因此乘客购买机票的效用由3个因素决定:估价V、机票价格、乘客在Hotelling线上的位置。

|
图 2 航空公司A、B的Hotelling博弈示意图 Fig. 2 Hotelling game graph with Airlines A and B |
以下标j(j=A, B)表示航空公司,本文符号定义如下。
c为单位距离成本,假设c>0。乘客从A公司购买机票将产生cx的成本,从B公司购买机票将产生c(1–x)的成本。
β为航空公司A和B的收益分享比例之和,中介的收益分享比例为1–β。
θ表示乘客预期购买的折扣因子,也称作策略程度[17],θ∈[0, 1]。
pI为中介制定的机票价格。
xj为航空公司j所能覆盖的最远乘客的位置。
πI为中介的收益。
πjI为航空公司j在中介主导的供应链模式下的收益。
πjD为航空公司j在直销模式下的收益。
∆πj为航空公司j在中介主导的供应链模式下的收益与直销模式下的差额收益。
进一步作如下假定。
1) 本文仅分析航空机票售卖淡季,即供大于求的情况(K>J)。在供小于求的情况下,航空公司往往作为“区域垄断者”(regional monopoly)进行销售,形成卖方市场。因此分析供大于求的情况更具有现实意义[9]。
2) 理性预期均衡,即航空公司和乘客的预期值与实际值相同,表现为航空公司和乘客的行为均是理性决策,Su等[13]都采用过此类假设。
3) 信息完全, 航空公司和乘客均知道市场上的所有信息。
4)
由于Hotelling模型的对称性,本文对航空公司A进行分析,B类似。
2 中介主导的销售供应链模型 2.1 基本模型根据传统的收益管理理论,航空公司A、B为实现收益最大化,在供大于求的情况下,有如下两种销售状态。
1) 选择高价,形成非竞争状态。具体表现在乘客坐标x位于[0, xA]区间内,只能在A购买;乘客坐标x位于[xB, 1]区间内,只能在B购买,此时市场上有部分乘客买不到机票。
2) 选择低价,形成竞争状态。具体表现在位于xB右侧的乘客可能在A购买机票,位于xA左侧的乘客可能在B购买机票,此时机票将全部卖完[19]。
在中介主导的供应链模式下,关于航空公司的定价和期望收益大小,有如下定理。
定理1 在供大于求的情况下,当采用中介主导的供应链模式时,航空公司的均衡结果如表1所示。
| 表 1 供大于求时航空公司的均衡状态 Tab. 1 The equilibrium of the airline in oversupply |
证明 首先考虑选择高价,形成非竞争状态。在此情况下,部分乘客有可能买不到机票。为了获得额外收益,在第2周期航空公司将机票交由中介销售,中介可以覆盖(xA, xB)区间里的所有乘客,第2周期每个乘客都可能获得机票。因此有[0, xA]区间内的乘客从A购买机票,[xB, 1]区间内的乘客从B购买机票。
在理性预期的情况下,乘客在第2周期购买的机票来自于A、B的概率均为
对A公司来说,位于临界点xA处的乘客效用满足
|
$\quad\quad V - p_{\rm{A}}^1 - c{x_{\rm{A}}} = \theta V - {p_{\rm{I}}} - \frac{1}{2}c{x_{\rm{A}}} - \frac{1}{2}c\left( {1 - {x_{\rm{A}}}} \right){\text{。}}$
|
为使得收益最大化,以上等式的右边等于0。因此,
|
$\begin{aligned}& \quad\quad {\pi _{{\rm{AI}}}} = \left( {V - c{x_{\rm{A}}}} \right){x_{\rm{A}}}J + \frac{{\beta {\pi _{\rm{I}}}}}{2} = \left( {V - c{x_{\rm{A}}}} \right){x_{\rm{A}}}J + \\& \frac{\beta }{2}\left( {\theta V - \frac{c}{2}} \right)\left( {{x_{\rm{B}}} - {x_{\rm{A}}}} \right)J{\text{。}}\end{aligned}$
|
令
|
$\begin{split}\quad\quad & {x_{\rm{A}}} = \frac{V}{{2c}} - \frac{\beta }{2}\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right),\\& p_{\rm{A}}^1 = V - c{x_{\rm{A}}} = \frac{V}{2} + \frac{\beta }{2}\left( {\theta V - \frac{c}{2}} \right){\text{。}}\end{split}$
|
(1) |
为保证此时航空公司A处于非竞争状态,需要
航空公司A的总收益为
|
$\begin{split}& \quad\quad {\pi _{{\rm{AI}}}} = p_{\rm{A}}^1{x_{\rm{A}}}J + \frac{{\beta {\pi _{\rm{I}}}}}{2} = \left[ {\frac{V}{2} + \frac{\beta }{2}\left( {\theta V - \frac{c}{2}} \right)} \right]\times\\& \left[ {\frac{V}{{2c}} - \frac{\beta }{2}\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right)} \right]J + \frac{{\beta {\pi _{\rm{I}}}}}{2}{\text{。}}\end{split}$
|
(2) |
最后考虑选择低价,形成竞争状态的情况。此时乘客偏好位于区间
由定理1可知,当
定理2 当
|
$\begin{split}& \quad\quad{\pi _{\rm{I}}} \!=\! cJ\left\{ {\left[ {{\theta ^2}\beta \left( {1 - \beta } \right) - \theta \left( {1 - \beta } \right)} \right]{{\left( {\frac{V}{c}} \right)}^2} \!+\! \biggr[ {\theta \left( {1 - \beta } \right) \!+} } \right.\\& \left. {\left. { \! \frac{1}{2}\left( {1 \!-\! \beta } \right)- \theta \beta \left( {1 - \beta } \right)} \right]\frac{V}{c} + \frac{1}{4}\beta \left( {1 - \beta } \right) - \frac{1}{2}\left( {1 - \beta } \right)} \right\}{\text{。}}\end{split}$
|
(3) |
证明 中介的收益为
将中介定价和最优市场覆盖率代入上式,整理可得式(3)。
证毕。
由上面两个定理可知:在中介主导的销售供应链模式下,航空公司的收益为式(2),中介的收益为式(3)。
2.2 收益分享比例的确定中介确定收益分享比例使自身收益最大化,因此有以下定理。
定理3 中介主导的供应链模式下,最优收益分享比例
|
$\quad\quad {\beta ^{\rm{*}}}{\rm{ = }}\displaystyle\frac{1}{2}{\rm{ + }}\frac{{\displaystyle\frac{V}{c}{\rm{ - }}1}}{{2\left( {\theta \displaystyle\frac{V}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)}}{\text{。}}$
|
证明 对πI求关于β的一阶导数,令其为0,得
|
$\begin{array}{l}\displaystyle\frac{{\partial {\pi _{\rm{I}}}}}{{\partial \beta }}\! \!=\!\! cJ\left[ {2\left( {\frac{{\theta V}}{c} \!\!-\!\! \frac{{{\theta ^2}{V^2}}}{{{c^2}}} \!\!-\!\! \frac{1}{4}} \right)\beta \!\!+\!\! \left( {\frac{{{\theta ^2}{V^2} \!\!+\!\! \theta {V^2}}}{{{c^2}}} \!\!-\!\! \frac{{4\theta V \!\!+\!\! V}}{{2c}} \!\!+\!\! \frac{3}{4}} \right)} \right] \!\!=\!\! 0,\\[15pt]{\beta ^*} = \displaystyle\frac{{ {\displaystyle\frac{{4\theta V + V}}{{2c}} - \displaystyle\frac{{{\theta ^2}{V^2} + \theta {V^2}}}{{{c^2}}} - \displaystyle\frac{3}{4}} }}{{2\left( {\displaystyle\frac{{\theta V}}{c} - \displaystyle\frac{{{\theta ^2}{V^2}}}{{{c^2}}} - \displaystyle\frac{1}{4}} \right)}}{\text{。}}\end{array}$
|
(4) |
对πI求关于β的二阶导数得
|
$\quad\quad \frac{{{\partial ^2}{\pi _{\rm{I}}}}}{{\partial {\beta ^2}}} = 2cJ\left( {\frac{{\theta V}}{c} - \frac{{{\theta ^2}{V^2}}}{{{c^2}}} - \frac{1}{4}} \right) = - \frac{{J{{\left( {c - 2\theta V} \right)}^2}}}{{2c}} {\text{<}} 0{\text{。}}$
|
因为
|
$\quad\quad {\beta ^{\rm{*}}}{\rm{ = }}\frac{1}{2}{\rm{ + }}\frac{{\displaystyle\frac{V}{c}{\rm{ - }}1}}{{2\left( {\theta \displaystyle\frac{V}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)}}{\text{。}}$
|
(5) |
所以
由定理3可得航空公司和中介在中介主导的供应链模式下的最优期望收益。
将式(3)和式(4)分别代入式(2)和式(3),得航空公司和中介在中介主导的供应链模式下的最优期望收益:
|
$\begin{array}{l} \quad\quad \pi _{{\rm{AI}}}^* \!=\! \pi _{{\rm{BI}}}^{\rm{*}}{\rm{ \!= \!}}\Biggr[ \!{\displaystyle\frac{{\left( {\theta V\! - \displaystyle\frac{c}{2}} \right)J}}{2}\! - \!\displaystyle\frac{{\left( {\displaystyle\frac{{\theta V}}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)VJ}}{4} \!-\! \displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)VJ}}{{4c}}} \Biggr]\times\\ \displaystyle\frac{{8c\theta V + 2cV - 3{c^2}{\rm{ - }}4{\theta ^2}{V^2} - 4\theta {V^2}}}{{8c\theta V - 8{\theta ^2}{V^2} - 2{c^2}}} + \displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)\left( {\displaystyle\frac{{\theta V}}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)J}}{4} \times \\\displaystyle\frac{{{{\left( {8c\theta V + 2cV - 3{c^2}{\rm{ - }}4{\theta ^2}{V^2} - 4\theta {V^2}} \right)}^2}}}{{{{\left( {8c\theta V - 8{\theta ^2}{V^2} - 2{c^2}} \right)}^2}}} + \displaystyle\frac{{{V^2}J}}{{4c}},\end{array}$
|
(6) |
|
$\begin{split} & \quad\quad\pi _{\rm{I}}^* = \frac{{4\theta {V^2} + {c^2} - 4{\theta ^2}{V^2} - 2cV}}{{8c\theta V - 8{\theta ^2}{V^2} - 2{c^2}}}\left\{ {1 - 2\left[ {\frac{V}{{2c}} - } \right.} \right.\\ & \left. {\left. {\frac{{8c\theta V + 2cV - 3{c^2}{\rm{ - }}4{\theta ^2}{V^2} - 4\theta {V^2}}}{{16c\theta V - 16{\theta ^2}{V^2} - 4{c^2}}}\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right)} \right]} \right\}J \times \left( {\theta V - \frac{c}{2}} \right) {\text{。}}\end{split}$
|
由定理3可得以下推论。
推论1 中介主导的供应链模式下,最优收益分享比例随乘客策略程度的增加而增加。
证明 由式(5),对β*求关于θ的一阶导数,得
|
$\quad\quad \frac{{\partial {\beta ^{\rm{*}}}}}{{\partial \theta }}{\rm{ = }}\displaystyle\frac{{{\rm{ - }}2\left( {\displaystyle\frac{V}{c}{\rm{ - }}1} \right)\displaystyle\frac{V}{c}}}{{4{{\left( {\theta \displaystyle\frac{V}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)}^2}}}{\text{。}}$
|
因为
证毕。
推论1表明:乘客策略程度越大,收益分享比例越大。事实上,乘客策略程度越大,将会有更多的乘客选择等待至第2周期购买,为平衡供应链契约,需要增加最优收益分享比例,让渡一部分收益给航空公司,以弥补其第1周期减少的收益,这与现实情况相符。
3 供应链模式的分析和比较本节主要分析中介主导的供应链模式的有效性,下面通过以下定理来证明。
定理4 航空公司决定收益分享比例的供应链模式不能实现协调。
证明 将式(3)代入式(2),对航空公司的总收益进行整理得
|
$\begin{align}& \quad\quad {\pi _{{\rm{AI}}}} = \frac{{{V^2}J}}{{4c}} + \biggr[ {\frac{J}{2}\left( {\theta V - \frac{c}{2}} \right) - \frac{{VJ}}{4}\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right) -}\\& { \frac{{VJ}}{{4c}}\left( {\theta V - \frac{c}{2}} \right)} \biggr]\beta + \frac{J}{4}\left( {\theta V - \frac{c}{2}} \right)\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right){\beta ^2}{\text{。}}\end{align}$
|
对πAI求关于β的一阶导数,令其为0,得
|
$\begin{align}& \quad\quad\frac{{\partial {\pi _{{\rm{AI}}}}}}{{\partial \beta }}{\rm{ = }}\frac{J}{2}\left( {\theta V - \frac{c}{2}} \right) - \frac{{VJ}}{4}\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right) - \frac{{VJ}}{{4c}}\left( {\theta V - \frac{c}{2}} \right) + \\ & \frac{{J\beta }}{2}\left( {\theta V - \frac{c}{2}} \right)\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right) = 0{\text{。}}\end{align}$
|
求得此时的最优收益分享比例
|
$\quad\quad {\beta ^*} = \frac{{2(V - c)}}{{2\theta V - c}}{\text{。}}$
|
再对其求二阶导数得
|
$\quad\quad \frac{{{\partial ^2}{\pi _{{\rm{AI}}}}}}{{\partial {\beta ^2}}}{\rm{ = }}\frac{J}{2}\left( {\theta V - \frac{c}{2}} \right)\left( {\frac{{\theta V}}{c} - \frac{1}{2}} \right) = \frac{{J{{\left( {2\theta V - c} \right)}^2}}}{{8c}} {\text{>}} 0{\text{。}}$
|
可以看出,当取β*时,航空公司的收益是极小值。
当β*取1时,此时是航空公司收益的最大值,由于没有将收益分配给中介,因此无法实现供应链协调,证毕。
接下来分析中介主导的供应链的有效性。首先分析航空公司采用直销模式的收益,假定航空公司存在两个销售周期,令xD为第1周期与第2周期航空公司直销时,乘客效用的无差异点。
理性均衡时,对航空公司A而言,在xD处有
|
$\quad\quad V - p_{\rm{A}}^1 - c{x_{\rm{D}}} = \theta V - p_{\rm{A}}^2 - c{x_{\rm{D}}},$
|
解得
|
$\quad\quad p_{\rm{A}}^1 = (1 - \theta )V + p_{\rm{A}}^2{\text{。}}$
|
(7) |
在
|
$\quad\quad \theta V - p_{\rm{A}}^2 - cx_{\rm{D}}' = 0,$
|
解得
|
$\quad\quad p_{\rm{A}}^2 = \theta V - cx_{\rm{D}}'{\text{。}}$
|
(8) |
所以航空公司A直销时的期望收益为
|
$\begin{split} & \quad\quad {\pi _{{\rm{AD}}}} = [p_{\rm{A}}^1{x_{\rm{D}}} + p_{\rm{A}}^2(x_{\rm{D}}' - {x_{\rm{D}}})]J = \\ & [(V - cx_{\rm{D}}'){x_{\rm{D}}} + (\theta V - cx_{\rm{D}}')(x_{\rm{D}}' - {x_{\rm{D}}})]J{\text{。}}\end{split}$
|
(9) |
令
将上式代入式(9),得
|
$\begin{align}\quad\quad & {\pi _{{\rm{AD}}}} = \Biggr[\left(V - \frac{{\theta V}}{2}\right){x_{\rm{D}}} + \frac{{\theta V}}{2}\left(\frac{{\theta V}}{{2c}} - {x_{\rm{D}}}\right)\Biggr]J = \\ & \Biggr[V(1 - \theta ){x_{\rm{D}}} + \frac{{{\theta ^2}{V^2}}}{{4c}}\Biggr]J{\text{。}}\end{align}$
|
航空公司的收益函数随xD增加而增加,当xD取极大值
将上式代入式(9),得航空公司的最优期望收益为
|
$\quad\quad \pi _{{\rm{AD}}}^* = p_{\rm{A}}^1{x_{\rm{D}}}J = \frac{{{V^2}J}}{{4c}}{\text{。}}$
|
(10) |
即直销模式下航空公司的最优期望收益为
有了以上分析,可得以下定理。
定理5 当
证明 在最优收益分享比例β*下,将航空公司在中介主导的供应链模式下的收益与直销模式的收益比较,式(6)减式(10),得
|
$\begin{array}{*{20}{l}}{\quad \quad \Delta \pi = \Biggr\{ \Biggr[\displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)}}{2} - \displaystyle\frac{{\left( {\displaystyle\frac{{\theta V}}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)V}}{4} - \displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)V}}{{4c}}\Biggr] + }\\{\displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)\left( {\displaystyle\frac{{\theta V}}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)}}{4} \cdot \left. {\displaystyle\frac{{8c\theta V + 2cV - 3{c^2}{\rm{ - }}4{\theta ^2}{V^2} - 4\theta {V^2}}}{{8c\theta V - 8{\theta ^2}{V^2} - 2{c^2}}}} \right\} \times}\\{ J{\beta ^*}}{\text{。}}\end{array}$
|
因为β*>0,J>0,得
|
$\begin{split}& \quad\quad\displaystyle\frac{{\Delta \pi }}{{J\beta ^{\rm{*}}}}{\rm{ = }}\Biggr[ {\displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)}}{2} - \displaystyle\frac{{\left( {\displaystyle\frac{{\theta V}}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)V}}{4} - \displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)V}}{{4c}}} \Biggr]{\rm{ + }}\\ & \displaystyle\frac{{\left( {\theta V - \displaystyle\frac{c}{2}} \right)\left( {\displaystyle\frac{{\theta V}}{c}{\rm{ - }}\displaystyle\frac{1}{2}} \right)}}{4} \cdot \displaystyle\frac{{8c\theta V + 2cV - 3{c^2}{\rm{ - }}4{\theta ^2}{V^2} - 4\theta {V^2}}}{{8c\theta V - 8{\theta ^2}{V^2} - 2{c^2}}}{\text{。}}\end{split}$
|
化简得
|
$\quad\quad \frac{{\theta V}}{{\rm{4}}} - \frac{{{\rm{5}}c}}{{32}}{\rm{ + }}\frac{{3V}}{{16}} - \frac{{\theta V}}{{2c}}{\rm{ + }}\frac{{{\theta ^2}{V^2}}}{{8c}} + \frac{{\theta {V^2}}}{{8c}}{\text{。}}$
|
由
因为
得证。
由定理5可以看出,对航空公司而言,在中介主导的供应链模式存在的情况下,其收益恒大于直销模式。其原因在于在中介主导的供应链模式下,航空公司可以通过中介将机票卖给偏好较小的乘客。因此,较之于直销模式,航空公司在该模式下会获得更多的收益。
4 算例分析本节将通过数值模拟验证以上结果,讨论不同参数对中介主导的供应链中的收益分享比例、中介收益和航空公司收益的影响。为了计算方便,假定J=1。
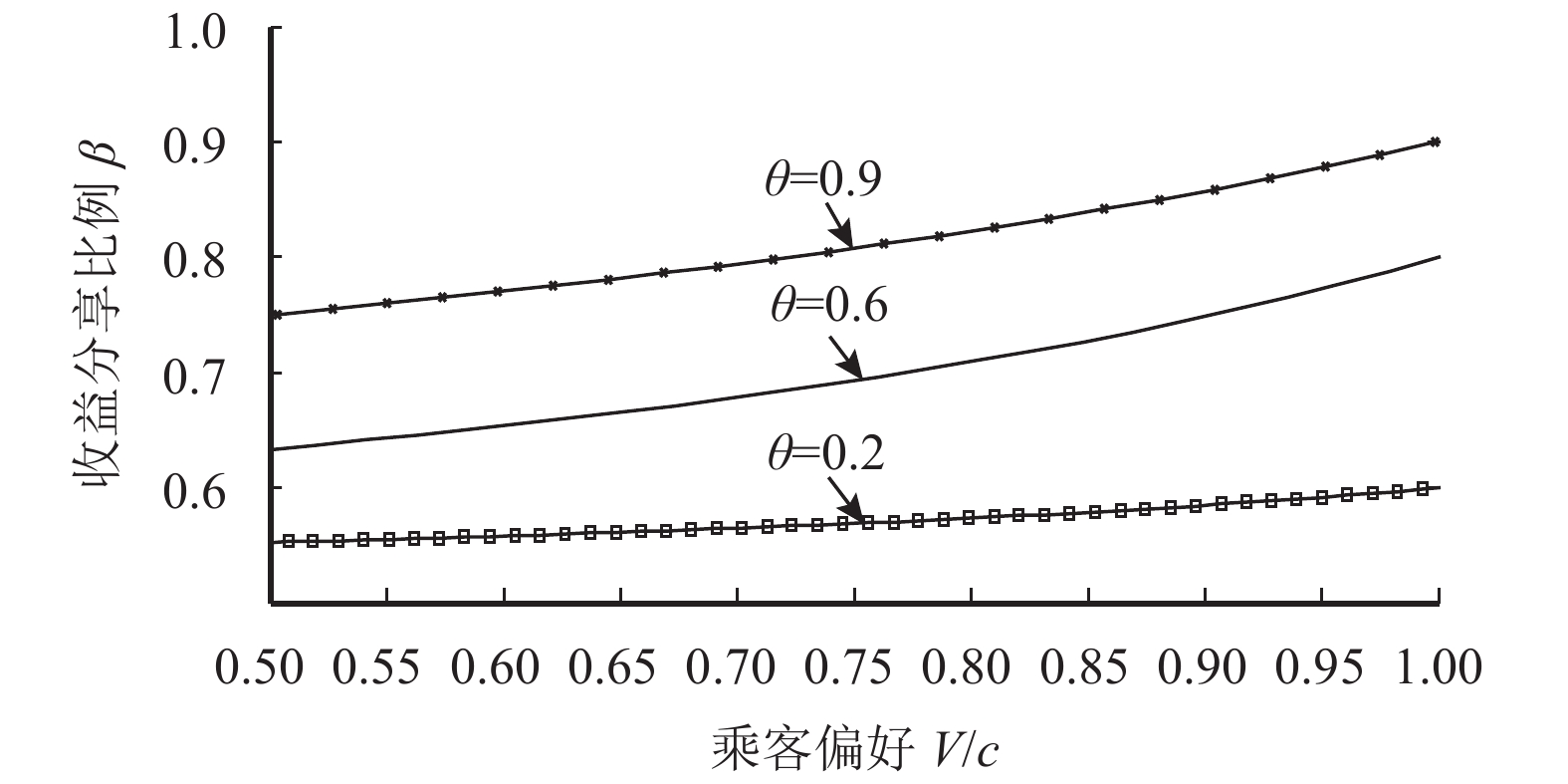
4.1 不同策略程度对收益分享比例的影响首先考虑不同策略程度和乘客偏好对收益分享比例的影响,采用3种不同的θ值:0.2,0.6,0.9,模拟乘客偏好与收益分享比例的关系。如图3所示,可知对相同偏好的乘客,其策略程度越大,收益分享比例也越大,与推论1相符。随着乘客策略程度的增加,图形的单调性越明显。同时,对策略程度相同的乘客,乘客偏好越大,收益分享比例也越大。
不同于市场争夺效应(competitive effect of the market),航空公司面对策略程度越大的乘客时,在第1周期卖出机票的数量越少,导致需求转移到第2周期,销售给偏好较小的乘客,获得更多的收益。
|
图 3 不同参数对收益分享比例的影响 Fig. 3 The influence of different parameters on the revenue sharing proportion |
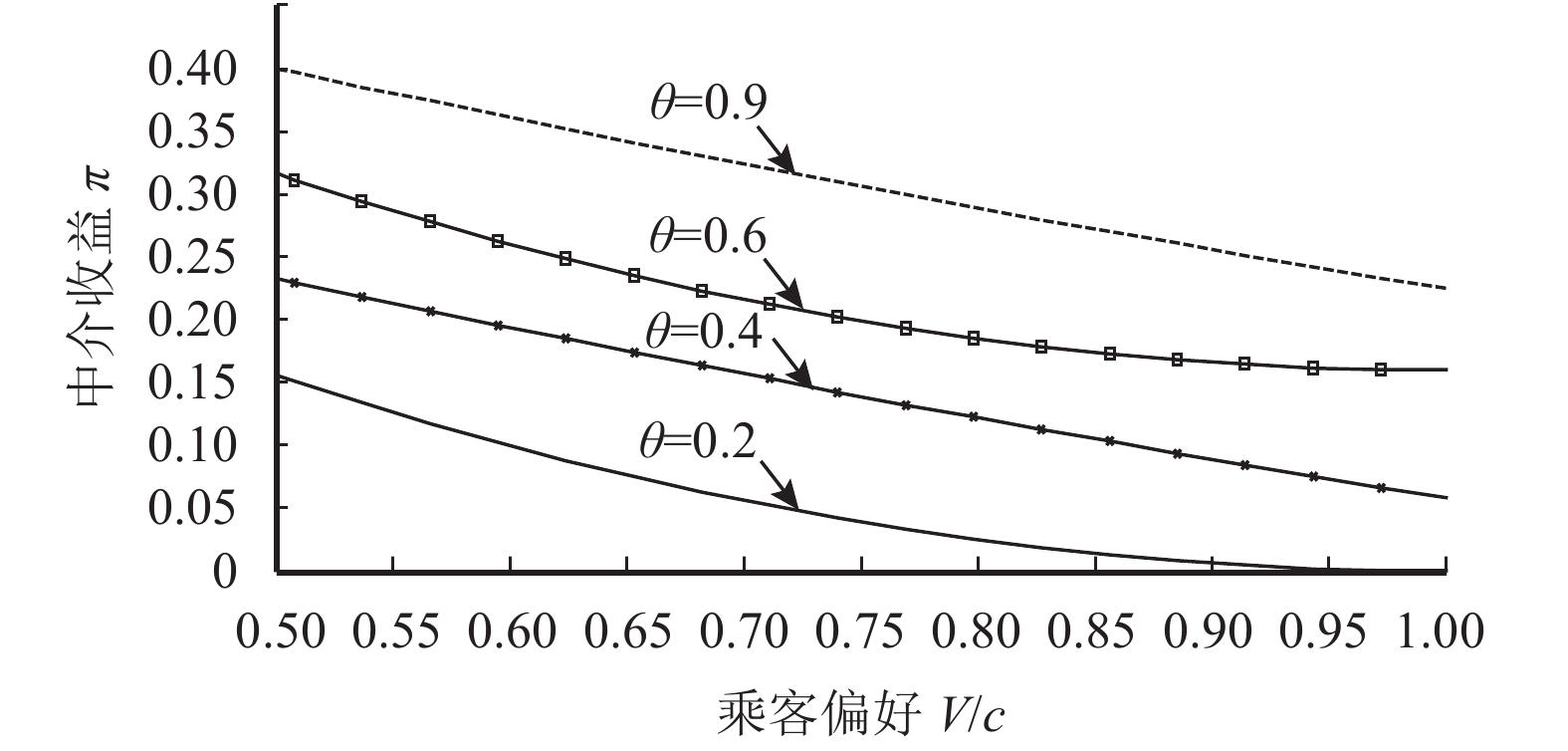
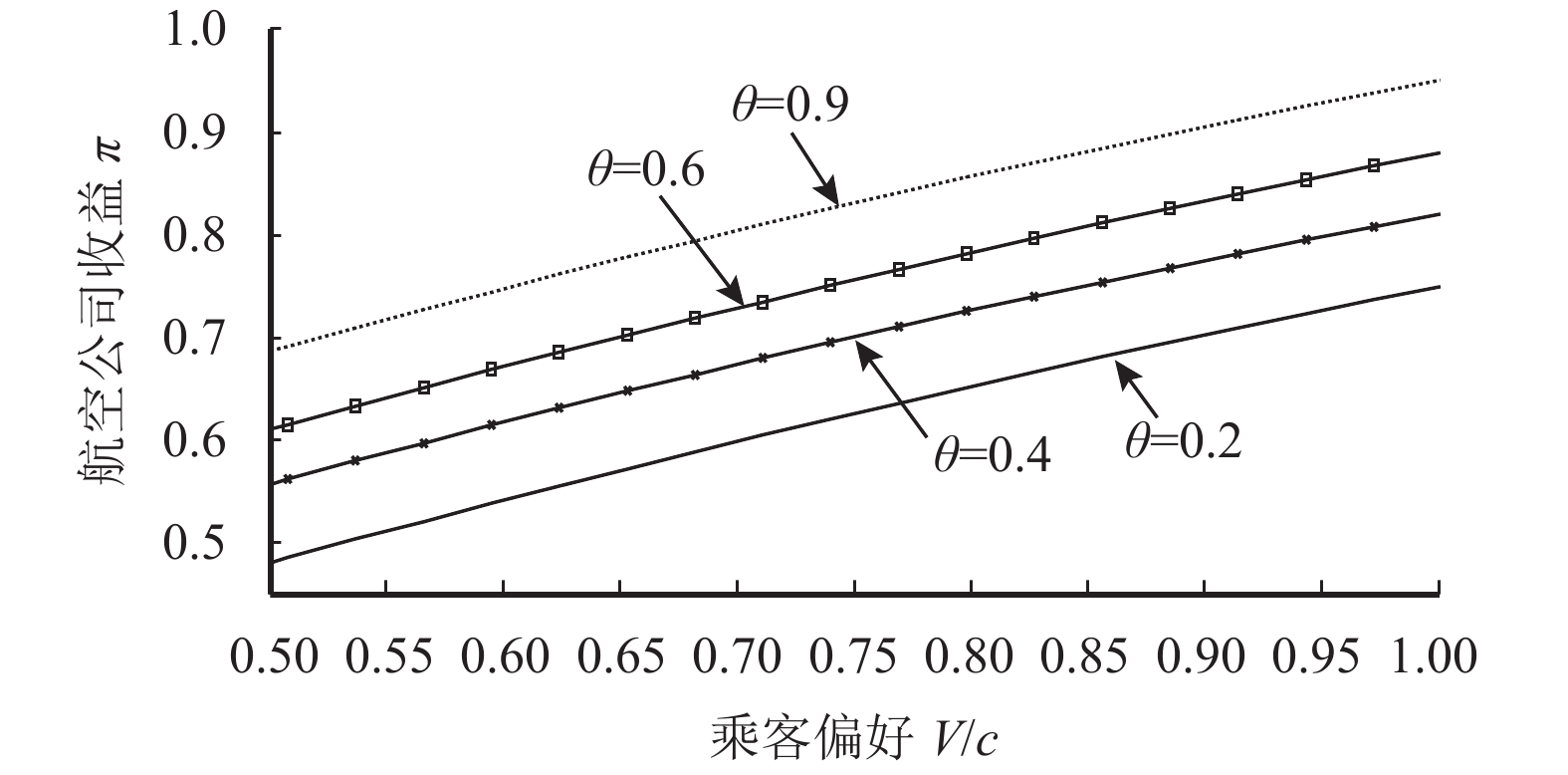
采用4种不同的θ值:0.2,0.4,0.6,0.9,考察不同策略程度对中介和航空公司收益的影响。如图4所示,可知对策略程度相同的乘客,中介收益随着乘客偏好增加而减小。对相同偏好的乘客,其策略程度越大,中介收益越大。如图5所示,可知对策略程度相同的乘客,航空公司收益随着乘客偏好增加而增加。对相同偏好的乘客,其策略程度越大,航空公司收益越大。
|
图 4 不同参数对中介收益的影响 Fig. 4 The influence of different parameters on the intermediary agent’s revenue |
|
图 5 不同参数对航空公司收益的影响 Fig. 5 The influence of different parameters on the airline’s revenue |
采用5种不同的θ值:0,0.2,0.4,0.6,0.9,考察中介主导的供应链模式的有效性。如图6所示,可知在相同的策略程度下,航空公司在中介主导的供应链模式与直销模式下的差额收益随乘客偏好的增加而增加。在乘客偏好相同的情况下,策略程度越大,航空公司的差额收益也越大。即乘客策略行为越明显,采取中介主导的供应链模式更优于直销模式。但是当乘客偏好趋于1时,差额收益趋于一个定值。当乘客的品牌偏好一旦建立,其策略的有效性并不会无限增加。总体来说,在乘客偏好较小的情况下,中介主导的供应链模式能一定程度上缓解乘客的策略行为。
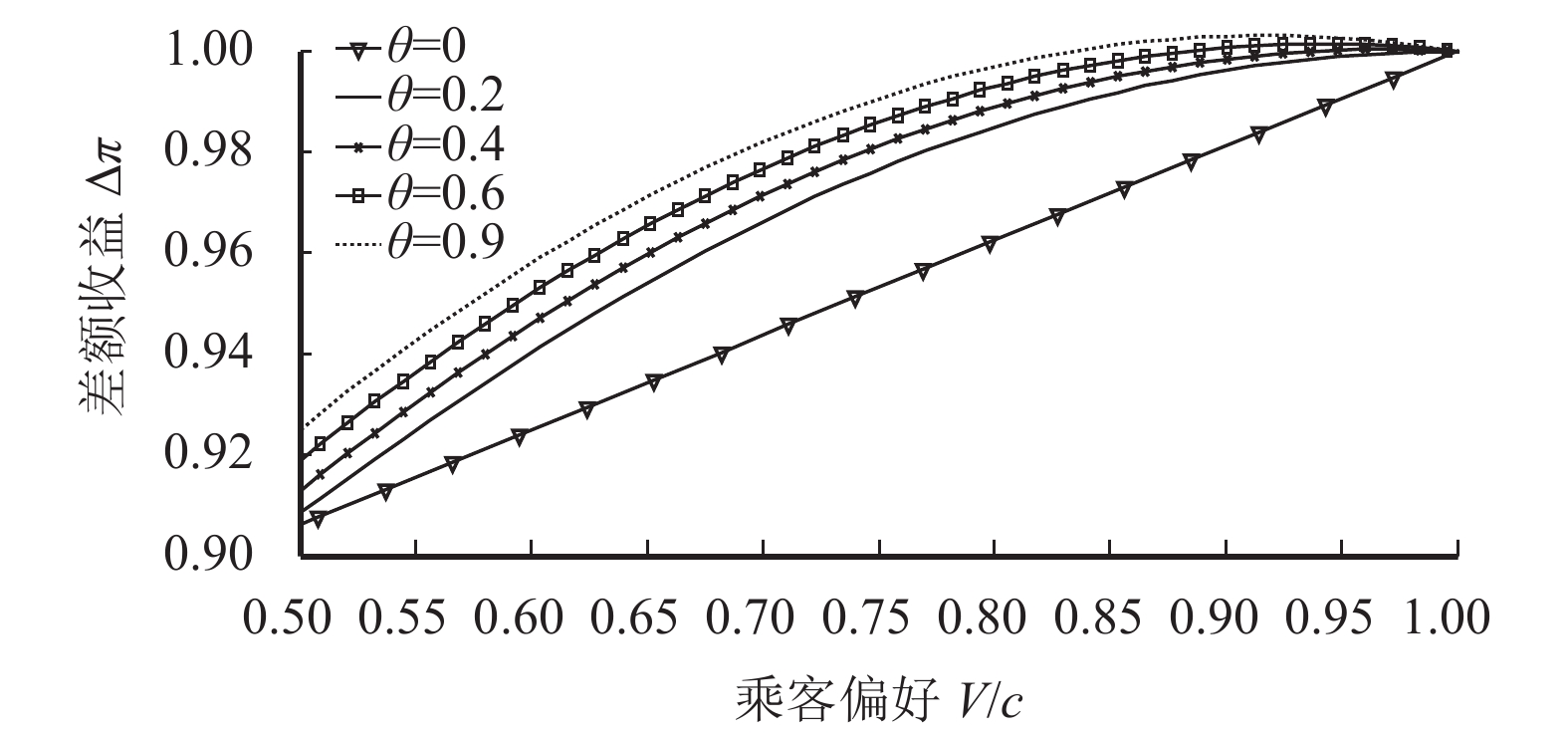
|
图 6 不同参数对差额收益的影响 Fig. 6 The influence of different parameters on the difference of revenue |
本文在供大于求的情况下,构建了中介主导的机票销售双渠道供应链模式。在该供应链模式中,两航空公司处于竞争状态,乘客具有策略行为。通过建立模型,本文首先求得航空公司和中介的收益,以及最优收益分享比例,在此基础上分析了中介主导的供应链模式的有效性。研究表明:1)中介主导的供应链模式存在于乘客偏好较小的情况;2)传统由航空公司主导的供应链模式不能实现协调;3)航空公司在中介主导的供应链模式下的收益大于直销模式的收益。最后通过算例分析,讨论了不同参数对中介主导的供应链中的收益分享比例、中介收益和航空公司收益的影响,同时分析中介主导的供应链模式的有效性。得出:1)策略程度相同的乘客,随乘客偏好的增加,收益分享比例、航空公司的收益和差额收益均增加,而中介的收益随乘客偏好的增加而减小;2)偏好相同的乘客,随策略程度的增加,收益分享比例、中介的收益、航空公司的收益和差额收益均增加。
本文的结论可在供大于求的情况下,对航空公司与中介建立新的利益共享机制,提高收益具有一定的指导意义。
后续研究还可以从以下两个方面加以讨论:1)考虑乘客的策略程度是一个随机函数时中介主导的供应链模式对策略乘客的缓解效果;2)可扩展至多个中介、多个航空公司竞争情况下,研究航空公司的供应链协调机制。
| [1] |
张丽, 丁晓东, 孙占芳. 航空客票销售渠道的博弈研究[J].
数学的实践与认识, 2014, 44(19): 155-161.
ZHANG Li, DING Xiaodong, SUN Zhanfang. An game model of airline tickets marketing channel[J]. Mathematics in Practice and Theory, 2014, 44(19): 155-161. |
| [2] |
国航等5家航空公司宣布: 机票代理手续费降为零[EB/OL]. (2016-02-05). http://www.Chinanews.com/gn/2016/02-25/7773318.shtml, 2016-02-25.
|
| [3] |
CACHON G P, LARIVIERE M A. Supply chain coordination with revenue-sharing contracts: strengths and limitations[J].
Management Science, 2005, 51(1): 30-44.
DOI: 10.1287/mnsc.1040.0215. |
| [4] |
张贵磊, 刘志学. 主导型供应链的Stackelberg利润分配博弈[J].
系统工程, 2006, 24(10): 19-23.
ZHANG Guilei, LIU Zhixue. A Stackelberg game of profit division in supply chains with dominant firms[J]. Systems Engineering, 2006, 24(10): 19-23. DOI: 10.3969/j.issn.1001-2362.2006.10.012. |
| [5] |
LIU X, LI J, WU J. Coordination of supply chain with a dominant retailer under government price regulation by revenue sharing contracts[J].
Annals of Operations Research, 2016, 5(1): 1-26.
|
| [6] |
BESANKO D, WINSTON W L. Optimal price skimming by a monopolist facing rational consumers[J].
Management Science, 1990, 36(5): 555-567.
DOI: 10.1287/mnsc.36.5.555. |
| [7] |
ANDERSON C K, WILSON J G. Wait or buy? The strategic consumer: pricing and profit implications[J].
Journal of the Operational Research Society, 2003, 54(3): 299-306.
DOI: 10.1057/palgrave.jors.2601497. |
| [8] |
LIU Q, VAN RYZIN G J. Strategic capacity rationing to induce early purchases[J].
Management Science, 2008, 54(6): 1115-1131.
DOI: 10.1287/mnsc.1070.0832. |
| [9] |
JERATH K, NETESSINE S, SENTHIL K. Revenue management with strategic customers: last-minute selling and opaque selling[J].
Management Science, 2010, 56(3): 430-448.
DOI: 10.1287/mnsc.1090.1125. |
| [10] |
PRASAD A, VENKATESH R, MAHAJAN V. Product bundling or reserved product pricing? Price discrimination with myopic and strategic consumers[J].
International Journal of Research in Marketing, 2015, 32(1): 1-8.
DOI: 10.1016/j.ijresmar.2014.06.004. |
| [11] |
YAN B, KE C. Two strategies for dynamic perishable product pricing to consider in strategic consumer behavior[J].
International Journal of Production Research, 2015, 24(4): 1-16.
|
| [12] |
杨道箭, 齐二石, 魏峰. 顾客策略行为与风险偏好下供应链利润分享[J].
管理科学学报, 2011, 14(12): 50-59.
YANG Daojian, QI Ershi, WEI Feng. Supply chain profit sharing under strategic customer behavior and risk preference[J]. Journal of Management Sciences in China, 2011, 14(12): 50-59. |
| [13] |
SU X M, ZHANG F Q. Strategic customer behavior, commitment, and supply chain performance[J].
Management Science, 2008, 54(10): 1759-1773.
DOI: 10.1287/mnsc.1080.0886. |
| [14] |
YANG D J, QI E, LI Y J. Quick response and supply chain structure with strategic consumers[J].
Omega, 2015, 52: 1-14.
DOI: 10.1016/j.omega.2014.10.006. |
| [15] |
Virgin Australia[EB/OL]. [2016-08-21]. http://www.virginaustralia.com/au/en/.
|
| [16] |
Su X M. Intertemporal pricing with strategic customer behavior[J].
Management Science, 2007, 53(5): 726-741.
DOI: 10.1287/mnsc.1060.0667. |
| [17] |
LEVIN Y, MCGILL J. Optimal dynamic pricing of perishable items by a monopolist facing strategic consumers[J].
Production and Operations Management, 2009, 50(1): 128-143.
|
| [18] |
NEVEN D. Two stage (perfect) equilibrium in Hotelling’s model[J].
The Journal of Industrial Economics, 1985, 33(3): 317-325.
DOI: 10.2307/2098539. |
| [19] |
周杰, 李豪. 考虑乘客策略行为的航空客运机票模糊销售机制研究[J].
工业工程与管理, 2016, 21(1): 150-158.
ZHOU Jie, LI Hao. The study of opaque selling mechanism for airline with strategic passengers[J]. Industrial Engineering and Management, 2016, 21(1): 150-158. |
 2017, Vol. 20
2017, Vol. 20