生产线平衡的研究已有多年，1954年由Bryton提出^[1]。在Balancing of A Continuous Production Line一文中，他首次提出了生产线平衡的问题并运用“会聚过程法”对装配生产线的问题进行了研究和改善，其研究结果使得装配生产线上总的空闲时间达到最小化^[2]。

组装生产线平衡优化一般有3种方法:数学模型法、启发式方法和IE方法。Salveson在1955年首次运用数学模型方法解决生产线平衡问题，他用线性规划模型模拟生产线，并求出模型解^[3]。1956年Jackson提出了一种解决生产线平衡的启发式方法——杰克逊列举法^[4]，但由于耗时长、操作困难，因此实用性大打折扣。孙建华等^[5]从实际生产情况出发，针对生产线上出现的问题，提出了一种基于精益生产的改善生产线方法。该方法运用现场管理的工具——“6S”管理和目视管理，并将生产平衡率作为衡量评价生产线优劣的标准之一。郭伏等^[6]使用MOD法(模特排时法)对生产线上所有工位操作动作进行分析，利用IE方法中的动作经济和“ECRS”原则进行改善。3种方法各有利弊，本文通过对比分析三者优缺点，见表1。

表 1(Tab. 1)

表 1 生产线平衡方法对比 Tab. 1 Comparison of assembly line balancing methods 方法 优点 缺点 数学分析法 复杂问题抽象成数学模型求解。 运算量较大，实用性不强。 启发式方法 通俗易懂，克服运算量大的缺点。 得出的解是理想解，但不是最优解。 IE方法 结合实际，通过合理的改变提高效率。 数据需要测量，会受到主观因素影响。

表 1 生产线平衡方法对比 Tab. 1 Comparison of assembly line balancing methods

因此，本文选择基础IE方法对A公司3号组装生产线进行分析改善，并结合Flexsim软件对改善效果进行评价，确保改善方案的科学性和有效性。本文不仅完成了对A公司生产线平衡的改善，还为制造企业和将来研究人员提供启发和借鉴意义。

基础IE解决问题主要有两大手段，方法研究和作业测定。前者是优化改善的原理，后者则是优化改善过程中常用的方法。

方法研究是对现有的作业系统和工作方法进行分析，进而改善优化，从而达到提高生产效率和降低成本的最终目的。

方法研究包括程序分析、操作分析和动作分析3个部分。程序分析是研究和分析整条流水线的流程程序，寻求最佳作业内容和操作顺序。目的是以最低时间消耗完成最高的效益^[7-8]。操作分析是研究人机活动配合程度，发现问题改善操作^[9]。动作分析是从微观层面以人体活动部位为研究对象，分析不必要的动作进行剔除，进行简化。

作业测定是制定标准工时的方法，通过测量作业时间，再经评比宽放之后得到标准工时，用来计算生产线平衡指标。进而对生产线现状进行分析研究，提出改善方案^[10]。

制定标准时间的方法一般有3种：经验判断法、历史记录法和作业测定法。通过对比最终选择作业测定方法测工时，具体比较如表2所示。

表 2(Tab. 2)

表 2 3种测量工时方法对比表 Tab. 2 Comparison of three methods for measuring working hours 方法 内容 优点 缺点 经验判断 凭实践经验估算出工时消耗。 简便易行。 误差较大。 历史记录法 根据过去统计的生产同类型产品的资料，估计作业的标准工时。 历史真实数据具有一定的科学性。 所得标准工时包括其他时间，一般比实际时间多。 作业测定法 用秒表等测量操作时间，加入评比和宽放系数后得到标准工时。 所得数据更准确，具有很强的科学性。 容易受主观影响。

表 2 3种测量工时方法对比表 Tab. 2 Comparison of three methods for measuring working hours

生产线的运行状况可以定量衡量平衡状态，一般有3种平衡的评价指标：生产线平衡率、生产线平衡损失率和平滑性指数。

生产线平衡率是衡量生产线各工位作业负荷状况和生产效率的指标，计算时要使用标准工时^[11]。

用公式表达为

其中，LBR为生产线平衡率；T_i为各工序标准工时；CT为瓶颈工序时间；n为作业人员数。

一般地，生产线的生产平衡率达到85%及以上，则可以说该生产线是比较有效率的。

在生产线中，因工作负荷不均衡导致的时间浪费，称为生产线平衡损失率。

用公式表达为

其中，d为生产线平衡损失率；T_j为各工序损失的标准工时；CT为瓶颈工序时间；n为作业人员数。

对生产线平衡损失率的评判标准如表3所示。

表 3(Tab. 3)

表 3 平衡损失率评价表 Tab. 3 Evaluation of balance loss rate 生产平衡损失率d/% 评判效果 ≤10 优 10~20 良 ≥20 差

表 3 平衡损失率评价表 Tab. 3 Evaluation of balance loss rate

平滑性指数是通过计算生产线上不同工位工时的关系来衡量工时的波动情况的指标^[12]。其具体公式为

其中，SI为平滑性指数；T_i为各工序的标准工时；CT为瓶颈工序时间；n为作业人员数。

SI值越大则表示各工位作业时间分布越分散，SI值越小则表示各工位作业时间分布越集中，操作时间比较接近。

A公司三号组装生产线为流水生产线采用链式传送带进行产品运输，共有9个工位分别为：底托组装与上胆、套玻璃棉、上探头、压筒子、装堵帽、打控制盒、装挂架、装拍上盖、蒸汽加热。A公司3号生产线具体布局如图1。

图 1(Fig. 1)

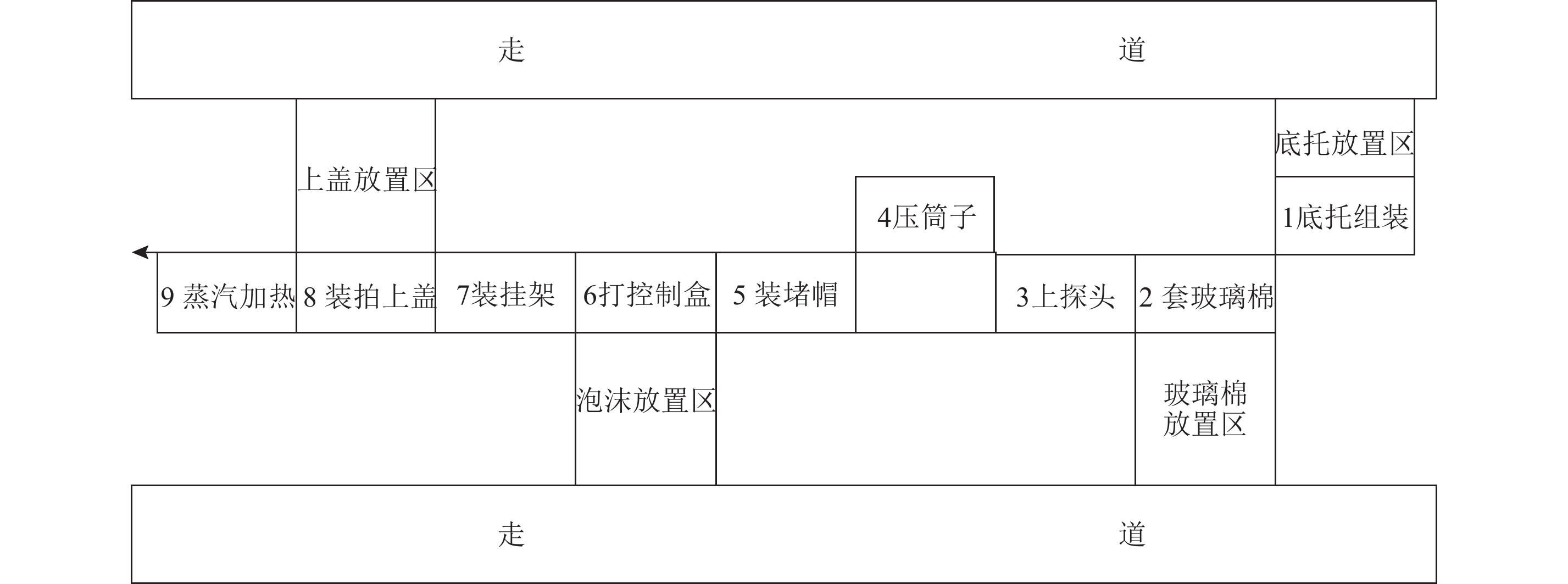
图 1 A公司组装生产线布局图 Fig. 1 Assembly line layout of Company A

图中2、3、4、5、7、8、9为工位位置，放置区表示物料位置，1和6为表示无法移动的工位。由图可见，生产线布局不当，明显偏向于图的下侧。可能会影响生产工艺流程的设计和工人的生产操作。

A公司3号组装生产线中的9个工序可以细化分为30个作业内容，操作工人10名，详细的作业内容及操作工时见表4。为便于直观观察生产瓶颈及平衡状况，本文根据表4测得的数据绘制标准作业山积图见图2。

表 4(Tab. 4)

表 4 作业内容和工时测定表 Tab. 4 Job contents and time determination 序号 作业名称 测量时间 标准工时 序号 作业名称 测量时间 标准工时 1 拉胆到提胆机下 3 3.70 16 检查控制盒 1 1.23 2 放底托上胆 7 8.62 17 拿贴二维码 4 4.93 3 推胆到传送带 3 3.70 18 整理塑料套 4 4.93 4 放保温棉 5 6.16 19 装泡沫 3 3.70 5 塑料袋扎口 6 7.39 20 正螺丝孔 2 2.46 6 将进出水口掏出 4 4.93 21 拿支架上支架 7 8.62 7 掏出排污阀 4 4.93 22 拧螺丝 6 7.39 8 接探头线 5 6.16 23 检查上盖 2 2.46 9 上探头 4 4.93 24 放上盖 10 检查筒体 3 3.70 25 收塑料套 4 4.93 11 上筒 2 2.46 26 压紧上盖 7 8.62 12 按压结实 5 6.16 27 装红蓝堵帽 7 8.62 13 扫码 2 2.46 28 压紧堵帽 14 贴二维码 2 2.46 29 贴螺丝盖膜 4 4.93 15 装大堵帽 4 4.93 30 充蒸汽 5 6.16

表 4 作业内容和工时测定表 Tab. 4 Job contents and time determination

由表4中的数据，可以计算A公司3号生产线目前的生产平衡指标：

生产平衡率= $\displaystyle\frac{{141.67}}{{9 \times 23.41}}$ =67.24%；

平衡损失率=1–67.24%=32.76%；

平滑性指数= $\sqrt {\displaystyle\frac{{680.41}}{9}} $ =8.69。

由计算结果可知，生产平衡率远小于85%，损失率较高，可见目前A公司3号组装生产线的生产效率不高，存在很大的改善空间。根据表4测得的数据，可以绘制山积图以便于观察生产线的工时平衡情况，发现瓶颈。

图 2(Fig. 2)

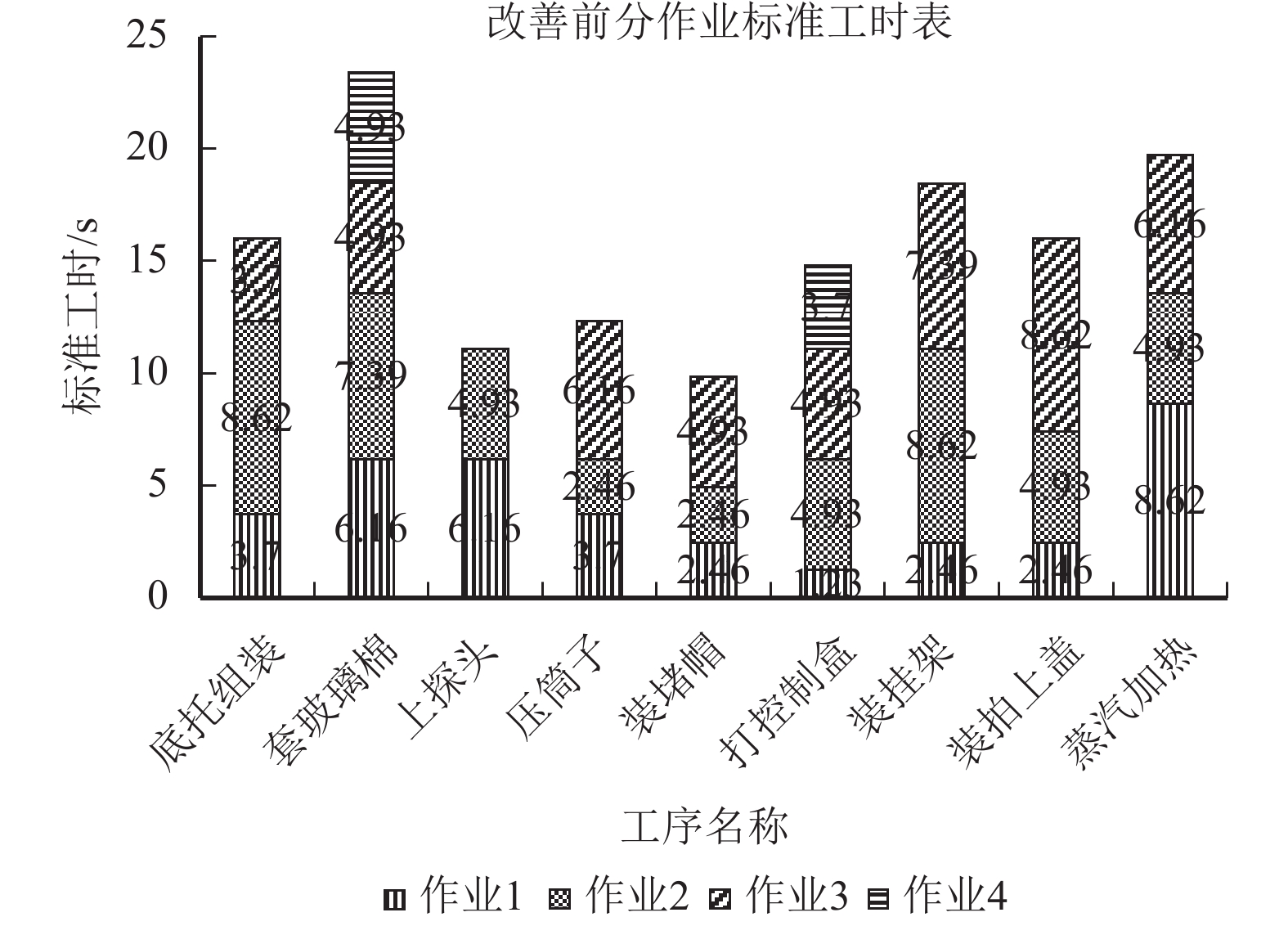
图 2 A公司改善前生产线工时山积图 Fig. 2 Operating loading chart of Company A before improvement

由图2可以看出第2工序所用工时最长，为该生产线的瓶颈，9道工序的工时差异较大，工作负荷出现严重不均的现象。

本文选用模特排时法，对A公司操作工人进行动作分析，分析结果如表5。

表 5(Tab. 5)

表 5 工作动作因素分析 Tab. 5 Action factor analysis 工序 左手 右手 左右手 其他 时间/MOD 底托组装与上胆 W5G1W5P2 M3G1M3P0、M3G1M3P0 27 套玻璃棉 W5G1W5P0 M3P2M3P0 M3P2M3G1M1P2M3P0 34 上探头 W5G1 W5G1M2P5 W5G0M1P5 24 压筒子 (M3G1×2)E2(L1×2)M3A4P0 19 装堵帽 M2G1、M1G1M3P2 M2G1M2P0、M1G1M3P2 17 打控制盒 W5G1M2P2 M3G1M3P2 M2P2 E2 25 装挂架 (M3G1M1P2×2)、M2P2 M1G1M3P2M3G1、(M3G1M1P2×2)、M3G1M3P2 32 装拍上盖 M2G1 M3P0、M2P2 M3G1E2、A4M3P2 25 蒸汽加热 M3G1、M3P0 M1P2、M3P2 M3G1M3P2、M3G1M3P2 33

表 5 工作动作因素分析 Tab. 5 Action factor analysis

由表4可以得出1-9工序的MOD值共计236 MOD。动作分析从微观层面上了解每个工序的动作情况，可以解决宏观层面无法改善的情况。

对生产线布局改善时，需遵守几点原则。

1) 符合生产工艺。生产线要为生产服务，这是最基本的原则。

2) 利用率最大化。人、机、物料尽可能达到效率最大化。

3) 搬运最少化。减少物料和在制品的搬运，有助于减少浪费。

基于以上原则并结合A公司的实际问题，本文对生产线做出改善如图3。

图 3(Fig. 3)

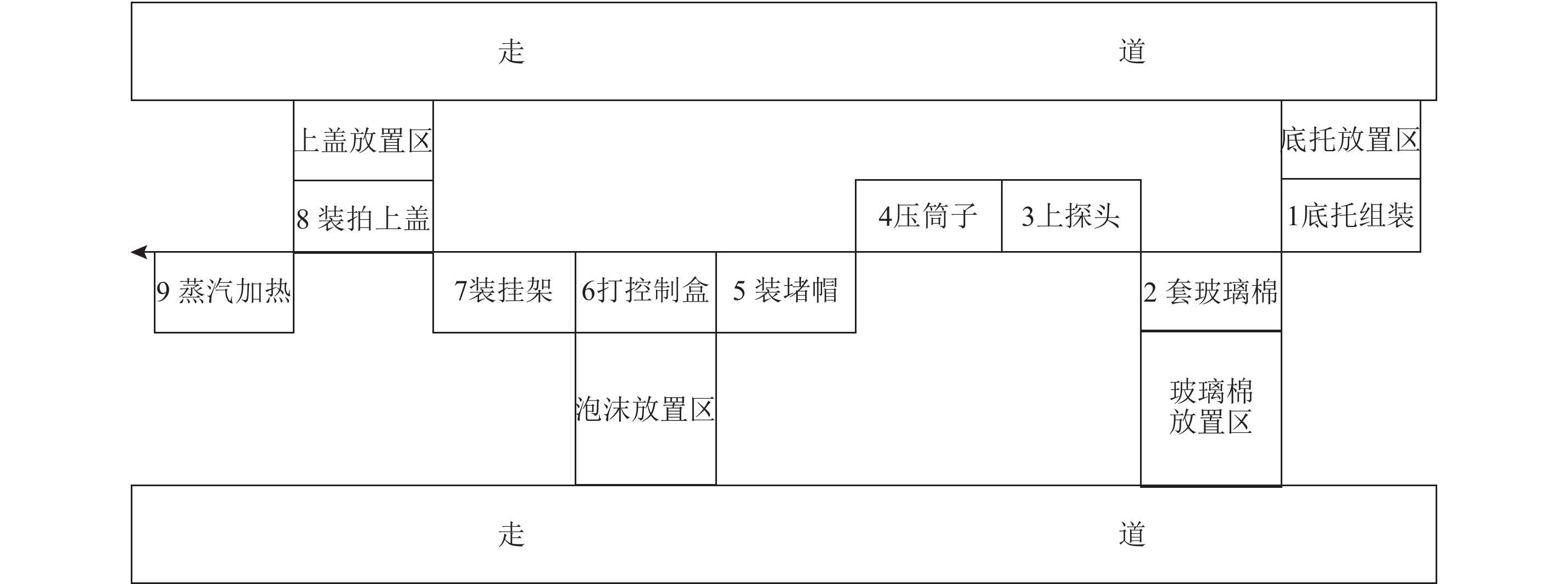
图 3 改善后的A公司组装生产线布局图 Fig. 3 Improved assembly line layout of Company A

图中3和8为调整的工位位置，其他区域不变。经改善后，原来的一侧偏型变为交叉型布局，可有效节省空间。第8工位原本因布局不合理造成的两人负责可减少为一人完成。经过生产线布局调整后，3种生产平衡评价指标分别为

经过布局调整，减少了一名操作人员，生产平衡率较之前的60.52%有了小幅提升。但仅是减少操作人员的数量，工时并没有改变，因而平滑性指数不降反升，由原来的8.25变为8.69，各工序工时分散程度略增。因此，单纯的减少工人数来提升生产平衡率的办法是不恰当的。

程序改善是经过改善工艺或调整作业顺序，使各工序作业时间接近，平衡工作负荷。在改善过程中一般遵循几点原则。

1) 对作业瓶颈进行改善。找出生产线中的瓶颈并予以消除，使得每一个工序工时尽可能接近。

2) 分担转移。将工作负荷较大的工序作业分担给空闲时间较多的工序。

3) 重组合并。合并工时较少的工序，重新组合，以提高生产效率。

4) 分解短程序。将作业时间较短且可以分解的工序分解重新分配到其他工序中。

根据程序改善的原则与方法，本文对9个程序分别提出改善方案，改善后的山积图如图4所示。

图 4(Fig. 4)

图 4 改善后的标准工时山积图 Fig. 4 Improved operating loading chart of Company A

其中经过程序改善的工序有：套玻璃棉、压筒子、装堵帽、装挂架，本文分别提出改善方案。

②套玻璃棉改善方案：该工序是瓶颈工序，根据改善瓶颈的原则，将该工序作业时间进行压缩。从时间的合适性来说，可以把第3作业部分或第4作业部分调整到第5工序中。改善后的工时为18.48 s。

④压筒子改善方案：该工序用时较短，根据程序改善中分担转移原则，可以承担第7工序正螺丝孔这一作业。改善后的工时为14.78 s。

⑤装堵帽改善方案：该工序用时较短，由②的改善方案可知，改善后的工时为14.78 s。

⑦装挂架改善方案：根据分担转移原则，将正螺丝孔这一作业调整到第4工序。改善后的工时为16.01 s。

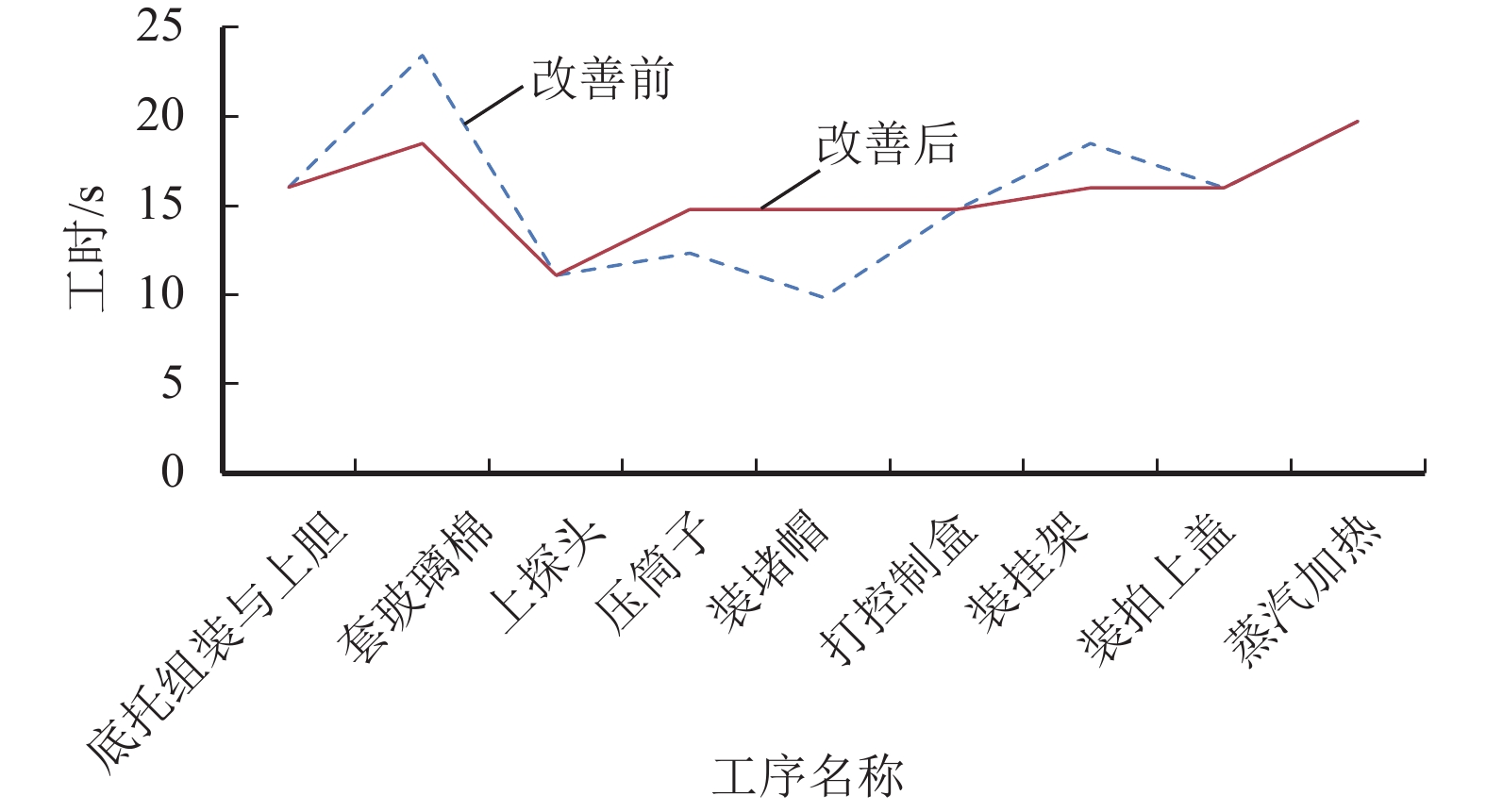
改善后工时有所变化，瓶颈也发生变化，改善前后工时变化折线图如图5。

图 5(Fig. 5)

图 5 程序改善前后工时对比 Fig. 5 Comparison of process before and after improvement

改善前生产平衡率= $\displaystyle\frac{{141.67}}{{9 \times 23.41}}$ =67.24%；

改善前平滑性指数= $\sqrt {\displaystyle\frac{{680.41}}{9}} $ =8.69；

改善后生产平衡率= $\displaystyle\frac{{141.67}}{{9 \times 19.71}}$ =79.86%；

改善前平滑性指数= $\sqrt {\displaystyle\frac{{189.63}}{9}} $ =4.59。

对比改善前后各工序的工时折线图，可以清晰看到改善后的工时更加趋于均衡，从生产线平衡率和平滑性指数来看，生产线平衡率得到了明显提高，说明该生产线的生产效率有所提高；同时平滑性指数降低说明每个工序的工时更加接近，改善效果有效。

在动作分析中常用到的ECRS 4种改善原则，即：取消(Eliminate)、合并(Combine)、重排(Rearrange)、简化(Simple)。

根据以上4点原则，对A公司3号生产线中操作工人的动作进行分析改善，对程序分析中宏观层面无法做出改善的工位进行改善优化。

②套玻璃棉

该工序动作多而繁琐是瓶颈工序。根据动作改善的第3个原则对其予以重排。第5工序中有安装排污阀堵帽是该动作的紧后工序，适合重排之后放到第5工序中。因此，改善后的MOD值为：11+15=26。

③上探头

该工序中动作幅度较大，需转身操作。根据动作改善原则中第4个简化原则，降低其动作幅度：由原来的转身变为大臂伸展。因此，改善后的MOD值变为：5+7+10=22。

④压筒子

该工序动作负荷较小，根据动作改善原则中重排原则，可以接受第7工序中的正螺丝孔动作，详细见第7工序分析。因此，调整后的MOD值为：19+7=26。

⑤装堵帽

根据动作改善的重排原则本文将第2工序中掏出排污阀的动作重排之后放到此工序中，②中已经提到。因此，改善后的MOD值为：17+8=25。

⑦装挂架

该工序中有检查和纠正螺丝孔动作，增加了工人工作负荷，但由于该动作只能是在④后和⑦之前才能出现，因此只能调整到第④~⑥工序中。根据动作改善原则中的重排原则，把该动作调整到第4工序。因此，改善后的MOD值为：4+3×2+3×2+9=25。

⑨蒸汽加热

在该工序中动作较多但多为不必要的动作，如左手拿起纸片之后右手揭掉螺丝盖膜，然后左手再将纸片放回桌面。根据动作改善取消原则予以取消多余动作，改为直接由左手按住右手揭下。因此，改善后的MOD值为：9+6+9=24。

从生产线布局调整来看，生产线平衡率由60.52%提高到了67.24%，但平滑性指数由8.25增加到8.69。这说明单纯减少工人数量会有一定的改善效果，但无形中又增加了其他工位的工作负荷，这并不是最优的改善方案。

从程序分析改善方面来看，生产线平衡率由67.24%提高到了79.86%，平滑性指数也从8.69下降到4.59。这说明从宏观层面对生产线的改善是卓有成效的。但同时应注意到，程序分析只是从宏观层面把程序进行分解或重组，考虑到实际生产情况中某些程序可能无法调整，因此微观层面还存在继续优化的可能性。

从动作改善方面来看，可以从微观层面对程序分析中宏观分析无法调整的工序进行改善，从更微观的层面分析后，得到的改善方案更加符合现实情况且效果也更好。

综上所述，3种方法都有一定的效果，但尚不完美。因此，本文综合3种改善方法，从微观和宏观多层面对A公司生产线进行改善。综合改善的结果如表6所示。

表 6(Tab. 6)

表 6 基于IE方法的综合改善前后对比 Tab. 6 Comparison before and after improvement on IE methods s 工序 改善前工时 改善后工时 底托组装与上胆 16.02 16.02 套玻璃棉 23.41 13.55 上探头 11.09 15.10 压筒子 12.32 14.78 装堵帽 9.85 14.78 打控制盒 14.79 14.79 装挂架 18.47 16.01 装拍上盖 16.01 16.01 蒸汽加热 19.71 14.33

表 6 基于IE方法的综合改善前后对比 Tab. 6 Comparison before and after improvement on IE methods

改善前生产平衡率= $\displaystyle\frac{{141.67}}{{9 \times 23.41}}$ =67.24%；

改善前平滑性指数= $\sqrt {\displaystyle\frac{{680.41}}{9}} $ =8.69；

改善后生产平衡率= $\displaystyle\frac{{135.37}}{{9 \times 16.02}}$ =93.89%；

程序改善前平滑性指数= $\sqrt {\displaystyle\frac{{14.39}}{9}} $ =1.26。

综合3种平衡方法最终得出生产平衡率为93.89%，平滑性指数为1.26。结果较单独使用3种方法得到的结果都好，且优于未做出改善之前的结果。运用IE方法改善后的生产平衡率为93.89%，平衡损失率为6.11%，远小于15%，因此该生产线此时的效率较优。平滑性指数显著降低说明各工序生产工时更为接近，生产作业负荷接近均衡。

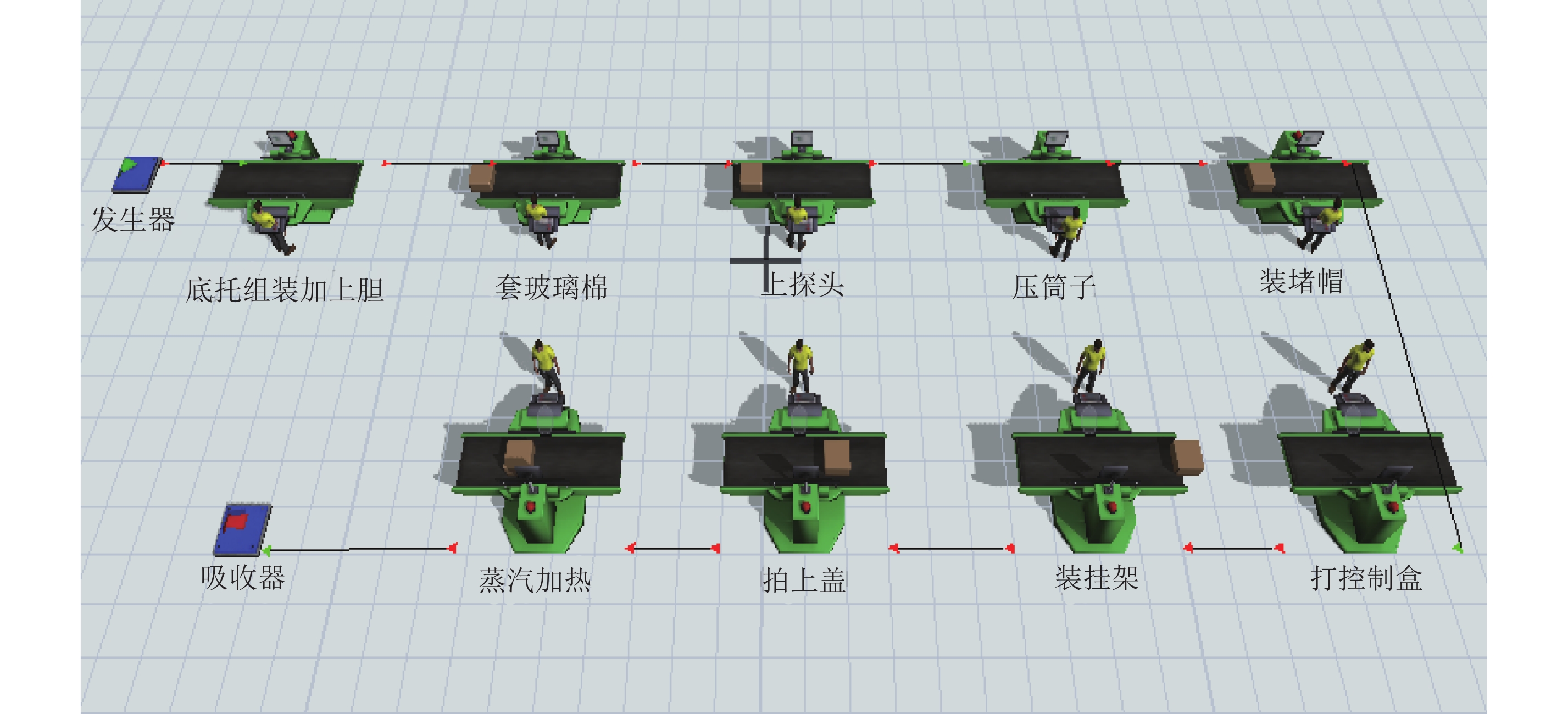
为验证基于IE方法的改善方案是否有效，本文利用Flexsim软件进行仿真评价。以A公司的生产线流程为依据，处理器代表工位，以发生器来代替产品的来源，以吸收器来代替产品的去向，建立如图6的模型。

图 6(Fig. 6)

图 6 Flexsim建模仿真图 Fig. 6 Flexsim modeling and simulation

模型建立以后，对模型中的对象分别进行参数设置。参数设置时间来自表4，参数设置见图7(其他几个参数设置与此类似)。

图 7(Fig. 7)

图 7 建模参数设置图 Fig. 7 Model parameter setting

建模完成，参数设置成功后，运行Flexsim软件，得到结果如表7所示。

表 7(Tab. 7)

表 7 Flexsim运行结果报告1) Tab. 7 Flexsim operating results % 对象 Class idle Processing generating collecting 发生器 Source 0.00 0.00 100.00 0.00 底托组装加上胆 Processor 0.00 100.00 0.00 0.00 套玻璃棉 Processor 15.42 84.58 0.00 0.00 上探头 Processor 5.75 94.25 0.00 0.00 压筒子 Processor 7.75 92.25 0.00 0.00 装堵帽 Processor 7.75 92.25 0.00 0.00 打控制盒 Processor 7.69 92.31 0.00 0.00 装挂架 Processor 0.08 99.92 0.00 0.00 拍上盖 Processor 0.08 99.92 0.00 0.00 蒸汽加热 Processor 10.57 89.43 0.00 0.00 吸收器 Sink 0.00 0.00 0.00 100.00 处理器平均值 6.11 93.89 1) 为得到准确而理想的结果，本文以一个月的工作时间为模拟运行工作时间。按照每天工作8 h，每月20工作日计算，则工作时长共为8×60×60×20=576 000 s。

表 7 Flexsim运行结果报告1) Tab. 7 Flexsim operating results

由表7可以看到该生产线有效工作时间占比为93.89%，空闲时间占比为6.11%，与本文前面运用基础IE方法得到的生产平衡率一致。因此，可以认为改善方案是科学有效的，得到的生产平衡指标也是在一定条件下最优的结果。

生产线是制造业的根本，生产线的工作效率将会直接影响企业的生产能力和竞争力^[13]。A公司3号组装生产线存在严重生产不平衡现象。本文使用基础工业工程中生产线布局分析、程序分析和动作分析等方法并依据作业测定测得的标准工时定性、定量地分析了A公司3号组装生产线的问题所在并提出改善方案。为评价改善方案的合理性和有效性，又引入Flexsim仿真软件进行仿真分析，证明改善方案有效可行，改善后效果显著。

1)生产线平衡率明显提高，由原来的67.24%提高到现在的93.89%，说明该生产线的生产效率有了很大的提高；

2)生产线平衡损失率明显下降，由原来的32.76%降低到现在的6.11%，达到并优于一条优秀生产线平衡损失率标准，这说明该生产线工时浪费得到了很大改善；

3)生产平衡平滑性指数显著改善，由原来的8.69降低到现在的1.26，这说明该生产线每个工序的作业负荷更加均衡，工时波动减小。

组装生产线平衡不仅是A公司亟待解决的问题，也是制造业乃至所有行业需要重视的问题。实现组装生产线的平衡对提高企业的生产效率形成企业核心竞争力从而提高生存和竞争能力有着十分重要的意义。