2. 暨南大学 电气信息学院,广东 珠海 519070;
3. 暨南大学 物联网与物流工程研究院 广东 珠海 519070;
4. 香港大学 工业及制造系统工程系,中国 香港
2. School of Electrical and Informatics Engineering, Jinan University(Zhuhai Campus), Zhuhai 519070, China;
3. Institute of Physical Internet, Jinan University (Zhuhai Campus), Zhuhai 519070, China;
4. Department of Industrial and Manufacturing Systems Engineering, The University of Hong Kong, Hong Kong, China
生产物流是指生产中发生的物流活动,是将多个生产活动进行前后关联的重要过程,通常占据生产时间的95%,决定着整个生产过程的效率[1]。在德国政府提出的工业4.0战略部署中,已将生产物流定义为着重关注的智能环节[2]。生产物流高效运作的核心是生产(子系统)与物流(子系统)的协同联动运作,通常被称为“生产—物流”联动。随着物联网技术的出现,大量学者开始研究物联网技术理论及其在工业环境中的应用[3-5]。其中,屈挺等[6]、张凯[7]、雷水平[8]首次提出基于物联网技术的“生产—物流”动态联动决策方法,旨在通过“生产—物流”各子系统动态联动决策来有效应对可能出现的动态性。在物联网环境下,“生产—物流”所体现出的联动决策形式为:由某个子系统根据系统运行的动态性触发某些或全部子系统建立动态关联关系,并协同决策产生下一阶段运行指导。但过去关于该方面研究多考虑单个环节之间的动态联动,而在实际制造企业(特别是齐套制造企业)的生产中,需要控制所需各种零件的生产节拍来保证其尽可能同时完成,以满足装配的齐套要求[9]。再如家具生产中,必须保证木质部分和玻璃部分齐套后才能进行组装配送[10]。最终装配产品和家具作为一个套件订单实质由多个产品(或套件)订单组成。由于不同产品在不同的地理位置进行生产,任意产品生产节奏的不确定性,都会影响到其关联产品的生产节奏,进而影响整个订单的生产节奏,最终可能影响整个“生产—物流”系统的有效执行。严重的情况下会造成在制品增加,订单在仓库积压,甚至延长交货期影响客户体验。
套件是具有相同使命的一组物料或条件,齐套是这一组物料或条件齐备的程度或状态[11]。从最初Ronen[12]教授对齐套进行全面的定义后,齐套概念广泛地应用在医疗、装配和工程等领域[13-14]。其后研究表明,齐套制造能够有效缩短订单的生产周期,减少在制品[11]。在齐套制造企业中,因为“生产—物流”某一环节(子系统)对齐套的需求,在动态性产生后,不仅需要考虑横向联动上下游部门(运输、仓储),还要考虑套件各产品生产进度的纵向齐套性联动。相比传统的“生产—物流”联动,齐套联动从一维度联动向二维度联动转变,使得其对联动信息架构、联动决策机制以及数学模型提出更高要求。
在物联网理论引起学术界广泛研究,物联网技术在生产物流全流程普及的背景下,本文以齐套制造类企业的“生产—物流”各环节之间动态的联动为对象进行研究。分析了齐套制造在实际“生产—物流”运作过程中的动态性;结合AUTOM解决方案,研究齐套动态联动的物联网信息架构;研究在物联网设备应用的环境下面向齐套控制的大型“生产—物流”系统动态联动机制,以及“生产—物流”计划精确制定的联动优化方法。
1 生产物流齐套联动运作分析 1.1 生产—物流齐套联动概念Volmajer等[15]指出“生产—物流”是指从原材料的采购开始,然后下料运送到各加工点和存储点,并以在制品形态从一个生产单元流入另一个生产单元进行加工、储存,始终体现着物料实物形态的流转过程的一个有机系统。生产物流在执行过程中,因为诸多不确定因素,导致生产物流执行与计划不一致,而调整内部资源成本过高或者无法解决不确定性带来的影响。为有效解决该问题,屈挺等[6]、张凯[7]、雷水平[8]提出了“生产—物流”动态联动决策方法,旨在通过获取生产物流各环节实时信息,采取最优的联动策略来将动态性地对“生产—物流”系统造成的损失降低到最小。
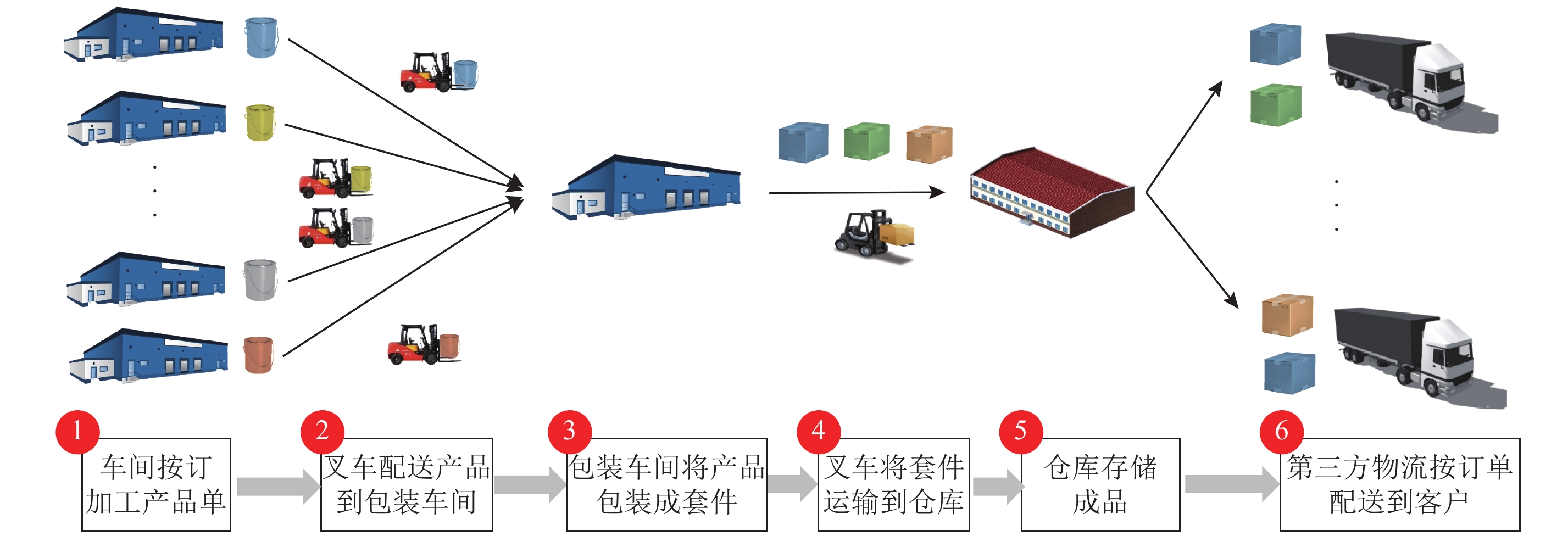
但过去的“生产—物流”联动的研究多考虑在单个车间和仓库之间的联动,而对于多个车间与仓库的联动,尤其齐套制造中同一订单的不同套件在不同车间进行生产时,在动态发生后,为了在尽可能保证关联产品的齐套性的前提下降低整体成本,企业不仅需要对车间与仓储之间实现横向维度联动,还需要考虑不同车间之间的纵向联动。本文所考虑的“生产—物流”运作包含生产、包装和仓储3个环节,如图1所示,客户的需求(订单)通常包含多类套件,而套件所包含的不同产品在不同的车间进行生产,如木器漆套装包含固化剂、稀释剂和主漆3种产品。同一套件的不同产品在车间生产完后同一时间运输到包装车间,套装在包装车间包装完后运输到仓库进行存储,等待同一订单的所有套件全部到齐后由同一车辆运输到客户手中。
|
图 1 生产物流运作流程图 Fig. 1 Production logistics operation flow chart |
在当前企业和社会背景下,随着消费者需求的不断变化,企业资源的局限性,企业内部各环节之间的决策独立性以及信息脱节等原因,齐套制造企业开始面临诸多问题。
1) 动态二维影响范围大。在“生产—物流”系统中,任何一个生产车间引起的动态性,不仅会横向地影响其上下游部门的正常运作,同时,还会纵向联动影响同一层级关联车间。如:当某订单的某一个产品下线时间因为机器维护等原因延迟下线,其不仅会在横向维度上影响下一环节的加工或入库;同时,为满足产品在下一个层级的齐套要求,还会在纵向维度上影响到关联车间的生产进度。
2) 动态实时捕获困难。在传统的制造企业中,缺乏有效的技术手段来实时获取“生产—物流”执行过程中各环节产生的动态性,如:机器故障、临时订单增减与修改、车辆故障、仓库不可用等。同时,没有定性的科学方法来判断(识别)不同时刻不同动态所带来的影响程度。
3) 资源最优重配置难。当员工发现动态性导致执行与计划不一致后,通常通过经验来重新配置资源和调整计划。但随着工作量的增加,人工方式的出错率增加,且很难实现资源最优重配置,从而造成不必要的成本损失。
2 基于物联网的生产—物流联动解决方案针对上一节中描述的问题,简单的单个部门间动态联动决策已经无法有效应对。本节将从源头对动态性进行分析,基于物联网技术搭建联动信息架构来实时获取“生产—物流”系统执行过程中的动态信息,同时提出面向齐套制造的三层两阶段齐套联动机制,其对动态性的定性分析结合下一节提出的定量联动方法能实现不同动态性下的最优重配置。
2.1 动态性分析下面以车间为动态发生源为例,根据车间产生的不同动态因素,分析其影响范围和应对不同动态性需要调整的资源,并将动态性分为3种强度。
1) 内部制造单元间联动。对于物联网信息架构在车间捕获到的最低强度动态性,只需要对动态性发生的车间进行内部调整,而不影响“生产—物流”系统其他模块的执行。如:车间某工序机器故障,此时刚好有空闲机器替代,则此时只需要重新调整车间调度计划,不影响其他车间和仓储。
2) 车间与车间纵向联动。对于物联网信息架构在车间捕获到的中级强度动态性,除了对动态性发生的车间进行内部调整外,还会影响其他关联车间生产计划的执行。如:订单1为生产计划最后一个订单,其含有a、b产品分别在A、B车间生产,预规划a比b先完工。如果动态性为增加b产品数量,为尽可能保证下游包装车间或者仓库的齐套需求,需要调整B车间的生产计划。
3) 车间与仓储横向联动。对于物联网信息架构在车间捕获到的高强度动态性,动态性发生车间和其关联车间以及下游包装车间或仓库需要同时进行调整。如:在生产结束前,临时增加订单1,其交货期在所有订单的交货期集合里靠前,此时需要同时调整订单1所有关联车间的生产计划,而生产计划的调整间接影响到仓储计划。
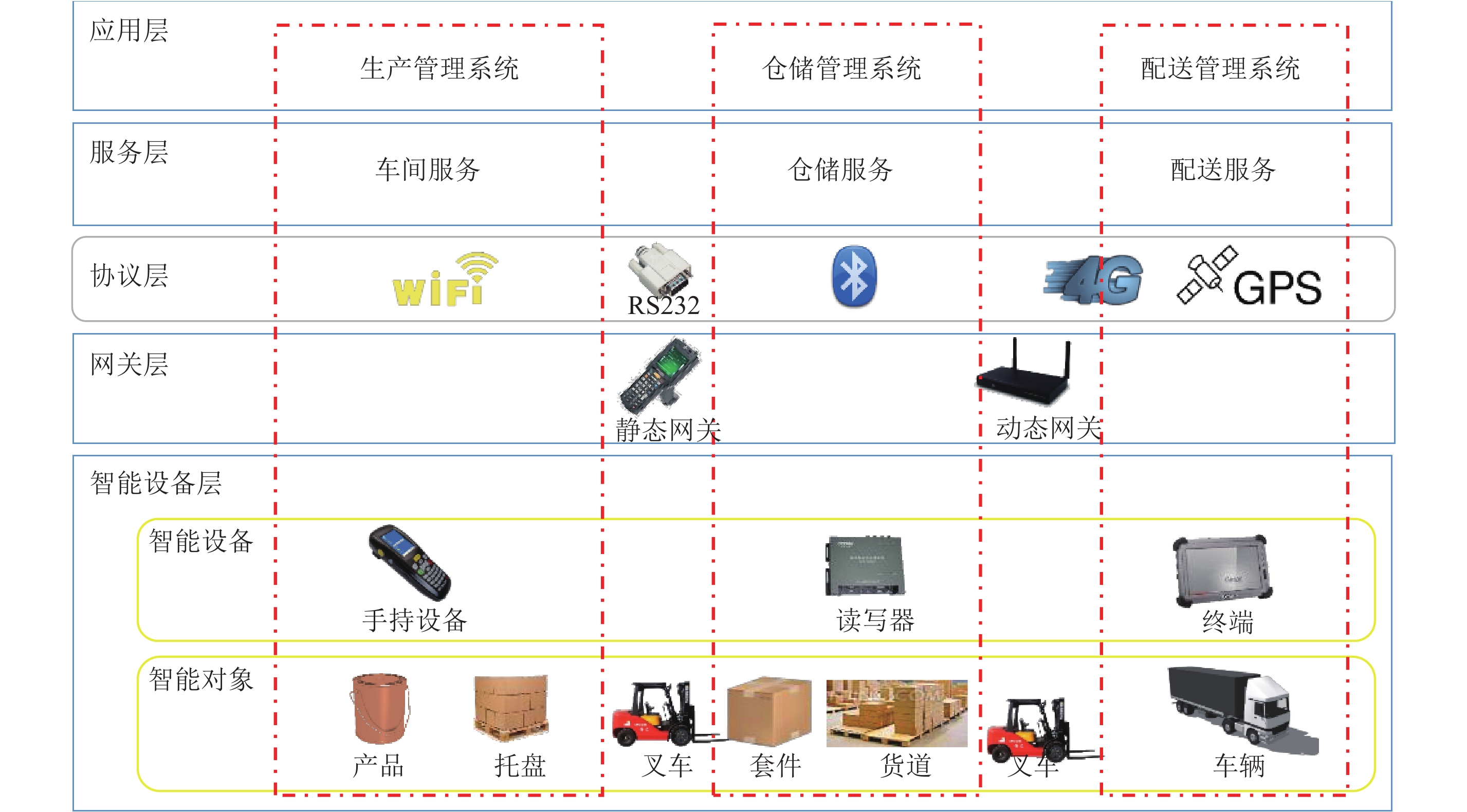
2.2 基于物联网的“生产—物流”齐套联动信息架构AUTOM解决方案是一种符合ISA-95国际标准的开放式、可扩展物联网实时信息架构,提供了一种有效的搭建物联网环境的方式[16]。利用AUTOM实时信息架构可扩展性特征,针对本文研究对象搭建了基于物联网的“生产—物流”齐套联动信息架构。该架构通过物联网设备实时采集“生产—物流”各环节实时数据,并将其转换为安全标准的有效信息,为生产物流计划的制定与动态联动的控制机制提供数据支撑,为各部门用户执行任务提供相关应用系统。如图2所示该信息架构的3个技术层面直接支撑本文提出的“生产—物流”动态联动架构。
|
图 2 生产物流齐套联动信息架构 Fig. 2 Production logistics kitting synchronization information framework |
感知层:又称为智能设备层,该层通过将RFID、条形码、PDA、车载平板、GPS等物联网设备部署到“生产—物流”各环节的设备与物品上来实现对“生产—物流”运作的信息采集。其包括两部分:被动感知设备,如“生产—物流”各环节部署的被动式物联网设备;主动感知设备,用来采集“生产—物流”各环节执行的实时数据信息,其与被动感知设备结合后形成物联网感知环境,实时监控各环节的动态信息。
智能网关层:该层的主要作用是作为现场物联网设备的信息汇集枢纽,缓存和交换实时数据和事件,控制各企业各环节数据信息安全性,将各环节异构物联网数据转换为符合生产物流计划制定的标准数据,使得企业信息系统和决策系统相互连接并有效交互。
服务层:针对应用层的不同需求,开发出的标准化服务组件系列。如Web Service,该层能够将实时信息转化为功能性服务,并将服务提供给最上层应用系统。
应用层:面向生产、配送、仓储等关键用户提供相关物联网应用系统。如:在PDA上配置生产管理系统,对订单生产包装的数据进行采集等;在叉车的车载平板上配置配送管理模块,方便叉车对订单配送任务的执行等;在仓库管理员终端配置仓储管理模块,方便对订单排库情况的监控与人工调整等。
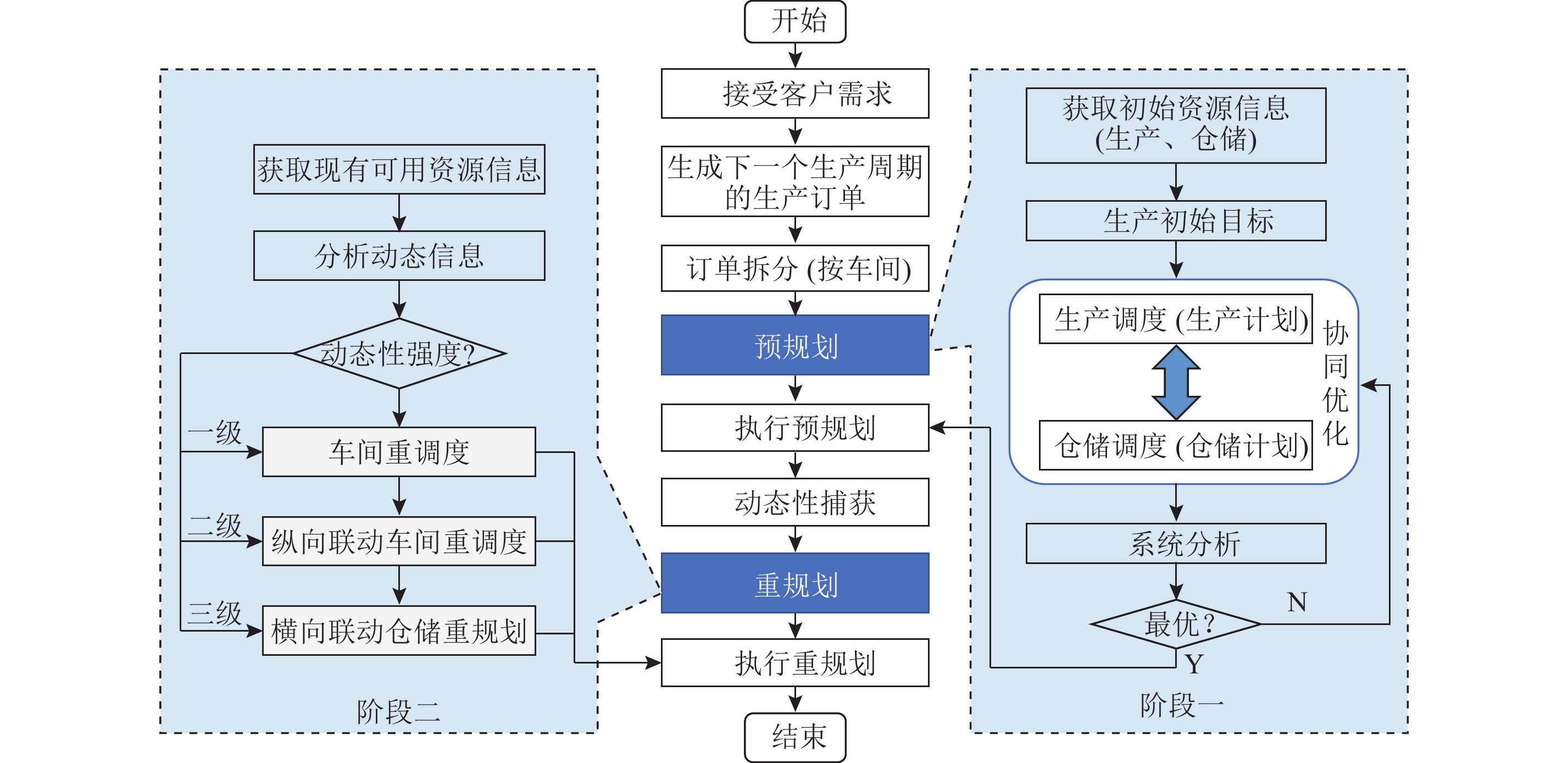
2.3 三层两阶段齐套联动机制针对上一节提出的联动信息架构,为了有效利用实时资源信息来支撑“生产—物流”系统高效的运行,提出三层两阶段齐套联动机制,来应对齐套制造中出现的不同强度等级的动态性。三层指车间、包装、仓储3个环节部门,两阶段指预规划和为应对动态性执行的修正重规划。如图3所示,其具体执行流程如下。
|
图 3 生产物流三层两阶段联动机制图 Fig. 3 Production logistics three-level two-stage synchronization mechanism chart |
1) 接收客户的需求并生成下一个生产周期的生产订单,同时按车间将订单拆分为子生产订单。
2) 预规划。通过2.2节提出的信息架构获取“生产—物流”系统各环节初始资源信息,并产生初始优化目标。根据初始资源信息和优化目标,生产与仓储层进行相互迭代优化,直到系统分析该结果为最优解。
3) 执行预规划。系统根据预规划最优结果进行“生产—物流”运作。同时在执行过程中,信息架构的智能设备实时收集执行信息,将实时捕获各环节执行信息上传给决策层进行决策。
4) 重规划。当决策层判断执行信息与预规划不一致时,通过分析动态性强度,确定其联动范围,以及需要联动优化的对象。
5) 执行重规划。“生产—物流”系统根据重规划结果继续进行“生产—物流”运作。
3 “生产—物流”动态齐套联动方法本节用目标级联法(ATC)求解“生产—物流”动态齐套联动问题。详细论述联动方法中仓储规划模型和车间调度模型的设计,并结合实验例证该模型的有效性。
3.1 ATC介绍目标级联(target cascading, TC)是Michelen[17]于1999年提出的一种解决复杂工程系统中目标优化问题的新方法,又称analytical target cascading(ATC)法。在多学科优化领域(MDO)中,CSSO和BLISS方法因为每次迭代都要进行系统分析,计算量比较大,且其收敛性没有经过理论证明[18]。CO方法虽然可以避免复杂的系统分析,各学科可以并行地进行分析和优化,但其分解后的分析模型必须在同一层次,对问题的分解要求比较严格[19],不适用于多层次的复杂系统。而ATC对于解决可分解为层级式体系结构的复杂大系统优化具有可并行优化、层级数不受限制和经过严格的收敛证明等优点[20]。
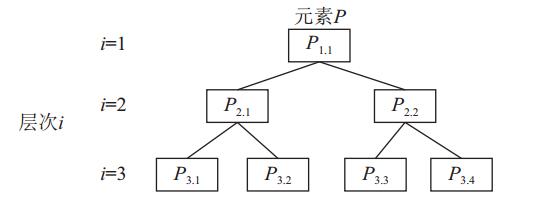
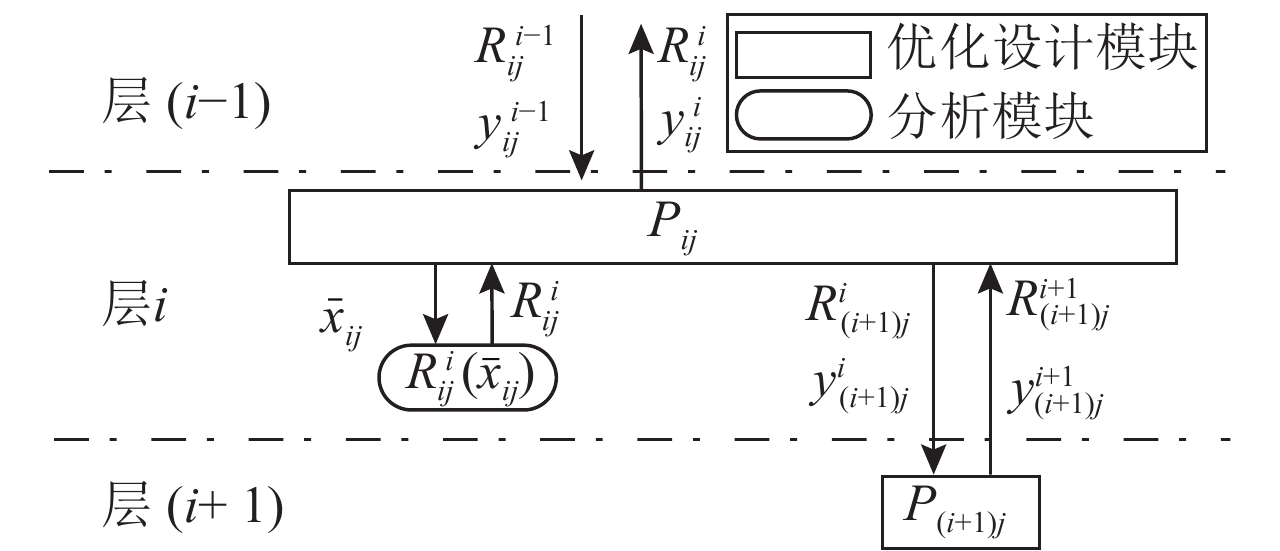
ATC方法把整个联动系统的动态目标传递过程转化为具有多个层次结构的子系统实时优化过程:各个子系统由其上一级父系统来协调优化,最后达到整个系统的优化。其层次结构如图4所示。在ATC模型中包括两类模块:优化设计模块和分析模块。优化设计模块负责元素目标的优化。分析模块用于计算元素的反应,局部设计变量、参数和子代元素的反应为其输入,而传递给优化设计模块的反应为其输出[21]。图5是ATC优化模型中元素Pij的原理图,Pij的优化目标Riji-1和联系变量yiji-1由父代系统传递下来,Pij的优化问题结束后,把响应变量
|
图 4 目标级联法层次结构图 Fig. 4 Target cascading hierarchical structure diagram |
|
图 5 ATC优化模型元素Pij原理图 Fig. 5 Schematic of element Pi,j in ATC optimization model |
基于ATC的“生产—物流”齐套联动优化,其考虑的是在齐套制造企业的“生产—物流”系统中,当动态性产生后,如何通过最优的资源重配置,来实现整个“生产—物流”过程产生的成本最小。“生产—物流”系统通常包含有生产、运输、仓储等多个部门,过去联动优化模型通常只考虑单个环节间的联动优化,如单个车间与单个仓库[6-8]。本文面向的“生产—物流”系统包含多个生产车间、1个包装车间和1个仓库,其所建立的基于ATC的联动优化模型更加复杂。为简化模型而不失一般性,假设包装车间的产能无限,且加工时间确定,则生产车间的同步即是为了满足下游包装车间的齐套需求,也是为了满足齐套入库的需求。其具体的参数符号如表1所示。
| 表 1 参数符号信息表 Tab. 1 Parameter symbol information table |
根据ATC的设计思想,将“生产—物流”系统分为车间调度层和仓储规划层。车间调度层的任务是完成所有订单在不同车间的生产任务规划,而仓储规划层的任务是完成所有订单的包装计划和库位规划。
3.2.1 仓储规划层模型仓储规划层的任务是根据车间调度层的结果,给订单进行包装调度和库位规划,使同一订单的不同套件的下线时间尽可能满足下一个包装环节的齐套需求,该层目标是在降低系统总成本的同时协调各车间订单下线时间。其数学模型如下。
| $\qquad\min {f_w} = ||{C_{{\rm{sys}}}} - {\rm{T}}{{\rm{C}}^0}|| + {\varepsilon _0}\text{。}$ | (1) |
| $\qquad\max ||{R^0} - {R^1}|| \text{≤} {\varepsilon _0}\text{。}$ | (2) |
| $\qquad{C_{{\rm{sys}}}} = {\rm{T}}{{\rm{C}}_{\rm{plant}}} + {\rm{T}}{{\rm{C}}_{{\rm{buffer}}}} + {\rm{T}}{{\rm{C}}_{{\rm{pac}}}} + {\rm{T}}{{\rm{C}}_{{\rm{ware}}}} + {\rm{T}}{{\rm{C}}_{{\rm{tar}}}};$ | (3) |
| $\qquad{\rm{T}}{{\rm{C}}_{{\rm{plant}}}} = {C_{{\rm{plant}}}} + \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^{n + {\alpha _T}} {\sum\limits_{j = 1}^m {(t_{{\rm{e}}{{\rm{p}}_{i,j}}}^h - t_{{\rm{s}}{{\rm{p}}_{i,j}}}^h)} \times } } {C_{{\rm{pro}}}};$ | (4) |
| $\qquad{\rm{T}}{{\rm{C}}_{{\rm{buffer}}}} = \sum\limits_{h = 1}^H {\sum\limits_{i = 1}^{n + {\alpha _T}} {{C_{{\rm{BIC}}}} \times } |t_{{\rm{e}}{{\rm{p}}_{i,m}}}^h - {t_{{\rm{De}}{{\rm{l}}_i}}}} | \times {Q^h}_i;$ | (5) |
| $\qquad{\rm{T}}{{\rm{C}}_{{\rm{pac}}}} = \sum\limits_{i = 1}^{n + {\alpha _T}} {{C_{{\rm{pac}}}} \times ({t_{{\rm{epa}}{{\rm{c}}_i}}} - {t_{{\rm{spa}}{{\rm{c}}_i}}})} ;$ | (6) |
| $\!\!\!\begin{array}{l}{\rm{T}}{{\rm{C}}_{{\rm{ware}}}} = \displaystyle\sum\limits_{l = 1}^{\rm{NC}} {{u_{l,t}}} \times {C_{{\rm{c}}\arg {\rm{o}}}} \!+\!\! \displaystyle\sum\limits_{i = 1}^{n + {\alpha _T}} {{Q_i} \times ({t_{{\rm{I}}{{\rm{n}}_i}}} - {t_{{\rm{O}}{{\rm{u}}_i}}})} \times {C_{{\rm{War}}}};\end{array}$ | (7) |
| $\qquad{\rm{T}}{{\rm{C}}_{{\rm{tar}}}} = \sum\limits_{i = 1}^{n + {\alpha _T}} {{\rm{flag}} \times |{t_{{D_i}}} - {t_{{\rm{O}}{{\rm{u}}_i}}}| \times } {Q_i} \times {C_{{\rm{tar}}}};$ | (8) |
| $\qquad{Q_i} = \sum\limits_{h = 1}^H {{Q^h}_i} ;$ | (9) |
| $\qquad{t_{{\rm{spa}}{{\rm{c}}_i}}} = {t_{{\rm{De}}{{\rm{l}}_i}}};$ | (10) |
| $\qquad{t_{{\rm{epa}}{{\rm{c}}_i}}} = {t_{{\rm{spa}}{{\rm{c}}_i}}} + {T_{{\rm{pac}}}} \times {Q_i};$ | (11) |
| $\qquad{t_{{\rm{I}}{{\rm{n}}_i}}} = {t_{{\rm{epa}}{{\rm{c}}_i}}};$ | (12) |
| $\qquad{t_{{\rm{O}}{{\rm{u}}_i}}} - {t_{{\rm{I}}{{\rm{n}}_i}}} \text{>} 0;$ | (13) |
| $\qquad\sum\limits_{l = 1}^{{\rm{NC}}} {{O_{t,i,l}} \times {p_{t,i,l}}} = {Q_i},i = 1,2,...,n + {\alpha _T};$ | (14) |
| $\qquad\sum\limits_{l = 1}^{{\rm{NC}}} {{u_{l,t}}} \text{≤} {\rm{NC;}}$ | (15) |
| $\qquad\sum\limits_{l = 1}^{{\rm{NC}}} {{\rm{pu}}{{\rm{t}}_{t,i,l}} \times {p_{t,i,l}}} = {Q_i},i = 1,2,...,n + {\alpha _T};$ | (16) |
| $\qquad\begin{split}\displaystyle & \sum\limits_{a,b = 1}^{n + {\alpha _T}} {{\rm{pu}}{{\rm{t}}_{t,a,l}} \times {p_{t,a,l}} + {\rm{pu}}{{\rm{t}}_{t,b,l}} \times {p_{t,b,l}}} \text{≤}{\rm{P}}{{\rm{C}}_l},\\& l = 1,2,...,{\rm{NC}};a \ne b;\end{split}$ | (17) |
| $\qquad\sum\limits_{i = 1}^{n + {\alpha _T}} {{\rm{pu}}{{\rm{t}}_{t,i,l}}} \text{≤} 2,l = 1,2,...,{\rm{NC}}{\rm{。}}$ | (18) |
其中:式(1)、(2)为仓储层系统层优化目标,
车间调度层的任务是给各个车间合理的分配子订单的加工顺序,使同一套件的不同产品在不同车间尽可能同时完成。该层目标是加工完所有产品的时间最短,将各车间订单的下线时间
| $\qquad\min {f_p} = {[{f_1},f{}_2]^{\rm{T}}}\text{。}$ | (19) |
| $\qquad{f_1} = \max t_{{\rm{e}}{{\rm{p}}_{i,m}}}^h|i = 1,2,...,n + {\alpha _T};$ | (20) |
| $\qquad{f_2} = \max \left( {t_{{\rm{e}}{{\rm{p}}_{i,m}}}^h - {R^0}} \right)|i = 1,2,...,n + {\alpha _T};$ | (21) |
| $\qquad\sum\limits_{{k_j} = 1}^{{M_j}} {x_{i,j,{k_j}}^h = 1} ,i \in \{ 1,2,...,n + {\alpha _T}\} ,j \in \{ 1,2,...,m\} ;$ | (22) |
| $\qquad\sum\limits_{i = 1}^n {{y^h}_{i,p} = 1} ,p \in \{ 1,2,...,n + {\alpha _T}\} ;$ | (23) |
| $\qquad\begin{split}& t_{{\rm{e}}{{\rm{p}}_{i,{\rm{j}}}}}^h = t_{{\rm{s}}{{\rm{p}}_{i,j}}}^h + \displaystyle\sum\limits_{k = 1}^{{M_j}} {{x^h}_{i,j,{k_j}} \times {T^h}_{i,j,{k_j}} \times {Q_i}^h,} \\& i \in \{ 1,2,...,n + {\alpha _T}\} ,j \in \{ 1,2,...,m\} ;\end{split}$ | (24) |
| $\qquad t_{{\rm{e}}{{\rm{p}}_{i,j - 1}}}^h \text{≤} t_{{\rm{s}}{{\rm{p}}_{i,j}}}^h,i \in \{ 1,2,...,n + {\alpha _T}\} ,j \in \{ 1,2,...,m\} ;$ | (25) |
| $\qquad{t_{{\rm{De}}{{\rm{l}}_i}}} = \max t_{{\rm{e}}{{\rm{p}}_{i,m}}}^h|i = 1,2,...,n + {\alpha _T}\text{。}$ | (26) |
其中:式(19)为车间调度层目标函数;式(20)、(21)分别为目标1(最小最大完工时间)和目标2(车间优化结果与上层目标的最大差值,即齐套差值最小);式(22)表示机器约束,即订单i的第j道工序在并行机器Mj上只能选择1台机器;式(23)表示订单加工顺序中,每个优先级位置只能对应1张订单;式(24)表示订单加工完成时间;式(25)表示工序约束,订单开始某一工序时必须先完成前一工序;式(26)表示订单从下线点配送到包装区的时间,即同一订单不同产品齐套配送到包装车间的时间。
4 算例分析对本团队所合作的某大型化工企业的油漆化工产品的“生产—物流”实际订单数据进行仿真分析,以验证文中提出的生产物流齐套联动方法。
4.1 数据参数表2为该企业2016年9月25日客户订单信息。每个订单为1类套件,每个套件包含2种产品在不同车间生产(表3为各车间机器信息),为满足包装的齐套需求,且包装区无临时存放点,优先加工完的产品需存放在下线点缓存区,等另外一种产品下线后同时送到包装区,叉车将包装完的产品配送到仓库预规划库位(表4为仓库库位信息),第三方物流在交货期将成品配送到客户手中。该企业正常生产开始时间为08:00 am,生产物流成本如表5所示。另外,本算例所考虑动态性为新增订单,该订单需要车间1和车间2各生产10个托盘,交货期为当天15:00,动态性发生时间为10:00。
| 表 2 客户订单信息表 Tab. 2 Customer order information table |
| 表 3 车间设备信息表 Tab. 3 Plant machine information table |
| 表 4 仓库库道信息表 Tab. 4 Warehouse cargo information table |
| 表 5 生产物流成本信息表 Tab. 5 Production logistics cost information table |
采用Matlab R2010b软件对上述生产物流联动方法的应用实例进行编程仿真。该实例仿真运行环境配置参数是:内存为8GB,CPU为Intel(R)Core(TM)i5-4200M 2.5 GHz,操作系统为Windows7 64位。
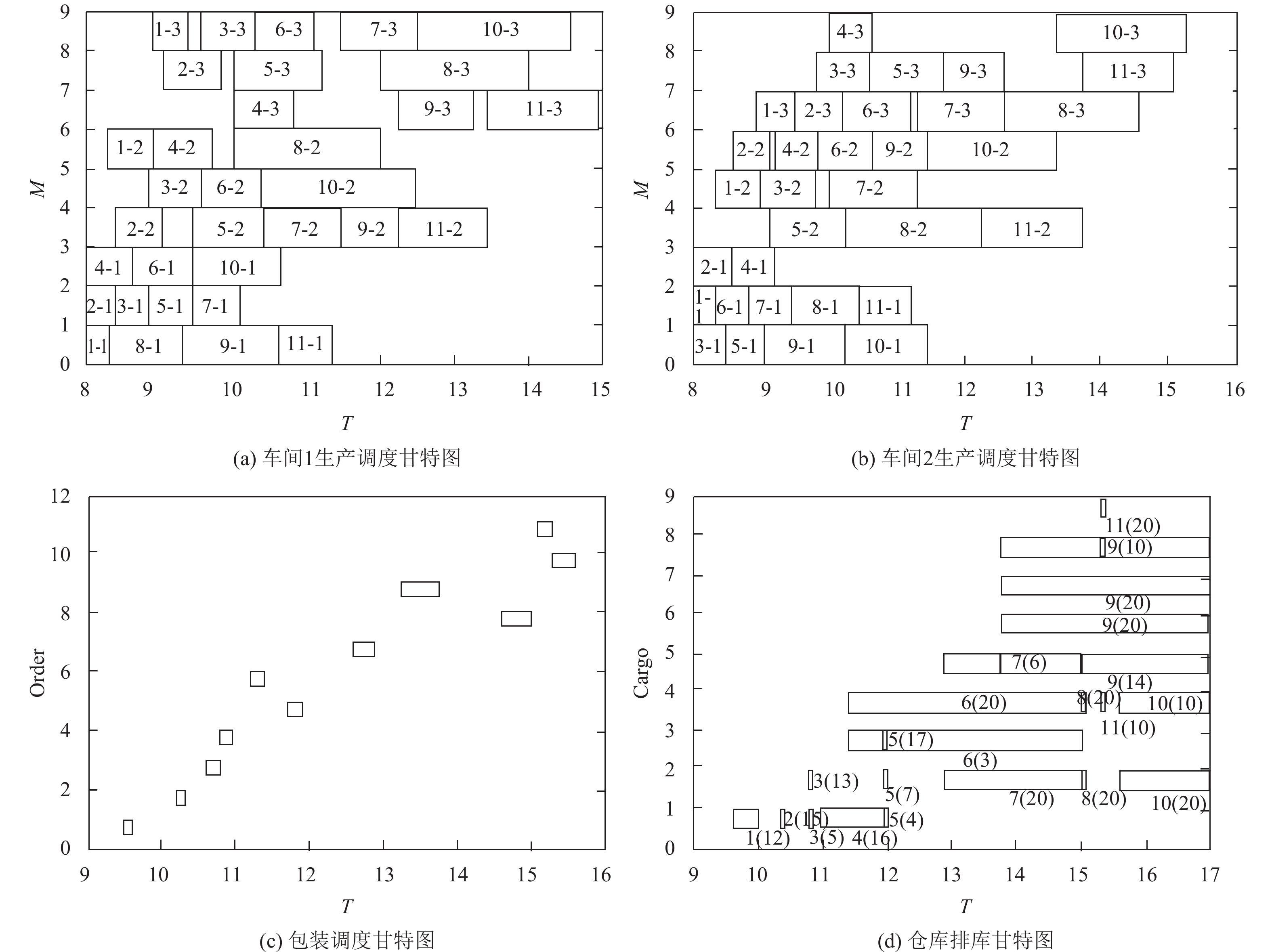
仿真过程中,生产调度子模型的遗传算法参数设置为:种群规模为pop=100个,遗传代数为n=100次,交叉概率为Pc=0.6,变异概率为Pm=0.06,仓储层与车间调度层迭代次数Count=19次。通过仿真得到的结果如表6和图6所示。对比表6中不同重规划方法的结果可以看出:1)与没有设定齐套目标的非齐套联动方法,基于ATC的齐套联动能在降低系统总成本1.6%的同时,将因包装车间产生的缓存成本降低24.7%左右,有效提高了套件各产品的齐套水平;2)相比基于AIO的齐套联动方法和非齐套联动方法,基于ATC的齐套联动方法将系统成本分别降低了0.7%和1.6%,将生产成本分别降低了0.1%和1.1%,降低了动态性对系统造成的经济损失;3)相比基于AIO的齐套联动方法和非齐套联动方法,基于ATC的齐套联动方法将拖期成本分别降低了15.6%和63%,有效降低了动态性对客户满意度的影响。
|
图 6 动态齐套联动结果图 Fig. 6 Gantt chart of dynamic kitting synchronization result |
| 表 6 结果分析表 Tab. 6 Result analysis chart |
本文以齐套制造企业的“生产—物流”运作为背景,在传统的“生产—物流”动态联动决策基础上,分析了齐套联动中动态因素对整个“生产—物流”系统带来的多层级、多维度影响,并基于制造物联网技术将传统的AUTOM信息架构扩展为面向齐套制造的齐套联动信息架构,提出面向多维度动态性和实时重规划的三层两阶段齐套联动机制,来定性地区分不同动态所需要重新配置的资源模块。最终,运用企业实际订单数据进行算法分析,结果表明,基于ATC的齐套联动优化能有效降低动态性引起的成本损失,且对其他齐套制造企业在制造物联网环境下实现生产物流有效的动态联动提供了有益参考。
作者将基于本文作如下扩展研究。1)结合企业的具体需求,对更加复杂多样化的“生产—物流”系统进行扩展研究。2)配送是生产物流的关键环节,下一阶段的研究将考虑生产物流的配送环节,且考虑更多环节的齐套性;如齐套出入库。3)实际生产物流执行过程中存在着诸多未知动态性,针对不同类型的动态性,需要提出更加灵活的应对策略,从而使生产物流齐套联动方法可以解决更多的动态性问题。
| [1] |
屈挺, 张凯, 罗浩, 等. 物联网驱动的" 生产—物流”动态联动机制、系统及案例[J].
机械工程学报, 2015, 51(20): 36-44.
QU Ting, ZHANG Kai, LUO Hao. Internet-of-things based dynamic synchronization of production and logistics: mechanism, system and case study[J]. Journal of Mechanical Engineering, 2015, 51(20): 36-44. |
| [2] | 德国联邦政府的高科技战略举措行动" 工业4. 0”. 控制工程在线. [DB/OL]. (2013-02-21). http://c.iot-online.com/News/2013/022123662.html. |
| [3] | BREWER A, SLOAN N. Intelligent tracking in manufacturing[J]. Journal of Intelligent Manufacturing, 1999, 10(3-4): 245-250. |
| [4] | LI Z, GADH R, PRABHU B S. Applications of RFID technology and smart parts in manufacturing[C/OL]. (2004-10-28). http://wireless.ucla.edu/gadh/pdf/04b.pdf. |
| [5] |
戴青云, 罗天友. 基于RFID的在制品追踪与管理系统[J].
电脑与电信, 2006(7): 10-15.
DAI Qingyun, LUO Tianyou. Produce pursuing and management system based on RFID[J]. Computer & Telecommunication, 2006(7): 10-15. |
| [6] |
屈挺, 贾东元, 王宗忠, 等. 基于物联网的" 生产—物流”实时联动方法和系统[J].
物流科技, 2014, 37(7): 1-4.
QU Ting, JIA Dongyuan, WANG Zongzhong. " Manufacturing-Logistics” real-time joint method and system based on IOT[J]. Logistics Sci-tech, 2014, 37(7): 1-4. |
| [7] |
张凯. 物联网环境下基于" 生产—物流”联动的动态成品入库优化方法[D]. 广州: 广东工业大学, 2015.
ZHANG Kai. Synchronization of production and logistics based dynamic optimization method for product warehousing under the internet-of-things environment [D]. Guangzhou: Guangdong University of Technology, 2015. |
| [8] |
雷水平. 物联制造系统中考虑云资源的" 生产—物流”两级联动控制方法[D]. 广州: 广东工业大学, 2016.
LEI Shuiping. Two level control method for an IoT-based production logistics synchronization system with cloud resources [D]. Guangzhou: Guangdong University of Technology, 2016. |
| [9] |
王卫国, 王耀. 一种齐套制造模型的研究及实现[J].
计算机集成制造系统, 2013, 19(11): 2795-2801.
WANG Weiguo, WANG Yao. Research and implement for kit-manufacturing model[J]. Computer Integrated Manufacturing Systems, 2013, 19(11): 2795-2801. |
| [10] | LI Chunglun, VAIRAKTARAKIS George. Coordinating production and distribution of jobs with bundling operations[J]. IIE Transactions, 2007, 39(2): 203-215. DOI: 10.1080/07408170600735561. |
| [11] |
王林平. 应用齐套概念的离散制造业生产调度问题研究[D]. 大连: 大连理工大学, 2009.
WANG Linping. Production scheduling of discrete manufacturing under complete kit concept [D]. Dalian: Dalian University of Technology, 2009. |
| [12] | RONEN B. The complete kit concept[J]. International Journal of Production Research, 1992, 30(10): 2457-2466. DOI: 10.1080/00207549208948166. |
| [13] | LESHNO M, RONEN B. The complete kit concept-implementation in the health care system[J]. Human Systems Management, 2001, 20(4): 313-318. |
| [14] | GÜNTHER H O, GRONALT M, PILLER F. Component kitting in semi-automated printed circuit board assembly[J]. International Journal of Production Economics, 1996, 43(2): 213-226. |
| [15] | VOLMAJER M, KEGL B. Cavitation phenomena in the injection nozzle: theoretical and numerical analysis[J]. Journal of KONES Internal Combustion Engines, 2004, 11(3-4): 295-303. |
| [16] | HUANG G Q, QU T, FANG M J. RFID-enabled gateway product service system for collaborative manufacturing alliances[J]. CIRP Annals-Manufacturing Technology, 2011, 60(1): 465-468. DOI: 10.1016/j.cirp.2011.03.040. |
| [17] | KIM H M. Target cascading in optimal system design [D]. Michigan: University of Michigan, 2001. |
| [18] | SOBIESZCZANSKI-SOBIESKI J, ALTUS T D, PHILLIPS M. Bilevel integrated system synthesis for concurrent and dis-tributed processing[J]. AIAA Journal, 2012, 41(10): 1996-2003. |
| [19] | BRAUN R D, MOORE A A, KROO I M. Collaborative approach to launch vehicle design[J]. J Spacecraft Rockets, 1997, 34(4): 478-486. DOI: 10.2514/2.3237. |
| [20] | ALLISON J, KOKKOLARAS M, ZAWISLAK M, et al. On the use of analytic target cascading and collaborative optimization for complex system design [C/OL]. (2005-03-03). http://ode.engin.umich.edu/publications/PapalambrosPapers/2005/217.pdf. |
| [21] | LING L Y, LIANG L, PU X J. ATC based coordination of distributed production planning and supplier selection[J]. Applied Mathematics & Computation, 2006, 182(2): 1154-1168. |
 2017, Vol. 20
2017, Vol. 20