伴随着我国经济的快速发展，民航行业也获得了较快增长，2015年全行业运输周转量实现13.8%的增长^[1]。由此对航班的安全飞行提出了更高要求。但近年来航空安全领域发生的事故及事故征候有明显的上升趋势。如2016年10月11日，东航一架客机在上海虹桥机场发生跑道入侵事件，险些酿成重大事故，调查初步结论确定为人为原因造成的严重事故征候。可见航班安全是民航安全管理中应重点关注的问题。

航班安全评估问题一直都是国内外研究热点。相关研究主要集中在对不确定性数据和信息的推理分析和建模。1)应用贝叶斯网络推理的研究。Brooker^[2]利用贝叶斯网络进行了飞行安全评价的可行性分析，借助专家意见确定条件概率，并验证了贝叶斯网络可对民航安全的风险预测提供较准确的结果。王岩韬等^[3]利用基于事故树的贝叶斯网络分析方法，预测出不安全事件发生的概率。2)应用模糊推理的研究。Skorupski^[4]将模糊风险矩阵的概念应用于航班运输风险分析，用模糊语言变量表示事故发生概率与严重程度，构造模糊推理系统，对航班飞行事故风险进行仿真分析。高扬等^[5]以人为差错严重度为指标，结合灰色综合评价法，定量评估出机组人为差错风险。王新等^[6]对国内5年内的事故及事故征候数据进行统计分析，建立了飞行安全评估的指标体系，使用模糊综合评价法对飞行安全系统进行风险评估。张晓燕等^[7]对基于物元分析理论的空管安全系统进行了模糊综合评价。3)应用主观推理的研究。文兴忠^[8]提出结合熵权和AHP来确定风险指标的影响权重。孙瑞山等^[9]利用AHP结合模糊函数，研发了用于事前评估的飞行航班风险评估工具。

航班运行安全系统是一种复杂的动态系统，指标间往往存在相互作用，并且很多指标难以精确量化，在一定程度上影响了航班风险评估的准确性。而现有文献研究中鲜有涉及航班风险评估中指标间的影响关系，限制了研究成果的应用价值。针对以上问题，本文综合运用FCM、ANP和DEMATEL 3种工具对航班风险的评估和改进，进行系统理论研究。

图1给出了本文研究的整体框架，主要包括两大部分：航班风险评估与航班风险改进。其中FCM是由Kosko^[10]在1986年提出，是针对Axelord认知图，通过引入模糊集理论，将概念间的因果关系由简单的{-1，0，1}三值关系扩展到区间[-1, 1]上的模糊隶属关系。FCM用图解的方式来描述复杂动力系统，节点表示系统中的概念或实体，有向弧表示概念或实体之间的因果关系。FCM通过节点之间的因果关系来进行模糊推理，分析整个图中各节点的相互作用来仿真整个系统的动态变化行为。FCM对无法用精确函数关系描述的复杂动态系统具有较强的知识表达和推理能力，广泛应用于商业管理^[11]、数据预测^[12]等领域。

图 1(Fig. 1)

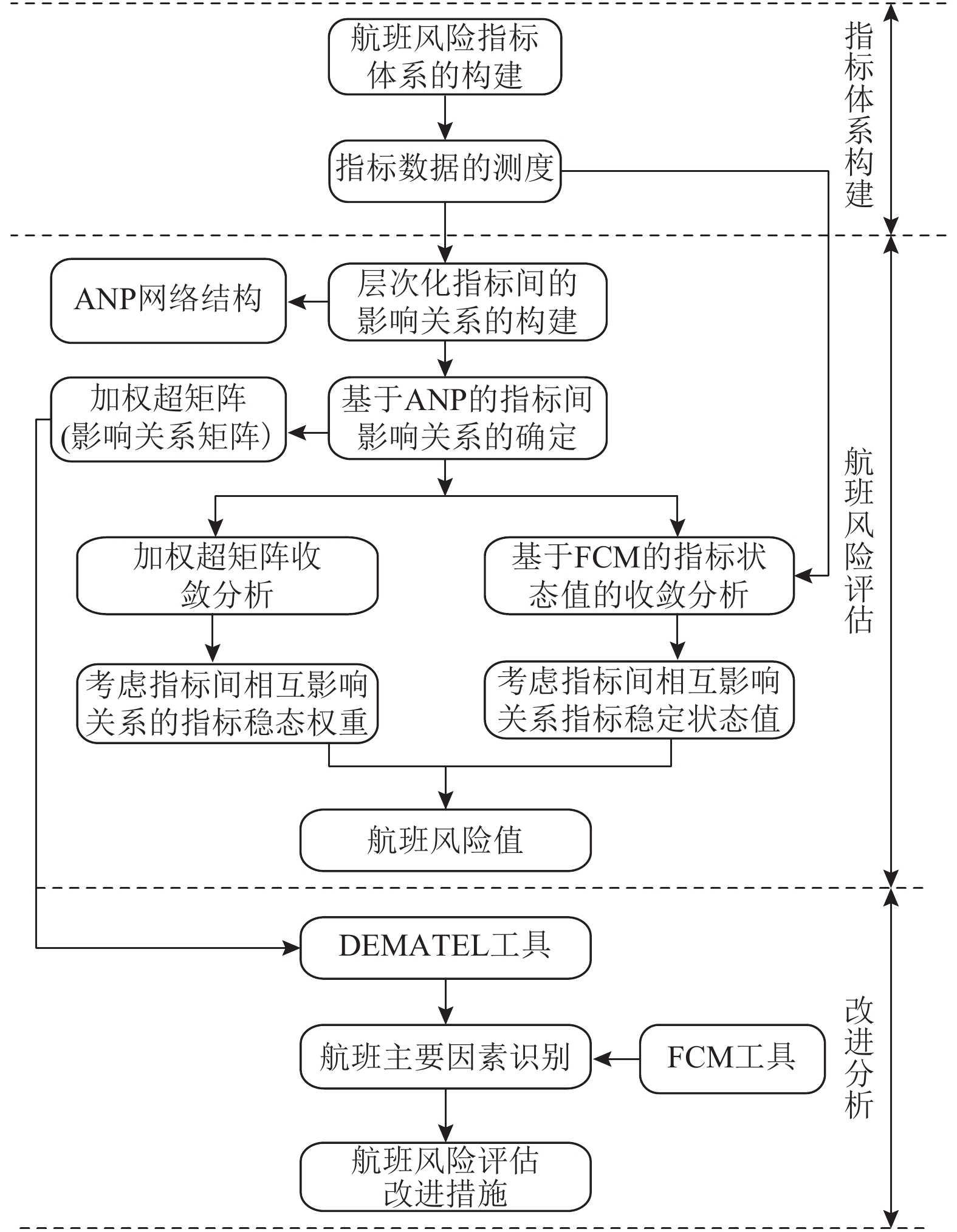
图 1 总体研究框架 Fig. 1 General research framework

本文在综合现有文献的基础上，从“人-机-环-管”的系统学角度出发，进一步完善了航班风险评估指标体系，构建了图2所示的航班风险评估指标体系。

图 2(Fig. 2)

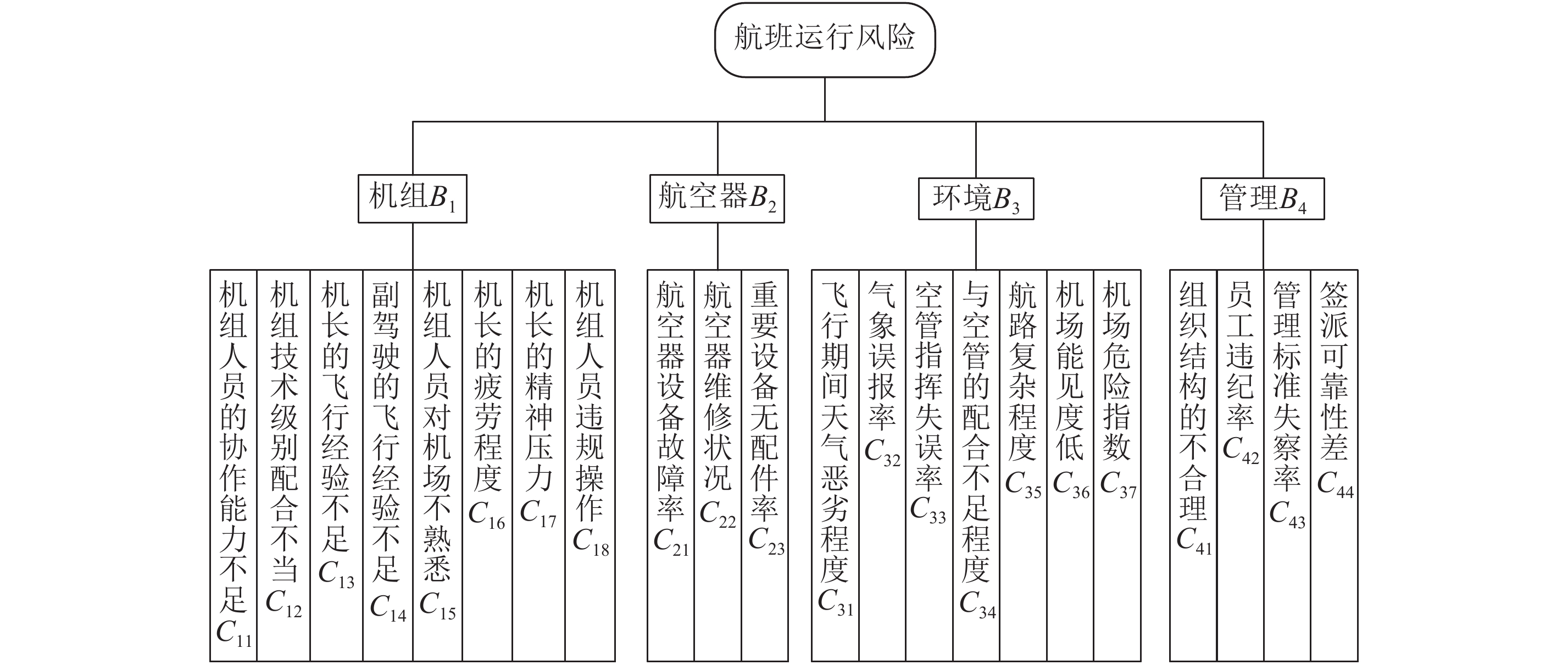
图 2 航班风险评估指标体系 Fig. 2 Flight risk assessment index system

表1给出了图2中指标的测度计算方法。

表 1(Tab. 1)

表 1 风险指标的计算方法 Tab. 1 Calculation method of risk criteria 指标 指标性质 计算方法 机组B1 机组人员的协作能力不足C11 定性指标 专家评价 机组技术级别配合不当C12 定性指标 专家评价 机长的飞行经验不足C13 定量指标 实际飞行时间 副驾驶的飞行经验不足C14 定量指标 实际飞行时间 机组人员对机场不熟悉C15 定量指标 机组执行该机场任务的次数 机长的疲劳程度C16 定量指标 执行一个飞行任务的时间 机长的精神压力C17 定性指标 专家评价 机组人员违规操作C18 定量指标 违规操作事件次数/操作事件总数 航空器B2 航空器设备故障率C21 定量指标 航空器出现故障的次数/航空器执行任务次数 航空器维修状况C22 定量指标 检查维护未达标次数/设备维护检查次数 重要设备无配件率C23 定量指标 无配件的重要设备数量/重要设备总数 环境B3 飞行期间天气恶劣程度C31 定性指标 专家评价 气象误报率C32 定量指标 一段时间内机场气象误报次数/机场气象误报总数 空管指挥失误率C33 定量指标 统计数据 与空管的配合不足程度C34 定性指标 专家评价 航路复杂程度C35 定性指标 专家评价 机场能见度低C36 定量指标 统计数据 机场危险指数C37 定性指标 专家评价 管理B4 组织结构的不合理C41 定性指标 专家评价 员工违纪率C42 定量指标 违纪员工人数/员工总数 管理标准失察率C43 定量指标 检查到低于标准的次数/检查次数 签派可靠性差C44 定量指标 不符合规定次数/检查次数

表 1 风险指标的计算方法 Tab. 1 Calculation method of risk criteria

1) 定量指标的标准化。

根据表1中的定量指标，可以根据其对整体航班风险的影响方向进行相应的标准化，即指标值越大航班风险就越大，可以采用 $x{\rm{' = }}\displaystyle\frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{{\rm{min}}}}}}$ ；其中， $x{\rm{'}}$ 表示定量指标数据标准化处理后得到的值， ${x_{\min }}$ 与 ${x_{\max }}$ 分别是统计一段时间内的航班数据的最小值和最大值。

2) 定性指标的标准化。

定性指标无法通过具体的定量数据来刻画，需要依靠专家的经验进行主观评估，可构建如下模糊语言评估：1)邀请多位专家对定性指标进行语言评估，可设{很低(VL)、低(L)、中等(M)、高(H)、很高(VH)}；2)定性语言的定量转化：通过表2方法将定性语言评价转换到[0, 1]区间上；3)基于重心法的解模糊化：为了便于FCM模型计算，进行解模糊化处理^[13]。设有n位专家，对应可信度分别为 ${\alpha _1}, {\alpha _2}, \ldots , {\alpha _n}$ 且 ${\alpha _1} + {\alpha _2} + \ldots + {\alpha _n} = 1$ 。假设指标C_i对指标C_j有影响，设指标C_i对指标C_j影响关系的专家评价分别为 $O_{ij}^1$ 、 $O_{ij}^2$ … $O_{ij}^n$ ， $O_{ij}^k = ({l_k},{m_k},{u_k})$ ， $(k = 1,2, \ldots , n)$ 。通过加权求和后，得到 ${\overline O _{ij}} = (\mathop \sum \nolimits {\alpha _k}{l_k},\mathop \sum \nolimits {\alpha _k}{m_k},\mathop \sum \nolimits {\alpha _k}{u_k})$ 。利用重心法对模糊评估值 ${\overline O _{ij}}$ 解模糊化，重心法计算公式为： ${w_{ij}} = \displaystyle\frac{{\mathop \smallint \nolimits x{\mu _{{{\overline O }_{ij}}}}(x){\rm{d}}x}}{{\mathop \smallint \nolimits {\mu _{{{\overline O }_{ij}}}}(x){\rm{d}}x}}$ ，其中 ${\mu _{{{\overline O }_{ij}}}}$ 表示专家评价语言所对应的隶属函数， ${w_{ij}}$ 表示指标i对指标j的影响程度。

表 2(Tab. 2)

表 2 定性指标定量转化 Tab. 2 Quantitative transformation of qualitative criteria 定性评价 很低(VL) 低(L) 中等(M) 高(H) 很高(VH) 对应定量区间 (0, 0.1, 0.2) (0.1, 0.3, 0.5) (0.3, 0.5, 0.7) (0.5, 0.7, 0.9) (0.8, 0.9, 1)

表 2 定性指标定量转化 Tab. 2 Quantitative transformation of qualitative criteria

1) 层次化指标间影响关系的确定。

首先基于ANP方法，在已构建好的层次化指标体系的基础上，利用专家知识来分析和评估指标间是否存在影响关系。应用ANP概念，构建如图3所示的航班风险系统ANP网络层次结构，该结构的控制层包含系统的目标，即航班运行风险，同时也是决策准则。网络层包含4个影响目标层的风险元素组，即图2中人、机、环和管4个元素组。

图 3(Fig. 3)

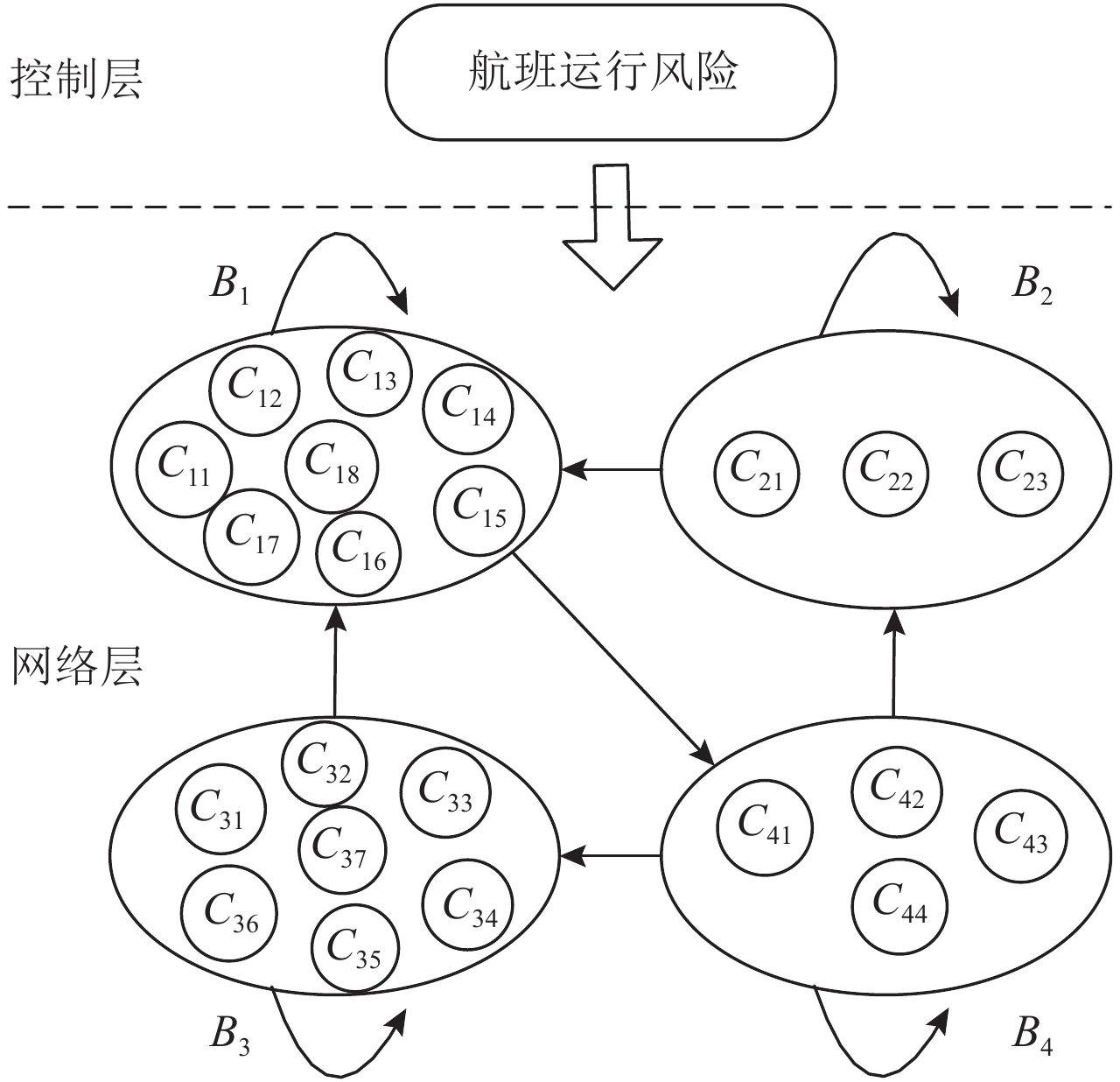
图 3 基于ANP指标间影响关系网络结构 Fig. 3 Network structure of criteria influence relationship based on ANP

设定如下元素组之间的影响关系：(1)元素组内影响关系设定：4个元素组内指标间均存在相关影响，即图3中 ${B_1} - {B_4}$ 的自环。(2)组间影响关系设定：存在5个组间影响关系， ${B_1} \to {B_4}$ (机组相关指标对管理相关指标存在影响关系，即机组成员的某些操作会影响航空公司的管理行为，如机组成员违规操作会增加员工的违纪率； ${B_2} \to {B_1}$ (航空器相关指标对机组相关指标存在影响关系，即航空器涉及物理性能会影响驾驶员的主观状态指标，如航空器维修质量不过关会增加驾驶员的精神压力等； ${B_3} \to {B_1}$ (环境相关指标对机组相关指标存在影响关系，即环境涉及的外部状态会影响驾驶员的主观状态指标，如飞行期间天气恶劣、航路复杂、机场能见度差等情况都可能会对驾驶员带来心理压力； ${B_4} \to {B_2}$ (管理相关指标对航空器相关指标存在影响关系，如管理标准失察可能会导致航空器的维修质量不高，给航班飞行带来很高的风险； ${B_4} \to {B_3}$ (即管理相关指标可以消减或者增强环境相关指标的作用，如签派放行时的失误会增加机场的危险指数等)。

2) 指标间影响关系的测度。

以航班运行风险为主准则，通过两两比较，构建无权重超矩阵W来反映指标间的影响关系。

其中 ${ W_{ij}}$ 表示元素组B_i对B_j的影响程度。

3) 加权超矩阵的构建及收敛分析。

进一步考虑不同元素组的影响权重，进行数据归一化处理，通过矩阵连乘迭代，可获得一个收敛的超级矩阵。通过该矩阵可获得各个指标在充分考虑相互影响关系后的稳定权重，该权重集可用于对航班的风险进行综合计算。

具体计算如下。

(1) 以目标为准则，对各风险元素组之间的重要性进行比较，构造权重矩阵

则可得到加权超矩阵 ${{W}_{\rm{A}}} = {A} \cdot {W}$ 。

(2) 通过求极限超矩阵的方法确定风险指标的影响权重，计算各个风险指标的权重Q^A。

4) 基于FCM的状态值收敛分析。

利用FCM推理方法，结合构建的指标间影响关系矩阵W，对航班风险各个指标的初始状态进行迭代推理，可得到充分考虑指标影响关系的指标状态稳态值。推理过程如图4所示，其中v_i(k)表示指标i迭代k次后的状态值。

图 4(Fig. 4)

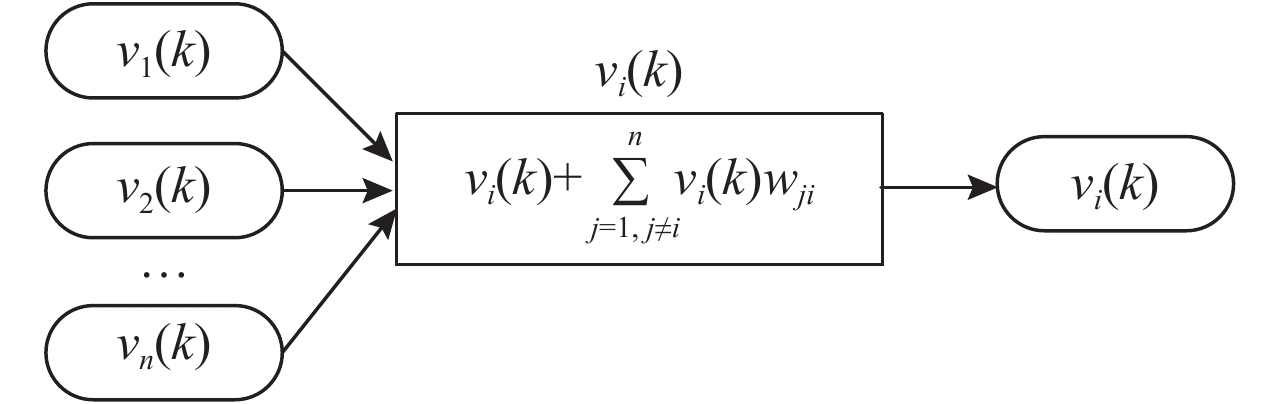
图 4 指标状态的FCM推理过程 Fig. 4 Reasoning process of criteria state based on FCM

步骤1：确定指标的初始状态。

按照2.2节指标数据的计算方法结合专家经验，对实际航班的风险指标值进行评估。设定V(0)= $({v_{11}}\left( 0 \right),\,\, \ldots,\, {v_{18}}\left( 0 \right),\,{v_{21}}\left( 0 \right),\,\, \ldots,\, {v_{23}}\left( 0 \right),\,{v_{31}}\left( 0 \right),\,\, \ldots,\, {v_{37}}\left( 0 \right),\,$ $ {v_{41}}\left( 0 \right), \ldots, {v_{44}}\left( 0 \right))$ 为FCM模型中指标的初始状态值，其中， $v\left( 0 \right) \in [0,1]$ 。

步骤2：确定FCM影响关系矩阵。

构建的指标间影响关系矩阵W_A，可用于FCM的各个指标节点影响关系矩阵W′_A测度，即W′_A=W_A，进而应用FCM模型进行模糊推理。

步骤3：指标状态的收敛分析。

根据FCM推理机制，将初始状态 $V\left( 0 \right)$ 与影响关系矩阵 ${W}_{\rm{A}}'$ 相乘，再经过特定阈值函数转换，则下一时刻各节点的状态值 $V\left( 1 \right) = F\left[ {V\left( 0 \right) + V\left( 0 \right) \cdot {W}} \right]$ ，其中 $F\left[ \cdot \right]$ 为阈值函数，本文选择Sigmoid函数(双弯曲函数)，目的是保证节点的状态值在[0, 1]区间上，F[x]公式为： $F[x] = \displaystyle \frac{1}{{1 + {\rm{e}^{ - x}}}}$ 。

设定 $V\left( 0 \right) \!=\! ({v_{11}}\left( t \right),\! \ldots,\! {v_{18}}\left( t \right),\!{v_{21}}\left( t \right),\! \ldots,\! {v_{23}}\left( t \right),\!{v_{31}}\left( t \right), $ $ \ldots, {v_{37}}\left( t \right),{v_{41}}\left( t \right), \ldots, {v_{44}}\left( t \right))$ 为FCM模型经过迭代推理后风险指标的稳定状态值，其中，t表示迭代的次数。

在应用案例部分，本文将使用国际上已有基于Matlab开发的FCM工具包，FCM_tool^[14]，进行分析计算。

5) 航班风险的评估与分级。

对获得的收敛指标状态值与稳态指标权重值Q^A，进行线性加权可以得到航班风险综合评估值，其公式如下：

参考《航空承运人运行控制风险管控系统实施指南》^[15]，将航班飞行风险分为3个等级，即可接受的、缓解后可接受的和不可接受的，数值划分见表3。

表 3(Tab. 3)

表 3 风险等级划分 Tab. 3 Risk classification 等级 可接受的 缓解后可接受的 不可接受的 对应数值区间 [0，0.5) [0.5，0.8) [0.8，1]

表 3 风险等级划分 Tab. 3 Risk classification

对于风险值和风险等级高的航班，可采用DEMATEL的风险改进方法，进一步分析影响航班运行风险的主要因素，针对性地提出相应缓解方案，为在运行过程中的航班提供实时的有效管控和决策支持。具体分析步骤如下。

1) 构建规范化的影响矩阵：对FCM影响关系矩阵W进行规范化处理，计算得到规范化后的影响矩阵 ${M} = {[{m_{ij}}]_{22 \times 22}}$ ，即 ${M} = s \cdot {W}$ ，其中

$s = \min \left[ \displaystyle \frac{1}{{\mathop {\max }\limits_{_{\displaystyle\scriptstyle 1 {\text{≤}} i {\text{≤}} 22}} \displaystyle \sum\limits_{j = 1}^{22} {{w_{ij}}} }}, \frac{1}{{\mathop {\max }\limits_{_{\displaystyle\scriptstyle 1 {\text{≤}}j {\text{≤}} 22}} \displaystyle \sum\limits_{i = 1}^{22} {{w_{ij}}} }} \right] $ ；

${m_{ij}} \in [0,1]$ ，i, j=1, 2, 3, …,22。

s为矩阵M中行和与列和的最大值的倒数。

2) 计算风险指标间的总影响矩阵：设T= $ {[{t_{ij}}]_{22 \times 22}}$ 为总影响矩阵，该矩阵综合了指标间的直接和间接影响关系。

当 $n \to + \infty $ 时， ${T} = {M}{({E} - {M})^{ - 1}}$ ，其中E为单位矩阵。

3) 计算各指标的影响度R与被影响度J：第i个指标的影响度R_i通过计算矩阵T中第i行的元素之和得到，被影响度J_i通过计算矩阵T中第i列的元素之和得到。计算公式如下：

其中，i=1, 2, 3, …,22，R_i表示指标i对其他指标影响的程度，J_i表示指标i受到其他指标影响的程度。

4) 计算各指标的R+J和R-J：R+J表示各个指标间的相互作用程度，而通过R-J可分析得到航班风险的主要影响指标。指标i的R-J值越大，表明指标i状态的增加会对其他指标产生非常大的影响，航空承运人在风险管控中可以通过降低这类指标的风险程度来减小航班运行风险。

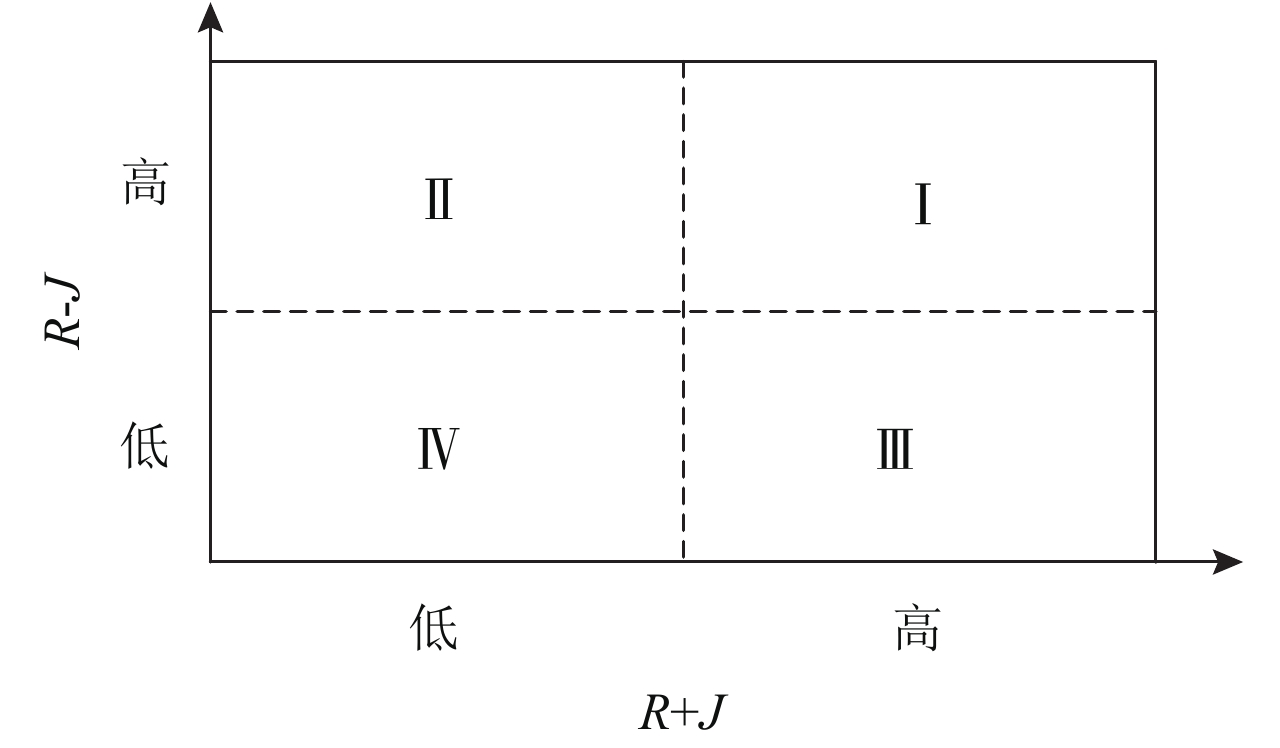
5) 构建指标影响度—被影响度二维图：以R+J、R-J为横纵坐标轴建立直角坐标系，如图5所示。在坐标系上标出各个指标的位置，从而通过指标影响其他指标程度与被其他指标影响程度的对比，分析各个指标的重要性。

图 5(Fig. 5)

图 5 影响度-被影响度二维图 Fig. 5 Two-dimensional graph of influencing-being influenced degree

当风险指标处于区域(I)时，指标的R+J和R-J值均处于较高水平，这类指标对其他指标的影响程度大且受其他指标的影响也大，是影响航班风险的主要指标，因此，在评估航班风险时应高度重视这些指标，确保这类指标处于安全范围。处于区域(II)的指标R-J值处于较高水平，这类指标对其他指标的影响程度大但自身受到的影响小，需要特别考虑它们的影响。区域(III)的指标R+J值处于较高水平，这类指标自身影响程度小，容易受到其他指标的影响，在风险管控中应重点关注影响这类指标的因素。区域(IV)的指标与其他指标间的相互作用小，不需要重点关注。

6) 针对关键指标，设计改进情景，计算改进效果：本文仅针对区域(I)内的指标分别进行分析，改变其中一个风险指标的状态值，其他指标不变，计算稳定后的航班综合风险值。

本文作者依托自身行业背景，获取了某航空公司近3年北京至上海某航班飞行记录数据。邀请了从事民航管理工作的3位资深飞行员及2位安全理论研究人员，组成专家组。在分析这些数据资料的基础上，依据设定的指标体系，对定性指标以及指标间影响关系进行综合评估。然后应用所提方法进行模拟仿真计算，分析该航班目前所处的风险等级以及可能的改进措施，以验证方法的可行性。

1) 构造超矩阵。

采用1~9评估标度，以打分的方式对指标间的影响关系进行评估，构造指标间影响关系超矩阵。

2) 构造权重超矩阵。

以目标为准则，对目标准则下各风险元素组之间的影响程度进行比较，得到如表4所示的权重矩阵A。

表 4(Tab. 4)

表 4 风险元素组间的权重矩阵 Tab. 4 Comparison matrix among the groups of risk criteria A B1 B2 B3 B4 B1 0.638 0.000 0.000 0.250 B2 0.109 0.667 0.000 0.000 B3 0.253 0.000 0.800 0.000 B4 0.000 0.333 0.200 0.750

表 4 风险元素组间的权重矩阵 Tab. 4 Comparison matrix among the groups of risk criteria

则可得到加权超矩阵

加权超矩阵 ${{W}_{\rm{A}}} = {A} \cdot {W}$ ，计算得到各个风险指标的权重 ${{Q}^{\rm{A}}}$ =(0.008，0.011，0.032，0.021，0.036，0.010，0.010，0.014，0.008，0.007，0.006，0.130，0.044，0.066，0.062，0.062，0.134，0.067，0.089，0.072，0.067，0.045)。

3) 风险指标状态的收敛分析。

表3中各指标间的影响关系较多，但有些指标间的影响较小，考虑在风险评估中会增加计算的复杂性，且对实际评估的风险值影响较小，因此设定一个阈值以过滤掉这些影响较小的指标间关系。从W_A可以看出各指标对自身影响最大值为0.096，指标值对自身影响可忽略不计，因此将阈值设定为0.096，矩阵中元素小于0.096的指标间影响关系可忽略不计。则指标间影响关系矩阵W′_A如下所示：

按照2.2节数据采集和处理方法，可获得如下航班各指标的初始状态值

V(0)=(0.39，0.21，0.35，0.68，0.3，0.19，0.1，0.2，0.16，0.05，0，0.25，0，0.6，0.62，0.2，0.3，0.4，0.7，0.4，0.42，0.1)。

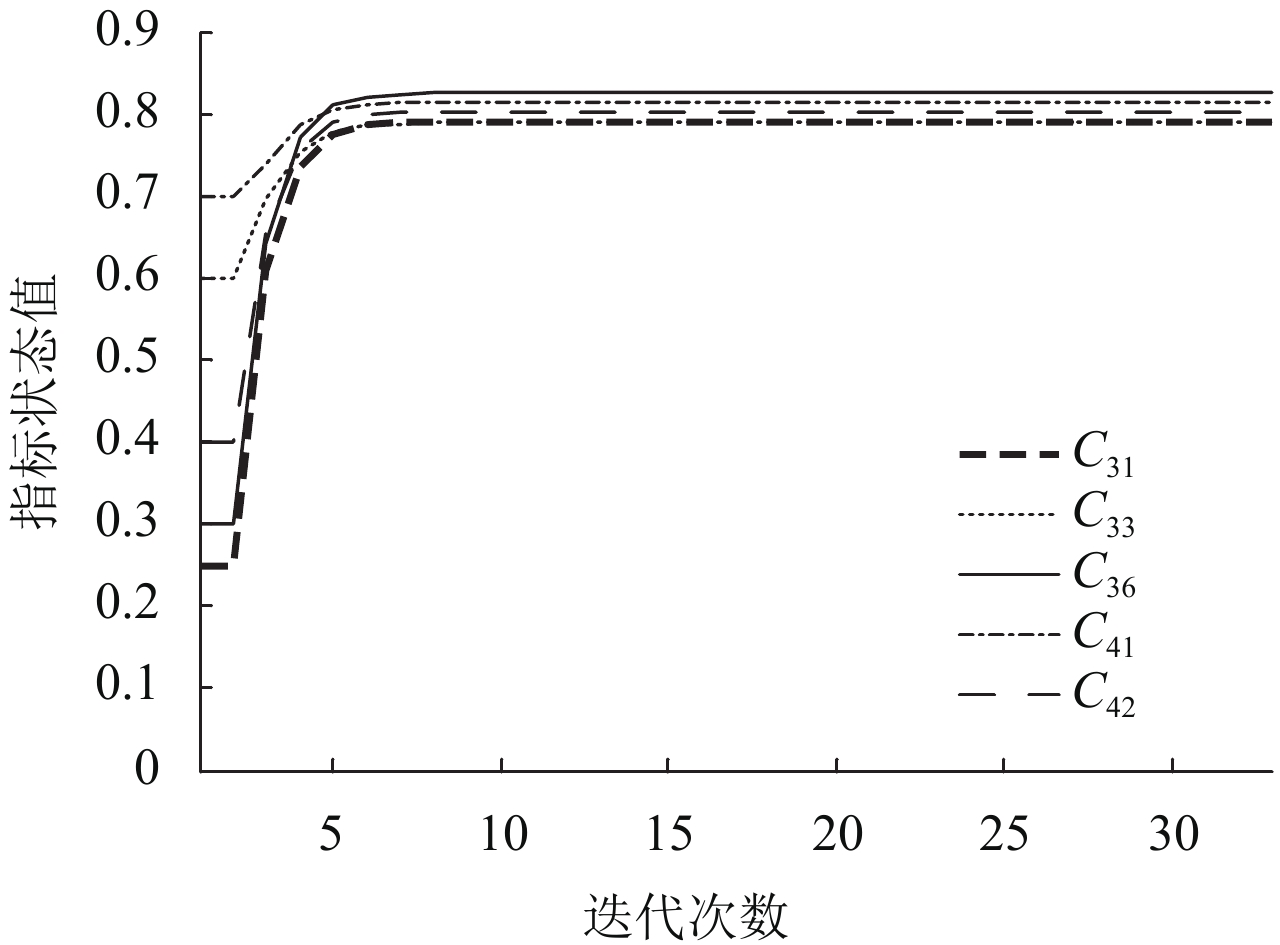
由初始状态开始，应用FCM_tool，通过Matlab软件进行FCM推理计算各节点下一个时刻状态值，该结果又作为下一次迭代输入状态，依次进行多次迭代，直到FCM模型中各节点的状态值不再发生变化或者变化十分微小。本文设定最小变化值为0.000 1，经过32次迭代，各节点的状态值变化小于该设定，由此表明系统最终收敛到一个稳定状态。

V(32)=(0.798，0.776，0.772，0.774，0.777，0.771，0.795，0.803，0.827，0.829，0.819，0.791，0.8，0.791，0.797，0.804，0.827，0.797，0.815，0.803，0.789，0.79)。

其中影响权重较大的几个主要风险指标随着迭代次数的变化情况如图6所示。

图 6(Fig. 6)

图 6 主要风险指标状态值迭代变化 Fig. 6 Iterative variation of the main risk states

5) 航班风险的评估与分级。

根据2.3节计算方法，得到R_i=0.800 6，属于“不可接受”风险，表明此时系统状态影响威胁到航班的飞行安全，需要制定相应措施直至风险降至合理范围。

以4.1节中的FCM影响关系矩阵为DEMATEL工具中的初始影响矩阵，按照第3节的分析步骤得到各个风险指标的R+J和R-J值，如表5所示。

表 5(Tab. 5)

表 5 DEMATEL分析结果 Tab. 5 DEMATEL analysis result 风险指标 R+J R-J C11 0.736 -0.736 C12 0.843 -0.359 C13 1.743 0.603 C14 1.019 -0.157 C15 1.93 0.716 C16 0.855 -0.291 C17 0.845 -0.587 C18 0.843 -0.647 C21 1.77 0.042 C22 1.556 -0.278 C23 1.543 -0.129 C31 2.025 0.917 C32 0.967 -0.507 C33 1.652 0.308 C34 1.628 0.196 C35 1.263 -0.245 C36 1.96 0.5 C37 1.103 -0.297 C41 2.399 0.713 C42 1.963 0.455 C43 1.447 0.135 C44 1.06 -0.268

表 5 DEMATEL分析结果 Tab. 5 DEMATEL analysis result

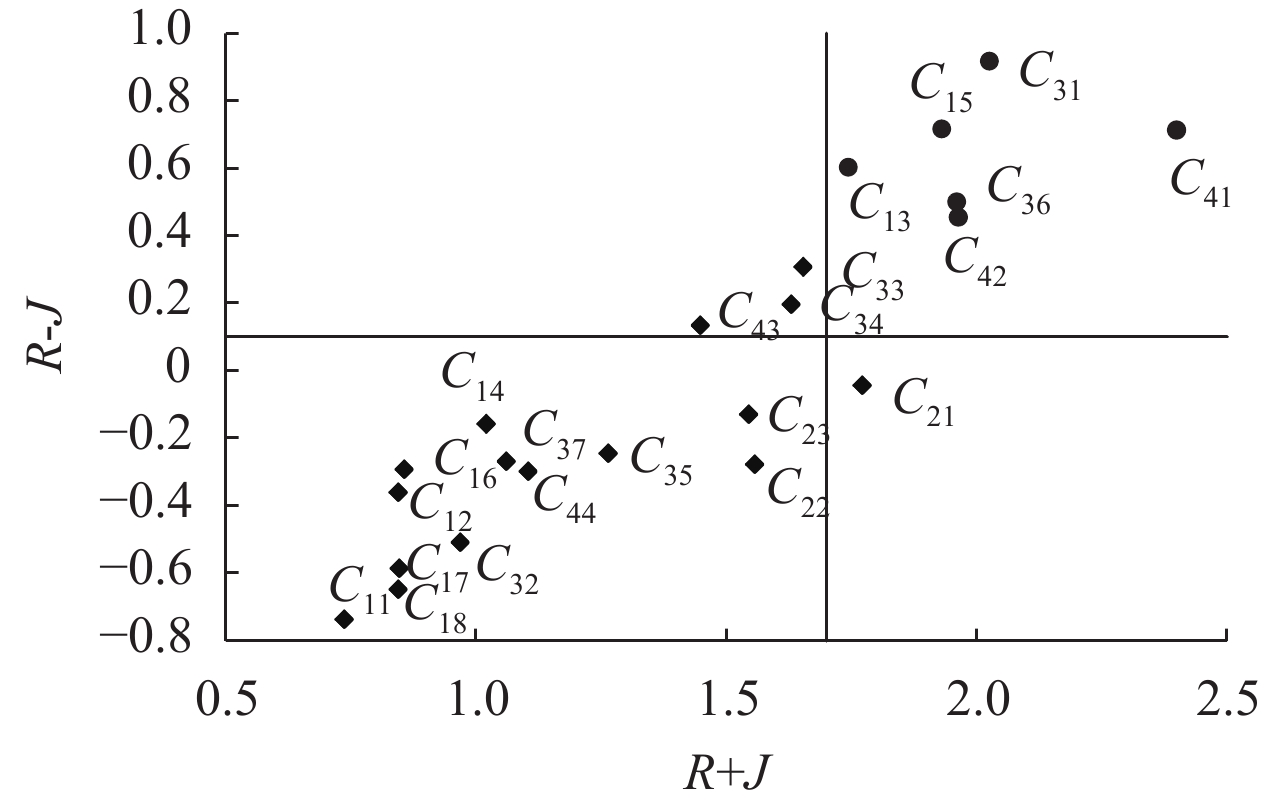
分别以R+J为横坐标、R-J为纵坐标建立如图7所示的直角坐标系，图中的每个点对应一个风险指标。

图 7(Fig. 7)

图 7 指标影响度—被影响度二维图 Fig. 7 Two-dimensional graph of influencing-being influenced degree

如图6所示，C₁₃、C₁₅、C₃₁、C₃₆、C₄₁以及C₄₂与其他指标间的相互影响程度大，需要重点考虑。而C₃₃、C₃₄、C₄₃对其他指标的影响大，自身受到的影响小，需要特别关注。因此，在航班运行前进行风险管控时，应对这些风险因素进行重点分析，判断其是否处于安全范围。

本文考虑需要重点关注的区域(I)内的风险指标，通过设计改进情景，分别对这些指标进行处理，计算得到航班综合风险的变化程度。为了能更好地理解后续的航班风险改进措施，这里将定量指标依据其状态值的大小划分为5个等级。由于设定的风险指标均为正向影响指标(指标值越大，对航班风险影响越大)，可统一划分为如表6所示的5个等级。

表 6(Tab. 6)

表 6 定量指标风险等级 Tab. 6 Quantitative criteria risk classification 等级 很低 低 中等 高 很高 对应数值区间 [0, 0.2) [0.2, 0.4) [0.4, 0.6) [0.6, 0.8) [0.8, 1]

表 6 定量指标风险等级 Tab. 6 Quantitative criteria risk classification

以4.1节算例为基础，将区域(I)内的风险指标的状态值分别降低一个等级，计算最后的航班风险以及风险等级，与4.1节计算得到的风险值进行对比。

表 7(Tab. 7)

表 7 风险改进情景 Tab. 7 Risk improvement scenarios 改进情景 风险指标 指标状态值 综合风险 1 C13 $\scriptstyle 0.35 \to 0.15$ $\scriptstyle 0.800\ 3 \to 0.798$ 2 C15 $\scriptstyle 0.3 \to 0.1$ $\scriptstyle 0.800\ 3 \to 0.791$ 3 C31 $\scriptstyle 0.25 \to 0.05$ $\scriptstyle 0.800\ 3 \to 0.778$ 4 C36 $\scriptstyle 0.3 \to 0.1$ $\scriptstyle 0.800\ 3 \to 0.782$ 5 C41 $\scriptstyle 0.7 \to 0.5$ $\scriptstyle 0.800\ 3 \to 0.790$ 6 C42 $\scriptstyle 0.4 \to 0.2$ $\scriptstyle 0.800\ 3 \to 0.791$

表 7 风险改进情景 Tab. 7 Risk improvement scenarios

根据上述计算结果，可以总结形成如下对该航班风险改进建议措施。

通过DEMATEL分析得到影响航班风险的关键指标主要有：机长的飞行经验不足、机组人员对机场不熟悉、飞行期间天气恶劣程度、机场能见度低、组织结构的不合理性以及员工违纪率等。这些指标不仅对其他指标的影响程度大，自身也会受到一定的影响，因此航空公司在风险管控中应多关注这些指标的变化以及它们是否处于安全的范围。

根据表7所示的改进情景结果可知，指标C₃₁和C₃₆对航班风险的影响程度更大，恶劣的天气会对航班飞行带来很大的风险，机场能见度差对飞机的安全起飞和降落也带来了不小的挑战，因此为减小飞行风险，针对飞行环境条件不好的航班，航空公司应做好相应措施，防止航空事故的发生。

本文以航班风险评估中指标间影响关系研究为目标，建立了基于FCM-DEMATEL的航班风险评估与改进模型，通过FCM推理方法进行仿真分析得到各指标的动态演化过程，结合ANP确定指标的影响权重，最终计算得到航班综合风险值。根据指标间的影响关系矩阵，利用DEMATEL方法分析得到影响航班风险的关键指标，进而设置不同情景来分析关键指标的影响程度。本文的研究是以单架航班为研究对象，从航空公司风险优化的视角来进行分析。将来研究可以进一步从包括机场、空管和航空公司三方在内的多角度协同决策来分析如何评估和降低航班风险，以期研究成果具有更好的实际应用价值。